Programa para seguir el punto de máxima potencia basado en la solución analítica del modelo circuital de una celda solar usando la función W de Lambert

Víctor Guzmán

Resumen: Este trabajo presenta el programa LAMP (Lambert Analytic Maximum Power Point), que calcula el punto de máxima potencia de un arreglo de celdas solares resolviendo la ecuación analítica del modelo circuital de las celdas para el voltaje correspondiente a la potencia máxima, empleando la función W de Lambert. LAMP incluye un método para calcular los parámetros del arreglo de celdas solares y un algoritmo que calcula la curva característica del arreglo de celdas con un error no mayor del 1%. LAMP corre en un microcontrolador de bajo costo, implementando un sistema de seguimiento del punto de máxima potencia (MPPT) preciso y económico, que puede utilizarse en instalaciones pequeñas y en localidades remotas que no están servidas por la red principal. Los resultados del programa se compararon con mediciones experimentales, mostrando un margen de error inferior al 1%.

Palabras clave: Función W de Lambert, Celdas Solares, Microcontrolador, MPPT.

A maximum power point tracking program based on the analytical solution of the solar cell circuital model using the Lambert-W function.

Abstract: This work presents the development of the LAMP (Lambert Analytic Maximum Power Point) program, that calculates the maximum power point of a solar cells array solving the analytical equation of the solar cell circuital model for the voltage related to the maximum power, using the Lambert-W function. LAMP includes a method to calculate the solar cells array parameters and an algorithm to calculate the solar cells array characteristic curve with less that 1% error. LAMP runs on a low cost microcontroller, implementing an inexpensive and precise maximum power point tracking (MPPT) system, which can be used in small installations and in remote locations not served by the main supply. The program results were compared with experimental measurements, showing a 1% error margin.

Keywords: Lambert W-function, Solar Cell, Microcontroller, MPPT.

1. INTRODUCCIÓN

La energía solar es una alternativa capaz de sustituir, o por lo menos complementar, a los sistemas convencionales de generación de energía eléctrica que consumen combustibles fósiles, produciendo una energía no contaminante y sostenible. Los sistemas fotovoltaicos son una solución muy buena para suministrar energía eléctrica a localidades remotas o aisladas, que no pueden estar conectadas al sistema eléctrico nacional, especialmente en los países en vías de desarrollo que están situados en la zona inter-tropical y naturalmente presentan alta irradiación solar [1].

Las celdas solares comerciales son capaces de convertir entre el 18 y el 20% de la energía solar recibida en electricidad, mientras que las multi-juntura más avanzadas (mucho más costosas) disponibles en el mercado alcanzan eficiencias en el rango del 39 al 41% y superan el 44,5% en los prototipos experimentales de cuatro uniones. Siempre es importante obtener el mejor rendimiento posible, sea cual sea el tipo de celdas empleado en el arreglo, y esto requiere lograr que las celdas operen en el punto que produce la máxima transferencia de energía, el llamado “punto de máxima potencia”, el cual está dado por una combinación instantánea única y específica de tensión y corriente en cada celda; si la corriente que circula por las celdas en esas condiciones aumenta o disminuye, la potencia entregada se reduce de forma exponencial. Para operar en el punto óptimo es necesario incluir a la salida del arreglo de celdas un sistema de “seguimiento del punto de máxima potencia”, o MPPT por sus siglas en inglés (Maximum Power Point Tracking) que regula la corriente extraída para mantener la potencia entregada por el arreglo en el valor máximo posible [2]. Las técnicas de seguimiento más usadas son variantes del método “perturbar y observar” (Hill Climbing/Perturb and Observe (P & O)), o algoritmos basados en la Lógica Difusa (Fuzzy Logic) o en el método fraccional [3]. La mayoría de los autores no consideran el uso de soluciones analíticas para describir el comportamiento de la celda solar, debido a que la corriente y el voltaje en una celda solar están relacionados por una función transcendente. Una vez que se publicaron métodos numéricos eficientes para evaluar la función de Lambert con precisión arbitraria y un método para la integración analítica de funciones que contienen la variable W [4], ha sido posible aplicar esta herramienta para la solución exacta de las ecuaciones transcendentes que definen el comportamiento de junturas tipo diodo. Aplicando esta herramienta a las celdas fotovoltaicas, se ha encontrado la solución analítica exacta para los parámetros eléctricos de una celda solar real [5], y esta solución se ha usado para estudiar varios aspectos del funcionamiento de las celdas solares, tales como las características de las celdas solares orgánicas [6], la determinación del “factor de idealidad del diodo” [7], la extracción de parámetros del modelo de la celda [8-10], el cálculo de parámetros de arreglos de celdas solares [11], y la determinación de la carga óptima [12].

Cuando se emplea la solución analítica es necesario conocer todos los parámetros de la celda considerada. Estos parámetros incluyen, entre otros, la resistencia en serie, Rs, y la conductancia en paralelo, G_p. Varios autores han presentado métodos experimentales para determinar estos parámetros [13-15], los cuales serán analizados posteriormente en la sección 2.5, buscando el más adecuado para este trabajo. Finalmente, una vez que se define el método analítico apropiado, es necesario establecer la potencia de cálculo requerida para aplicar los resultados del método analítico a fin de poder aplicar los resultados a un sistema de control MPPT práctico.

Este trabajo presenta el desarrollo de un control MPPT que usa la función W de Lambert para encontrar la tensión que corresponde con el punto de máxima transferencia de energía, deducida en base al modelo de diodo único de la celda solar. Para esto se resuelve la ecuación de la celda, escribiendo el voltaje en forma explícita como una función de la corriente de la celda para calcular la potencia instantánea disponible. Hecho esto, se calcula el máximo valor de la función de la potencia disponible, derivando la función de la potencia con respecto al voltaje de celda, igualando a cero el resultado y resolviendo para encontrar el valor del voltaje que produce la máxima potencia, valor éste que debe ser fijado en la celda por el sistema de control. Dada la necesidad de conocer los parámetros de la resistencia en serie, R_s y de la conductancia en paralelo G_p, de la celda para realizar los cálculos antes indicados, se incluye en el trabajo un método experimental para determinarlos.

Para implementar este método de cálculo del punto de máxima potencia de un arreglo de celdas en un sistema MPPT práctico, se desarrolló el programa LAMP (Lambert Analytical Maximum Power point). LAMP calcula los parámetros del modelo del arreglo de celdas, considerando un arreglo serie, y a continuación determina el punto de máxima potencia disponible empleando la solución analítica del voltaje de salida del arreglo en base a la función W de Lambert. LAMP se desarrolló inicialmente en lenguaje C en una computadora personal y luego fue migrado a un procesador de bajo costo. Esta implementación de bajo costo hace posible la aplicación de este control en sistemas de generación solar fotovoltaica pequeños, destinados a aplicaciones domésticas, especialmente en localidades aisladas.

Para validar el sistema MPPT propuesto se realizaron mediciones experimentales con tres arreglos de celdas solares en condiciones diferentes; la comparación de los resultados obtenidos en estas pruebas experimentales concuerdan con los producidos por el programa LAMP con un margen de error del 1%.

2. DESARROLLO DEL MODELO EQUIVA­LENTE DE LA CELDA SOLAR EMPLEADO EN EL CÁLCULO DEL CONTROLADOR MPPT

2.1 Circuito equivalente de la celda solar.

Las celdas solares pueden modelarse con diferentes circuitos equivalentes. Los autores de [16] presentan un modelo con cuatro componentes, mostrado en la figura 1, que se usa ampliamente para representar el comportamiento de la celda solar.

Este modelo incluye una fuente de corriente, que representa la corriente foto-generada, un diodo que representa la unión P-N, y una resistencia en serie y una conductancia en paralelo que, en conjunto, representan las pérdidas que ocurren en la celda solar. En base a este circuito, la corriente I en la celda se puede escribir como:

Donde: I y V son la corriente y el voltaje en los terminales de la celda expresados respectivamente en amperios (A) y voltios (V), I₀ es la corriente de saturación en amperios (A), I_ph es la corriente foto-generada en la juntura en amperios (A), v_th es el voltaje térmico en voltios (V), n es el factor de idealidad de la celda, R_s es la resistencia en serie en ohmios (Ω, y G_p es la conductancia en paralelo en siemens (S=1/Ω).

Esta ecuación permite calcular la curva característica de corriente-voltaje, y la curva de potencia en función de las características de corriente o voltaje de cada celda. En base a estas curvas es posible calcular los otros parámetros de interés, tales como la tensión en circuito abierto, V_oc, la corriente de cortocircuito, I_sc, el voltaje en el punto de la máxima potencia, V_mpp, la corriente en el punto de máxima potencia, I_mpp, y la potencia máxima, P_mpp, que puede suministrar la celda bajo unas condiciones de iluminación y temperatura ambiental específicas.

2.2. Solución analítica para el modelo equiva­lente de la celda solar aplicando la función W de Lambert.

La ecuación (1) incluye una combinación de funciones lineales y exponenciales, por lo tanto no es fácil encontrar una expresión del voltaje en función de la corriente, o de la corriente en función del voltaje, usando funciones matemáticas comunes. Por esta razón usualmente se han empleado diversas aproximaciones para simplificar los cálculos matemáticos. En [3] se presenta una revisión de los diferentes algoritmos usados en la literatura para calcular el punto de máxima potencia, con sus respectivas ventajas y desventajas. En todo caso, dado que se trabaja con aproximaciones simplificadoras, el resultado no es exacto. Este problema no se presenta si se usa una solución exacta, lo que es posible para la ecuación (1) aplicando la función W de Lambert, también conocida como la función Omega o producto logarítmico, que es la función inversa de la expresión:

f(W) = We^(W)     (2)

Donde e es la función exponencial y W es un número complejo. La función W de Lambert es derivable e integrable, lo que permite manipulaciones matemáticas una vez que ha sido aplicada a cualquier ecuación. La función W de Lambert queda definida entonces como:

Si x = ye^y, entonces

y = W(x)       (3)

Se ha demostrado [5] que, cuando se aplica la función W de Lambert a la ecuación (1), es posible obtener la siguiente expresión analítica para la corriente entregada por la celda solar en función del voltaje entre los terminales:

De la misma manera, es posible escribir una ecuación del voltaje en función de la corriente de la celda:

Empleando las ecuaciones (4) y (5) la curva de potencia de la celda solar puede dibujarse respectivamente como una función de la corriente o del voltaje de la celda. Siguiendo el mismo procedimiento se pueden obtener soluciones analíticas para cualquiera de las variables incluidas en la ecuación (1).

2.3. Efectos resistivos parasíticos.

Los efectos resistivos en la estructura de la celda solar, representados en el modelo por R_s y G_p, reducen la eficiencia de conversión del dispositivo ya que disipan energía. La resistencia serie de la celda solar es resultado del efecto de la corriente base-emisor del dispositivo y de la resistencia de contacto en la unión Si-metal, entre otras razones. El efecto principal de esta resistencia es reducir la máxima potencia que el dispositivo puede entregar, pero valores muy altos de R_s también pueden reducir la corriente de cortocircuito de la celda solar. La figura 2(a) muestra el efecto de la resistencia serie sobre la curva I-V de la celda solar, incluyendo la reducción en la corriente de cortocircuito, que es el peor efecto de R_s en el dispositivo (simulación ejecutada en el programa Maple).

La conductancia en paralelo en una celda solar es usualmente el resultado de defectos de fabricación del dispositivo, que permiten la existencia de corrientes de fuga en los bordes del elemento y entre los contactos de diferente polaridad. Las pérdidas de potencia producidas por G_p son importantes porque la corriente foto-generada encuentra un camino indeseado por los defectos fuera de la juntura activa del dispositivo; una resistencia en paralelo baja (esto es, una G_p alta) causa reducciones en el voltaje de circuito abierto. Las celdas comerciales que se encuentran en el mercado actualmente ofrecen en general una resistencia paralela alta (superior a 100Ω), por lo que las pérdidas asociadas con G_p son generalmente muy bajas y pueden ser despreciadas. La figura 2(b) muestra el efecto de la conductancia en paralelo sobre las características I-V de la celda solar, llegando a valores de G_p que producen una reducción significativa en el voltaje de circuito abierto, causando pérdidas de potencia importantes (simulación ejecutada en el programa Maple).

2.4. Parámetros requeridos para el cálculo del punto de máxima potencia

Para calcular el punto de máxima potencia de la red es necesario conocer el valor de todos los parámetros que aparecen en la ecuación (1). La resistencia en serie, la conductancia en paralelo, la corriente de saturación inversa, y el factor de idealidad dependen de la estructura de la celda. La corriente foto-generada depende de la irradiación solar que esté recibiendo la celda y de su eficiencia de conversión. El voltaje térmico está dado por:

Donde v_th es el voltaje térmico en voltios (V), k es la constante de Boltzman en electrón-voltios por grado Kelvin (eV/Kº), T es la temperatura de la juntura en grados Kelvin (Kº), y q es la carga del electrón en Coulombs (C). La temperatura de la juntura se puede estimar midiendo la temperatura en la superficie de la celda en varios puntos y promediando el resultado.

El factor de idealidad, n, es un indicador que determina el grado de similitud existente entre el comportamiento de la juntura PN en la celda solar y en la ecuación de un diodo ideal. En celdas solares mono-cristalinas el factor de idealidad cambia con la tensión de juntura, y debe ser seleccionado en función del punto de operación específico. En todo caso, para voltajes cercanos al del punto de máxima potencia, el factor de idealidad es aproximadamente 1,5 [7].

La corriente foto-generada es la corriente producida en la celda por el efecto fotovoltaico. Su medición directa no es posible, pero considerando el caso de una celda cortocircuitada, se puede aproximar el valor a partir de la siguiente ecuación:

Manipulando términos, y considerando en primera aproximación una celda cuasi-ideal, se puede demostrar que:

Esta aproximación se hizo progresivamente más exacta a medida que fue aumentando la calidad de las celdas disponibles y en la actualidad es en general casi exacta para las celdas comerciales mono-cristalinas. La figura 2(c) muestra el efecto de la corriente foto-generada en la curva de una celda solar simulada en el programa Maple.

2.5. Métodos experimentales para determinar aproximadamente el valor de las resistencias parásitas en una celda solar.

La resistencia en serie y la conductancia en paralelo son parámetros que definen las pérdidas y afectan directamente la eficiencia de conversión del dispositivo fotovoltaico. Para determinar el mejor valor de estos parámetros para este trabajo se consideraron tres métodos a fin de estimar estos valores:

Método 1: Trabajando con la hipótesis de que la resistencia en paralelo es mucho más grande que la resistencia en serie. Dhifaoui [14] propone que R_s puede ser despreciada en la ecuación (1) sin que se causen errores notables en el modelo.

Método 2: Carrol [17] propone un método basado en el voltaje de circuito abierto, V_oc, y la corriente de cortocircuito, I_sc. Como primer paso se define la resistencia característica del arreglo solar, R_ch, mediante la ecuación:

Y, a partir de esta resistencia característica, las resistencias parásitas del arreglo se calculan como:

Método 3: Por último Cheegar [13] señala que, tal como se muestra en la figura 3, es posible calcular el valor de las resistencias parásitas a partir de las pendientes de la curva I-V de la celda.

De acuerdo con esta propuesta, el valor de la resistencia paralela, R_sh, puede calcularse como:

Y el valor de la resistencia en serie puede calcularse como:

Donde R_sO es la pendiente de la curva I-V en la zona de voltaje en circuito abierto, y N_s es el número de celdas en serie en el arreglo.

Estos tres métodos se aplicaron al análisis de dos arreglos de celdas diferentes, uno ensamblado en el laboratorio, formado con 12 celdas JAM individuales conectadas en serie y el otro, un panel solar comercial de la firma BP, compuesto por 72 celdas en serie ensambladas en fábrica, a fin de calcular la potencia máxima que se obtiene cuando los parámetros se calculan con cada uno de dichos métodos y compararla con la potencia máxima medida experimentalmente. Cada uno de los tres métodos producen resultados distintos, mostrados en la Tabla I, que también presenta los errores porcentuales cometidos en cada caso, asumiendo como valor de referencia en cada caso el correspondiente medido experimentalmente. Como puede observarse en la tabla, el error cometido al calcular la potencia calculando los parámetros según el método Dhifaoui es superior al 10% en los dos arreglos, mientras que con el método de Carrol el error para el arreglo JAM es pequeño (1,5%), pero en el panel comercial sube a mas del 50% (52,9%). En base a esto se puede considerar que el segundo método parece ser capaz de producir buenos resultados cuando el número de celdas es bajo, pero resulta inaceptable cuando aumenta el número de celdas o, alternativamente, que los resultados son excesivamente sensibles al tipo de celda considerado.

En cualquier caso ni el método Dhifaoui ni el Carrol resultan adecuados para esta aplicación.

Por otra parte, al aplicar el método Cheegar para el cálculo de las resistencias del modelo, los errores porcentuales entre la potencia calculada y la medida son apreciablemente menores al 1% en ambos arreglos de celdas solares, por lo que éste es el método seleccionado para estimar las resistencias parásitas en el presente trabajo.

2.6. Cálculo de la corriente de saturación inversa, I_O, a partir de los valores aproximados de las resistencias parásitas.

Conocidos todos los parámetros del modelo descrito por la ecuación (1), es posible calcular un valor aproximado para la corriente de saturación inversa I₀. Para esto es necesario conocer adicionalmente el valor de la tensión de circuito abierto de la celda y el de la corriente de cortocircuito. En estas condiciones, la corriente de saturación inversa resulta:

2.7. Cálculo analítico del voltaje en el punto de máxima potencia.

Para encontrar el punto de máxima potencia de la celda y el voltaje asociado con el mismo, es necesario trabajar a partir de la ecuación (1). El primer paso es generar una ecuación de la corriente de la celda en función del voltaje de la celda. Esto se hizo aplicando la función W de Lambert con ayuda del programa de cálculo matemático Maple. Así, la ecuación de la corriente en función del voltaje es:

El segundo paso es definir la potencia de salida, trabajando a partir de la definición estándar de la potencia DC:

P = VI        (16)

De la ecuación (15), multiplicando ambos lados por el voltaje, se encuentra que la potencia de salida de la fuente en función del voltaje es:

El tercer paso para encontrar el punto de máxima potencia es calcular la función dP/dV. Debido a la complejidad de la función, resultó necesario realizar una serie de cambios de variables, para agrupar términos y simplificar las operaciones analíticas. Las funciones auxiliares definidas fueron:

Aplicando las funciones auxiliares definidas en (18), (19) y (20) a la ecuación (17), tomando la derivada en función del voltaje de esta ecuación e igualando la derivada a cero, se obtiene la siguiente expresión:

Esta es la ecuación que debe ser resuelta para encontrar el valor del voltaje de celda en el cual se genera la máxima potencia de salida de la celda. Dado que la variable V está presente en forma explícita en la ecuación (21) y también en forma implícita en las funciones auxiliares X y Z, la ecuación (21) no puede resolverse analíticamente, y por lo tanto la solución debe ser encontrada por métodos numéricos.

3. EL PROGRAMA LAMP

3.1 Diseño del programa LAMP.

La biblioteca de funciones del programa Maple incluye la función fsolve, que es capaz de encontrar soluciones analíticas para las ecuaciones. Esta función fue usada en este trabajo para simular el algoritmo diseñado para resolver la ecuación (21). Una vez que se probó este algoritmo, se pudo desarrollar el programa LAMP (Lambert Analytic Maximum power point Program), cuyo diagrama de flujo se presenta en la figura 4.

Este programa determina los parámetros requeridos para modelar el arreglo de celdas solares en base a la solución analítica de la ecuación (1), para calcular el punto de máxima potencia del arreglo. Como primer paso se adquieren los valores iniciales de los parámetros ambientales, a continuación se calculan los parámetros del modelo y finalmente se determina el valor del voltaje en el punto de máxima potencia, V_mpp, en base a la ecuación (21), aplicando un algoritmo de solución por métodos numéricos.

Cuando el sistema está operando en el campo, naturalmente se producirán cambios en los parámetros ambientales, cambios que afectarán al valor V_mpp previamente calculado. Tomado esto en cuenta, el programa calcula un nuevo valor del voltaje Vmpp cada 500ms. Dado que las resistencias parásitas también dependen de las condiciones ambientales, ya que son función tanto de la temperatura de la celda como de la insolación, sus valores se recalculan cada 30 minutos para minimizar los posibles errores en el seguimiento del punto de máxima potencia.

La versión inicial de LAMP fue desarrollada en lenguaje C, con entrada de datos manual, como prototipo para calcular fuera de línea los puntos de máxima potencia de los paneles probados en el laboratorio. El programa se consideró depurado cuando logró reproducir exactamente los resultados obtenidos en las pruebas experimentales realizadas en el laboratorio sobre los arreglos de celdas solares indicados en la Tabla I.

3.2 Implementación del programa LAMP en un microcontrolador.

La selección del microcontrolador se hizo en base a dos criterios: velocidad de cálculo y costo. En esta aplicación el microcontrolador debe ser capaz de calcular un nuevo valor para el voltaje del punto de máxima potencia en cada intervalo de 500 ms, por lo que el primer criterio es rechazar todos los microcontroladores que no cumplan con este requisito. Hecho esto, el microcontrolador seleccionado será el de menor precio entre los que sean capaces de realizar los cálculos requeridos en el lapso de 500 ms.

Establecidos los criterios de selección, se probó un grupo de los microcontroladores disponibles en el mercado; de éstos el seleccionado por cumplir con los criterios de velocidad de ejecución y costo fue el MSP430F5438 de Texas Instruments (TI). Este dispositivo se presenta en una carcasa de 100 patas, tiene 87 puertos de entrada/salida (I/O), 16 KB de memoria RAM y doce canales de conversión analógico/digital, proporcionando toda la capacidad necesaria para adquirir los datos y realizar los cálculos requeridos para que el programa LAMP determine los valores de las resistencias parásitas y el punto de máxima potencia en el tiempo asignado para las operaciones en el campo. El prototipo experimental fue montado en una tarjeta de desarrollo modelo MSP430F5438 Experimenter Board de TI, de la cual se emplearon tres entradas en modo conversión analógico/digital, una entrada digital y una salida digital programada como una salida generadora de señal modulada en ancho de pulso (PWM).

4. RESULTADOS EXPERIMENTALES

4.1 Caracterización inicial de las celdas solares en el laboratorio.

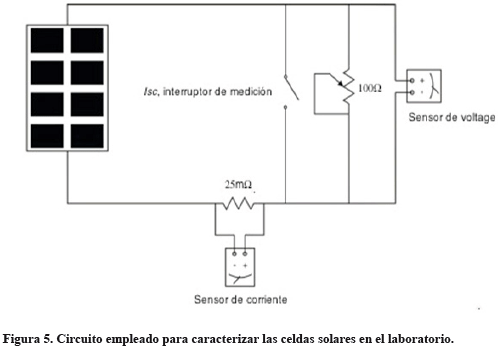
La figura 5 muestra el circuito empleado para caracterizar en el laboratorio las celdas solares usadas en las pruebas experimentales del programa LAMP.

El protocolo de pruebas empleado fue el siguiente: En cada caso se medía el voltaje de circuito abierto, a continuación se conectaba el máximo valor de carga resistiva externa, y se tomaba un conjunto de medidas de corriente y voltaje de salida mientras la carga resistiva se reducía hasta el mínimo. Alcanzado este valor se desconectaba la carga externa, se cortocircuitaba la celda y se medía la corriente de corto circuito. Los datos obtenidos se graficaban, y el punto de máxima potencia se determinaba por inspección de la gráfica obtenida.

4.2. Comparación entre las medidas experi­mentales y los valores calculados con el progra­ma LAMP.

Se realizaron tres experimentos para probar el programa LAMP. El primero, operando bajo condiciones controladas, se realizó en el laboratorio, empleando el arreglo de 12 celdas individuales tipo JAM conectadas en serie. Todas las mediciones se obtuvieron en condiciones de iluminación constante proporcionada por una lámpara halógena de 1000 W. Adicionalmente la temperatura del arreglo se mantuvo también constante ventilándolo con un soplador. Este experimento se realizó en condiciones correspondientes a insolación baja, ya que la irradiación proporcionada por la lámpara era de unos 100 W/m2. El segundo y tercer experimento se realizaron con el panel solar de BP, bajo insolación natural, en el techo del laboratorio, situado a 1300 metros de altitud a 10º 24’ 32’’ N y 66º 52’ 55’’ W en el mes de marzo. Estas pruebas se realizaron en el “ambiente natural”, esto es, incontrolado, con condiciones de viento y cobertura parcial de nubes variable. El segundo experimento se realizó al medio día solar (12 m), con una insolación solar fuerte, directa y perpendicular, de entre 800 y 900 W/m2 (variaciones debidas a cambios atmosféricos durante las pruebas). El tercer experimento, se realizó a las tres de la tarde hora solar (3 p.m.), bajo insolación natural media. A esta hora la insolación en un día despejado era del orden del 50% de la insolación al medio día.

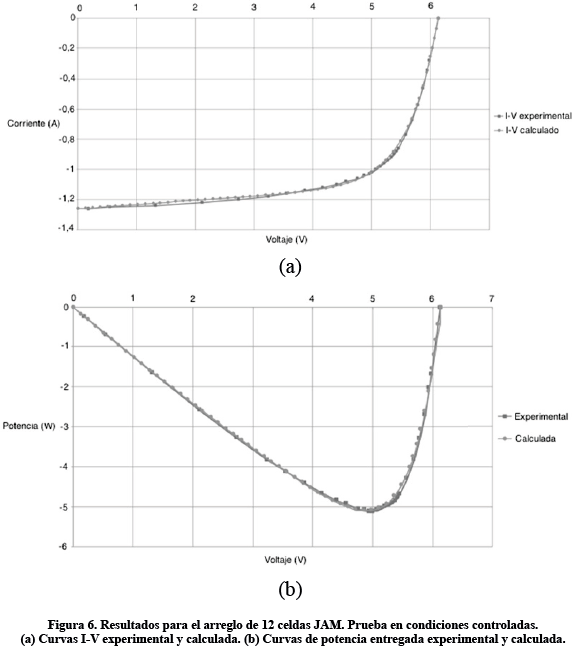
La figura 6(a) muestra la comparación entre la curva I-V medida experimentalmente y la calculada por LAMP en el experimento controlado (iluminación artificial y ventilación forzada) y la figura 6(b) muestra la comparación entre la curva de potencia de salida calculada con los datos experimentales y la calculada por LAMP para el arreglo de celdas JAM.

La figura 7 presenta los resultados de la prueba realizada con el panel PB con insolación natural fuerte, al aire libre a las 12m. La figura 7(a) muestra la comparación entre la curva I-V medida experimentalmente y la calculada por LAMP mientras que la figura 7(b) muestra la comparación entre la curva de potencia de salida calculada con los datos experimentales y la calculada por LAMP.

La figura 8 presenta los resultados de la prueba realizada con el panel PB con insolación natural media, al aire libre a las 3 pm. La figura 8(a) muestra la comparación entre la curva I-V medida experimentalmente y la calculada por LAMP mientras que la figura 8(b) muestra la comparación entre la curva de potencia de salida calculada con los datos experimentales y la calculada por LAMP.

Como puede observarse comparando los tres conjuntos de curvas, el comportamiento de los arreglos corresponde con lo esperado en las tres condiciones de insolación probadas (baja, media y alta) y no hay diferencias significativas apreciables entre los valores calculados y medidos. Entrando en el análisis detallado, la Tabla II muestra la comparación entre los resultados medidos experimentalmente en los tres casos y los correspondientes valores calculados por LAMP. Como puede observarse, los errores de los valores de potencia calculados por el programa LAMP referidos a los medidos experimentalmente son en los tres casos inferiores o apenas superiores al 1%, alcanzando el objetivo de diseño propuesto.

5. CONCLUSIONES

Las pruebas para validar el desarrollo del programa LAMP realizadas tanto en condiciones controladas de laboratorio como al aire libre demuestran que el porcentaje de error cometido en la predicción de la curva I-V y en la determinación del punto de máxima potencia de los arreglos de celdas solares es siempre menor al 1% en el área de interés, alrededor del punto de operación deseado, para lograr la máxima eficiencia de conversión solar-eléctrica. Por lo tanto se puede concluir que el programa LAMP, trabajando a partir de la ecuación básica de la celda fotovoltaica y resolviéndola mediante la función W de Lambert, es capaz de proporcionar muy buenos resultados en el seguimiento del punto de máxima potencia cuando se trabaja tanto con arreglos de celdas ensamblados con celdas individuales como con paneles solares comerciales disponibles en el mercado.

También queda demostrado en la práctica que el programa LAMP puede ser ejecutado en un microcontrolador comercial de propósitos generales. Por lo tanto el método de seguimiento del punto de máxima potencia o MPPT en base a la solución analítica de la ecuación de la celda solar presenta una solución económica, que puede usarse para controlar sistemas de generación fotovoltaica de potencia moderada y bajo costo, adecuados para suministrar electricidad en aplicaciones domésticas y para localidades aisladas.

En base a estos resultados se puede concluir que se justifica pasar a la siguiente etapa de desarrollo, implementando un sistema generador fotovoltaico prototipo completo que opere en base al programa LAMP.

En base a la experiencia obtenida con las mediciones realizadas, se debe señalar también la conveniencia de disponer de un laboratorio equipado con fuentes de luz más poderosas y controlables en intensidad, para poder realizar mediciones en condiciones controladas que emulen el amplio rango de las insolaciones posibles en un país tropical. Esta instalación será necesaria para homologar bajo condiciones completamente controladas la operación de diferentes equipos operando bajo diversas leyes de control del MPPT.

6. REFERENCIAS

1. Ochieng, R. M. Solar Collectors and Panels, Theory and Applications. Rijeka, Scijo, 2010, p. 444.        [ Links ]

2. Kalogirous, S. Solar Energy Engineering, Processes and Systems. Burlington, Elsevier, 2009, p. 756.        [ Links ]

3. Chapman, P., Esran, T. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Transactions on Energy Conversion, vol. 22, nº 2, June 2007, pp 439-449.        [ Links ]

4. Corless, R.M., Gonnet, G.H., Hare, D.E.G., Jeffrey, D.J., Knuth, D.E. On the Lambert W-Function. Advances in Computational Mathematics, vol. 5, issue 1, 1996, pp. 329-359.        [ Links ]

5. Jain, A., Kapoor, A. Exact analytical solutions of the parameters of real solar cells using Lambert-W functions. Solar Energy Materials and Solar Cells, vol. 81, nº 2 February 2004, pp. 269–277.        [ Links ]

6. Jain, A., Kapoor, A. A new approach to study organic solar cell using Lambert W-function. Solar Energy Materials and Solar Cells, vol. 86, nº 2, March 2005, pp. 197-205.        [ Links ]

7. Jain, A., Kapoor, A. A new method to determine the diode ideality factor of real solar cell using Lambert W-function. Solar Energy Materials and Solar Cells, vol. 85, nº 3, January 2005, pp. 391-396.        [ Links ]

8. Ortiz-Conde, A., García Sánchez, F., Muci, J. New method to extract the model parameters of solar cells from the explicit analytic solutions of their illuminated I–V characteristics. Solar Energy Materials and Solar Cells, vol. 90, nº 3, February 2006, pp. 352-361.        [ Links ]

9. Ghani, F., Duke, M., Carson, J. Extraction of solar cell modeling parameters using the Lambert W-function. Proceedings of the 50th Annual Conference, Australian Solar Energy Society, Melbourne, Australia, December 2012, pp. 1-10.        [ Links ]

10. Ghani, F., Duke, M. Numerical determination of parasitic resistances of a solar cell using the Lambert W-function. Solar Energy, vol. 8, nº 9, September 2011, pp. 2386-2394.        [ Links ]

11. Jain, A., Sharma, S., Kapoor, A. Solar cell array parameters using LambertW function. Solar Energy Materials and Solar Cells, vol. 90, nº 1, January 2006, pp. 25-31.        [ Links ]

12. Ding, J., Radhakrishnan, R. A new method to determine the optimum load of a real solar cell using the Lambert W-function. Solar Energy Materials and Solar Cells, vol. 92, nº 12, December 2008, pp. 1566-1569.        [ Links ]

13. Chegaar, M., Ouennoughi, Z., Guechi, F., Langueur, H. Determination of Solar Cells Parameters under Illuminated Conditions. Journal of Electron Devices, vol. 2, 2003, pp. 17-21.        [ Links ]

14. Dhifaoui, R., Faouzi, M., et al. Analytical Expressions for the Determination of the MPPT Under Different Insolation Levels for a PV Cell. World Renewable Energy Congress, Londres, 2008, CD.        [ Links ]

15. Wagner, A., Kunz, G. Internal series resistance determinated of only one IV-Curve under illumination. 19th European Photovoltaic Solar Energy Conference, Paris, France, June 2004, Paper No. 5BV.2.70.        [ Links ]

16. Fernández, H., Martínez, A., Guzmán, V., Giménez, M. Modelo genérico de celdas fotovoltaicas. UCT, vol.12, nº 48, Julio 2008, pp.157-162.        [ Links ]

17. Carrol, D. The Winning Solar Car. SAE International, Warrendale, Pennsylvania, USA, 2003, pp. 375.        [ Links ]