Electronic structure and the half-metallic ferromagnetic behavior of the ti-doped bn system studied using first-principles

Gladys Casiano Jiménez¹, César Ortega López¹, Miguel J. Espitia R.²*

¹: Grupo Avanzado de Materiales y Sistemas Complejos GAMASCO, Universidad de Córdoba, Montería Colombia.

²: Grupo GEFEM. Universidad Distrital Francisco José de Caldas. Bogotá D.C., Colombia * e-mail: mespitiar@udistrital.edu.co

ABSTRACT

In this work using the first-principles in the framework of Density Functional Theory the structural properties, electronic structure and magnetism of Ti-doped w-BN are studied. Our calculations were performed with the ultrasoft pseudopotentials method, employed exactly as implemented in Quantum ESPRESSO code. For the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N concentrations it is found a ferromagnetic and half-metallic behavior with 100% carrier spin polarization of the conduction carriers in the ground state. The calculations showed that the substitution of a Ti atom at the B site (B0.9375Ti0.0625N compound) introduces a magnetic moment of 1.0 μB, while two Ti atoms substitutions (B_0.875Ti_0.125N compound) introduce a magnetic moment of 2.0 μB. These magnetic properties come from hybridization and polarization of states Ti-3d and their first neighboring B-2p and first neighboring N-2p atoms. Calculated magnetic properties indicate that Ti-doped w-BN compound can potentially be used in diluted magnetic semiconductors or as spin injectors.

Keywords: w-BN, half-metallic behavior, electronic and magnetic properties.

Estructura electrónica y comportamiento semimetálico y ferromagnético del sistema bn dopado con ti estudiado usando primeros principios

RESUMEN

En este trabajo usando primeros principios en el marco de la Teoría del funcional de la Densidad, se estudiaron las propiedades estructurales, la estructura electrónica y magnetismo del w-BN dopado con Ti. Nuestros cálculos fueron ejecutados con el método de pseudopotenciales ultrasuaves, tal como está implementado en el código Quantum ESPRESSO. Se encontró que las concentraciones B_0.9375Ti_0.0625N y B0.875Ti_0.125N poseen un comportamiento ferromagnético y semimetálico con una polarización de espín del 100% de los portadores de conducción en el estado base. Los cálculos muestran que la sustitución con un átomo de Ti en el sitio del B (compuesto B_0.9375Ti_0.0625N) introduce un momento magnético de 1.0 μB, mientras que la sustitución con dos átomos de Ti (compuesto B_0.875Ti_0.125N) introduce un momento magnético de 2.0 μB. Estas propiedades magnéticas provienen de la hibridación y polarización de los estados Ti-3d y de sus primeros vecinos N-2p y B-2p. Estas propiedades indican que w-BN dopado con Ti puede ser potencialmente usado como un semiconductor magnético diluido o como inyectores de espín.

Palabras Claves: w-BN, comportamiento semimetálico, propiedades electrónicas y magnéticas.

Recibido: 28-10-2015 ; Revisado: 14-12-2015 Aceptado: 17-12-2015 ; Publicado: 01-04-2016

In recent years, many experimental and theoretical studies on the properties of boron nitride (BN) [1-5] due to its excellent physical, mechanical, and thermal properties, such as high-temperature stability, chemical inertia, a high degree of hardness, a low coefficient of thermal expansion, a high melting point, and high thermal conductivity [6-9]. BN is a semiconducting material BN and has a broad range of potential applications, such as in high-temperature ceramic material that can withstand an extremely harsh environment, radio frequency and high-frequency high-power laser diodes, light-emitting diodes operating in the ultraviolet region, solar detectors, field-effect transistors, and high electron mobility transistors [10-15]. Owing to the variable bonding character, BN can exist in different crystallographic phases, such as zincblende (cubic) boron nitride (c-BN) [16–18], wurtzite (w), boron nitride (w-BN) [17, 19, 20], hexagonal (h) boron nitride (h-BN) [4, 5], and rhombohedral (r) boron nitride (r-BN) [1, 2]. Boron nitride has been experimentally grown in hexagonal [5], zinblende [18], and wurtzite [20] phases. At the same time, theoretical and experimental investigations have shown that h-BN and r-BN are easily compressible, while the sp3 hybridized in c-BN and w-BN phase belongs to the class of superhard materials. Over the last few years, BN has received extensive attention because of its possible use as a diluted magnetic semiconductor (DMS) with potential applications in the field of spintronic. For these applications, ferromagnetism at room temperature is a requirement. Recently, high-temperature ferromagnetism has been reported by many researchers for several types of transition-metal (TM)-doped semiconducting oxides and nitrides [21-23]. Kurdyumov et al. [19] and Soma et et al. [20] grew and characterized w-BN. Ohba et al. [24] studied the structural, dielectric and dynamic properties of w-BN using first-principles calculations. He et al. [25], by means of DFT, proved that TM (TM = V, Cr, and Mn)-doped BN nanotubes can be used in spintronic. Boukra et al. [26], using first-principles calculations, showed that Mn-doped c-BN exhibits half-metallic and magnetic behavior. Lopez et al. [27] investigated the electronic and magnetic properties of Mn adsorption on the w-BN(0001) surface. However, investigations of Ti-, V- and Cr-doped w-BN in volume, whether theoretical or experimental, are rare. For this reason, in the present paper we present a systematic theoretical study of the structural, electronic, and magnetic properties of the Ti-doped w-BN, B_0.9375Ti_0.0625N and B_0.875Ti_0.125N concentrations, due to potential applications in dilute magnetic semiconductors, spin injectors, and other applications in spintronic.

The calculations were performed within the DFT framework using the Quantum ESPRESSO package [28]. The correlation and exchange effects of the electrons were dealt with using the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) [29]. Electron-ion interactions were treated with the pseudopotential method [30, 31]. The electron wave functions were expanded into plane waves with a kinetic energy cutoff of 40 Ry. For the charge density, a kinetic energy cutoff of 400 Ry was used. A 6×6×4 Monkhorst-Pack mesh [32] was used to generate the k-points in the unit cell. The calculations were performed taking into account the spin polarization. To calculate the structural, electronic, and magnetic properties of pure BN, a 32-atom 2a x 2b x 2c wurtzite supercell was considered. The B_0.9375Ti_0.0625N and B_0.875Ti_0.125N concentrations were obtained by substituting one and two B-atoms in the supercell in the positions shown in Fig.1. Pure w-BN and the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds were modeled according to the special quasirandom structures approach [33], and the disorder aspects were ignored.

To determine the structural properties in the ground state, such as the lattice constant (a₀), the bulk modulus (B₀), the c/a ratio, and the total energy (E₀) of pure BN, B_0.9375Ti_0.0625N and B_0.875Ti_0.125N concentrations in the wurtzite structure, the total energy of the crystal was minimized as a function of supercell volume. The results were fit to the Murnaghan equation of state [34]. Additionally, the total energy variation was calculated as a function of the volume for the ferromagnetic (FM) and antiferromagnetic (AFM) phases in order to find the most favorable magnetic phase of the Ti-doped w-BN compounds. For this purpose, the B_0.875Ti_0.125N compound was used to get even numbers of Ti atom for switching spin state up and down. Figure 2 shows the energy-volume curves for B_0.9375Ti_0.0625N and B_0.875Ti_0.125N concentrations.

We can see in Figure 2(a) for the B_0.9375Ti_0.0625N compound the calculated total energy of spin polarized state (FM phase) is lower than that of the non-spin polarized state (non-magnetic phase) by about 66.4 meV, while for the B_0.875Ti_0.125N compound in the ground state the calculated total energy of spin polarized state (FM phase) is lower the AFM state, being the total energy differences between the FM and AFM states (ΔE = E_FM -E_AFM) by about 45,23 meV, which indicates that the ground state of Ti-doped BN is ferromagnetic.

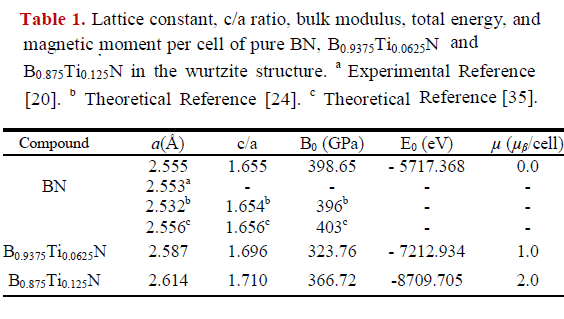
The lattice constant, the c/a value, the bulk modulus (B₀), the total energy (E₀), and the magnetic moment (μβ) per cell are listed in Table 1, along with available experimental data and from other theoretical studies.

The calculated lattice constant (2.555 Å) for pure BN is in excellent agreement with that of experimental results (2.553 Å) [20]. Additionally, the lattice constant and c/a ratio agree well with values reported in other theoretical studies [24, 35], since they differ by less than one percent. The bulk modulus of w-BN agrees well with other theoretical studies [24, 35], with an error of about 0.97%. Calculated bulk modulus for w-BN is close to that of diamond (442 GPa). This may be attributed to the strong sp3 B-N bonding and to a structure similar to diamond. We note that the values of the bulk modulus of the pure BN, B_0.9375Ti_0.0625N and B_0.875Ti_0.125N concentrations are higher, which confirms that they are quite rigid, making them good candidates for possible application in devices operated at high temperature and high power, as well as in hard coatings.

For the B_0.9375Ti_0.0625N compound a similar result was obtained for Casiano et al. [36] in your study of B_1-xTi_xN (x = 0.0625) using first-principles calculations.

We can see in the table 1, when one and two B atoms in the 2a x 2b x 2c supercell is substituted with Ti atoms, the lattice constant in the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compound increases with respect to pure w-BN. This increase in the parameters may be due the radius of the Ti atom (1.47 Å) is much bigger than the atomic radius of B (0.98 Å). A similar behavior has been reported by Fan et al. [37] for Al_0.9375Ti_0.0625N compound in the wurtzite structure.

The theoretical lattice constants and the c/a ratio of pure BN, B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds in the wurtzite structure, listed in Table 1, were used to calculate the band structure and the spin-polarized density of states (DOS) along the high-symmetry paths in the first Brillouin zone. The band structure for pure BN and the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds are shown in Fig. 3.

Fig. 3(a) shows the band structure of pure BN. This confirms the indirect semiconductor behavior, with the top of the valence band located at the Γ point and the bottom of the conduction band at the K point of the Brillouin zone. We found an indirect band gap of about 5.4 eV. This value was calculated using the pseudopotential method and the GGA approximation; the magnitude of this gap agrees well with values reported in other theoretical papers, for example, 5.23 eV [35] calculated via the FP-LAPW-GGA method, 5.45 eV [38] calculated via LMTO-LDA, and 5.81 eV [39, 40] calculated via the OLCAO-LDA method. We note that the band gap calculated in the present paper (5.4 eV) is very close to the value of reference [38] calculated with the LDA approximation. This can be attributed to the fact that B and N atoms are light, and "since the variation of the electronic charge density in the light elements is small, the charge density gradient corrections involved in GGA are not large, and consequently this exchange correlation functional gives results similar to LDA, which is based on a uniform electron gas approximation with no gradient correction" [41].

Figures 3(b) and 3(c) show the band structure of the ternary B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds, respectively. We can observe that the minority spin (down) states preserve a band gap, with an energy gap 3.13 eV and 3.16 eV, respectively; but in the majority spin (up) states there is a penetration

The allowed ternary compounds exhibit half-metallic behavior, because spins up are conductors and spins down are semiconductors. We can see that the spin up orientation of the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds is partially filled and exhibits dispersed bands near the Fermi level. High polarization of the conduction carriers is confirmed by the fact that the Ti atom dopants couple ferromagnetically and that there is a high presence of conduction carriers in the majority spin channel. These compounds exhibit a spin polarization of 100% of the conduction carriers, and they are responsible for the conduction in Ti-doped w-BN. This is a requirement for spin injectors [42, 43]. This finding suggests that these ternary compounds can be efficiently used in spintronics.

In order to study the atomic contribution to the ferromagnetism, we calculated the total density of states (TDOS) and partial density of states (PDOS) for the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds. The TDOS and PDOS are shown in Fig. 4 (a and b). The total density of states confirms that due to the Ti-atom substitution at the B site, the compounds have a half-metallic character. Fig. 4 (a and b) shows that the valence band between -10 and -3 eV originate mainly from hybrid states 2p-B and 2p-N. Additionally, in the valence band near the Fermi level, the spin-up density is mainly dominated by the 3d-Ti states and to a lesser extent by the 2p-B and 2p-N states, which cross the Fermi level. This indicates that all the magnetic properties come from strong hybridization between 3d-Ti and 2p-N states mainly, with a minimum contribution by 2p-B. A similar result was obtained by Boukra et al. [26] in their first-principles study of the magnetic properties of B_0.9375Mn_0.0625N in the zincblende phase.

As we can see in Fig. 4 (a and b), the TDOS confirms the presence of some unoccupied states at the top of the valence band near the Fermi level, because there is no contribution of spin down in the valence band and the majority spin exhibits a hybridization between the 3d-Ti, 2p-B, and 2p-N states, resulting in a magnetic moment of 1.0 μβ/cell for the B_0.9375Ti_0.0625N and 2.0 μβ/cell for B_0.875Ti_0.125N compounds, respectively. These magnetic moment values are integers; therefore, this again confirms that each compound is half-metallic.

In Figure 1 (a and b) and Figure 4 (a and b), we note that the tetrahedral crystal field formed by N-ions split fivefold 3d-MT (Ti, V and Cr) states into threefold degenerate high-energy t_2g (d_xy, d_xz, and d_yz) and twofold degenerate low-energy e_g ( and ) states. The crystal field splitting energy (defined as the energy difference between the e_g and t_2g states) is lesser than the exchange splitting energy (defined as the energy necessary to pair up electrons in the same orbitals), resulting in empty spin-down states which merge with the conduction band states. The hybridization between the 3d-Ti, 2p-B, and p- 2p states induces finite magnetization in Ti as well as neighboring N- and B-atoms. We calculated the contribution of each atom to the total magnetic moment: for B_0.9375Ti_0.0625N we found that main contribution to the magnetic moment is by the 3d-Ti orbitals (0.88 μβ), while each of the neighboring N and B atoms also contribute a small part (0.011 μβ and 0.034 μβ, respectively.Whereas for the B_0.875Ti_0.125N compound the local contribution is 0.86 μβfor the Ti atom and 0.019 μβ and 0.031 μβ for the N and B atoms, respectively. In both compounds, the main contribution to the magnetic moment comes from the Ti atom. Boukra et al. [26] obtained a similar result in their first-principles study of the magnetic properties of the Mn-doped c- BN compound. Additionally, a similar behavior has been found for other III nitrides, for example V-doped GaN [44], Ti-doped AlN [45], V-doped AlN [46], and MT (MT = V, Cr, Mn, Fe, Co, Ni)-doped AlN [47], where the main contribution to the total magnetic moment comes from the MT ion.

First-principles total energy calculations to determine the structural, electronic, and magnetic properties of the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds were carried out. The calculated values of the bulk modules were quite high; therefore, the ternary compounds are quite rigid. Therefore, could be used in devices operating high temperatures and for hard coatings. Also, we found that the compounds exhibit ferromagnetic and half-metallic behavior, due to the hybridization and polarization of 2d-Ti, 2p-N, and 2p-B orbitals that cross the Fermi level. Finally, we found that the B_0.9375Ti_0.0625N and B_0.875Ti_0.125N compounds exhibit magnetic properties with magnetic moments 1 μβ and 2 μβ per supercell, respectively. Therefore, these compounds are possible candidates for spintronic applications.

The authors wish to thank the Research Division of Córdoba University for its financial support.

1. Furthmuller J, Hafner J, Kresse G. Phys. Rev. B 1994; 50: 15606.        [ Links ]

2. Liu L, Feng YP, Shen ZX. Phys. Rev. B 2003; 68: 104102.        [ Links ]

3. Kharlamov VS, Kulikov DV, Trushin YV. Vacuum 1999; 52: 407-410.        [ Links ]

4. Gao SP. Solid State Commun. 2012; 152: 1817-1820.        [ Links ]

5. Wittkowski T, Jorzick J, Jung K, Hillebrands B. Thin Sol. Films 1999; 353: 137-143.        [ Links ]

6. Wena G, Wu GL, Lei TQ, Zhou Y, Guo ZX. J. Europ. Ceram. Soc. 2000; 20: 1963-1928.        [ Links ]

7. Eicheler J, Lesniak C. J. Europ. Ceram. Soc. 2008; 28: 1105-1109.        [ Links ]

8. Lin Z, Yan-Liu A, Moon K, Wong CP. Comp. Sci. and Tech. 2014; 90: 123-128.        [ Links ]

9. Evans DA, McGlyn AG, Towlson BM, Gunn M, Jones D, Jenkins TE, Winter R, Poolton NR, J. Phys: Condens. Matt. 2008; 20: 075233.        [ Links ]

10. Wang H, Taychatanapat T, Hsu A, Watanabe K, Taniguchi T, Jarillo P, Palacios T. Elect. dive. Lett. 2011; 32 (9): 1209-1211.        [ Links ]

11. Pittroff W, Erbert G, Beister G, Bugge F, Klein A, Knauer A, Maege J, Ressel P, Sebastian J, Staske R, Traenkle G. IEEE Trans. 2001; 24: 434-441.        [ Links ]

12. Subramani S, Devarajan M. IEEE Trans. 2014; 61: 3213-3216.        [ Links ]

13. Takahashi S, Yusuke I, Akinori K, Yuji H, Hirotaka O. J. Allo. And Comp. 615 (2014) 141-145.        [ Links ]

14. Watanave K, Taniguchia T, Miya K, Sato Y, Nakamura K, Niiyama T, Taniguchi M. Diam. and Relat. Mat. 2011; 20: 849-852.        [ Links ]

15. Ishida H, Rimdusit S. Thermochimica Acta 1998; 320: 177-186.        [ Links ]

16. Kanoun MB, Mera A. E, Mera G, Cibert J, Aourag H. Solid-State Elect. 2014; 48: 1601-1606.        [ Links ]

17. Cappellini G, Satta G, Tenelsen K, Bechstedt F. Phys. Status Sol. B 2000; 217: 861.        [ Links ]

18. Bundy FP, Wentorf RH. J. Chem. Phys. 1963 38: 1144.        [ Links ]

19. Kurdyumov AV, Solozhenko VL, Zelyavski WB. J. Appl. Cryst. 1995; 28: 540-545.        [ Links ]

20. Soma T, Sawaoka S, Saito S. Mater. Rese. Bulle. 1974; 9: 755-762.        [ Links ]

21. Gonzalez N, Majewski JA, Dietl T. Phys. Rev. B 2011; 83: 184417.        [ Links ]

22. Vargas-Hernandez C, Espitia-Rico M, Báez R. Comp. Conden. Matt. 2015; 4: 1-5.        [ Links ]

23. Cui XY, Fernandez-Hevia D, Delley B, Freeman AJ, Stampfl C. J. Appl. Phys. 2007; 101: 103917.        [ Links ]

24. Ohba N, Miwa K, Nagasako N, Fukumoto A. Phys. Rev. B 2001; 63: 115207.        [ Links ]

25. He KH, Zheng G, Chen G, Wan M, Ji GF. Phys. B Conden. Matt. 2008; 403: 4213–4216.        [ Links ]

26. Boukra A, Zaoui A, Ferhat M. Superla. and Microstru. 2012; 52: 880–884.        [ Links ]

27. Lopez W, Rodríguez JA, Fajardo F, Cardona R. J. Mag. and Mag. Mat. 2008; 320: e249-e252.        [ Links ]

28. Giannozzi P, Baroni S, Bonin NJ. Condens. Matt. 2009; 21: 395502.        [ Links ]

29. Perdew J, Burke K, Ernzerhof M. Phys. Rev. Lett. 1996; 77: 3865.        [ Links ]

30. Vanderbilt D. Phys. Rev. B 1990; 41: 7892.        [ Links ]

31. Laasonen K, Pasquarello A, Car R, Lee C, Vanderbilt D. Phys. Rev. B 1993; 47: 10142.        [ Links ]

32. Monkhorst H, Pack J. Phys. Rev. B 1976; 13: 5188.        [ Links ]

33. Zunger A, Wei SH, Ferreira L, Bernard J. E. Phys. Rev. Lett. 1990; 65: 353.        [ Links ]

34. Murnaghan FD. Proceedings of the National Academy Science U.S.A 1944; 30: 244-24.        [ Links ]

35. Shimada K, Sota T, Suzuki K. J. Appl. Phys. 1998; 84: 4951.        [ Links ]

36. Fan SW, Yao KL, Huang ZG, Zhang J, Gao GY, Du GH. Chem. Phys. Lett. 2009; 482: 62-65.        [ Links ]

37. Casiano Jiménez G, Ortega C, Espitia-Rico M. J. Mag. and Mag. Mat. 2016; 402: 156-160.        [ Links ]

38. Christensen N. E, Gorczyca I. Phys. Rev. B 1994; 50: 4397.        [ Links ]

39. Xu Y.-N, Ching W. Y. Phys. Rev. B 1991; 44: 7787.        [ Links ]

40. Xu Y.-N, Ching W.Y. Phys. Rev. B 1993; 48: 4335.        [ Links ]

41. Ahmed R, Aleem F, Javad Hashemifar S, Akbarzadeh H. Phys. B 2007; 400: 297–306.        [ Links ]

42. Ohno Y, Young D.K, Beschoten B, Matsukura F, Awschalom D.D. Nat. 1999; 402: 790.        [ Links ]

43. Espitia-Rico M, Díaz J, Ortega C. Rev. Latin Am. Metal. Mat. 2015; 35 (2): 165-172.        [ Links ]

44. G. Yao, G. Fan, H. Xing, S. Zheng, J. Ma, S. Li, Y. hang, M. He, Chem. Phys. Lett., 529 (2012) 35–38.        [ Links ]

45. Fan S.W, Yao K.L, Huang Z.G, Zhang J, Gao G.Y, Du G.H. Chem. Phys. Lett. 2009; 482: 62–65.        [ Links ]

46. Yao G, Fan G, Xing H, Zheng S, Ma J, Zhang Y, He L. J. Mag. and Mag. Mat. 2013; 331: 117–121.        [ Links ]

47. Kaczkowski J, Jezierski A. Acta Phys. Pol. A 2009; 115: 1-3.        [ Links ]