Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Paradígma
versión impresa ISSN 1011-2251
Paradìgma v.27 n.2 Maracay dic. 2006
Análisis y valoración de la idoneidad didáctica de procesos de estudio de las matemáticas1
Juan D. Godino, Delisa Bencomo,Vicenç Font y Miguel R. Wilhelmi
Universidad de Granada
Con seguridad, las teorías y la investigación son las mejores herramientas que tenemos para mejorar la práctica y tomar decisiones pedagógicas apropiadas (Sfard, 2002, p. 3)
Resumen
Presentamos un sistema de nociones teóricas para describir los procesos de enseñanza y aprendizaje de las matemáticas y valorar la idoneidad didáctica de tales procesos desde una perspectiva global. Dicha idoneidad se concibe como la articulación coherente y eficaz de las distintas dimensiones implicadas en los procesos de estudio matemático: epistémica, cognitiva, interaccional, mediacional, emocional y ecológica. El enfoque ontosemiótico de la cognición e instrucción matemática aporta una categorización de los elementos intervinientes en cada una de dichas dimensiones, estructurándolos en configuraciones de procesos, objetos y relaciones. Esta categorización y estructuración permiten explicar algunos fenómenos didácticos en términos de la complejidad ontosemiótica implicada. Las nociones teóricas introducidas se aplican al análisis del proceso de estudio realizado en una experiencia de enseñanza de la noción de función con estudiantes universitarios.
Palabras clave: instrucción matemática; metodología de análisis; enfoque ontosemiótico; significados; conflictos semióticos; enseñanza de funciones.
Abstract
We propose a system of theoretical notions to describe teaching and learning mathematics processes and to assess the didactical suitability of these processes from a global perspective. The didactical suitability is conceived as the coherent and efficient articulation of the different dimensions involved in teaching and learning mathematics: epistemic, cognitive, interactive, mediational, emotional and ecological dimensions. The onto-semiotic approach to mathematical cognition and instruction provides a categorization of elements composing each dimension, structuring these elements into epistemic cognitive and didactical configurations. This categorization and structuring allow explaining some didactical phenomena in terms of the onto-semiotic complexity involved. The set of theoretical notions are applied to analyze a teaching experience on the function notion with university students.
Recibido: 02/07/2006 Aceptado: 18/10/2006
Introducción
Con frecuencia la investigación didáctica se ha centrado, y continúa centrada en gran medida, en estudios descriptivos sobre aspectos cognitivos del aprendizaje, pensamiento del profesor, etc., y en ciertos casos proporcionando explicaciones de las dificultades y factores condicionantes de los procesos de enseñanza y aprendizaje. Sin embargo, consideramos necesario abordar de manera sistemática la cuestión tecnológica del diseño, desarrollo y evaluación de propuestas de intervención en el aula. La Didáctica de la Matemática debería aportar conocimientos para el análisis de:
-
La adaptación y pertinencia de los contenidos matemáticos a un determinado proyecto educativo.
-
Los medios tecnológicos y temporales adecuados para la puesta en marcha de un proceso de estudio matemático.
-
El tipo de interacción entre profesor y alumnos que permita identificar y resolver las dificultades y conflictos en los procesos de estudio matemático.
-
La adaptación entre los objetivos formativos y las capacidades y competencias previas de los alumnos, así como a sus intereses, afectividad y motivaciones.
-
La pertinencia de los significados pretendidos (e implementados), de los medios usados y de los patrones de interacción al proyecto educativo de la escuela y el contexto social en que se desarrolla el proceso de estudio.
El objetivo de mejorar los procesos de enseñanza y aprendizaje de las matemáticas está en la base de cualquier esfuerzo de investigación e innovación; pero la complejidad de tales procesos nos lleva a ser extremadamente precavidos en la proposición de normas y reglas para la intervención en los sistemas didácticos. Si preguntamos actualmente a cualquier investigador en educación matemática sobre, qué matemáticas enseñar y cómo en un contexto específico, posiblemente, nos dirá no lo sabemos, o algo parecido. ¿Significa esto que todos los esfuerzos de investigación realizados hasta la fecha han sido baldíos?
Ciertamente no disponemos de recetas de cómo enseñar, pero esto no significa que no tengamos ciertos conocimientos que nos permiten tomar algunas decisiones locales preferentes. Aceptamos la siguiente hipótesis metodológica: Fijadas unas circunstancias (sujetos, recursos, restricciones, ), un experto en didáctica de las matemática puede razonar (apoyándose en resultados teóricos contrastados empíricamente) que ciertas tareas y modos de interacción en el aula son preferibles a otras diferentes.
Nos parece necesario indagar sobre los criterios que ayuden a determinar en qué medida un proceso de estudio o instrucción matemática2 reúne ciertas características que permitan calificarlo como idóneo3 para los fines pretendidos y adaptado a las circunstancias e instrumentos disponibles. En este sentido, Sfard (2002) hace un análisis de las características educativas de los estándares curriculares (NCTM, 1989)4 teniendo en cuenta diez necesidades de los estudiantes en relación con el aprendizaje de las matemáticas. Para Sfard, la necesidad central es la de dotar de significado a las manipulaciones simbólicas.
La necesidad de significado, culturalmente matizada, pero universal, y la necesidad de comprendernos a nosotros mismos y al mundo que nos rodea, es ampliamente reconocida como la fuerza básica tras todas nuestras actividades intelectuales (Sfard, 2002, p. 5).
El resto de necesidades que describe Sfard hacen referencia a aspectos epistémicos (naturaleza relacional de las matemáticas; las matemáticas como actividad humana; las matemáticas como proceso, antes que como producto), cognitivos (adaptación consistente de los nuevos conocimientos a los previamente establecidos; interacción social y comunicación como motores del aprendizaje; complejidad del aprendizaje) o emocionales (el aprendizaje como proceso de participación e integración en una comunidad, para la aceptación en la misma).
Estas diez necesidades del aprendiz de matemáticas deben ser tenidas en cuenta en el diseño e implementación de los procesos de estudio. Además de estas necesidades nosotros consideramos que es necesario tener en cuenta necesidades docentes, en particular las que denominamos mediacionales (disponibilidad de recursos materiales y temporales) y ecológicas (relativas a la institución de referencia, al contexto social, a las directrices en política educativa, a las limitaciones económicas, etc.).
En diversos trabajos, Godino y colaboradores5 (Godino y Batanero, 1994; Godino, 2002; Contreras, Font, Luque y Ordóñez, 2005; Font y Ramos, 2005; Godino, Contreras y Font, 2006; Godino, Font y Wilhelmi, 2006) han elaborado un sistema de nociones teóricas sobre la naturaleza, origen y significado de los objetos matemáticos desde una perspectiva educativa, tratando de articular de manera coherente las dimensiones epistémica (significados institucionales o socioculturales) y cognitiva (significados personales, psicológicos o individuales). Estas nociones constituyen un primer paso para abordar los problemas de enseñanza y aprendizaje de las matemáticas, ya que se centran en modelizar los propios conocimientos matemáticos a enseñar y los aprendizajes logrados por los estudiantes. Sin embargo, las cuestiones de diseño, implementación y evaluación de intervenciones didácticas efectivas requiere la adopción (o el desarrollo) de teorías instruccionales, esto es, herramientas que ayuden a describir las interacciones en el aula, explicar por qué ocurren ciertos hechos y fenómenos (Wilhelmi et al., 2005) y, a ser posible, orientar posibles acciones de mejora.
Godino, Contreras y Font (2006) han desarrollo algunas nociones teóricas para el análisis de la instrucción matemática, modelizándola, de manera metafórica, como procesos estocásticos compuestos de seis subprocesos y sus correspondientes trayectorias muestrales:
1. Trayectoria epistémica, que es la distribución a lo largo del tiempo de la enseñanza de los componentes del significado6 institucional implementado. Estos componentes (problemas, lenguaje, definiciones, propiedades, procedimientos, argumentos) se van sucediendo en un cierto orden en el proceso de instrucción.
2. Trayectoria docente: distribución de las tareas/acciones docentes a lo largo del proceso de instrucción.
3. Trayectorias discentes: distribución de las acciones desempeñadas por los estudiantes.
4. Trayectoria mediacional: distribución de los recursos tecnológicos utilizados (libros, apuntes, manipulativos, software, etc.), y del tiempo asignado al estudio.
5. Trayectorias cognitivas: cronogénesis y evolución de los significados personales de los estudiantes.
6. Trayectorias emocionales: distribución temporal de los estados emocionales (motivaciones, actitudes, valores, afectos, ) de cada alumno con relación a los objetos matemáticos y al proceso de estudio seguido.
Godino, Contreras y Font introducen la noción de idoneidad (pertinencia, adecuación, ) de un proceso de estudio matemático como herramienta para establecer un puente entre una didáctica descriptiva y una didáctica normativa o técnica7. En este trabajo vamos a desarrollar la noción de idoneidad didáctica de un proceso de estudio matemático, teniendo en cuenta las distintas dimensiones implicadas, así como el modelo epistemológico y cognitivo propuesto por el enfoque ontosemiótico de la cognición matemática (EOS). Con el fin de ejemplificar el uso del sistema de nociones teóricas del EOS en el análisis didáctico8 vamos a aplicarlas a una experiencia de enseñanza de la noción de función a estudiantes de un primer curso de matemáticas en una escuela de ingeniería (Godino, Wilhelmi y Bencomo, 2005).
La Noción de Idoneidad Didáctica, sus dimensiones y componentes
En Godino, Contreras y Font (2006) se introducen cinco criterios a tener en cuenta para valorar la idoneidad de los procesos de enseñanza y aprendizaje matemático, usando en su formulación nociones teóricas del EOS. A continuación describimos estos criterios con algunas precisiones respecto de la versión inicialmente formulada:
1. Idoneidad epistémica, se refiere al grado de representatividad de los significados institucionales implementados (o previstos), respecto de un significado de referencia.
2. Idoneidad cognitiva, expresa el grado en que los significados pretendidos/implementados estén en la zona de desarrollo potencial de los alumnos, así como la proximidad de los significados personales logrados a los significados pretendidos/implementados.
3. Idoneidad interaccional, grado en que las configuraciones y trayectorias didácticas permiten, por una parte, identificar conflictos semióticos9 potenciales (que se puedan detectar a priori), y, por otra parte, resolver los conflictos que se producen durante el proceso de instrucción mediante la negociación de significados.
4. Idoneidad mediacional, grado de disponibilidad y adecuación de los recursos materiales y temporales necesarios para el desarrollo del proceso de enseñanza-aprendizaje.
5. Idoneidad emocional, grado de implicación (interés, motivación) del alumnado en el proceso de estudio.
6. Idoneidad ecológica, grado de adaptación del proceso de estudio al proyecto educativo del centro10, las directrices curriculares, las condiciones del entorno social, etc.
Estas idoneidades deben ser integradas teniendo en cuenta las interacciones entre las mismas, lo cual requiere hablar de la idoneidad didáctica como criterio sistémico de pertinencia (adecuación al proyecto de enseñanza) de un proceso de instrucción, cuyo principal indicador empírico puede ser la adaptación entre los significados personales logrados por los estudiantes y los significados institucionales pretendidos/ implementados (Godino, Wilhelmi y Bencomo, 2005).
En la figura 1 sintetizamos los componentes de la noción idoneidad didáctica de un proceso de estudio matemático. La idoneidad didáctica supone la articulación coherente y armónica de las siguientes idoneidades parciales: epistémica, cognitiva, mediacional, emocional, interaccional y ecológica. Representamos mediante un hexágono regular la idoneidad correspondiente a un proceso de estudio pretendido o programado, donde a priori se supone un grado máximo de las idoneidades parciales. El hexágono irregular interno correspondería a las idoneidades efectivamente logradas en la realización de un proceso de estudio implementado.
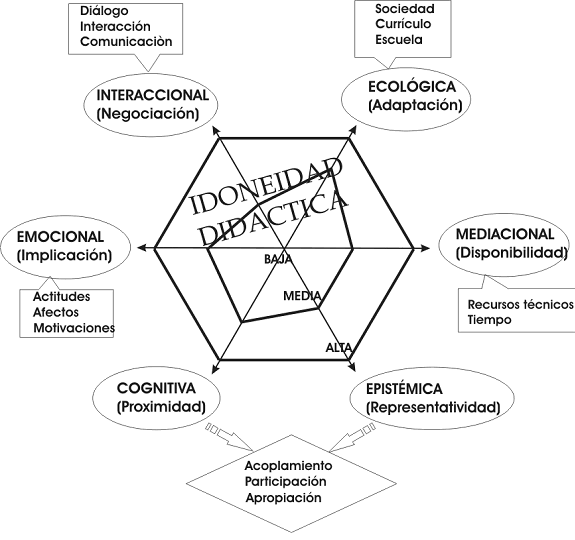
Figura 1: Componentes de la idoneidad didáctica
Situamos en la base las idoneidades epistémica y cognitiva al considerar que el proceso de estudio gira alrededor del desarrollo de unos conocimientos específicos. En el EOS, cuando se habla de conocimiento se incluye comprensión y competencia. La dimensión epistémica se refiere a los conocimientos institucionales (o sea, compartidos en el seno de instituciones o comunidades de prácticas) mientras que la dimensión cognitiva se refiere a los conocimientos personales (o del sujeto individual). El aprendizaje tiene lugar mediante la participación del sujeto en las comunidades de prácticas, el acoplamiento progresivo de los significados personales a los institucionales y la apropiación de los significados institucionales por los estudiantes.
En la figura 2 se indican los distintos tipos de significados institucionales y personales que se ponen en juego en el diseño, implementación y evaluación de procesos de instrucción matemática. Los significados aquí mencionados son interpretados como los sistemas de prácticas operativas y discursivas que se ponen en juego por una persona (o compartidas en el seno de una institución) para resolver una cierta clase de situaciones – problemas (Godino y Batanero, 1994, p. 340). Estos significados son descritos mediante configuraciones de objetos intervinientes y emergentes de los sistemas de prácticas (Godino, Batanero y Font, 2006)

Figura 2: Tipos de significados institucionales y personales
En la parte central de la figura 2 indicamos las relaciones dialécticas entre enseñanza y aprendizaje, que supone el acoplamiento progresivo entre los significados personales e institucionales. Así mismo, la enseñanza implica la participación del estudiante en la comunidad de prácticas que soporta los significados institucionales, y el aprendizaje, en última instancia, supone la apropiación por el estudiante de dichos significados.
Las idoneidades epistémica y cognitiva no se pueden reducir a los componentes conceptuales, procedimentales y actitudinales, como habitualmente se considera en las propuestas curriculares. El primer paso para poder confeccionar un programa de estudio es determinar qué es idóneo desde los puntos de vista epistémico y cognitivo (así como la coordinación de estas idoneidades). La ontología matemática (junto con las facetas duales) propuesta por el EOS permite describir las idoneidades epistémica y cognitiva en términos de configuraciones epistémicas y cognitivas (conglomerado de situaciones-problema, definiciones (conceptos), procedimientos, proposiciones, lenguajes y argumentos). El núcleo de dichas configuraciones son las situaciones-problemas seleccionadas para contextualizar y personalizar los significados.
Tal y como hemos definido con anterioridad, tanto la idoneidad epistémica (representatividad de los significados implementados y pretendidos) como la idononeidad cognitiva (adaptación de los significados implementados/ pretendidos con respecto a los significados personales iniciales y finales de los estudiantes) están definidas sobre la noción de significado. En el EOS, el significado se concibe en términos de sistemas de prácticas operativas y discursivas (institucionales y personales). Tales sistemas de prácticas se hacen operativos mediante las correspondientes configuraciones (epistémicas o cognitivas).
Todas estas nociones se han revelado útiles para el análisis de proyectos y experiencias de enseñanza (Contreras et al., 2005; Godino et al., 2005; Godino et al., 2006). Los distintos elementos pueden interactuar entre sí, lo que sugiere la extraordinaria complejidad de los procesos de enseñanza y aprendizaje. El logro de una idoneidad alta en una de las dimensiones, por ejemplo, la epistémica, puede requerir unas capacidades cognitivas que no posean los estudiantes a los que se dirige la enseñanza. Una vez logrado un cierto equilibrio entre las dimensiones epistémica y cognitiva es necesario que la trayectoria didáctica optimice la identificación y solución de conflictos semióticos. Los recursos técnicos y el tiempo disponible también interaccionan con las situaciones-problemas, el lenguaje, etc.
El aprendizaje individual es una criatura compleja con muchas necesidades las cuales tienen que satisfacerse para que el aprendizaje tenga éxito. El principio de una dieta equilibrada es por tanto aplicable tanto para nuestras mentes como para nuestros cuerpos (Sfard, 2002, p. 30).
Las herramientas descritas se pueden aplicar al análisis de un proceso de estudio puntual implementado en una sesión de clase, a la planificación o el desarrollo de una unidad didáctica, o de manera más global, al desarrollo de un curso o una propuesta curricular. También pueden ser útiles para analizar aspectos parciales de un proceso de estudio, como un material didáctico, un manual escolar, respuestas de estudiantes a tareas específicas, o incidentes didácticos puntuales.
El centro de atención del análisis didáctico debiera progresar desde la situación –problema (o del concepto/ estructura conceptual) a la configuración epistémica/ cognitiva, y de ésta hacia la configuración didáctica –que incluye no sólo el saber y los sujetos sino también el papel del profesor, los recursos y las interacciones entre los diversos componentes. En la siguiente etapa la unidad de análisis didáctico debe contemplar la trayectoria o secuencia de configuraciones didácticas, esto es, el progresivo crecimiento matemático de los aprendizajes (Figura 3). Con la expresión metafórica crecimiento matemático queremos expresar la intencionalidad del proceso educativo hacia la formación de ciudadanos o profesionales competentes y creativos en el área de las matemáticas.

Figura 3. Centros de atención del análisis didáctico
Descripción de un Proceso de Estudio Observado
En esta sección describimos una experiencia de enseñanza de la noción de función con estudiantes de primer curso de una escuela de ingeniería, que utilizaremos para ejemplificar algunos aspectos de la noción de idoneidad didáctica y sus componentes. Somos conscientes del reto metodológico que plantea la evaluación de las distintas dimensiones del constructo teórico idoneidad didáctica, de la cantidad y tipo de datos que se han de recoger y de la complejidad del análisis de los datos. Ahora bien, puesto que en el ejemplo que vamos a utilizar como contexto de reflexión sólo disponemos de información de las actividades realizadas y de las interacciones profesor – estudiantes observadas mediante grabaciones audio-visuales, ejemplificaremos con más detalle sólo algunas de las idoneidades.
Descripción del proceso de estudio observado
El objetivo de la enseñanza observada consiste en que los estudiantes recuerden, interpreten, consoliden y formalicen las definiciones de correspondencia, función, rango, dominio y tipos de funciones, aplicándolas en una situación que pone en juego conocimientos de física: el lanzamiento vertical hacia arriba de una pelota con una velocidad inicial. Los alumnos han estudiado previamente las definiciones de dichas nociones y el profesor propone una tarea matemática que es un problema contextualizado evocado de aplicación (Ramos y Font, en prensa)11. El profesor presupone que los estudiantes son capaces de aplicar estas definiciones junto a otros conocimientos previos necesarios (graficación de la parábola, velocidad, etc.). Las consignas dadas a los alumnos se incluyen en la tabla 1.

Tabla 1. Cuestiones propuestas a los estudiantes
El profesor organizó el proceso de estudio dividiendo la clase en equipos de cuatro alumnos, asignando a cada uno de ellos una parte de la tarea. Un alumno de cada grupo explicó al resto de la clase la solución encontrada en el seno del grupo. El profesor completaba o corregía la explicación del alumno. La trayectoria didáctica implementada, es decir, la secuencia de modos de gestión de los significados implementados a propósito de un objeto matemático específico, incluye, por tanto, configuraciones de tipo cooperativo, dialógico y magistral (Godino, Contreras y Font, 2006). Para trabajar las cuestiones propuestas se dedicaron cuatro clases de 45 minutos.
El análisis del proceso instruccional descrito es consustancial a la teoría didáctica, como en general lo es todo hecho o fenómeno didáctico. Los criterios de idoneidad se apoyan en la noción de significado y en los tipos de significado identificados (institucionales y personales).
Para poder valorar la idoneidad epistémica de un proceso de instrucción realmente implementado (significado implementado) o bien de un proceso de instrucción planificado en un libro de texto (significado pretendido) es necesario establecer primero el significado de referencia que sirva de comparación.
Significado de referencia del objeto función
El concepto de función es un buen ejemplo para mostrar la diversidad de sistemas de prácticas y contextos de uso, progresivamente más amplios, en los cuales podemos mostrar la pluralidad de significados parciales (Biehler, 2005) (entendidos en el EOS como subsistema de prácticas). La reconstrucción de los significados de la función es un primer paso necesario para poder comprender los procesos de enseñanza efectivamente implementados y elaborar criterios para su mejora. Diversos autores se han interesado por dicha reconstrucción desde un punto de vista histórico y epistemológico (Youschkevitch, 1976; Sierpinska, 1992). En concreto, Ruiz (1998) hace un estudio sistemático y caracteriza siete concepciones epistemológicas del objeto función, las cuales describe usando la tripleta conceptual de Vergnaud (1990) (situaciones, invariantes y representaciones). Nosotros preferimos interpretar tales concepciones en términos de subsistemas de prácticas institucionales ligadas a contextos de uso particulares, y de objetos emergentes (tipos de problemas, lenguaje, definiciones, proposiciones, procedimientos y argumentos); cada una de estas configuraciones epistémicas y sus prácticas asociadas modeliza aspectos parciales del holo-significado (Wilhelmi, Godino y Lacasta, 2004) del objeto función, el cual desempeñará el papel de significado global del objeto función y que constituye el referente en una investigación específica.
En la figura 4 sintetizamos algunos elementos intervinientes en la configuración global12 de la noción de función que vamos a utilizar como significado institucional de referencia para analizar el proceso de estudio observado. En la práctica escolar actual (significados pretendidos e implementados) las configuraciones parciales que aquí llamamos tabular, gráfica y analítica suelen presentarse simultáneamente y centradas en su aplicación a la solución de problemas de modelización de problemas extramatemáticos. Se obtiene de este modo una configuración epistémica que podemos considerar como informal/empírica que contrasta con la configuración conjuntista, la cual, dada su generalidad y carácter intramatemático podemos describir como formal (Ramos y Font, en prensa; Font y Godino, en prensa).

Figura 4. Configuraciones epistémicas asociadas al concepto de función.
En la siguiente sección desarrollamos y ejemplificamos la noción de idoneidad didáctica aplicándola al proceso de estudio descrito. Las cuestiones que nos planteamos son:
-
¿En qué medida es idóneo el proceso de instrucción observado?
-
¿Qué cambios se podrían introducir en el proceso para incrementar la idoneidad?
-
¿Qué información es necesario recoger para poder evaluar los distintos aspectos de la idoneidad didáctica?
Pauta de Evaluación de la Idoneidad Didáctica
La valoración de la idoneidad didáctica de un proceso de estudio es un asunto sumamente complejo puesto que, como hemos visto en la sección 2, involucra diversas dimensiones, que a su vez están estructuradas en distintas componentes. Además, tanto las dimensiones como los componentes no son observables directamente y, por lo tanto, es necesario inferirlos a partir de indicadores empíricos.
En las definiciones presentadas de las distintas idoneidades parciales juega un papel central la noción de significado, entendido, como sistema de prácticas operativas y discursivas. Este enfoque proporciona herramientas para operativizar la noción de idoneidad de las configuraciones y trayectorias didácticas. En esta sección presentamos algunos criterios o indicadores de las distintas idoneidades parciales y los aplicamos al proceso de enseñanza descrito en la sección 3, centrándonos principalmente en las dimensiones epistémica, cognitiva e interaccional.
Idoneidad epistémica
El análisis de la idoneidad epistémica precisa de la definición previa de un significado de referencia para el proceso de estudio matemático (efectivo o potencial) que se desea analizar. De las categorías de objetos primarios introducidas en el EOS, fijaremos nuestra atención en las situaciones-problemas, las cuales deben, por un lado, ser representativas de las incluidas en el significado de referencia y, por otro lado, permitir contextualizar los conocimientos pretendidos, ejercitarlos y aplicarlos a situaciones relacionadas. Más aún, desde el punto de vista de los procesos, una idoneidad alta estará asociada a la presencia de momentos de generación del problema (problematización), de modo que los propios alumnos tengan ocasión de formular o reformular los problemas y plantear cuestiones relacionadas, en definitiva, de asumir los problemas como propios13.
Los lenguajes utilizados deben ser una muestra representativa de los identificados en el significado de referencia; también se tienen en cuenta las transformaciones, traducciones y conversiones entre los mismos. Se descartan notaciones innecesarias o inconsistentes. Los estudiantes tienen ocasión de expresar y comunicar sus conjeturas, procedimientos operatorios, argumentaciones, en general, sus conocimientos.
Las definiciones, proposiciones y procedimientos son representativos de los identificados en el significado de referencia y adaptados al nivel, capacidades y recursos disponibles en el marco institucional correspondiente. El proceso incluye momentos en los que se generan y negocian las reglas mejor adaptadas a las circunstancias, existiendo momentos en que operan como herramientas implícitas (Douady, 1986). Tales reglas conceptuales, proposicionales y procedimentales son explicadas y justificadas mediante argumentos representativos y adaptados.
El juicio positivo sobre la idoneidad epistémica del proceso de estudio debe tener en cuenta las conexiones e interacciones entre los elementos mencionados14. Los elementos conceptuales, proposicionales y procedimentales deben haber sido contextualizados mediante las situaciones, explicados y justificados con argumentos pertinentes y todos estos elementos soportados mediante recursos expresivos eficaces.
Idoneidad epistémica de la enseñanza observada
La observación del proceso de estudio descrito en la Sección 3.1 nos permite caracterizar el sistema de prácticas operativas y discursivas efectivamente implementadas, relativas al objeto matemático función. La comparación de estas prácticas con el significado de referencia de dicho objeto nos permite identificar diversos desajustes y formular hipótesis sobre la idoneidad del proceso de estudio, en cuanto a su faceta epistémica.
El primer aspecto que hay que destacar es el que el profesor presenta una situación problema que pretende ser representativa de las dos configuraciones epistémicas en las que se puede subdividir el significado de referencia (la empírica y la formal o conjuntista). De hecho, se puede considerar que la tarea es una mezcla de dos problemas diferentes (las cuestiones 1,5, 6 y 7 por una parte y las cuestiones 2, 3 y 4 por otra).
En el EOS (Ramos y Font, en prensa) se consideran dos usos del término contexto. Uno consiste en considerar el contexto como un ejemplo particular de un objeto matemático, mientras que el otro consiste en considerar el entorno. En el primer caso se trata de ver que la situación problema cae dentro del campo de aplicación de un objeto matemático. En el segundo caso, se trata de un uso que vamos a llamar, metafóricamente, ecológico (se trataría de responder a preguntas del tipo: ¿En qué lugar se halla? ¿Qué tiene a su alrededor? ¿Dónde vive? ¿Con qué otros objetos matemáticos se relaciona?, ¿En qué institución se utiliza?, etc. Si consideramos el primer uso vemos que el problema que nos ocupa pretende ser una caso particular del objeto función. El contexto (entendido en términos ecológicos) de las cuestiones 2, 3 y 4 es una configuración epistémica de tipo formalista mientras que las cuestiones 1, 5, 6 y 7 tendrían por contexto una configuración empirista.
Lo que en principio podría ser positivo: la mayor representatividad posible del significado implementado puede resultar contraproducente si no se consigue armonizar, de manera coherente, las dos configuraciones epistémicas (la empírica y la formal). Esta falta de armonización puede ser la causa de conflictos semióticos (de tipo epistémico). A continuación comentamos dos de dichos conflictos.
Conflicto 1
El primer conflicto semiótico de tipo epistémico que encontramos es la ruptura brusca entre la primera cuestión propuesta en la tarea y las dos que le siguen. La cuestión 1 plantea un problema de modelización de un problema físico (previsión del espacio conocido el tiempo) mediante una función dada mediante una fórmula algebraica. Las cuestiones que siguen piden determinar si la correspondencia definida por la fórmula es o no una función, su dominio, codominio, rango y tipo de función (inyectiva, sobreyectiva, biyectiva).
Estas cuestiones se refieren a una problemática de naturaleza formal que es ajena al problema de modelización. La razón de ser del sistema de objetos puestos en juego por el modelo conjuntista es la descripción, generalización y estructuración de conocimientos matemáticos, ajenos a la práctica de modelización funcional.
Conflicto 2
El segundo conflicto lo podemos observar en la siguiente explicación del profesor:
P: Entonces, fíjense esta función d, me relaciona un conjunto de números reales positivos; se tiene que usar incluyendo el cero, y dónde va a parar ese conjunto; ¿en qué conjunto numérico va a parar? Enteros otra vez, los enteros y el veintisiete y medio ¿positivos o negativos? ¿Y el cero, lo van a dejar afuera? Ahí tienen entonces esta función, la función altura relaciona al conjunto de los números reales más el cero con el conjunto de los números reales con el cero.
Se trata de una explicación confusa que puede llevar a que los alumnos hagan interpretaciones discordantes con la que el profesor pretende transmitir (conflictos semióticos de tipo interaccional). Ahora bien, en nuestra opinión su origen es un conflicto de tipo epistémico, puesto que mientras la configuración conjuntista requiere explicitar cuáles son los conjuntos inicial y final cuyos elementos se corresponden (de modo que si se cambia alguno de estos conjuntos se tiene una función diferente), la configuración empírica no lo requiere.
El problema físico que se modeliza con la fórmula algebraica pone en juego dos intervalos de números reales que pueden tomarse como conjuntos iniciales, o dominios de definición de la función, [0; 3,2] (tiempo hasta que la pelota alcanza la altura máxima), o [0; 6,4] (tiempo hasta que vuelve al suelo); el conjunto imagen es el intervalo [0; 51,2] en ambos casos. La naturaleza de la variable independiente, tiempo, hace que los valores que puede tomar sean números reales positivos, pero la fórmula algebraica que establece el criterio de correspondencia es válida para todo número real. El conjunto final (codominio) de la función ![]() queda completamente indefinido, y por tanto, carece de sentido preguntar si la función (¿cuál?) es o no sobreyectiva.
queda completamente indefinido, y por tanto, carece de sentido preguntar si la función (¿cuál?) es o no sobreyectiva.
La tensión entre la configuración empírica y la conjuntista se puede observar claramente cuando el profesor dice: Ahí tienen entonces esta función, la función altura relaciona al conjunto de los números reales más el cero con el conjunto de los números reales con el cero.. Matemáticamente, la fórmula ![]() , con v0 = 32 m / s y g = 10 m / s2 es válida para todo t real y su imagen es el intervalo (-8; 51,2]. Desde el punto de vista de la modelización física, en la función altura, tal como dice el profesor, la variable t varía entre 0 y 3,2 segundos (intervalo en que se alcanza la altura máxima pedida), ambos extremos incluidos y el rango varía entre 0 y 51,2 metros y no de los positivos a los positivos como el profesor estableció en la clase.
, con v0 = 32 m / s y g = 10 m / s2 es válida para todo t real y su imagen es el intervalo (-8; 51,2]. Desde el punto de vista de la modelización física, en la función altura, tal como dice el profesor, la variable t varía entre 0 y 3,2 segundos (intervalo en que se alcanza la altura máxima pedida), ambos extremos incluidos y el rango varía entre 0 y 51,2 metros y no de los positivos a los positivos como el profesor estableció en la clase.
Si en lugar de una ruptura brusca entre los dos tipos de configuraciones epistémicas se hubiese buscado su articulación coherente, este hecho podía haberse utilizado para matizar la diferencia entre rango y conjunto final y para introducir o desarrollar la noción de función sobreyectiva.
Idoneidad cognitiva
En el EOS se introduce la noción de significado personal para designar los conocimientos del estudiante. Estos significados son concebidos, al igual que los significados institucionales, como los sistemas de prácticas operativas y discursivas que son capaces de realizar los estudiantes a propósito de cierto tipo de problemas. Los significados personales se van construyendo progresivamente a lo largo del proceso de instrucción, partiendo de unos significados iniciales al comienzo del proceso, y alcanzando unos determinados significados finales (logrados o aprendidos)
Hemos definido que una configuración didáctica tiene idoneidad cognitiva cuando el material de aprendizaje está en la zona de desarrollo potencial (Vygotski, 1934) de los alumnos; con otras palabras, que el desfase entre los significados institucionales implementados y los significados personales iniciales sea el máximo abordable teniendo en cuenta las restricciones cognitivas de los alumnos y los recursos humanos, materiales y temporales disponibles (Godino, Wilhelmi y Bencomo, 2005). Además se exige que los significados personales logrados por los estudiantes en el proceso de estudio concuerden con los significados pretendidos/ implementados.
Esta definición se puede relacionar con la necesidad de dificultad descrita por Sfard:
Puesto que las personas rehuyen la dificultad tratando instintivamente de evitarla, es importante enfatizar que cuando se trata del aprendizaje, la dificultad es de hecho una buena cosa, siempre que sea básicamente manejable. Se puede decir que la dificultad es para el aprendizaje lo que la fricción es para el movimiento: Es la condición necesaria para su existencia. Sin dificultad no hay aprendizaje, de igual modo que no hay movimiento sin fricción (Sfard, 2002, p. 13).
El juicio positivo sobre la idoneidad cognitiva de un proceso de estudio se basará en: a) la existencia de una evaluación inicial de los significados personales de los estudiantes, a fin de comprobar que los significados pretendidos suponen un reto manejable; b) la existencia de adaptaciones curriculares que tengan en cuenta las diferencias individuales15; y, finalmente, c) que los aprendizajes logrados estén lo más próximos posible a los significados institucionales pretendidos/ implementados.
Idoneidad cognitiva de la enseñanza observada
Para evaluar la idoneidad cognitiva del proceso de instrucción en términos de proximidad de la zona de desarrollo potencial del alumno es necesario hacer un seguimiento detallado de los alumnos (test, entrevistas, evaluaciones orales y escritas, etc.) para conocer sus significados previos y determinar si las explicaciones dadas por el profesor fueron efectivas.
Con relación a los significados personales previos de los alumnos (representación gráfica de la parábola, velocidad, etc.), necesarios para resolver la tarea propuesta, sólo sabemos que el profesor los considera de manera implícita como logrados.
Para determinar si las explicaciones dadas por el profesor fueron efectivas disponemos únicamente de las grabaciones de las sesiones. De esta forma, únicamente es posible obtener indicadores para valorar la idoneidad cognitiva del proceso basados en secuencias concretas. A continuación mostramos dos fragmentos observados.
En el siguiente diálogo podemos observar tres alumnos A2 , A3 y A4 que manifiestan diferentes significados personales del objeto función. Por una parte, se observa que A3 aplica incorrectamente la definición de función. A4 hace una afirmación en la que usa de manera incorrecta la definición de función, en la que inicialmente confunde los conjuntos inicial y de partida, aunque a continuación rectifica su error. Por último, A2 realiza afirmaciones en las que aplica correctamente, aunque con titubeos, la definición general de función.
P: Ahora la pregunta clave es: ¿además de una correspondencia, qué se necesita para que sea una función? ¿Qué hace falta añadirle para que se convierta o se constituya en una función?
A2: Que cada elemento del conjunto de partida tenga un elemento del conjunto de llegada. Que cada elemento del conjunto de partida no tenga dos elementos en el conjunto de llegada.
[ ]
P: ¿Entendieron el concepto de ella? Ahora preguntamos: Entonces, eso, [señalando a la gráfica de la pizarra] ¿Eso es una función? ¿No? Allá dijeron que no. ¿Hay algún elemento del conjunto de partida que tenga dos imágenes, o tres o cuatro?
A3: Sí. Por ejemplo, en y, yo coloqué el valor en x igual cero y me da cero; en x igual seis coma cuatro, también.
P: ¿Y eso significa que eso no es función? ¿Por qué no es función?
A2: Bueno Sí es función, pero aparte de eso tiene otra función.
P: ¿Otra función?
A2: Sí.
P: ¿Por qué dices tú que no es función?
A2: Yo no he dicho que no es función, yo no puedo explicarlo, pero cumple dos tipos de funciones.
P: ¿Dos tipos de funciones o dos tipos de aplicaciones?
A2: A través de esa gráfica uno puede saber si es sobreyectiva, porque, aparte de que se cumple la definición de que cada elemento tiene una y sólo una imagen en el rango, también se cumple que un elemento tiene dos imágenes.
P: ¿Ahí tiene un elemento dos imágenes?
A2: Sí.
P: ¿Cuál elemento tiene dos imágenes?
A2: No, ninguno.
A4: Profesor, un elemento del conjunto de partida tiene dos elementos del conjunto de llegada; por ejemplo, el cero y el seis coma cuatro Ahí se ve que dos elementos del conjunto de partida caen en un mismo elemento del conjunto de llegada.
P: ¿Y eso rompe la continuidad de una función?
A2: No.
P: [ ] ¿Cómo es la definición de función? A cada elemento del conjunto de partida le corresponde uno y sólo un elemento del conjunto de llegada. Eso no significa que tres elementos del conjunto de partida puedan tener la misma imagen.
En este diálogo se puede observar la existencia de un conflicto semiótico de tipo cognitivo en el discurso de A2 (cuando éste intenta explicar por qué es una función) y también se puede observar como, en cierta manera, logra superarlo. Se puede observar también un aspecto claramente relacionado con las limitaciones que presentan los significados personales del objeto función de estos tres alumnos. Nos referimos al hecho de que el profesor se refiere al dibujo trazado en la pizarra (objeto ostensivo) como si fuera el propio objeto función (no ostensivo): Entonces, eso, [señalando a la gráfica de la pizarra] ¿Eso es una función?. Si bien un profesor experto está en condiciones, según convenga, de identificar o diferenciar el signo del objeto, un alumno corre el peligro de confundir el signo con el objeto) Esta identificación implícita del profesor puede producir el efecto de la identificación entre representación y objeto en el significado personal del alumno. En esta interacción el profesor, sin darse cuenta, puede estar propiciando la aparición de un conflicto semiótico de tipo interaccional (disparidad de interpretaciones entre el profesor y el alumno). El gráfico es visto por el profesor como una entidad transparente, elemental, cuando en realidad constituye un sistema de convenios que es necesario explicitar y compartir para que adquiera sentido la pregunta: ¿Eso es una función?.
Otro segmento instruccional en el que se observa claramente que las explicaciones dadas por el profesor no fueron efectivas es el siguiente:
P: .. ¿Cuál es el codominio?
[A2 señaló el eje equis de la gráfica]
P: ¡Co-co-codomio!
A2: Si el rango vendría siendo el conjunto y , de llegada, el co-dominio tendría que ser el reflejo de ambos conjuntos, o sea,
P: ¿Qué el codominio y rango son los mismos?
A2: No, no, tendría que ser el recorrido que hace la pelota, desde que parte hasta que llega.
En este diálogo se observa que el significado personal del objeto codominio del alumno A2 se aleja mucho del pretendido por el profesor.
Idoneidad interaccional
Diremos que un proceso de estudio tiene una idoneidad interaccional16 alta en la medida en que las configuraciones didácticas posibilitan que el profesor y los alumnos identifiquen conflictos semióticos potenciales (a priori), efectivos (durante el proceso de instrucción) y residuales (a posteriori) y resolver dichos conflictos mediante la negociación de significados.
Los formatos de interacción de tipo dialógico y de trabajo cooperativo tendrán potencialmente mayor idoneidad interaccional que las de tipo magistral y de trabajo individual, puesto que los estudiantes muestran su relación con los objetos matemáticos y, por lo tanto, el profesor tiene indicadores explícitos de dicha relación. Estos indicadores pueden permitir al profesor valorar la relación de los estudiantes con los objetos matemáticos y, eventualmente, determinar la intervención más adecuada (según las restricciones matemático-didácticas asociadas a la situación).
Idoneidad interaccional de la enseñanza observada
Si nos fijamos en la interacción que se ha producido en el primer diálogo podemos observar como la actuación del profesor propicia la emergencia del conflicto cognitivo del alumno A2 y su posterior resolución, pero en cambio no soluciona el problema del alumno A3. Por otra parte, su última intervención: ¿Y eso rompe la continuidad de una función? sólo puede ser causa de un nuevo conflicto semiótico (de tipo interaccional). Si nos fijamos en la interacción que se produce en el segundo diálogo vemos que ésta no resuelve la disparidad que se produce entre la interpretación de A2 y la que previamente había explicado el profesor.
Si nos fijamos más en general en el modo de interacción entre el profesor y los estudiantes observamos algunos hechos importantes relacionados con la idoneidad interaccional.
Un problema pedagógico general
El profesor asigna cada uno de los siete apartados de la tarea a un grupo de alumnos diferente, de modo que cada grupo, formado por 5 estudiantes, se responsabiliza de resolver una de tales cuestiones y de presentarla al resto de la clase. Esta manera de organizar el trabajo en el aula implica que los estudiantes que no han trabajado alguna de las cuestiones tendrán dificultades para seguir las explicaciones del resto de los compañeros. El resultado es que las presentaciones de los estudiantes se convierten en explicaciones magistrales para la mayor parte de los estudiantes. Una trayectoria didáctica pretendida inicialmente por el profesor con un cierto grado dialógico y adidáctico resulta finalmente en varias configuraciones magistrales, pero en este caso, conducidas por profesores inexpertos (los representantes de los distintos equipos).
Configuración didáctica pretendida e implementada
A partir de un estudio personal previo el profesor plantea un diálogo contextualizado cuyo fin es el desarrollo de la noción de función (configuración didáctica dialógica.). El papel que el profesor atribuye a los alumnos en la construcción y comunicación del conocimiento es central: supone que los estudiantes serán capaces de identificar los objetos pretendidos en la situación modelizada y descontextualizarlos para la construcción del significado de función pretendido. Con otras palabras, el profesor intenta gestionar un aprendizaje de tipo constructivista: los estudiantes, por intermedio de la situación y en interacción con el profesor, deberán ser capaces de hacer evolucionar el significado personal atribuido a la noción de función (producto del proceso de estudio personal) y obtener una adaptación fiel al significado institucional pretendido.
Sin embargo, la configuración didáctica efectiva no puede considerarse como dialógica. La mayor parte de los estudiantes no ha realizado el estudio personal anterior a la sesión de aprendizaje. El profesor es consciente de ello, empero no modifica el diseño del proceso instruccional pretendido. Poco a poco, el carácter dialógico de la configuración didáctica implementada se diluye en una mayéutica ficticia en la que el profesor toma a su cargo la formulación y la validación. De esta forma, detrás del diálogo efectivo, la sesión de aprendizaje esconde una configuración didáctica magistral, irreflexivamente asumida por el profesor.
Evidentemente, esta distorsión entre las configuraciones didácticas pretendida y efectiva es origen de conflictos. En concreto, un problema didáctico prototípico se da cuando el profesor no es consciente, en el curso del proceso efectivo de enseñanza, de dichas discrepancias y tiene la ilusión de que el proceso se desarrolla en los términos que él había establecido a priori.
El papel de la institucionalización
Al finalizar la primera clase el primer equipo ha escrito en la pizarra una tabla de valores para representar la gráfica de la función, en la que incluye valores negativos para el tiempo.
En la gráfica aparecen marcados el valor de t en que se alcanza la altura máxima, y el valor de dicha altura, (3,2; 51,2).

Pero en cuanto el alumno comienza a explicar la solución el profesor le interrumpe y plantea cuestiones ajenas al trabajo realizado y cuyo interés es meramente formal:
P: ¿Cuál es la variable independiente y la variable dependiente?
El momento de institucionalización de la solución de la tarea de modelización se aborta y en su lugar se institucionalizan nociones imprevistas (variable dependiente, variable independiente). No se aprovecha la interacción para generar y superar un conflicto cognitivo en el alumno (los valores negativos del tiempo), ni para identificar los intervalos de números reales que constituyen el dominio y rango de la función que modeliza el problema de física planteado.
Indoneidad mediacional
En Godino, Contreras y Font (2006) se define la idoneidad mediacional como el grado de disponibilidad y adecuación de los recursos materiales y temporales necesarios para el desarrollo del proceso de enseñanza-aprendizaje. Si el profesor y los alumnos tuvieran a su disposición medios informáticos pertinentes al estudio del tema en cuestión (Cabri, p.e., para la geometría plana), el proceso de estudio que se apoye en estos recursos tendría mayor idoneidad mediacional que otro tradicional basado exclusivamente en la pizarra, lápiz y papel. Asimismo, un ejemplo de un proceso de enseñanza-aprendizaje con un alto grado de idoneidad mediacional con relación a los medios temporales sería una clase magistral, donde el profesor reproduce de manera íntegra y sin interacción con los estudiantes el significado pretendido.
Los recursos materiales pueden ser manipulativos, utilidades informáticas de graficación y cálculo, libros de texto, Estos medios interaccionan con los distintos elementos de las configuraciones epistémicas y cognitivas (tipos de problemas abordables, representaciones, definiciones, proposiciones y argumentaciones). La idoneidad del proceso de estudio se verá afectada positivamente si el profesor y los estudiantes tienen a su alcance los medios materiales mejor adaptados a los significados pretendidos.
En cuanto al tiempo didáctico interesa tener en cuenta no sólo el tiempo presencial colectivo (donde básicamente tiene lugar la enseñanza), sino también el tiempo no presencial, de trabajo individual. La planificación y el desarrollo del proceso de estudio se valorará positivamente si la cantidad y gestión del tiempo dedicado al estudio es adecuado a los objetivos de aprendizaje.
En la enseñanza observada, el profesor podría haber utilizado diversos medios o recursos como dispositivos de ayuda al estudio: por ejemplo, medios de presentación de la información (retroproyector, etc.) o dispositivos de cálculo y graficación (calculadoras, ordenadores). Este hecho, junto a la gran cantidad de tiempo invertido en esta actividad (4 sesiones de 45 minutos), es un indicador de una baja idoneidad mediacional, Una mejor planificación y diseño de la actividad habría economizado el tiempo invertido.
Idoneidad emocional
Diremos que un proceso de estudio tiene idoneidad emocional alta en la medida en que las configuraciones didácticas motiven a la acción y participación a los alumnos; esto supone la creación de un ambiente de trabajo que tiene en cuenta los intereses, afectos y emociones de los alumnos hacia las matemáticas.
La selección de las situaciones – problemas de iniciación o contextualización que pertenezcan al campo de intereses de los alumnos será un factor a tener en cuenta en esta dimensión. La creación de un clima de respeto mutuo y de trabajo cooperativo será un factor positivo para el aprendizaje.
En el ejemplo de enseñanza observada, sin duda la elección de la situación de modelización de espacio recorrido por la pelota lanzada verticalmente hacia arriba aporta significación y relevancia al estudio del tema de las funciones, de donde podemos inferir que los estudiantes podrían adoptar una actitud positiva hacia la tarea y el estudio. Sin embargo, la interferencia de la configuración conjuntista con la empirista introduce una problemática esencialmente dispar respecto del uso genuino de la función como herramienta de previsión. Los estudiantes pueden preguntarse legítimamente, ¿esto para qué sirve?; y ante la ausencia de una respuesta convincente se pueden sentir desmotivados. Por otra parte, se debe valorar positivamente en esta dimensión la fase de trabajo en equipo y la presentación de las soluciones por los propios estudiantes.
Idoneidad ecológica
En la sección 2 hemos definido la idoneidad ecológica como el grado de adaptación del proceso de estudio al proyecto educativo del centro, las directrices curriculares, las condiciones del entorno social-profesional, etc., en que se implementa. También se tendrán en cuenta las conexiones que se establezcan con otros contenidos (significados) intradisciplinares (otros temas de matemáticas) e interdisciplianres (otras materias del programa de estudios.
Puesto que la institución investigada tiene por objetivo la formación inicial de ingenieros, debe asegurar su competencia para su futuro ejercicio profesional. Por este motivo, se considera que un primer criterio (de tipo ecológico) útil para la selección de objetivos y contenidos, que tiene en cuenta tanto los intereses de estudiantes como de la sociedad en su conjunto, es la contextualización sociocultural de la práctica profesional. Un segundo criterio es que los objetos matemáticos estudiados por estos profesionales sean, a ser posible, los nucleares en la disciplina.
En el ejemplo considerado (la enseñanza de las funciones) se cumplen estos dos criterios. La noción de función desempeña un papel esencial dentro de la matemática y en sus aplicaciones prácticas, por ser una herramienta de previsión de los valores de una variable conocidos los valores de otra, u otras variables. Queda, por tanto, plenamente justificada su inclusión en los programas de formación de ingenieros. Sin embargo, una visión más profunda del objeto función revela diversos tipos de prácticas discursivas y operativas, algunas de las cuales, como es el caso de la configuración que hemos descrito como conjuntista, podría no ser imprescindible, dada su generalidad y formalidad. El tiempo requerido para el aprendizaje de las sutilezas que distinguen las correspondencias de las aplicaciones, las definiciones de dominio, rango, codominio, tipos de funciones, etc, no debería ocultar la verdadera utilidad de las funciones como herramientas de modelización y previsión en situaciones tanto externas como internas a las matemáticas.
Reflexiones Finales
En este trabajo hemos descrito la noción de idoneidad didáctica, aplicable a las configuraciones y trayectorias de enseñanza y aprendizaje de contenidos matemáticos específicos. Se trata de un constructo muldimensional, compuesto de seis facetas o dimensiones (epistémica, cognitiva, mediacional, emocional, interaccional y ecológica) mediante las cuales se pretende abordar de manera integral la complejidad de factores que intervienen en el diseño, desarrollo y evaluación de cualquier proceso de estudio matemático. El Enfoque Ontosemiótico de la cognición e instrucción matemática (EOS) proporciona un sistema de supuestos y categorías para hacer operativas las diversas idoneidades parciales, particularmente las correspondientes a las dimensiones epistémica y cognitiva.
La idoneidad didáctica es una herramienta para el análisis y la síntesis didáctica que puede ser útil para la formación de profesores. Como afirman Hiebert, Morris y Glass (2003), un problema persistente en educación matemática es cómo diseñar programas de formación que influyan sobre la naturaleza y calidad de la práctica de los profesores. La ausencia de efectos significativos de los programas de formación de profesores en dicha práctica se puede explicar, en parte, por la falta de un conocimiento base ampliamente compartido sobre la enseñanza y la formación de profesores.
La preparación de programas de formación puede ser más efectiva centrándola en ayudar a los estudiantes a que adquieran las herramientas que necesitarán para aprender a enseñar, en lugar de competencias acabadas sobre una enseñanza efectiva (Hiebert, Morris y Glass, 2003, p. 202).
Pensamos que entre estas herramientas deben figurar los criterios para analizar la propia práctica docente, las lecciones de los textos escolares como fuente próxima para el diseño de unidades didácticas, o experiencias de enseñanza observadas. Consideramos importante introducir en la formación (inicial y continua) de profesores de matemáticas criterios para valorar la idoneidad de los procesos de estudio matemático, tanto si son basados en el uso de libros de texto, como si se trata de procesos apoyados en el uso de materiales y documentos de trabajo elaborados por el propio profesor.
La noción de idoneidad didáctica y las herramientas para su análisis y valoración que introducimos en este trabajo permiten establecer un puente entre una didáctica descriptiva – explicativa y su aplicación para el diseño, implementación y evaluación de intervenciones educativas específicas. En consecuencia, la formación de profesores de matemáticas puede orientarse de manera global y sistemática hacia el análisis y valoración de la idoneidad didáctica de propuestas curriculares, programaciones de aula, así como de experiencias de enseñanza y aprendizaje.
La noción de idoneidad didáctica, y sus seis dimensiones principales epistémica, cognitiva, mediacional, emocional, interaccional y ecológica - permite centrar la atención del análisis didáctico en las interacciones entre los significados institucionales y personales, en el contexto de un proyecto educativo. El profesor necesita tener criterios que le ayuden a dilucidar qué aspectos de su práctica docente puede mejorar, bien en la etapa de diseño, implementación y evaluación.
El análisis epistemológico de los objetos matemáticos, realizado con un enfoque y herramientas conceptuales apropiadas, debe ser un objetivo esencial en la formación del profesor de matemáticas. Hemos visto cómo un objeto matemático tan elemental y aparentemente conocido, como la función, ha planteado grandes complicaciones tanto al profesor como a los estudiantes. Algunas de las complicaciones observadas se derivan, probablemente, de una falta de reflexión del profesor sobre la ruptura brusca que se produce entre las configuraciones informal/ empírica y conjuntistas de las funciones.
Es necesario que los profesores planifiquen la enseñanza teniendo en cuenta los significados institucionales que se pretenden estudiar, adoptando para los mismos una visión amplia, no reducida a los aspectos discursivos (idoneidad epistémica). Asimismo, es necesario diseñar e implementar una trayectoria didáctica que tenga en cuenta los conocimientos iniciales de los estudiantes (idoneidad cognitiva), identificar y resolver los conflictos semióticos que aparecen en todo proceso de estudio, empleando los recursos materiales y temporales necesarios (idoneidad interaccional y mediacional). Estas idoneidades deben ser integradas teniendo en cuenta las interacciones entre las mismas, lo cual requiere hablar de la idoneidad didáctica como criterio sistémico de pertinencia (adecuación al proyecto de enseñanza) de un proceso de instrucción, uno de cuyos indicadores empíricos puede ser la adaptación entre los significados personales logrados por los estudiantes y los significados institucionales pretendidos/ implementados (idoneidad cognitiva).
Reconocimiento:
Trabajo realizado en el marco del proyecto MCYT – FEDER: SEJ2004-00789, Ministerio de Ciencia y Tecnología, Plan Nacional de Investigación Científica, Desarrollo e Innovación Tecnológica. Madrid.
Referencias
1. Artigue, M. (1989). Ingenierie didactique. Recherches en Didactique des Mathématiques, 9 (3): 281–308. [ Links ]
2. Biehler, R. (2005). Reconstruction of meaning as a didactical task –the concept of function as an example. En J. Kilpatrick, C. Hoyles and O. Skovsmose (Eds.), Meaning in Mathematics Education. Springer. [ Links ]
3. Brousseau, G. (1997). Theory of didactical situation in mathematics. Dordrecht: Kluwer. [ Links ]
4. Contreras A., Font, V., Luque, L. y Ordóñez, L. (2005). Algunas aplicaciones de la teoría de las funciones semióticas a la didáctica del análisis. Recherches en Didactique des Mathématiques, 25 (2): 151-186. [ Links ]
5. DAmore, B., Fandiño, M. I. y Marazzani, I. (2003). Ejercicios anticipados y Zona de desarrollo próximo: comportamiento estratégico y lenguaje comunicativo en actividad de resolución de problemas. Epsilon, 57: 357-378. [ Links ]
6. Douady, R. (1986). Jeux de cadres et dialectique outil-objet. Recherches en Didactique des Mathématiques, 7(2), 5-31. [ Links ]
7. Font, V. y Godino, J. D. (en prensa). La noción de configuración epistémica como herramienta de análisis de textos matemáticos: Su uso en la formación de profesores. Educaçao Matemática Pesquisa (aceptado) [ Links ]
8. Font, V. y Ramos, A. B. (2005). Objetos personales matemáticos y didácticos del profesorado y cambio institucional: El caso de la contextualización de funciones en una Facultad de Ciencias Económicas y Sociales. Revista de Educación, 338: 309-346. [ Links ]
9. Gallardo, J. y González, J. L. (2006). El análisis didáctico como metodología de investigación en educación matemática. Ponencia invitada. X Simposio de la SEIEM, Huesca. [ Links ]
10. Godino, J. D. y Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14 (3): 325–355. [ Links ]
11. Godino, J. D. (2002). Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactique des Mathématiques 22, (2/3): 237–284. [ Links ]
12. Godino, J. D., Batanero, C. y Font, V. (2006). Un enfoque ontosemiótico para la Didáctica de las Matemáticas. Departamento de Didáctica de la Matemática. Universidad de Granada. Disponible en Internet: http://www.ugr.es/ local/jgodino [ Links ]
13. Godino, J. D., Batanero, C. y Roa, R. (2005). An onto-semiotic analysis of combinatorial problems and the solving processes by university students. Educational Studies in Mathematics, 60: 3-36. [ Links ]
14. Godino, J. D., Contreras, A. y Font, V. (2006). Análisis de procesos de instrucción basado en el enfoque ontológico-semiótico de la cognición matemática. Recherches en Didactique des Mathématiques, 26 (1): 39-88. [ Links ]
15. Godino, J. D., Font, V. y Wilhelmi, M. R (2006). Análisis ontosemiótico de una lección sobre la suma y la resta. Revista Latinoamericana de Investigación en Matemática Eductiva, 9 (Especial): 133-156. [ Links ]
16. Godino, J. D., Wilhelmi, M. R. y Bencomo, D. (2005). Suitability criteria for a mathematical instruction process: A teaching experience with the function notion. Mediterranean Journal for Research in Mathematics Education, 4.2, 1-26. [ Links ]
17. Gómez, P. (2002). Análisis didáctico y diseño curricular en matemáticas. Revista EMA, 7 (3): 252-292. [ Links ]
18. Hiebert, J., Morris, A. K. y Glass, B. (2003). Learning to learn to teach: An "experiment" model for teaching and teacher preparation in mathematics. Journal of Mathematics Teacher Education, 66: 201-222. [ Links ]
20. NCTM (2000). Principies and standards for school mathematics. Reston. VA: NCTM. [ Links ]
21. Ramos, A. B. y Font, V. (2006). Contexto y contextualización en la enseñanza y el aprendizaje de las matemáticas. Una perspectiva ontosemiótica. La Matematica e la sua didattica (en prensa) [ Links ]
22. Ruiz, L. (1998). La noción de función: Análisis epistemológico y didáctico. Jaén: Publicaciones de la Universidad de Jaén. [ Links ]
23. Sfard, A. (2002). Balancing the unbalanceable: The NCTM Standards in the light of theories of learning mathematics. En J. Kilpatrick, Martin, G., & Schifter, D. (Eds.), A Research Companion for NCTM Standards. Reston, VA: National Council for Teachers of Mathematics. [ Links ]
24. Sierpinska, A. (1992). On understanding the notion of function. En G. Harel and E. Dubinsky (Eds.), The Concept of Function: Aspects of Epistemology and Pedagogy. MAA Notes # 25 (pp. 3–58). Washington, DC: Mathematical Association of America [ Links ]
25. Vergnaud, G. (1990). La théorie des champs conceptuels. Recherches en Didactiques des Mathématiques, 10 (2/3): 133-170. [ Links ]
26. Vygotski, L.S. (1934). El desarrollo de los procesos psicológicos superiores, 2ª edición. Barcelona, ESP: Crítica-Grijalbo, 1989. [ Links ]
27. Youschkevitch, A. P. (1976). The concept of function up to the middle of the 19th century. Archive for History of Exact Sciences, 16: 39–85. [ Links ]
28. Wilhelmi, M. R., Godino, J. D. y Lacasta, E. (en prensa). Configuraciones epistémicas asociadas a la noción de igualdad de números reales. Recherches en Didactique des Mathematiques (aceptado) (Disponible en: http://www.ugr.es/local/jgodino). [ Links ]
29. Wilhelmi M. R., Godino J. D., Font V. (2005). Bases empiriques de modèles théoriques en didactique des mathématiques: réflexions sur la théorie de situations didactiques et le point de vue ontologique et sémiotique. Colloque International «Didactiques: quelles références épistemologiques?». Bordeaux, France: AFIRSE et IUFM dAquitaine. [ Links ]
Notas:
1 Versión ampliada de la ponencia invitada en el X Simposio de la Sociedad Española de Investigación en Educación Matemática (SEEM), Huesca (España), 7-9 Septiembre de 2006.
2 Designamos como «instrucción matemática» - o proceso de estudio matemático - a los procesos de enseñanza y aprendizaje de contenidos matemáticos especifico, organizados en el seno de sistemas didácticos.
3 Segun le diccionario de la RAE, idóneo, «adecuado y para algo». En nuestro caso lo aplicamos no a la competencia o capacidad de una persona para una función o tarea sino al grado en que un proceso de estudio matemático (o una parte del mismo) permite el logro de los fines pretendidos.
4 Análisis similares pueden ser realizados sobre los estándares currículares propuestos más recientemente (NCTM, 2000).
5 Estos trabajos estándisponibles en Internet, http://www.ugr.es/local/jgodino. En godino, Btanero y Font (2006) se presenta una síntesis actualizada del «enfoque ontosemiótico» para la Didáctica de las Matemáticas.
6 Significado pragmático: sistema de prácticas operativas y discursivas.
7 La noción de idoneidad busca valorar las diferencia trayectorias en procesos de estudio efectivos por contraste con procesos de estudios potenciales . En este sentido, supone una reformulación en términos ontosemióticos de los instrumentos de contraste del análisis a priori y el análisis a posteriori propuestos en la metodología de la ingenieria didáctica (Artigue, 1989).
8 Consideramos como «análisis didáctico» el estudio sistemático de los factores que condicionan los procesos de enseñanza y aprendizaje de un contenido curricular - o de aspectos parciales del mismo - con una herramientas teóricas y metodológicas específicas. Gallardo y González (2006) describen dicho análisis como una metodología de investigación educativa (busqueda de fuentes y tipos de información de las distintas áreas de conocimientos implicadas, meta-ánalisis de las investigaciones previas, delimitación de cuestiones abiertas y formulación de conjeturas). Por su parte, Gómez (2002) llama "ánalisis didáctico" a una metodología de diseño, implementación y evaluación de programaciones curriculares de aula en el contexto de la formación de profesores de matemáticas.
9 Un conflito semiótico es cualquier disparidad o discordancia entre los significados atributos a una expresión por dos sujetos (personas o instituciones). Si la disparidad se prduce entre significados institucionales hablamos de conflitos semióticos de tipo epistémico, mientras que si la disparidad se produce entre prácticas que forman el significado personal de un mismo sujeto los designamos como conflitos semióticos de tipo cognitivo. Cuando la disparidad se produce entres las prácticas (discursivas y operativas) de dos sujetos diferentes en interacción comunicativa (por ejemplo, alumno-alumno o alumno-profesor) hablaremos de conflitos (semióticos) interaccionales
10 Parece deable suponer que el «proyecto educativo» asume unos principios educativos en concordancia, por ejemplo, con los descritos por el NCTM (2000) (equidad, uso de tecnología, etc.), pero la nación de idoneidad es independiente de los fines y principios asumidos.
11 D' Amore, Fandiño y Marazzani (2003) proponen clasificar los problemas contetextualizados en función del momento en que se proponen a los alumnos. Se pueden proponer, por ejemplo, a continuación de un proceso de instrucción en el que se han enseñado los objetivos matemáticos adquiridos y, por otra parte, para que los alumnos vean las aplicaciones de las matemáticas al mundo real. A este tipo de problemas, Ramos y Font (en prensa) les llaman problemas contextualizados evocados de aplicación si son relativamente sencillos o problemas contextualizados evocados de consolidación cuando su resolución resulte más compleja. En ambos casos, se trata fundamentalmente de aplicar los conocimientos matemáticos adquiridos previamente en el proceso de instrucción.
12 En una institución de enseñanza concreta el significado de referencia será una parte del significado holístico del objeto matemático. La determinación de dicho significado global requiere realizar un estudio histórico - epistemológico sobre el origen y evolución del objeto en cuestión, así como tener en cuenta la diversidad de contextos de uso donde se pone en juego dicho objeto.
13 En Teoría de Sustitución Didácticas (Brousseau, 1997), estas situaciones-problemas implican la defición de un medio adidáctico que actúe de manera antagonista a las acciones de los alumnos, así como la defición de un conjunto de variables didácticas que el profesor pueda manipular arbitrariamente para devolver la responsabilidad matemática a los alumnos.
14 La necesidad de estructura que plantea Sfard (2002) para los conocimientos matemáticos: «While seeing structure is helpful in any domain of knowledge, in mathematics it may be the very essence of learning » (p.8)
15 No nos referimos aquí a la llamada "atención a la diversidad", sino a la dualidad institucional - personal de los objetos matemáticos, que determina la necesidad de contemplar en los currículos instrumentos de valoración tanto de los significados institucionales como personales.
16 En Godino, Contreras y Font (en prensa) designamos esta dimensión como « idoneidad semiótica » Preferimos ahora designarla como mediacional ya que el componente semiótico está presente tambien en la deficinión de las idoneidades epistémica y congnitiva. En Godino, Wilhelmi y Bencomo (2005) se agrupa esta dimensión con la mediacional y se designan conjuntamente como «idoneidad instruccional ».
LOS AUTORES
Juan D. Godino, Universidad de Granada (España), Departamento de Didáctica de la Matemática, Línea de investigación: Fundamentos teóricos y metodológicos de la investigación en Didáctica de la Matemática. jgodino@ugr.es
Vicenç Font, Universitat de Barcelona (España), Facultat de Formació del Professorat, Departament de Didàctica de les Ciències Experimentals i la Matemàtica. Línea de investigación: Fundamentos teóricos y metodológicos de la investigación en Didáctica de la Matemática. vicencfont@menta.net
Miguel R. Wilhelmi, Universidad Pública de Navarra (España), Departamento de Matemáticas e Informática. Profesor Ayudante. Línea, Fundamentos teóricos y metodológicos de la investigación en Didáctica de la Matemática. miguelr.wilhelmi@unavarra.es
Delisa Egleé Bencomo Moncada,Universidad Nacional Experimental de Guayana (UNEG). Área de Matemática del Departamento de Ciencia y Tecnología. Docente investigador. Teoría y Método de investigación matemática. dbencomo@uneg.edu.ve













