EFECTOS DE LOS CAMPOS MAGNÉTICOS SOBRE EL CRECIMIENTO DE Saccharomyces cerevisiae

José E. Zapata M., Germán Moreno O. y Edna J. Márquez F.

José E. Zapata M. Ingeniero Químico. M.Sc. en Biotecnología. Profesor, Departamento de Alimentos, Facultad de Química Farmacéutica, Universidad de Antioquia, Colombia. Dirección: A.A. 1226, Medellín, Colombia. e-mail: joseedgar@epm.net.co.

Germán Moreno O. Ingeniero Electricista. M.Sc. y D.Sc. en Ingeniería Eléctrica. Profesor, Departamento de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia, Colombia. e-mail: gmoreno@jaibana.udea.edu.co.

Edna J. Márquez F. Bióloga. M.Sc. en Genética. Profesora, Departamento de Biología, Facultad de Ciencias, Universidad Nacional de Colombia, Medellín, Colombia. e-mail: ejmarque@perseus. unalmed. edu.co.

Resumen

Cultivos de Saccharomyces cerevisiae fueron sometidos al efecto de campos magnéticos variables de alta frecuencia (hasta 100kHz) y bajas densidades de flujo (hasta 620mG). Se aplicó la metodología estadística de superficies de respuesta para evaluar en qué rangos de las variables densidad de campo, frecuencia y tiempo de aplicación, se obtenían efectos significativos sobre la concentración celular (CB). En los valores de las variables predichos como significativos por los modelos obtenidos de las superficies de respuesta, se hicieron comparaciones entre el crecimiento del cultivo a diferentes densidades de flujo, tiempos de exposición al campo y frecuencias, para evaluar el comportamiento de la CB ante la modificación de una sola variable a la vez. Se utilizó el método de la mínima diferencia significativa (LSD) para comparar los resultados de los ensayos correspondientes a cada variable. Los resultados mostraron que se puede estimular el crecimiento del cultivo tratado con campos magnéticos, cuando se utilizan campos con densidades de flujo de 20mG, frecuencias de 100kHz y tiempos de aplicación de 30s. Los porcentajes de estimulación obtenidos con este tratamiento fueron del 30% con respecto a un cultivo control.

Summary

Cultures of Saccharomyces cerevisiae were submitted to magnetic fields of high frequency (up to 100kHz) and low flux density (up to 620mG). Statistical designs of response surfaces were used to assess the ranges in which flux density, frequency and application time produce significant effects on cell concentration (CB). In the values of the variables predicted as significant by the models derived from this methodology, comparisons were performed among cell growths under diverse flux densities, exposition to field durations and field frequencies in order to assess the CB behavior for one variable at a time. The least significant difference (LSD) method was used to compare test results corresponding to each variable. The results showed that it is possible to stimulate the culture growth under magnetic fields by applying flux densities of 20mG, frequencies of 100kHz and application times of 30s. The stimulation reached 30% with reference to a control culture.

Resumo

Cultivos de Saccharomyces cerevisiae foram submetidos ao efeito de campos magnéticos variáveis de alta frequência (até 100kHz) e baixas densidades de fluxo (até 620mG). Aplicou-se a metodologia estatística de superfícies de resposta para avaliar em que faixas das variáveis densidade de campo, frequência e tempo de aplicação, se obtinham efeitos significativos sobre a concentração celular (CB). Nos valores das variáveis preditos como significativos pelos modelos obtidos das superficies de resposta, fizeram-se comparações entre o crescimento do cultivo a diferentes densidades de fluxo, tempos de exposição ao campo e frequências, para avaliar o comportamento CB diante da modificação de uma só variável por vez. Utilizou-se o método da mínima diferença significativa (LSD) para comparar os resultados dos ensaios correspondentes a cada variável. Os resultados mostraram que se pode estimular o crescimento do cultivo tratado com campos magnéticos, quando se utilizam campos com densidades de fluxo de 20mG, frequências de 100kHz e tempos de aplicação de 30s. As percentagens de estimulação obtidas com este tratamento foram de 30% com respeito a um cultivo controle.

PALABRAS CLAVE / Campos Magnéticos / Crecimiento de Hongos / Saccharomyces cerevisiae /

Recibido: 06/03/2002. Modificado: 02/08/2002. Aceptado: 13/08/2002

Introducción

Las variables más importantes en cualquier proceso biotecnológico y que requieren ser controladas para el buen desempeño de los organismos implicados son, entre otras, temperatura, pH, concentración de nutrientes, presión, luminosidad, grado de agitación y concentración de O2. Además, cualquier cuerpo sobre la faz de la tierra, está sometido al efecto de otras variables menos tangibles, pero igualmente importantes, como los campos electromagnéticos (Polk y Postow, 1986; Ueno y Harada, 1982).

El efecto que los campos electromagnéticos ejercen sobre el crecimiento celular ha sido estudiado desde el punto de vista biofísico, pero su aplicación a la biotecnología no se ha estudiado de forma profunda; sólo en la última década algunos estudios se han dedicado a microorganismos de interés biotecnológico (Hirano et al., 1998; Jung y Sofer, 1997; Phillip et al. 1997; Ruzic et al. 1998; Goldsworthy et al., 1999).

Los campos electromagnéticos afectan la dirección de la migración (Blakemore y Frankel, 1981; Farina et al., 1982, 1983; Mottas y Lins, 1986; Adamkiewicz et al., 1987) y alteran el crecimiento y la reproducción de los microorganismos (Jennison, 1937; Kimball, 1938; Moore, 1979), causan cambios en la síntesis de ADN (Liboff et al., 1984), en la orientación de biomoléculas y biomembranas (Maret y Dransfeld, 1977) y alteran el flujo de iones a través de la membrana plasmática (Conti et al. 1985; Collis y Segal, 1988), generando como resultado neto una modificación en la velocidad de reproducción celular (Gerencser et al., 1962; Pothakamury et al., 1993a; Goldsworthy et al., 1999).

El efecto que generan los campos magnéticos sobre el crecimiento celular se puede clasificar (Pothakamury et al., 1993b) en inhibitorio, estimulatorio o no observable. Los efectos de estimulación o inhibición de los campos magnéticos se han atribuido a cambios en la orientación de las biomoléculas (proteínas), cambios en las biomembranas (lipídicas y plasmáticas), alteraciones del flujo de iones a través de la membrana plasmática y/o cambios en la estructura de las biomoléculas (Pothakamury et al., 1993a).

Con base en el conocimiento del efecto que los campos magnéticos ejercen sobre los microorganismos, resulta de interés desarrollar sistemas que, haciendo uso de los campos electromagnéticos, estimulen el crecimiento de microorganismos de importancia industrial, lo que podría redundar en la disminución de los tiempos de fermentación, aumento en los rendimientos y disminución de costos en procesos como la producción de cerveza, vino, pan, derivados lácteos, productos farmacéuticos, enzimas, entre muchos otros.

Por otro lado, los campos electromagnéticos pueden usarse para inhibir el crecimiento de los microorganismos, lo que se presenta como una posibilidad para la conservación de alimentos, al eliminar los microorganismos presentes en ellos y que pueden alterarlos (Gerencser et al., 1962; Van Nostran et al., 1967; Pothakamury et al., 1993a, b; Mertens y Knorr, 1992; Dallas, 1997).

Los mecanismos por los cuales los campos magnéticos afectan el desarrollo de los microorganismos están sin esclarecer completamente, pero se interpreta que se desarrollan por efecto sobre la membrana plasmática, con posibles repercusiones metabólicas y acción directa sobre las partículas coloidales del medio de cultivo. Se han propuesto varias teorías para explicar el efecto de los campos magnéticos débiles sobre los organismos y todas hacen mención de un fenómeno denominado la resonancia del ciclotrón, como uno de los responsables de dichos efectos (Liboff, 1985; Pothakamury et al., 1993a; Goldsworthy et al., 1999). Los campos magnéticos pueden activar las partículas coloidales del medio de cultivo, haciendo que estas remuevan parte del Ca unido a los fosfolípidos de las membranas plasmáticas, incrementando su permeabilidad y de esta forma, afectando el crecimiento de los microorganismos (Goldsworthy et al., 1999).

Según Baker y Judd (1996), el mejor efecto sobre las partículas coloidales se obtiene cuando el medio líquido se hace pasar varias veces a través del dispositivo generador de campo, pero estos dispositivos utilizan densidades de flujo magnético relativamente altas (0,01-0,5T), lo cual presenta limitaciones económicas. La forma de eliminar este problema, es usando una bobina alrededor del tubo con el medio a tratar y aplicando una señal de corriente alterna, la cual genera sobre un medio estático el mismo efecto que si el medio se estuviera moviendo con respecto al dispositivo generador del campo (Goldsworthy et al., 1999).

En el presente trabajo se estudió el efecto de campos magnéticos de densidad de flujo baja y alta frecuencia (hasta 100kHz), sobre un cultivo de Saccharomyces cerevisiae, usando diferentes tiempos de exposición.

Materiales y Métodos

Microbiológicos

La cepa. Se utilizó una cepa holandesa de Saccharomyces uvarum, código 1320 de Laboratorios Alfred Jorgesen. Saccharomyces uvarum está clasificada como una raza fisiológica de Saccharomyces cerevisiae (Bourgeois y Larpent, 1995). Se cultivó a 30ºC y pH de 5,0.

El medio de cultivo. La cepa inicial fue cultivada en agar Sabouraud sólido al 4% y mantenida a 4ºC en tubos cerrados. Para los diferentes ensayos con campos magnéticos se tomaron inóculos de este medio sólido y se inocularon medios líquidos previamente esterilizados en autoclave a 121ºC durante 15min. El medio líquido usado contiene (% p/p): Glucosa 10; KH2PO4 0,2; (NH4)SO4 0,3; MgSO47H2O 0,1; extracto de levadura 0,4; peptona 0,36.

Determinación de la concentración celular. Se adoptó el método de peso seco (Garcia et al., 1991) para realizar el recuento celular en todos los ensayos.

Condiciones de cultivo. Para los cultivos en los ensayos con campos magnéticos, se partió de los microorganismos en los tubos en agar Saboureaud sólido, de éstos se tomaron varias azadas y se colocaron en 100ml de medio líquido con la composición mencionada, el cual se dejó cultivando a 30ºC por 24h. El medio líquido inoculado se diluyó en medio fresco, hasta llevar su absorbancia a un valor entre 0,15-0,2 y se repartió en tubos plásticos de 50ml, los cuales se sometieron a los campos magnéticos y se dejaron creciendo entre 15-18h, después de las cuales se les evaluó la concentración celular por medio del método de peso seco.

Para el tratamiento con campos magnéticos se usaron tubos plásticos de 50ml, estériles, en los que se colocó el inóculo en medio líquido. Los tubos permanecieron tapados durante el tratamiento magnético en las bobinas y, durante el tiempo de incubación posterior, el cierre no fue hermético para evitar la anaerobiosis en su interior.

Magnéticos

El sistema para generación de campos magnéticos consta de dos componentes principales, el generador de señal y el sistema de bobinas. La medición del campo se realizó con un Gausimetro marca F.W. Bell, modelo 9550, de efecto Hall.

Generador de señal. La señal eléctrica usada para alimentar las bobinas se basó en el sistema propuesto por Goldsworthy et al. (1999), con algunas modificaciones. El generador entregó una onda cuadrada de amplitud pico-pico variable de 0-25V, con frecuencia entre 10-120kHz, la cual fue modulada en amplitud por otra onda cuadrada de frecuencia entre 0-3kHz. La señal, la cual se monitoreó con un osciloscopio, se liberaba como una serie de pulsos con una relación marca:espacio 1:1 y con una frecuencia de repetición definido por la onda moduladora de 1kHz. Esta señal se generó modulando ondas cuadradas de 10, 50, 70, 80 ó 100kHz, con otra onda cuadrada de 1kHz. La amplitud fue variable, dependiendo de la densidad de flujo usada en cada caso. La señal se entregaba a una bobina en el interior de la cual se colocaba un tubo plástico con el cultivo de levadura, por un tiempo definido, entre 30 y 300s.

Diseño de las Bobinas. Se diseñaron bobinas para 10, 50, 60, 70, 80 y 100kHz, las cuales se elaboraron en alambre trenzado, con un tubo de cartón como soporte, un diámetro interior de 3,8cm, altura de 10cm y núcleo de aire, en el interior del cual se colocó el cultivo microbiano durante el tratamiento con campos magnéticos. Se diseñaron bobinas para cada frecuencia con el objetivo de poder aplicar el teorema de la máxima transferencia de potencia y de esa forma conseguir el mejor comportamiento del equipo generador de señal (Giacoletto, 1977). Las dimensiones de las bobinas se definieron con base en las dimensiones de los tubos plásticos usados para contener el cultivo durante la aplicación del campo, buscando que el cultivo se ubicara en la región donde el campo es más uniforme, es decir el centro geométrico del cilindro conformado por la bobina (Kaufman y Seidman, 1982). Por está razón se presentó la necesidad de colocar varias capas en algunas bobinas, en las que el número de vueltas fue muy grande. Las bobinas se construyeron con alambre trenzado de dos o tres hilos, según el calibre usado (19-22).

Diseños experimentales

Las variables que se evaluaron en este estudio, desde el punto de vista electromagnético fueron: La densidad de flujo del campo aplicado (ó densidad de campo), la frecuencia del mismo y el tiempo de aplicación del tratamiento. 

Para buscar los rangos de valores de estas variables en los que se produjera algún efecto sobre el crecimiento de S. cerevisiae, se adoptaron dos diseños experimentales de forma consecutiva, centrando el estudio en los intervalos que presentaran mayor concentración celular (CB) en el cultivo. Se realizaron dos diseños Factorial Central Compuesto, en los cuales se evaluó el efecto de los factores (densidad de flujo de campo 120-620mG; frecuencia 10-100kHz y tiempo 30-300s) sobre la CB. En estos diseños se usó el software estadístico ESTAT-EASE, cada diseño Factorial Central Compuesto se hizo por duplicado. Los datos experimentales obtenidos de estos diseños factoriales, se ajustaron a un polinomio de la forma de la ecuación 1 (Montgomery, 1991)

                                        CB=a0+a1X1+a2X2+a3X3+

                                        a12X1X2+a13X1X3+a23X2X3+

                                        a123X1X2X3+a11X12+a111X13+

                                        a22X22+a222X23+a33X32+a333X33

(1)

donde los a, son las constantes de ajuste y X1, X2 y X3, son variables codificadas para densidad de flujo de campo, frecuencia y tiempo, respectivamente. La codificación de las variables se realiza según la ecuación

(2)

donde Ci, Cih y Cil son los factores en el valor dado, alto y bajo respectivamente.

Al modelo obtenido de cada diseño, se le aplicó un proceso de optimización para maximizar el valor de la respuesta (CB), y con base en ese resultado se intentó localizar las combinaciones de las variables que mejor respuesta entregaran en el rango evaluado.

En la región que mejores resultados se obtuvo para la CB, se hicieron gráficas de barras, para observar el efecto individual de cada una de las variables sobre la variable respuesta. La comparación entre las barras de una misma gráfica se hizo usando el método de la mínima diferencia significativa LSD (Montgomery, 1991), por medio del software estadístico Statgraphics.

Resultados y Discusión

Secuencia de diseños de experimentos

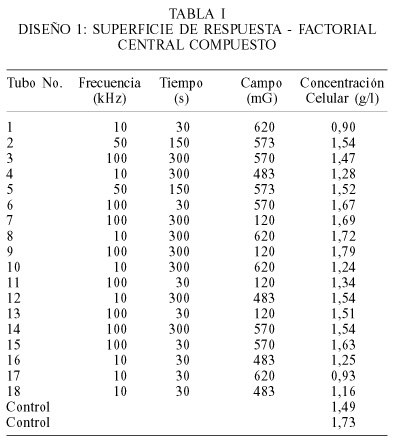
Diseño 1: Primera aproximación al problema. Se planteó un diseño de experimento con superficies de respuesta, en el cual se utilizó como factores la frecuencia, el tiempo y la densidad de campo, y la variable respuesta fue la concentración celular (CB). Los niveles de cada factor fueron frecuencia (10-100kHz), tiempo (30-300s) y densidad de campo (120-620mG). En la Tabla I se presenta el diseño Factorial Central Compuesto, con las corridas en forma aleatoria. Los resultados del análisis de varianza del diseño 1 se presentan en la Tabla II, donde los coeficientes corresponden a los factores en términos de sus valores codificados.

En el análisis de varianza del diseño 1 (Tabla II), el valor del coeficiente de variación (10,25%) denota que los valores de la respuesta no se encuentran muy dispersos con respecto a la media. Se observa que la frecuencia tiene un efecto positivo estadísticamente significativo (P= 0,0032) sobre la respuesta, consecuente con lo reportado por Goldsworthy et al. (1999), quienes afirman que la componente de alta frecuencia en la onda modulada es muy importante, debido a los bajos niveles de campo usados, porque el rápido movimiento de la onda compensa el muy bajo valor de densidad de campo. Esto se evidencia en el trabajo de Chibowski et al. (1994) el cual demostró que la utilización de ondas RF puede activar partículas coloidales de CaCO3.

En la Tabla II también se observa una interacción negativa significativa (P= 0,0119) entre la frecuencia y el tiempo, es decir si se utilizan frecuencias altas y tiempos altos se podrían generar efectos negativos sobre el crecimiento celular, similar a lo reportado por Goldsworthy et al. (1999). Para la interacción positiva entre el tiempo y el término cuadrático del campo (P= 0,0434) es difícil hacer una inferencia en esta parte del estudio. Además, se ha encontrado en otros tipos de células (fibroblastos humanos) que la interacción entre la frecuencia y la densidad de campo puede tener un efecto positivo pero saturable (Liboff et al., 1984).

La optimización del modelo del diseño 1, para maximizar el valor de CB como función objetivo, entregó los resultados presentados en la Tabla III, donde se presentan varios resultados de óoptimos locales con diferentes valores para la respuesta máxima. Ya que varios de los óptimos locales y el máximo de ellos, se obtuvieron con una frecuencia de 100kHz, en la Figura 1 se presenta la respuesta gráfica tridimensional del modelo fijando la frecuencia en 100kHz. En esta Figura y la Tabla III se observa que el modelo predice un valor máximo de la respuesta (CB), cuando el tiempo de exposición es de 30s y se trabaja en las proximidades de 390mG como densidad de flujo de campo aplicado.

Figura 1. Superficie de Respuesta del Factorial Central Compuesto (Diseño 1). Concentración celular en función de la densidad de campo y del tiempo, a una frecuencia de 100kHz.

Teniendo en cuenta que las soluciones 1 y 2 de la Tabla III son las mejores y ambas presentan un valor de frecuencia de 100kHz, se definió esta frecuencia para los ensayos posteriores y se evaluó el comportamiento de las otras dos variables (campo y tiempo). Por ello se diseñó un segundo grupo de experimentos, que evaluaría el comportamiento de la respuesta en un rango más estrecho de las variables campo y tiempo. El rango de valores de campo a evaluar, estaría un poco por debajo del valor predicho en el proceso de maximización, consecuente con lo observado por Goldsworthy et al. (1999), quienes recomiendan valores de campo muy bajos cuando se está trabajando con frecuencias altas, si se quiere obtener estimulación del crecimiento del cultivo de S. cerevisiae; además, las soluciones 2 y 3 de la Tabla III, predijeron valores óptimos de la respuesta usando valores de campo en el límite inferior del rango evaluado.

Diseño 2: Evaluación del efecto del tiempo y de la densidad de flujo del campo, con frecuencia constante de 100kHz. Se planteó un diseño de experimento con superficies de respuesta, en el cual se utilizó como factores el tiempo y la densidad de campo y la variable respuesta fue CB. Los niveles de cada factor fueron tiempo (30-300s) y densidad de campo (60-180mG). El diseño 2 con las corridas en forma aleatoria se presenta en la Tabla IV y el análisis de varianza de este diseño en la Tabla V. Los coeficientes en esta Tabla corresponden a los factores en términos de sus valores codificados.

En la Tabla V, el valor del coeficiente de variación (10,33%) denota que los valores de la respuesta no se encuentran muy dispersos con respecto a la media. No se observa un efecto significativo del tiempo ni del campo, como variables individuales, pero sí se presenta un efecto positivo de la interacción de estos dos factores (P= 0,0887), la cual tiene una acción limitada debido a que la interacción entre el término cuadrático del campo y el tiempo tiene un efecto negativo (P= 0,0243).

La optimización del modelo del diseño 2, para maximizar el valor de CB como función objetivo, generó los resultados presentados en la Tabla VI, que presenta varios resultados de óptimos locales, con diferentes valores para la respuesta máxima. En la Figura 2 se presenta la superficie de respuesta tridimensional del diseño 2. En ella se aprecia que los valores máximos de respuesta se obtendrían en el límite inferior tanto de valores de campo como de tiempo. Ello sugiere que se podría encontrar mejores resultados usando valores de campo y de tiempo en ese punto o aun menores. Se debe resaltar que el tiempo obtenido para los máximos locales, tanto en el diseño 1 como en el diseño 2 (Tablas III y VI), correspondió a 30s, lo cual es consecuente con lo reportado por Goldsworthy et al. (1999).

Figura 2. Superficie de respuesta del Factorial Central Compuesto (Diseño 2). Concentración celular en función de la densidad de campo y del tiempo, a una frecuencia de 100 kHz.

La diversidad de soluciones entregadas en la optimización de los diseños 1 y 2 (Tablas III y VI) denota que existen diferentes combinaciones de las variables que pueden entregar resultados de estimulación del crecimiento de la S. Cerevisiae. En este trabajo se pretende encontrar una de las combinaciones, pero se debe tener en cuenta que no es la única.

Se planteó un nuevo diseño de experimentos (diseño 3) que cubriera los valores correspondientes a los óptimos locales del diseño 2, manteniendo el valor de frecuencia en 100kHz. Los resultados del diseño 3 (no mostrados), entregaron un R2= 0,2816 y coeficiente de variación CV= 21,69. Dichos resultados mostraron un efecto del campo en los términos lineal, cuadrático y cúbico, y no mostraron efecto del tiempo en el rango evaluado. Debido al bajo R2 y al alto CV, estos resultados no permiten definir condiciones concluyentes, por lo cual se decidió evaluar el efecto único de cada variable manteniendo las otras dos fijas.

Efecto de la densidad de flujo del campo aplicado sobre el crecimiento de S. cerevisiae

En la Figura 3 se presentan los valores promedio del crecimiento celular a diferentes densidades de flujo. Cada concentración celular de la Figura 3, corresponde al promedio de 3 valores. Se observa que el campo de 20mG tiene un efecto marcado sobre el crecimiento del cultivo, con un porcentaje de células extra de 30% con respecto al cultivo control (0mG).

Figura 3. Concentración celular de S. cerevisiae en función de la densidad de flujo magnético, con un campo de 100 kHz aplicado por 30 s.

Al aplicar el método de la mínima diferencia significativa (LSD) a los resultados de la Figura 3, se encontró que el tratamiento con 20mG, presenta un crecimiento del cultivo mayor que todos los demás (significativo al 95% de confianza), excepto el tratamiento de 100mG. Este comportamiento de la respuesta con respecto a la variable campo, permite inferir que estos valores solo son máximos locales y que pueden encontrarse otros máximos en otros rangos. Por otra parte, demuestra la dependencia no lineal de la respuesta con respecto al campo, similar a lo reportado por varios autores (Kimball, 1938; Moore, 1979; Galar y Martínez, 1985; Hirano et al., 1998; Goldsworthy et al., 1999) y a lo observado en los diseños 1 y 2.

Estos resultados con tan bajos valores en la densidad de campo representan un avance en el estudio de la estimulación del desarrollo de cultivos microbianos con campos magnéticos, ya que la gran mayoría de los estudios reportados en la literatura utilizan campos de densidad media y alta (Kimball, 1938; Gerencser et al., 1962; Van Nostran et al., 1967; Maret y Dransfeld, 1977; Moore, 1979; Dihel et al., 1985; Galar y Martínez, 1985; Aoki et al., 1990; Malko et al., 1994; Jung y Sofer, 1997; Hirano et al., 1998). La utilización de campos de extremadamente baja densidad posibilita la utilización de esta tecnología en sistemas de cultivo de mayor tamaño, sin que el costo de los dispositivos necesarios se incremente considerablemente.

Efecto del tiempo de aplicación del campo sobre el crecimiento de S. cerevisiae

En la Figura 4 se presentan resultados de la evaluación del efecto del tiempo de tratamiento magnético sobre el crecimiento del cultivo. Cada concentración celular de la Figura 4, corresponde al promedio de 3 o más valores. Se observa que el tratamiento con 30s de aplicación del campo tiene el mayor efecto positivo sobre el crecimiento del cultivo de S. cerevisiae (significativo al 95% de confianza por el método LSD).

Figura 4. Concentración Celular en función del tiempo de aplicación de un campo de 20 mG y 100 kHz.

Este resultado corrobora lo predicho con los diseños experimentales 1 y 2, en los cuales la maximización de los respectivos modelos siempre entregó como óptimo local un tiempo de 30s. Además es similar al reportado en la literatura para un tratamiento con un campo magnético de esta misma naturaleza (Goldsworthy et al., 1999). Los bajos valores en el tiempo de aplicación del campo se explican porque la activación de las partículas coloidales por campos magnéticos es un fenómeno que permanece en el tiempo, incluso varias horas después de terminada la exposición (Higashitani et al., 1992; Chibowski et al., 1994).

Estos resultados en tan cortos tiempos de exposición, representan un avance en el estudio de la estimulación del desarrollo de cultivos microbianos con campos magnéticos, ya que la gran mayoría de los estudios reportados en la literatura (ver referencias del apartado anterior) utilizan tiempos de exposición del orden de minutos e incluso horas. La utilización de tiempos tan cortos de exposición facilita el diseño de los equipos de tratamiento con campos magnéticos, permitiendo incluso que se apliquen en sistemas de tuberías con velocidades de flujo líquido moderadas (Baker y Judd, 1996).

Efecto de la frecuencia de oscilación del campo sobre el crecimiento de S. cerevisiae

Se comparó el crecimiento celular presentado por los cultivos sometidos al efecto de campos magnéticos de diferentes frecuencias, todos con un tiempo de exposición de 30s y una densidad de campo de 20mG (ensayo A). Adicionalmente, se escogieron aleatoriamente otras condiciones de trabajo diferentes, y se evaluó el mismo efecto para observar si la respuesta tenía un comportamiento similar. Las otras condiciones de trabajo fueron un campo de 162mG, un tiempo de exposición de 60s y una concentración de inóculo inicial mayor que el usado normalmente (ensayo B). Los resultados de estos ensayos se presentan en la Figura 5, en la cual cada uno de los valores de concentración celular corresponden al promedio de tres valores.

Figura 5. Concentración celular en función de la frecuencia del campo aplicado, para dos densidades de flujo y tiempos diferentes

En la Figura 5 se observa que en el ensayo A, en todos los casos excepto en 70kHz, las condiciones del tratamiento generan estimulación del crecimiento del cultivo con respecto a los controles, es decir se presentan porcentajes de células extra positivos; mientras que en el ensayo B, todos los tratamientos magnéticos generan inhibición del crecimiento del cultivo con respecto a los controles. Se debe resaltar el hecho de que, aunque un tratamiento es inhibitorio (B) y el otro estimulatorio (A), los dos ensayos tienen el mismo patrón de comportamiento del crecimiento con respecto a la frecuencia, es decir, en los dos tratamientos la frecuencia que mayor crecimiento permite con respecto a los controles, es la de 100kHz, seguida por la de 50kHz y en ambos casos la frecuencia de 70kHz, fue la que menor crecimiento permitió.

La similitud de la respuesta gráfica de los ensayos A y B permite inferir que los aumentos de frecuencia tienden a aumentar el valor de la concentración celular de la levadura, consecuente con lo observado en el diseño 1 y con algunos reportes de literatura. Galar y Martínez (1985), encontraron que campos magnéticos con frecuencias de 120, 60 y 0Hz tenían efectos diferentes sobre el crecimiento de S. cerevisiae, siendo estimulatorios, inhibitorios y nulos, respectivamente. Moore (1979), trabajó con 5 tipos de bacterias y una levadura, y encontró que al aumentar la frecuencia del campo magnético aplicado desde 0 hasta 0,3Hz se pueden obtener niveles de estimulación del cultivo.

El efecto que tiene la frecuencia sobre el crecimiento de S. cerevisiae, está asociado con el efecto que genera sobre las partículas coloidales en el medio de cultivo, fundamentado en el fenómeno denominado resonancia del ciclotrón, el cual puede generar una cascada de respuesta en el sistema metabólico celular, después de que los iones circundantes han interactuado con la membrana por acción de un campo magnético externo sobre el sistema de cultivo (Liboff, 1985). La utilización de frecuencias en el orden de 100kHz, permite que los valores de densidad de campo usados puedan ser muy bajos, siendo particularmente importante la componente interna de la onda, por ser la de mayor frecuencia (Chibowski et al., 1994; Goldsworthy et al., 1999).

Conclusiones

- El crecimiento de S. cerevisiae es afectado al exponerla a un campo magnético variable. El efecto que genera el campo depende de su densidad, frecuencia y del tiempo de exposición, y puede ser para estimular el crecimiento o para inhibirlo. En los rangos evaluados en este trabajo la mejor combinación de las variables para estimular el crecimiento se encuentra en 20mG, 100kHz y 30s.

- Estos tres factores, siendo importantes como variables independientes, pueden también generar interacciones importantes entre ellas, que repercutan en el crecimiento de S. cerevisiae.

- La posibilidad de obtener efectos con densidades de campo extremadamente bajas y tiempos de exposición muy cortos pone de manifiesto la potencialidad que tiene este tipo de tecnologías, de ser escaladas a niveles de producción industrial, dado que los dispositivos que se requerirían no tendrían grandes consumos de energía, ni tamaños exageradamente grandes.

- Se debe tener en cuenta que los resultados obtenidos en este trabajo, corresponden a una combinación, entre varias posibles de las variables estudiadas, que pueden generar efectos sobre el crecimiento de la S. cerevisiae.

AGRADECIMIENTOS

Los autores agradecen al CINDEC, Universidad Nacional de Colombia, por la financiación, y a la Facultad de Ciencias de la Universidad Nacional y al Departamento de Alimentos de la Universidad de Antioquia por el apoyo logístico.

REFENCIAS

1. Adamkiewicz VW, Bassous C, Morency D, Lorranin P, Lepage JL (1987) Magnetic response in cultures of Streptococcus mutans ATCC-27607. Exper. Biol. 46: 127-132.        [ Links ]

2. Aoki H, Yamazaki H, Yoshino T, Akagi T (1990) Effects of static magnetic fields on membrane permeability of a culture cell line. Res. Comm. Chem. Pathol. Pharmacol. 69: 103-106.        [ Links ]

3. Baker JS, Judd SJ (1996) Magnetic amelioration of scale formation. Water Res. 30: 247-260.        [ Links ]

4. Blakemore R, Frankel R (1981) Magnetic navigation in bacteria. Scientific American 245: 58.        [ Links ]

5. Bourgeois CM, Larpent JP (1995) Microbiología Alimentaria. Editorial Acribia. Zaragoza. España. 366 pp.        [ Links ]

6. Chibowski E, Holysz L, Wójcik W (1994) Changes in zeta potential and surface free energy of calcium carbonate due to exposure to radiofrequency electric fields. Physicochemi. Eng. Aspects 92: 79-85.        [ Links ]

7. Collis CS, Segal MB (1988) Effects of pulsed electromagnetic fields on Na+ fluxes across stripped rabbit colon epithelium. J. Appl. Physiol. 65: 124-130.        [ Links ]

8. Conti P, Gigante GE, Alesse E, Fieschi C, Reale M, Angeletti PU (1985) A role for Ca2+ in the effect of low frecuency electromagnetic fields on the blastogenesis of human lymphocytes. FEBS Lett. 181: 28-32.        [ Links ]

9. Dallas G (1997) Minimally Processed Fruits and Vegetables: Reducing Microbial Load by Nonthermal Physical Treatments. Food Technol. 51: 66.        [ Links ]

10. Dihel L, Smith J, Middaugh R (1985) Effects of extremely low frequency electromagnetic fields on the cell division rate and plasma membrane of Paramecium tetraurelia. Bioelectromagnetics 6: 61-71.        [ Links ]

11. Farina M, Lins H, Mottas D y Danon J (1982) Microorganismes magnetotactiques de la region de Rio de Janeiro. Centro Brasilero de Pesquisas Físicas-CBPF-039. Rio de Janeiro, Brasil. pp. 1-5.        [ Links ]

12. Farina M, Lins H, Mottas D, Danon J (1983) Electron microscopy and ultrastructure of a magnetic microorganism. Centro Brasilero de Pesquisas Físicas-CBPF-022. Rio de Janeiro. Brasil. pp. 1-5.        [ Links ]

13. Galar I, Martínez S (1985) Efectos de campos magnéticos variables sobre el crecimiento de Saccharomyces cerevisiae. Revista Latinoamericana Microbiología 27: 283-291.        [ Links ]

14. García MJ, Zúñiga M, Uruburu F (1991) Métodos directos de medida del crecimiento microbiano. Alimentaria: 31-34.        [ Links ]

15. Gerencser V, Barnothy M, Barnothy J (1962) Inhibition of bacterial growth by magnetic fields. Nature VOL 196: 539-541.        [ Links ]

16. Giacoletto LJ (1977) Electronics Designers’ Handbook 2nd Ed. McGraw Hill. New York. 82 pp.        [ Links ]

17. Goldsworthy A, Whitney H, Morris E (1999) Biological effects of physically conditioned water. Water Res. 33: 1618-1626.        [ Links ]

18. Higashitani K, Okuhara K, Hatade S (1992) Effects of magnetic fields on stability of nonmagnetic ultrafine colloidal particles. J. Coll. Interface Sci. 152: 125-131.        [ Links ]

19. Hirano M, Ohta A, Abe K (1998) Magnetic fields effects on photosynthesis and growth of the cyanobacterium. J. Fermentat. Bioeng. 86: 313-316.        [ Links ]

20. Jennison M (1937) The growth of bacteria, yeast and molds in a strong magnetic field. J. Bateriol. 33: 15-16.        [ Links ]

21. Jung JT, Sofer S (1997) Enhancement of phenol biodegradation by south magnetic field exposure. J. Chem. Technol. Biotechnol. 70: 299-303.        [ Links ]

22. Kaufman M, Seidman A (1982) Manual para ingenieros y técnicos en electrónica. McGraw Hill. México. 25 pp.        [ Links ]

23. Kimball G (1938) The growth of yeast in a magnetic field. J. Bateriol. 35: 109-122.        [ Links ]

24. Liboff A (1985) Cyclotron resonance in membrane transport. Schwann Series A: Life Sci. 97: 281-296.        [ Links ]

25. Liboff A, Williams T, Strong D, Wistair R (1984) Time varying magnetic fields: Effect on DNA synthesis. Science 223: 818-820.        [ Links ]

26. Malko JA, Constantinidis I, Dilleha D (1994) Search for influence of magnetic fields on growth of yeast cell. Bioelectromagnetics 15: 495-501.        [ Links ]

27. Maret G, Dransfeld K (1977) Macromolecules and membranes in high magnetic fields. Physica 86-88B: 1077-1083.        [ Links ]

28. Mertens B, Knorr D (1992) Developments of Nonthermal Processes for Food Preservation. Food Technol. Vol 46: 124-133.        [ Links ]

29. Montgomery D (1991) Diseño y Análisis de Experimentos. Iberoamérica. México. 589 pp.        [ Links ]

30. Moore R (1979) Biological effects of magnetic fields: studies with microorganisms. Can. J. Microbiol. 25: 1145-1151.        [ Links ]

31. Mottas D, Lins H (1986) Motion of magnetotactic microorganims. J. Exp. Biol. 121: 153-163.        [ Links ]

32. Phillip E, Kovacs PE, Valentine RL, Alvarez PJJ (1997) The effect of static magnetic fields on biological systems – Implications for enhanced biodegradation (Review). Critical Rev. Env. Sci. Technol. 27: 319-382.        [ Links ]

33. Polk C, Postow E (1986) Handbook of biological effects of electromagnetic fields. CRC Press. Boca Ratón. 140 pp.        [ Links ]

34. Pothakamury U, Barbosa G, Swanson B (1993a) Magnetic Fields Inactivation of Microoganisms and Generation of Biological Changes. Food Technol. VOL 47: 85-93.        [ Links ]

35. Pothakamury U, Barletta B, Barbosa G, Swanson B (1993b) Inactivación de microorganismos en alimentos usando campos magnéticos oscilantes. Revista Española de Ciencia y Tecnología de Alimentos 33: 479-489.        [ Links ]

36. Ruzic R, Jerman I, Gogala N (1998) Effects of weak low-frequency magnetic fields on spruce seed germination. Can. J. Forest Res. 28: 609-616.        [ Links ]

37. Ueno S, Harada K (1982) Redistribution of dissolved oxygen concentration under strong DC magnetic fields. IEEE Trans. Magnetics 18: 1704-1706.        [ Links ]

38. Van Nostran F, Reynolds R, Hedrick H (1967) Effects of a high magnetic field at different osmotic pressures and temperatures on multiplication of Saccharomyces cerevisiae. Appl. Microbiol. 15: 561-563.        [ Links ]