BIODIVERSIDAD: INFERENCIA BASADA EN EL ÍNDICE DE SHANNON Y LA RIQUEZA

Laura Pla

Laura Pla. Magister Scientiarum en Estadística y Doctora en Ciencias Agrícolas, Universidad Central de Venezuela. Profesora, Universidad Nacional Experimental Francisco de Miranda, Venezuela. Dirección: Apartado 7434, Coro 4101, Venezuela. e-mail: laura@reacciun.ve.

RESUMEN

Se describen los estimadores puntuales y por intervalos de confianza (IC) de la riqueza y del índice de Shannon; se aplican a un ejemplo con datos de vegetación y a otro con conteo de aves, y se comparan los resultados obtenidos sobre la base de simulaciones originales y de consideraciones teóricas. Se ofrecen recomendaciones para la aplicación de la técnica de remuestreo adecuada, con énfasis en casos de muestras pequeñas o sin repeticiones. Se orienta también en el uso del software disponible.

Biodiversity: Inference about richness and Shannon index

SUMMARY

Point estimators and confidence intervals for richness and Shannon index are described and applied to a vegetation example and a bird inventory survey. Results of various techniques are compared based on original simulation performance and theoretical formulation conditions. A guide to proceed with emphasis on small real data set and bootstrap estimation is provided, including available software use orientation.

Biodiversidade: Inferência baseada no índice de Shannon e a riqueza

RESUMO

Descrevem-se os estimadores pontuais e por intervalos de confiança (IC) da riqueza e do índice de Shannon; se aplicam a um exemplo com dados de vegetação e a outro com contagem de aves, e se comparam aos resultados obtidos sobre a base de simulações originais e de considerações teóricas. Oferecem-se recomendações para a aplicação da técnica de reamostragem adequada, com ênfase em casos de amostras pequenas ou sem repetições. Orienta-se também no uso do software disponível.

PALABRAS CLAVE / Bootstrap / Diversidad Biológica / Intervalo de Confianza / Remuestreo /

Recibido: 28/10/2005. Modificado: 14/07/2006. Aceptado: 18/07/2006.

Introducción

En estudios de biodiversidad, a partir del muestreo de comunidades, el tamaño de la muestra o número de unidades de observación puede ser pequeño, para realizar inferencia paramétrica sobre la diversidad existente. No obstante, es deseable lograr estimaciones con niveles de confianza conocidos. Una alternativa a la estimación paramétrica para los índices de diversidad es la construcción de intervalos de confianza (IC) mediante técnicas de computación intensiva tales como remuestreo (Pla y Matteucci, 2001), que no se basan en supuestos distribucionales.

Este trabajo aborda el problema con un enfoque aplicado. Se describen los métodos de estimación de la biodiversidad expresada mediante la riqueza y el índice de Shannon, se propone un método de remuestreo para la inferencia, y se discuten los resultados de dos ejemplos, orientando también en el uso del software disponible.

En una comunidad con un número total S de clases (típicamente especies en estudios de biodiversidad) no superpuestas, identificadas por i=1, 2, ..., S, designaremos con p_i la proporción de i-ésima clase. Estas clases son excluyentes, es decir que un mismo elemento o individuo no puede pertenecer a más de una clase, y por lo tanto los p_i están sujetos a la restricción que   Si se toma una muestra aleatoria de esta comunidad, llamaremos n_i al número de individuos o abundancia de la clase i; si n_i=0, entonces la i-ésima especie no se ha observado en la muestra. Al número total de especies observadas en la muestra la llamamos r, que nunca podrá ser mayor que S.

Denominaremos f_k al número de clases con frecuencia o abundancia k y así, el número total de individuos o abundancia total (N) en la muestra puede calcularse como

que puede ser expresado en función de los f_k como

recordando que el símbolo " indica ‘para todos los posibles valores de k’.

Asimismo, la estimación de los p_i en una muestra aleatoria puede hacerse a partir de las frecuencias relativas como

   (1)

Los estimadores de la riqueza se basan en las frecuencias (los f_k) y en el número de clases o especies efectivamente observadas (r). Los estimadores de los índices de biodiversidad se basan directamente en las p_i o frecuencias relativas de cada especie, e indirectamente en la riqueza.

Índice de Shannon

Uno de los índices más utilizados para cuantificar la biodiversidad específica es el de Shannon, también conocido como Shannon-Weaver (Shannon y Weaver, 1949), derivado de la teoría de información como una medida de la entropía. El índice refleja la heterogeneidad de una comunidad sobre la base de dos factores: el número de especies presentes y su abundancia relativa. Conceptualmente es una medida del grado de incertidumbre asociada a la selección aleatoria de un individuo en la comunidad. Esto es, si una comunidad de S especies es muy homogénea, por ejemplo porque existe una especie claramente dominante y las restantes S-1 especies apenas presentes, el grado de incertidumbre será más bajo que si todas las S especies fueran igualmente abundantes. O sea, al tomar al azar un individuo, en el primer caso tendremos un grado de certeza mayor (menos incertidumbre, producto de una menor entropía) que en el segundo; porque mientras en el primer caso la probabilidad de que pertenezca a la especie dominante será cercana a 1, mayor que para cualquier otra especie, en el segundo la probabilidad será la misma para cualquier especie.

El índice de Shannon (Shannon y Weaver, 1949) se define como      

  (2)

La diversidad máxima (H_max= lnS) se alcanza cuando todas las especies están igualmente presentes. Un índice de homogeneidad asociado a esta medida de diversidad puede calcularse como el cociente H/H_max=H/lnS, que será uno si todas las especies que componen la comunidad tienen igual probabilidad (p_i = 1/S).

El antilogaritmo de H (e^H) cuantifica el número de especies, igualmente abundantes, suficiente para producir el mismo grado de incertidumbre, o sea el mismo valor de H. Cuanto mayor sea la diferencia entre e^H y S, el total de especies, menos diversa será la comunidad. Esta cuantificación puede ser útil al comparar gráficos de dispersión del índice de Shannon en función de la riqueza en varias comunidades. Con datos muestrales, H_max=ln(r) indica qué índice de diversidad de Shannon podría haberse alcanzado con las especies presentes, mientras S_H=e^H indica cuántas especies equiabundantes serían necesarias para obtener ese índice observado. Diferencias promedio entre estos valores potenciales y los observados pueden contribuir a la comparación entre comunidades (Figura 1).

El uso de datos muestrales aplicando la Ec. 2 produce estimadores sesgados que subestiman siempre el valor del índice en la población, especialmente cuando se trata de muestras relativamente pequeñas donde es poco probable que estén incluidas todas las especies presentes en la comunidad. Dado que esta es la situación más frecuente en los estudios ecológicos y ambientales, es necesario encontrar un procedimiento que corrija el sesgo y asocie al índice un nivel de incertidumbre que permita separar las fluctuaciones aleatorias no atribuibles a causas identificables, de aquellas que poseen un patrón de comportamiento peculiar. La corrección del sesgo puede hacerse si se dispone de una buena (en el sentido de que se acerca al verdadero valor en la población) estimación de la riqueza.

Generalizando, se trata de construir un intervalo de confianza con probabilidad conocida (1-a) para un parámetro de interés q, en este caso el índice de Shannon, del que existe un estimador calculado a partir de una muestra aleatoria x₁, x₂, ..., x_n, tomada de la población de interés, con una distribución de probabilidad F desconocida, y generalmente a partir de una muestra relativamente pequeña. Esta estimación puede ser puntual cuando solo se estima un valor del índice o por intervalo cuando se estiman los límites inferior y superior con probabilidad fijada de antemano. El segundo procedimiento, más informativo y que permite comparaciones estadísticamente válidas entre comunidades requiere la estimación del índice y de una medida de variabilidad.

Estimadores de la riqueza

A continuación se detallan procedimientos de estimación puntual de la riqueza. No se considerarán aquí las estimaciones asintóticas y las basadas en curvas de rarefacción (Gotelli y Colwell, 2001).

Cuando se cuantifica la riqueza observada en la muestra (r), como el número total de especies presentes en ella, se obtiene siempre un límite inferior para la riqueza de la comunidad. Una propuesta para corregir el sesgo de esta estimación se basa en el concepto de ‘cobertura muestral’ que corresponde a la proporción que representa la abundancia total de las especies presentes en una muestra, con relación a la abundancia total de la comunidad (Good, 1953). En las dos últimas décadas se han propuesto varios estimadores de la riqueza, muchos de ellos derivados de los métodos de estimación de totales poblacionales en animales con métodos de captura-recaptura.

a) ACE (abundance coverage estimator). Chao y colaboradores (Chao y Lee, 1992; Chao et al., 2000) dividen las especies presentes en una muestra en abundantes (r_abun: cuando tienen más de k individuos en la muestra) y raras (r_rara: aquellas con k o menos individuos). La estimación del número de especies ausentes, utilizado para corregir el sesgo, se basa enteramente en las especies consideradas raras, ya que las abundantes serán observadas en toda muestra (Chao y Shen, 2003). El estimador propuesto es

   

el coeficiente de variación de la abundancia de las especies. Este estimador requiere la selección a priori de k, y no está definido para aquellos casos en que todas las especies raras tienen un solo individuo. Chao y Shen (2003) han sugerido fijar k=10 sobre base empírica.

b) r_pot (de potencia ponderada). Pla et al. (2004) han propuesto un estimador de naturaleza no-paramétrica, que no requiere especificar parámetros de distribución de las abundancias por especie, y ajusta la riqueza observada r por adición de la suma de las frecuencias de especies, inversamente ponderada por la potencia de su abundancia muestral,

         (4)

donde r=1/2 es un coeficiente seleccionado sobre evidencia empírica, f_k es el número de especies con k individuos en la muestra, con k=1,…, max_k (abundancia máxima observada). El término que se adiciona es la parte entera de la sumatoria. Supone que las especies de las que no se encontraron individuos en la muestra son más similares a aquellas con menor abundancia y no requiere fijar un valor de abundancia para separar especies raras de abundantes.

Estimadores puntuales del índice de Shannon

a) Máximo verosímil (MV). El estimador máximo verosímil a partir de datos de la abundancia de cada especie es

           (5)

siendo p_i, el definido en la Ec. 1. Este método produce un estimador sesgado (Hutcheson, 1970), con esperanza

       (6)

y cuando no se conoce el total de especies en la población (S), que es el caso más frecuente en la práctica, no es posible corregir el sesgo sin estimar a su vez el número de especies presentes en la población (Peet, 1974).

b) Máximo verosímil corregido por sesgo (MVr, MV_ACE y MVr_pot). Se trata de ajustar el estimador puntual de la Ec. 5 sumándole el sesgo estimado por la Ec. 6 sustituyendo S, que es desconocida, por su estimador: la riqueza observada (r), el estimador ACE, o r_pot.

c) Basado en Horvitz-Thompson (HT). Chao y Shen (2003) combinaron la propuesta de Horvitz y Thompson (1952) para estimar el total de una población bajo un diseño de muestreo no equiprobable con el concepto de ‘cobertura muestral’ para ajustar el sesgo producido por las especies no observadas. El estimador resultante puede calcularse como

siendo el estimador de la ‘cobertura muestral’ basado en todas las especies. Así, si todas las especies están presentes con dos o más individuos en la muestra, ésta puede considerarse ‘completa’ en el sentido de que todas las especies están representadas y la estimación de la cobertura muestral será 1 y no afectará la estimación. La diferencia con el estimador máximo verosímil (Ec. 5) reside en el denominador que corresponde al ajuste basado en Horvitz-Thompson.

d) Ajustado empíricamente (HA). Propuesto por Pla (2004) para muestras con frecuencias o abundancias totales £2000, se basa en la estimación del sesgo por bootstrap y su uso para corregir el sesgo del estimador máximo verosímil como

Ĥ_HA = 2,73Ĥ - 1,75Ĥ* + 0,0003r    (8)

siendo Ĥ el índice calculado con la Ec. 5, Ĥ* la media bootstrap del índice y r la riqueza observada.

Estimación del intervalo de confianza del índice de Shannon

Como se ha señalado arriba, la definición de los límites del intervalo de confianza requiere una estimación de la variabilidad aleatoria asociada a la estimación. En el caso del estimador máximo verosímil, la varianza puede calcularse como (Hutcheson, 1970)

   (9)

y la riqueza (S) deberá ser sustituida por su estimación. Surgirán así tres variantes del intervalo de confianza máximo verosímil según se utilice r, ACE o r_pot.

Con la corrección por ACE, Chao (1987) ha sugerido el uso de una transformación logarítmica para ajustar los límites del intervalo que garantiza la obtención de un límite inferior >0. Se considera que la variable aleatoria l n(MV_ACE-Ĥ) tiene una distribución que se aproxima a la normal y el límite inferior del IC puede calcularse como Ll=Ĥ+D/L, mientras que el límite superior será LS=Ĥ+D * L, siendo D=(MV_ACE-Ĥ) y

   (10)

En la discusión de los ejemplos podremos ver la diferencia entre estas aproximaciones.

La estimación del índice por Horvitz-Thompson permite el cálculo de la varianza por aproximación asintótica como (Chao y Shen, 2003)

siendo côv(f_i,f_j)=f_i(1-f_i/ACE) cuando i=j, y côv(f_i,f_j)=f_if_j/ACE cuando i¹j. Esta ecuación requiere la evaluación de las derivadas para cada par de individuos. Una alternativa es el uso de la estimación bootstrap de la varianza. Comparando resultados entre ambos procedimientos no se encontraron diferencias significativas, y en este trabajo se aplicó la segunda opción.

En el caso del ajuste empírico propuesto por Pla (2004), la construcción de los IC se basa en la desviación estándar bootstrap y sus límites se calculan como Ĥ_HA ± z_a/2 sd*_Ĥ* siendo sd*_Ĥ* la desviación estándar bootstrap del índice. Para muestras con frecuencias o abundancias totales >2000 se recomienda el método de remuestreo corregido por el sesgo y por la aceleración: BCA, por sus siglas en inglés (bias-corrected and accelerated). Mientras que con presencia de varias muestras por unidad de análisis o estructuras jerárquicas de clasificación se recomienda el uso del IC por BCA para el promedio (Pla y Matteucci, 2001).

Materiales y Métodos

Se comparan los estimadores de riqueza (Ec. 3 y 4) y del índice de Shannon (Ec. 5, 6, 7 y 8) a través de su aplicación a dos conjuntos de datos, uno de vegetación y otro de aves. Se presentan los dos conjuntos de datos usados y el método de estimación de la variabilidad por remuestreo.

Bases de datos utilizadas

Vegetación de Falcón. Es una base amplia de datos de vegetación y ambiente georeferenciada del estado Falcón, Venezuela (Matteucci et al., 2001). Se tomaron cuatro formaciones de Beard (Matteucci, 1987): cardonales (C), cardonales secundarios (CS), espinares (E) y espinares deciduos (ED). La sub-base posee datos de abundancia de 151 especies en 37 sitios de muestreo. Las cuatro formaciones corresponden a bosques secos tropicales que han sido estudiados en su relación con el ambiente en otros trabajos (Matteucci et al., 1999a, b).

Aves de Misiones. Es una base de datos resultante del muestreo de aves en la selva atlántica de la Provincia de Misiones, Argentina (Giraudo et al., 2005). Se realizaron campañas en los meses de octubre, diciembre 2004 y abril 2005 en 94 unidades de observación divididas en fragmentos grandes (n=53) y fragmentos pequeños (n=41). Del total de 155 especies detectadas para toda la selva (26 generalistas y 129 exclusivas del bosque), 86 están tanto en los fragmentos grandes como en los pequeños (de esas, 76 son exclusivas del bosque y 10 son generalistas). De las especies que faltan en los fragmentos grandes, 11 son generalistas y 8 exclusivas del bosque; mientras que de las especies que faltan en los fragmentos pequeños y sí fueron detectadas en los grandes, 5 son generalistas y 45 exclusivas del bosque. La probabilidad de que en los fragmentos pequeños falte una especie de bosque tiene un riesgo 4.55 veces mayor a que falte una especie generalista.

Para comparar los subgrupos se aplicó la prueba no paramétrica de Wilcoxon para muestras independientes, a no ser que se indique lo contrario.

Estimación por remuestreo

No es razonable suponer una distribución normal y tampoco conocida para el índice de Shannon, por lo que no es posible aplicar métodos paramétricos de estimación por intervalos. La estimación por remuestreo del índice de Shannon se basa en la abundancia de las especies observadas en una muestra y el único supuesto que debe cumplirse es que la población de la cual provenga la muestra sea homogénea a la escala de análisis seleccionada. Para aplicar métodos de remuestreo se puede entonces asumir que la abundancia total puede subdividirse en ‘porciones unitarias’ cada una tan grande como el mínimo tamaño identificable (Pla, 2004), expresado en las unidades de abundancia utilizadas (área basal, cobertura, biomasa, frecuencia).

Así, la abundancia de cada especie se subdivide en ni porciones unitarias que pueden ser remuestreadas. Como la abundancia se expresa en la misma escala para todas las especies, tanto en la población como en la muestra (y en las remuestras) podemos hacer una selección aleatoria de ‘porciones unitarias’ caracterizadas por la especie que se registra en ella. Estos son N objetos virtuales, que se suponen mutuamente independientes y que tienen la misma distribución (no conocida) de probabilidad. Este valor de N es el que se toma en estos casos como ‘tamaño de la muestra’. El caso más simple es aquel dónde cada ‘porción unitaria’ corresponde a un individuo que pertenece a la especie ‘i’, el cuál puede o no ser incluido en la muestra según el resultado del remuestreo aleatorio.

En este trabajo se usó el intervalo estándar por aproximación normal. Esta técnica se basa en suponer que existe una transformación monotónica del estimador que llamaremos genéricamente I con una distribución aproximadamente normal con media m y desviación estándar s; y que por lo tanto hay una probabilidad de (1-a) que

I + z_a/2s_I < I* < I + z_I-a/2s_I

para toda muestra aleatoria usada en la estimación I* (Efron 1979).

Sobre esta base es posible estimar los límites del intervalo de confianza usando la estimación bootstrap de la desviación estándar como

Ī* ± z_a/2s₁*

siendo Ī* la media del estimador bootstrap del índice, s₁* el estimador bootstrap de la desviación estándar y z_a/2 el correspondiente valor de la distribución normal estándar.

Detalles de éste y otros métodos de estimación de intervalos de confianza pueden encontrarse por ejemplo en Efron y Tibshirani (1998). Para el cálculo de los índices y sus IC existe software específico de acceso libre como por ejemplo EstimateS (Colwell, 2005) o SPADE (Chao y Shen, 2003-2005). En el programa InfoStat se ha desarrollado un módulo de aplicación que calcula éstos y otros índices de biodiversidad y sus IC (InfoStat, 2004). Los cálculos en este trabajo se hicieron con InfoStat y las simulaciones utilizando ResamplingStats (Simon, 2003) con rutinas desarrolladas especialmente que pueden ser solicitadas a la autora.

Resultados

Biodiversidad en la Base de Vegetación

Las estimaciones aplicadas al ‘espinar’ se presentan en la Tabla I. La variabilidad entre muestras de una misma formación influye en el tamaño o amplitud (diferencia entre los límites) del intervalo de confianza para toda la formación. Se ha evitado expresamente el término "promedio" al final de la Tabla I, ya que en este caso no se trata de un promedio de los índices a nivel de la formación, sino del valor obtenido con el amalgamiento de la información de todas las muestras. La diferencia entre uno y otro procedimiento al calcular un indicador y su intervalo de confianza, dependerá del plan de muestreo utilizado para relevar la información a campo.

Los intervalos utilizando el estimador máximo verosímil sin corregir o corregido por r o r_pot son comparativamente menores que aquellos corregidos por ACE. La amplitud del ajuste empírico propuesta por Pla (2004) resulta en IC menos amplios que la estimación de Horvitz-Thompson propuesta por Chao y Shen (2003). Los valores excesivamente altos que se registran para los intervalos corregidos por ACE están asociados directamente a una estimación de la riqueza que discrepa altamente de la observada. Estos casos se presentan cuando predominan especies con muy baja abundancia, como por ejemplo en el espinar identificado como e4, con 36 especies, donde la estimación de la riqueza por ACE fue de 739. El efecto en la corrección del estimador máximo verosímil produce un aumento excesivo del límite superior, tornando no informativo al IC. Los resultados obtenidos para otras tres formaciones (resultados no mostrados) permiten generalizar estas conclusiones en relación al comportamiento de los estimadores.

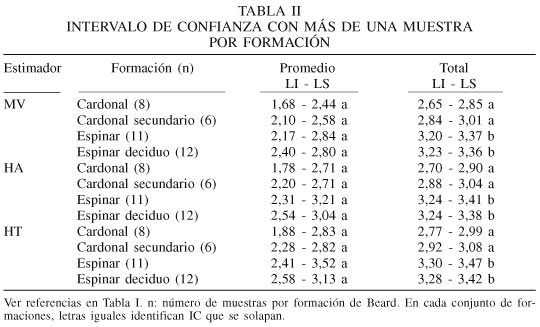
Los intervalos de confianza estimados para el promedio de los censos de cada formación y para el total amalgamado de la formación utilizando el estimador máximo verosímil sin corrección, el propuesto por Pla (2004) y el propuesto por Chao y Shen (2003), se presentan en la Tabla II. Mientras que al utilizar el promedio por formación no se detectan diferencias significativas entre cardonales y espinares; al amalgamar las muestras éstas se ponen de manifiesto. Sin embargo, siguen siendo no significativas las diferencias entre las formaciones secundarias y aquellas que les dieron origen.

La amplitud de los IC construidos a partir del promedio de los índices por muestra es entre 3 y 4 veces mayor que la de aquellos calculados amalgamando la información de todas las muestras. La amplitud del intervalo por aproximación normal refleja la variabilidad aleatoria entre las muestras y la variabilidad dentro de muestras (la debida a la necesidad de estimar la abundancia relativa de cada especie). En el caso de las muestras amalgamadas no existe variabilidad entre muestras, y toda la variabilidad aleatoria está asociada a la estimación de la abundancia relativa de las especies. El número de individuos incluidos en la muestra amalgamada es siempre mayor que el de cada muestra individual, permitiendo que la estimación de la proporción por especie se base en una muestra más grande (y por lo tanto más eficiente) de la misma comunidad. No debe sorprender al investigador obtener esta diferencia de amplitudes.

Muestras independientes que constituyan repeticiones al azar pueden ser tratadas en cualquiera de las dos formas, mientras que muestras sistemáticas o provenientes de un plan de muestreo no aleatorio deberían ser amalgamadas a fin de aprovechar la variabilidad observada en campo para mejorar la estimación de la abundancia relativa de cada especie, en lugar de considerar un promedio. El uso del error estándar (desvío del promedio: que podría tender a declarar significativas diferencias atribuibles al azar, en realidad produce IC más amplios por la falta de ‘cobertura muestral’. Por este motivo la correcta construcción de los intervalos de confianza contribuirá a que el investigador efectivamente identifique aquellas diferencias de interés, y sobre ellas concentre su atención.

Estudios por simulación de poblaciones con patrones de abundancia de especies similares a los del ejemplo indican que la cobertura (probabilidad de que el intervalo calculado con 95% de confiabilidad efectivamente cubra el parámetro) depende no solo del tamaño de cada muestra y del número de muestras que se promedien, sino también del método de estimación utilizado. Acorde a lo esperado, el estimador máximo verosímil y el ajustado de Pla mejoran su estimación tanto al aumentar el número de individuos por muestra, como el número de muestras tomadas en cada caso (Figura 2). Al contrario, el estimador de Horvitz-Thompson si bien mejora la estimación cuando se utiliza el promedio de varias muestras a medida que su número aumenta, cuando las muestras se amalgaman las estimaciones son menos confiables a medida que aumenta el número de individuos muestreados. Para cualquier situación la estimación máximo verosímil no es confiable, cuando se trata de muestras amalgamadas la estimación ajustada de Pla ofrece los intervalos más informativos (menor amplitud) y cuando se trata de promedios de varias muestras la mejor opción se logra al utilizar el método Horvitz-Thompson, que ofrece intervalos más amplios pero con una cobertura óptima.

El comportamiento observado es esperable ya que la propuesta de Chao y Shen (2003) está definida para situaciones donde el número de individuos es bajo y la capacidad de una sola muestra de incluir una buena proporción de las especies es también baja. Así, al amalgamar muestras disminuye su efectividad. En el caso de la estimación ajustada por Pla (2004) la amplitud del intervalo se mantiene reducida; la estimación puntual (centro del intervalo) corresponde al ajuste por el número de especies presentes y la estimación bootstrap del índice que reproduce la diferencia entre población y muestra se utiliza para corregir el sesgo de la estimación puntual.

Cuando se poseen muestras independientes, la diferencia entre los procedimientos de amalgamiento y por promedio, también pueden ser aprovechados por el investigador. Mientras que al utilizar el amalgamiento se obtiene información de la diversidad alfa (de un solo sistema considerado homogéneo a la escala de análisis), el uso del promedio de las muestras permite cambiar la escala de observación al considerar la variación dentro del sistema (diversidad beta) y asociar la biodiversidad con algún patrón del ambiente, ya que se dispondría de una estimación para cada muestra y una para el promedio. En la Figura 2 puede observarse, en especial para las muestras de hasta 60 individuos, que el índice estimado por promedios es menor que el estimado con la muestra amalgamada. Si el objetivo es estimar la diversidad alfa, el segundo procedimiento corrige con mayor eficiencia el sesgo negativo de la estimación aunque siempre se subestima el índice poblacional.

Biodiversidad en la Base de Aves

Dado que el objetivo de los investigadores es detectar posibles diferencias entre la riqueza y la abundancia de fragmentos grandes y pequeños con fines de manejo del ecosistema, una primera aproximación es comparar los promedios de riqueza y de abundancia suponiendo que las variables fueran aproximadamente normales o que el número de muestras fuese suficientemente grande para justificar la aplicación del teorema central del límite. En este caso las pruebas de falta de bondad de ajuste a la normal para la riqueza observada fueron no significativas (p=0,4932 y p=0,7353) y para la abundancia también (p=0,5608 y p=0,8192) en ambos tipos de fragmentos. Las pruebas t de Student permiten concluir que no existieron diferencias significativas del número de aves observadas por muestra entre los fragmentos grandes y los pequeños (p=0,2431), pero que los primeros tienen significativamente mayor número de especies (p=0,0017). El índice de Shannon se estimó usando Horvitz-Thompson ya que el número máximo de aves fue 55 en los fragmentos grandes y 46 en los pequeños. Si se amalgaman las muestras debe usarse HA.

Los fragmentos pequeños (con una superficie promedio de 67,36ha) que varían entre 3,45 y 129,67ha no presentan diferencias de biodiversidad asociadas a su superficie (p=0,3279), como tampoco difieren en su abundancia (p=0,1291). Los fragmentos grandes tienen sólo dos tamaños (24060ha y 21879ha) y su riqueza promedio no difiere significativamente (p=0,4696) como tampoco difiere la abundancia promedio (p=0,6452). Asimismo, la diferencia entre la abundancia promedio de los fragmentos grandes (30) y los pequeños (27) no es estadísticamente significativa (p=0,2431), todo lo cuál permite comparar la biodiversidad sobre la base de los índices (riqueza e índice de Shannon) en muestras que pueden considerarse de tamaño homogéneo. La pregunta que resta es si el tamaño fue suficiente para ambos tipos de fragmentos, solo para uno, o bien para ninguno.

Una opción para encontrar esta respuesta podemos obtenerla si amalgamamos las muestras que provienen del mismo fragmento y el mismo día, y comparamos los resultados. En 8 sitios de muestreo provenientes de un mismo fragmento pequeño de 129,67ha se calculó un promedio de 18 especies y se estimó la riqueza con ACE en 28 y con r_pot en 24. Sin embargo, si se amalgaman esas mismas muestras se encuentran 55 especies presentes con un valor estimado para ACE de 63 y para r_pot de 65. El promedio de las abundancias fue 34 individuos, mientras que en la muestra amalgamada se totalizaron 271 individuos. Si se expresa la riqueza en forma relativa al número de ejemplares (por ejemplo, expresada como número de especies por cada 10 aves avistadas), se obtiene un valor de 5,3 para el promedio y de 2,0 para la muestra amalgamada.

Esta discrepancia es el resultado de cómo se procesó la información del muestreo para estimar tanto la riqueza como el índice de Shannon. En el presente ejemplo se requieren en cada muestra aproximadamente 2 individuos para detectar una nueva especie, mientras que en el total amalgamado se requieren 5; es decir que se debe tener al menos 2,5 muestras (5/2) para amalgamar, a fin de obtener la misma efectividad. Pero cualquier incremento en el número de muestras amalgamadas resultará en una ganancia en la capacidad de detectar especies raras (o poco frecuentes). Si disponemos de 8 muestras la ganancia debería ser significativa, como efectivamente se observa al comparar la potencia de ambos procedimientos. En la Figura 3 se muestra la capacidad de detectar cierto porcentaje de las especies (abscisas) en función de la potencia (proporción de veces en que se alcanza dicho porcentaje). La muestra amalgamada es capaz de detectar con certeza (potencia 1) el 80% de las especies, mientras que para el promedio este porcentaje baja al 50%. Si bien el amalgamiento no garantiza una estimación no sesgada de riqueza, mejora considerablemente la inferencia utilizando los estimadores ACE o r_pot al disminuir el número de especies no incluidas en la muestra.

Así, al amalgamar todas las muestras según el tipo de fragmento del que provengan se obtienen los resultados que se muestran en la Tabla III. Los intervalos de confianza de ACE no se solapan, lo que mantiene la conclusión inicial de que los fragmentos grandes tienen comparativamente mayor número de especies que los pequeños y poseen una diversidad estimada por el índice de Shannon significativamente mayor.

Conclusiones

El uso generalizado del índice de Shannon como una expresión sintética de la biodiversidad ha estimulado la aparición de estimadores que corrigen el sesgo y mejoran la cuantificación de la variabilidad aleatoria para permitir la construcción de intervalos de confianza. Hasta la década pasada el estimador máximo verosímil constituyó la única opción y su uso generalizado produjo con toda seguridad subestimaciones de los valores reportados en la literatura. La aparición de alternativas que mejoran la estimación puntual porque corrigen el sesgo negativo, como la de Chao y Shen (2003) o de Pla (2004), revitalizan la utilidad de este índice.

El estimador máximo verosímil, aun corrigiendo con una estimación mejorada de la riqueza, resulta en valores puntuales e IC más bajos que cualquiera de las otras propuestas. La revisión de la literatura y los resultados de nuestra simulación nos hacen descartar su aplicación. Esta recomendación, sin embargo, conlleva una dificultad para comparar resultados anteriores ya publicados con nuevas estimaciones, salvo que se disponga de los datos originales. En estos casos siempre podrán considerarse las dos opciones y utilizar la máxima verosímil para comparaciones cualitativas.

Cuando el estimador máximo verosímil del índice de Shannon se corrige usando ACE para estimar la riqueza el límite inferior del IC puede ser negativo y el superior excesivamente alto. Como alternativa, se sugiere el uso de una transformación logarítmica que resuelve la negatividad del límite inferior, pero mantiene la amplitud del IC muy alta. Se pueden obtener estimaciones de la riqueza que discrepan en más de un 2000% de la observada, en particular cuando se trata de muestras con muchas especies muy poco abundantes.

La propuesta de Pla (2004) permite la estimación por IC con límites ajustados y ofrece comportamiento óptimo cuando se trata de muestras con d»2000 individuos, independientemente de la abundancia de las especies, mejorando la confiabilidad a medida que aumenta el número de individuos en la muestra. Por ello es la opción recomendada cuando se pueden amalgamar muestras.

La propuesta de Chao y Shen (2003) ofrece IC más amplios pero su cobertura es óptima. Se lo recomienda para casos donde abundan las especies raras, ya sea para una muestra única como para el promedio de varias muestras. La desventaja de este estimador reside en que a medida que aumenta el número de individuos en la muestra, desmejora la corrección por sesgo y, al contrario de lo esperado, aumenta la amplitud del intervalo.

La cuantificación de la biodiversidad será apreciada en tanto pueda utilizarse con fines comparativos y por ello el énfasis está en la construcción de intervalos de confianza. La investigación metodológica está en desarrollo y los estudios que comparan estimadores en diversas condiciones por métodos de simulación Monte Carlo se han generalizado. La dependencia del desempeño de los estimadores del patrón de distribución de la abundancia de las especies, hoy ampliamente aceptada, es un obstáculo para la generalización descontextuada.

Por ello, una vez más es posible afirmar que la colaboración entre biólogos, ecólogos y biómetras permitirá definir la mejor estrategia de análisis para casos particulares y aumentará el conocimiento sobre la biodiversidad para manejar adecuada y sosteniblemente el ecosistema.

AGRADECIMIENTOS

La autora agradece a Alejandro Giraudo por facilitar la base de datos de aves.

REFERENCIAS

1. Chao A (1987) Estimation the population size for capture-recapture data with unequal catchability. Biometrics 43: 783-791.        [ Links ]

2. Chao A, Lee S-M (1992) Estimating the number of classes via sample coverage. J. Am. Stat. Assoc. 87: 210-217.        [ Links ]

3. Chao A, Shen T-J (2003) Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Env. Ecol. Stat. 10: 429-443.        [ Links ]

4. Chao A, Shen TJ (2003-2005) Program SPADE (Species Prediction And Diversity Estimation). Program and User’s Guide. http://chao.stat.nthu.edu.tw.        [ Links ]

5. Chao A, Hwang W-H, Chen Y-C, Kuo C-Y (2000) Estimating the number of shared species in two communities. Stat. Sinica 10: 227-246.        [ Links ]

6. Colwell RK (2005) EstimateS: Statistical estimation of species richness and shared species from samples Version 7.5. User’s Guide and application. http://purl.oclc.org/estimates.        [ Links ]

7. Efron B (1979) Bootstrap methods: An other look to the Jacknife. Ann. Stat. 7: 1-26.        [ Links ]

8. Efron B, Tibshirani RJ (1998) An introduction to the bootstrap. 1^a reimpresión. CRC. Boca Ratón, FL, EEUU. 436 pp.        [ Links ]

9. Giraudo AR, Matteucci SD, Morello J, Alonso J, Herrera J, Abramson RR (2005) Efectos de la fragmentación sobre la riqueza y abundancia de aves en la Selva Atlántica de Argentina. Un análisis preliminar en parches grandes y pequeños. XI Reunión Argentina de Ornitología. Buenos Aires, Argentina. www.avesargentinas.org.ar/rao/resumenes.htm        [ Links ]

10. Good IJ (1953) The population frequencies of species and the estimation of population parameters. Biometrika 40: 237-264.        [ Links ]

11. Gotelli NJ, Colwell RK (2001) Quantifying biodiversity: procedures and pitfalls in the measurement and comparison of species richness. Ecol. Lett. 4: 379-391.        [ Links ]

12. Horvitz DG, Thompson DJ (1952) A generalization of sampling without replacement from a finite universe. J. Am. Stat. Assoc. 47: 1475-87.        [ Links ]

13. Hutcheson K (1970) A test for comparing diversities based on Shannon formula. J. Theor. Biol. 29: 151–154.        [ Links ]

14. InfoStat (2004) InfoStat versión 1.5. Grupo InfoStat, FCA, Universidad Nacional de Córdoba, Argentina. www.infostat.com.ar        [ Links ]

15. Matteucci SD (1987) The vegetation of Falcón State, Venezuela. Vegetatio 70: 67-91.        [ Links ]

16. Matteucci SD, Colma A, Pla L (1999a) Biodiversidad vegetal en el árido falconiano (Venezuela). Interciencia 24: 300-307.        [ Links ]

17. Matteucci SD, Colma A, Pla L (1999b) Bosques secos tropicales del estado Falcón, Venezuela. En Matteucci SD, Solbrig OT, Morello J, Halffter G (Eds.) Biodiversidad y Uso de la Tierra. Conceptos y ejemplos de Latinoamérica. Colección CEA-UBA Vol. 23. EUDEBA. Buenos Aires, Argentina. pp. 399-420.        [ Links ]

18. Matteucci SD, Colma A, Pla L (2001) Falcón y sus recursos naturales: base electrónica de información biofísica. UNEFM-CONICIT. Coro, Venezuela. ISBN: 980-858-7        [ Links ]

19. Peet RK (1974) The measurement of species diversity. Ann. Rev. Ecol. Sistem. 5: 285-307.        [ Links ]

20. Pla L (2004) Bootstrap Confidence Intervals for the Shannon Biodiversity Index: A Simulation Study. J. Agric. Biol. Env. Stat. 9: 42–56.        [ Links ]

21. Pla L, Matteucci SD (2001) Intervalos de confianza bootstrap del índice de biodiversidad de Shannon. Rev. Fac. Agron. (LUZ) 18: 222-234.        [ Links ]

22. Pla L, Balzarini M, DiRienzo JA (2004) The Assessment of Biodiversity: Inference about richness. XXII International Biometric Conference, Cairns, Australia. pp. 134.        [ Links ]

23. Shannon CE, Weaver W (1949) The mathematical theory of communication. University of Illinois Press. Urbana, IL, EEUU. 144 pp.        [ Links ]

24. Simon JL (2003) Resampling Stats, version 5.02. www.resample.com.        [ Links ]