Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de Obstetricia y Ginecología de Venezuela
versión impresa ISSN 0048-7732
Rev Obstet Ginecol Venez vol.75 no.1 Caracas mar. 2015
Sistema Internacional de Unidades (SI)*
Dr. Rogelio Pérez DGregorio
Director de Editorial Ateproca
* Esta publicación realizada por R. Pérez DGregorio con apoyo de ATEPROCA no tiene derechos de autor y está disponible en www. ateproca.com. En vista de que se intenta difundir una información importante a una audiencia lo más amplia posible puede reproducirse, imprimirse, copiarse y distribuirse gratuitamente con propósitos educativos.
El Sistema Internacional de Unidades, del francés Le Système International dUnités, abreviado universalmente como SI, también denominado sistema internacional de medidas, es la norma que se utiliza en casi todo el mundo a excepción de Birmania, Liberia y Estados Unidos (1,2).
Junto con el antiguo sistema métrico decimal que es su antecedente y que ha mejorado el SI también es conocido como sistema métrico.
Se estableció en 1960 en la XI Conferencia General de Pesos y Medidas (CGPM) con seis unidades básicas y en 1971 fue añadido el mol como la séptima unidad básica (1).
El 1º de septiembre de 2005 en Venezuela entra en vigencia la Ley de Metrología (3). En su Artículo 6 se establece que El Sistema Internacional de Unidades (SI), adoptado por la Conferencia General de Pesas y Medidas, regirá como el Sistema Legal de Unidades de Medida en el territorio nacionaL. Las definiciones, símbolos, múltiplos y submúltiplos, usos y aplicaciones del SI se establecerán en las disposiciones legales respectivas.
Las unidades del SI se basan en fenómenos físicos fundamentales con la excepción del kilogramo, unidad de masa, como se discute más adelante. Las unidades SI constituyen una referencia internacional de las indicaciones de los instrumentos de medición, a los cuales están referidas mediante una concatenación ininterrumpida de calibraciones o comparaciones (1,2).
Esto permite lograr equivalencia de las medidas realizadas con instrumentos similares, utilizados y calibrados en lugares distantes sin la necesidad de duplicación de ensayos y mediciones (4,5).
Para nuestras revistas biomédicas es de sumo interés, en vista de que acogidos a la norma de las Recomendaciones para la realización, informe, edición y publicación de trabajos académicos en revistas médicas del Comité Internacional de Editores de Revistas Médicas (ICMJE) (6,7), las unidades de medida deben ser expresadas de acuerdo con los lineamientos del SI.
Las tres clases de unidades SI y los prefijos SI
La unidades SI se dividen en tres clases:
unidades básicas o fundamentales
unidades derivadas
unidades suplementarias
las cuales en conjunto conforman el sistema coherente de unidades SI. El SI también incluye prefijos de los múltiplos y submúltiplos de las unidades SI.
Unidades básicas SI
En el Cuadro 1 se presentan las siete unidades básicas, mutualmente independientes entre sí, en las cuales se fundamenta el SI; y los nombres y los símbolos de sus unidades respectivas, llamadas unidades base SI (4).
A continuación se presenta la definición de las mismas (1,2,4).
Metro (m): es la longitud del trayecto del recorrido por la luz en el vacío durante un intervalo de 1/299.792.458 segundos.
Kilogramo (kg): es la unidad de masa. Es igual a la masa del prototipo internacional del kilogramo sancionado por la Conferencia General de Pesas y Medidas en 1889 y depositado en el Pabellón de Breteuil, de Sévres. Un duplicado de este prototipo se encuentra depositado en el Servicio Nacional de Metrología de Venezuela. Es la única unidad básica que tiene un prefijo de múltiplo (kilo) en el nombre, que se ha respetado por razones históricas. Los múltiplos y submúltiplos de esta unidad se forman anteponiendo prefijos a la palabra gramo y sus símbolos al símbolo g.
Segundo (s): es la unidad de tiempo que expresa la duración de 9.192.631.770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133.
Ampere (A): es la unidad de corriente eléctrica. Es la intensidad de una corriente constante que, mantenida en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y colocados a una distancia de un metro uno del otro en el vacío, produce entre estos conductores una fuerza igual a 2 x 10–7 newton por metro de longitud.
Kelvin (K): es la unidad de temperatura termodinámica, y es la fracción 1/273,16 de la temperatura termodinámica del punto triple del agua. Un intervalo de temperatura puede también expresarse en grados Celsius ºC.
Mol (mol): es la unidad de cantidad de materia de un sistema que contiene tantas entidades elementales como átomos hay en 0,012 kilogramos de carbono 12. Cuando se use el mol, deben especificarse las entidades de los elementos que pueden ser átomos, moléculas, iones, electrones, otras partículas, o grupos especificados de esas partículas.
Candela (cd): es la unidad de intensidad luminosa. Representa la intensidad luminosa, en una dirección dada, de una fuente que emite radiación monocromática de frecuencia 540 x 1012 hertz y que tiene una dirección de (1/683) watt por estereorradián.
Radián (rad): es el ángulo plano entre dos radios de un círculo que corta en la circunferencia un arco igual en longitud a los radios.
Estereorradián (sr): es el ángulo sólido que, teniendo su vértice en el centro de la esfera, corta un área de la superficie de la esfera igual a un cuadrado con lados de longitud igual a los radios de la esfera.
Unidades SI derivadas
Las unidades SI derivadas se expresan algebraicamente en términos de unidades base u otras unidades derivadas (incluyendo el radián y el estereorradián que son dos unidades suplementarias). Los símbolos de las unidades derivadas se obtienen mediante operaciones matemáticas de multiplicación y división. Por ejemplo, la unidad derivada de la cantidad de masa molar (masa dividida por cantidad de sustancia) es el kilogramo por mol, símbolo kg/mol. En el Cuadro 2 se presentan ejemplos adicionales de unidades derivadas en términos de unidades SI base (1,2,4).
Unidades SI derivadas con nombres y símbolos especiales
Ciertas unidades SI derivadas tienen nombres y símbolos especiales y se presentan en los Cuadros 3 y 4. En los Anexos 1 y 2 se presentan, respectivamente, las unidades SI con y sin nombres especiales.


Grado Celsius
Además de la cantidad de temperatura termodinámica (símbolo T), expresada en la unidad kelvin, se usa también la cantidad de temperatura Celsius (símbolo t) definida por la ecuación t = T – T0, donde T0 = 273,15 K por definición. Para expresar la temperatura Celsius, se utiliza la unidad de grados Celsius, símbolo °C, el cual es igual en magnitud a la unidad kelvin; en este caso, grado Celsius es un nombre especial usado en lugar de kelvin. Un intervalo o diferencia de temperatura Celsius puede ser expresado en unidades kelvin, así como en unidades de grados Celsius [Note que la temperatura termodinámica T0 es exactamente 0,01 K por debajo de la temperatura termodinámica del triple punto de agua].
Uso de las unidades derivadas del SI con nombres y símbolos especiales
En el Cuadro 5 se presentan ejemplos de unidades derivadas de SI que pueden ser expresadas con la ayuda de unidades derivadas de SI que tienen nombres y símbolos especiales (incluyen el radián y estereorradián).
Las ventajas de usar los nombres especiales y símbolos de unidades derivadas de SI son aparentes en el Cuadro 5. Considere, por ejemplo, la unidad de entropía molar: la unidad J/(mol · K) es obviamente más fácil de entender que su unidad base equivalente, m2 · kg · s–2 · K–1 · mol–1. Sin embargo, debe reconocerse que existen, por conveniencia, los nombres y símbolos especiales (1,4).
Los Cuadros 3, 4 y 5 muestran también que los valores de diferentes cantidades se expresan en la misma unidad SI. Por ejemplo, el joule por kelvin (J/K) es la unidad SI para capacidad de calor y para entropía. Así, el nombre de la unidad no es suficiente para definir la cantidad medida (1,4).
Una unidad derivada puede ser expresada, frecuentemente, en varias vías diferentes mediante el uso de unidades base y unidades derivadas con nombres especiales. En la práctica, con algunas cantidades, se prefiere usar ciertas unidades con nombres especiales, o combinaciones de unidades para facilitar la distinción entre cantidades de aquellos valores que tienen expresiones idénticas en términos de unidades base SI. Por ejemplo, la unidad SI de frecuencia es el hertz (Hz) en vez de la recíproca de segundo (s–1), y la unidad SI de momento de fuerza es el newton metro (N · m) en vez del joule (J) (1,4).
Similarmente, en el campo de la radiación ionizante, la unidad SI de actividad es el becquerel (Bq) en vez de la recíproca de segundo (s–1), y las unidades SI de dosis absorbida y dosis equivalente son designadas como el gray (Gy) y el sievert (Sv), respectivamente, en vez del joule por kilogramo (J/ kg).
Unidades SI suplementarias
Como se mencionó anteriormente, hay dos unidades en esta clase: el radián, símbolo rad, la unidad SI de cantidad de ángulo plano; y el estereorradián, símbolo sr, la unidad SI de cantidad de ángulo sólido.
Las unidades suplementarias son interpretadas ahora como unidades derivadas sin dimensión, por lo cual, se pueden usar en expresiones para unidades derivadas SI, y se incluyen en el Cuadro 3 junto con las otras unidades derivadas con nombres y símbolos especiales (1,4).
Esta interpretación de las unidades suplementarias implica que el ángulo plano y el ángulo sólido se consideren cantidades derivadas de dimensión uno (llamadas cantidades sin dimensión), cada una de las cuales tiene la unidad uno, símbolo 1, como su unidad SI coherente. Sin embargo, en la práctica, cuando se expresan los valores de cantidades derivadas que involucren el ángulo plano o el ángulo sólido, ayuda su comprensión si se usan los nombres (o símbolos) especiales radián (rad) o estereorradián (sr) en lugar del número 1. Por ejemplo, aunque los valores derivados de velocidad angular (ángulo plano dividido por tiempo) pueden expresarse en la unidad s–1, esos valores se expresan usualmente en la unidad rad/s.
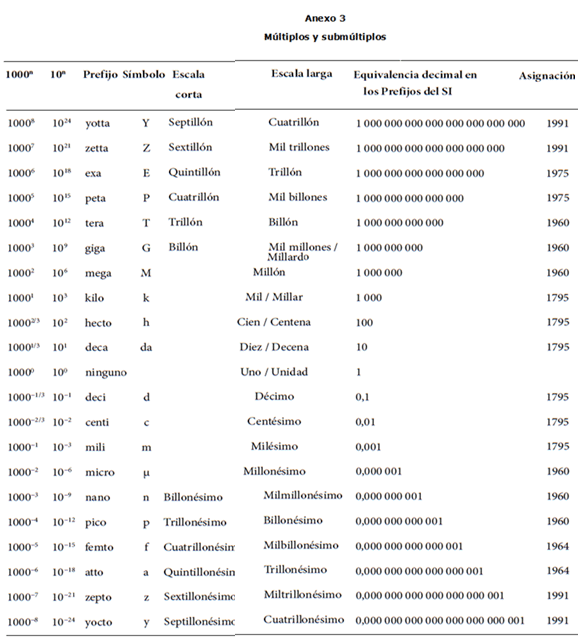
Múltiplos y submúltiplos decimales de las unidades SI: prefijos SI
En el Cuadro 6, se presentan los prefijos SI que se usan para múltiplos y submúltiplos de las unidades SI. Mediante estos se evita el uso de valores numéricos muy largos o muy pequeños. Un prefijo se une directamente al nombre de la unidad o al símbolo de la misma. Por ejemplo, un kilómetro, símbolo 1 km, es igual a mil metros, símbolo 1 000 m o 103 m. Cuando los prefijos se agregan a las unidades SI, las unidades así formadas se denominan múltiplos y submúltiplos de unidades SI a fin de distinguirlas de las unidades SI del sistema coherente (Anexo 3).
Nota: No se permiten definiciones alternativas para los prefijos SI y sus símbolos. Por ejemplo, no se acepta usar kilo (k) para representar 210 = 1024, mega (M) para representar 220 = 2201048576, o giga (G) para representar 230 = 1073741824.
Unidades fuera del SI
Las unidades que están fuera del SI pueden dividirse en tres categorías:
unidades aceptadas para su uso en el SI
unidades aceptadas temporalmente para su uso en el SI
unidades no aceptadas para su uso en el SI y deben evitarse estrictamente.
Unidades aceptadas para su uso en el SI
Existen cuatro categorías de unidades aceptadas para su uso en el SI
Hora, grado, litro y similares.
Neper, bel, shannon, y similares.
Electronvolt y unidad de masa atómica unificada.
Unidades naturales y atómicas.
Hora, grado, litro y similares
Ciertas unidades que no son parte del SI son esenciales, se usan ampliamente y son aceptadas por el Comité Internacional de Pesos y Medidas (CIPM), y para uso en el SI. Estas unidades se presentan en el Cuadro 7. La combinación de unidades de ese cuadro con las unidades SI para formar unidades derivadas debe restringirse a casos especiales a fin de no perder las ventajas de la coherencia de las unidades SI.
Además, se reconoce que en ocasiones puede ser necesario utilizar otras unidades de tiempo como las suministradas en el Cuadro 7; en particular, en algunas circunstancias, se puede requerir que se expresen intervalos en semanas, meses, o años. En esos casos, si no existe un símbolo estandarizado debe escribirse la palabra completa (4).
Neper, bel, shannon, y similares
Hay otras pocas unidades altamente especializadas que no aparecen en el Cuadro 7 y son usadas por la Organización Internacional de Estandarización (International Organization for Standardization ISO) y la Comisión de Electrotécnica Internacional (International Electrotechnical Commission IEC) que no pertenecen al SI, pero que se aceptan para su uso. Estas incluyen el neper (Np), bel (B), octave, phon, y sone, y unidades usadas en información de tecnología, como el baud (Bd), bit (bit), erlang (E), hartley (Hart), y shannon (Sh) (4).
Electronvolt y unidad de masa atómica unificada
Se aceptan para su uso las dos unidades que se presentan en el Cuadro 8. Esas unidades se usan en campos especializados; sus valores en unidades SI deben obtenerse de experimentación y no se conocen exactamente.
Nota: En algunos campos, la unidad de masa atómica unificada es llamada dalton, símbolo DA; sin embargo, este nombre y símbolo no es aceptado por SI. Similarmente, UMA no es un símbolo aceptado para unidad de masa atómica. El único nombre permitido es unidad de masa atómica y el único símbolo permitido es u.
Unidades naturales y atómicas
En algunos casos, particularmente en ciencias básicas, los valores de cantidad se expresan en términos de constantes fundamentales de la naturaleza, conocidas como unidades naturales. El uso de estas se permite cuando sea necesario para una comunicación más efectiva de la información. En esos casos, deben identificarse las unidades naturales utilizadas. Esto se aplica también para el sistema de unidades denominadas unidades atómicas usadas en física atómica teórica y química. Ejemplos de cantidades físicas usadas como unidades naturales, se presentan en el Cuadro 9 (4).
Unidades aceptadas temporalmente para su uso en el SI
Debido a la práctica existente en ciertos campos o países, en 1978 el CIPM consideró el uso de ciertas unidades hasta que se considerara que su uso no era necesario. Sin embargo, esas unidades no deben ser introducidas donde no se usen actualmente. Se recomienda el uso de esas unidades excepto por milla náutica, nudo, área, y hectárea; y excepto curie, roentgen, rad, y rem hasta el año 2000.
Unidades no aceptadas para su uso en SI
En el Cuadro 10, se presentan algunas unidades aceptadas, temporalmente, para su uso en el SI, y en los Cuadros 11 y 12 ejemplos de otras unidades no aceptadas.
Unidades CGS (Sistema Cegesimal)
En el Cuadro 11, se dan ejemplos de unidades del Sistema Cegesimal (centímetrogramo-segundo CGS) que tienen nombres especiales. Esas unidades no son aceptadas en el SI. Tampoco se aceptan otras unidades de varios sistemas de CGS que incluyen los sistemas electrostático, electromagnético, y gausiano, a excepción de unidades del centiempotro, gramo, y segundo que están definidas también en el SI.
Otras unidades inaceptables
Existen muchas otras unidades ademas de las del CGS que estan fuera del SI y no son aceptadas en este, e incluyen todas las unidades comunes de EE.UU (pulgada, libra). Estas unidades deben restringirse y evitarse y usar las unidades SI con sus multiplos y submultiplos. Esta restriccion tambien aplica a nombres especiales para unidades SI o nombres especiales para multiplos o submultiplos de las unidades SI, asi como mho para siemens (S) y micron para micrometro (µm). El Cuadro 11 presenta ejemplos de algunas de esas unidades inaceptables.
REGLAS Y CONVENCIONES DE ESTILO PARA IMPRIMIR Y USAR LAS UNIDADES
Reglas y convenciones de estilo para los símbolos de unidades
Tipo de letra
Los símbolos de las unidades se imprimen en letras romanas (normales) del mismo tipo usado en el texto.
Mayúsculas
Los símbolos de las unidades se imprimen en letra minúscula a excepción de:
a. cuando el nombre de la unidad se derive del nombre de una persona
b. el simbolo recomendado para litro en Estados Unidos es L
c. el simbolo del ohm (Ω¶) letra mayuscula del alfabeto griego
Ejemplos:
m (metro) s(segundo) V (volt)
Pa (pascal) lm (lumen) Wb (weber)
Plurales
Los símbolos de las unidades no se alteran en el plural Ejemplo:
l = 75 cm y no l = 75 cms
Nota: l es el símbolo de cantidad para longitud.
Puntuación
Los símbolos de las unidades no van seguidos de un punto a menos que vayan al final de una frase.
Ejemplo:
Su largo es de 75 cm. o Es de 75 cm de largo.
Y no: Es de 75 cm. de largo.
Vive a 200 km de su residencia
Y no: Vive a 200 km. de su residencia

Símbolos de unidades obtenidos por multiplicación
Los símbolos de unidades que se forman por la multiplicación de otras unidades se indican por medio de un punto en la mitad (centrado) o por un espacio. Sin embargo, se prefiere el punto porque es menos probable que haya confusión (4).
Ejemplo:
N · m o N m
Notas:
1. Un punto centrado o un espacio es usualmente imperativo. Por ejemplo, m · s–1 es el símbolo de metro por segundo mientras que ms–1 es el símbolo de la recíproca de un milisegundo (103 s–1).
2. Se sugiere que si se usa un espacio para indicar unidades formadas por multiplicación, se omita el espacio si no causa confusión. Esta posibilidad se refleja en la práctica común de usar el símbolo kWh en vez de kW · h o kWh por el kilovatio hora.
Símbolos de unidades obtenidos por división
Los símbolos de unidades formadas por división de otras unidades se indican mediante una línea sólida (raya oblicua /), una línea horizontal o un exponente negativo.
Ejemplo:
m/s, , o m · s–1
Sin embargo, para evitar ambigüedad, no debe repetirse la misma línea a menos que se usen paréntesis.
Ejemplos:
m/s2 o m · s–2 y no: m/s/s
m · kg/(s3 · A) o m · kg · s–3 · A–1 y no: m · kg/s3/A
En casos complicados debe usarse exponentes negativos.
No usar simultáneamente símbolos y nombres de unidades
Los símbolos y las unidades no deben usarse juntos.
Ejemplo:
C/kg, y no: coulomb/kg
C · kg–1, coulomb por kg;
coulomb por kilogramo C/kilogramo;
coulomb · kg–1; o
C por kg; coulomb/
kilogramo
No usar abreviaturas para unidades
Debido a que las unidades aceptables tienen, generalmente, símbolos y nombres reconocidos internacionalmente, no se permite utilizar abreviaturas para los símbolos o nombres de unidades, así como seg (para s o segundo), mm cuad. (para mm2 o milímetro cuadrado), cc (para cm· o centímetro cúbico), mins (para min o minuto), hrs (para hora u horas), lit (para L o litro), apms (para A o ampers), UMA (para u o unidad de masa atómica unificada) o mps (por m/s o metro por segundo). Aunque los valores de cantidad se expresan, normalmente, mediante el uso de símbolos por números y símbolos por unidades, si por alguna razón el nombre de una unidad es más apropiado que el símbolo, debe escribirse el nombre completo.
Reglas y convenciones de estilo para prefijos SI
Letras y espacios
Los símbolos de los prefijos se imprimen en letra romana normal del mismo tipo del texto circundante, y se unen a los símbolos de las unidades sin dejar espacio entre el símbolo del prefijo y el símbolo de la unidad. Esto aplica también a los prefijos agregados a nombres de unidades
Ejemplos:
mL (mililitro), pm (picometro), GÙ(gigaohm), THz (terahertz)
Mayúsculas
Los símbolos de los prefijos Y (yota), Z (zeta), E (exa), P (peta), T (tera), G (giga), y M (mega) se escriben con letra mayúscula mientras que los otros prefijos se escriben con minúscula (ver Cuadro 6). Los prefijos se escriben, normalmente, con letras minúsculas.
Inseparabilidad de prefijo y unidad
Las agrupaciones formadas por la unión del símbolo de un prefijo al símbolo de una unidad constituyen una unidad inseparable (forman un múltiplo o submúltiplo de la unidad correspondiente) lo cual puede dar lugar a una potencia positiva o negativa que se puede combinar con otros símbolos de unidades para formar símbolos de unidades compuestos.
Ejemplos:
2,3 cm3 = 2,3 (cm)3 = 2,3 (10–2 m)3 = 2,3 x 10–6 m3
1 cm–1 = 1 (cm)–1 = 1 (10–2 m)–1 = 102 m–1
5000 µ–1 = 5000 (µs)–1 = 5000 (10–6 s)–1
= 5000 x 106 s–1 = 5 x 109 s–1
1 V/cm = (1 V)/(10–2 m) = 102 V/m
Los prefijos son también inseparables de los nombres de las unidades a los que estén unidos. Así, por ejemplo, milímetro, micropascal, y meganewton son una sola palabra.
No se aceptan prefijos compuestos
No está permitido el uso de símbolos prefijos compuestos, esto es, símbolos formados por la yuxtaposición de dos o más símbolos de prefijos. Esta regla aplica también a los prefijos compuestos.
Ejemplo:
nm (nanometro) y no: mìm (milimicrometro)
Uso de prefijos múltiples
En una unidad derivada formada por división, el uso de un símbolo prefijo (o un prefijo) en el numerador y el denominador puede causar confusión. Así, por ejemplo,
10 kV/mm
es aceptable, pero
10 MV/m
se considera, frecuentemente, preferible porque contiene solo un símbolo prefijo y está en el numerador.
En una unidad derivada de multiplicación, el uso de más de un símbolo prefijo (o más de un prefijo) puede también causar confusión. Así, por ejemplo,
10 MV · ms
es aceptable, pero
10 kV · s
se considera preferible.
Nota: Estas consideraciones no aplican, usualmente, a las unidades derivadas de kilogramo. Por ejemplo,
0,13 mmol/g
no se considera preferible a
0,13 mol/kg
No se aceptan prefijos por sí solos
Los símbolos prefijos no deben usarse solos y no pueden agregarse al número 1, el símbolo para la unidad uno. De manera similar, los prefijos no se pueden agregar al nombre de la unidad uno, esto es, la palabra uno.
Ejemplo:
la densidad del número de átomos de Pb es 5 x 106/ m3
y no:
la densidad del número de átomos de Pb es 5 M/m3.
Prefijos y el kilogramo
Como ya mencionamos, por razones históricas, el nombre kilogramo para la unidad base SI de masa contiene el nombre kilo, el prefijo SI para 103. Así, debido a que no se aceptan los prefijos compuestos, los múltiplos y submúltiplos decimales de la unidad de masa se forman al agregárseles los símbolos prefijos a g, el símbolo de gramo, y los nombres de sus múltiplos y submúltiplos se forman cuando se agregan los prefijos al nombre gramo.
Ejemplo:
10–6 kg = 1 mg (1 miligramo)
y no
10–6 kg = 1 µkg (1 microkilogramo)
Prefijos con el grado Celsius y las unidades aceptadas para su uso en el SI
Los símbolos de prefijos se pueden usar con la unidad símbolo °C y los prefijos se pueden usar con el nombre de la unidad grado Celsius. Por ejemplo, 12 m°C (12 miligrados Celsius) es aceptable. Sin embargo, para evitar confusión, los símbolos de los prefijos (y los prefijos) no se usan con los símbolos de las unidades relacionadas con el tiempo (nombres) min (minuto), h (hora), d (día); ni con los símbolos (nombres) relacionados con ángulos ° (grado), (minuto), y (segundo) (ver Cuadro 7).
Los símbolos de los prefijos (y los prefijos) se pueden usar con los símbolos (nombres) de las unidades L (litro), t (tonelada métrica), eV (electronvolt), y u (unidad de masa atómica unificada) (ver Cuadros 8 y 9). Sin embargo, aunque los submúltiplos de litro como mL (mililitro) y dL (decilitro) son de uso común, los múltiplos de litro así como kL (kilolitro) y ML (megalitro) no lo son. De forma similar, aunque se usan, comúnmente, múltiplos de tonelada métrica como kt (tonelada kilométrica), los submúltiplos así como mt (tonelada milimétrica), que es igual al kilogramo (kg), no se usa. Ejemplos del uso de símbolos de prefijos con eV y u son 80 MeV (80 megaelectronvoltios) y 15 nu (15 unidades de masa atómica nanounificada) (1).
REGLAS Y CONVENCIONES DE ESTILO PARA EXPRESAR VALORES DE CANTIDADES
Valor y valor numérico de una cantidad
El valor de una cantidad es la magnitud expresada como el producto de un número y una unidad, y el número multiplicado por la unidad es el valor numérico de la cantidad expresada en la unidad.
Espacio entre valor numérico y símbolo unidad
En la expresión del valor de una cantidad, el símbolo de la unidad se coloca después del valor numérico y se deja un espacio entre el valor numérico y el símbolo de la unidad.
La única excepción a esta regla es para los símbolos de unidades de grado, minuto y segundo para ángulo plano, respectivamente: °, , y , (ver Cuadro 7), en cuyo caso no se deja espacio a la izquierda entre el valor numérico y el símbolo de la unidad.
Ejemplo:
α= 30°228
Nota:α es un simbolo de cantidad para angulo plano.
Esta regla significa que:
a. El símbolo °C para el grado Celsius es precedido por un espacio cuando se expresan valores de temperatura Celsius.
Ejemplo:
t = 30,2 °C y no: t = 30,2°C o t = 30,2° C
b. Aun cuando el valor de una cantidad es usada en sentido adjetivo, se deja un espacio a la izquierda entre el valor numérico y el símbolo de la unidad (esta regla reconoce que los símbolos de las unidades no son como otras palabras corrientes o abreviaturas, sino que son entidades matemáticas, y que el valor de una cantidad debe expresarse de manera tal que sea tan independiente del lenguaje como sea posible.
Ejemplos:
un calibre final de 1 m
y no:
un calibre final de 1-m
Una resistencia de 10 kΩ
y no:
una resistencia de 10-kΩ
Sin embargo, si hay ambigüedad, las palabras deben reacomodarse adecuadamente. Por ejemplo, la aseveración las muestras fueron colocadas en viales de 22 mL debería ser reemplazada por las muestras fueron colocadas en viales con un volumen de 22 mL.
Nota: Cuando se escriban los nombres completos, aplican las normas del lenguaje. Por ejemplo un rollo de película de 35 milímetros es aceptable.
Número de unidades por valor de una cantidad
El valor de una cantidad se expresa, al usar no más de una unidad.
Ejemplo:
l = 10,234 m y no: l = 10 m 23 cm 4 mm
Nota: Son excepciones a esta regla, las expresiones de valores de intervalos (tiempo) y de ángulos planos. Sin embargo, es preferible escribir 22,20° en vez de 22°12, excepto en campos como cartografía y astronomía.
No se acepta agregar información a las unidades
Cuando se da el valor de una cantidad, es incorrecto agregar letras u otros símbolos a la unidad a fin de proveer información acerca de la cantidad o de sus condiciones de medición. En vez, deben agregarse letras u otros símbolos a la cantidad.
Ejemplo:
Vmax = 1000 V y no: V = 1000 Vmax
Nota: V es un símbolo de cantidad para diferencia de potencial.
No se acepta mezclar información con las unidades
Cuando se den valores de una cantidad, cualquier información concerniente a sus condiciones de medición debe ser presentada de manera que no se asocien con la unidad. Esto significa que las cantidades deben ser definidas de manera que puedan ser expresadas solamente en unidades aceptadas (esto incluye a la unidad uno).
Ejemplo:
El contenido de Pb is 5 ng/L y no:
5 ng Pb/L o 5 ng de plomo/L
La sensibilidad para las moléculas de NO3 es 5 x 1010/cm3
y no la sensibilidad es 5 x 1010 moléculas de NO3 / cm3
La tasa de emisión de neutrón es 5 x 1010/s
y no: la tasa de emisión es 5 x 1010 n/s
El número de densidad de los átomos de O2 is 3 x 1018/cm3
y no la densidad es 3 x 1018 átomos de O2 / cm3
La resistencia por cuadrado es 100 Ω
y no: la resistencia es 100 Ω/cuadrado
Símbolos por números y unidades versus nombres completos de números y unidades
Los elementos clave de un trabajo científico o técnico, particularmente los resultados de mediciones y los valores de cantidades que influyan en las medidas, deben presentarse tan independientemente del lenguaje como sea posible. Esto permitirá que el documento sea entendido por una audiencia más amplia, inclusive a los lectores con conocimientos limitados de la lengua extranjera. Así, para promover la comprensión de información cuantitativa en general y tener un entendimiento amplio en particular, los valores de cantidades deberían expresarse en unidades aceptadas mediante el uso de:
los símbolos arábigos para los números, esto es, los números arábigos, no los nombres de los mismos, y:
los símbolos de las unidades, no el nombre completo de las mismas.
Ejemplo:
la longitud del láser es 5 m y no: la longitud del láser es cinco metros.
La muestra fue calentada a una temperatura de 955 K por 12 h y no: la muestra fue calentada a una temperatura de 955 kelvins por 12 horas.
Notas:
1. Si se utiliza un símbolo en particular que puede no ser conocido por la audiencia, debe definirse la primera vez que se mencione.
2. Debido a que el uso del nombre completo de un número arábigo con el símbolo de una unidad puede causar confusión, debe evitarse esta combinación. Por ejemplo, no debe decirse el largo del láser es cinco m.
3. Ocasionalmente, se usa un valor en una obra descriptiva o literaria y es correcto usar el nombre completo y no el símbolo. Se considera aceptable: la lámpara para leer se diseñó para aceptar bombillos de luz de 60 vatios o el cohete viajó sin problemas a través de 380 000 kilómetros en el espacio, o ellos compraron un rollo de película de 35 milímetros para su cámara.
Claridad en la escritura de valores y cantidades
El valor de una cantidad se expresa como el producto de un número y una unidad. Para evitar
confusiones, los valores de cantidades deben escribirse de manera nítida para que sea completamente claro a qué símbolos de unidades pertenecen los valores numéricos. Se recomienda el uso de la letra a para indicar rango de valores de cantidades en vez del guion porque puede confundirse con el signo menos (la primera de estas recomendaciones nuevamente reconoce que los símbolos de las unidades no son palabras ordinarias ni abreviaturas sino entidades matemáticas).
Ejemplos:
51 mm x 51
mm x 25 mm
y no:
51 x 51 x 25 mm
225 nm a 2400 nm
o (225 a 2400) nm
y no:
225 a 2400 nm
0 °C a 100 °C o (0 a 100) °C
y no:
0 °C - 100 °C 0 V a 5 V o (0 a 5) V
y no:
0 - 5 V
(8,2, 9,0, 9,5, 9,8, 10,0) GHz
y no:
8,2, 9,0, 9,5, 9,8, 10,0 GHz
63,2 m ± 0,1 m o (63,2 ± 0,1) m
y no
63,2 ± 0,1 m o 63,2 m ± 0,1
129 s - 3 s = 126 s o (129 - 3) s = 126 s
y no:
129 - 3 s = 126 s
No se aceptan símbolos aislados de unidades
Los símbolos de unidades nunca deben usarse sin valores numéricos o símbolos de cantidades (estos no son abreviaturas).
Ejemplos:
hay 106 mm in 1 km y no: hay muchos mm en un km
Se vende por metro cúbico y no: se vende por el m3
Selección de los prefijos SI
La selección de los múltiplos o submúltiplos decimales apropiados de una unidad para expresar el valor de una cantidad, y así la elección del prefijo, se basa en varios factores; estos incluyen:
la necesidad de indicar qué dígitos de un valor numérico son significativos;
la necesidad de tener valores numéricos que sean fácilmente entendidos; y,
el ejercicio de un campo particular de ciencia o tecnología.
Un dígito es significativo si es requerido para explicar el valor numérico de una cantidad. En la expresión l = 1200 m, no es posible decir si los últimos dos ceros son significativos o solo indican la magnitud del valor numérico de l . Sin embargo, en la expresión l = 1,200 km, que usa el símbolo prefijo para 103 (kilo, símbolo k), los dos ceros se asume que son significativos porque si no lo fueran el valor de l hubiera sido escrito l = 1,2 km.
Frecuentemente, se recomienda, que para un mejor entendimiento, deben elegirse símbolos prefijos de manera tal que los valores numéricos estén entre 0,1 y 1000, y que se usen solo símbolos prefijos que representen el número 10 elevado a la potencia que es múltiplo de 3.
Ejemplos:
3,3 x 107 Hz puede ser escrito como
33 x 106 Hz = 33 MHz
0,009 52 g puede ser escrito como
9,52 x 10–3 g = 9,52 mg
2703 W puede ser escrito como
2,703 x 103 W = 2,703 k
5,8 x 10–8 m puede ser escrito como
58 x 10–9 m = 58 nm
Sin embargo, los valores de cantidades no siempre permiten seguir esta recomendación, ni es obligatorio realizarla.
recomienda usar un solo símbolo prefijo aun si los valores numéricos no se encuentran entre 0,1 y 1 000. Por ejemplo, es preferible escribir el tamaño de la muestra es 10 mm x 3 mm x 0,02 mm en vez de "el tamaño de la muestra es de 1mm x 3mm x 20 µm"
En cierto tipo de dibujos de ingeniería, es costumbre expresar todas las dimensiones en milímetros. Esto es un ejemplo de selección del prefijo basado en la práctica de un campo particular de la ciencia o tecnología.
Valores de cantidades expresadas simplemente como números: la unidad uno, símbolo 1
Ciertas cantidades, así como índice de refractariedad, permeabilidad relativa, y fracción de masa, se definen como la relación de dos cantidades comparables mutuamente y así son de dimensión uno. La unidad SI coherente para esa cantidad es la relación de dos unidades idénticas y puede ser expresada por el número 1. Sin embargo, el número 1, generalmente, no aparece en la expresión por el valor de una cantidad de dimensión uno. Por ejemplo, el valor del índice refractivo de un medio dado se expresa como
n = 1,51 x 1 = 1,51.
De otro lado, ciertas cantidades de dimensión uno tienen unidades con nombres y símbolos especiales que pueden ser usados o no dependen de las circunstancias. Ángulo plano y ángulo sólido, cuyas unidades SI son el radián (rad) y el estereorradián (sr), respectivamente, son ejemplos de esas cantidades.
Múltiplos y submúltiplos decimales de la unidad uno
Debido a que los símbolos prefijos no pueden agregarse a la unidad uno, se usan potencias de 10 para expresar múltiplos y submúltiplos de la unidad uno.
Ejemplo:
µr = 1,2 x 10–6 y no: µr
Nota: µ es el simbolo de cantidad para permeabilidad relativa.
Por porcentaje, %, fracción
Es aceptable y reconocido internacionalmente el uso del símbolo.% (porcentaje) para el número 0,01 con el SI y así expresar los valores de cantidades de dimensión mediante este. Cuando se usa, se deja un espacio entre el símbolo % y el número por el cual es multiplicado. Además, debe usarse el símbolo % y no el nombre porciento.
Ejemplo:
χ
Nota: χB es el símbolo para cantidad de sustancia fracción de B.
Debido a que el símbolo % representa simplemente a un número, este no tiene significado si se le añade información. Deben, por tanto, evitarse las frases como porcentaje por peso, porcentaje por masa, porcentaje por volumen, o porcentaje por cantidad de sustancia. Igualmente, debe evitarse escribir por ejemplo
% (m/m), % (por peso), % (V/V), % (por volumen),
o % (mol/mol).
Del mismo modo, debido a que el símbolo % representa simplemente al número 0,01, es incorrecto escribir, por ejemplo, cuando las resistencias R1 y R2 difieren por 0,05 %, o cuando la resistencia R1 excede la resistencia R2 por 0,05 %. En cambio, debe escribirse, por ejemplo, donde R1 = R2(1 + 0,05 %), o definir una cantidad ∆ via la relacion ∆ = (R1 . R2)/ R2 y escribir gdon∆ = 0,05 %.h Alternativamente, en ciertos casos, puede usarse la palabra gfraccion deh o grelativoh. Por ejemplo, seria aceptable escribir gel aumento de fraccion de la resistencia del estandar de referencia 10 k en 1994 fue 0,002 %.h
ppm, ppb, y ppt
Los términos partes por millón, partes por billón y partes por trillón, y sus abreviaturas respectivas, ppm, ppb, y ppt (y términos similares y abreviaturas), no se aceptan para expresar valores de cantidades en el SI. Deben usarse en su lugar, formas como las que se suministran en los siguientes ejemplos.
Ejemplos:
una estabilidad de 0,5 (µA/A)/min
y no:
una estabilidad de 0,5 ppm/min
un cambio de 1,1 nm/m
y no:
un cambio de 1,1 ppb un cambio de frecuencia de 0,35 x 10–9 f
y no:
un cambio de frecuencia de 0,35 ppb
una sensibilidad de 2 ng/kg
y no:
una sensibilidad de 2 ppt
Debido a que los números 109 y mayores no son uniformes mundialmente, es mejor que se eviten completamente (en la mayoría de los países, 1 billón = 1 x 1012, no 1 x 109 como en Estados Unidos); la manera preferida para expresar grandes números es usar potencias de 10. La ambigüedad de los nombres de los números es una de las razones de por qué no deben usarse ppm, ppb, ppt, y similares. Otra, y la más importante, es que es inapropiado el uso de abreviaturas que son dependientes del lenguaje junto con signos y símbolos reconocidos internacionalmente así como MPa, ln, 1013, y %, para expresar los valores de cantidad y en ecuaciones y otras expresiones matemáticas.
Nota: En ciertas circunstancias, el uso de ppm, ppb, y similares, puede ser requerido por una ley o regulación.
Números romanos
No se acepta el uso de números romanos para expresar valores de cantidades. En particular, no debe usarse C, M, y MM como sustitutos de 102, 103, and 106, respectivamente (ver Anexo 4).
Ecuaciones de cantidad y ecuaciones de valores numéricos
Una ecuacion de cantidad expresa una relacion entre cantidades. Un ejemplo es l = ut, donde l es la distancia de una particula en movimiento uniforme de velocidad que viaja en el tiempo t.
Debido a que una ecuación de cantidad así como l= t es independiente de las unidades usadas para expresar los valores de las cantidades que componen la ecuacion, y porque l, u, y t representan cantidades y no valores numericos, es incorrecto asociar la ecuación con afirmación como "donde l es en metros, u es en metros por segundos, y t es en segundos."
Por otra parte, una ecuacion valor numerico expresa una relacion entre valores numericos de cantidades y, por tanto, depende de las unidades usadas para expresar los valores de las cantidades. Por ejemplo, {l}m = 3,6-1 {u}km/h {t}s expresa la relacion entre los valores numericos de l, u, y t solo cuando los valores de l, u, y t son expresados en unidades metro, kilometro por hora, y segundo, respectivamente. (Aqui {A}X es el valor numerico de cantidad A cuando su valor es expresado en la unidad X).
Nombres propios de cantidades cocientes
Al escribirse las cantidades formadas de otras cantidades por división se usan las palabras dividido por en vez de las palabras por unidad a fin de evitar la apariencia de asociación de una unidad particular con la cantidad derivada.
Ejemplo:
presión es fuerza dividida por área
y no:
presión es fuerza por unidad de área
Distinción entre un objeto y un atributo
Para evitar confusión, cuando se discuten cantidades o se reportan sus valores, se debe distinguir entre un fenómeno, cuerpo o sustancia, y un atributo adscrito a este. Por ejemplo, debe reconocerse la diferencia entre un cuerpo y su masa, una superficie y su área, un capacitador y su capacitancia, y un espiral y su inductancia. Esto significa que aunque es aceptable decir un objeto de 1 kg masa se agregó a una cuerda para formar un péndulo no es aceptable decir una masa de 1 kg se agregó a una cuerda para formar un péndulo.
COMENTARIOS ACERCA DE ALGUNAS CANTIDADES Y SUS UNIDADES
Tiempo y frecuencia de rotación
La unidad de tiempo SI (intervalo actualmente) es el segundo (s) y debe usarse en todos los cálculos técnicos. Cuando el tiempo se relacione con ciclos calendarios, pueden ser necesarios el minuto (min), la hora (h), y el día (d). Por ejemplo, el kilómetro por hora (km/h) es la unidad usual para expresar velocidades de los vehículos. Aunque no se ha aceptado universalmente un símbolo para el año, se sugiere que sea el símbolo a.
La frecuencia de rotación n de un cuerpo se define como el número de revoluciones que este hace en un intervalo dividido por ese intervalo. La unidad SI para esta cantidad es la recíproca de segundo (s–1). Sin embargo, la designación de revoluciones por segundo (r/s) y revoluciones por minuto (r/min) son usadas ampliamente como unidades de frecuencia de rotación en especificaciones de maquinarias de rotación.
Volumen
La unidad SI de volumen es el métro cúbico (m3) y puede usarse para expresar el volumen de cualquier sustancia en estado sólido, líquido o gaseoso. El litro (L) es un nombre especial para el decímetro cúbico (dm3), pero se recomienda que no se use el litro para dar resultados de mediciones precisas de volúmenes. Tampoco es una práctica común el uso del litro para expresar los volúmenes de sólidos y usar los múltiplos del litro así como el kilolitro (kL).
Peso
En ciencia y tecnología, el peso de un cuerpo en un marco de referencia particular se define como la fuerza que da el cuerpo una aceleración igual a la aceleración local de caída libre en ese marco de referencia. Así, la unidad SI de cantidad de peso definido en esta forma es el newton (N). Cuando el marco de referencia es un objeto celestial, la Tierra, por ejemplo, el peso de un cuerpo es llamado comúnmente la fuerza local de gravedad en el cuerpo.
Ejemplo: La fuerza de gravedad de una esfera de cobre de masa 10 kg localizada en la superficie de la Tierra, el cual es su peso en esa ubicación, es aproximadamente 98 N.
Nota: La fuerza local de gravedad de un cuerpo, esto es, su peso, es la resultante de todas las fuerzas gravitacionales en el cuerpo y la fuerza centrífuga local debida a la rotación del objeto celestial. El efecto de la presión atmosférica es excluido usualmente, y así el peso de un cuerpo es, generalmente, la fuerza de gravedad en un cuerpo en el vacío.
En uso comercial y diario, y especialmente el lenguaje cotidiano, el peso es expresado con el uso de sinónimos de masa. Así, la unidad SI de cantidad de peso usado en este sentido es el kilogramo (kg) y el verbo pesar significa determinar la masa de o tener una masa de.
Ejemplos:
el peso del niño es de 23 kg
el maletín pesa 6 kg
Peso neto 227 g
Masa atómica relativa y masa molecular relativa
Los términos peso atómico y peso molecular son obsoletos y por tanto deben evitarse. Han sido reemplazados por los términos equivalentes, pero preferidos de masa atómica relativa, símbolo Ar, y masa molecular relativa, símbolo Mr, respectivamente, las cuales reflejan mejor sus definiciones. Como el peso atómico y el peso molecular, la masa atómica relativa y la masa molecular relativa son cantidades de dimensión uno y se expresan simplemente como números. Las definiciones de esas cantidades son las siguientes:
Masa atómica relativa (anteriormente peso atómico): relación de la masa promedio por átomo de un elemento a la 1/2 de la masa del átomo de un nucleido 12C.
Masa molecular relativa (anteriormente peso molecular): relación de la masa promedio por molécula o entidad especificada de una sustancia a la 1/2 de la masa de un átomo del nucleido 12C.
Ejemplos:
Ar (Si) = 28,0855
Mr (H2) = 2,0159
Ar (12C) = 12 exactamente
Intervalo de temperatura y diferencia de temperatura
La temperatura Celsius (t) se define en términos de temperatura termodinámica (T) por la ecuación t = T – T0, donde T0 = 273.15 K por definición. Esto implica que el valor numérico de un intervalo de temperatura o diferencia de temperatura cuyo valor es expresado en la unidad grado Celsius (°C) es igual al valor numérico del mismo intervalo o diferencia cuando su valor se expresa en la unidad kelvin (K); {t}°C = {T}K. Así, intervalos de temperatura o diferencias de temperatura pueden ser expresadas tanto en grados Celsius como en kelvin con el uso del mismo valor numérico.
Ejemplo:
La diferencia en temperatura entre el punto de congelación del galio y el punto triple del agua es t = 29,7546 °C = T = 29,7546 K.
REGLAS Y CONVENCIONES DE ESTILO PARA ESCRIBIR LOS NOMBRES DE LAS UNIDADES
Mayúsculas
Cuando los nombres de las unidades se escriban completos, se tratan como nombres ordinarios de la lengua española. Así, deben comenzar con letra minúscula, a menos que se encuentren al comienzo de una frase.
Manteniendo esta regla, la forma correcta de escribir la unidad °C es grado Celsius (la unidad grado comienza con la letra minúscula g y el modificador Celsius comienza con mayúscula porque es el nombre de una persona).
Plurales Los nombres de las unidades en plural se usan cuando son requeridos por la gramática española.
Ejemplo:
SINGULAR PLURAL
henry henries
metro metros
gramo gramos
lux lux
hertz hertz
siemmens siemmens
Escritura de nombres de unidades y prefijos
Cuando se escriba el nombre de una unidad que contenga un prefijo, no deben usarse guiones entre el prefijo y el nombre de la unidad Ejemplos:
miligramo y no: mili-gramo
kilopascal y no: kilo-pascal
Hay tres casos en los que se omite la vocal final del prefijo: megohm (no megaohm), kilohm (no kiloohm), y hectárea (no hectoárea). En todos los otros casos donde el nombre de la unidad comience con una vocal, se retienen la vocal final del prefijo y la vocal inicial del nombre.
Escritura de nombres obtenidos por multiplicación
Al escribir el nombre de una unidad derivada formada por multiplicación de otras unidades, se deja un espacio entre estas, o un guion.
Ejemplo: pascal segundo o pascal-segundo
Escritura de nombres obtenidos por división
Al escribir el nombre de una unidad derivada formada por división de otras unidades, se usa la palabra por en vez de una barra oblicua (/).
Ejemplo:
ampere por metro (A/m) y no: ampere/metro
Escritura de nombres de unidades elevadas a una potencia
Al escribir los nombres de unidades elevadas a una potencia se colocan los modificadores como cuadrado o cúbico después del nombre de la unidad.
Ejemplo:
metro por segundo cuadrado (m/s2)
milímetro cúbico (mm3)
ampere por metro cuadrado (A/m2)
kilogramo por metro cúbico (kg/m3)
No se acepta aplicar nombres de unidades en operaciones matemáticas
Para evitar confusión, no se deben aplicar operaciones matemáticas a nombres de unidades, deben usarse únicamente los símbolos de las unidades.
Ejemplo:
joule por kilogramo o J/kg o J · kg–1
y no:
joule/kilogramo o joule · kilogramo–1
Tipos de símbolos
Existen tres categorías de símbolos: (a) símbolos para cantidades, (b) símbolos para unidades y (c) símbolos para términos descriptivos. Los símbolos de cantidad, que se imprimen siempre en letra itálica, son, con pocas excepciones, letras simples de los alfabetos latino y griego que pueden tener subíndices o superíndices u otros signos de identificación. Los símbolos para unidades, en particular aquellos para unidades aceptables, se han descrito en detalle en párrafos anteriores. Los símbolos para términos descriptivos incluyen los símbolos de los elementos químicos, ciertos símbolos matemáticos, y modificadores superíndices y subíndices de símbolos de cantidad.
Símbolos de cantidad estandarizados Debe evitarse el uso de palabras, acrónimos, u otro grupo de letras como símbolos de cantidad. Por ejemplo, uso del símbolo de cantidad Zm para impedancia mecánica y no MI.
Ejemplos:
Ω (angulo solido)
Zm (impedancia mecanica)
LP (nivel de una cantidad de potencia)
∆r (exceso de masa relativa) p (presion)
stot (seccion transversal total)
E (fuerza de campo electrico)
TN (temperatura Neel)
Signos y símbolos matemáticos estandarizados
Así como para los símbolos de cantidad, la mayoría de los signos y símbolos matemáticos usados en ciencias físicas y tecnología están estandarizados.
Ejemplos:
^ (signo de conjunción, p ^ q significa p y q)
¹ (a ¹ b, a no es igual a b) .
» (a » b, a es aproximadamente igual a b)
~ (a ~ b, a es proporcional a b)
loga c (logaritmo de la base a de c)
tipo itálico (itálica) para área de cantidad de escala: A;
tipo romano (normal) para la unidad ampere: A;
itálica negrita (bold) para la cantidad de vector potencial: A.
Más específicamente, las tres categorías mayores de símbolos encontrados en publicaciones científicas y técnicas, deben escribirse en tipo itálico o romano, como sigue:
símbolos para cantidades de variables: itálicas;
símbolos para unidades: romana;
símbolos para términos descriptivos: romana.
Esas reglas implican que un subindice o un superindice en un simbolo de cantidad se escribe en tipo romano si es descriptivo (por ejemplo, si es un numero o representa el nombre de una persona o una particula); pero se escribe en italica si representa una cantidad, o es una variable, asi como c en Eco un indice asi como i en åici que representa un numero.
Notas: La regla anterior tambien implica, por ejemplo, que µ, el simbolo para el prefijo SI micro (10-6), que Ω, el simbolo para la unidad SI derivada ohm, y que F, el simbolo para la unidad SI derivada farad, se imprimen en tipo romano; pero cuando se imprimen en italica representan cantidades (µ, Ω, y F son los simbolos recomendados para las cantidades de momento magnetico de una particula, angulo solido y fuerza, respectivamente).
Alfabeto griego en tipo de letra romana e itálica
En el Cuadro 13 se muestran los tipos de letras del alfabeto griego en letra romana.
Símbolos para los elementos
Tipo de letra y puntuación para los símbolos de los elementos
Los símbolos para los elementos se imprimen, normalmente, en tipo de letra romana sin tomar en cuenta el tipo de letra del texto circundante. No van seguidas de un punto a menos que estén al final de un párrafo.
SUBÍNDICES Y SUPERÍNDICES EN SÍMBOLOS DE ELEMENTOS
El número nucleón (número masa) de un nucleido se escribe como un superíndice izquierdo: 28Si.
El número de átomos de una molécula de un nucleido en particular se muestra como un subíndice a la derecha: 1H2.
El número protón (número atómico) se indica como un subíndice izquierdo: 29Cu.
El estado de ionización o excitación se indica como un superíndice derecho. Ejemplos:
Estado de ionización: Ba++
Co(NO2)6 --- o Co(NO2)6 3- o [Co(NO2)6]3-
Estado de excitación electrónica: Ne*, CO*
Estado de excitación nuclear: 15N* o 15Nm
Impresión de números
Tipo de letra para números
Los números arábigos que expresan valores de cantidades se imprimen en letras romanas (normal), independientemente del tipo de letra circundante en el texto. Otros números arábigos que no son valores numéricos o cantidades se imprimen en letra romana normal, o itálica negrita o negrita normal, pero se prefiere, usualmente, el tipo romano normal.
Agrupación de dígitos
Los dígitos deben separarse en grupos de tres y no deben emplearse puntos como separadores (o coma en Estados Unidos), se centa desde el separador decimal hacia la izquierda y hacia la derecha, y se deja un espacio fijo entre estos.
Ejemplos:
76 483 522 y no: 76.483.522
43 279,168 29 y no: 43.279,168 29
8012 u 8 012 y no: 8.012
0,491722 3 y no: 0,4917223
0,5947 o 0,594 7 y no: 0,59 47
8012,5947 y no: 8 012,5947
u 8 012,594 7 u 8012,594 7
Nota: La práctica de usar un espacio entre los grupos de dígitos no es, usualmente, seguida en ciertas aplicaciones especializadas, así como dibujos de ingeniería y balances financieros.
Multiplicación de números
Cuando se usa el punto como marcador decimal (Estados Unidos), el signo preferido para la multiplicación es la equis (que es el signo de multiplicación) (x), no el punto a media altura (esto es, centrado) ( · ).
Ejemplos:
25 x 60.5 y no: 25 · 60.5
5m/s x 10.2 s y no: 53 m/s · 10.2 s
15 x 72 kg y no: 15 · 72 kg
Cuando se usa la coma como marcador decimal, el signo preferido de multiplicación es el punto a media altura. Sin embargo, aun cuando se use la coma, preferimos el uso de la equis para la multiplicación de valores de cantidades.
La multiplicación de símbolos de cantidad (o números en paréntesis o valores de cantidades en paréntesis) puede indicarse en una de las siguientes maneras: ab, a b, a · b, a x b.
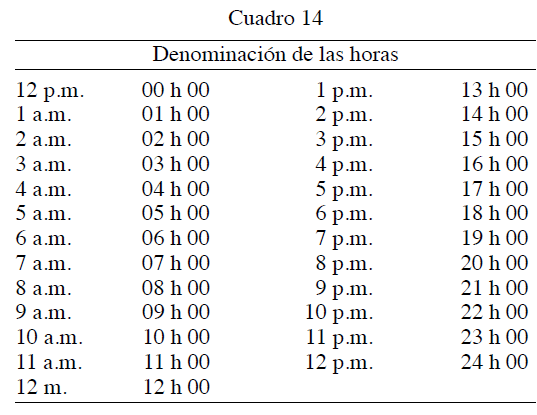
Denominación correcta del tiempo
El día está dividido en 24 horas, por tanto, las horas deben denominarse desde las 00 hasta las 24 (ver Cuadro 14)
Nota: siguiendo las recomendaciones de la RAE de 2010, antemeridiano, meridiano y posmeridiano) se abrevian a.m., m. y p.m. (10).
Ejemplos:
3 de la tarde 30 minutos: 15 h 30
9 de la noche 18 minutos: 21 h 18
Escritura numérica de fechas
Para la escritura numérica de fechas se utilizarán únicamente cifras arábigas, en tres agrupaciones separadas por un guion.
La primera agrupación corresponde a los años y tendrá 4 cifras.
La segunda agrupación consta de dos dígitos, entre el 01 y el 12, y corresponderá a los meses.
La tercera consta también de dos dígitos, entre el 01 y el 31, y corresponderá a los días.
Ejemplos:
24 de mayo 1982 = 1982-05-24
10 de agosto de 1982 = 1982-08-10
1ro de enero de 1983 = 1983-01-01
Por qué la coma como marcador decimal
Las razones por las cuales se escogió la coma como signo para separar en un número la parte entera de la decimal, pueden considerarse en cierta forma como un cúmulo de razones sencillas y hasta un tanto humildes en su concepción individual. Sin embargo, todas estas, en conjunto, explican por qué la coma fue escogida como único signo ortográfico en la escritura de números (1):
1. La coma es reconocida por la Organización Internacional de Normalización ISO (esto es, por alrededor de 90 países de todo el mundo) como único signo ortográfico en la escritura de números.
2. La importancia de la coma para separar la parte entera de la decimal, es enorme. Esto se debe a la esencia misma del Sistema Métrico Decimal, por ello debe ser visible, no se debe perder durante el proceso de aplicación o reducción de documentos.
3. La grafía de la coma se identifica y distingue mucho más fácilmente que la del punto.
4. La coma es una grafía que, por tener forma propia, demanda del escritor la intención de escribirla, el punto puede ser accidental o producto de un descuido.
5. El punto facilita el fraude, puede ser transformado en coma, pero no viceversa.
6. En matemática, física y, en general en los campos de la ciencia y de la ingeniería, el punto es empleado como signo operacional de multiplicación. Esto podría llevar a error o causar confusión, no es recomendable usar un mismo signo ortográfico para dos diferentes propósitos.
7. En nuestro lenguaje común, la coma separa dos partes de una misma frase, mientras que el punto detalla una frase completa. Por consiguiente y teniendo esto en cuenta, es más lógico usar la coma para separar la parte entera de la parte decimal de una misma cantidad.
8. Es una regla estricta que el marcador decimal debe tener siempre, por lo menos, una cifra a su izquierda y a su derecha. Sin embargo, en países donde se usa el punto como marcador decimal, se escribe, muy a menudo, expresiones como .25 en vez de lo correcto 0.25. Esta forma incorrecta de escribir números decimales puede tener consecuencias muy graves: si un médico prescribe .25 mg en una receta y no marca claramente el punto, la enfermera o el farmacéutico pueden fácilmente leer 25 mg y como consecuencia pueden preparar para el paciente una dosis cien veces mayor de la medicina recetada, lo cual podría ocasionarle, inclusive, la muerte. Si el médico hubiera escrito 0,25 mg esto no pasaría, aun en el caso de no haber escrito con claridad el punto, se leería 0 25 mg, grafía que inmediatamente y por su misma naturaleza hace comprender que el marcador decimal no se ha escrito. En los países métricos donde se usa la coma como separador decimal, el caso anteriormente descrito es prácticamente imposible que se dé, puesto que la coma es una grafía mucho más visible y fácil de identificar. Además, si el que escribe está tentado de escribir, .25 por ser esta una forma de escritura totalmente no acostumbrada, resalta de inmediato la necesidad de escribir el cero antes de la coma.
9. Una de las más importantes razones para aceptar el Sistema Internacional de Unidades SI que no es otra cosa que el Sistema Métrico Decimal modernizado, es el de facilitar el comercio y el intercambio de conocimientos e informes en un mundo métrico. La coma se usa como marcador decimal en toda Europa continental y en casi toda Sudamérica. Al adoptar la coma, pues, se adopta una práctica aceptada mundialmente, lo que nos permite usufructuar, sin confusiones ni dudas, el intercambio mundial de ciencia y experiencia.
REFERENCIAS
1. Pérez DGregorio R. Sistema Internacional de Unidades SI. En: Pérez DGregorio R, editor. Normas para autores y editores. Volumen I. Caracas: Editorial Ateproca; 2011.p.361-420.
2. Sistema Internacional de Unidades. Disponible en: http://es.wikipedia.org/wiki/Sistema_Internacional_ de_Unidades. Consultado 28 de enero 2015.
3. Gaceta Oficial de la República Bolivariana de Venezuela. Número 38.263. Disponible en: http:// historico.tsj.gov.ve/legislacion/LeyesOrdinarias/46.- GO_38263.pdf
4. Physical Measurement Laboratory of NIST. International System of Unis (SI). http://physics.nist. gov/cuu/Units/index.html
5. Servicio Nacional de Metrología de Venezuela. Sistema Internacional de Unidades SI. Rev Obstet Ginecol Venez. 1992;52(3):183-189. [ Links ]
6. International Committee of Medical Journal Editors. Recommendations for the Conduct, Reporting, Editing, and Publication of Scholarly work in Medical Journals. http://www.icmje.org
7. Comité Internacional de Editores de Revistas Médicas (ICMJE). Recomendaciones para la realización, informe, edición y publicación de trabajos académicos en revistas médicas. Actualizado diciembre 2014. Traducción: Rogelio Pérez DGregorio. Rev Obstet Ginecol Venez. 2014;74(4):259-284.
8. Real Academia Española. Diccionario de la Lengua Española. Vigésima segunda edición. Madrid: Editorial Espasa Calpe, S.A.; 2001.
9. Real Academia Española. Asociación de Academias de la Lengua Española. Nueva gramática de la lengua española. Volumen I y II. Madrid: Espasa Libros, S.L.U; 2009.
10. Real Academia Española. Asociación de Academias de la Lengua Española. Ortografía de la lengua española. Madrid: Espasa Libros, S.L.U; 2010.
11. Pérez D Gregorio R. Los números en los textos escritos. Gac Méd Caracas. 2012;120(3):320-343.
12. Rozman C. Medicina Clínica. Manual de Estilo. Publicaciones médicas. Barcelona, España; Ediciones Doyma; 1993.
13. Medicina Clínica. Manual de Estilo. Barcelona: Doyma, 1993.