Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Técnica de la Facultad de Ingeniería Universidad del Zulia
versión impresa ISSN 0254-0770
Rev. Téc. Ing. Univ. Zulia v.31 n.2 Maracaibo ago. 2008
Computer model to predict drillstring lateral vibration modes and frequencies using the finite-element-method and modal analysis.
David Bukowitz1, Joaquín Morán1 y Rafael Bravo2
1Escuela de Mecánica, Facultad de Ingeniería, Universidad del Zulia. Apartado 4011-A-526, Maracaibo, Venezuela. Tel: +58-261-7598772. dbukowitz@luz.edu.ve.
2Mechanical Engineering Department. McMaster University. Hamilton, ON, Canada.
Abstract
A computer program based on the finite element method was developed to predict the lateral vibration modes and frequencies in the Bottom Hole Assembly (BHA) of a drillstring. This model is applicable in both a planning and a real time mode of operation to avoid resonance problems. The analysis used in this model proceeds in two stages. The first stage solves the two-dimensional nonlinear static deformation of the drillstring; this gives the deformed shape of the BHA and the side forces at points where the BHA touches the wellbore wall. In this way, the length of the BHA that is free to vibrate in the lateral direction is obtained. The second stage consists in a dynamic analysis of the system, to obtain the lateral vibration modes and frequencies. The model was compared with experimental and simulated results obtained from several BHA configurations, giving excellent results.
Key words: Drillstring vibration, BHA, vibration modes.
Programa computacional para predecir las frecuencias y modos de vibración transversales en sartas de perforación mediante el método de elementos finitos y análisis modal.
Resumen
Se desarrolló un programa computacional mediante el método de elementos finitos, que permite predecir las frecuencias y modos transversales de vibración en el Ensamblaje de Fondo (BHA) de las sartas de perforación. Este modelo se puede aplicar tanto en la planificación como en tiempo real durante la operación de perforación, con la finalidad de evitar problemas de resonancia en el sistema. Este análisis se lleva a cabo en dos etapas. En la primera se resuelve el problema bidimensional y no lineal de la deformación estática de la sarta; esto proporciona su perfil deformado y las fuerzas en los puntos donde contacta las paredes del hoyo. De esta forma se determina la longitud efectiva del ensamblaje de fondo que está libre de vibrar lateralmente. La segunda, consiste en un análisis dinámico del sistema para obtener las frecuencias y modos de vibración transversales. El modelo fue validado con varias configuraciones de sartas de perforación utilizadas en otros estudios y en mediciones experimentales, obteniéndose excelentes resultados.
Palabras clave: Sartas de perforación, BHA, Modos de vibración.
Recibido el 30 de Julio de 2007 En forma revisada el 24 de Marzo de 2008
Introducción
Las vibraciones mecánicas presentes en las sartas de perforación tienen gran influencia en el rendimiento de la perforación de pozos petroleros. Éstas se pueden clasificar en tres tipos según su dirección: axial, torsional y lateral o transversal [1]; ésta última es la responsable en la mayoría de los casos, de las fallas en las herramientas y componentes del ensamblaje de fondo [2].
Dentro de una metodología integrada de control de vibraciones, el modelaje y simulación de las sartas de perforación constituye una actividad fundamental en la fase de análisis y planificación de los programas de perforación de los pozos. Por lo que se ha detectado la importancia de la misma, para lograr el incremento del rendimiento en el proceso de perforación.
En este estudio, se presentan los fundamentos teóricos y la metodología de modelaje mediante el método de elementos finitos, para obtener como producto un programa computacional que permite simular las condiciones dinámicas de la sarta de perforación cuando se encuentra en operación. De esta manera se podrán conocer las frecuencias y los modos de vibración transversales a las cuales está sometida el Ensamblaje de Fondo (BHA) de la Sarta de Perforación, para así evitar el efecto de resonancia y hacer más efectivo el proceso
Vibraciones en la sarta de perforación
Los desplazamientos y esfuerzos asociados con las vibraciones, no son significativamente grandes hasta que el sistema es excitado con una señal a una de sus frecuencias naturales, lo que causa la resonancia. La mayor fuente de excitación es la velocidad de giro. Si el BHA posee una frecuencia natural transversal, axial o torsional cercana a la velocidad de rotación y ese modo no se encuentra bien amortiguado, entonces existe un peligro de resonancia en el ensamblaje de fondo que puede originar una falla debido a fatiga [3].
La interacción roca-mecha es otra de las fuentes de excitación, la cual puede estar bien amortiguada si la formación es blanda; pero si la formación es dura, se generan frecuencias debido al impacto de los dientes o insertos de la mecha. En el caso de una mecha tricónica se pueden esperar por ejemplo, frecuencias de 3xRPM [4].
Otras fuentes potenciales de excitación la constituyen las bombas de lodo y los estabilizadores. Un estabilizador con 4 aletas rectas por ejemplo, puede generar una señal con frecuencias de 4xRPM [4].
Vibraciones transversales de la sarta
Las frecuencias resonantes transversales dependen principalmente de las dimensiones y rigidez de los elementos de la sarta, de la ubicación y holgura de los estabilizadores, del peso aplicado sobre la mecha y de la inclinación del hoyo. Este último parámetro es de suma importancia, ya que es uno de los factores que determina el punto en el cual la tubería por encima del último estabilizador hace contacto con las paredes del hoyo, estableciendo efectivamente la longitud del sistema vibratorio transversal. Por este motivo, la vibración transversal no se puede apreciar en la superficie, a menos que se acople con los modos axiales y torsionales.
Descripción general del modelo
Para obtener la información requerida sobre el comportamiento del sistema, se utiliza el Método de Elementos Finitos (MEF), de amplia aceptación para la solución numérica de problemas de ingeniería, particularmente en el área de elasticidad tanto estática como dinámica [5]. El comportamiento de la sarta de perforación se analiza en un plano longitudinal que contiene al sistema (Figura 1), fijándose las condiciones de contorno en el tope, fondo y puntos de contacto entre la sarta-hoyo [6], y se divide en tres problemas desacoplados entre si: vibraciones transversales, axiales y torsionales. El objetivo del presente análisis numérico del sistema es determinar los modos y frecuencias de vibración transversales.
Análisis dinámico transversal
De los tres tipos de análisis, el caso más complejo es el de vibraciones transversales. Esto es debido a que las condiciones de contorno no están predeterminadas antes de obtener la solución, dado que los puntos de contacto de la sarta con el hoyo, debido a las fuerzas estáticas aplicadas, determinarán las condiciones de contorno, pero estos puntos a su vez no se conocen hasta que se haga un análisis no lineal geométrico estático en el rango elástico lineal del modelo. Por lo tanto, antes de efectuar el análisis dinámico transversal, es necesario efectuar un análisis estático para determinar la forma deformada de la sarta, con lo que se obtienen los puntos de contacto entre sarta y agujero que se usarán como condiciones de contorno en el análisis dinámico transversal.
Análisis estático
En el análisis estático se busca obtener la forma deformada de la sarta debido a las cargas aplicadas, tales como el peso propio de la misma, las fuerzas de flotación debidas a lodo de perforación, y el peso sobre la mecha especificado, tomando en cuenta las restricciones de desplazamiento a lo largo del sistema, debidas a los miembros (mecha, estabilizadores, mesa rotatoria), y al confinamiento de la sarta en el agujero. Dado que no se conocen a priori los puntos de contacto entre la sarta y el agujero, que dependen de la configuración deformada de la sarta, que a su vez depende de los puntos de contacto, el problema es de naturaleza no lineal y tiene que ser resuelto iterativamente.
En el análisis estático de un sistema elástico usando el MEF, se busca reducir el problema continuo a uno discreto, mediante la ecuación algebraica matricial de la forma:
![]() (1)
(1)
en donde K es la matriz de rigidez del sistema, Q es el vector de grados de libertad (GDL), formado por los desplazamientos de los nodos de los elementos, y F es el vector de cargas nodales equivalentes del sistema. La matriz K y el vector F se obtienen de superponer o “ensamblar”, las matrices de rigidez de los elementos.
Como se mencionó anteriormente, la sarta de perforación se modelará como una estructura plana con elementos conectados rígidamente. Durante el análisis estático se utilizan elementos tipo marco, de 3 grados de libertad por nodo (Figura 2).
Elemento Marco Bidimensional
Los grados de libertad nodales son los desplazamientos axiales y transversales, y la rotación transversal. Basándose en esta configuración, se puede obtener la matriz de rigidez elástica y el vector de cargas nodales equivalentes del elemento como:
 (2)
(2)
 (3)
(3)
con ![]() . La matriz
. La matriz ![]() es simétrica y las constantes involucradas son:
es simétrica y las constantes involucradas son:
E: Módulo de Young del material
A: Área de la sección transversal
L: Longitud del elemento finito
Iz: Momento de Inercia de Área centroidal con respecto a un eje transversal
Px' Py': Cargas distribuidas por unidad de longitud (por gravedad) en las direcciones axial y transversal, respectivamente.
Para resolver el problema estático, hay que tomar en cuenta el debilitamiento o reforzamiento geométrico de los elementos de la sarta debido a fuerzas de compresión o tensión a las que estos se encuentran sometidos. Esto se manifiesta a través de una matriz de rigidez geométrica que se presenta a continuación [4]:
 (4)
(4)
La matriz ![]() es simétrica, donde F es la fuerza axial promedio en el elemento, negativa si es a compresión y positiva si es a tracción, de tal manera que la matriz de rigidez del elemento es la suma de la rigidez elástica más la rigidez geométrica del elemento:
es simétrica, donde F es la fuerza axial promedio en el elemento, negativa si es a compresión y positiva si es a tracción, de tal manera que la matriz de rigidez del elemento es la suma de la rigidez elástica más la rigidez geométrica del elemento:
![]() (5)
(5)
La matriz de rigidez y el vector de cargas nodales equivalentes del sistema completo, se obtienen ensamblando las matrices locales, tomando en cuenta la orientación de cada elemento respecto al sistema de coordenadas global:
 (6)
(6)
en donde la matriz R representa la transformación de rotación entre el sistema de coordenadas local del elemento e y el sistema de referencia global, y el signo sumatoria representa el proceso de ensamble de la matrices tomando en cuenta la conectividad inter-elementos.
Antes de resolver el sistema ![]() para los GDL nodales Q, hay que eliminar la singularidad de la matriz K introduciendo las condiciones de contorno de desplazamiento prescrito, e incluir las fuerzas concentradas aplicadas a la sarta (peso sobre la mecha, tensión en el malacate).
para los GDL nodales Q, hay que eliminar la singularidad de la matriz K introduciendo las condiciones de contorno de desplazamiento prescrito, e incluir las fuerzas concentradas aplicadas a la sarta (peso sobre la mecha, tensión en el malacate).
El procedimiento descrito anteriormente resuelve el problema elástico lineal, sin tomar en cuenta el problema de contacto de la sarta con el hoyo. El proceso iterativo necesario para resolver este problema se basa en la solución del problema lineal repetidas veces, variando las condiciones de contorno, hasta que se cumpla el criterio de convergencia que está relacionado con el hecho de que la sarta no puede penetrar en la pared, y que la pared no puede “halar” a la sarta para mantener el contacto, por lo que las reacciones en los puntos de contacto tienen que tener signos opuestos al desplazamiento nodal en cada nodo de la sarta en contacto con las paredes del hoyo. En el diagrama de flujo de la Figura 3 se muestra el proceso iterativo antes descrito.
Análisis dinámico
Una vez determinada la forma deformada de la sarta a través del análisis estático, se puede efectuar el análisis dinámico para obtener los modos y frecuencias de vibración del sistema en la dirección transversal a la sarta. En este caso, el sistema dinámico de la sarta se modela como una viga unidimensional, utilizando el método de elementos finitos. Esto implica nuevamente convertir el problema continuo en un problema discreto, mediante la siguiente ecuación algebraica matricial:
![]() (7)
(7)
en donde M es la matriz de masa del sistema, C es la matriz de amortiguamiento, K es la matriz de rigidez y F es el vector de cargas nodales equivalentes del sistema. El elemento tipo viga usado en esta etapa del problema se muestra en la Figura 4.
En este caso, cada nodo tiene dos grados de libertad, que son los desplazamientos transversales y la rotación transversal. Basándose en esta configuración, se pueden obtener las matrices de masa y rigidez elástica del elemento como:
 (8)
(8)
 (9)
(9)
en donde las propiedades geométricas y mecánicas involucradas en las matrices se definen a continuación:
r: Densidad del material
A: Área de la sección transversal
L: Longitud del elemento
E: Módulo de Young
I: Momento de Inercia de Area centroidal con respecto a un eje transversal.
Adicionalmente, en el problema de vibraciones transversales hay que tomar en cuenta el debilitamiento o reforzamiento geométrico debido a fuerzas de compresión o tensión aplicadas a cada uno de los elementos de la sarta. Esto se manifiesta a través de una matriz de rigidez geométrica que se presenta a continuación [4]:
 (10)
(10)
en donde F es la fuerza axial promedio en el elemento, negativa si es a compresión y positiva si es a tracción, de tal manera que la matriz de rigidez del elemento es la suma de la rigidez elástica mas la rigidez geométrica del elemento:
![]() (11)
(11)
Como se explicó en la sección anterior, las matrices de masa y rigidez del sistema completo se obtienen ensamblando las matrices locales, tomando en cuenta la conectividad inter-elementos:
 (12)
(12)
En este punto, se introducen las condiciones de contorno de desplazamiento prescrito al sistema, modificando K y M. Para el análisis de las vibraciones transversales, estas condiciones de contorno incluyen los desplazamientos prescritos debido a la presencia de elementos como la mecha y los estabilizadores, que están en contacto con el hoyo e introducen condiciones de contorno articuladas, y la mesa rotatoria, que introduce una condición de contorno empotrada [7, 8], así como las condiciones de contorno articuladas debido al contacto de secciones de la sarta con el hoyo debido a la deflexión estática, que fue determinada durante el análisis estático descrito anteriormente.
Dado que en este trabajo el propósito es obtener las frecuencias y modos de vibración del sistema y no la respuesta en el tiempo, el sistema se resuelve utilizando análisis modal, mediante las matrices de rigidez y masa obtenidas en esta sección.
Resultados y Discusión
Se realizaron comparaciones con varios modelos y mediciones experimentales en cuanto a las frecuencias y los modos de vibración transversales, y se verificó la longitud del ensamblaje de fondo que estaba libre de vibrar.
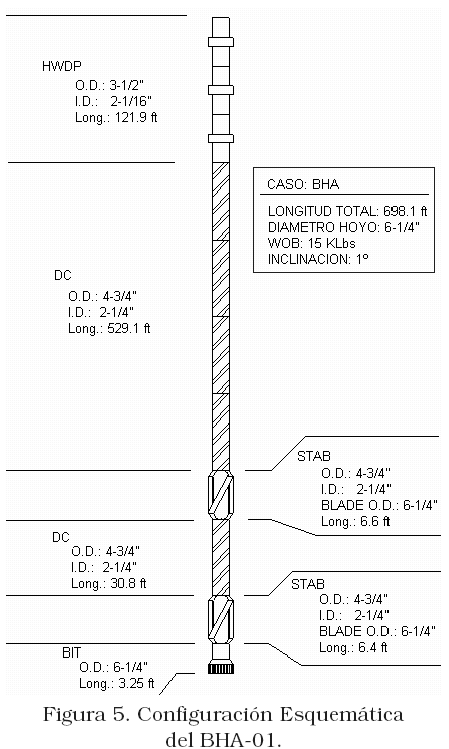
El BHA-01 se ha usado en numerosos estudios, posee una longitud de 698 pies, fue utilizada para recolectar datos de un pozo experimental perforado en cemento [9], también fue analizada por Burgess-McDaniel-Das [4] para los casos de vibración transversal.
En la Figura 5 se representan esquemáticamente los componentes del BHA-01 y su ensamble. Se consideró un diámetro del hoyo de 6.25 pulg, una densidad de lodo de 10 lbs/gal, se utilizó un peso sobre la mecha de 15 KLbs y una inclinación de hoyo de 1°.
Se discretizó el sistema para cada 2.5 pies de longitud de la sarta, ya que estudios de sensibilidad realizados indican que este espaciado es necesario para obtener una información de autovalores confiables; para valores mucho menores los resultados se mantienen sin mucho cambio, pero el tiempo de computación se incrementa considerablemente; mientras que para longitudes mucho mayores se mejora el tiempo de cómputos pero se sacrifica la confiabilidad de los resultados.
Del análisis estático se obtuvo el primer punto de contacto tubería-hoyo por encima del último estabilizador a 104 pies desde la mecha (Figura 6), lo cual concuerda con datos experimentales y otros estudios realizados a este BHA [4, 9], los cuales utilizaron métodos y discretizaciones similares a los aplicados.
En la Figura 7 se muestran los dos primeros modos de vibración del ensamblaje de fondo, los cuales muestran patrones similares a los obtenidos por Burgess-McDaniel-Das [4].
En la Tabla 1, se comparan las frecuencias de resonancia obtenidas mediante el programa desarrollado, pruebas experimentales [9] y las obtenidas por Burgess-McDaniel-Das [4]. Se puede apreciar que tanto para el primer y segundo modo los valores obtenidos concuerdan con los de las referencias.
Tabla 1. Comparación de Resultados para el BHA [6]
| Modos de Vibración del BHA | Modelo Desarrollado | Spanos-Rice-Payne3 |
| Primer modo Lateral (Hz) | 1.68 | 1.70 |
| Segundo modo Lateral (Hz) | 4.20 | 4.20 |
| Tercer modo Lateral (Hz) | 5.42 | 5.20 |
Se efectuaron tres pruebas mas con el BHA-01 [4], con diferentes longitudes de la sarta y usando la misma discretización anterior, obteniéndose excelentes resultados. Además se realizaron pruebas con el modelo de Sarta utilizado por Spanos-Rice-Payne [7], donde se obtuvieron modos de vibración laterales y frecuencias similares; estas últimas se comparan en la Tabla 1.
Conclusiones
Se desarrolló un programa computacional basado en el método de elementos finitos, que permite determinar las frecuencias y los modos de vibración transversales de la sarta de perforación, el cual fue validado mediante la comparación con otros estudios de simulación y pruebas experimentales.
El programa determina efectivamente los puntos de contacto entre la sarta y el hoyo, de tal manera se puede determinar la longitud de la sarta que está libre de vibrar transversalmente.
Se obtuvieron excelentes resultados usando longitudes de los elementos menores a 2.5 pies.
En función de la rapidez de ejecución, el programa puede ser utilizado en campo para precisar los rangos de operación segura o los cambios a realizar en la configuración del BHA, para minimizar los riesgos de fallas durante el proceso de perforación. La rapidez del programa depende de la longitud de la sarta y de la longitud de los elementos seleccionada. En el caso de la prueba realizada con el BHA-01, la simulación duró aproximadamente 6 segundos en un computador con procesador de 1.6 GHz.
Agradecimiento
Los autores agradecen a la Empresa Core Services de Venezuela por su ayuda y colaboración en la ejecución de este proyecto.
Referencias Bibliográficas
1. P.C. Kriesels, W.J.G. Keultjes, Shell EP Technology Applications and Research, P. Dumont (SPE), Issam Huneidi, Al Furat Petroleum Company, O.O. Owoeye (SPE), R.A. Hartmann (SPE), Shell Petroleum Development Company Nigeria: “Cost Savings Through an Integrated Approach to Drillstring Vibration Control”. SPE/IADC 57555 (1999) 2. [ Links ]
2. S.L. Chen, K. Blackwood, Security DBS, A Halliburton Company, and E. Lamine, Consultant: “Field Investigation of the Effect of Stick-Slip, Lateral, and Whirl Vibrations on Roller Cone Bit Performance”. SPE 56439 (1999) 1. [ Links ]
3. J.W. Nicholson, Shell Research B.V.: “An Integrated Approach to Drilling Dynamics Planning, Identification and Control”. IADC/SPE-27537 (1994) 949. [ Links ]
4. T.M. Burgess, G.L. McDaniel & P.K. Das.: “Improving BHA Tool Reliability with Drillstring Vibration Models: Field Experience and Limitations”. SPE/IADC 16109 (1987) 517-530. [ Links ]
5. Y. A. Khulief, M. A. Mohiuddin: “On the dynamic analysis of rotors using modal reduction, Finite Elements in Analysis and Design” v.26 n.1, p.41-55, May 15, 1997. [ Links ]
6. Clayer, F., Vandiver, J.K. & Lee, H.Y.: “The Effect of Surface and Downhole Boundary Conditions on the Vibration of Drillstrings”. SPE 20447 (1990) 431-439. [ Links ]
7. P.D. Spanos, Rice, U. & M.L. Payne: “Advances in Dynamic Bottomhole Assembly Modeling and Dynamic Response Determination”. IADC/SPE 23905 (1992) 581-590. [ Links ]
8. M.C. Apostal, G.A. Haduch, J.B. Williams: “A study to determine the effect of damping on finite-element-based, forced-frequency-response models for bottomhole assembly vibration analysis”. SPE 20458, Proceedings of the 65th SPE Annual Technical Conference & Exhibition, New Orleans (1990). [ Links ]
9. A.A. Besaisow & M.L. Payne: “A Study of Excitation Mechanism and Resonances Inducing BHA Vibrations”. SPE 15560 (1986) 1-10. [ Links ]