Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Técnica de la Facultad de Ingeniería Universidad del Zulia
versión impresa ISSN 0254-0770
Rev. Téc. Ing. Univ. Zulia v.31 n.2 Maracaibo ago. 2008
Direct torque control of induction machines with current limitation and ripple reduction using fuzzy logic.
Marcel Ortega1, José A. Restrepo2, Julio Viola2, María I. Giménez2 y Víctor Guzmán2
1Dpto. Electrónica, Universidad Nacional Experimental Politécnica Antonio José de Sucre. Puerto Ordaz, Venezuela. mortega_unexpo@yahoo.com.
2Dpto. Electrónica y Circuitos, Universidad Simón Bolívar, Apartado postal 89000. Valle de Sartenejas, Baruta, Venezuela. Tel: 58 212 906 3630. Fax: 58 212 906 3631. restrepo@usb.ve, jcviola@usb.ve, mgimenez@usb.ve, vguzman@usb.ve
Abstract
The classic Direct Torque Control scheme proposed by Takahashi y Noguchi [1] obtains fast torque responses of the induction machine. This control scheme however does not regulate the current demand, and the developed torque presents high ripple levels. In this paper a modification to the DTC algorithm is presented where a control loop is added to limit the stator current to a preset value. The proposed control strategy also allows for stator voltage regulation, resulting in a reduction of the electric torque ripple. In the proposed scheme the control voltage vector amplitude modulation is accomplished by a fuzzy controller with two inputs. The proposed control scheme was analized in simulations performed in C language, and afterwards experimental results were obtained with an 1 ½ HP induction motor and the Plataforma III system developed by the SIEP group of the Simón Bolívar University.
Key words: Direct torque control, induction machine, fuzzy logic.
Control directo de par de máquinas de inducción con limitación de corriente y reducción del rizado mediante lógica difusa.
Resumen
El esquema de Control Directo de Par clásico (DTC, Direct Torque Control) presentado por Takahashi y Noguchi [1] logra una respuesta rápida del par de la máquina de inducción. Sin embargo, este esquema de control no permite la regulación de la demanda de corriente y adicionalmente el par generado presenta un fuerte rizado. En este artículo se presenta una modificación del algoritmo DTC clásico que emplea un lazo de control para limitar la corriente de estator a un valor prefijado. La estrategia de control propuesta permite también regular el voltaje aplicado al estator, con lo cual se obtiene una reducción en el rizado de par eléctrico. La modulación de la magnitud del vector de voltaje de control en el esquema de control propuesto se realiza mediante un controlador difuso de dos entradas. El esquema propuesto se analizó mediante simulaciones en lenguaje C y posteriormente los resultados obtenidos se corroboraron experimentalmente en un motor de inducción de 1 ½ HP con el sistema Plataforma III, desarrollado por el Grupo SIEP de la Universidad Simón Bolívar.
Palabras clave: Control directo de par, máquina de inducción, lógica difusa.
Recibido el 18 de Junio de 2007 En forma revisada el 02 de Junio de 2008
1. Introducción
La máquina de inducción (MI) se utiliza ampliamente en convertidores de corriente alterna (CA), pero su control es complejo y costoso debido a que la MI es una planta de control multivariable altamente no-lineal. Inicialmente, las posibilidades de control de la MI se restringían a la conexión directa a la red eléctrica, o a la utilización de estrategias de control escalar, como el control Voltaje/Frecuencia (CVH, Constant Volts/Hertz). Aunque esta técnica de control es simple, tiene un rango limitado de operación, es imprecisa en el rango de baja velocidad, y presenta una respuesta pobre del par.
En la década de los 70, F. Blaschke [2] propone el Control de Campo Orientado para máquinas de inducción (FOC, Field Oriented Control), en el que las corrientes del estator son orientadas en fase (d) y en cuadratura (q) con el vector del flujo del rotor. Bajo estas condiciones el par desarrollado es proporcional a la corriente en cuadratura y el flujo del rotor a la corriente en fase, por lo que se pueden controlar de manera independiente mediante la regulación de las corrientes del estator en las componentes d-q; sin embargo el buen funcionamiento de esta técnica depende del conocimiento de los parámetros del modelo de la MI y de las variaciones de la carga [3].
En la década de los 80, Takahashi y Noguchi [1] proponen el Control Directo de Par, (DTC, Direct Torque Control), adecuado para aplicaciones de mediana y baja potencia. El DTC selecciona directamente la conectividad de los interruptores del puente inversor para controlar el flujo del estator y el par desarrollado, empleando un conjunto de reglas cualitativas. Con el DTC se obtiene una respuesta rápida del par, ya que es posible desacoplar las variables de par y de flujo del estator en la MI. En este esquema de control, el par presenta un fuerte rizado y la corriente del estator se eleva drásticamente durante el arranque y en los cambios de referencia del flujo del estator. Esta sobre-corriente puede destruir los interruptores del puente inversor, por lo tanto es necesario implementar un método para limitar la corriente del estator. En consecuencia, en este trabajo se propone un esquema de limitación de la corriente del estator, implementado mediante un algoritmo de DTC que emplea SV-PWM (Space Vector Pulse Width Modulation) y una función lineal para modular la magnitud del vector de voltaje de control. Las pruebas de laboratorio se han realizado en una MI de 1 ½ HP controlada con el sistema de pruebas experimentales Plataforma, desarrollado por el Grupo SIEP de la Universidad Simón Bolívar [4].
2. Modelo de la Máquina de Inducción
El modelo equivalente de la máquina de inducción que permite calcular las cantidades básicas, cuando el motor opera en el estado estacionario o en el estado transitorio, está basado en los conceptos de cantidades vectoriales introducidos por Kovacs [10, 11]. La forma compacta de las ecuaciones que modelan la máquina de inducción en un marco de referencia estacionario orientado al estator es la presentada en las ecuaciones (1)-(3).
 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
donde
Vs (t), Vr (t): Tensión de estator y de rotor.
is (t), ir (t): Corriente de estator y de rotor.
Rs, Rr: Resistencia de estator y de rotor.
Lm, Ls, Lr: Inductancia de magnetización, de estator y de rotor.
Y r (t): Flujo de rotor.
P: Número de pares de polos.
Te, TL: Par eléctrico y par de carga.
JL: Inercia del sistema mecánico más inercia del rotor.
w m : Velocidad mecánica del motor.
3. Lógica Difusa
El primer controlador difuso lo desarrolló Mamdani [5] basado en la teoría de conjuntos difusos propuesta por Zadeh [6]. En 1985 Takagi y Sugeno [7] proponen un modelo de inferencia difusa, en un esfuerzo para desarrollar una aproximación sistemática para las reglas difusas generadas a partir de un conjunto de datos de entrada/salida dado. La forma típica de la regla difusa propuesta por el modelo de Takagi-Sugeno es:
SI “x” es A y “y” es B Entonces z = f(x,y)
donde “x” e “y” son las variables de entrada, A y B son los correspondientes conjuntos difusos y z la salida. La Figura 1 muestra el razonamiento difuso de un modelo difuso de Takagi-Sugeno (T-S) de orden cero, en el cual las funciones de pertenencia de los conjuntos de salida, Zi,j, son constantes. En forma general, la salida del modelo difuso de T-S de orden cero está dada por (4), donde Zi es la salida correspondiente a la regla i-ésima y im() es el grado de pertenencia de la variable de entrada al i-ésimo conjunto.
 (4)
(4)
El modelo difuso de T-S es más fácil de calcular que el modelo difuso de Mamdani y se considera adecuado cuando se desea reducir el tiempo de cómputo del controlador.
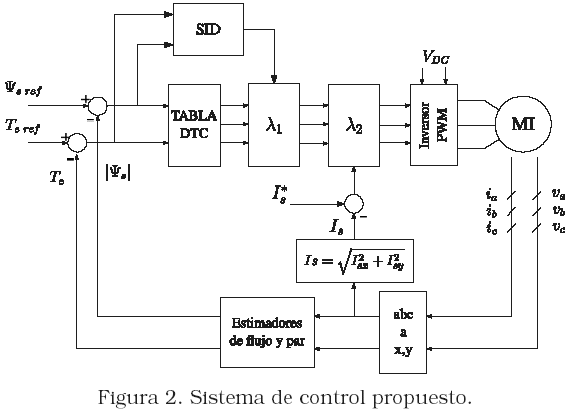
4. Esquema de Control Propuesto
El esquema de control propuesto se muestra en la Figura 2. Está conformado por un estimador de par y de flujo del estator, un Sistema de Inferencia Difusa (SID) y un lazo de control de corriente.
4.1. Estimadores de par y flujo
El flujo desarrollado por la MI se estima mediante las ecuaciones (5) y (5) y el par desarrollado se estima mediante la ecuación (7).
![]() (5)
(5)
![]() (6)
(6)
 (7)
(7)
4.2. Control difuso
El controlador difuso empleado en el diseño del sistema propuesto es del tipo T-S de orden cero [8]. Tiene como entradas el error de flujo de estator, eYs, y el error de par, eTe. Los voltajes de referencia para la generación del vector espacial de voltaje de estator se obtienen de la tabla de selección de voltajes óptimos del DTC clásico o DTC de Takahashi-Noguchi [1].
 (8a)
(8a)
 (8b)
(8b)
Este vector espacial de voltaje se modula por un factor l1 que está en el rango 0 a 1, obtenido como indica la ecuación (8a) antes de alimentar al bloque de modulación por ancho de pulso (PWM). Los valores de wi,j se obtienen multiplicando las funciones de pertenencia evaluadas para los valores de error de flujo y de par dados, tal como se indica en (8b). Los indices i,j toman los valores NG (Negativo Grande), NP (Negativo Pequeño), C (Cero), PP (Positivo Pequeño), PG (Positivo Grande), seleccionando de esta forma las distintas funciones de pertenencia. Las Figuras 3 y 4 presentan las funciones de pertenencia para el error de flujo de estator y el error de par respectivamente. Los valores de Ci,j corresponden a los elementos de la matriz de reglas de 5×5 mostrada en la Tabla 1. En este trabajo los valores asociados con las reglas son constantes seleccionadas heurísticamente e iguales a: C=0; P=0,15; M=0,5; G=1,0
Tabla 1. Matriz de Reglas
| eYs | ||||||
| PG | PP | C | NP | NG | ||
| eTs | PG | G | G | M | G | G |
| PP | G | P | P | P | G | |
| C | C | C | C | C | C | |
| NP | G | P | P | P | G | |
| NG | G | G | M | G | G | |
4.3. Lazo de control de corriente
El lazo de control de corriente permite modular la magnitud del vector de voltaje de control con un factor l2, limitando la corriente del estator a un valor pre-fijado I*s. El factor l2 se calcula con la ecuación (9), donde f(e Is), para el sistema de control propuesto, es una función de amplitud máxima igual a 1, cuya forma se muestra en la Figura 5. Así se varía la magnitud del vector de voltaje de control gradualmente en función del error de la corriente del estator dado por la ecuación (10), donde el módulo de la corriente de estator está dado por (11).
l2 = f(e Is) (9)
e Is = I*s - Is (10)
![]() (11)
(11)
La corriente también se puede limitar al aplicar el vector de voltaje cero para detener la progresión del flujo del estator e impedir el crecimiento de la corriente del estator [9]. Nótese que este método es un caso particular del expresado en el párrafo anterior, cuando la función f(e Is) es un escalón. El valor de DI utilizado en este trabajo fue de 4 A.
5. Resultados de las Simulaciones
A continuación se presentan los resultados de la simulación del esquema de control mostrado en la Figura 2. Los parámetros de la MI empleados tanto en las simulaciones como durante la pruebas experimentales se presentan en la Tabla 2 y los datos de placa se presentan en la Tabla 3.
Tabla 2. Parámetros de la MI utilizados en las simulaciones y en las pruebas experimentales
| Rs | 1.486 W |
| Rr | 1.3 W |
| Ls | 0.080 H |
| Lr | 0.080 H |
| Lm | 0.066 H |
| J | 0.089 kg.m2 |
Tabla 3. Datos de placa de la MI
| Fabricante | Baldor |
| Volts | 208-230/460 |
| Amp | 5-4/2.6 |
| Hz | 60 |
| RPM | 3450 |
En la Figura 6 se muestra las respuestas del par y flujo del estator en la MI con el DTC de Takahashi-Noguchi [1]. El par crece rápidamente y el flujo del estator se mantiene en una trayectoria circular. Sin embargo, como se muestra en la Figura 7, en el arranque la corriente se eleva aproximadamente a siete veces el valor de la corriente en estado estacionario.
La primera estrategia de limitación de la corriente del estator consiste en aplicar el vector de voltaje cero cuando la corriente alcanza un valor límite, como proponen Chapuis et al. [9]. La Figura 8 muestra el comportamiento de las variables par generado y flujo de estator de la MI con la primera estrategia de limitación de corriente en el sistema de control propuesto. La corriente resultante, mostrada en la Figura 9(a), presenta un rizado de alta frecuencia cuando actúa la limitación de corriente. La segunda estrategia de limitación de la corriente del estator consiste en graduar la magnitud del vector de voltaje de control en función de la señal de error de la corriente del estator. La Figura 9 (b) muestra la corriente del estator cuando se implementa esta segunda estrategia. El rizado de la corriente disminuye en la zona donde se limita la corriente mientras que el par y el flujo del estator son análogos a los mostrados en la Figura 8.
6. Resultados Experimentales
Las pruebas de laboratorio se realizaron con una MI de 1 ½ HP, en el banco de pruebas experimentales desarrollado por el Grupo SIEP de la Universidad Simón Bolívar [4]. Las Figuras 10 y 11 presentan la respuesta de la MI con el esquema propuesto, cuando se aplica la primera estrategia de limitación de corriente. Como se esperaba de las simulaciones, la corriente presenta un rizado de alta frecuencia en la zona donde se limita la corriente.
La Figura 12 muestra la corriente del estator en el esquema propuesto, cuando se aplica la segunda estrategia de limitación de la corriente del estator. Todos los resultados experimentales coinciden esencialmente con las simulaciones realizadas, pero presentan una magnitud de rizado mayor.
7. Conclusiones
En el esquema del DTC de Takahashi-Noguchi se aplica el vector de voltaje cero para detener la progresión del flujo y por ende reducir el crecimiento del par. En este trabajo se presenta un esquema de DTC que controla el par y el flujo de la MI, sin aplicar el vector de voltaje nulo. El rizado del par mostrado es similar al DTC de Takahashi-Noguchi. Este trabajo propone una estrategia de limitación de corriente que reduce el rizado de la corriente cuando ésta se limita. Esta aplicación está inspirada en la teoría de los conjuntos difusos, y permite variar gradualmente la magnitud del vector de voltaje de control en función del error de la corriente del estator.
Las estrategias de limitación de corriente mostradas en este trabajo se aplican con un retardo en la respuesta del par, el cual se logra al hacer crecer el flujo en un sola dirección. Sin embargo, es posible limitar la corriente del estator cuando el flujo crece de forma natural como se muestra en la Figura 11. En esta situación se empobrece la respuesta del par y el rizado de la corriente depende de la estrategia de limitación de la corriente.
Es posible diseñar un controlador difuso de dos salidas para modular la magnitud y la fase del vector de voltaje de control. Sin embargo, tanto las simulaciones como las pruebas experimentales demuestran que la respuesta del sistema depende del ajuste del controlador y que la inercia del sistema afecta el ajuste del controlador difuso. Por otra parte, la modulación de sólo la magnitud del vector de voltaje de control mediante un controlador difuso cuando se aplica la tabla de voltajes óptimos del DTC de Takahashi-Noguchi no requiere de ajustes rigurosos del controlador difuso. También es posible diseñar un controlador difuso de tres entradas donde se considere como entrada el error de la corriente del estator. Sin embargo, el ajuste de este controlador es mucho más complejo debido a la matriz de reglas de tres dimensiones generada por las funciones de pertenencia [8].
Referencias Bibliográficas
1. Takahashi I., Noguchi T., A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor, IEEE Trans. on Industry Applications, Vol. IA-22, No. 5, pp. 820-827, September/October 1986. [ Links ]
2. Blaschke F., A New Method for the Structural Decoupling of A.C Induction Machines, in Conf. Rec. IFAC Düsseldorf, Germany, Oct. 1971. [ Links ]
3. Nordin K., Novotny D., Zinger D, The Influence of Motor Parameter Deviations in Feedforward Field Orientation Drive Systems, IEEE Transactions on Industry Applications, Vol IA-21. No. 4, pp. 1009-1015, July 1985. [ Links ]
4. Giménez M., Restrepo J., Millán A., Guzmán V., Viola J., Aller J., Bueno A., Nuevos Desarrollos para el Sistema Plataforma III, Universidad Simón Bolívar, IV Congreso de Ingeniería Eléctrica, Caracas, Venezuela, Septiembre 2004. [ Links ]
5. Mamdani E., Assilian S., An experiment in linguistic synthesis with a fuzzy logic controller, Int. J. Man-Mach stud, vol 7 pp. 1-13, 1975. [ Links ]
6. Zadeh L., Fuzzy Sets, Information and Control 8 338-353, 1965. [ Links ]
7. Takagi T., Sugeno M., Fuzzy identification of systems and its applications to modeling and control, IEEE Transactions on Systems Man, and Cybernetics Vol SMC-15. No 1, January/February 1985. [ Links ]
8. Ortega M., Control Directo del Par de Motores de Inducción Empleando Lógica Difusa con limitación de Corriente, Tesis de Maestría, Universidad Simón Bolívar, Enero 2005. [ Links ]
9. Chapuis Y., Kosaka T., Matsui N., Performance Improvement up Condition for DSP-Based Direct Torque Control of an Induction Machine, Fourth International Power Electronics Conference, IPEC’2000, Tokio, Japan, April, 2000. [ Links ]
10. K. P. Kovacs, Transiente Vorgänge in Wechselstrommachinen Verein der Ungarischen Akademic der Wissenschaften Budapest, Hungary, 1959. [ Links ]
11. K. P. Kovacs, Transient Penomena in Electrical Machines, Amsterdam: Elsevier,1984. [ Links ]