Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Técnica de la Facultad de Ingeniería Universidad del Zulia
versión impresa ISSN 0254-0770
Rev. Téc. Ing. Univ. Zulia v.33 n.1 Maracaibo abr. 2010
Directed hyper-graphs for RDF documents
Amadís Antonio Martínez-Morales 1, 2 and María-Esther Vidal 2
1 Departamento de Computación, Facultad Experimental de Ciencias y Tecnología, Universidad de Carabobo. Valencia, Venezuela. Teléfono: +58-241-6004000, Ext. 375200. aamartin@uc.edu.ve.
2 Departamento de Computación y Tecnología de la Información, Universidad Simón Bolívar. Valle de Sartenejas, Baruta, Venezuela.
Teléfono: +58-212-9063268. mvidal@ldc.usb.ve
Abstract
Resource Description Framework (RDF) is a W3C proposal to express metadata about resources in the Web. The RDF data model has been formalized using several graph-based representations; each one offers different expressive power and support for the tasks of query answering and semantic reasoning. In this paper, we propose a directed hyper-graph formal model to represent and manage RDF documents efficiently. We have developed algorithms that exploit the properties of the proposed representation, and conducted an experimental study to analyze the space and time savings of our solution with respect to the labeled directed graph representation. Our study has been performed over synthetic and real-world RDF documents, and we could observe that our approach reduces the space required to store an RDF document and speeds up the task of query answering, overcoming the labeled directed graph representation.
Key words: Data model, directed hyper-graphs, Resource Description Framework (RDF).
Hipergrafos dirigidos para documentos RDF
Resumen
Resource Description Framework (RDF) es una propuesta del W3C para expresar metadatos acerca de recursos en el Web. El modelo de datos de RDF ha sido formalizado utilizando diversas representaciones basadas en grafos, cada una de las cuales ofrece diferente poder expresivo y soporte para las tareas de responder consultas y razonamiento semántico. En este trabajo se propone el desarrollo de un modelo formal, basado en hipergrafos dirigidos, para el almacenamiento y administración eficiente de documentos RDF. A tal fin, se han desarrollado algoritmos que explotan las propiedades de la representación propuesta y se ha realizado un estudio experimental para analizar las mejoras en espacio y tiempo de esta solución con respecto a la representación basada en grafos dirigidos etiquetados. El estudio fue realizado sobre documentos RDF sintetizados y reales, los resultados obtenidos confirman que el enfoque propuesto reduce el espacio requerido para almacenar un documento RDF y acelera la tarea de responder consultas, mejorando los resultados obtenidos por la representación basada en grafos dirigidos etiquetados.
Palabras clave: Hipergrafos dirigidos, modelo de datos, Resource Description Framework (RDF).
Received: December 10, 2008 Revised: November 23, 2009
Introduction
Resource Description Framework (RDF) [1, 2, 3, 4] is a language proposed by the World Wide Web Consortium (W3C) to express metadata about resources in the Web. The main goal of RDF is to describe resources in a machine-interpretable way such that these descriptions can be processed by applications. An RDF management system requires support for two main tasks: (1) answering queries posed by users and software agents and (2) semantic reasoning to discover relationships between resources. In the literature, the RDF data model has been formalized using different graph-based representations: labeled directed graphs [3, 5], undirected hyper-graphs [6], and bipartite graphs [6, 7]. Each one of these representations has its own limitations with respect to the expressive power of the RDF data model and support for the tasks of query answering and semantic reasoning.
In this paper we propose a directed hyper-graph formal model for RDF to represent, store, and process RDF documents efficiently, overcoming the limitations of the existing representations. Basically, a directed hyper-graph is defined by a set of nodes and a set of hyper-arcs; each hyper-arc connects a set of source nodes to a set of target nodes. Directed hyper-graphs have been successfully used as a modeling tool to represent concepts and structures in many application areas (e.g., formal languages, relational databases, production and manufacturing systems, public transportation systems, and topic maps [8, 9, 10]).
In an RDF directed hyper-graph, the information is only stored in the nodes, and the hyper-arcs only preserve the role of each node and the concept of direction of RDF graphs. Thus, each resource (subject, property, or value) is stored only once, and the space complexity of an RDF document is reduced if a resource appears several times in the document. Besides, RDF directed hyper-graphs define implicit position-based indexes [11] for an RDF document, which can support efficient evaluation of queries over the document.
We have developed algorithms that exploit the properties of the proposed approach, and conducted an empirical study to analyze the space and time savings of our solution with respect to the labeled directed graph (LDG) representation. Our study has been performed over a variety of synthetic and real-world RDF documents, and we could observe that our approach scales better than the LDG representation in terms of space and time complexity. These results encourage us to develop algorithms to solve the tasks of query answering and semantic reasoning, and to extend the proposed approach to represent RDF Schema (RDFS) [12, 13] data models.
The main contributions of this paper are: (1) an efficient representation of RDF documents based on the directed hyper-graph formal model, (2) an analysis of the expressive power of the directed hyper-graph model, (3) a formal space complexity study of the proposed representation to store RDF documents, (4) query answering algorithms that exploit the properties of the directed hyper-graphs, and (5) an empirical study of the impact of our approach on the task of query answering. This paper extends and updates the work reported in [14].
The rest of this paper is structured as follows. Section 2 describes the existing approaches to represent the RDF data model, including their limitations. In Section 3, we present our RDF model based on directed hyper-graphs. Section 4 reports our preliminary experimental results. Finally, in Section 5, the concluding remarks and future work are pointed out.
Related Work
An RDF document can be represented as a graph, where each node is a resource and each arc represents a property. Formally, an RDF graph is defined as follows [5, 15]: Suppose there is an infinite set U (URI references), an infinite set B = { bj: j ³ 0 } (blank nodes), and an infinite set L (RDF literals). A triple (s, p, o) Î (U È B) × U × (U È B È L) is called an RDF triple, where s represents a subject, p a predicate, and o an object.
Definition 1
An RDF graph T is a set of RDF triples.
T = {(s, p, o): (s, p, o) Î (U È B) × U × (U È B È L)}
The universe of T, univ(T), is the set of elements of U È B È L that occur in the triples of T. The vocabulary of T is the set vocab(T) = univ(T) - B. sub(T) (resp. pred(T), obj(T)) is the set of all elements in univ(T) that occur as a subject (resp. predicate, object) in an RDF graph T. The size of T, |T|, is the number of RDF triples in T. An RDF graph is simple if it does not use vocabulary with a predefined semantics in RDF Schema (RDFS). Let Var be a set of variables disjoint from U, B, and L. A triple (v1, v2, v3) Î (U È Var) × (U È Var) × (U È L È Var) is a triple pattern. A graph pattern is a set of triple patterns. Given a graph pattern P, we denote by var(P) the set of variables mentioned in P. An elemental query Q is an expression of the form Q: H ¬ B, where H = (H1,..., Hn) is a list of variables such that (“i: 1 £ i £ n: Hi Î var(B)) (safety condition), and B is a graph pattern. We denote H by Head(Q) and B by Body(Q). If |B| = 1 then Q is a basic query, if |B| > 1 then Q is a conjunctive query.
Given an RDF graph T, the required space complexity to store the RDF document represented by T is O(|T|). If there are no blank nodes in T, then the required time complexity to answer an elemental query Q against the RDF document represented by T is O(|T|k), where k ³ 1 is an integer that represents the number of triple patterns in Body(Q). RDF graphs allow several representations: labeled directed graphs [3, 5], undirected hyper-graphs [6], and bipartite graphs [6, 7]. Each one of these representations has its own limitations with respect to the RDF data model, in terms of expressive power, space complexity, and support for the tasks of query answering and semantic reasoning.
In the labeled directed graph model, given an RDF graph T, the set of nodes W is comprised of elements in sub(T) È obj(T), and the set of arcs E is composed of elements in pred(T) [3, 5]. Thus, each RDF triple (s, p, o) Î T is represented by a labeled arc, s —p ® o. The number of nodes and arcs for directed labeled graphs representing RDF graphs is |W| £ 2 |T| and |E| = |T| [6]. Thus, given an RDF graph T, the required space complexity to store the RDF document represented by T using this model is O(|T|).
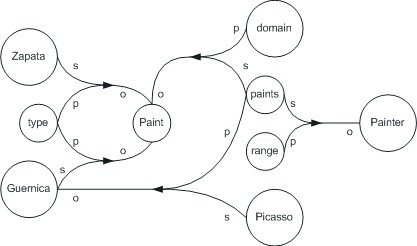
This approach has two main drawbacks [6]. First, a resource may simultaneously appear as a predicate, a subject and/or an object in the same RDF graph. For example, in the RDF graph T1 = {(Picasso, paints, Guernica), (Guernica, type, Paint), (Zapata, type, Paint), (paints, range, Paint), (paints, domain, Painter)}, the resource paints occurs as a predicate and a subject. This situation can be modeled by allowing multiple occurrences of the same resource in the resulting labeled directed graph, as arcs or nodes labels (Figure 1). However, this compromises one of the more important properties of graph theory: the intersection between the nodes and arcs labels must be empty. Second, a predicate may relate other predicates in an RDF graph. For example, in the RDF graph T2 = {(Painter, paints, Paint), (Artist, creates, Artifact), (paints, subPropertyOf, creates)}, the predicate subPropertyOf relates the predicates paints and creates. This situation can be modeled by extending the notion of arc by allowing the connection between arcs (Figure 2). However, the resulting structure is not a graph in the strict mathematical sense, because the set of arcs must be a subset of the Cartesian product of the set of nodes. Since these two simple situations violate some graph constraints, it is not possible to use concepts and search algorithms of graph theory to manipulate RDF graphs. Thus, while labeled directed graph model is the most widely used representation, it can not be considered a formal model for RDF [16].
Figure 1. RDF graph allowing multiple occurrences of the same resource.
Figure 2. RDF graph extending the notion of arc.
In the undirected hyper-graph model, given an RDF graph T, each RDF triple t = (s, p, o) Î T is a hyper-edge and each element of t (subject s, predicate p, and object o) is a node (Figure 3) [6]. The number of nodes and hyper-edges for undirected hyper-graphs representing RDF graphs is |W| = |univ(T)| and |E| = |T| [6]. Thus, given an RDF graph T, the required space complexity to store the RDF document represented by T using this model is O(max(|univ(T)|, |T|)). However, this representation loses the concept of direction in RDF graphs, which impacts the task of semantic reasoning. Additionally, it may not be easy to graphically represent large RDF graphs, like the museum example [17].
Figure 3. Undirected hyper-graph for (s, p, o).
In the bipartite graph model, given an RDF graph T, there are two types of nodes in W: statement nodes St (one for each RDF triple (s, p, o) Î T) and value nodes Val (one for each element w Î univ(T)). Arcs in E relate statement and value nodes as follows: each t Î St has three out-coming arcs that point to the corresponding node for the subject, predicate, or object of the RDF triple represented by the statement node t (Figure 4). The number of nodes and arcs of bipartite graphs representing RDF graphs is |St| = |T|, |Val| = |univ(T)|, and |E| = 3 |T| [6, 7]. Thus, given an RDF graph T, the required space complexity to store the RDF document represented by T using this model is O(max(|univ(T)|, |T|)). While bipartite graphs satisfy the requirement of a formal graph representation for RDF, issues such as reification, entailment, and semantic reasoning have not been addressed yet [16].
Figure 4. Bipartite graph for (s, p, o).
Proposed Solution
In this work we propose a directed hyper-graph formal model for RDF. Basically, a directed hyper-graph is defined by a set of nodes and a set of hyper-arcs, each one of them connecting a set of source nodes to a set of target nodes. Directed hyper-graphs have been successfully used as a modeling tool to represent concepts and structures in many application areas (e.g., formal languages, relational databases, production and manufacturing systems, public transportation systems, and topic maps [8, 9, 10]). An RDF directed hyper-graph is formally defined as follows:
Definition 2
Let T be an RDF graph. The RDF directed hyper-graph representing T is a tuple H(T) = (W, E, r) such that:
-
W = { w: w Î univ(T) } is the set of nodes.
-
E = { ei: 1 £ i £ |T| } is the set of hyper-arcs.
-
r: W × E ® {‘s’, ‘p’, ‘o’} is the role function of nodes w.r.t. hyper-arcs. Let t Î T be an RDF triple, e Î E an hyper-arc, and w Î orig(e) È dest(e) a node. Then, the following must hold:
-
(r(w, e) = ‘s’) Û (w Î orig(e)) Ù (w Î sub({t}))
-
(r(w, e) = ‘p’) Û (w Î orig(e)) Ù (w Î pred({t}))
-
(r(w, e) = ‘o’) Û (w Î dest(e)) Ù (w Î obj({t}))
Figures 5 and 6 show RDF directed hyper-graphs representing the RDF graphs T1 and T2 of Section 2, respectively. To understand the relationship between hyper-arcs and RDF triples consider, for example, the right topmost hyper-arc in Figure 6, which corresponds with the RDF triple e = (Artist, creates, Artifact). In this case, r(Artist, e) = ‘s’, r(creates, e) = ‘p’, and r(Artifact, e) = ‘o’. In our approach, given an RDF graph T, each node corresponds to an element w Î univ(T). Thus, the information is only stored in the nodes, and the hyper-arcs only preserve the role of each node and the concept of direction of RDF graphs. An advantage of this representation is that each resource (subject, property, or value) is stored only once, and the space required to store an RDF document is reduced if a resource appears several times in the document. In this way, the space complexity of our approach may be smaller than the complexity of representations presented in Section 2. In addition, concepts, techniques, and algorithms of hyper-graph theory may be used to manipulate RDF graphs under this representation.
Figure 5. RDF directed hyper-graph for RDF graph T1.
Figure 6. Directed hyper-graph for T2.
The number of nodes and hyper-arcs required for directed hyper-graphs representing RDF graphs can be obtained from Definition 2, and it is stated in Proposition 1.
Proposition 1
Let T be an RDF graph and H(T) = (W, E, r) the RDF directed hyper-graph representing T. Then, we have that |W| = |univ(T)| and |E| = |T|.
Thus, given an RDF graph T, the required space complexity to store the RDF document represented by T using this model is O(max(|univ(T)|, |T|)). The transformation from an RDF graph to the corresponding RDF directed hyper-graph is shown in Algorithm 1 and Proposition 2. Given an RDF graph T, Algorithm 1 scans all the triples in T (line 4). For each triple t = (s, p, o) in T, it adds the elements s, p, and o to the set of nodes (line 5), the identifier for the hyper-arc corresponding to the triple t to the set of hyper-arcs (line 6), and the roles (subject, predicate, or object) of each node w.r.t. the hyper-arc to the role function (lines 7-9). Note that, using this approach, RDF directed hyper-graphs define implicit position-based indexes [11] for an RDF document, which can support efficient evaluation of queries over the document.
Algorithm 1. Directed hyper-graph construction.
Proposition 2
Algorithm GETHYPERGRAPH takes an RDF graph T as input and computes the RDF directed hyper-graph representing T, H(T), as output.
The cost of the transformation from an RDF graph T to the corresponding RDF directed hyper-graph H(T) is defined in terms of the size of T in Proposition 3.
Proposition 3
Algorithm GETHYPERGRAPH computes H(T) in O(|T|) time.
Intuitively, the most expensive operation performed at each iteration of the for loop in Algorithm 1 is a set-add for the nodes. If W is implemented as a hashed set of the elements labels, this operation can be performed in O(1) time. Thus, the time complexity of Algorithm 1 is O(|T|). We found that this result is better than the O(|T| lg(|T|)) time complexity obtained in [6, 7].
Given an RDF simple graph without blank nodes T, a basic query with one unbound argument (a basic query Q is an elemental query Q: H ¬ B, where |B| = 1), and an RDF directed hyper-graph representing T, Algorithm 2 and Proposition 4 present the task of basic query answering over H(T). Algorithm 2 determines the role (subject, predicate, or object) of the variable in the query (lines 1, 7, and 12). In each case, it identifies the relevant hyper-arcs according to the instantiations on the query (lines 2-3, 8-9, and 13-14). The query answer set is comprised of the hyper-arcs that are relevant to these instantiations (lines 4-5, 10-11, and 15-16).
Algorithm 2. Basic query answering, one variable.
Proposition 4
Let T be an RDF simple graph without blank nodes. Algorithm BASICQANSONEVAR receives a basic query Q with one variable and the RDF directed hyper-graph representing T, H(T), and computes the answer set of Q w.r.t. T.
Time complexity of Algorithm 2 is defined in terms of the size of H(T) in Proposition 5.
Proposition 5
Let T be an RDF simple graph without blank nodes, Q a basic query with one variable, and H(T) the RDF directed hyper-graph representing T. Algorithm BASICQANSONEVAR computes the answer set of Q in O(|T|) time.
Intuitively, to identify the relevant hyper-arcs for the query answer is the most expensive operation performed in Algorithm 2. Note that it is a two-fold operation. In the first step, the relevant hyper-arcs set for each instantiation of the query Q has to be identified, while, in the second step, these sets of instantiations are intersected. Assuming that W is implemented as a hashed set of the elements labels, the first step is done through a hash lookup which returns the relevant hyper-arcs set for the instantiations; this step can be performed in O(1) time. The time complexity of the second step depends on the size of the relevant hyper-arcs set for the instantiations which, in the worst case, is |T|. Thus, the time complexity of Algorithm 2 is O(max(1, |T|)) = O(|T|) time.
Algorithm 2 can be modified in a straightforward way for the task of basic query answering with two unbound arguments. Finally, we briefly analyze the behavior of our approach in the presence of updates/insertions on an RDF document. If these operations occur toward the start of the document, then they can require the update of the whole structure, because of the existing order on the elements labels over this representation. Thus, our approach is adequate on environments where updates/insertions are not frequent operations.
Experimental Results
An initial prototype was developed based on definitions 1 and 2, and algorithms 1 and 2. Labeled directed graph (LDG) and directed hyper-graph (DH) representations were studied empirically; we considered a set of ten synthetic RDF documents randomly generated using a uniform distribution. RDF documents syntax was expressed using N-Triples format [2]. Synthetic documents considered in this experimental study corresponded to simple RDF graphs (i.e., an RDF graph that does not use vocabulary with a predefined semantics in RDF Schema). Document sizes were increased, ranging from 100000 RDF triples to 1000000 RDF triples. Our prototype was developed using PYTHON programming language and all the experiments were performed on a machine with a 3.0 GHz Intel Core2 Duo processor, 2 GB of RAM, and 420 GB of local SATA disk, running Fedora 9 Linux operating system.
We reported three metrics to accomplish this preliminary experimental study: (1) the time required to load each document (in secs.), (2) the space in memory needed to load each document (in MB), and (3) the time required to answer a basic query (in secs.).
Figure 7 reports the time required to load each document; note that DH time shows a linear behavior and it is about a half-order of magnitude smaller than LDG time. In Figure 8, we can observe that the space complexity of both approaches (LDG and DH) linearly increases as the number of triples in the documents. However, DH space is smaller than LDG space; due to the fact that there are resources which can appear several times in the same document, and in our approach each element is stored only once.
Figure 7. Load time (secs).
Figure 8. Structure size (MB).
Additionally, we evaluated our prototype on four real-world RDF datasets: the Mindswap research group (www.cs.umd.edu/~hendler/2003/MindPeople4-30.rdf), a webcrawl of arbitrary RDF (activerdf.org/webcrawl_10k.nt), a FOAF dataset (rdfweb.org/2003/02/28/cwm-crawler- output.rdf), and the ontoworld.org Semantic Wiki (ontoworld.org/RDF/ontoworld.xml) [18]. These datasets have different characteristics (Table 1), and they were converted to N-Triples format using an RDF/XML parser [19]. The space and load time required for each dataset, with respect to DH and LDG, is shown in Table 2. Again, the difference between the two approaches is due to the fact that there are resources which appear several times in the same document, and in our approach each element is stored only once.
Table 1. Evaluation datasets
| Dataset | Classes | Resources | Triples | Size (KB) |
| Mindpeople | 14 | 273 | 1082 | 140.3362 |
| Webcrawl | 2 | 112 | 10000 | 1398.1409 |
| FOAF | 4 | 3123 | 9758 | 1476.4329 |
| Ontoworld | 42 | 4467 | 55619 | 9878.6468 |
Table 2. Space and load time required for the evaluation datasets
| Dataset | DH | LDG | |||
| Size (KB) | Load Time (secs.) | Size (KB) | Load Time (secs.) | ||
| Mindpeople | 81.167 | 0.0190 | 92.246 | 0.0570 | |
| Webcrawl | 565.453 | 0.1410 | 805.080 | 0.5379 | |
| FOAF | 1039.294 | 0.1440 | 902.356 | 0.5829 | |
| Ontoworld | 6255.260 | 0.8589 | 6304.939 | 4.1184 | |
Finally, we ran twenty basic queries over each synthetic dataset: ten of these queries contained one variable, and they were characterized by the access patterns (?s, p, o), (s, ?p, o), and (s, p, ?o); the other ten queries contained two variables, and they were characterized by the access patterns (?s, ?p, o), (?s, p, ?o), and (s, ?p, ?o). Figures 9 and 10 report, for each dataset, the time required to answer a basic query with one and two variables, respectively, for DH and LDG.
Figure 9. Basic query answering time (one variable).
Figure 10. Basic query answering time (two variables).
Note that, although the behavior of both approaches is similar, DH time is smaller than LDG time. Thus our approach requires less time than the LDG representation for the task of basic query answering. These results depend on the selectivity of the instantiations on each query. Large selectivity requires more time than a small one to determine the answer set, because it implies larger sets of relevant triples.
Conclusions and Future Work
We proposed a directed hyper-graph formal model to represent RDF documents. In our initial experimental results we could observe that our proposed representation requires less space to represent RDF documents; in addition, it is able to speed up the task of basic query answering. Accordingly, the directed hyper-graph formal model seems to be an alternative to represent RDF documents efficiently, which may scale up better than existing representations to manage large RDF documents. These results have encouraged us to define RDF query evaluation techniques based on this RDF model.
In the future, we plan to compare our approach against other existing models, e.g., the bipartite graph model. Also, we will extend this initial representation to model RDF Schema (RDFS) graphs, and implement query evaluation algorithms for conjunctive and SPARQL [20] queries. We will formally study the impact of this model on issues like blank nodes, reification, entailment, and on the tasks of query answering and semantic reasoning. Finally, we will conduct a more extensive empirical study to analyze the suitability of the RDF hyper-graph model.
References
1. D. Beckett, “RDF/XML Syntax Specification (Revised),” Tech. Rep. Recommendation, W3C, February 2004. [ Links ]
2. J. Grant and D. Beckett, “RDF Test Cases,” Tech. Rep. Recommendation, W3C, February 2004. [ Links ]
3. G. Klyne and J.J. Carroll, “Resource Description Framework (RDF): Concepts and Abstract Syntax,” Tech. Rep. Recommendation, W3C, February 2004. [ Links ]
4. F. Manola and E. Miller, “RDF Primer,” Tech. Rep. Recommendation, W3C, February 2004. [ Links ]
5. C. Gutiérrez, C.A. Hurtado, and A.O. Mendelzon, “Foundations of Semantic Web Databases,” in Proc. of the 23rd SIGMOD/ PODS, pp. 95-106, France, 2004. [ Links ]
6. J. Hayes, “A Graph Model for RDF,” Master’s thesis, Technische Universität Darmstadt, Department of Computer Science, Darmstadt, Germany, October 2004. [ Links ]
7. J. Hayes and C. Gutiérrez, “Bipartite Graphs as Intermediate Model for RDF,” in Proc. of the 3rd ISWC, pp. 47-61, Japan 2004. [ Links ]
8. P. Auillans, P.O. de Mendez, P. Rosenstiehl, and B. Vatant, “A Formal Model for Topic Maps,” in Proc. of the 1st ISWC, pp. 69-83, Italy 2002. [ Links ]
9. G. Gallo, G. Longo, S. Pallottino, and S.V. Nguyen, “Directed Hypergraphs and Applications,” Discrete Applied Mathematics, vol. 42, pp. 177-201, April 1993. [ Links ]
10. G. Gallo and M.G. Scutellà, “Directed Hypergraphs as a Modelling Paradigm,” Tech. Rep. TR-99-02, Università di Pisa, February 1999. [ Links ]
11. R. Sacks-Davis, T. Dao, J.A. Thom, and J. Zobel, “Indexing Documents for Queries on Structure, Content, and Attributes,” in Proc. of the International Conference on Digital Media Information Bases, pp. 236-245, Japan 1997. [ Links ]
12. D. Brickley and R. V. Guha, “RDF Vocabulary Description Language 1.0: RDF Schema,” Tech. Rep. Recommendation, W3C, February 2004. [ Links ]
13. P. Hayes, “RDF Semantics,” Tech. Rep. Recommendation, W3C, February 2004. [ Links ]
14. A.A. Martínez-Morales and M.E. Vidal, “A Directed Hypergraph Model for RDF,” in Proc. of the 2nd KWEPSY, pp. 96-97, Austria, 2007. [ Links ]
15. C. Gutiérrez, C.A. Hurtado, and A.O. Mendelzon, “Formal aspects of querying RDF databases,” in Proc. of the 1st SWDB, pp. 293-307, Germany, 2003. [ Links ]
16. F. Dau, “RDF as Graph-Based, Diagrammatic Logic,” in Proc. of the 16th ISMIS, pp. 332-337, Italy, 2006. [ Links ]
17. G. Karvounarakis, V. Christophides, D. Plexousakis, and S. Alexaki, “Querying RDF Descriptions for Community Web Portals,” in Actes des 17ème Journées Bases de Données Avancées (BDA 2001), Agadir, Maroc, pp. 133-144, Cépaduès Edition, October 2001. [ Links ]
18. E. Oren, S. Gerke, and S. Decker, “Simple Algorithms for Predicate Suggestions using Similarity and Co-Occurrence,” in Proc. of the 4th ESWC, pp. 160-174, Austria, 2007. [ Links ]
19. S.B. Palmer, “An RDF/XML Parser in Python.” http://infomesh.net/2003/rdfparser, August 2003. [ Links ]
20. E. Prud’hommeaux and A. Seaborne, “SPARQL Query Language for RDF,” Tech. Rep. Recommendation, W3C and Hewlett-Packard Laboratories, Bristol, January 2008. [ Links ]