New method for geometrical design of spur gears with asymmetric involute-trochoid profile 

J.A. Cárdenas Oliveros ^1,2, D.R. Hernández Ochoa ², G.A. Babilonia Sánchez ^1,2, J.L. Moya Rodríguez ³ 

¹ Dpto. de Mecánica, Instituto Universitario Experimental de Tecnología La Victoria. Apartado 109. La Victoria 2121, Venezuela. Tlf. 0058–244-3214620. tariba2006@gmail.com, gbabilonia@yahoo.es

² Centro de Estudios CAD/CAM, Facultad de Ingeniería, Universidad de Holguín “Oscar Lucero Moya”. Ave. XX Aniv. GP 57. CP 80 100.  Holguín, Cuba. Daniel@cadcam.uho.edu.cu

³ Facultad de Ingeniería Mecánica, Universidad Central “Marta Abreu” de Las Villas.Santa Clara, Villa Clara, Cuba. Tlf. 0053–42-214408. CP 50 300. jorgemr@uclv.edu.cu 

Abstract 

This paper establishes a general mathematical model of the geometry of asymmetric spur gears with involute - trochoid tooth profile. This method is different of currently used for obtain three-dimensional models of that spur gear kind those, and it can be manipulated by CAD tools, with the geometry and accuracy needed to be used as objects of CAE analysis in subsequent testing. 

Key words:  spur gear, involute, trochoid, asymmetric, CAD. 

Resumen 

En el presente trabajo se establece un modelo matemático general de la geometría de los engranes cilíndricos con dientes rectos asimétricos de perfil evolvente y trocoide, que es un método alternativo a los actualmente usados para la obtención de modelos tridimensionales de estos tipos de engranes. El modelo establecido permite la manipulación de los mencionados engranes con herramientas CAD, con la geometría y exactitud necesarias para poder ser utilizados como objetos de ensayo en posteriores análisis con herramientas CAE. 

Palabras clave:  engranes cilíndricos rectos, evolvente, trocoide, asimetría, CAD. 

Recibido el 27 de Abril de 2010 

En forma revisada el 9 de Mayo de 2011 

Introducción 

En el año de 1997, según referencian Di Francesco y Marini [1], se efectuaron unos de los primeros estudios sobre las utilidades en peso y tamaño del engrane cilíndrico recto con diente de perfil asimétrico. En 1998 Novikov y col. [2], publicaron la variante de uso de engranajes asimétricos, iniciándose así una nueva etapa en las transmisiones por engranajes. Por su parte, Kapelevich [3] desarrolló un procedimiento de diseño directo del engrane para la síntesis del par asimétrico del engranaje. En esa línea, destacan aportes de autores como Muni y col. [4, 5], Chira y col. [6, 7]. 

De otra manera también han abordado el problema Litvin y Fuentes [8], Fetvaci e Imrak [9], Spitas [10], Cavdar y col. [11], Yang [12] quienes usan la teoría cinemática de generación de la evolvente. Estos últimos, utilizan un modelo de transformación de coordenadas a partir de la geometría de la herramienta de corte y el proceso cinemático del par herramienta-rueda para la generación de los perfiles asimétricos. 

También los autores Cotaquispe [13], González y col. [14], Hernández y Vega [15] han logrado la síntesis del engrane considerando las funciones evolvente y trocoide, usando herramientas computacionales, pero esto ha sido en el ámbito de los engranes simétricos. 

En el presente trabajo se expone el método desarrollado para la modelación de dientes rectos asimétricos de perfil de evolvente y trocoide en engranes cilíndricos rectos. Este método permite producir de una manera exacta el diente asimétrico, a partir de la intersección de las funciones evolvente y trocoide y los parámetros normalizados de los engranes. 

Método de síntesis del diente recto asimétrico con perfil de evolvente trocoide 

El método usado para obtener el modelo CAD se sintetiza en la Figura 1 (ver al final de este documento la nomenclatura utilizada). Se siguió el siguiente procedimiento: 

Paso 1 

(1.a) Establecimiento del modelo matemático general de generación del diente (ambiente Wolfram Mathematica7.0^®). (1.b) Discretización del perfil (Figura 2) en cada lado y definición de las coordenadas inicial y final de cada una de las partes, las rectas, el arco de la punta y las evolventes y trocoides de cada lado. (1.c) Exportación (archivos tipo texto) de las coordenadas de los segmentos descriptivos de la partición de las funciones representativas de los componentes constituyentes del perfil, en forma numérica, así como las pendientes inicial y final de las funciones representativas de los diferentes componentes. 

Paso 2 

(2.a) Captura de la data exportada mediante la ejecución de macros diseñados en el entorno VisualBasic del Mechanical Desktop©6.0. (2.b) Creación de curvas B-Spline, utilizando las coordenadas de los segmentos de las funciones componentes como puntos de control y las pendientes de inicio y final exportadas por partición. (2.c) Generación del perfil total, mediante la unión de las curvas B-Spline y extrusión virtual del perfil bidimensional generado. 

Paso 3 

(3.a) Exportación del modelo tridimensional en formato de archivo de intercambio STEP, (3.b) Captura del modelo CAD, en este caso SolidWorks2010© para análisis con CAE. 

Modelo matemático 

Coeficiente de asimetría 

El perfil total del diente asimétrico está compuesto por dos lados (Figura 2), que se denominarán ataque y respaldo, correspondientes respectivamente a los ángulos de presión menor y mayor. El perfil de ataque y el respaldo se relacionan geométricamente por un valor que se llamará coeficiente de asimetría c, definido como la relación entre los ángulos de presión de los perfiles de respaldo y de ataque (1), Moya y col. [16]. 

            (1) 

Las ecuaciones de las funciones evolvente y trocoide (2), (3), (4) y (5), han sido descritas por Buckingham [17] y más recientemente Fuentes [18] y Hernández [19], entre otros. 

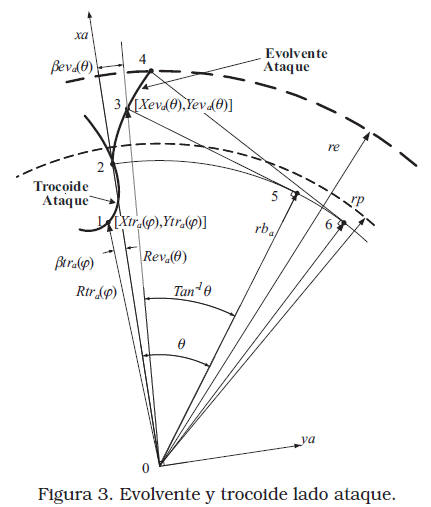
Evolvente. El perfil generado por la parte recta de la herramienta de tallado por encima del radio rpCos(fh) es una evolvente de circunferencia. El radio de base de esa circunferencia se conoce como radio básico rb del engrane. Las ecuaciones paramétricas de la función evolvente (2) y (3), están en función del parámetro q, como se muestra para el perfil de ataque en la Figura 3. 

        (2) 

        (3) 

Trocoide. La trocoide es el lugar geométrico de los puntos del radio de acuerdo de la cabeza de la herramienta sobre la rueda generada. Las ecuaciones paramétricas están en función del parámetro j, ángulo formado por la recta que une un punto cualquiera del acuerdo de la herramienta y el centro de la circunferencia de acuerdo con su horizontal Figura 4 (ver ecuaciones (4) y (5) abajo). 

El radio de salida de trocoide r₀, se define como la distancia desde el centro de la rueda tallada hasta el punto la trayectoria donde la parte recta del diente de la herramienta de generación se une con el radio de acuerdo de cabeza o de finalización de la herramienta rf, Fuentes [14], ecuación (6), detalle de Figura 4. 

    (6) 

Procedimiento de generación del diente 

Intersección de funciones evolvente y trocoide 

Para cada lado se calculan los valores (q_0,j₀) de los parámetros q y j, correspondientes a las intersecciones de las ecuaciones paramétricas polares de la evolvente (2), (3) con la trocoide (4), (5). Ecuaciones (7) y (8). 

        (7) 

        (8) 

Estimación de parámetros angulares para valor máximo y mínimo del perfil del diente 

La altura de la cabeza del diente limita superiormente a la evolvente. Cuando el radio de la evolvente es igual al radio externo o de cabeza de diente re (9), (como se observa en la Figura 3) el arco circular 2-6 es igual al cateto 4-6, obteniéndose (10) y en consecuencia el ángulo máximo de la evolvente q_max (11). 

        (9) 

        (10) 

        (11) 

El valor límite inferior del perfil del diente, se encuentra en el valor mínimo radial de la trocoide, localizado en  

Trazado de perfil 

A partir de las ecuaciones paramétricas polares para la evolvente (2) y (3), así como (4) y (5) para la trocoide, se consiguen las ecuaciones paramétricas cartesianas del sector con perfil evolvente (12) y con perfil trocoide (13), (Figura 3). 

,
,    (12) 

,
,    (13) 

La evolvente va desde la intersección hasta y la trocoide desde hasta . Se unen ambas curvas, en el lado de ataque y del respaldo, generando el perfil completo al considerar la asimetría, el espesor angular D del diente medido entre los círculos básicos (14), el ángulo d formado entre las líneas centrales (CL) o ejes de simetría de la trocoide (15), el ancho de cabeza y el coeficiente de corrección x. 

Espesor angular del diente D (14) 

             (14) 

Distancia angular d (15), entre trocoides del diente z_i+1 y z_i 

    (15) 

Trocoide del respaldo. Se consigue a partir de las ecuaciones paramétricas (16), desde el inicio de la intersección con la evolvente hasta su punto mínimo en , para cada i diente requerido. El rango de i es y el rango de j es , (Figura 5) para i=1. 

    (16) 

Evolvente del respaldo. Las ecuaciones paramétricas (17) se evalúan en el rango , para i número de dientes, obteniendo el sector de perfil mostrado en la Figura 6. 

    (17) 

Cabeza. Con el radio de la cabeza re, se parametriza dicho sector (18), el rango es , produciendo el arco circular de la Figura 7. 

    (18) 

Evolvente del lado de ataque. Tomando en cuenta la distancia angular entre los puntos de inicio de la evolvente en el respaldo y el ataque, se traza la función evolvente para el ataque según (19), entre el rango de los valores paramétricos y los i dientes, Figura 8. 

    (19) 

Trocoide lado de ataque. Usando las ecuaciones (20), entre para los i dientes requeridos, se ejecuta el trazado de la Figura 9. 

    (20) 

Unión de sectores del diente. Se unen los trazados precedentes, resultando el perfil del diente mostrado en la Figura 10. 

Generación de rueda total. Si la trocoide en el punto p/2 del lado de ataque del diente z_i no coincide con el de la trocoide del respaldo en p/2 del diente z_i+1, significa que existe una holgura angular d (15), entre las líneas centrales CL de las mismas i e i+1, tal como se muestra en la Figura 11. 

El trazado de dicho sector circular, que corresponde al radio mínimo, se efectúa con las ecuaciones paramétricas (21), variando q según y los i dientes. 

            (21) 

La Figura 12 muestra el resultado del procedimiento descrito para m={1}, a/m={1}, b/m={1.25}, y={0}, z={10},{16},{20},{50}, c={1.0},{1.5},{1.7}, x/m={0},{-0.2},{-0.5}, rf/m= {0},{0.25} 

Una vez ejecutada la síntesis del diente recto asimétrico, es inmediata la síntesis de la herramienta de corte por generación, como se indica en la Figura 13 (sin coeficiente de corrección x) y Figura 14 (caso con x+ o alejamiento de la herramienta de corte). 

Generación en ambiente CAD 

Cada perfil evolvente y trocoide de las caras de ataque y respaldo, se particiona en j partes, con j+1 puntos de control (se usó j = 5), determinando los puntos de inicio y final de los sectores así como sus pendientes iniciales y finales. 

Se procede a exportar las coordenadas de los 7 sectores (Figura 15), 2 trocoides, 2 evolventes, la punta y las líneas que cierran el dominio, en forma de archivos de texto, que serán usadas para la creación del modelo mediante herramientas de CAD (Figura 16), mediante macros diseñados en ambiente VBasic y una vez logrado el sólido, se procede a la exportación con archivo de intercambio tipo STEP, disponible para ser usado en análisis por el método de elementos finitos MEF, aportado por la herramienta de CAE seleccionada. 

Macros para generación de diente CAD 

Para sistematizar el procedimiento, se divide en pasos las tareas desarrolladas por las macros. 

Paso 1 macro. Captura de la data exportada por el modelo matemático. Se cargan los datos de cada sector, con las rutinas de lectura secuencial comúnmente usadas en VBasic (Figura 17). 

Paso 2 macro. Conversión de data en curvas B-Spline, con las coordenadas de los puntos de control e inicio, final y pendientes respectivas, capturadas en Paso 1 (Figura 18). 

Paso 3 macro. Generación del perfil total mediante la unión de las curvas B-Spline, se crea una superficie y se procede a extruir virtualmente, logrando el modelo tridimensional (Figura 19). 

Conclusiones 

1. Se desarrolla un método alternativo para la modelación geométrica del diente asimétrico de perfil evolvente trocoide de engranes cilíndricos rectos. 

2. La geometría de los engranajes asimétricos es equivalente a la unión de dos dientes, donde el lado de menor ángulo representa al lado de ataque y el de mayor ángulo al respaldo. 

3. El modelo matemático desarrollado y sus expresiones permiten realizar la síntesis métrica de los engranajes asimétricos de perfil de evolvente y trocoide, de manera rápida, confiable y para cualquier configuración aceptable de engranajes rectos asimétricos. 

4. El modelo matemático permite la exportación de los datos del perfil del diente discretizado. 

5. Las macros producidas, capturan la data del modelo matemático y generan el modelo tridimensional en ambiente CAD del diente asimétrico de perfil evolvente trocoide de los engranes cilíndricos rectos. 

Nomenclatura 

a    :  Altura adendo diente (mm) 

b    :  Altura dedendo diente (mm) 

c    ^:  Coeficiente de asimetría 

h_a0    :  Altura adendo de la herramienta de generación (mm) 

i    :  Número deseado de dientes 

invfh    :  Ángulo polar del ángulo de presión 

m    :  Módulo 

r_0    :  Radio de salida de la trocoide (mm) 

rb    :  Radio básico de la rueda dentada (mm) 

re    : 

Radio de la cabeza del diente (mm) 

rf    :  Radio de finalización de herramienta (mm) 

rp    :  Radio de paso de la rueda dentada (mm) 

rt    :  Radio de la punta del diente (mm) 

x    :  Coeficiente de corrección (mm) 

z    :  Número total de dientes 

Rev[q]    :  Radio polar de la evolvente (mm) 

Rtr[j]    :  Radio polar de la trocoide (mm) 

Xev,tr,e,base    :  Abscisa para sector: evolvente, trocoide, cabeza, base 

14.  González Rey G., García Martín R. José, Frechilla Fernández P. “Modelo matemático y procedimiento para la generación gráfica de los contornos de dientes de engranajes cilíndricos”. Ingeniería Mecánica, Vol.8, n2, (2005), 31-55. 

15.  Hernández Daniel y Vega Manuel. “Análisis del socavado en engranajes cilíndricos de perfil evolvente aplicados en mecanismos de minería”, Minería y Geología, ISSN 0258 5979, v. 22 n. 3, (2006). 

16.  Moya Rodríguez J. L., Velázquez Pérez J. A., Goytisolo Espinosa R. A., Machado Rodríguez A. S.: “Determinación del factor de forma para engranajes de dientes rectos asimétricos”, 8º Congreso Iberoamericano de Ingeniería Mecánica, Cusco, (2007). 

17.  Earle Buckingham. “Analytical mechanics of gears”. Dover Publications, Inc., New York, (1949).         [ Links ] 

18.  Fuentes Aznar Alfonso. “Modelo de cálculo a flexión de engranajes cilíndricos de perfil de evolvente”. Tesis Doctoral. UNED, España, (1995).         [ Links ] 

19.  Hernández Daniel. “Método para el diseño de engranes cilíndricos con dientes rectos de perfil de evolvente basado en el indicador del grado de socavado”. Tesis Doctoral. Universidad de Holguín, Cuba, (2005).         [ Links ]