A Mathematical Model for the Dimensioning of Combined Footings of Rectangular Shape

Un Modelo Matemático para el Dimensionamiento de Zapatas Combinadas de Forma Rectangular

Arnulfo Luévanos Rojas

Facultad de Ingeniería, Ciencias y Arquitectura Universidad Juárez del Estado de Durango Av. Universidad S/N, Fracc. Filadelfia , CP 35010, Gómez Palacio , Durango, México Tel: 8717147119. Fax: 8717152017. Email: arnulfol_2007@hotmail.com

Abstract

This paper presents a mathematical model to obtain the most economical dimension of the contact surface in combined footings of rectangular shape subjected to an axial load and moment in two directions (bidirectional bending), when the load that must support said structural member is applied. The cases presented in this paper are: 1) Combined footings of boundary; 2) Combined footings intermediate. The classic model considers an axial load and a moment around the axis “ X ” (transverse axis) applied to each column, i.e., the force resulting from the applied loads are located on the axis “ Y ” (longitudinal axis), and once obtained the resultant force and its position is necessary to adjust the length thereof such that the centroid of loads coincides with the geometrical center. The main part of this research is that the proposed model considers the bending moments around the axis “ Y ” and the classic model neglected the moments around the axis “ Y ”. Then, the proposed model is more suited to the general conditions and is more economical.

Keywords: combined footings of boundary, combined footings intermediate, permissible capacity of soil, contact surface, bidirectional bending.

Resumen

En este trabajo se presenta un modelo matemático para determinar la medida más económica de la superficie de contacto en zapatas combinadas de forma rectangular sometidas a una carga axial y momento en dos direcciones (flexión bidireccional), cuando la carga que debe soportar dicho miembro estructural se aplica. Los casos que se presentan en este documento son: 1) Zapata combinada de lindero, 2) Zapata combinada intermedia. El modelo clásico considera una carga axial y un solo momento alrededor del eje “ X ” (eje transversal) aplicada en cada columna, es decir, la fuerza resultante de las cargas aplicadas se localiza sobre el eje “ Y ” (eje longitudinal), y una vez obtenida la fuerza resultante y su posición es necesario ajustar la longitud de ésta de tal manera que el centroide de cargas coincida con el centro geométrico. La parte principal de esta investigación es que el modelo propuesto considera momentos flexionantes alrededor del eje “ Y ” y el modelo clásico no los toma en cuenta. Entonces, el modelo propuesto se ajusta más a las condiciones generales y es más económico.

Palabras clave: zapatas combinadas de lindero, zapatas combinadas intermedias, capacidad permisible del suelo, superficie de contacto, flexión bidireccional.

Introducción

La cimentación es la parte de la estructura que transmite las cargas al suelo. Cada edificación demanda la necesidad de resolver un problema de cimentación. Las cimentaciones se clasifican en superficiales y profundas, las cuales presentan importantes diferencias en cuanto a su geometría, al comportamiento del suelo, a su funcionalidad estructural y a sus sistemas constructivos [1, 2].

Una cimentación superficial es un elemento estructural cuya sección transversal es de dimensiones grandes con respecto a la altura y cuya función es trasladar las cargas de una edificación a profundidades relativamente cortas, menores de 4m aproximadamente, con respecto al nivel de la superficie natural del terreno [1-4]. Las cimentaciones superficiales, cuyos sistemas constructivos generalmente no presentan mayores dificultades pueden ser de varios tipos, según su función: zapata aislada, zapata combinada, zapata corrida o losa de cimentación [1, 2].

En el diseño de cimentaciones superficiales, en cuanto a la aplicación de cargas son: 1) Zapatas sujetas a carga axial concéntrica; 2) Zapatas sujetas a carga axial y momento en una dirección (flexión unidireccional); 3) Zapatas sujetas a carga axial y momento en dos direcciones (flexión bidireccional) [1-4].

La zapata combinada es un elemento que sirve de cimentación para dos o más columnas. [1, 3, 4]. Las zapatas combinadas se utilizan cuando: a) La relación existente entre cargas, capacidad admisible del suelo de la cimentación y distancia entre columnas adyacentes imposibilitan la construcción de zapatas aisladas; b) Una columna exterior queda tan cerca del lindero de la propiedad que no es posible centrar una zapata aislada bajo ella [5-7].

Existen dos tipos de zapatas combinadas: las de lindero y las intermedias, las cuales se diferencian solo por la posicion de los elementos que van a soportar [5-7]. La zapata combinada puede ser rectangular, trapezoidal o en forma de T en planta. La zapata rectangular se proporciona cuando una de las proyecciones de la zapata está restringido o el ancho de la zapata está restringido. La zapata trapezoidal cuando se proporciona una carga de la columna es mucho más que la otra. Como resultado, se restringirán las proyecciones tanto de la zapata más allá de las caras de las columnas [5-7].

Las hipótesis usadas en el modelo clásico considera la carga axial y momento alrededor de un eje transversal a la zapata combinada, para las proporciones y la forma geométricas se fija de manera que el centroide del área de la zapata coincida con la resultante de las cargas de columna.

Esto se traduce en una presión uniforme por debajo de toda la superficie de contacto de la zapata. A continuación, la ecuación de la flexión bidireccional se utiliza para obtener los esfuerzos que actúan sobre la superficie de contacto de la zapata, que deben cumplir con las condiciones siguientes: 1) El esfuerzo mínimo debe ser igual o mayor que cero, debido a que el suelo no es capaz de soportar esfuerzos de tensión, 2) El esfuerzo máximo debe ser igual o menor que la capacidad admisible que puede soportar el suelo [1, 2, 8, 9].

Recientemente se han desarrollado modelos matemáticos para el dimensionamiento de zapatas aisladas de forma rectangular, cuadrada y circular sujetas a carga axial y momentos en dos direcciones (flexión bidireccional), que cumple con las dos condiciones ya mencionadas anteriormente [10-12].

En este documento se presenta un modelo matemático para obtener el dimensionamiento de zapatas combinadas de forma rectangular sometidas a una carga axial y momento en dos direcciones (flexión bidireccional) en cada una de las columnas, que debe cumplir las siguientes condiciones: 1) La primera condición es que el esfuerzo mínimo debe ser igual o mayor que cero, ya que el suelo no es capaz de soportar tensiones; 2) La segunda condición es que el esfuerzo máximo debe ser igual o menor que la capacidad admisible del suelo. Los casos que se presentan en este documento son: 1) Zapata combinada de lindero, 2) Zapata combinada intermedia.

Desarrollo matemático del nuevo modelo

1. Zapata combinada de lindero

En la Figura 1 se muestra una zapata combinada de lindero soportando dos columnas rectangulares de diferentes dimensiones (una columna de lindero y otra interior) sujetas a carga axial y momento en dos direcciones (flexión bidireccional).

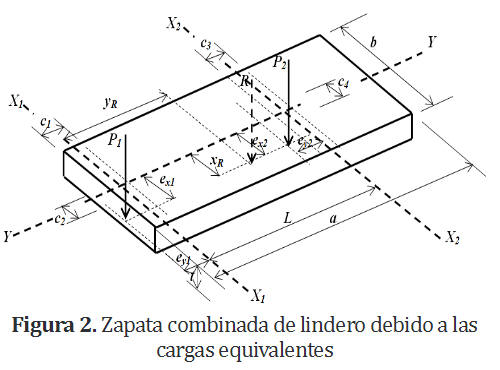
En la Figura 2 se presenta una zapata combinada de lindero debido a las cargas equivalentes. Las solicitaciones normales de las componentes de P₁, M_x1, My1, es equivalente a una fuerza normal P₁ actuando en los puntos con coordenadas ( e_x1 , e_y1 ), y para las componentes de P₂ , M_x2 , M_y2 , es equivalente a una fuerza normal P 2 actuando en los puntos con coordenadas ( e x2 , e y2 ).

Si se obtiene la suma de momentos alrededor del eje “ X₁ ” de la zapata 1 para encontrar la posición de la resultante “ R=P₁ +P₂ ” y considerando que esta se localiza entre las dos columnas: 

donde: y R es la distancia a partir de “ X₁ ” hasta donde se encuentra la resultante. Si se sustituye “ M_x1 =P₁ e y1 ”, “ M x2 =P₂e_y2 ” y el valor de “ R ” en la ecuación (2) para presentar la ecuación en función de los elementos mecánicos que actúan en la zapata:

Ahora se hace coincidir el centro del área de la zapata con la posición de la resultante en el sentido “ Y ”, entonces se presenta lo siguiente:

 

Y se sustituye la ecuación (3) en la ecuación (4), esto es:

Ahora se encuentra la suma de momentos alrededor del eje “ Y ” de la zapata:

Si se sustituye “ M_y1 =P₁ e_x1 ”, “ M _y2 =P₂ e_x2 ” y el valor de “ R ” en la ecuación (7) para presentar la ecuación en función de los elementos mecánicos que actúan en la zapata:

donde: x R es la distancia a partir de “ Y ” hasta donde se encuentra la resultante.

1.1. Cuando la resultante cae dentro del núcleo central, es decir, x R ≤ b/6.

La ecuación general para cualquier tipo de zapata sujetas a flexión bidireccional es [13, 14]:

donde: σ es el esfuerzo que ejerce el suelo sobre la zapata (presión del terreno), A es el área de contacto de la zapata, P es la carga axial aplicada en el centro de gravedad de la zapata, M_x es el momento alrededor del eje “ X ”, M y es el momento alrededor del eje “ Y ”, C _x es la distancia en dirección “ X ” medida a partir del eje “ Y ” a la fibra más alejada, C _y es la distancia en dirección “ Y ”, medida a partir del eje “ X ” a la fibra más alejada, I y es el momento de inercia alrededor del eje “ Y ” e I _x es el momento de inercia alrededor del eje “ X ”.

La ecuación general de la flexión bidireccional se transforma de la siguiente manera:

donde: σ_adm es la capacidad de carga admisible disponible del suelo, y_c es la distancia a partir del centro del área de contacto de la zapata en dirección “ Y ” a la resultante y en este caso es cero, x _c es la distancia a partir del centro del área de contacto de la zapata en dirección “ X ” a la resultante y en este caso es x _R. 

Ahora como se hizo coincidir la resultante con el centro del área de la zapata con la posición de la resultante en el sentido “ Y ”, por lo tanto no existe momento alrededor del eje “ X ”, y la ecuación (10) queda de la siguiente manera:

Se puede expresar de la siguiente manera:

Enseguida, la ecuación (12) se hace igual a cero para obtener “ b ” para el cual es el valor mínimo para que satisfaga esta ecuación es:

Si se sustituye el valor de “ R ” y “ x_R ” en la ecuación (13) para presentar la ecuación en función de los elementos mecánicos que actúan en la zapata:

Dimensionamiento de Zapatas Combinadas Rectangulares

En seguida se debe verificar el valor de “ b ” de la ecuación (14), y el valor de “ x _R ” por la ecuación (8) se obtiene, si cumple con “ x _R ≤ b/6 ”, esto significa que la resultante se encuentra dentro del núcleo central de la zapata, y por lo tanto este valor se debe tomar.

1.2. Cuando la resultante cae fuera del núcleo central, es decir, x R ≥ b/6.

En la Figura 3 se observa el diagrama de presiones, cuando la resultante cae fuera del núcleo central, es decir, las presiones se generan en una parte de la cara de la zapata.

La suma de fuerzas se encuentra:

donde: x es la distancia donde se localiza la presión bajo la zapata. La suma de momentos alrededor del eje “ Y ” se realiza:

La ecuación (15) se sustituye en la ecuación (16) para encuentra “ x ”:

 

2. Zapata combinada intermedia

En la Figura 4 se muestra una zapata combinada intermedia soportando dos columnas rectangulares de diferentes dimensiones (dos interiores) sujetas a carga axial y momento en dos direcciones (flexión bidireccional).

En la Figura 5 se presenta una zapata combinada intermedia debido a las cargas equivalentes. Las solicitaciones normales de las componentes de P₁ , M_x1 , M_y1 , es equivalente a una fuerza normal P₁ actuando en los puntos con coordenadas ( e_x1 , e_y1 ), y para las componentes de P ₂ , M _x2 , M _y2 , es equivalente a una fuerza normal P 2 actuando en los puntos con coordenadas ( e _x2 , e _y2 ).

La ecuación (3) se utiliza para encontrar la posición “ y_R ” de la resultante “ R ” y considerando que esta se localiza entre las dos columnas. Ahora se considera que la distancia del centro de la columna sometida a la menor carga al extremo libre de la zapata es “ b/2 ” en dirección “ Y ”:

 

Ahora se encuentra la posición “ x_R ” de la resultante “ R ” en dirección “ X ” de la zapata por la ecuación (8).

2.1. Cuando la resultante cae dentro del núcleo central, es decir, xR≤ b/6.

2.2. Cuando la resultante cae fuera del núcleo central, es decir, x R ≥ b/6.

La ecuación (20) se usa para obtener el valor de “ b ”.

Entonces la dimensión mínima propuesta para una zapata combinada intermedia será: el valor de “ a ” presentado en la ecuación (22), y el valor de “ b ” es la ecuación (24) para “ x _R ≤ b/6 ” o la ecuación (20) para “ x _R ≥ b/6 ”.

Aplicación

A continuación se muestran tres casos de zapatas combinadas de lindero y los mismos casos para zapatas combinadas intermedias, en cada caso se presentan las mismas cargas aplicadas a la cimentación, variando la capacidad de carga del suelo y la separación entre las columnas. Las dimensiones de las dos columnas son de 40x40 cm .

Entonces la dimensión mínima propuesta para una zapata combinada será: 1) Para zapatas combinadas de lindero: la dimensión “ a ” se obtiene por medio de la ecuación (5), la dimensión de “ b ” es la ecuación (14) para “ x _R ≤ b/6 ” o la ecuación (20) para “ x _R ≥ b/6 ”. 2) Para zapatas combinadas intermedias: la dimensión “ a ” se presenta en la ecuación (22), la dimensión de “ b ” es la ecuación (24) para “ x _R ≤ b/6 ” o la ecuación (20) para “ x _R ≥ b/6 ”.

Una vez que se tiene definida la dimensión de la zapata combinada, se procede a obtener los esfuerzos generados por las cargas que se aplican a la cimentación, para verificar que estos esfuerzos estén dentro de los parámetros establecidos, es decir, que el esfuerzo máximo debe ser igual o menor que la capacidad admisible que pueda resistir el suelo y el esfuerzo mínimo debe ser igual o mayor que cero, porque el suelo no es capaz de resistir esfuerzos de tensión. Los resultados para zapatas combinadas de lindero se presentan en la Tabla 1, y para las zapatas combinadas intermedias se muestran en la Tabla 2.

Resultados

En la Tabla 1 se presentan los resultados por el modelo propuesto de los tres casos de zapatas combinadas de lindero para las 4 diferentes tipos de capacidades de carga del suelo. En todos los casos rige la condición de “ x _R ≤ b/6 ”, con excepción en el caso 3 en la cual el primer tipo de capacidad de carga del suelo es dominante la condición de “ x _R ≥ b/6 ”.

Para la condición de “ x _R ≤ b/6 ”, esto significa que rige el esfuerzo máximo, es decir, la capacidad de carga admisible del suelo, y por lo tanto toda la superficie de la zapata en contacto con el suelo está sujeta a compresión. Para el caso 3 en la cual el primer tipo de capacidad de carga del suelo es dominante la condición de “ x _R ≥ b/6 ”, estos significa que rige el esfuerzo mínimo, es decir, el esfuerzo mínimo es cero, y por lo tanto una parte de la superficie de la zapata en contacto con el suelo está sujeta a compresión, si se usa la ecuación (17) se obtiene x = 135 cm , esto significa que 135 cm está sujeta a compresión y el excedente para b = 150 cm carece de esfuerzos.

En la Tabla 2 se muestran los resultados por el modelo propuesto de los tres casos de zapatas combinadas intermedias para las 4 diferentes tipos de capacidades de carga del suelo. También en la mayoría de los casos rige la condición de “ x _R ≤ b/6 ”, con excepción en el caso 2 en el primer tipo y en el caso 3 en los dos primeros tipos de capacidad de carga del suelo es dominante la condición “ x _R ≥ b/6 ”.

Para la condición de “ x _R ≤ b/6 ”, esto significa que rige el esfuerzo máximo, es decir, la capacidad de carga admisible del suelo, y por lo tanto toda la superficie de la zapata en contacto con el suelo está sujeta a compresión.

Para la condición de “ x _R ≥ b/6 ”, estos significa que rige el esfuerzo mínimo, es decir, el esfuerzo mínimo es cero, y por lo tanto una parte de la superficie de la zapata en contacto con el suelo está sujeta a compresión, si se usa la ecuación (17) se obtiene para el caso 2 del primer tipo es x = 120 cm , y para el caso 3 de los dos primeros tipos son x = 120 cm y x = 165 cm , respectivamente, esto significa que “ x ” está sujeta a compresión y el excedente para “ b ” carece de esfuerzos para cada caso.

Conclusiones

La cimentación es el elemento de la estructura que es la parte esencial de la misma debido a que ella va a permitir la trasmisión de las cargas de la estructura al terreno, con lo que ayudan al suelo, a resistir esta cargas, por lo que el mismo no sufrirá y se comportara idealmente para las condiciones a las que será sometido. Por lo tanto la cimentación viene a conforma las bases de la estructura y de ahí que el comportamiento de la edificación u obra civil va a estar forzado a como está trabaje y se comporte.

Debido a la importancia que cobra la cimentación, la misma esta forzada a cumplir con ciertos parámetros geométricos, de presión, de conformación que responden a las características del suelo y de las cargas de la estructura. Por lo tanto el diseño de una cimentación no es algo que se realiza de manera intuitiva sino que cumple con una metodología de diseño que evalué desde la forma de la cimentación hasta la profundidad la que se desplante, así como también las características naturales del suelo.

El enfoque matemático propuesto en este trabajo produce resultados que tienen una precisión tangible para todos los problemas que se investigan para encontrar la solución más económica.

Entonces se recomienda el modelo propuesto para el diseño estructural de zapatas combinadas de forma rectangular sujetas a carga axial y flexión bidireccional. Además, esta situación la hace más económica y se apega más a las condiciones reales de las presiones del suelo que se aplican a la cimentación.

El modelo matemático desarrollado en este documento sólo se aplica a los suelos rígidos que cumplen con la ecuación de la flexión bidireccional, es decir, la variación de las presiones es lineal. Las sugerencias para investigaciones futuras: 1) cuando se presenta otro tipo de suelo, por ejemplo, en suelos cohesivos y suelos granulares el diagrama de presiones no es lineal y deben ser tratados de manera diferente; 2) Cuando se desee otro tipo de forma de zapata combinada, por ejemplo, las zapatas trapezoidales o en forma de “T”.

Referencias  

[1] Bowles J.E.: “Foundation analysis and design”, McGraw-Hill, New York, 1996.         [ Links ]

[2] Das B.M., Sordo-Zabay E., Arrioja-Juarez R.: “Principios de ingeniería de cimentaciones”, Cengage Learning Latín América, México, 2006.         [ Links ]

[3] Calabera-Ruiz J.: “Cálculo de Estructuras de Cimentación”, Intemac Ediciones, México, 2000.         [ Links ]  

[4] Tomlinson M.J.: “Cimentaciones, Diseño y Construcción”, Trillas, México, 2008.         [ Links ]  

[5] McCormac J.C.: “Design of Reinforced Concrete”, John Wiley & Sons, Inc, New York, 2008.         [ Links ]  

[6] Mosley W.H., Bungey J.H. & Hulse R.: “Reinforced Concrete Design”, Palgrave, New York, 1999.         [ Links ]  

[7] Parker A.: “Diseño Simplificado de Concreto Reforzado”, Limusa, México, 1996.         [ Links ]  

[8] Gambhir M.L.: “Fundamentals of Reinforced Concrete Design”, Prentice-Hall, New York, 2008.         [ Links ]  

[9] González-Cuevas O.M., Robles-Fernández-Villegas F.: “Aspectos fundamentales del concreto reforzado”, Limusa, México, 2005.         [ Links ]  

[10] Luévanos-Rojas A.: “A Mathematical Model for Dimensioning of Footings Rectangular”. ICIC Express Letters Part B: Applications, Vol. 4, No. 2, (2013) 269-274.  

[11] Luévanos-Rojas A.: “A Mathematical Model for Dimensioning of Footings Square”. International Review of Civil Engineering, Vol. 3, No. 4, (2012) 346-350.  

[12] Luévanos-Rojas A.: “A Mathematical Model for the Dimensioning of Circular Footings”. Far East Journal of Mathematical Sciences, Vol. 71, No. 2, (2012) 357- 367.  

[13] Gere J.M., Goodo B.J.: “Mecánica de Materiales”, Cengage Learning, México, 2009.         [ Links ]  

[14] Punmia B.C., Kumar Jain Ashok & Kumar Jain Arun.: “Limit State Design of Reinforced Concrete”, Laxmi publications (P) LTD, India, 2007.         [ Links ]

Recibido el 22 de Enero de 2015 En forma revisada el 29 de Febrero de 2016