Aplicación de la mecánica de la fractura post-cedencia a polímeros

Maria Lluisa Maspoch*, Edgar Franco-Urquiza, José Gámez-Pérez, Miguel Sánchez-Soto, José I. Velasco, Orlando O. Santana, Antonio B. Martínez

Centre Català del Plàstic. Universitat Politècnica de Catalunya (UPC) C/Colom 114, 08222 Terrassa

* E-mail: maria.lluisa.maspoch@upc.edu

Publicado On-Line el 30-Jul-2010

Disponible en: www.rlmm.org

Resumen

La técnica del trabajo esencial de fractura (EWF) se ha utilizado en la caracterización a fractura de materiales que desarrollan una amplia ductilidad y donde ocurre una completa cedencia antes del inicio de la propagación de la grieta. De esta manera, la técnica EWF caracteriza la fractura post-cedencia determinando dos parámetros: el trabajo esencial específico de fractura (w_e), relacionado con la superficie donde ocurre el proceso real de fractura, y el trabajo no esencial específico de fractura (w_p), relacionado con el trabajo plástico realizado en la zona exterior de la zona de fractura. La técnica EWF ha sido utilizada satisfactoriamente, especialmente en polímeros, permitiendo el estudio de la influencia de distintas variables sobre el comportamiento a fractura. Su elevada sensibilidad así como su fácil aplicabilidad le confieren amplias ventajas sobre otras técnicas tales como la integral J. En este trabajo se describen los fundamentos de la técnica EWF y se recopilan algunos ejemplos de su aplicación, presentando un breve resumen de las aportaciones más relevantes realizadas por nuestro grupo de investigación sobre la técnica del EWF.

Palabras Clave: Mecánica de la fractura post-cedencia (PYFM), trabajo esencial de fractura (EWF), fractura de polímeros, nanocompuestos

Abstract

The Essential Work of Fracture (EWF) technique has been used for the ductile materials characterization, where yielding phenomenon occurs before crack propagation. The EWF method characterizes the post-yielding fracture, determining two parameters: the specific essential work of fracture, w_e related with the real fracture process area, and the specific non-essential work of fracture, w_p that corresponds with the work done in the outer region of the crack tip. The EWF technique has been successfully employed especially with polymers, allowing the study of the influence of many variables on the fracture behavior, unavailable using other techniques such as J integral. In this work, the fundamentals of the technique and examples of application are reviewed, presenting a brief summary of the most relevant contributions of our group to the EWF method.

Keywords: Post-yielding fracture mechanics (PYFM), essential work of fracture (EWF), Fracture of polymers, nanocomposites

Recibido: 07-May-2010; Revisado: 28-May-2010; Aceptado: 21-Jun-2010

1. INTRODUCCIÓN

La mecánica de la fractura tiene sus inicios en 1913 cuando Inglis [1] estudió la rotura de placas sometidas a tracción, las cuales contenían un defecto en forma de elipse. Poco después, en 1920, Griffith [2] llevó más allá el trabajo de Inglis al estirar la elipse hasta convertirla en una grieta, relacionando por primera vez el tamaño del defecto con la tensión aplicada. Sin embargo, este método estaba limitado únicamente a materiales frágiles, y no fue hasta la década de los 50 que Irwin extendió ésta teoría a materiales más dúctiles a través del concepto de la tasa de liberación de energía [3]. Posteriormente, Irwin utilizó el método de Westergaard [4] para mostrar que los esfuerzos locales y los desplazamientos cercanos a la punta de la grieta tenían una solución general, la cual podría ser descrita por una simple constante [5]. Este parámetro sería conocido poco después como el factor de intensidad de tensiones (K), el cual caracteriza por completo las condiciones de tensión en la punta de la grieta para un material linealmente elástico, relacionando el esfuerzo aplicado y el esfuerzo localizado en la punta de la grieta.

Después de que los fundamentos de la Mecánica de la Fractura Elástico Lineal (LEFM) fueran establecidos (alrededor de la década de los 60), diversos científicos comenzaron a estudiar la plasticidad desarrollada en la punta de la grieta. De esta forma, Wells [6], en 1961, presentó el concepto de desplazamiento de apertura en la punta de la grieta (CTOD), el cual serviría para modelar la fractura bajo condición de deformación plástica significativa. Por otra parte, Rice [7], en 1968, extendió el método de la tasa de liberación de energía hacia materiales más dúctiles, al considerar la deformación plástica como un comportamiento elástico no lineal y definiendo el concepto de la integral de contorno J (o simplemente integral J), para describir el flujo de energía en la región de la punta de la grieta, mostrando que la tasa de liberación de energía puede ser expresada como una integral de contorno independiente de la línea de integración. Este concepto llevó al desarrollo de la Mecánica de la Fractura Elastoplástica (EPFM), la cual involucra una deformación plástica extensa por delante de la punta de la grieta. Por su parte, Broberg [8,9], en 1968, planteó el uso de un simple parámetro relacionado con la descripción del proceso de fractura durante el crecimiento estable de una grieta. De esta manera se desarrolló la teoría de la Mecánica de la Fractura Post-Cedencia (PYFM), donde la fractura de un material se desarrolla bajo condiciones previas de cedencia [8, 9]. Sin embargo, no fue hasta 1977 cuando Cotterel y Reddel [10] aplicaron las teorías de Broberg en el desarrollo de la técnica del trabajo esencial de fractura (EWF), la cual permite determinar las propiedades a fractura de materiales dúctiles.

A pesar de que los numerosos trabajos publicados demuestran la satisfactoria aplicación de la técnica EWF sobre materiales dúctiles (láminas metálicas y/o poliméricas), existen todavía algunas controversias sobre la influencia de algunas variables experimentales tales como: la velocidad de deformación, el espesor de la probeta, la calidad de la entalla, etc., las cuales pueden llegar a limitar la aplicabilidad de ésta técnica.

2. METODOLOGÍA DEL TRABAJO ESENCIAL DE FRACTURA

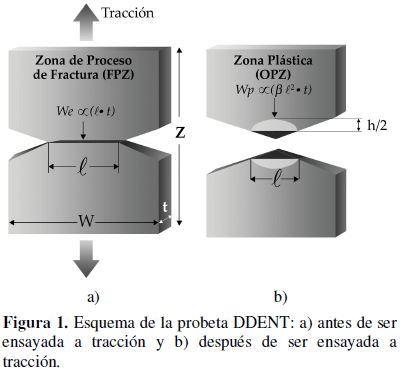
La idea fundamental de Broberg [9] consiste en separar en dos términos la energía total de fractura (W_f) de una probeta de doble entalla sometida a tracción (DDENT): la zona interior del proceso de fractura (FPZ) y la zona plástica exterior de fractura (OPZ). Ambas zonas son fácilmente identificables, tal y como se esquematiza en la Figura 1.

En la zona interior del proceso de fractura ocurre el proceso real de fractura, dando lugar a la creación de dos nuevas superficies. La energía asociada a este proceso es el trabajo esencial de fractura (W_e), el cual es proporcional a la sección del ligamento ℓ· t (Figura 1a).

En la zona plástica exterior de fractura tienen lugar el resto de fenómenos asociados a la fractura dúctil, tales como la deformación plástica y otros procesos disipativos (cizalla, crazes o cavitación, entre otros). La energía involucrada en la OPZ, denominada trabajo no-esencial de fractura o trabajo plástico (W_p), es proporcional al volumen de la región deformada (Figura 1b). Esto queda resumido mediante la siguiente expresión:

W_f = W_e +W_p = w_e·ℓ t + b·w_p ℓ²· t          (1)

donde w_e es el trabajo esencial específico de fractura por unidad de área de ligamento, ℓ es la longitud del ligamento, t es el espesor de la probeta, b es el factor de forma de la zona plástica y w_p es el trabajo noesencial específico de fractura por unidad de volumen. Dividiendo ambos términos de la ecuación 1 por la sección de ligamento (ℓ· t), se obtiene que el trabajo específico de fractura (w_f) es:

w_f = W_f / ℓ t = w_e + βw_p       (2)

El procedimiento experimental consiste en ensayar varias probetas DDENT con distinta longitud de ligamento, y a partir de las curvas fuerza vs. desplazamiento (Figura 2a) se determina la energía de fractura (W_f) como el área bajo la curva L-d.

De acuerdo con la ecuación 2, es posible determinar w_e y bw_p representando los valores de w_f en función de ℓ, y ajustándolos a la ecuación de una recta por regresión lineal, correspondiendo la ordenada en el origen a w_e y la pendiente al término plástico, tal y como se representa en la Figura 2b.

Teóricamente, el trabajo esencial específico de fractura (w_e) es una constante del material que depende únicamente del espesor y es equivalente a J_IC [12], lo cual ha sido sustentado experimentalmente por diferentes autores [13-16] y contrastado con los valores de CTOD [17]. No obstante, en comparación con el método de la integral J, la técnica EWF presenta ciertas ventajas de procedimiento, tales como su simplicidad en el desarrollo experimental o su aplicabilidad a espesores muy delgados [18-21].

A pesar de que la técnica EWF ha ganado adeptos por parte de diversos centros de investigación, su aplicación se ve limitada ya que actualmente no existen modelos matemáticos que permitan utilizar los datos obtenidos por la técnica EWF para la simulación de la fractura de los materiales. En este sentido, se pueden resaltar tanto los trabajos desarrollados por Knockaert, Pardoen, Chen y Cotterell en la simulación numérica para la fractura de probetas tipo DDENT [22-25], como el trabajo realizado recientemente por Chen et al [26], quienes investigaron la correlación entre los parámetros de fractura y la estructura molecular de polímeros amorfos y dúctiles.

Es igualmente destacable que la aplicación del método EWF se haya extendido, a parte del Modo I de apertura, a los otros dos modos de propagación de grieta: cizalla (Modo II) [27, 28] y desgarre (Modo III) [29, 30]. Adicionalmente, la técnica EWF ha sido utilizada para evaluar la energía de adhesión en juntas y uniones adhesivas [31-33].

3. CONSIDERACIONES EXPERIMENTALES PARA LA APLICACIÓN DEL ENSAYO EWF

En 1993, Gray llevó a cabo el primer intento de normalizar el método EWF dentro del comité técnico número 4 de la European Structural Integrity Society (ESIS TC-4) [34], en donde se establecieron las siguientes recomendaciones:

a) La zona del ligamento debe estar completamente en cedencia antes de que la grieta inicie su propagación.

b) Para poder emplear la ecuación 2, las probetas deben estar realmente bajo un estado de tensión plana, lo cual se verifica al aplicar el criterio de Hill [35].

c) La forma de las curvas fuerza vs. desplazamiento (L-d) deben ser similares para todas las probetas ensayadas de diferente longitud de ligamento, ya que produce el desarrollo de una geometría de fractura común a todas las probetas (Figura 2a).

d) Las longitudes de ligamento deben encontrarse dentro del siguiente rango:

max (3t-5mm) < ℓ < min (W/3, 2r_p)       (3)

Siendo W el ancho de la probeta DDENT, mientras que r_p es el radio de la zona plástica, el cual se define como:

2r_p = (p/8)(Ew_e/s_y²)                (4)

donde E y s_y representan el módulo de elasticidad y la tensión de cedencia, respectivamente. Ambos parámetros deberán ser obtenidos para un mismo material, mediante ensayos a tracción y bajo condiciones de ensayo similares.

También se recomendó medir la altura de la zona plástica (h en la Figura 1b) para poder determinar el factor de forma (b), proponiendo tres formas geométricas distintas: rombo, círculo o elipse.

Este primer protocolo de norma se revisó en 1997 [36] y posteriormente en el 2001 [37], acordando que el criterio de Hill se podría complementar por la existencia de una uniformidad en el estado de tensiones. Lo anterior se verifica a través de un valor de tensión máxima (s_max), el cual debe ser similar en todas las probetas ensayadas, independientemente de la longitud de ligamento (ℓ).

A pesar de todas las revisiones y trabajos realizados por el comité TC-4 de la ESIS [38,39] aún existen algunas cuestiones que causan controversia, representando un desafío para la investigación. En la literatura, se pueden encontrar muchos trabajos que profundizan en aspectos experimentales y/o metodológicos de la técnica EWF, así como en la mejora del análisis de los datos o incluso en relacionar los parámetros EWF con otros parámetros intrínsecos del material. En la Tabla 1 se indican algunos de estos temas, introduciendo la bibliografía encontrada.

En un intento por profundizar en la técnica EWF, algunos de los temas presentados en la Tabla 1 han sido desarrollados dentro del Centre Català del Plàstic, a continuación se describen brevemente una selección de los mismos.

Dimensiones de la probeta DDENT [42]

De acuerdo con la teoría del trabajo esencial de fractura, el parámetro w_e representa la tenacidad del material, por lo que es independiente de la geometría de la probeta. Para verificar lo anterior, se han realizado trabajos [76-81] que reflejan la dependencia de los parámetros EWF con distintas variables, que en el caso de estudio con un polipropileno isotáctico (iPP) fueron las siguientes:

• Ancho de la probeta DDENT (W): 30-60 mm

• Longitud de la probeta DDENT (Z): 20-150 mm

• Rango de longitud del ligamento de la probeta DDENT

• Espesor de la probeta DDENT (t): 38-2500 mm

En este trabajo se concluyó que el ancho de la probeta (W en la Figura 1) no influye drásticamente en los valores de w_e ni en bw_p, en los rangos estudiados, lo cual indicaría que ambos parámetros de fractura son propiedades intrínsecas del material, siempre y cuando los mecanismos de fractura no varíen. La longitud de la probeta (Z en la Figura 1) tampoco parece influir en los parámetros EWF, ya que al variar Z en el rango de 40 hasta los 100 mm, los valores del trabajo esencial y no esencial específico de fractura fueron constantes. Con respecto a la longitud del ligamento se observó que la longitud mínima no parece estar supeditada al criterio ℓ > (3-5)· t, ya que se encontró que ℓ era válida para valores comprendidos entre 5 y 6 mm, y que era independiente del espesor de la probeta. Finalmente, el espesor (t) de la probeta DDENT tuvo un efecto significativo en los parámetros de fractura del iPP estudiado, ya que un incremento de t produjo una clara disminución en los valores de w_e, un resultado que puede estar relacionado tanto con la morfología como con los mecanismos de fractura, según se pudo apreciar a través de microscopía electrónica de barrido (SEM)[42].

Utilización de videoextensómetro [47]

La teoría del trabajo esencial de fractura indica que toda la energía involucrada durante el proceso de fractura es absorbida tanto en la zona de proceso de fractura como en la zona plástica. Sin embargo, se argumenta que parte de la energía viscoelástica puede encontrarse almacenada en la probeta DDENT (fuera de la OPZ), siendo liberada lentamente posterior a la fractura. Esto puede ser una fuente de error en la medición de los parámetros EWF, tal como ha sido indicado por Fung et al. [82], debido a que esta energía viscoelástica no se encuentra incluida dentro de la energía total de fractura, al ser recuperable.

Por tal motivo, se propuso medir la deformación de las probetas DDENT con la ayuda de un videoextensómetro [47]. En este procedimiento se propone la colocación de dos marcas extensométricas separadas por una distancia igual a la longitud del ligamento (ℓ) de cada probeta.

Después de comparar el procedimiento con y sin videoextensómetro, se concluyó que su uso no afectaba significativamente los valores de w_e ni su precisión, encontrando desviaciones estándar muy similares. Por otro lado, el uso del extensómetro supuso una reducción significativa (aproximadamente 10 %) en los valores de bw_p, lo que indicaría que la energía viscoelástica almacenada fuera de las marcas extensométricas introduce un error sistemático en la determinación del trabajo plástico. Las deformaciones de las probetas DDENT, durante el ensayo hasta la fractura, se han podido cuantificar mediante un sistema de correlación digital de imágenes (GOMAramis ^TM) que permite visualizar el campo de deformaciones en 3D [11] (Figura 3).

Método de agudización de la entalla [43]

La normalización de la técnica EWF supone aún un reto, siendo la calidad y la agudización de la entalla uno de los puntos clave para ello, tal como se ha podido constatar en diversas series de Round Robin del TC-4 de la ESIS [38,39].

En un trabajo reciente [43], se utilizó un nuevo procedimiento para la agudización de las entallas de las probetas DDENT, el cual se basó en la técnica de ablación térmica por pulsos de radiación láser en periodos de femtosegundos (femtoláser). Este procedimiento se comparó con el método convencional de agudización de la entalla con hoja de afeitar.

Los resultados de este trabajo [43] muestran que el radio del fondo de la entalla no parece ser crítico por debajo de 10 μm. No obstante, los parámetros de fractura son muy sensibles a la deformación plástica inducida durante el proceso de entallado, afectando considerablemente los valores de w_e. Así, se comprobó que para obtener parámetros intrínsecos es necesario, por un lado, medir la deformación a través de un videoextensómetro y además utilizar un proceso de entallado que evite inducir deformación plástica, tal y como es el caso de la agudización por femtoláser.

Aplicación de la técnica EWF en Modo III [29]

La técnica EWF se ha aplicado principalmente en la caracterización a fractura de películas de polímeros dúctiles bajo la configuración de apertura (Modo I). No obstante, la técnica también se ha utilizado en la configuración de desgarro (Modo III). Habitualmente, ésta es la configuración más utilizada en los ensayos de control de calidad a nivel industrial, aunque únicamente se suele determinar la energía de desgarro (ensayo de Elmendorf). Durante la fractura de una probeta de desgarro (también conocida como probeta “trouser”) se pueden identificar dos zonas de deformación plástica diferenciadas, las cuales se esquematizan en la Figura 4.

La zona A es la región de la zona plástica (OPZ) en la que él ancho (h) varía proporcionalmente con la longitud de ligamento (ℓ_A). En la zona B, por el contrario, h es constante e independiente de la longitud de ligamento que ha sufrido el desgarro. Los parámetros de fractura se pueden determinar para cada una de estas zonas, siguiendo dos modelos.

Modelo de la zona A

En la zona A, el tamaño de la OPZ aumenta durante el desgarro, por lo que se deduce que:

W_f = w_IIIe.ℓ_A.t + w_IIIp. S_A.t = w_IIIe.ℓ_A.t + w_IIIp.a·ℓ_A².t    (5)

w_IIIf = w_IIIe + w_IIIp.a.ℓ_A          (6)

donde S_A es el área de la zona deformada plásticamente, la cual puede expresarse como S_A = a·ℓ_A²; mientras que el término a es el factor de forma que, en este modelo, es igual a la relación h/2ℓ_A. Ensayando probetas con diferentes longitudes de ligamento que cumplan con este modelo, se puede determinar (aplicando la ecuación 6) el trabajo esencial específico de fractura de desgarro (w_IIIe) mediante la intersección en el eje-y de la gráfica w_IIIf vs. ℓ_A.

Modelo de la zona B

En el modelo de la zona B, el ancho de la OPZ (h_B) se encuentra totalmente saturado (Figura 4), por lo que el trabajo total de desgarro en la zona B viene dado por:

W_IIIf = w_IIIe.ℓ_B.t + w_IIIp. S_B.t = w_IIIe.ℓ_B.t + w_IIIp.h·ℓ_B.t    (7)

w_IIIf = w_IIIe + w_IIIp.h_B          (8)

donde ℓ_B es la longitud del ligamento de la Zona B, y S_B es el área de la zona plástica correspondiente a la zona B, la cual puede representarse como S_B = h_B·ℓ_B.

De acuerdo con la ecuación 8, al ensayar varias probetas “trouser”, se pueden obtener distintos anchos (h_B) correspondientes a la OPZ, por lo que el trabajo específico de desgarro w_IIIe se podría obtener por regresión lineal representando en una gráfica los valores de w_IIIf vs. h_B.

Sin embargo, para algunos polímeros, la variación del valor de h_B puede llegar a ser demasiado pequeña, por lo que sería inviable obtener unos parámetros de fractura precisos. Otra alternativa para poder evaluar el w_IIIe sería utilizando el valor de w_IIIp calculado en la Zona A (ecuación 6) y determinando los parámetros w_IIIf y h_B de la zona B. La energía de saturación de desgarro (w_IIIf) en esta zona se obtendría mediante el valor de la carga constante de propagación de fractura (P_B):

y el ancho desarrollado (h_B) en saturación. Este último, puede ser medido directamente en las probetas post-mortem. El valor de w_IIIe en la zona B se puede obtener, de esta manera, para varias probetas (ecuación 8).

Propuesta de partición de energía [40, 66]

Según la teoría del EWF, w_f considera toda la energía disipada dividida por la sección del ligamento ℓ· t (ecuación 2). No obstante, si se llega a observar cuidadosamente las probetas DDENT, y si se relaciona el proceso de fractura con la forma de las curvas obtenidas, se sugiere que al separar las contribuciones energéticas de iniciación y de propagación, se pueden interpretar mejor los términos involucrados en el proceso de deformación y fractura de probetas DDENT.

Hasta la fecha, se han propuesto dos métodos para dividir la energía consumida durante la fractura de una probeta DDENT [66,75], los cuales se representan en la Figura 5.

En el método de trabajo a cedencia y trabajo de estricción y propagación, propuesto por Karger-Kocsis et al [75], la fuerza máxima de la curva fuerza vs. desplazamiento (Figura 5a) divide la energía de fractura en dos componentes: el trabajo de cedencia (W_f,y) y el trabajo de estricción y propagación (W_f,n):

w_f = w_f,y + w_f,n = (w_e,y + bw_p,y·ℓ) + (w_e,n + bw_p,n·ℓ)          (10)

En el método de trabajo de iniciación, propuesto por Ferrer-Balas et al [66], el punto para la partición de la energía se define al final de la estricción del ligamento (Figura 5b), justo antes del inicio de la propagación de la grieta. Así, la energía de fractura se separa en dos términos, W_I (proceso de iniciación, el cual se refiere al proceso de estricción de la sección de ligamento, que es un fenómeno de deformación plástica incluido en éste término) y W_II (propagación de grieta y disipación de energía en zona plástica). La energía elástica absorbida durante la cedencia del ligamento se consume durante la propagación de la grieta, por lo tanto, se considera parte de W_II (propagación) y se resta de W_I (iniciación).

w_f = w_f,I + w_f,II = (w_e,I + bw_p,I·ℓ) + (w_e,II + bw_p,II·ℓ) (11)

Cuando se compararon ambos métodos en láminas de u-PVC [40], el método de trabajo a cedencia pareció dar mejores resultados al relacionar los parámetros con los valores obtenidos a velocidades de impacto. Sin embargo, para materiales con una marcada estricción antes de que ocurra la propagación de grieta, el método de trabajo de iniciación mostró mejores resultados.

Propuesta de la nueva forma de la zona plástica [67]

Bajo condiciones geométricas y de ensayo similares, el término plástico (bw_p) puede utilizarse como un parámetro comparativo entre diferentes materiales. El factor de forma (b) depende del material, y está relacionado con la geometría de la zona plástica desarrollada durante la fractura de la probeta DDENT. Por otra parte, el valor de w_p no se puede determinar directamente a través de la regresión lineal obtenida de la representación gráfica de w_f vs. ℓ, lo que justifica la necesidad de medir b con la mayor precisión posible.

En el primer protocolo de norma del EWF [34], se sugirió representar la forma de la zona plástica en base a tres diferentes geometrías: circular, elíptica y romboidal, las cuales se esquematizan en la Figura 6. No obstante, es común observar que la zona plástica desarrolla una forma intermedia entre las geometrías elíptica y romboidal [78, 83, 84]. Por esta razón, se propuso una nueva geometría de la zona plástica, la cual es el resultado de la intersección entre dos parábolas, y se identifica también como “forma de ojo”. Dichas geometrías se pueden definir utilizando la siguiente ecuación:

h = k·b·ℓ            (12)

donde k es una constante que depende de la forma de la zona plástica, la cual toma los valores de 1.27 para las geometrías circular y elíptica, y de 2 y 1.5 para las geometrías romboidal y parabólica respectivamente.

De esta manera, b se puede determinar como la pendiente de la regresión lineal [34], obtenida al representar gráficamente la altura total de la zona plástica (h) frente a la longitud de ligamento (ℓ), dividida por el factor k.

Índice de ductilidad [85-87]

En algunos trabajos de investigación, se ha detectado que al ensayar probetas DDENT de polipropileno (PP) y/o copolímeros (EPBC) se podían presentar distintos tipos de fractura, que van desde los que presentan una extensa ductilidad en la punta de la grieta hasta los que desarrollan una fractura totalmente frágil. En el primer caso se produce una notoria estricción de la sección del ligamento sin que la grieta llegue a propagar, mientras que en el otro extremo, la fractura frágil va acompañada de la aparición de crazes [68, 85-88], los cuales forman parte de un micromecanismo de deformación asociado a un proceso de cavitación, desarrollándose microvacíos y fibrillas (similares a microgrietas).

Las diferencias encontradas se revelaron en la forma de las curvas L-d, y su evaluación ha permitido clasificar los diferentes comportamientos a fractura, al aplicar la técnica EWF, en:

1. Frágil: rápida propagación de la grieta, sin apenas deformación plástica. Las superficies de fractura son lisas, y a contra luz se pueden apreciar pequeñas grietas localizadas por debajo de la sección fracturada.

2. Inestabilidad dúctil: la grieta comienza a deformarse plásticamente. Mientras tanto, la energía acumulada de forma elástica se almacena en la punta de las entallas, donde se alcanza un valor crítico, ocasionando una propagación inestable de la grieta y una rotura repentina. Las probetas post-mortem muestran un emblanquecimiento en los extremos del ligamento, lo que indica el desarrollo de una deformación plástica.

3. Post-cedencia: se presentan todas las condiciones establecidas para poder aplicar satisfactoriamente la técnica EWF.

4. Enromamiento: se caracteriza por una extensa deformación plástica en la punta de la entalla, la cual evita la propagación estable de la grieta.

5. Estricción: las probetas DDENT no muestran propagación de la grieta durante la cedencia de la sección del ligamento, la cual continúa deformándose plásticamente, comportándose casi como una probeta de tracción, resultando en la formación de un cuello.

En un intento por relacionar los diferentes tipos de fractura observados, se definió un índice de ductilidad:

este índice de ductilidad (D_L) se determina como el cociente del desplazamiento a rotura (d_r) de una probeta DDENT y de su respectiva longitud de ligamento.

La Tabla 2 muestra la correspondencia obtenida al comparar la ductilidad promedio con los diferentes tipos de fractura.

Se puede postular que para poder cumplir satisfactoriamente con todas las condiciones establecidas para la aplicación de la técnica EWF, D_L deberá estar dentro del rango: 0.15 < D_L < 1.

4. APLICACIONES DEL EWF

Las primeras publicaciones acerca del uso de la técnica EWF son atribuidas a Cotterel, Reddel y Mai [10, 89, 90] siendo aplicada a polímeros por primera vez en 1986 [91]. Desde entonces, la técnica EWF se ha utilizado principalmente en películas y láminas poliméricas, aunque también se pueden encontrar estudios en metales [16, 22, 24, 79, 92-102] y otros materiales, tales como asfaltos [103, 104], papel [105-107] u hormigón [108].

En la Tabla 3 se muestra una selección de publicaciones en las cuales se ha utilizado la técnica EWF para caracterizar el comportamiento a fractura de distintos materiales poliméricos.

Por otra parte, la técnica EWF ha sido de gran utilidad tanto para caracterizar y optimizar la composición de mezclas [15, 18, 45, 57, 60, 72, 109-133] y polímeros reforzados (compuestos) [17, 19, 50, 56, 60, 134-163], así como para evaluar el efecto de distintos agentes de acoplamiento [17, 50, 51, 53, 117, 136, 141, 143, 144, 149, 164-167]. Además, la técnica EWF también ha sido utilizada en sistemas poliméricos multicapas [30, 168, 169].

La técnica EWF permite analizar la relación que existe entre los procesos de fractura y diversos parámetros microestructurales [170]. De este modo, algunos casos en los cuales aparecen fenómenos complejos tales como el envejecimiento o la degradación [134, 171-173] así como la transición dúctil-frágil [42, 174, 175], han podido ser evaluados a través de la aplicación de la técnica EWF.

La elevada sensibilidad de la técnica EWF hace que sea de un particular interés para estudiar la relación procesado-propiedades [13, 87, 121, 169, 176-182], optimizar los parámetros de procesado [183, 184], e incluso para evaluar la influencia del recocido en diferentes sistemas poliméricos [67, 185, 186].

La técnica EWF ha sido utilizada satisfactoriamente para estudiar la influencia que distintos parámetros morfológicos tales como: el peso molecular [12, 171, 175, 187, 188], la anisotropía [26, 189-191], la densidad de enredos moleculares [180, 192, 193] y la estructura cristalina o morfología [41, 176, 186, 194-196] tienen sobre la tenacidad a fractura de películas y láminas delgadas.

5. APLICACIONES DE LA TÉCNICA EWF EN NANOCOMPUESTOS POLIMÉRICOS

Hace pocos años que la técnica EWF comenzó a utilizarse en la caracterización a fractura de nanocompuestos poliméricos [160, 239-242], aunque es preciso destacar que en éste trabajo solamente se hará referencia a los polímeros reforzados con arcillas modificadas. La elevada sensibilidad de la técnica EWF ha permitido evaluar la influencia de variables como el tipo de modificador orgánico, el contenido de carga, el grado de exfoliación o la orientación de las láminas de arcilla, sobre la tenacidad de películas de nanocompuestos. En este sentido, algunos autores [160, 239] emplearon la técnica EWF para comparar el efecto tanto del contenido de arcilla como del uso de un agente de acoplamiento, sobre la tenacidad a fractura de películas de PP. Los autores encontraron que al añadir arcilla, la tenacidad de los nanocompuestos (w_e) disminuía considerablemente con respecto a la del PP sin modificar, y no se observaron cambios considerables al introducir a los nanocompuestos el agente de acoplamiento. No obstante, la presencia de la arcilla promovió un incremento apreciable en el trabajo plástico disipado, independientemente del contenido de arcilla montmorillonita (MMT).

Diversos autores han aplicado la técnica EWF para evaluar el efecto que produce la compatibilidad molecular, la morfología y el contenido de arcilla sobre los parámetros de fractura [160, 242]. Es conocido que la mayoría de las arcillas utilizadas en la preparación de nanocompuestos poliméricos se encuentran modificadas orgánicamente [243]. Esta modificación favorece la difusión molecular siempre y cuando exista una afinidad entre el modificador orgánico y la matriz polimérica [244-247]. En un estudio reciente[240], se demostró que la compatibilidad molecular puede influir drásticamente en la morfología de las láminas de arcilla (Figura 7) y en su grado de exfoliación. Los nanocompuestos EVOH/OMMT compatibles desarrollaron una morfología laminar, marcada por el deslizamiento de las láminas durante el procesado (Figura 7a); mientras que en los nanocompuestos no compatibles se desarrolló una morfología con láminas dobladas y enrolladas (Figura 7b).

Por otra parte se observó que el grado de exfoliación disminuía a medida que aumentaba el contenido de arcilla, promoviendo el desarrollo de partículas aglomeradas.

El comportamiento a fractura, evaluado a través de la técnica EWF, resultó ser muy sensible a la morfología desarrollada en ambos tipos de nanocompuestos. En ambos casos, el trabajo esencial específico de fractura se vio influenciado tanto por el contenido de arcilla como por la cristalinidad, correspondiente al primer calentamiento. La evolución del factor de forma con respecto al porcentaje de arcilla, indicó que en los nanocompuestos compatibles, las partículas de arcilla transfieren los esfuerzos de forma efectiva; mientras que en los nanocompuestos no compatibles, las partículas de arcilla promueven la deformación plástica a bajos niveles de tensión, de acuerdo con los valores obtenidos del trabajo plástico específico y las observaciones realizadas por SEM.

En nanocompuestos EVOH/OMMT compatibles [241] se observó, a través de microscopía electrónica de transmisión (TEM), una marcada orientación de las láminas de arcilla. El eje longitudinal de la arcilla se encontraba dispuesto paralelamente a la dirección del flujo. Para poder evaluar el efecto de la orientación de las partículas sobre el comportamiento a fractura, se prepararon probetas DDENT en la dirección del flujo de fundido (MD) y en la dirección transversal al flujo (TD). Así, la sección de ligamento quedaba perpendicular o paralela al flujo del fundido. A través de observaciones por SEM de las superficies de fractura de las probetas DDENT en ambas configuraciones (MD y TD), se cuantificó la estricción del ligamento (Fig. 8). Para un contenido de arcilla similar (2.5 %), las probetas DDENT correspondientes a los nanocompuestos ensayados en la dirección MD, mostraron una estricción del ligamento menor que en los nanocompuestos ensayados en TD, siendo ésta última muy similar al valor obtenido en el EVOH sin modificar [241]. A mayores aumentos, las superficies de fractura de los nanocompuestos presentaron un alto nivel de fibrilación, siendo más evidente para las probetas DDENT ensayadas en MD que en TD, lo cual se atribuyó a la disposición de las partículas de arcilla dentro de la matriz polimérica. Todo lo anterior permitió sugerir que las partículas de arcilla restringen el flujo plástico durante el proceso de fractura.

Con respecto a los parámetros de fractura, los resultados mostraron que las partículas de arcilla actúan como efectivo refuerzo, ya que la tenacidad aumentó en ambas configuraciones (MD y TD). No obstante, el término plástico no mostró una tendencia clara, por lo que fue necesario determinar el factor de forma para poder explicar los valores encontrados en ambas configuraciones. En los nanocompuestos ensayados en MD, b aumentó con el contenido de arcilla; mientras que en TD, b tendió a disminuir debido a que en esta configuración, el eje más largo de las partículas de arcilla se encontraba orientado paralelamente a la propagación de la grieta, lo que promovió una transferencia de esfuerzos menor que en la dirección MD.

Por otra parte, w_p disminuyó para ambas configuraciones (MD y TD) debido a que las arcillas restringen el flujo plástico durante el proceso de fractura.

6. AGRADECIMIENTOS

Los autores desean agradecer tanto al Ministerio de Educación y Ciencia como al Ministerio de Ciencia y Tecnología Españoles la financiación de los proyectos MAT 2000-1112, MAT 2003-08480-C03- 02, MAT 2006-13354-C02-01 y MAT 2007-62450.

7. REFERENCIAS

1. Inglis CE. Trans R Inst Naval Architects 1913; 60: 219-241.        [ Links ]

2. Griffith AA. Philosophical Transactions of the Royal Society of London. Series A, 1921; 221: 163-198.        [ Links ]

3. Irwin GR. Fracture dynamics. in Fracturing of Metals (Proc. 1947 ASM Symposium, Cleveland) 1949. Cleveland, Ohio: American Society for Metals, p. 147-166.        [ Links ]

4. Westergaard HM. Journal of Applied Mechanics, 1939; 6: 49-53.        [ Links ]

5. Irwin GR. Journal of Applied Mechanics, 1957; 24(3): 361-364.        [ Links ]

6. Wells AA. British Welding Journal, 1961; 11: 563-570.        [ Links ]

7. Rice JR. Journal of Applied Mechanics, 1968; 35: 379-389.        [ Links ]

8. Broberg KB. Journal of the Mechanics and Physics of Solids, 1971; 19(6): 407.        [ Links ]

9. Broberg KB. Journal of the Mechanics and Physics of Solids, 1975; 23: 215.        [ Links ]

10. Cotterell B, Reddel JK. International Journal of Fracture, 1977; 13: 267-277.        [ Links ]

11. Gamez-Perez J, J. V, Franco-Urquiza E, Velasco JI, Maspoch ML, under review.        [ Links ]

12. Mai Y-W, Cotterell B, Horlyck R, Vigna G. Polym. Eng. Sci. 1987; 27: 804.        [ Links ]

13. Paton CA, Hashemi S. Journal Materials Science, 1992; 27: 2279-2290.        [ Links ]

14. Wu J, Mai YW, Cotterell B. J Mater Sci 1993; 28: 3373-3384.        [ Links ]

15. Sanchez JJ, Santana OO, Gordillo A, Maspoch ML, Martinez AB, "Essential Work of Fracture of Injection Moulded Samples of PET and PET/PC Blends", in Fracture of Polymers, Composites and Adhesives II, Blackman B, Pavan A, Williams JG, Editors. 2004, Elsevier Ltd. and ESIS. 77-84.        [ Links ]

16. Pardoen T, Marchal Y, Delannay F. Eng Fract Mech 2002; 69(5): 617-631.        [ Links ]

17. Xie XL, Yu ZZ, Zhang QX, Zhen GW, Mai YW. J. Polym. Sci. Pt. B-Polym. Phys. 2007; 45(12): 1448-1458.        [ Links ]

18. Lach R, Weidisch R, Janke A, Knoll K. Macromol. Rapid Commun. 2004; 25(24): 2019-2024.        [ Links ]

19. Antich P, Vazquez A, Mondragon I, Bernal C. Compos. Pt. A-Appl. Sci. Manuf. 2006; 37(1): 139-150.        [ Links ]

20. Rae PJ, Brown EN, Orler EB. Polymer 2007; 48(2): 598-615.        [ Links ]

21. Arkhireyeva A, Hashemi S. Polymer 2002; 43: 289-300.        [ Links ]

22. Knockaert R, Doghri I, Marchal Y, Pardoen T, Delannay F. International Journal of Fracture, 1996; 81(4): 383-399.        [ Links ]

23. Pardoen T, Marchal Y, Delannay F. Journal of the Mechanics and Physics of Solids, 1999; 47(10): 2093-2123.        [ Links ]

24. Cotterell B, Pardoen T, Atkins AG. Eng Fract Mech 2005; 72(6): 827-848.        [ Links ]

25. Chen YH, Mai YW, Tong P, Zhang LC, "Numerical Simulation of the Essential Fracture Work Method", in Fracture of Polymers, Composites and Adhesion,, Williams JG, Pavan A, Editors. 2000, Elsevier: Amsterdam. 175.        [ Links ]

26. Chen HB, Wu JS. Macromolecules 2007; 40(12): 4322-4326.        [ Links ]

27. Kwon HJ, Jar PYB. Polymer 2005; 46(26): 12480-12492.        [ Links ]

28. Kwon HJ, Jar PYB. International Journal of Fracture, 2007; 145(2): 123-133.        [ Links ]

29. Wong JSS, Ferrer-Balas D, Li RKY, Mai YW, Maspoch ML, Sue HJ. Acta Mater 2003; 51(16): 4929-4938.        [ Links ]

30. Kim HS, Karger-Kocsis J. Acta Mater 2004; 52(10): 3123-3133.        [ Links ]

31. Duan K, Hu XZ, Mai YW. J. Adhes. Sci. Technol. 2004; 18(1): 39-53.        [ Links ]

32. Haughie DW, Buckley CP, Wu JJ. Biomaterials 2006; 27(21): 3875-3881.        [ Links ]

33. Schuller T, Lauke B. Eng Fract Mech 2006; 73(16): 2252-2263.        [ Links ]

34. Gray A, Testing Protocol for Essential Work of Fracture, ESIS, Editor. 1993, European Structural Integrity Society (ESIS) - TC4.        [ Links ]

35. Hill R. Journal of the Mechanics and Physics of Solids, 1952; 1: 19.        [ Links ]

36. Clutton E, Testing Protocol for Essential Work of Fracture, ESIS., Editor. 1997, European Structural Integrity Society (ESIS) - TC4.        [ Links ]

37. Clutton E, "Essential Work of Fracture", in Fracture Mechanics testing methods for polymers, adhesives and composites, Moore DR, Pavan A, Williams JG, Editors. 2001, Elsevier Science, Ltd.: Oxford. 177-195.        [ Links ]

38. Clutton E, "ESIS TC4 Experience with the Essential Work of Fracture Method", in Fracture of polymers, composites and adhesives, Williams JG, Pavan A, Editors. 2000, Elsevier Science, Ltd.: Oxford. 187-199.        [ Links ]

39. Williams JG, Rink M. Eng Fract Mech 2007; 74(7): 1009-1017.        [ Links ]

40. Maspoch ML, Gamez-Perez J, Karger-Kocsis J. Polymer Bulletin 2003; 50(4): 279-286.        [ Links ]

41. Maspoch ML, Hénault V, Ferrer-Balas D, Velasco JI, Santana OO. Polymer Testing 2000; 19: 559-568.        [ Links ]

42. Maspoch ML, Ferrer D, Gordillo A, Santana OO. Journal of Applied Polymer Science, 1999; 73: 177-187.        [ Links ]

43. Martinez AB, Segovia A, Gamez-Perez J, Maspoch ML. Eng Fract Mech 2009; 76(9): 1247-1254.        [ Links ]

44. Pettarin V, Frontini PM, Elicabe GE. Polymer Testing 2005; 24(2): 189-196.        [ Links ]

45. Lach R, Schneider K, Weidisch R, Janke A, Knoll K. Eur. Polym. J. 2005; 41(2): 383-392.        [ Links ]

46. Duan K, Hu XZ, Stachowiak G. Compos.Sci. Technol. 2006; 66(16): 3172-3178.        [ Links ]

47. Gamez-Perez J, Santana O, Martinez AB, Maspoch ML. Polymer Testing 2008; 27(4): 491-497.        [ Links ]

48. Korsunsky AM, Nguyen GD, Kim K. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2006; 423(1-2): 192-198.        [ Links ]

49. Tjong SC, Bao SP, Hang GD. J. Polym. Sci. Pt. B-Polym. Phys. 2005; 43(21): 3112-3126.        [ Links ]

50. Bao SP, Tjong SC. Compos. Pt. A-Appl. Sci. Manuf. 2007; 38(2): 378-387.        [ Links ]

51. Ozkoc G, Bayram G, Bayramli E. J Mater Sci 2008; 43(8): 2642-2652.        [ Links ]

52. Wainstein J, Fasce LA, Cassanelli A, Frontini PM. Eng Fract Mech 2007; 74(13): 2070-2083.        [ Links ]

53. Tjong SC, Xu SA, Mai YW. J. Polym. Sci. Pt. B-Polym. Phys. 2002; 40(17): 1881-1892.        [ Links ]

54. Fayolle B, Verdu J. Polym. Eng. Sci. 2005; 45(3): 424-431.        [ Links ]

55. Light ME, Lesser AJ. J Mater Sci 2005; 40(11): 2861-2866.        [ Links ]

56. Saminathan K, Selvakumar P, Bhatnagar N. Polymer Testing 2008; 27(3): 296-307.        [ Links ]

57. Santana OO, Maspoch ML, Martinez AB. Polymer Bulletin 1997; 39(4): 511-518.        [ Links ]

58. Wong J, Ferrer-Balas D, Maspoch M, Li R, Mai Y. ABSTR PAP AM CHEM S 2002; 223: D93-D93.        [ Links ]

59. Fayolle B, Tcharkhtchi A, Verdu J. Polymer Testing 2004; 23(8): 939-947.        [ Links ]

60. Ragosta G, Musto P, Abbate M, Russo P, Scarinzi G. Macromol. Symp. 2005; 228: 287-298.        [ Links ]

61. Hashemi S, Xu Y. J Mater Sci 2007; 42(15): 6197-6204.        [ Links ]

62. Arkhireyeva A, Hashemi S. Eng Fract Mech 2004; 71(4-6): 789-804.        [ Links ]

63. Arkhireyeva A, Hashemi S. Polym. Eng. Sci. 2002; 42(3): 504-518.        [ Links ]

64. Korsunsky AM, Kim K. International Journal of Fracture, 2005; 132(3): L37-L44.        [ Links ]

65. Korsunsky AM, Nguyen GD, Houlsby GT. International Journal of Fracture, 2005; 135(1-4): L19-L26.        [ Links ]

66. Ferrer-Balas D, Maspoch ML, Martínez AB, Santana OO. Polymer Bulletin 1999; 42: 101-108.        [ Links ]

67. Ferrer-Balas D, Maspoch ML, Martínez AB, Santana OO. Polymer 2001; 42(4): 1697-1705.        [ Links ]

68. Ferrer-Balas D, Maspoch ML, Martínez AB, Ching E, Li RKY, Mai Y-W. Polymer 2001; 42(6): 2665-2674.        [ Links ]

69. Martínez AB, Segovia A, Gamez-Perez J, Maspoch ML. Eng Fract Mech 2010; En prensa.        [ Links ]

70. Karger-Kocsis J, Ferrer-Balas D. Polymer Bulletin 2001; 46(6): 507-512.        [ Links ]

71. Kwon HJ, Jar RYB. Polym. Eng. Sci. 2007; 47(9): 1327-1337.        [ Links ]

72. Liu Y, Xie BH, Yang W, Zhang WQ, Feng JM, Yang MB. Polymer Testing 2007; 26(3): 388-395.        [ Links ]

73. Pegoretti A, Ricco T. Eng Fract Mech 2006; 73(16): 2486-2502.        [ Links ]

74. Kwon HJ, Jar PYB. Eng Fract Mech 2007; 74(16): 2471-2480.        [ Links ]

75. Karger-Kocsis J, Czigány T, Moskala EJ. Polymer 1997; 38: 4587.        [ Links ]

76. Saleemi AS, Nairn JA. Journal of Applied Polymer Science, 1990; 30: 211.        [ Links ]

77. Chan WYF, Willams JG. Polymer 1994; 35: 1666.        [ Links ]

78. Hashemi S. Polym. Eng. Sci. 1997; 37(5): 912-921.        [ Links ]

79. Marchal Y, Delannay F. International Journal of Fracture, 1996; 80: 295-310.        [ Links ]

80. Maspoch ML, Santana OO, Grando J, Ferrer-Balas D, Martínez AB. Polymer Bulletin 1997; 39: 249-255.        [ Links ]

81. Karger-Kocsis J, Czigány T. Polym. Eng. Sci. 2000; 40(8): 1809-1815.        [ Links ]

82. Fung KL, Zhao HX, Wang JT, Meng YZ, Tjong SC, Li RKY. Polym. Eng. Sci. 2004; 44(3): 580-587.        [ Links ]

83. Mouzakis DE, Gahleitner M, Karger-Kocsis J. Journal of Applied Polymer Science, 1998; 70: 873-881.        [ Links ]

84. Karger-Kocsis J, Czigány T, Moskala EJ. Polymer 1998; 39: 3939.        [ Links ]

85. Maspoch ML, Gamez-Perez J, Gordillo A, Sánchez-Soto M, Velasco JI. Polymer 2002; 43: 4177-4183.        [ Links ]

86. Gamez-Perez J, Muñoz P, Santana OO, Gordillo A, Maspoch ML. Journal of Applied Polymer Science, 2006; 101: 2714–2724.        [ Links ]

87. Gamez-Perez J, Relación estructurapropiedades en placas y láminas de polipropileno y copolímeros en bloque etileno-propileno obtenidas por diferentes procesos de transformación. Tesis Doctoral, Terrassa (España): Universidad Politécnica de Cataluña, 2006.        [ Links ]

88. Gamez-Perez J, Muñoz P, Velasco JI, Martínez AB, Maspoch ML. J Mater Sci 2005; 40: 1967-1974.        [ Links ]

89. Mai YW, Pilko KM. J Mater Sci 1979; 14: 386-394.        [ Links ]

90. Mai YW, Cotterell B. J Mater Sci 1980; 15: 2296-2306.        [ Links ]

91. Mai YW, Cotterell B. International Journal of Fracture, 1986; 32: 105-125.        [ Links ]

92. Marchal Y, Delannay F, Froyen L. Scr. Mater. 1996; 35(2): 193-198.        [ Links ]

93. Levita G, Parisi L, Mcloghlin S. Journal of Material Science, 1996; 31: 1545-1553.        [ Links ]

94. Marchal Y, Walhin JF, Delannay F. International Journal of Fracture, 1997; 87(2): 189-199.        [ Links ]

95. Marchal Y, Delannay F. Mater Sci Tech Ser 1998; 14(11): 1163-1168.        [ Links ]

96. Wnuk MP, Read DT. International Journal of Fracture, 1986; 31(3): 161-171.        [ Links ]

97. Mai YW, Cotterell B. International Journal of Fracture, 1984; 24: 229-236.        [ Links ]

98. Monsalve A, Morales R. Rev. Metal. 2004; 40(6): 431-435.        [ Links ]

99. Pardoen T, Hachez F, Marchioni B, Blyth PH, Atkins AG. Journal of the Mechanics and Physics of Solids, 2004; 52(2): 423-452.        [ Links ]

100. Lu G, Yu TX, Huang X. Int. J. Veh. Des. 2005; 37(2-3): 224-251.        [ Links ]

101. Chehab B, Brechet Y, Glez JC, Jacques PJ, Mithieux JD, Veron M, Pardoen T. Scr. Mater. 2006; 55(11): 999-1002.        [ Links ]

102. Chia JYH, Cotterell B, Cheong AYH. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2006; 428(1-2): 67-72.        [ Links ]

103. Andriescu A, Hesp SAM, Youtcheff JS, "Essential and plastic works of ductile fracture in asphalt binders", in Bituminous Binders 2004. 2004, Transportation Research Board National Research Council: Washington. 1-8.        [ Links ]

104. Kodrat I, Sohn D, Hesp SAM. Transp. Res. Record 2007;1998: 47-55.        [ Links ]

105. Seth RS. Tappi J 1995; 78(10): 177-183.        [ Links ]

106. Seth RS, Robertson AG, Mai YW, Hoffmann JD. Tappi J 1993; 76(2): 109-116.        [ Links ]

107. Tanaka A, Otsuka Y, Yamauchi T. Tappi J 1997; 80(5): 222-226.        [ Links ]

108. Zhu PW, Edward G. Polymer 2004; 45(8): 2603-2613.        [ Links ]

109. Staudinger U, Satapathy BK, Thunga M, Lach R, Weidisch R, Knoll K. Acta Mater 2007; 55(17): 5844-5858.        [ Links ]

110. Li ZM, Yang W, Huang R, Fang XP, Yang MB. Macromol. Mater. Eng. 2004; 289(5): 426-433.        [ Links ]

111. Satapathy BK, Lach R, Weidisch R, Schneider K, Janke A, Knoll K. Eng Fract Mech 2006; 73(16): 2399-2412.        [ Links ]

112. Vincent L, Connolly SN, Dolan F, Willcocks PH, Jayaweera SAA. J. Therm. Anal. Calorim. 2006; 86(1): 155-164.        [ Links ]

113. Wan CY, Zhang Y, Zhang YX, Qiao XY, Teng GM. J. Polym. Sci. Pt. B-Polym. Phys. 2004; 42(2): 286-295.        [ Links ]

114. Fung KL, Li RKY. Polymer Testing 2005; 24(7): 863-872.        [ Links ]

115. Musto P, Ragosta G, Scarinzi G, Mascia L. Polymer 2004; 45(12): 4265-4274.        [ Links ]

116. Jing B, Dai WL, Liu PS. J Mater Sci 2006; 41(18): 6090-6094.        [ Links ]

117. Correa CA, Yamakawa RS, Razzino CA, Hage E. Polimeros-Ciencia y Tecnologia, 2007; 17(1): 36-45.        [ Links ]

118. Xie BH, Shen YX, Li ZM, Yang W, Feng JM, Yang MB. Acta Polym. Sin. 2006; 2: 335-339.        [ Links ]

119. Anuar H, Ahmad SH, Rasid R, Surip SN, Czigany T, Romhany G. J. Compos Mater. 2007; 41(25): 3035-3049.        [ Links ]

120. Baldi F, Bignotti F, Fina A, Tabuani D, Ricco T. Journal of Applied Polymer Science, 2007; 105(2): 935-943.        [ Links ]

121. Li B, Gong G, Xie BH, Yang W, Yang MB, Lai SM. J Mater Sci 2007; 42(11): 3856-3864.        [ Links ]

122. Na B, Lv RH, Zhao ZX. Journal of Applied Polymer Science, 2007; 104(2): 1291-1298.        [ Links ]

123. Shen YX, Xie BH, Yang W, Li ZM, Yang MB. J. Macromol. Sci. Part B-Phys. 2007; 46(6): 1127-1138.        [ Links ]

124. Lievana E, Bernal C, Frontini P. Polym. Eng. Sci. 2004; 44(9): 1707-1715.        [ Links ]

125. Mouzakis DE, Papke N, Wu JS, Karger-Kocsis J. Journal of Applied Polymer Science, 2001; 79(5): 842-852.        [ Links ]

126. Mouzakis DE, Mader D, Mulhaupt R, Karger-Kocsis J. J Mater Sci 2000; 35(5): 1219-1230.        [ Links ]

127. Marchal Y, Oldenhove B, Daoust D, Legras R, Delannay F. Polym. Eng. Sci. 1998; 38(12): 2063-2071.        [ Links ]

128. Okada O, Keskkula H, Paul DR. J. Polym. Sci. Pt. B-Polym. Phys. 2004; 42(9): 1739-1758.        [ Links ]

129. Pressly TG, Keskkula H, Paul DR. Polymer 2001; 42(7): 3043-3055.        [ Links ]

130. Lesser AJ, Jones NA. Journal of Applied Polymer Science, 2000; 76(6): 763-770.        [ Links ]

131. Pisharath S, Wong SC, Hu X. J Mater Sci 2004; 39(21): 6529-6538.        [ Links ]

132. Heino M, Hietajoa P, Seppälä T, Harmia T, Friedrich K. Journal of Applied Polymer Science, 1997; 66: 2209-2220.        [ Links ]

133. Inberg JPF, Gaymans RJ. Polymer 2002; 43(13): 3767-3777.        [ Links ]

134. Barany T, Karger-Kocsis J. J. Macromol. Sci.-Phys. 2004; B43(3): 671-683.        [ Links ]

135. Satapathy BK, Weidisch R, Pötschke P, Janke A. Macromol. Rapid Commun. 2005; 26(15): 1246-1252.        [ Links ]

136. Gong G, Xie BH, Yang W, Li ZM, Zhang WQ, Yang MB. Polymer Testing 2005; 24(4): 410-417.        [ Links ]

137. Qiao Y, Avlar S, Chakravarthula SS. Journal of Applied Polymer Science, 2005; 95(4): 815-819.        [ Links ]

138. Tjong SC, Bao SP. J. Polym. Sci. Pt. BPolym. Phys. 2005; 43(5): 585-595.        [ Links ]

139. Yang JL, Zhang Z, Zhang H. Compos. Sci. Technol. 2005; 65(15-16): 2374-2379.        [ Links ]

140. Baldi F, Bignotti F, Tieghi G, Ricco T. Journal of Applied Polymer Science, 2006; 99(6): 3406-3416.        [ Links ]

141. Bao SP, Tjong SC, "Fracture characterization of high density polyethylene/organoclay nanocomposites toughened with SEBS-g-MA", in Fracture of Materials: Moving Forwards. 2006, Trans Tech Publications LTD: Zurich-Uetikon. 187-192.        [ Links ]

142. Costa FR, Satapathy BK, Wagenknecht U, Weidisch R, Heinrich G. Eur. Polym. J. 2006; 42(9): 2140-2152.        [ Links ]

143. Gong G, Xie BH, Yang W, Li ZM, Lai SM, Yang MB. Polymer Testing 2006; 25(1): 98-106.        [ Links ]

144. Lim JW, Hassan A, Rahmat AR, Wahit MU. Plast. Rubber Compos. 2006; 35(1): 37-46.        [ Links ]

145. Wang K, Wu JS, Zeng HM. Journal of Applied Polymer Science, 2006; 99(3): 1207-1213.        [ Links ]

146. Yang W, Xie BH, Shi W, Li ZM, Liu ZY, Chen J, Yang MB. Journal of Applied Polymer Science, 2006; 99(4): 1781-1787.        [ Links ]

147. Zhang H, Zhang Z, Yang JL, Friedrich K. Polymer 2006; 47(2): 679-689.        [ Links ]

148. Ahmad SH, Rasid R, Surip SN, Anuar H, Czigany T, Razak SBA. J. Compos Mater. 2007; 41(17): 2147-2159.        [ Links ]

149. Arencon D, Velasco JI, Realinho V, Sanchez-Soto M, Gordillo A. J Mater Sci 2007; 42(1): 19-29.        [ Links ]

150. Gong G, Xie BH, Yang MB, Yang W, Zhang WQ, Zhao M. Compos. Pt. A-Appl. Sci. Manuf. 2007; 38(7): 1683-1693.        [ Links ]

151. Kobayashi H, Shioya M, Tanaka T, Irisawa T. Compos. Sci. Technol. 2007; 67(15-16): 3209-3218.        [ Links ]

152. Satapathy BK, Ganss M, Weidisch R, Potschke P, Jehnichen D, Keller T, Jandt KD. Macromol. Rapid Commun. 2007; 28(7): 834-841.        [ Links ]

153. Satapathy BK, Weidisch R, Potschke P, Janke A. Compos. Sci. Technol. 2007; 67(5): 867-879.        [ Links ]

154. Tjong SC, Bao SP. Compos. Sci. Technol. 2007; 67(2): 314-323.        [ Links ]

155. Wang XL, Li RY, Cao YX, Meng YZ. Materials and Design, 2007; 28(6): 1934-1939.        [ Links ]

156. Yoo YJ, Shah RK, Paul DR. Polymer 2007; 48(16): 4867-4873.        [ Links ]

157. Ganss M, Satapathy BK, Thunga M, Weidisch R, Potschke P, Jehnichen D. Acta Mater 2008; 56(10): 2247-2261.        [ Links ]

158. Saminathan K, Selvakumar P, Bhatnagar N. Polymer Testing 2008; 27(4): 453-458.        [ Links ]

159. Wong SC, Baji A, Gent AN. Compos. Pt. AAppl. Sci. Manuf. 2008; 39(4): 579-587.        [ Links ]

160. Bureau MN, Ton-That MT, Perrin-Sarazin F. Eng Fract Mech 2006; 73(16): 2360-2374.        [ Links ]

161. Cotterell B, Chia JYH, Hbaieb K. Eng Fract Mech 2007; 74(7): 1054-1078.        [ Links ]

162. Sui GX, Wong SC, Yue CY. J Mater Process Tech 2001; 113(1-3): 167-171.        [ Links ]

163. Velasco JI, Arencon D, Maspoch ML, Morhain C. Boletin de la sociedad española de ceramica y vidrio, 2000; 39: 514-519.        [ Links ]

164. Tjong SC, Xu SA, Li RKY, Mai YW. Compos. Sci. Technol. 2002; 62(6): 831-840.        [ Links ]

165. Lauke B, Schuller T. Int J Adhes Adhes 2001; 21(1): 55-58.        [ Links ]

166. Tjong SC, Xu SA. Journal of Applied Polymer Science, 2004; 94(4): 1539-1546.        [ Links ]

167. Jing B, Dai WL, Chen SB, Hu T, Liu PS. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2007; 444(1-2): 84-91.        [ Links ]

168. Poisson C, Fournier JE, Lacrampe MF, Krawczak P. Polymers and Polymer Composites 2006; 14(7): 671-689.        [ Links ]

169. Gamez-Perez J, Santana O, Gordillo A, Maspoch ML. Polym. Eng. Sci. 2007; 47(9): 1365-1372.        [ Links ]

170. Karger-Kocsis J, "Fracture and fatigue behaviour of semicristalline polymers as a function of microstructural and molecular parameters", in Structure Development during Polymer Processing, Cunha AM, Fakirov S, Editors. 1999, Kluwer Academic: Dordrechet. 163-179.        [ Links ]

171. Casellas JJ, Frontini PM, Carella JM. Journal of Applied Polymer Science, 1999; 74(4): 781-796.        [ Links ]

172. Barany T, Ronkay F, Karger-Kocsis J, Czigany T. International Journal of Fracture, 2005; 135(1-4): 251-265.        [ Links ]

173. Ho CH, Vu-Khanh T. Theoretical and Applied Fracture Mechanics, 2004; 41(1-3): 103-114.        [ Links ]

174. Kayano Y, Keskkula H, Paul DR. Polymer 1998; 39(13): 2835-2845.        [ Links ]

175. Van der Wal A, Mulder JJ, Thijs HA, Gaymans RJ. Polymer 1998; 39(22): 5467-5475.        [ Links ]

176. Cañizares R, Serrano P, Sánchez JJ, Gordillo A, Salazar D, Santana OO. Anales de Mecánica de la Fractura, 2002; 19: 153.        [ Links ]

177. Supatham P, Tabtiang A, Venables RA. Polym.-Plast. Technol. Eng. 2005; 44(3): 363-379.        [ Links ]

178. Na B, Lv RH. J. Polym. Sci. Pt. B-Polym. Phys. 2006; 44(19): 2880-2887.        [ Links ]

179. Wallner GM, Major Z, Maier G, Lang RW. Adv. Eng. Mater. 2006; 8(11): 1140-1145.        [ Links ]

180. Na B, Lv RH, Zhang Q, Fu Q. Polym. J. 2007; 39(8): 834-840.        [ Links ]

181. Rao YQ, Greener J, Avila-Orta CA, Hsiao BS, Blanton TN. Polymer 2008; 49(10): 2507-2514.        [ Links ]

182. Wallner GM, Major Z, Maier GA, Lang RW. Polymer Testing 2008; 27(3): 392-402.        [ Links ]

183. Yamakawa RS, Razzinoa CA, Correab CA, Hage Jr E. Polymer Testing 2004; 23(2): 195-202.        [ Links ]

184. Karger-Kocsis J, Mouzakis DE. Polym. Eng. Sci. 1999; 39(8): 1365-1374.        [ Links ]

185. Arkhireyeva A, Hashemi S, O'Brien M. J Mater Sci 1999; 34: 5961-5974.        [ Links ]

186. Monedero MT, Gamez-Perez J, Velasco JI, Maspoch ML. Anales de Mecánica de la Fractura, 2001; 19: 175-180.        [ Links ]

187. Karger-Kocsis J, Moskala EJ. Polymer Bulletin 1997; 39: 503-510.        [ Links ]

188. Wang XL, Li RKY, Cao YX, Meng YZ. Polymer Testing 2005; 24(6): 699-703.        [ Links ]

189. Hashemi S. J Mater Sci 2003; 38: 3055-3062.        [ Links ]

190. Wu JS, Chen HB. ABSTR PAP AM CHEM S 2005; 230: U3522-U3522.        [ Links ]

191. Satapathy BK, Staudinger U, Weidisch R, Lach R, Janke A, Knoll K. Macromol. Rapid Commun. 2006; 27(4): 266-273.        [ Links ]

192. Chen HB, Karger-Kocsis J, Wu JS. Polymer 2004; 45(18): 6375-6382.        [ Links ]

193. Karger-Kocsis J. ESIS Publ. "Fracture of Polymers, Composites and Adhesives" 2000; 27: 213-230.        [ Links ]

194. Martinez AB, Maspoch ML, Ferrer-Balas D. Anales de Mecánica de la Fractura, 2000; 17: 249-261.        [ Links ]

195. Kwon JA, Truss RW. Eng Fract Mech 2002; 69: 605-616.        [ Links ]

196. Wang SW, Yang W, Gong G, Xie BH, Liu ZY, Yang MB. Journal of Applied Polymer Science, 2008; 108(1): 591-597.        [ Links ]

197. Belzunce FJ, Bonhomme J, Rodriguez C, "Caracterización del proceso de fractura de polímeros dúctiles: trabajo esencial de fractura", en Anales de Mecánica de la Fractura. 1994. 273-276.        [ Links ]

198. Kwon HJ, Jar PYB. Polym. Eng. Sci. 2006; 46(10): 1428-1432.        [ Links ]

199. Peres FM, Schon CG. J Mater Sci 2008; 43(6): 1844-1850.        [ Links ]

200. Gupta P, Wilkes GL, Sukhadia AM, Krishnaswamy RK, Lamborn MJ, Wharry SM, Tso CC, DesLauriers PJ, Mansfield T, Beyer FL. Polymer 2005; 46(20): 8819-8837.        [ Links ]

201. Yang W, Shan GF, Tang XG, Xie BH, Li ZM, Zhou QC, Yang MB. Plast. Rubber Compos. 2006; 35(9): 368-374.        [ Links ]

202. Ching E C.Y., Li R K.Y., Mai Y-W. Polym. Eng. Sci. 2000; 40(2): 310-319.        [ Links ]

203. Riekel C, Karger-Kocsis J. Polymer 1999; 40: 541-545.        [ Links ]

204. Barany T, Foldes E, Czigany T, Karger-Kocsis J. Journal of Applied Polymer Science, 2004; 91(6): 3462-3469.        [ Links ]

205. Viana JC, Cunha EM, "Extensibility of the inter-lamellar amorphous layer and the mechanical behaviour of polyethylene", in Advanced Materials Forum Iii, Pts 1 and 2. 2006, Trans Tech Publications LTD: Zurich-Uetikon. 1186-1190.        [ Links ]

206. Li QG, Xie BH, Yang W, Li ZM, Zhang WQ, Yang MB. Journal of Applied Polymer Science, 2007; 103(5): 3438-3446.        [ Links ]

207. Sheng BR, Li B, Xie BH, Yang W, Feng HM, Yang MB. Polym. Degrad. Stabil. 2008; 93(1): 225-232.        [ Links ]

208. Ferrer-Balas D, Maspoch ML, Mai Y-W. Polymer 2002; 43: 3083-3091.        [ Links ]

209. Karger-Kocsis J, Czigány T. Polymer 1996; 37(12): 2433-2438.        [ Links ]

210. Liu C-H, Nairn J A. Polym. Eng. Sci. 1998; 38(1): 186-193.        [ Links ]

211. Arkhireyeva A, Hashemi S. Plast. Rubber Compos. 2001; 30(7): 337-350.        [ Links ]

212. Vincent L, Connolly SN, Dolan F, Willcocks PH, Jayaweera SAA, Pendlebury R. J. Therm. Anal. Calorim. 2006; 86(1): 147-154.        [ Links ]

213. Yakimets I, Wellner N, Smith AC, Wilson RH, Farhat I, Mitchell J. Mech. Mater. 2007; 39(5): 500-512.        [ Links ]

214. Karger-Kocsis J, Moskala EJ, Shang PP. J. Therm. Anal. Calorim. 2001; 63: 671-678.        [ Links ]

215. Poon WKY, Ching ECY, Cheng CY, Li RKY. Polymer Testing 2001; 20(4): 395-401.        [ Links ]

216. Kayano Y, Keskkula H, Paul DR. Polymer 1998; 39(4): 821-834.        [ Links ]

217. Vu-Khanh T. Polymer 1988; 29: 1979.        [ Links ]

218. Chiou KC, Chang FC, Mai YW. Polym. Eng. Sci. 2001; 41(6): 1007-1018.        [ Links ]

219. Huang J, Paul DR. Polymer 2006; 47(10): 3505-3519.        [ Links ]

220. Jing B, Dai W, Liu P, Zhang P. Polym. Int. 2007; 56(10): 1240-1246.        [ Links ]

221. Hashemi S. J Mater Sci 1993; 28: 6178.        [ Links ]

222. Hashemi S. J Mater Sci 1997; 32: 1563-1573.        [ Links ]

223. Wu J, Mai Y-W. Polym. Eng. Sci. 1996; 36(18): 2275.        [ Links ]

224. Hashemi S. J Mater Sci 2000; 35(23): 5851-5856.        [ Links ]

225. Yuan YL, Wu CML, Li RKY. Polymer Testing 2007; 26(1): 102-107.        [ Links ]

226. Luna P, Bernal C, Cisilino A, Frontini P, Cotterell B, Mai YW. Polymer 2003; 44(4): 1145-1150.        [ Links ]

227. Ching E C.Y., Poon WKY, Li R K.Y., Mai Y-W. Polym. Eng. Sci. 2000; 40(12): 2558-2568.        [ Links ]

228. Fasce L, Bernal C, Frontini P. Polym. Eng. Sci. 2001; 41(1): 1 - 14.        [ Links ]

229. Plummer CJG, Scaramuzzino P, Steinberger R, Lang RW, Kausch H-H. Polym. Eng. Sci. 2000; 40(4): 985-991.        [ Links ]

230. Whittle AJ, Burford RP, Hoffman MJ. Plast. Rubber Compos. 2001; 30(9): 434-440.        [ Links ]

231. Lau SW, Truss RW. J Mater Sci 2002; 37(6): 1115-1119.        [ Links ]

232. Hashemi S, O'Brien D. J Mater Sci 1993; 28: 3977-3982.        [ Links ]

233. Zhao HX, Li RKY. Mech. Mater. 2006; 38(1-2): 100-110.        [ Links ]

234. Pfaff FA. J. Coat. Technol. Res. 2007; 4(2): 151-159.        [ Links ]

235. Maspoch ML, Tafzi A, Ferrando HE, Velasco JI, Martinez AB. Filled PMMA: Mechanical Properties and Fracture Behaviour. in EURO-FILLERS'99 1999. Lyon, France.        [ Links ]

236. Chen HB, Wu JS. J. Polym. Sci. Pt. BPolym. Phys. 2007; 45(12): 1418-1424.        [ Links ]

237. Plucknett KP, Normand V. Polymer 2000; 41(18): 6833-6841.        [ Links ]

238. Chaleat CM, Halley PJ, Truss RW. Carbohydr. Polym. 2008; 71(4): 535-543.        [ Links ]

239. Bureau MN, Perrin-Sarazin F, Ton-That MT. Polym. Eng. Sci. 2004; 44(6):1142-1151.        [ Links ]

240. Franco-Urquiza E, Gamez-Perez J, Sanchez-Soto M, Santana O, Maspoch ML. Polym. Int. 2010; 59(6):778-786        [ Links ]

241. Maspoch ML, Franco-Urquiza E, Gamez-Perez J, Santana OO, Sanchez-Soto M. Polym. Int. 2009; 58(6): 648-655.        [ Links ]

242. Maspoch ML, L. Nascimento, E. Fanco-Urquiza, J. Gámez-Perez. Fracture Behaviour of Poly(Lactic Acid) and PLA/MMT Nanocomposites. in 5th ESIS TC4 Conference on Fracture Polymers Composites and Adhesives 2008. Les Diablerets, Switzerland.        [ Links ]

243. Franco-Urquiza E, Maspoch ML. Ingenierías 2009; 12: 35-40.        [ Links ]

244. Realinho VCdR, Caracterización estructural, térmica y mecánica de nanocompuestos termoplásticos de matriz amorfa (PS, SAN y PMMA), preparados por mezcla en fundido, con partículas laminares de hidrotalcita y montmorillonita modificadas. Tesis doctoral, Terrassa: (España) Universidad Politécnica de Cataluña, 2009.        [ Links ]

245. Franco-Urquiza E, Preparación y caracterización de nanocompuestos EVOH/Montmorillonita. Tesis doctoral, Terrassa (España): Universidad Politécnica de Cataluña, 2009.        [ Links ]

246. Vaia RA, Teukolsky RK, Giannelis EP. Chemistry of Materials, 1994; 6: 1017-1022.        [ Links ]

247. Vaia RA, Giannelis EP. Macromolecules 1997; 30(25): 7990-7999.        [ Links ]