A small-angle light scattering instrument to study soft condensed matter

Angel Romo-Uribe^1*, Bonifacio Alvarado-Tenorio², Maria Eugenia Romero-Guzmán¹

1: Laboratorio de Nanopolímeros y Coloides, Instituto de Ciencias Físicas, Universidad Nacional Autónoma de México. Av. Universidad s/n, Cuernavaca, Morelos. 62210 México

2: Facultad de Química, Departamento de Ingeniería Química (Programa de Maestría y Doctorado en Ingeniería), Universidad Nacional Autónoma de México, 04510 México D.F., México

* E-mail: aromo-uribe@fis.unam.mx

Publicado On-Line el 30-Jul-2010

Disponible en: www.rlmm.org

Abstract

A simple and inexpensive small-angle light scattering (SALS) instrument for soft condensed matter studies has been developed; the instrument has the advantage of simplicity of equipment, rapid detection and presentation of the entire small-angle pattern for investigation. A wide scattering vector range is achieved using a CCD detector; despite the lowbudget components utilized the instrument characteristics have enabled us to obtain high-quality light scattering data from soft matter systems. The setup is especially well suited to studies of systems with a weak scattering power and/or a timedependent structure evolution in a wide spatial range with sub-micrometer resolution. The technique enabled to measure the size, anisotropy, radial periodicity and internal structure of polymer spherulites at a resolution below that achieved by optical microscopy. Applications of this instrument to investigate the microstructure and spatial correlations in semicrystalline polymers using the Debye-Bueche theory, and in thermotropic liquid crystalline polymers are also reported. Furthermore, it is demonstrated that the technique is also suitable to study the evolution of microstructure with applied uniaxial tensile strain in thin polymer films.

Keywords: Small-angle light scattering, Microstructure, Polymers, Morphology

Resumen

Un instrumento sencillo y de bajo costo de difracción de luz a ángulo-pequeño (SALS, por sus siglas en inglés) para estudiar la materia condensada suave ha sido desarrollado; el instrumento tiene la ventaja de simplicidad de equipo, rapida detección y la presentación del patrón de ángulo-pequeño completo para su investigación. Un rango amplio del vector de difracción se logra al utilizar un detector CCD; a pesar del bajo costo de los componentes utilizados, las características del instrumento nos han permitido obtener datos de alta calidad de difracción de luz de sistemas de materia suave. El dispositivo está especialmente adaptado para el estudio de sistemas con difracción débil y/o con evolución de la microestructura dependiente del tiempo en una gama espacial amplia con resolución de sub-micras. La técnica permitió medir el tamaño, la anisotropía, la periodicidad radial y la estructura interna de las esferulitas de un polímero a una resolución por debajo de la alcanzada por microscopia óptica. Las aplicaciones de este instrumento para investigar la microestructura y las correlaciones espaciales en polímeros semicristalinos usando la teoría de Debye-Bueche, y en cristale líquidos poliméricos termotrópicos también son reportadas. Además, se muestra que la técnica es también conveniente para estudiar la evolución de la microestructura al aplicar una tensión uniaxial a películas poliméricas delgadas.

Palabras Claves: Difracción de luz a ángulo- pequeño, Microestructura, Polímeros, Morfología

Recibido: 19-May-2009; Revisado: 04-May-2010; Aceptado: 24-May-2010

1. INTRODUCTION

The light scattering (LS) technique and theoretical background were initially developed to characterize polymeric solutions and colloidal suspensions. Key physical properties such as molecular weight and radius of gyration were the major subjects [1, 2]. In the early days, commercial instrumentation for light scattering measurements was not available and the responsibility for the design and construction of this instrumentation relied on the scientists themselves [3-5]. This technique consists of scanning a wide scattering angle range (typically 90º), therefore the instruments were usually equipped with a photometer on a wide-angle goniometer. After developments for over half a century, this technique (sometimes termed wide-angle light scattering, WALS) is now well established [6, 7]. Nowadays commercial instruments are also equipped with autocorrelators thus enabling dynamic measurements for the determination of diffusion coefficients of polymeric chains in solution [8].

Along these developments, since the 1960’s Stein and coworkers pioneered a light scattering technique to investigate the higher ordered structures in condensed systems, especially the spherulitic microstructure of partially crystalline polymers [9,10], the microstructure in deformed polyethylene samples [11], and the influence of thermal annealing on polymer’s crystalline microstructure [12]. The value of the technique was rapidly recognized and successfully applied to investigate polymer microstructure in industrial laboratories [13]. In order to investigate the optically anisotropic structure a depolarized light scattering (DPLS) technique was employed, that is, a polarizer and an analyzer are inserted along the light beam path before and after the specimen, respectively. For the measurement of the higher ordered structure a small scattering angle range is scanned compared with the former technique, WALS. Therefore, this type of light scattering technique is often termed smallangle light scattering (SALS).

The usefulness of SALS is now well established and the technique is routinely utilized to investigate soft condensed matter as well as complex fluids. For instance, SALS has been utilized to investigate capillary flow behavior in worm-like micelles [14], phase separation dynamics in binary fluid mixtures [15], phase separation kinetics in polymeric blends [16, 17], orientation behavior of solutions of poly (g -benzyl-L-glutamate) in an electric field [18], domain texture coarsening in thermotropic polymers [19], aggregation kinetics during drying of particle monolayers [20] , and polymerization-induced phase separation kinetics [21]. There also a number of applications into biological systems as SALS has been applied to study the human cornea [22] and biological cells [23].

Due to the versatility of this technique and advances in instrumentation, in-situ studies of flowing complex fluids have been carried out. These studies include flow-induced texture orientation in lyotropic [24] and thermotropic [25] liquid crystalline polymers, flow-induce phase transitions in thermotropic polymers [26], shear-induced coalescence in polymer blends [27], and shearinduced crystallization on polyolefins [28, 29].

The SALS technique was initially implemented by using an arc lamp as light source and photographic film as the detector for the scattered light [9-12]. In order to produce a beam of parallel light and a monochromatic light from the diverging white light source, a lens and a pinhole device as well as monochromatic filters were, respectively, employed [9,10]. In order to carry out quantitative angular profile analysis, a photomultiplier tube on a smallangle goniometer was also employed in addition to the photographic film. Later on the He-Ne laser was introduced as the light source [13] further fueling the development of this technique.

Further developments in electronics made possible to build a photodiode array making possible to measure the angular profile at once and leading to time-resolved measurements [30]. In the same way, charge-coupled device (CCD) image sensors to record two-dimensional SALS patterns replaced photographic film. However, note that the exposure area of the CCD image sensor is usually very small. Accordingly, a condenser lens focusing the scattered light onto the CCD plane has been utilized [31,32]. In other cases, the scattering pattern has been projected on a white screen and indirectly recorded by a CCD camera equipped with an imaging lens [14, 25, 26]. A great advantage in the former method is that the scattered light can be directly brought into the CCD plane without loss of intensity. However, in order to obtain the scattering pattern on the CCD plane, the distance of the sample-to-condenser lens and the distance from the condenser lens to the CCD plane must be tightly arranged according to the focal length (F) of the condenser lens. That is, there is no flexibility in the camera length of the scattering geometry. On the other hand, imaging the scattered pattern on a screen is a flexible method because enables adjusting the camera length without compromising the optics of the instrument. There is a penalty to be paid however, and it is the lose of brightness and resolution due to the smearing effect on the screen when the scattered light is projected, however the correction factors are negligible for scattering angles less than 2q =15º [33].

In this work we describe a simple and inexpensive design of a SALS setup where the imaging screen method has been adopted. The following sections are devoted to the description of the setup and of the procedures for instrument adjustment and calibration. We then demonstrate through case studies that, despite the simplicity and low-budget components utilized to set this instrument, it is possible to characterize the submicron spherulitic microstructure in partially crystalline polymer thin films, the internal structure of a spherulite, the texture microstructure in thin films of liquid crystalline polymers and the characterization of microstructure in thin polymer films subjected to uniaxial tensile deformation.

2. EXPERIMENTAL

2.1 SALS instrument design

The apparatus developed for the SALS measurements is shown schematically in Figure 1a. The optical components were mounted on an optical breadboard manufactured by Edmunds Optics Co. (New Jersey, USA). The light source is a vertically polarized He-Ne laser (wavelength l = 632.8 nm) of 0.8 mW power (model 1500 manufactured by JDS Uniphase Corp., Santa Rosa California, USA). Immediately downstream from the laser there are iris diaphragms with adjustable apertures that work as pinholes (PH). The PH function is to collimate the main beam such that stray reflections are prevented from reaching the sample. The incident intensity was then attenuated by using neutral density filters (Edmunds Optics Co.). The polarization direction of the incident beam was set by a polarizer (P) with the polarization axis set vertically. The polarized light impinged on the sample (S) and the incident and scattered light passed through a 40 mm diameter polarizer whose polarization axis is now set at 90º, this is called the analyzer (A). The 0º-90º orientation of the polarizer and analyzer sets the so-called HV polarization condition. The scattered light falls onto a diffusing plate (sand blasted glass, manufactured by Edmunds Optics Co.) placed 126 mm downstream from the sample. The main function of the diffusing plate is to act as an image transfer screen onto which the light detection device can be focused. A circular beam stop made of black foam of 8.5 mm diameter was used to prevent the main beam to impinge directly on the detector. For image recording a charge-coupled device (CCD, model PC-23C, Super Circuits, Taiwan) with C-mount ring and wide-angle lens (manufactured by Computar, Japan) was used. The CCD has a resolution of 200 mm/pixel. The CCD was located 50 cm behind the diffusing plate. When enabled the CCD captures a two-dimensional image covering the scattering angles 2q between 2 and 15 degrees. The scattering patterns were displayed on the color monitor of a PC and recorded via an IMAQ frame grabber (model PCI-1405, National Instruments, USA). Frame grabbing was performed using National Instruments software. The image analysis was carried out using the software ImageTool v.3, a Windows XP . based application developed by The University of Texas Health Science Center in San Antonio (USA). The entire setup is encased in a black box made of acrylic polymer sheets. Figure 1b shows a picture of the instrument with the black box removed.

2.2 Instrument calibration

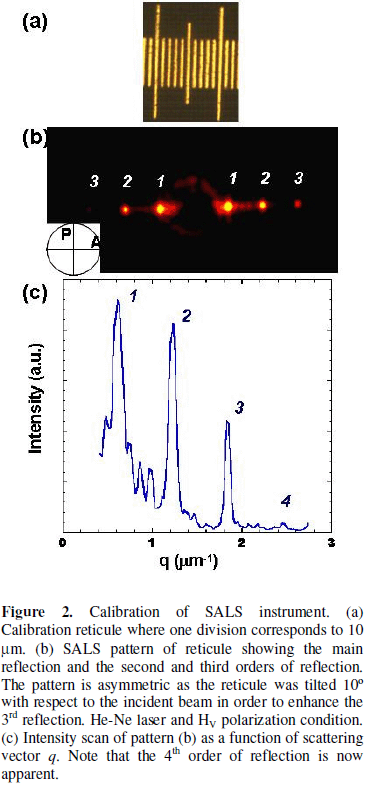
For the determination of the sample-to-detector distance, D, an optical microscopy calibration graticule 1 mm long was used (made by Graticules Ltd, Tonbridge, Kent, England). The reticule contains 100 divisions/mm and therefore there is a distance of 10 mm per division. The reticule can be considered a one-dimensional crystal. Figure 2a shows an optical micrograph of a section of the reticule. Figure 2b shows the corresponding SALS pattern where there are intense and sharp reflections on one axis; note that the diffraction pattern corresponds to the Fourier transform of an array of periodic slits and shows three orders of reflection.

From the digitized pattern an intensity scan was extracted along the reflections. The X-axis of the scan, in pixels, was converted to mm by applying the conversion factor specified by the CCD manufacturer of 200 mm/pixel. The scattering angle 2q for the first order reflection was obtained from Bragg’s relationship [34]

2d . Sinq = n . l ,      (1)

where q is half the scattering angle, n the order of reflection and l the radiation wavelength (632.8 nm). For a first order reflection n =1 and therefore

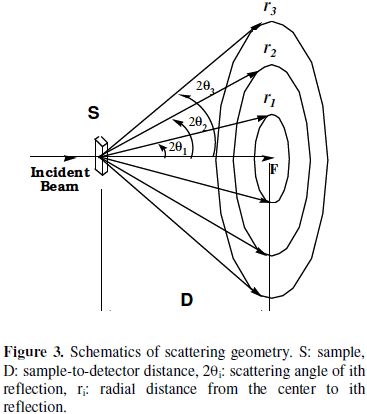
The sample-to-detector distance D was obtained from the scattering geometry (see Figure 3) using the trigonometric relationship

where r is the radial position to a given reflection, as shown schematically in Figure 3. The sample-todetector distance is then obtained from the relation

From equation (4) a sample-to-detector distance of D = (126.08 ± 0.10) mm was determined. The uncertainty in the value of D was estimated from at least five independent measurements. Figure 2c shows the intensity scan extracted from the SALS pattern 2b. The intensity is plotted as a function of the magnitude of the scattering vector = q

The plot shows the first, second, third and fourth orders of reflection located at q_m,1= 0.62 mm^-1, q_m,2= 1.23 mm^-1, q_m,3= 1.83 mm^-1, and q_m,4= 2.45 mm^-1. The d spacing associated with these reflections are d₁= 10.05 mm, d₂= 5.1 mm, d₃= 3.4 mm and d₄= 2.5 mm. Therefore, from the spacing of the first order reflection, d₁, we recover the value of the minimum spacing in the calibration graticule, i.e., 10 mm.

Moreover, note that the sample-to-detector distance chosen give a scattering angle range from 2q = 2º to 15º translating in a d-spacing of ca. 18 to 1.7 mm (the scattering space is reciprocal to the real space, therefore small angles mean large d-spacing). This spatial resolution is of course a function of the sample-to-detector distance and our instrument setup allows for easy reposition of the screen in order to change this range.

3. RESULTS AND DISCUSSION

The SALS instrument described here is simple in its concept and versatile; the following sections present a small selection of applications to study the microstructure in soft condensed matter.

3.1 Ring structure in polymeric spherulites

The usefulness of the SALS technique was first applied to investigate the internal structure of a polymeric spherulite. Figure 4 shows the optical micrographs of a well-crystallized sample of polyhydroxy butyrate (hereafter denoted PHB) obtained under cross-polarized light conditions. Figure 4a shows a crystalline morphology with well-defined Maltese crosses typical of lamellar crystalline morphology in some semicrystalline polymers [12, 35]. The scale in the micrograph shows that the spherulites have sizes ranging from 50 to over 400 mm, the smaller spherulites being trapped between the larger ones. Figure 4b shows a higher resolution micrograph of PHB where the internal ring structure can be clearly appreciated. Stein et al have shown that the ring structure arises from radially periodic orientation of crystals within the spherulites [36]. For instance, in polyethylene the ring structure arises from the angle describing the orientation of the tangential a- and c-axis about the radial b-axis, the angle being proportional to the distance from the center of the spherulite. The resolution of this SALS instrument enables then to study the spherulites internal structure.

Figure 5a shows the SALS pattern of PHB. The pattern is anisotropic and shows four reflections with scattering maxima positioned azimuthally at 45º to the polarization directions indicative of undeformed spherulitic morphology [12, 36]. The pattern also shows a second order of reflection. The azimuthal spread of the reflections is indicative of the imperfect crystalline morphology in the sample. Figure 5b shows the radial intensity scan obtained by scanning along 45º to the polarization direction, i.e., through the intensity maxima. The positions of the intensity maxima are q_m,1= 1.06 mm-1, and q_m,2= 2.14 mm-1, which correspond to a d-spacing of d₁= 5.91 mm, and d₂= 2.94 mm.

The theory for the scattering from the ring structure within spherulites has been developed by Stein [36], this theory predicts a scattering maximum when

 l » d_ring . sinq_m .    (6)

Equation (6) shows that the ring spacing d_ring can be obtained from half the angular position of the reflection maximum (2q)_m. In terms of the scattering vector q equation (6) is written as

Applying equation (7) to the q value obtained for the first order reflection (q_m,1=1.06 μm^-1) gives rise to a ring spacing of d_ring » (11.8±0.6) μm.

The ring spacing obtained from the SALS pattern is contrasted with the ring spacing obtained directly from the real space image shown in Figure 4b. For this an intensity scan was obtained by scanning inside a spherulite, Figure 6 shows the plot of intensity as a function of distance, note the spatial periodicity of intensity maxima. The ring spacing was determined from the position of intensity maxima, averaging over eleven maxima, giving a value of _ring  = (11.0±0.5) μm. This result is equal to that obtained from the SALS analysis.

3.2 Spherulitic morphology in semicrystalline polymers

The SALS technique was also applied to investigate the microstructure in extruded Nylon 6™ films of 35 mm thickness. The sample was kindly provided by Ticona, the Engineering Polymers Business of Celanese Co. Figure 7a shows the optical micrograph of the film under crossed polarizers, the extrusion direction is vertical. It can be seen that the micrograph shows little contrast if any and certainly no sign of sherulites despite being a semicrystalline polymer. On the other hand, figure 7b shows the H_V SALS pattern of this polymer film, and the pattern shows a “four-leaf clover” with intensity maxima at an azimuthal angle of f=45º with respect to the extrusion direction. This SALS pattern is typical of spherulitic microstructure in semicrystalline polymers [12,35]. Figure 7c shows the intensity scan as a function of scattering vector q; note that the intensity reaches a maximum at q_m= 0.78 μm^-1 and then decays monotonically.

Stein et al., developed a theory for small-angle scattering from spherulitic polymers and the theory was developed by assuming that scattering arises from a homogeneous anisotropic sphere embedded in an isotropic medium [12]. The equation derived by Stein et al for H_V scattering is

where V_o is the volume of the sphere, U=(4pR/l)sinq, where R is the radius of the sphere, l the wavelength of the light (in the medium), and 2q is the scattering angle. a_t and a_r are the tangential and radial polarizabilities of the sphere, and f is the azimuthal scattering angle.

The maxima of the “four-leaf clover” H_V patterns occur, according to equation (8), when

enabling the calculation of the spherulite size from the angular position of the intensity maximum.

Equation (9) is easily rewritten in terms of the scattering vector

Stein et al., [12, 36] have shown that this relation gives a good agreement between measured spherulite sizes and those deduced from equation (11). Furthermore, those and other authors have shown that the light scattering technique may be used for the measurement of smaller sizes than is possible by light microscopy. Applying equation (11) to the results shown in Figure 7 we obtained a spherulite radius for the Nylon 6 extruded film of R = 5 mm.

3.3 Uniaxial deformation in semicrystalline polymer film

Here are presented preliminary results of scattering arising from a polymer with spherulitic microstructure subjected to uniaxial tensile deformation. The Nylon 6 extruded film discussed above was uniaxially deformed along the extrusion direction. The polymer film was clamped at both ends and displaced symmetrically in such a way as the incident beam always impinged on the same point each time. Figure 8 shows a selection of SALS patterns obtained at (0), (b) 30, (c) 66 and (d) 134 % deformation. The scattering pattern at 30 % strain (Figure 8b) shows a slight rotation of the intensity maxima towards the equatorial (horizontal) axis as well as a shifting towards the beam stop. This pattern indicates that the spherulites have been deformed and stretched along the tensile axis (indicated by the arrow). There is additionally an intensity streak along the equatorial axis. This streak arises from an elongated microstructure along the tensile axis. Further stretching the sample up to 66% strain (Figure 8c) does not change the four lobe morphology indicating that the spherulitic morphology is preserved under the uniaxial elongation. Moreover, the shifting of the lobes towards the beam stop indicates a size increase of the spherulites. It can also be seen that the equatorial streak is more intense and elongated suggesting that more material has been aligned along the tensile axis.

Finally, Figure 8d shows the pattern corresponding to 134 % strain. The four lobe morphology is still appreciated although the maxima are now concentrated into the beam stop. Furthermore, the equatorial streak has grown in intensity, and it is more elongated along the equatorial axis. It is also noted that the equatorial streak shows some azimuthal broadening. The contraction of the four lobes indicates that the spherulitic microstructure has increased in size. On the other hand, the broadening of the equatorial streak indicates that there is some degree of misorientation of the microstructure along the tensile axis. The change in spherulite size as a function of strain has been characterized; the results will be reported elsewhere.

3.4 Diffuse scattering and correlation length

Here it is discussed diffuse scattering arising from a non-spherulitic microstructure in a semicrystalline polyester Vandar 9116™, a polymer film 35 mm thick and supplied by Ticona, The Engineering Polymer Business of Celanese Co. The polarized optical micrograph is shown in Figure 9a, where a “grainy” microstructure can be appreciated. Figure 9b shows the corresponding SALS pattern, note that there is only isotropic diffuse scattering intensity. The depolarized H_V intensity arises from orientation fluctuations [12]. Thus the diffraction pattern indicates that there is not preferred orientation in the film sample.

Figure 9c shows the plot of intensity as a function of scattering angle. Due to the isotropic nature of the pattern the intensity was azimuthally averaged, it can be seen that there is a rapid decays of intensity as q increases.

This type of diffuse scattering pattern can be analyzed using the Debye-Bueche equation in the nonspherically symmetrical form [37]. For the cross-polarized condition, H_V, and assuming that there are not cross correlation terms in the refractive index fluctuations and that they can be expressed as Gaussians, in the limit of small scattering angles (q ®0 ), the following expression for the correlation length, a, was obtained

I_HV (q) = Kn < n² > p^3/2 a³. exp(-q²a²),   (12) 

where I_HV is the depolarized intensity, K is a constant, n is the scattering volume, <n²> is the mean-squared fluctuation in refractive index, and q (= (4p /l )Sinq ) is the magnitude of the scattering vector. From the Guinier-type plots thus obtained (ln I_HV vs. q²) the correlation length can be calculated. Figure 10 shows the Guinier-type plot for Vandar, it can be seen that the experimental data conform very well to the Debye-Bueche equation; from the slope a correlation length a = 0.96 μm was determined.

3.5 Microstructure in thermotropic liquid crystalline polymers

Finally, the usefulness of the SALS instrument is applied in the investigation of the complex microstructure displayed by liquid crystalline polymers (LCPs). The LCP was kindly provided by Ticona and it is a random copolyesteramide based on hydroxybenzoic acid, terephthalic acid and aminophenol (denoted B-T-AP). Figure 11a shows the optical micrograph under crossed polarizers condition of the thermotropic B-T-AP which had been subjected to uniaxial shear (shear direction indicated by the arrow) at 310 ºC and then rapidly quenched onto a cold metal block to preserve the microstructure [38, 39]. The micrograph shows a periodic oriented structure oriented orthogonally to the velocity axis, it is the well-known "gbanded" texture. Note that the width of the bands is ca. 15 μm.

Figure 11b shows the corresponding SALS pattern. Firstly, the diffraction pattern shows the formation of intensity maxima on the velocity axis indicative of a periodic oriented structure along the vorticity axis (i.e., orthogonal to the velocity axis). The radial spread of the intensity is related to the regularity in bands spacing, whereas the position of the intensity maxima corresponds to the mean distance between bands. Moreover, the azimuthal concentration of intensity is related to the regularity of the bands orientation along the vorticity direction. Secondly, the diffraction pattern also shows intensity streaks along the vorticity axis which are the signature of some oriented defects along the velocity axis. Note that the optical micrograph (Figure 11a) does not show evidence of these defects oriented along the velocity axis. Therefore, SALS evidences a double oriented texture in the as-sheared LCP. This type of orientation had already been reported by Romo- Uribe and Windle during in-situ studies of this sort of LCP [39].

4. CONCLUSIONS

Recently a high-resolution SALS instrumentation has been described for soft condensed matter studies based on a potent laser source and a high resolution CCD camera [40]. Those authors demonstrated that with this sort of hardware is possible to achieve a good signal-to-noise ratio especially for complex fluids with relatively low contrast. In this work we have demonstrated that a simple and inexpensive small-angle light scattering instrument can enabled the study of a variety of soft condensed matter systems in the solid state. The instrument enabled the determination of size and anisotropy in polymer thin films, and in the defect texture of liquid crystalline polymer thin films. Despite the simplicity and low-budget components utilized the instrument also enabled the analysis of the internal structure of polymeric spherulites. Furthermore, it was demonstrated the capability of this instrument to characterize the evolution of spherulitic microstructure under uniaxial tensile deformation.

Nomenclature

a: correlation length

d: spacing

n: index of refraction

r: radial distance

q: scattering vector

A: analyzer

D: sample-to-detector distance

DPLS: depolarized light scattering

H_V: polarization condition

LS: light scattering

P: polarizer

PH: pinhole

PHB: poly hydroxy butyrate

R: spherulite radius

S: sample

Si: sine integral function

SALS: small-angle light scatter

WALS: wide-angle light scatter

l: wavelength

f: azimuthal angle

2q: scattering Bragg’s angle

5. ACKNOWLEDGEMENTS

The authors would like to thank Ticona, The Engineering Polymers of Celanese Co. (Summit, NJ, USA) for the provision of especially prepared samples. B Alvarado-Tenorio was supported by a graduate scholarship from CONACyT. M.E. Romero-Guzmán was supported by a postdoctoral fellowship from DGAPA-UNAM. This research was supported by CONACyT (CIAM-2006, 58646).

6. REFERENCES

1. Debye P. J. App. Phys. 1944; 15: 338-342.        [ Links ]

2. Zimm BH, Stein RS, Doty P. Polymer Bull. 1945; 1: 90-119.        [ Links ]

3. Debye P. J. Phys. and Colloid Chem. 1947; 51: 18-32.        [ Links ]

4. Zimm BH. J. Chem. Phys. 1948; 16: 1093-1099.        [ Links ]

5. Zimm BH. J. Chem. Phys. 1948; 16: 1099-1116.        [ Links ]

6. Kerker M. The scattering of Light, Academic Press, New York, 1969.        [ Links ]

7. Chu B. Laser Light Scattering: Basic Principles and Practice, 2nd Ed. Academic Press, Boston, 1991.        [ Links ]

8. <http://www.wyatt.com>        [ Links ]

9. Stein RS, Rhodes MB. J. Appl. Phys. 1960; 31: 1873-1884.        [ Links ]

10. Stein RS, Wilson PR. J. Appl. Phys. 1962; 33: 1914-1922.        [ Links ]

11. Sasaguri K, Hoshino S, Stein RS. J. Appl. Phys. 1964; 35: 47-54.        [ Links ]

12. Rhodes MB, Stein RS. J. Appl. Phys. 1961; 32: 2344-2352.        [ Links ]

13. Samuels RJ. Structured Polymers,Wiley, New York, 1966.        [ Links ]

14. Castelleto V, Hamley IW. Polym. Adv. Techn. 2006; 17: 137-144.        [ Links ]

15. Cumming A, Wiltzius P, Bates FS, Rosedale JH. Phys. Rev. A 1992; 45: 885-897.        [ Links ]

16. Cheung YW, Stein RS, Lin JS, Wignall GD. Macromolecules. 1994; 27: 2520-2528.        [ Links ]

17. Sakurai S, Izumitani T, Hasegawa H, Hashimoto T, Han CC. Macromolecules. 1991; 24: 4844-4851.        [ Links ]

18. Ozaki F, Ogita T, Matsuo M. Macromolecules. 1981; 14: 299-309.        [ Links ]

19. Shiwaku T, Nakai A, Hasegawa H, Hashimoto T. Macromolecules. 1990; 23: 1590-1599.        [ Links ]

20. Thill H, Spalla O. Colloids and Surfaces A: Physicochem. Eng. Aspects. 2003; 217: 143-151.        [ Links ]

21. Maugey J, van Nuland T, Navard P. Polymer 2001; 42: 4353-4366.        [ Links ]

22. Bettelheim FA, Kumbar M. Invest. Ophthalmol. Visual Sci. 1977; 16: 236-240.        [ Links ]

23. Mullaney PF, Dean PN. Biophys. J. 1970; 10: 764-772.        [ Links ]

24. Ernst B, Navard P, Hashimoto T, Takebe T. Macromolecules. 1990; 23: 1370-1374.        [ Links ]

25. Romo-Uribe A, Mather PT, Chaffee KF, Han CD. Mat. Res. Soc. Symp. Proc. 1997; 461: 63-68.        [ Links ]

26. Mather PT, Romo-Uribe A, Han CD, Kim SS. Macromolecules. 1997; 30: 7977-7989.        [ Links ]

27. Borschig C, Fries B, Gronski W, Weis C, Friedrich C. Polymer. 2000; 41: 3029-3035.        [ Links ]

28. Fukushima H, Ogino Y, Matsuba G, Nishida K, Kanaya T. Polymer. 2005; 46: 18978-1885.        [ Links ]

29. Pogodina NV, Lavrenko VP, Srinivas S, Winter HH. Polymer. 2001; 42: 9031-9043.        [ Links ]

30. Okada T, Saito H, Inoue T. Macromolecules. 1992; 25: 1908-1911.        [ Links ]

31. Kawai T, Strobl G. Macromolecules. 2004; 37: 2249-2255.        [ Links ]

32. Weber V, Schosseler F. Rev. Sci. Instrum. 2002; 73: 2537-2543.        [ Links ]

33. Alexander M, Hallet FR. Applied Optics. 1999; 38: 4158-4163.        [ Links ]

34. Alexander L. X-ray Diffraction Methods in Polymer Science, John Wiley and Sons, London, 1969.        [ Links ]

35. Yalcin B, Cakmak M. Polymer. 2004; 45: 2691-2710.        [ Links ]

36. Stein RS, in Newer Methods of Polymer Characterization, Interscience Publishers, New York, 1964, p 155.        [ Links ]

37. Stein RS, Hotta T. J. Appl. Phys. 1964; 35: 2237-2242.        [ Links ]

38. Viney C, Donald AM, Windle AH. J. Mater. Sci. 1983; 18: 1136-1142.        [ Links ]

39. Romo-Uribe A, Windle AH. Proc. Royal Soc. Lond. A. 1999; 455: 1175-1201.        [ Links ]

40. Nishida K, Ogawa H, Matsuba G, Konishi T, Kanaya T. J. Appl. Cryst. 2008; 41: 723-728.        [ Links ]