Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Latinoamericana de Metalurgia y Materiales
versión impresa ISSN 0255-6952
Rev. LatinAm. Metal. Mater. vol.34 no.1 Caracas jun. 2014
LATTICE PARAMETER VALUES AND PHASE TRANSITIONS FOR THE Cu2-II-IV-S4(Se4) (II=Mn, Fe, Co; IV=Si, Ge, Sn) MAGNETIC SEMICONDUCTOR COMPOUNDS
1*11,2222
Miguel Quintero, Ekadink Moreno, Silvana Alvarez, Jesús Marquina, Carlos Rincón, Eugenio Quintero, Pedro Grima2, José-Antonio Heano3, Mario Alberto Macías3
1: Centro de Estudios de Semiconductores (CES), Departamento de Física, Facultad de Ciencias, Universidad de los Andes, Mérida 5101, Venezuela. 2: Centro de Estudios Avanzados en Óptica (CEAO), Departamento de Física, Facultad de Ciencias, Universidad de los Andes, Mérida 5101, Venezuela. 3: Grupo de investigación en Química Estructural (GIQUE), Facultad de Ciencias, Escuela de Química, Universidad Industrial de Santander, Apartado aéreo 678, Bucaramanga, Colombia.
* e-mail: mquinter@ula.ve

ABSTRACT
X-ray powder diffraction measurements, at 300 K, and differential thermal analysis (DTA) were made on sixteen polycrystalline samples of Cu2-II-IV-S4(Se4) (II: Mn, Fe, Co; IV: Si, Ge, Sn) magnetic semiconductor compounds. The diffraction patterns were
analyzed to determine lattice parameter values. The results showed that ten have tetragonal stannite I42m structure, one has tetragonal
pseudo-cubic P4 structure, four an orthorhombic wurtz-stannite Pmn21 and two an orthorhombic pseudo-cubic F222 structure. When the values of the effective parameter ae = (V/N)1/3 are plotted against its molecular weight W, it was found that the tetragonal and orthorhombic materials lie on the same straight line. The peaks on the DTA measurements were used to determine the type of melting as well as the melting temperature. The resulting data together with the Lindemann relation were used to estimate values for the Debye temperature θD as well as for the sound velocity in the material vs.
Keywords: Semiconducting, X-ray diffraction (XRD), differential thermal analysis (DTA).
VALORES DE LOS PARAMETROS DE LA RED Y TRANSICIONES DE FASE PARA LOS COMPUESTOS SEMICONDUCTORES MAGNETICOS Cu2-II-IV-S4(Se4) (II=Mn, Fe, Co; IV=Si, Ge, Sn)
RESUMEN
Se hicieron medidas de difracción en polvo de rayos X (a 300 K) y análisis térmico diferencial (ATD) sobre dieciseis muestras policristalinas de los compuestos semiconductores magnéticos Cu2-II-IV-S4(Se4) (II: Mn, Fe, Co; IV: Si, Ge, Sn). Se analizaron los patrones de difracción para determinar los valores de los parámetros de la red. Los resultados muestran que diez de ellas tiene la
estructura estanita tetragonal I42m , una tiene la estructura tetragonal seudocúbica P4 , cuatro poseen una estructura wurtzitaestannita Pmn21 y dos tienen una estructura seudocúbica F222. Cuando los valores del parámetro efectivo ae = (V/N)1/3 se grafican contra su peso molecular W, se encuentra que los materiales tetragonales y ortorrómbicos caen sobre la misma línea recta. Los picos en las medidas de ATD fueron usados para determinar el tipo de fusión, así como, la temperatura de fusión. Los datos resultantes junto con la relación de Lindemann fueron utilizados para estimar los valores de la temperatura de Debye θD, así como, los valores de la velocidad del sonido en el material vs.
Palabras Claves: Semiconductores, difracción de rayos X (DRX), análisis térmico diferencial (ATD).
Recibido: 21-09-2012 ; Revisado: 18-10-2012 pISSN: 0255-6952 | eISSN: 2244-7113
28
Aceptado: 23-10-2012 ; Publicado: 19-02-2013 Rev. LatinAm. Metal. Mat. 2014; 34 (1): 28-38
1. INTRODUCTION
Quaternary semiconducting compounds of the I2-II-IV-VI4 type, where II = Zn, Cd, Hg, Mn, Fe or Co, IV = Si, Ge, Sn or Pb and VI = S, Se or Te, are of great interest because of both their applications in the fabrication of low cost solar cells [1] and their large magneto-optical effects which are observed when II are paramagnetic atoms [2, 3]. As reported by several authors [3-5], most of these compounds showed either the tetrahedral tetragonal stannite (
I42m ) structure based on zinc-blende, an orthorhombic superstructure derived from wurtzite (known as wurtz-stannite, Pmn21) or an orthorhombic face-centered unit cell (space group F222) [5]. More recently, it has been found that at room temperature the Cu2FeSnS4 compound crystalizes in a tetragonal structure with space group
P4 [6]. The crystallographic parameter values of the I2-Mn-IV-VI4, I2-Fe-IV-VI4 and of the set Cu2II-IV-S4(Se4) have been reported in [7, 8, and 4], respectively. The magnetic behavior of various I2(Mn,Fe,Co)-IV-VI4 have been given in [9,10 and 11]. However, the available information related to differential thermal analysis DTA and phase transition temperatures for these compounds is very scarce. The knowledgement of the crystallographic parameters as well as the phase relations of the materials are important to establish their crystal growth conditions. Here, a systematic study on the crystallographic parameters and phase transitions, carried out on Cu2-(Mn,Fe,Co)-IV-S4(Se4) compounds is presented. The obtained crystallographic parameters and melting temperature values together with the Lindemann’s relation have been used to estimate values of the Debye temperature as well as the sound velocity in the material.
2. EXPERIMENTAL PART
The samples were produced by the melt and anneal technique. In each case, highly pure components (copper 99.98 %, manganese 99.97 %, iron 99.9 %, cobalt 99.99 %, silicon 99.999%, germanium 99.999%, tin 99.999 %, sulphur 99.997 % and/or selenium 99.9997 %) of 1 g sample were sealed
10-5
under vacuum (≈ Torr) in a small quartz ampoule, and then the components were heated up to 200 °C and kept for about 1-2 h, then the temperature was raised to 500 °C using a rate of 40 K/h, and held at this temperature for 14 hour. After, the samples were heated from 500 °C to 800 °C at a rate of 30 K/h and kept at this temperature for another 14 hours. Then it was raised to 1150 °C at 60 K/h, and the components were melted together at this temperature. The furnace temperature was brought slowly (4 K/h) down to 600 °C, and the samples were annealed at this temperature for 1 month. Then, the samples were slowly cooled to room temperature using a rate of about 2 K/h.
A small amount of each compound was gently ground in an agate mortar and sieved to a grain size of less than 38 µm. Each sample was mounted on a zero-background specimen holder for the respective measurement. X-ray powder diffraction patterns of the samples were recorded using a D8 FOCUS BRUKER Rigaku D/MAX IIIB diffractometer operating in Bragg-Brentano geometry equipped with an X-ray tube (Cu Kα radiation: λ = 1.5406 Å, 40 kV and 40 mA) using a nickel filter and an onedimensional LynxEye detector. A fixed antiscatter slit of 8 mm, receiving slit of 1 mm, soller slits of
2.5 ° and a detector slit of 3 mm were used. The scan range was from 2 to 70 ° 2θ with a step size of
0.02 °2θ and a counting time of 0.4 s/step.
Phase transition temperatures were obtained from differential thermal analysis (DTA) measurements, in the temperature range between 20 ºC and 1150 ºC, using a Perkin-Elmer DTA-7 with aluminum and gold used as reference materials. The charge was of powdered alloy of approximately 100-mg weight. Both heating and cooling runs were carried out on each sample, the average rates of these runs being approximately 10 K/min. The error in determining these temperatures is of about ±10 K.
3. RESULTS
3.1 X-Ray
From the X-ray diffraction pattern obtained for each sample, which was indexed with the computer program DICVOL04 [12] using an absolute error of 0.03º (2θ) in the calculations, lattice parameter values were estimated. The space group was established using CHECKCELL program according to the systematic absences, and the unit cell parameters for each compound were refined with the NBS*AIDS83 program [13]. A complete crystal structure refinement was performed for each compound using the fitting program MAUD (Material Analysis Using Diffraction) [14]. The obtained crystallographic parameter values and
space groups are summarized in table 1. tetragonal pseudo-cubic P4 , four were orthorhombic wurtz-stannite Pmn21 and two were
It is seen from table 1 that, as indicated above, the orthorhombic pseudo-cubic F222. The x-ray
present materials crystallize in two tetragonal diffraction patterns obtained here are similar to
( I42m , P4 ) and two orthorhombic (Pmn21, F222) tetrahedral structure types. Out of the 16 slowly those shown in Ref. (15) for stannite I42m and cooled samples investigated in this work, ten were wurtz-stannite Pmn21, Ref. 6 for tetragonal P4 and found to be tetragonal stannite I42m , one was Ref. (5) for orthorhombic F222.
Table 1. Resulting lattice parameter, melting point (TM), Debye temperature (θD) and sound velocity (vS) values for each compound. N is the number of molecules per cell, SG the space group.
| N° | Compound | W | N | SG | a | b | c | V | ae | Dx | TM | θD | vs ×105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (g/mol) | (Å) | (Å) | (Å) | (Å3) | (Å) | (g/cm3) | (K) | (K) | (cm/s) | ||||
| 1 | Cu2MnSiS4 | 338.38 | 2 | Pmn21 | 7.5362 | 6.4416 | 6.1866 | 300.33 | 5.3152 | 3.74 | 1293 | 312 | 2.8 |
| 2 | Cu2MnGeS4 | 382.93 | 2 | Pmn21 | 7.6160 | 6.5130 | 6.2300 | 309.03 | 5.3661 | 4.12 | 1272 | 288 | 2.6 |
| 3 | Cu2MnSnS4 | 429.00 | 2 | I 42m | 5.5180 | 5.5180 | 10.8070 | 329.06 | 5.4796 | 4.33 | 1177 | 257 | 2.4 |
| 4 | Cu2FeSiS4 | 339.28 | 2 | Pmn21 | 7.4210 | 6.4170 | 6.1409 | 292.43 | 5.2682 | 3.85 | 1275 | 311 | 2.7 |
| 5 | Cu2FeGeS4 | 383.84 | 2 | I 42m | 5.3355 | 5.3355 | 10.5250 | 299.62 | 5.3111 | 4.25 | 1269 | 289 | 2.6 |
| 6 | Cu2FeSnS4 | 429.91 | 1 | P-4 | 5.4329 | 5.4329 | 5.4104 | 159.70 | 5.4254 | 4.47 | 1104 | 250 | 2.3 |
| 7 | Cu2CoSiS4 | 342.37 | 2 | I 42m | 5.2683 | 5.2683 | 10.3350 | 286.85 | 5.2345 | 3.96 | 1258 | 312 | 2.7 |
| 8 | Cu2CoGeS4 | 479.59 | 2 | I 42m | 5.2957 | 5.2957 | 10.4740 | 293.74 | 5.2761 | 4.37 | 1323 | 299 | 2.6 |
| 9 | Cu2CoSnS4 | 433.00 | 2 | I 42m | 5.3992 | 5.3992 | 10.8180 | 315.36 | 5.4025 | 4.56 | 1191 | 261 | 2.4 |
| 10 | Cu2MnGeSe4 | 570.51 | 2 | Pmn21 | 7.9958 | 6.8574 | 6.5717 | 360.33 | 5.6479 | 5.26 | 1085 | 207 | 2.0 |
| 11 | Cu2MnSnSe4 | 616.58 | 2 | I 42m | 5.7623 | 5.7623 | 11.3682 | 377.47 | 5.7361 | 5.42 | 967 | 185 | 1.8 |
| 12 | Cu2FeGeSe4 | 571.42 | 2 | I 42m | 5.6008 | 5.6008 | 11.0561 | 346.82 | 5.5764 | 5.47 | 1046 | 206 | 1.9 |
| 13 | Cu2FeSnSe4 | 617.49 | 2 | I 42m | 5.7054 | 5.7054 | 11.2710 | 366.89 | 5.6820 | 5.59 | 1045 | 194 | 1.9 |
| 14 | Cu2CoSiSe4 | 529.95 | 1 | F222 | 5.5680 | 5.5010 | 5.3980 | 165.34 | 5.4886 | 5.32 | 1112 | 224 | 2.1 |
| 15 | Cu2CoGeSe4 | 574.51 | 1 | F222 | 5.5983 | 5.5548 | 5.4993 | 171.01 | 5.5507 | 5.58 | 1054 | 207 | 1.9 |
| 16 | Cu2CoSnSe4 | 620.58 | 2 | I 42m | 5.6728 | 5.6728 | 11.3220 | 364.35 | 5.6689 | 5.66 | 1118 | 201 | 1.9 |
| a | Cu2CdGeSe4 | 627.98 | 2 | I 42m | 5.7482 | 5.7482 | 11.0533 | 365.22 | 5.6734 | 5.71 | 1103 | 198 | 1.9 |
| b | Cu2CdSnSe4 | 674.05 | 2 | I 42m | 5.8306 | 5.8306 | 11.399 | 387.52 | 5.7867 | 5.78 | 1040 | 182 | 1.8 |
| c | Cu2CdGeS4 | 440.40 | 2 | Pmn21 | 7.703 | 6.5549 | 6.312 | 318.71 | 5.4215 | 4.59 | 1282 | 267 | 2.4 |
| d | Cu2HgSnSe4 | 762.23 | 2 | I 42m | 5.818 | 5.818 | 11.48 | 388.59 | 5.7919 | 6.51 | 981 | 166 | 1.6 |
| e | Cu2ZnSnSe4 | 627.03 | 2 | I 42m | 5.681 | 5.681 | 11.34 | 365.98 | 5.6773 | 5.69 | 1063 | 195 | 1.9 |
a: Ref. [17]; b: Ref. [16]; c: Ref. [26]; d: Ref. [25]; e: Ref. [25].
3.2 Differential Thermal Analysis DTA
DTA runs were carried out on each prepared sample as indicated above. The transition temperatures as well as the type of melting were obtained from the peaks on the DTA heating and cooling curves. Each transition temperature was determined from the base intercept of the tangent to the leading edge of the peak in the differential signal. Values of the melting point temperature, denoted as TM, obtained from the congruent and/or peritectic peaks on the DTA curves are given in table 1. The DTA results for the investigated samples can be summarized as follow. The DTA curves for the Cu2FeSnS4 [6], Cu2MnGeSe4 [15], Cu2FeGeSe4 [15], Cu2MnSnSe4
[16] and Cu2FeSnSe4 [16] have been given in earlier works. The resulting transition temperature values, melting type and phase relations have been collected in table 2.
Table 2. Values of transition temperatures obtained from heating TH and cooling TC DTA runs.
| No | Compound | TH | TC | Melting Type | Phase relations | Ref. |
| (°C) | (°C) | |||||
| 1 | Cu2MnSiS4 | 1020 | 1146, 1002, 986 | Peritectic | δ • β + δ • β • L + β1 • L | PW |
| 2 | Cu2MnGeS4 | 999, 1029 | 986 | Undercooling | δ • L + δ1 • L | PW |
| Peritectic | ||||||
| 3 | Cu2MnSnS4 | 904 | 1004, 903 | Peritectic | α • L + δ1 • L | PW |
| 4 | Cu2FeSiS4 | 1002, 919 | 996, 920 | Congruent | δ‚α‚L | PW |
| 5 | Cu2FeGeS4 | 996,1024 | 960 | Undercooling | α • L + δ1 • L | PW |
| Peritectic | ||||||
| 6 | Cu2FeSnS4 | 831 | 831 | Congruent | γ • α• L | [6] |
| 7 | Cu2CoSiS4 | 985, 923 | 1047, 985, 870 | Peritectic | α • α + δ • δ • L + δ1 • L | PW |
| 8 | Cu2CoGeS4 | 1050 | 1014 | Undercooling | α • L | PW |
| Undetermined | ||||||
| 9 | Cu2CoSnS4 | 918 | 918, 871 | Congruent | α • δ • L | PW |
| 10 | Cu2MnGeSe4 | 812, 688 | 848 | Peritectic | δ • L + δ1 • L | [15] |
| 11 | Cu2MnSnSe4 | 694, 795, 613 | 700, 606 | Undercooling | α • α + δ • L + δ1 • L | [16] |
| Peritectic | ||||||
| 12 | Cu2FeGeSe4 | 773 | 734 | Undercooling | α • L | [15] |
| Undetermined | ||||||
| 13 | Cu2FeSnSe4 | 772 | 740 | Undercooling | α • α + δ • L + δ1 • L | [16] |
| Peritectic | ||||||
| 14 | Cu2CoSiSe4 | 839, 908, 711 | 907, 822 | Peritectic | δ • δ + β • β • L + β1 • L | PW |
| 15 | Cu2CoGeSe4 | 781, 866 | 811, 746 | Undercooling | γ’ • L + β • L | PW |
| Peritectic | ||||||
| 16 | Cu2CoSnSe4 | 845, 895, 675 | 854, 674 | Peritectic | α • β • L + β1 • L | PW |
PW: Present work. α: tetragonal stannite I42m structure; δ: orthorhombic wurtz-stannite Pmn21 structure; δ1: high temperature modification HT; γ: tetragonal pseudo-cubic P4 ; γ’: orthorhombic pseudo-cubic F222 structure; β and β1-HT: cubic zinc-blende.
3.2.1 Cu2MnSiS4, Cu2MnGeS4 and Cu2MnSnS4.
From the obtained DTA thermograms for Cu2MnSiS4, shown in fig. 1, it is seen that only one transition at about 1020 ºC appears in the heating curve, while the cooling run shows three transitions at 1146 and 1002 and 986 ºC. The effects observed at 1020 and 1146 ºC would correspond to the solid and liquid lines respectively, i.e. to the peritectic decomposition of the Cu2MnSiS4 (from β to liquid L+ β1) and to the transition to the liquid L state (from L+ β1 to L), respectively. Here, β1 and β must be cubic zinc-blende phases with different compositions since, at low temperatures, the
tetragonal stannite α phase ( I42m ) has lower symmetry than the wurtz-stannite δ phase (Pmn21) observed in the x-ray results given above. In the range between 1020 and 1002 ºC the phase is β, below 1002 ºC there is a two phase field β + δ, and at 986 ºC a solid-solid transition from β + δ to δ occurs, where once again δ has the wurtz-stannite structure shown by the present x-ray data . These results are similar to those reported in earlier works for the compounds Cu2CdGeSe4 [15, 17] and Cu2ZnGeSe4 [18, 19]. From the DTA results for Cu2MnGeS4 shown in fig. 2, it can be observed that the respective DTA curves exhibit two effects in both heating and cooling runs. Also, the onset temperature in the heating processes (999 ºC) is slightly higher than the one in the cooling run (986 ºC). This behavior would indicate that undercooling effects are present. The DTA results show that the Cu2MnGeS4 melts incongruently and the peritectic decomposition (from δ to L+δ1) occurs at 999 ºC and the liquid transformation (from L+δ1 to L) takes place at 1029 ºC. The DTA thermograms for the Cu2MnSnS4 are shown in fig. 3, which are similar to the ones in fig. 1. It is seen from this figure that one transition at about 904 ºC occurs in the heating curve, while the cooling run shows two transitions at 1004 and 904 ºC. The effects observed at around 904 ºC in both of these two runs and at 1004 ºC in the cooling one would correspond to the peritectic decomposition of the Cu2MnSnS4 (from α to liquid L+δ1) and to the liquid transformation (from L+ δ1 to L), respectively, where δ1 being the HT modification suggested in earlier works for similar compounds [15, 17, 18, 19] and α the tetragonal stannite observed in the present x-ray diffractogram, respectively.



3.2.2 Cu2FeSiS4 and Cu2FeGeS4.
From the DTA thermograms for Cu2FeSiS4 shown in fig. 4, it is seen that the DTA curves exhibit two effects in both heating (at 919 and 1002 ºC) and cooling (at 996 and 920 ºC) runs. In addition, no effects due to undercooling are observed, and the compound melts congruently at about 1002 ºC. The DTA results for Cu2FeGeS4 (see fig. 5) show that the compound melts incongruently and undercooling behavior is present. Thus, the peritectic decomposition (from α to L+δ1) occurs at 996 ºC and the liquid (from δ1+L to L) at 1024 ºC, where δ1 is the HT modification suggested in earlier works [15, 17, 18, 19] and α the tetragonal stannite
( I42m ) observed in the present x-ray results.


3.2.3 Cu2CoSiS4, Cu2CoGeS4 and Cu2CoSnS4.
The resulting DTA thermograms for Cu2CoSiS4 are illustrated in fig. 6. It is seen that the DTA curves exhibit two effects in the heating run at 923 and 1041 ºC, while the cooling run shows three transitions at 1047, 985 and 870 ºC. No effects due to undercooling are observed in this compound. The effects observed at 985 and 1041 ºC would correspond to the peritectic decomposition of the Cu2CoSiS4 (from δ to liquid L+δ1) and to the liquid L state (from L+δ1 to L), respectively. In the range between 985 and 923 ºC, the phase is δ and at 870ºC a transition occurs from δ+α to the tetragonal stannite α phase ( I42m ), which is the equilibrium structure at 300 K. From the DTA curves for Cu2CoGeS4 (see fig. 7) it is observed that the onset temperature in the heating process (1050 °C) is slightly higher than the one in the cooling run (1014 °C). This would indicate that undercooling effects are present so that the type of melting is uncertain in this case. The melting point of this compound is estimated to be TM ≈ 1050 ºC, from the heating process. The obtained DTA results for Cu2CoSnS4, shown in fig. 8, indicate that the compound melts congruently at 918 ºC whereas below 871 ºC the
phase is the tetragonal stannite α ( I42m ), which is the equilibrium structure at 300 K.



Figure 8. DTA thermograms for Cu2CoSnS4. The direction of heating run, or cooling run, is indicated by the corresponding arrow.
3.2.4 Cu2CoSiSe4, Cu2CoGeSe4 and Cu2CoSnSe4.
From the DTA curves for Cu2CoSiSe4, shown in fig. 9, three transitions occurring at about 711, 839 and 908 ºC and two transformations at 907 and 822 ºC can be observed in the heating and cooling runs, respectively. Undercooling effects are not observed in the present case. The peaks at 839 and 908 ºC in the heating curve are related to the peritectic decomposition of the compound (from β to L+β1) and to the liquid transformation (from L+β1 to L), respectively. Once again, β1 and β are cubic zinc blende phases of different compositions. A two phase field β+δ exits below 822 ºC and a transformation from β+δ to the wurtz-stannite δ phase (Pmn21) observed in the x-ray data occurs at 711 ºC. From the DTA results for the Cu2CoGeSe4, fig. 10, it was found that undercooling effects are present. Also, it is seen that this compound melts incongruently at 781 ºC and below this temperature the structure is γ orthorhombic pseudocubic (F222). The DTA thermograms for the Cu2CoSnSe4 are shown in fig. 11; it can be observed in this figure that it has a peritectic temperature of TM ≈ 845 ºC (β
• L+ β1) and the liquid (L + β1 • L) occurs at 895
ºC. Below 675 ºC, the phase is the tetragonal stannite α ( I42m ), which is the equilibrium structure at room temperature.



4. DISCUSSION
As has been shown previously [9] for these type of compounds, the quantity ae = (V/N)1/3, where V is the volume of the unit cell and N the number of molecules per cell, varied smoothly with the molecular weight W of the compound. For the present materials, N depends upon the corresponding space group, thus N = 2 for I42m or Pmn21 and N = 1 for P4 or F222. Values of ae for the compounds investigated here are given in table
1. Figure 12 shows the variation of ae vs W for the tetragonal and orthorhombic. It is seen from this figure that, within the limits of experimental errors, for the present Cu2(Mn,Fe,Co)-IV-S4(Se4), whether tetragonal or orthorhombic phases, the experimental points of ae lie on the same straight line. It is to be mentioned that, in a previous work, carried out on material involving Fe atoms [8], all of the compounds with Ag and Te atoms were found to be orthorhombic, and their ae values lied on a straight line different than the one for the tetragonal compounds. However, in the work made on the I2-Mn-IV-VI4 [7], the results showed that the tetragonal as well as the orthorhombic Cucompounds lie on the same straight line, while the Ag materials lie on a different one. The present results are in good agreement with the ones obtained for the Cu compounds in Ref. [7].
Another point of interest here is to use the obtained values of ae and the melting temperature TM to estimate values for the Debye temperature θD with the Lindemann’s expresion [20].
T ⎞1/ 2 1 θ D = C HM ⎟ (1)
⎜⎟
W a
⎠ e

Where W = W/n , n is the number of atoms per formula (n = 8 for the present quaternaries), V is the volume of unit cell (in Å3) and C is a constant. The Debye temperature is an important parameter in the understanding of thermal and electrical properties of semiconducting materials. A value of C = 450 has been used for NaCl structure type [21] and Garbato et al [22] have used C =341 for the tetrahedral bonded tetragonal chalcopyrite as well as hexagonal wurtzite materials. A value of C is not available for the I2-II-IV-VI4 tetrahedral bonded quaternary compounds as yet. Also, no directly experimental values of θD for the present compounds have been given in the literature. Since the ternary chalcopyrite structure of the I-III-VI2 materials is close to the tetragonal one of most of the present tetrahedral bonded quaternary compounds, available θD experimental data for ternary compounds can be used for an estimation of C. Thus, the values of θD determined from specific heat experiments for the I-III-VI2 [23, 24] have been plotted as a function of W-1/2 in fig. 13. Using these values together with the TM [22-24, 27-32] and W values in eq. (1), a value of C ≈ 300 is obtained from the average of the C values for the I-III-VI2 compounds. Hence, as first approximation, here the values of ae and TM listed respectively in table I have been used in Eq. (1), with C ≈ 300, to estimate initial values of θD for the
2
⎞ ⎠
kBθ
⎛
present
Cu2-(Mn,Fe,Co)-IV-S4(Se4) compounds.
(2)
v=
s
6π
The resulting θD values for the I2-II-IV-VI4, h
quaternaries together with the experimental ones for the I-III-VI2 are shown in fig. 13. In addition, values θD for some nonmagnetic I2-II-IV-VI4, for which experimental values of ae and TM are available, have also been included in this figure. The estimated values of θD for the materials are tabulated in table I. It seen from this fig. 13 that, within the limits of experimental errors, these curves of θD vs W-1/2 are linear, and the values for the quaternaries are higher than the ones for the ternaries. Since the TM and W values for ternary and quaternary compounds are very similar, then the separation between both θD vs
| W-1/2 | is | due | to | that | the | values | of | ae | for | the | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| quaternaries | are | greater | than | the | ones | for | the | ||||
| ternaries. | |||||||||||

(W)-1/2
. Close circles: tetragonal. Open circles: orthorhombic. The triangles represent the experimental θD values from specific heat for the I-III-VI2 compounds. A. CuInS2 [24], B. CuInSe2 [24], C. CuGaSe2 [24], D. CuInTe2 [24], E. CuGaTe2 [24], F.AgInTe2 [23], G.AgGaTe2 [23]. The squares represent some nonmagnetic I2-II-IV-VI4: a. Cu2CdGeSe4 [17], b. Cu2CdSnSe4 [16], c. Cu2CdGeS4 [26], d. Cu2HgSnSe4 [25], e. Cu2ZnSnSe4 [25]. The solid line represents the fit to a linear form in W-1/2. The dashed line is to guide the eyes.
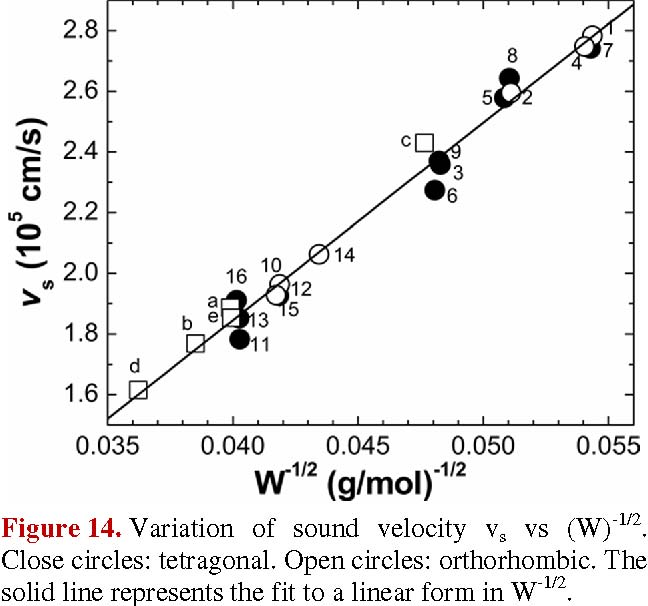
The sound velocity vs in a material can be estimated from the value of the Debye temperature θD by the well-known relation [33],
where kB is the Boltzmann constant, h is the reduced Planck's constant, V (= V/16) is the mean vs W-1/2
volume per atom. The resulting curve of vs , obtained using the values of V and θD from table I with eq. (2), is shown in fig. 14. It is seen from figs. 13 and 14 that, within the limits of the experimental errors, the values of θD and vs vary linearly with W1/2 . Hence, as a first approximation, using the molecular weight W of the compound reasonable values of θD and/or vs can be obtained from figs. 13 and 14, respectively, for similar materials. Then for extrapolation purposes, the values of θD and vs as a function of W-1/2 were least squared fitted to a linear form and the resulting relations are,
θD = -141.8 + 8392.0 W-1/2 (K) (3)
vs = -75849.8 + 6.5 x 106 W-1/2 (cm/s) (4)
(W)-1/2
5. CONCLUSIONS
The x-ray results show that the present materials crystallize in two tetragonal ( I42m , P4) and two orthorhombic (Pmn21, F222) tetrahedral structure types. When the values of the parameter ae (= (V/N)1/3) are plotted against values of the molecular weight W of the material, it is found that independent of the crystal structure all the compounds lie on the same straight line in agreement with earlier works made on compounds involving Cu, S and Se but neither Ag, Fe and Te. From the DTA data, it was found that Cu2FeSiS4, Cu2FeSnS4 and Cu2CoSnS4 melt congruently, for Cu2CoSnS4, Cu2FeSnSe4 the melting type could not be determined because undercooling effects are present. The rest of the materials were found to have peritectic melting type. Also, all of the materials were found to have polymorphous transformations. The Lidenmann relation, with C= 300, was found to be appropriated to estimate reasonable values of the Debye temperature θD and/or the sound velocity vs. These values were found to vary linearly with W of the compound, so that a value of θD and/or vs for a material can be obtained from W.
6. ACKNOWLEDGEMENTS
This work was partially supported by the CDCHT-ULA (Project No. C-1740-11-05-AA). E. Moreno would like to thank the Plan de Desarrollo de Talentos Humanos de Alto Nivel of FONACIT, through contract No. 200601411, Venezuela. M.A. Macías would like to thank COLCIENCIAS (Colombia) for his doctoral fellowship.
7.REFERENCIAS
[1].Katagiri H, Jimbo K, Maw WS, Oishi K, Yamazaki M, Araki H, Takeuchi A. Thin Solid Films 2009; 517: 2455-2460.
[2].Shapira Y, McNiff EJ, Oliveira NF, Honig ED, Dwight K, Wold A. Phys. Rev. B 1988; 37: 411418.
[3].McCabe GH, Fries T, Liu MT, Shapira Y, Ram-Mohan LR, Kershaw R, Wold A, Fau C, Averous M, McNiff EJ. Phys. Rev. B 1997; 56: 6673-6680.
[4].Shafer W, Nitsche R. Mater. Res. Bull. 1974; 9: 645-654.
[5].Gulay LD, Nazarchuk OP, Olekseyuk ID. J. Alloy Compd. 2004; 377: 306-311.
[6].Rincón C, Quintero M, Moreno E, Power Ch, Quintero E, Henao JA, Macías MA, Delgado GE, Tovar R, Morocoima M. Solid State Commun. 2011; 151: 947-951.
[7].Lamarche A-M, Willsher A, Chen L, Lamarche G, Woolley JC. J. Solid State Chem. 1991; 94: 313318.
[8].Quintero M, Barreto A, Grima P,Tovar R, Quintero E, Sanchez Porras G, Ruiz J, Woolley JC, Lamarche G and Lamarche A-M. Mater. Res. Bull. 1999; 34: 2263-2270.
[9]. Guen L, Glaunsinger WS. J. Solid State Chem. 1980; 35: 10-21.
[10]. Chen XL, Lamarche A-M, Lamarche G, Woolley JC. J. Magn. Magn. Mater. 1993; 118: 119-128.
[11]. Quintero E, Quintero M, Moreno E, Lara L, Morocoima M, Pineda F, Grima P, Tovar R, Bocaranda P, Henao JA, Macías MA. J. Phys. Chem. Solids 2010; 71: 993-998.
[12]. Boultif A, Louër D. J. Appl. Cryst. 1991; 24: 987
993. [13]. Laugier J, Bochu B. "Chekcell: Graphical powder indexing cell and space group assignment software" [On-Line], http://www.ccp14.ac.uk/tutorial/lmgp/. Miguel AD, Hubberd CR, Stalick JK. "NBS*AIDS80: A FORTRAN program for crystallographic data evaluation", National Bureau of Standards (USA), Tech. Note 1141. [14]. Lutterotti L. "Material Analysis using Diffraction-MAUD: Computer code JAVA." Trento: Universite of Trento. 1997-2009 [On-Line], http://www.ing.unitn.it/~maud/. [15]. Quintero E, Tovar R, Quintero M, Delgado GE,
Morocoima M, Caldera D, Ruiz J, Mora AE, Briceño M, Fernadez JL. J. Alloy Compd. 2007;
432: 142-148. [16]. Moreno E, Quintero M, Morocoima M, Quintero E, Grima P, Tovar R, Bocaranda P, Delgado GE, Contreras JE, Mora AE, Briceño JM, Ávila Godoy R, Fernández JL, Henao JA, Macías MA. J. Alloy Compd. 2009; 486: 212-218. [17]. Gulay LD, Romanyuk Ya. E, Parasyuk OV. J. Alloy Compd. 2002; 347: 193-197. [18]. Parasyuk OV, Gulay LD, Romanyuk Ya. E, Piskach LV. J. Alloy Compd. 2001; 329: 202-207. [19]. Caldera D, Quintero M, Morocoima M, Quintero
E, Grima P, Marchan N, Moreno E, Bocaranda P, Delgado GE, Mora AE. J. Alloy Compd. 2008;
457: 221-224. [20]. Lindemann F. Z. Phys. 1910; 11: 609. [21]. Neelakanda Pillai N, Mahadevan CK. Physica B
2008; 403: 2168-2172. [22]. Garbato L, Ledda F, Manca P, Rucci A, Spiga A, "Phase diagram, growth and properties of quaternary diamond-like alloys in the CuInSe4-CdSe System". Mérida (Venezuela) Prog. Cryst. Growth. Ch. 10, 1984 p. 199. [23]. Bachmann KJ, Hsu FS, Thiel FA, Kasper HM. J. Electron. Mater. 1977; 6: 431-448. [24]. Bonmhammel K, Deus P, Kühn, Möller. Phys. Status. Solidi (a) 2002; 71: 505-510. [25]. Olekseyuk ID, Gulay LD, Dydchak IV, Pichach
| LV, Parayuk OV, Marchuk OV. J. Alloy Compd. | |
|---|---|
| 2002; 340: 141-145. | |
| [26]. | Pisckach LV, Parasyuk OV, Romanyuk Ya. E. J. |
| Alloy Compd. 2000; 299: 227-231. | |
| [27]. | Komaki H, Yoshino K, Seto S, Yoneta M, Akaki |
| Y, Ikary T. J. Cryst. Growth 2002; 236: 253-256. | |
| [28]. | Meriono JM, Di Michiel M, León M. J. Phys. |
| Chem. Solids 2003; 64: 1649-1652. | |
| [29]. | Burger A, Ndap JO, Cui Y, Roy U, Morgan S, |
| Chattopadhyay K, Ma X, Faris K, Thibaud S, | |
| Miles R, Mateen H, Goldstein JT, Rawn CJ. J. | |
| Cryst. Growth 2001; 225: 505-511. | |
| [30]. | Roy UN, Mekonen B, Adetunji OO, |
| Chattopadhyay K, Kochari F, Cui Y, Burger A, | |
| Goldstein JT. J. Cryst. Growth 2002; 241: 135 | |
| 140. | |
| [31]. | Klimova AM, Ananichev VA, Blinov LN. Glass |
| Phys. Chem+ 2006; 32:643. | |
| [32]. | Jagomägi A, Krustok J, Raudoja J, Grossberg M, |
| Danilson M, Yakushev M. Physica B 2003; 337: | |
| 369-374. | |
| [33]. | G. Sánchez Porras, M. Quintero and S.M. Wasim. |
| J. Applied Physics 1990, 67 (7), 3382-3386. | |













