Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Boletín Técnico
versión impresa ISSN 0376-723X
IMME v.40 n.3 Caracas nov. 2002
EVALUACIÓN DE LAS REGLAS DE COMBINACIÓN ANTES DOS COMPONENTES SÍSMICOS HORIZONTALES Y VERTICAL
Julio J. Hernández1 Oscar A. López2
1. Investigador Asociado, IMME, Facultad de Ingeniería, Universidad Central de Venezuela; correo-e: julher@cantv.net
2. IMME, Facultad de Ingeniería, Universidad Central de Venezuela; correo-e: oslopez@reacciun.ve
RESUMEN
Se evalúan las respuestas ![]() , dadas por diversas reglas normativas de combinación a sismos multicomponentes, para el caso cuando una componente sísmica principal es vertical y las componentes horizontales principales pueden tener cualquier dirección. Las acciones sísmicas se expresan mediante espectros normativos de pseudoaceleraciones. Las reglas examinadas son la de la RCSC, la del 30%, la del 40% y una de las reglas del IBC.
, dadas por diversas reglas normativas de combinación a sismos multicomponentes, para el caso cuando una componente sísmica principal es vertical y las componentes horizontales principales pueden tener cualquier dirección. Las acciones sísmicas se expresan mediante espectros normativos de pseudoaceleraciones. Las reglas examinadas son la de la RCSC, la del 30%, la del 40% y una de las reglas del IBC.
La respuesta crítica ![]() , la máxima obtenida para todos los ángulos de incidencia de las componentes sísmicas, se obtiene mediante la regla CQC3. Las cotas superior e inferior de la relación
, la máxima obtenida para todos los ángulos de incidencia de las componentes sísmicas, se obtiene mediante la regla CQC3. Las cotas superior e inferior de la relación ![]() se presentan en función de la intensidad espectral entre las componentes principales horizontales y de las respuestas a una componente sísmica actuando según cada eje estructural. Se desarrollan expresiones analíticas para los valores extremos de
se presentan en función de la intensidad espectral entre las componentes principales horizontales y de las respuestas a una componente sísmica actuando según cada eje estructural. Se desarrollan expresiones analíticas para los valores extremos de ![]() , dada una determinada intensidad espectral.
, dada una determinada intensidad espectral.
Palabras clave: reglas de combinación, sismos multicomponentes, normas sísmicas, respuesta crítica, CQC3, componente sísmica vertical.
EVALUATION OF COMBINATION RULES WITH TWO HORIZONTAL AND ONE VERTICAL SEISMIC COMPONENTS
ABSTRACT
Responses ![]() , given by several multicomponent combination rules used in seismic codes, are evaluated for the case when one principal seismic component is vertical and two horizontal principal components can act along any direction. Seismic motions are described by code pseudoacceleration spectra. The SRSS-, 30%-, 40%- and one of the IBC- rules are examined.
, given by several multicomponent combination rules used in seismic codes, are evaluated for the case when one principal seismic component is vertical and two horizontal principal components can act along any direction. Seismic motions are described by code pseudoacceleration spectra. The SRSS-, 30%-, 40%- and one of the IBC- rules are examined.
Critical response ![]() , the largest one for all possible incident angles of the seismic components, is obtained by means of the CQC3-rule. The upper and lower bounds of ratio
, the largest one for all possible incident angles of the seismic components, is obtained by means of the CQC3-rule. The upper and lower bounds of ratio ![]() are presented as a function of the spectral intensity ratio of the horizontal principal components and of the responses to one seismic component acting along each structural axis. Analytical expressions are developed for the extreme bounds of the ratio
are presented as a function of the spectral intensity ratio of the horizontal principal components and of the responses to one seismic component acting along each structural axis. Analytical expressions are developed for the extreme bounds of the ratio ![]() , given a fixed spectral intensity ratio.
, given a fixed spectral intensity ratio.
Key words: combination rules, multicomponent ground motions, seismic codes, critical response, CQC3, vertical seismic component.
INTRODUCCIÓN
Las normas de diseño sismorresistente, tanto la venezolana [COVENIN, 2001] como las extranjeras, por ejemplo el 1997 UBC [ICBO, 1997], el 2000 IBC [ICC, 2000] y el Eurocódigo-8 [CEN, 1998], requieren la consideración de la acción simultánea de las tres componentes sísmicas de movimiento de traslación del terreno. En el marco del método de análisis espectral las respuestas máximas probables suelen calcularse según diversas reglas de combinación a sismos multicomponentes, tales como la regla de la Raíz Cuadrada de la Suma de Cuadrados (RCSC), o las reglas del 30% y del 40%.
Las reglas RCSC y del 30% son estipuladas por COVENIN y el Eurocódigo-8, mientras que en el 1997-UBC y el 2000-IBC estas reglas se aplican a las 2 componentes horizontales y el efecto de la componente vertical se incorpora aparte mediante un término lineal en las combinaciones de diseño. Estas normas suponen que una componente sísmica principal es vertical y que las dos componentes horizontales tienen intensidades similares; además la práctica de diseño normalmente considera que los tres componentes actúan a lo largo de los ejes estructurales. Sin embargo, aún manteniéndonos dentro del método de análisis espectral, es posible refinar la estimación de las respuestas máximas probables para una probabilidad de excedencia establecida.
Podemos tomar en cuenta el hecho de que las dos componentes horizontales principales tienen distintas intensidades y que pueden incidir con cualquier ángulo respecto a los ejes estructurales, (Figura 1), e incluso la posibilidad de que una componente principal no sea exactamente vertical (Figura 1(a)). Con este objetivo han sido desarrolladas algunas reglas de combinación; la regla denominada CQC3 ("Complete Quadratic Combination with 3 components") infiere la respuesta crítica como la mayor respuesta considerando todos los posibles ángulos de incidencia de las componentes horizontales, teniendo éstas espectros proporcionales de intensidades diferentes, y bajo el supuesto que una componente principal sea vertical (Figura 1(b)) [Smeby y Der Kiureghian, 1985; Menun y Der Kiureghian, 1998; López y Torres, 1997]. En el caso de que se considere la posibilidad de desviación de una componente principal respecto del eje vertical puede aplicarse una reciente generalización de este criterio, la regla GCQC3 ("Generalized Complete Quadratic Combination with 3 components") [López y Hernández, 2001 a; Hernández y López, 2002 a], la cual suministra la respuesta máxima para todas las direcciones posibles de las componentes cuasi-vertical y cuasi-horizontales.


Figura 1. Direcciones principales (1, 2, 3) del movimiento sísmico y direcciones (X, Y, Z) de los ejes estructurales; (a) Caso general; (b) Caso de una dirección principal vertical y dos direcciones principales horizontales
En un trabajo anterior se evaluaron varias reglas de combinación de las componentes sísmicas comparándolas con la respuesta crítica dada por la regla CQC3, en el supuesto de que los efectos de la componente vertical en la respuesta estructural estudiada sean despreciables [López et al., 2001; López y Hernández, 2001 b]. Para el caso más general en que la respuesta estructural a una componente sísmica vertical no es nula, este artículo se propone comparar los resultados de aplicar los criterios normativos de combinación mencionados al comienzo, con respecto a la respuesta crítica dada por la regla CQC3. Considerando la acción simultánea de las tres componentes sísmicas, se logra así evaluar los efectos peculiares de la direccionalidad de las componentes sísmicas horizontales principales y su distinta intensidad, respecto a la usual omisión de este fenómeno. Se amplía así el programa de estudio de los efectos de la direccionalidad de las componentes sísmicas, llevado a cabo a través del conjunto de referencias citadas. Estos resultados se presentan también en un par de artículos conexos [Hernández y López, 2002 b; Hernández y López, 2003], en los cuales se incluyen además los resultados correspondientes a la consideración de que la componente principal 3 pueda sufrir una desviación del eje vertical. Igualmente estos últimos resultados se presentarán en español en un trabajo paralelo a éste.
2. MOVIMIENTOS SÍSMICOS
El movimiento sísmico de traslación se puede describir a lo largo de tres ejes principales 1, 2 y 3, (Figura 1), cuyas aceleraciones no están correlacionadas [Penzien y Watabe, 1975]. Llamamos 1 a la dirección de la mayor componente cuasi-horizontal, 2 a la dirección de la menor componente cuasi-horizontal y 3 a la dirección de la componente cuasi-vertical (la más cercana al eje vertical). En muchos casos la desviación (ψ ) entre esta componente y el eje vertical es despreciable, y por tanto en este trabajo se toma ψ = 0°. Sin embargo, en ocasiones ψ puede tomar valores significativos, posibilidad que se considera en la referencia Hernαndez y Lσpez, 2003. En el caso que nos ocupa basta considerar el αngulo θ para precisar la posiciσn de las componentes sνsmicas principales (Figura 1(b)).

Figura 2. Intensidad espectral suavizada, γ
2, entre las componentes sísmicas horizontales menor y mayor
Para la aplicación del método de análisis espectral cada componente k ![]() se describe mediante un espectro de pseudoaceleraciones. Simplificadamente, suponemos que los espectros de las componentes horizontales son proporcionales entre sí, tomando a
se describe mediante un espectro de pseudoaceleraciones. Simplificadamente, suponemos que los espectros de las componentes horizontales son proporcionales entre sí, tomando a ![]() como el espectro correspondiente a la componente 2, donde T es el periodo de vibración y
como el espectro correspondiente a la componente 2, donde T es el periodo de vibración y ![]() es el espectro de la componente 1. Denominamos intensidad espectral al parámetro
es el espectro de la componente 1. Denominamos intensidad espectral al parámetro ![]() . El error en las respuestas, proveniente de suponer espectros proporcionales, suele ser pequeño dado que dichas respuestas están principalmente contenidas en un modo dominante. Esta simplificación tiene la ventaja de permitir la realización de evaluaciones paramétricas, que es el objetivo principal de este trabajo. Para la componente vertical
. El error en las respuestas, proveniente de suponer espectros proporcionales, suele ser pequeño dado que dichas respuestas están principalmente contenidas en un modo dominante. Esta simplificación tiene la ventaja de permitir la realización de evaluaciones paramétricas, que es el objetivo principal de este trabajo. Para la componente vertical ![]() empleamos el espectro
empleamos el espectro ![]() .
.
Podemos utilizar valores razonables de la intensidad espectral ![]() entre las componentes sísmicas horizontales a partir de un reciente estudio estadístico [López y Hernández, 2002; López et al., 2002]. En la Figura 2 se observan los valores medios suavizados obtenidos para los casos de sismos cercanos y lejanos; en general los valores de
entre las componentes sísmicas horizontales a partir de un reciente estudio estadístico [López y Hernández, 2002; López et al., 2002]. En la Figura 2 se observan los valores medios suavizados obtenidos para los casos de sismos cercanos y lejanos; en general los valores de ![]() oscilan entre 0.5 y 0.8 aproximadamente.
oscilan entre 0.5 y 0.8 aproximadamente.
3. RESPUESTA CRÍTICA ANTE DOS COMPONENTES SÍSMICAS HORIZONTALES Y UNA VERTICAL
Consideramos una respuesta estructural que pueda expresarse como combinación lineal de los desplazamientos generalizados de un sistema elástico de m grados de libertad. Llamamos r al valor máximo probable de la respuesta. Particularmente definimos a ![]() y
y ![]() como las respuestas máximas probables a una única componente sísmica de espectro
como las respuestas máximas probables a una única componente sísmica de espectro ![]() aplicada sucesivamente según los ejes X y Y, respectivamente. Y denominamos
aplicada sucesivamente según los ejes X y Y, respectivamente. Y denominamos ![]() a la respuesta máxima probable ante la aplicación de la componente sísmica
a la respuesta máxima probable ante la aplicación de la componente sísmica ![]() de espectro
de espectro ![]() .
.
Las respuestas ![]() ,
, ![]() y
y ![]() las calculamos con la regla CQC ("Complete Quadratic Combination") [Chopra, 2001]:
las calculamos con la regla CQC ("Complete Quadratic Combination") [Chopra, 2001]:
![]() ,
, ![]() ,
, ![]() (1a-c)
(1a-c)
El término cruzado de las respuestas ![]() y
y ![]() se define como:
se define como:
![]() (2)
(2)
En las expresiones (1) y (2) ![]() es la respuesta máxima probable del modo de vibración i, ante la componente sísmica de espectro
es la respuesta máxima probable del modo de vibración i, ante la componente sísmica de espectro ![]() aplicada según la dirección k (k = X, Y) y
aplicada según la dirección k (k = X, Y) y ![]() es la correspondiente respuesta ante la componente sísmica de dirección
es la correspondiente respuesta ante la componente sísmica de dirección ![]() y espectro
y espectro ![]() , tomadas todas con su respectivo signo algebraico;
, tomadas todas con su respectivo signo algebraico; ![]() es el coeficiente de correlación modal entre los modos i y j.
es el coeficiente de correlación modal entre los modos i y j.
Admitiendo que los espectros de las componentes principales horizontales guardan la relación de proporcionalidad ![]() , la respuesta máxima probable ante las tres componentes conjuntas puede ponerse en función del ángulo de incidencia θ usando la regla CQC3 [Smeby y Der Kiureghian, 1985; Menun y Der Kiureghian, 1998; López y Torres, 1997]:
, la respuesta máxima probable ante las tres componentes conjuntas puede ponerse en función del ángulo de incidencia θ usando la regla CQC3 [Smeby y Der Kiureghian, 1985; Menun y Der Kiureghian, 1998; López y Torres, 1997]:
![]() (3)
(3)
La respuesta crítica, definida como el máximo valor de r considerando todos los valores posibles de θ , y el correspondiente αngulo crνtico para el cual ocurre, vienen dados por [Anastassiadis et al., 1998; Lσpez et al., 2000]:
 (4a)
(4a)
 (4b)
(4b)
4. REGLAS DE COMBINACIÓN NORMATIVAS PARA DISEÑO CON TRES COMPONENTES SÍSMICAS
Se examinan aquí las siguientes reglas de combinación a sismos multicomponentes: la regla de la Raíz Cuadrada de la Suma de Cuadrados (RCSC), la regla del 30%, la regla del 40% y una de las reglas especificadas en el UBC 1997 y el IBC 2000, la cual designamos como regla IBC#1. Las dos primeras se prescriben en el Eurocódigo 8, COVENIN 2001 y en otras normas. La regla del 40% se recomienda para el análisis de plantas nucleares [ASCE, 1986] y de puentes [Nutt, 1996]. En [Hernández y López, 2003] se estudia también otra regla (IBC#2) especificada en el UBC 1997 y el IBC 2000. Conviene destacar que en todas las reglas de combinación de las normativas actuales se omite la consideración de la relación de intensidad espectral, ![]() , entre las componentes sísmicas horizontales.
, entre las componentes sísmicas horizontales.
El valor de la respuesta combinada calculada utilizando cualquiera de estas reglas de combinación la llamaremos "respuesta estimada" y la designaremos con ![]() ; ella depende de las respuestas máximas probables ante una única componente sísmica actuando a lo largo de los ejes estructurales,
; ella depende de las respuestas máximas probables ante una única componente sísmica actuando a lo largo de los ejes estructurales, ![]() ,
, ![]() y
y ![]() , dadas por las expresiones (1a), (1b) y (1c), respectivamente. Sin pérdida de generalidad podemos suponer que
, dadas por las expresiones (1a), (1b) y (1c), respectivamente. Sin pérdida de generalidad podemos suponer que ![]() , y con la finalidad de normalizar las expresiones definimos las siguientes razones de respuesta:
, y con la finalidad de normalizar las expresiones definimos las siguientes razones de respuesta:
![]() ;
; ![]() (5)
(5)
4.1 Regla de la RCSC
La aplicación de esta regla equivale a suponer que las respuestas a cada componente sísmica en la dirección de los ejes estructurales son estadísticamente independientes, y que ambas componentes horizontales tienen la misma intensidad espectral:
![]() (6)
(6)
4.2 Regla del 30%
Esta regla es una aproximación lineal que supone componentes sísmicas horizontales de igual intensidad y no correlacionadas entre sí [Rosenblueth y Contreras, 1977]:
![]() (7)
(7)
4.3 Regla del 40%
Esta regla igualmente supone componentes sísmicas horizontales de igual intensidad no correlacionadas. Pretende ser conservadora para la mayoría de los casos [Newmark, 1975]:
![]() (8)
(8)
4.4 Regla IBC#1
Una de las reglas prescritas en el IBC combina las respuestas a las dos componentes horizontales mediante la regla de la RCSC, y añade al resultado (tras multiplicarlo por cierto coeficiente de redundancia estructural ρ ) la contribuciσn de la componente vertical, la cual es estimada en ![]() , donde
, donde ![]() es la respuesta a carga permanente, y
es la respuesta a carga permanente, y ![]() es la aceleración espectral horizontal para periodos cortos. Esto equivale a adoptar como espectro para la componente vertical a 2/3 del espectro de las componentes horizontales,
es la aceleración espectral horizontal para periodos cortos. Esto equivale a adoptar como espectro para la componente vertical a 2/3 del espectro de las componentes horizontales, ![]() , y tomar luego 30% de su valor como contribución simultánea de la componente vertical:
, y tomar luego 30% de su valor como contribución simultánea de la componente vertical: ![]() . Por consiguiente, la respuesta combinada (tomando
. Por consiguiente, la respuesta combinada (tomando ![]() ) se puede escribir como:
) se puede escribir como:
![]() (9)
(9)
5. COMPARACIÓN ENTRE LAS RESPUESTAS ESTIMADAS Y LA CRÍTICA
Comparamos la respuesta estimada, ![]() , obtenida con cada una de las reglas de combinación normativas (expresiones (6) -( 9)) con la respuesta crítica calculada con la regla CQC3 (expresión (4)). Realizamos evaluaciones para los valores extremos aproximados de
, obtenida con cada una de las reglas de combinación normativas (expresiones (6) -( 9)) con la respuesta crítica calculada con la regla CQC3 (expresión (4)). Realizamos evaluaciones para los valores extremos aproximados de ![]() , 0.5 y 0.8 (Figura 2), y para el valor intermedio
, 0.5 y 0.8 (Figura 2), y para el valor intermedio ![]() . Presentamos los valores máximo y mínimo de la relación
. Presentamos los valores máximo y mínimo de la relación ![]() , la cual corresponde a los valores mínimo y máximo de la respuesta crítica
, la cual corresponde a los valores mínimo y máximo de la respuesta crítica ![]() , respectivamente. Estos valores,
, respectivamente. Estos valores, ![]() y
y ![]() se determinan con la expresión (4) para los casos
se determinan con la expresión (4) para los casos ![]() y
y ![]() respectivamente, los cuales corresponden a las situaciones extremas de correlación nula y correlación perfecta entre las respuestas rx y ry [López et al., 2000]:
respectivamente, los cuales corresponden a las situaciones extremas de correlación nula y correlación perfecta entre las respuestas rx y ry [López et al., 2000]:
![]() (10a,b)
(10a,b)
Observemos que las respuestas estimadas ![]() (expresiones (6) -( 9)) tienen la forma
(expresiones (6) -( 9)) tienen la forma ![]() , donde f representa una relación funcional genérica. Por tanto, para valores prefijados de β y
, donde f representa una relación funcional genérica. Por tanto, para valores prefijados de β y ![]() tenemos:
tenemos:
![]() (11a)
(11a)
![]() (11b)
(11b)
donde ![]() y
y ![]() representan relaciones funcionales. Si ahora consideramos toda la variación posible de los parámetros β y
representan relaciones funcionales. Si ahora consideramos toda la variación posible de los parámetros β y ![]() , manteniendo constante
, manteniendo constante![]() , obtenemos las cotas inferior y superior del cociente
, obtenemos las cotas inferior y superior del cociente ![]() correspondientes a cada
correspondientes a cada ![]() :
:
![]() (12)
(12)
Es decir, la cota superior es una relación funcional S que depende de ![]() , mientras que la cota inferior I es independiente de este parámetro. La función S y la constante I evidentemente están relacionadas con la función f que define
, mientras que la cota inferior I es independiente de este parámetro. La función S y la constante I evidentemente están relacionadas con la función f que define ![]() , es decir son particulares de cada criterio de combinación. En lo que sigue hablaremos de subestimación de
, es decir son particulares de cada criterio de combinación. En lo que sigue hablaremos de subestimación de ![]() cuando la respuesta estimada
cuando la respuesta estimada ![]() sea menor que aquella, y de sobreestimación cuando sea mayor.
sea menor que aquella, y de sobreestimación cuando sea mayor.
Nótese que los casos particulares que se obtengan de la expresión (12) serán válidos para cualquier sistema estructural y cualesquiera formas espectrales (con espectros horizontales proporcionales). Las razones de respuesta β y ![]() engloban las propiedades de cualquier respuesta, las intensidades relativas de los espectros horizontales se incorporan en
engloban las propiedades de cualquier respuesta, las intensidades relativas de los espectros horizontales se incorporan en ![]() , mientras que la intensidad relativa entre la componente vertical y las horizontales está incluida en
, mientras que la intensidad relativa entre la componente vertical y las horizontales está incluida en ![]() .
.
Cuando ![]() diremos que la respuesta estimada
diremos que la respuesta estimada ![]() subestima la respuesta crítica, y cuando
subestima la respuesta crítica, y cuando ![]() diremos que la sobreestima.
diremos que la sobreestima.
5.1 Regla de la RCSC
En la regla de la RCSC, ![]() (expresión (6)) es igual a
(expresión (6)) es igual a ![]() (expresión (10b)). Por tanto
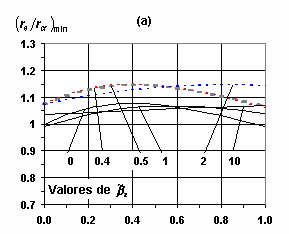
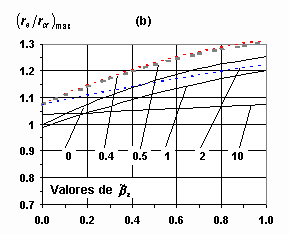
(expresión (10b)). Por tanto ![]() , y esta regla siempre sobreestima la respuesta crítica (Figura 3(a)). En las Figuras 3(b), 3(c) y 3(d) se presentan las variaciones de la relación
, y esta regla siempre sobreestima la respuesta crítica (Figura 3(a)). En las Figuras 3(b), 3(c) y 3(d) se presentan las variaciones de la relación ![]() en función de β , para valores de
en función de β , para valores de ![]() comprendidos entre 0 y 10, y para los casos de
comprendidos entre 0 y 10, y para los casos de ![]() igual 0.5, 0.65 y 0.8.
igual 0.5, 0.65 y 0.8.
Los mayores valores de ![]() ocurren para valores pequeños de
ocurren para valores pequeños de ![]() y para el menor valor de
y para el menor valor de ![]() . Para valores grandes de
. Para valores grandes de ![]() la respuesta calculada con la RCSC tiende a la respuesta crítica
la respuesta calculada con la RCSC tiende a la respuesta crítica ![]() . Mediante manipulación algebraica de la expresión (12), usando las funciones f,
. Mediante manipulación algebraica de la expresión (12), usando las funciones f, ![]() y
y ![]() derivadas de la expresión (6), obtenemos las siguientes cotas inferior y superior de la relación
derivadas de la expresión (6), obtenemos las siguientes cotas inferior y superior de la relación ![]() para el conjunto de valores posibles de β y
para el conjunto de valores posibles de β y ![]() y un valor fijo de
y un valor fijo de ![]() :
:
![]() ;
; ![]() (13)
(13)
Para esta regla las cotas superior e inferior son iguales a las correspondientes al caso de respuesta vertical nula [López et al., 2001; López y Hernández, 2001 b], ya que éste es el caso más desfavorable. La máxima sobreestimación encontrada es 26.5% para ![]() ; mientras que para
; mientras que para ![]() las mayores sobreestimaciones son 18.6% y 10.4%, respectivamente.
las mayores sobreestimaciones son 18.6% y 10.4%, respectivamente.




Figura 3. Cotas de ![]() para la regla de la RCSC: (a)
para la regla de la RCSC: (a) ![]() para todo
para todo ![]() ; ( b)
; ( b) ![]() para
para ![]() = 0.5; (c)
= 0.5; (c) ![]() para
para ![]() = 0.65; (d)
= 0.65; (d) ![]() para
para ![]() = 0.8
= 0.8
5.2 Regla del 30%
Al aplicar la regla del 30% resultan subestimaciones o sobreestimaciones de ![]() dependiendo de los valores de los parámetros β,
dependiendo de los valores de los parámetros β, ![]() y
y ![]() . La Figura 4 muestra las variaciones de
. La Figura 4 muestra las variaciones de ![]() y
y ![]() en función de β , para valores de
en función de β , para valores de ![]() entre 0 y 10, y
entre 0 y 10, y ![]() igual a 0.5, 0.65 y 0.8.
igual a 0.5, 0.65 y 0.8.
El cociente ![]() puede aumentar o disminuir por efecto de la respuesta a la componente vertical (
puede aumentar o disminuir por efecto de la respuesta a la componente vertical (![]() >0) respecto del caso con dicha respuesta nula
>0) respecto del caso con dicha respuesta nula ![]() detallada en [López et al., 2001; López y Hernández, 2001 b]. En general los valores de
detallada en [López et al., 2001; López y Hernández, 2001 b]. En general los valores de ![]() tienden a crecer al pasar
tienden a crecer al pasar ![]() de 0 a ~0.3; disminuyen con
de 0 a ~0.3; disminuyen con ![]() de ~0.3 a 1; vuelven a crecer para
de ~0.3 a 1; vuelven a crecer para ![]() de 1 a ~3, para tender a 1
de 1 a ~3, para tender a 1 ![]() con valores grandes de
con valores grandes de ![]() . Mediante manipulación algebraica de la expresión (12), usando las funciones f,
. Mediante manipulación algebraica de la expresión (12), usando las funciones f, ![]() y
y ![]() derivadas de la expresión (7), obtenemos las siguientes cotas inferior y superior de la relación
derivadas de la expresión (7), obtenemos las siguientes cotas inferior y superior de la relación ![]() para el conjunto de valores posibles de β y
para el conjunto de valores posibles de β y ![]() y un valor determinado de
y un valor determinado de ![]() :
:
![]() ;
; ![]() (14)
(14)




Figura 4. Cotas de ![]() para la regla del 30%: (a)
para la regla del 30%: (a) ![]() para todo γ 2 ; ( b)
para todo γ 2 ; ( b) ![]() para
para ![]() = 0.5; (c)
= 0.5; (c) ![]() para
para ![]() = 0.65; (d)
= 0.65; (d) ![]() para
para ![]() = 0.8.
= 0.8.
La cota inferior es igual a la del caso de respuesta vertical nula [López et al., 2001; López y Hernández, 2001 b] mientras que la cota superior es una función cercana a la de ese caso ![]()
![]() . Las subestimaciones no pasan de 8.1%, mientras que las sobreestimaciones alcanzan hasta un 20.1% cuando
. Las subestimaciones no pasan de 8.1%, mientras que las sobreestimaciones alcanzan hasta un 20.1% cuando ![]() , un 14.1% para
, un 14.1% para ![]() , y un 10.9% para
, y un 10.9% para ![]() .
.
5.3 Regla del 40%
Aplicando la regla del 40% siempre resultan sobreestimaciones de ![]() , salvo pocos casos con subestimaciones escasas. La Figura 5 muestra las variaciones de
, salvo pocos casos con subestimaciones escasas. La Figura 5 muestra las variaciones de ![]() y
y ![]() en función de β , para valores de
en función de β , para valores de ![]() entre 0 y 10, y
entre 0 y 10, y ![]() igual a 0.5, 0.65 y 0.8. El cociente
igual a 0.5, 0.65 y 0.8. El cociente ![]() puede aumentar o disminuir por efecto de la respuesta a la componente vertical
puede aumentar o disminuir por efecto de la respuesta a la componente vertical ![]() respecto del caso con dicha respuesta nula
respecto del caso con dicha respuesta nula ![]() detallada en [López et al., 2001; López y Hernández, 2001 b]. Los valores de
detallada en [López et al., 2001; López y Hernández, 2001 b]. Los valores de ![]() tienden a crecer al pasar
tienden a crecer al pasar ![]() de 0 a ~0.4; disminuyen con
de 0 a ~0.4; disminuyen con ![]() de ~0.4 a 1; vuelven a crecer para
de ~0.4 a 1; vuelven a crecer para ![]() de 1 a ~2, para tender a 1
de 1 a ~2, para tender a 1 ![]() con valores grandes de
con valores grandes de ![]() .
.
Mediante manipulación algebraica de la expresión (12), usando las funciones f, ![]() y
y ![]() derivadas de la expresión (8), obtenemos las siguientes cotas inferior y superior de la relación
derivadas de la expresión (8), obtenemos las siguientes cotas inferior y superior de la relación ![]() para el conjunto de valores posibles de β y
para el conjunto de valores posibles de β y ![]() y un valor prefijado de
y un valor prefijado de ![]() :
:
![]() ;
; ![]() (15).
(15).


Figura 5. Cotas de ![]() para la regla del 40%: (a)
para la regla del 40%: (a) ![]() para todo
para todo ![]() ; ( b)
; ( b) ![]() para
para ![]() = 0.5; (c)
= 0.5; (c) ![]() para
para ![]() = 0.65; (d)
= 0.65; (d) ![]() para
para ![]() = 0.8
= 0.8
La cota inferior es igual a la del caso de respuesta vertical nula [López et al., 2001; López y Hernández, 2001 b], mientras que la cota superior es una función cercana a la de ese caso ![]()
![]() . Las subestimaciones nunca sobrepasan el 1%, mientras que las sobreestimaciones pueden ir desde un 31.5% cuando
. Las subestimaciones nunca sobrepasan el 1%, mientras que las sobreestimaciones pueden ir desde un 31.5% cuando ![]() , un 24% para
, un 24% para ![]() , hasta un 18.7% para
, hasta un 18.7% para ![]() .
.
5.4 Regla IBC#1
Los resultados presentados en la Figura 6 indican que la regla IBC#1 sobreestima la respuesta crítica para pequeños ![]() , pero conduce a grandes subestimaciones para valores grandes del mismo. La sobreestimación aumenta al variar
, pero conduce a grandes subestimaciones para valores grandes del mismo. La sobreestimación aumenta al variar ![]() de 0 a ~0.3, para disminuir luego con mayores valores de
de 0 a ~0.3, para disminuir luego con mayores valores de ![]() . Para
. Para ![]() =1 la mayor subestimación es solo de 8.1%, pero se incrementa en gran medida para valores grandes de
=1 la mayor subestimación es solo de 8.1%, pero se incrementa en gran medida para valores grandes de ![]() .
.




Figura 6. Cotas de ![]() para la regla IBC#1 : (a)
para la regla IBC#1 : (a) ![]() para todo
para todo ![]() ; ( b)
; ( b) ![]() para
para ![]() = 0.5; (c)
= 0.5; (c) ![]() para
para ![]() = 0.65; (d)
= 0.65; (d) ![]() para
para ![]() = 0.8
= 0.8
Mediante manipulación algebraica de la expresión (12), usando las funciones f, ![]() y
y ![]() derivadas de la expresión (9), obtenemos las siguientes cotas inferior y superior de la relación
derivadas de la expresión (9), obtenemos las siguientes cotas inferior y superior de la relación ![]() para el conjunto de valores posibles de β y
para el conjunto de valores posibles de β y ![]() y un valor prefijado de
y un valor prefijado de ![]() :
:
![]() ;
; ![]() (16)
(16)
La tan pequeña cota inferior está gobernada por el término ![]() de la expresión (9); la cota superior se aproxima linealmente pues la expresión exacta es muy compleja. Las subestimaciones pueden llegar a valer tanto como 70%, mientras que las sobreestimaciones pueden llegar hasta un máximo de 30% cuando
de la expresión (9); la cota superior se aproxima linealmente pues la expresión exacta es muy compleja. Las subestimaciones pueden llegar a valer tanto como 70%, mientras que las sobreestimaciones pueden llegar hasta un máximo de 30% cuando ![]() , un 22.3% para
, un 22.3% para ![]() , y 14.4% para
, y 14.4% para ![]() . Es de interés observar que para valores grandes de
. Es de interés observar que para valores grandes de ![]() esta regla subestima la respuesta crítica en todas las situaciones. Estas situaciones de subestimación se compensan parcialmente mediante las combinaciones de diseño normativas, gracias a la adición de las correspondientes solicitaciones gravitacionales a cada solicitación sísmica, conduciendo a una menor subestimación de las solicitaciones combinadas que de una solicitación sísmica aislada.
esta regla subestima la respuesta crítica en todas las situaciones. Estas situaciones de subestimación se compensan parcialmente mediante las combinaciones de diseño normativas, gracias a la adición de las correspondientes solicitaciones gravitacionales a cada solicitación sísmica, conduciendo a una menor subestimación de las solicitaciones combinadas que de una solicitación sísmica aislada.
6. EJEMPLO
A continuación ilustramos las comparaciones de las reglas de combinación sísmicas mediante un caso sencillo pero de características reales. Sea una plataforma de un piso formada por una losa rectangular de lados 8.00 m y 5.00 m y espesor 0.17 m, apoyada en cuatro vigas que a su vez apoyan en cuatro columnas de 4 m de altura (Figura 7). La sección de las vigas es de 0.40 m de ancho por 0.65 m de altura, y la de las columnas es de 0.60 m por lado. El material de los elementos estructurales es concreto armado con f'c = 27.5 MPa. La plataforma se diseña para soportar equipos con una carga distribuida de 5.64 kN/m2 en el área de la losa y una carga concentrada de 480 kN en el centro de la misma.
Conviene anotar que en un modelo de un piso puede evaluarse el comportamiento de prácticamente cualquier tipo de respuesta, respecto al problema que nos ocupa. Lo que interesa evaluar es la sensibilidad a la componente vertical del sismo y a las direcciones de incidencia de las componentes sísmicas. Ella depende de la razón de las respuestas a la componente vertical y a la componente horizontal mayor, ![]() , y de la correlación entre las respuestas a cada par de componentes horizontales,
, y de la correlación entre las respuestas a cada par de componentes horizontales, ![]() . Estos parámetros pueden tomar el mismo rango de valores en edificaciones de un piso y de varios pisos. En consecuencia, los resultados que se muestren con un sistema de un piso son semejantes a los que se obtendrían con sistemas de varios pisos.
. Estos parámetros pueden tomar el mismo rango de valores en edificaciones de un piso y de varios pisos. En consecuencia, los resultados que se muestren con un sistema de un piso son semejantes a los que se obtendrían con sistemas de varios pisos.

Figura 7. Planta de plataforma de un piso
Consideramos la estructura sometida a un sismo cercano con tres componentes, dos horizontales que pueden obrar según cualquier dirección en su plano y una vertical (Figura 1(b)). Definimos el espectro ![]() en términos de pseudoaceleración (Figura 8(a)) para la aceleración, velocidad y desplazamientos picos del terreno iguales a 0.5 g, 61 cm/seg y 45.7 cm respectivamente, percentil de 84.1 % y coeficiente de amortiguamiento de 5 %. La componente sísmica 1 está caracterizada por el espectro
en términos de pseudoaceleración (Figura 8(a)) para la aceleración, velocidad y desplazamientos picos del terreno iguales a 0.5 g, 61 cm/seg y 45.7 cm respectivamente, percentil de 84.1 % y coeficiente de amortiguamiento de 5 %. La componente sísmica 1 está caracterizada por el espectro ![]() y la componente 2 por
y la componente 2 por ![]() donde
donde ![]() la tomamos de la línea de campo cercano de la Figura 2. Igualmente utilizamos un espectro típico de campo cercano
la tomamos de la línea de campo cercano de la Figura 2. Igualmente utilizamos un espectro típico de campo cercano ![]() (Figura 8(b)) para caracterizar a la componente vertical
(Figura 8(b)) para caracterizar a la componente vertical ![]() .
.


Figura 8. Espectros de pseudoaceleración para campo cercano: (a) de la componente mayor horizontal 1; (b) de la componente vertical 3=Z
TABLA 1. Modos significativos y sus valores básicos
| Modo (i) |
(seg) | Valores espectrales | Masas participativas (%) | ||||
|
|
Intensidad espectral |
| |||||
|
X | Y | Z | |||||
| 1 | 0.2874 | 1.355 | 0.701 | 1.200 | 0 | 84.58 | 0 |
| 2 | 0.2632 | 1.355 | 0.701 | 1.200 | 0 | 0 | 62.99 |
| 3 | 0.2276 | 1.355 | 0.701 | 1.200 | 94.92 | 0 | 0 |
| 6 | 0.0834 | 0.981 | 0.797 | 1.046 | 0 | 15.37 | 0 |
| 7 | 0.0713 | 0.871 | 0.788 | 0.934 | 5.07 | 0 | 0 |
| 9 | 0.0551 | 0.726 | 0.776 | 0.783 | 0 | 0 | 6.36 |
| 10 | 0.0312 | 0.500 | 0.751 | 0.561 | 0 | 0 | 10.86 |
| 21 | 0.0095 | 0.500 | 0.724 | 0.550 | 0 | 0 | 19.52 |
El sistema estructural se modeló tomando 9 nodos desplazables de una malla de elementos de losa de 4 m x 2.5 m (Figura 7), para un total de 27 grados de libertad, con elementos finitos planos para la losa y elementos lineales para las vigas y columnas. En la Tabla 1 se exponen los periodos propios significativos con sus respectivas masas participativas a cada componente sísmica y los valores espectrales ante los espectros ![]() y
y ![]() .
.
Como respuestas r a estudiar escogemos: a) la fuerza axial de la columna inferior izquierda de la Figura 7 (tomada positiva para compresión); b) la fuerza cortante de dirección X en la misma columna; c) el momento flector según el eje X en el tope de la misma columna; d) la fuerza cortante de dirección Z en un extremo de la viga inferior de dirección X; y e) el momento flector según el eje Y de la misma viga.
En la Tabla 2 se presentan las respuestas ![]() de los modos de vibración i ante cada componente sísmica horizontal (k = X, Y) de espectro
de los modos de vibración i ante cada componente sísmica horizontal (k = X, Y) de espectro ![]() , y las respuestas
, y las respuestas ![]() de los modos i ante la componente vertical de espectro
de los modos i ante la componente vertical de espectro ![]() .
.
TABLA 2. Valores de las respuestas modales espectrales
| RESPUESTA | Direc. comp. sísm. | M O D O S D E V I B R A C I Ó N | |||||||
| 1 | 2 | 3 | 6 | 7 | 9 | 10 | 21 | ||
| Fuerza axial en columna (kN) |
|
0 | 0 | 111.33 | 0 | 3.97 | 0 | 0.12 | 0.10 |
|
|
175.64 | 0 | 0 | 24.81 | 0 | 0 | 0 | 0.20 | |
|
|
0 | 178.02 | 0 | 0 | 0 | 11.73 | 14.36 | 25.28 | |
| Fuerza cortante X en columna (kN) |
|
0 | 0 | 302.93 | 0 | 10.41 | 0 | 0 | 0 |
|
|
5.74 | 0 | 0 | 1.11 | 0 | 0 | 0 | 0 | |
|
|
0 | 101.90 | 0 | 0 | 0 | 6.77 | 0.19 | 0.19 | |
| Momento flector X en tope de columna (mkN) |
|
0 | 0 | 4.64 | 0 | 0.18 | 0 | 0.09 | 0.004 |
|
|
437.53 | 0 | 0 | 57.49 | 0 | 0 | 0 | 0 | |
|
|
0 | 120.78 | 0 | 0 | 0 | 2.91 | 11.29 | 0.94 | |
| Fuerza cortante vertical en viga (kN) |
|
0 | 0 | 100.67 | 0 | 3.46 | 0 | 0 | 0 |
|
|
7.60 | 0 | 0 | 2.19 | 0 | 0 | 0 | 0 | |
|
|
0 | 129.21 | 0 | 0 | 0 | 11.27 | 0.03 | 0.31 | |
| Momento flector Y en extremo de viga (mkN) |
|
0 | 0 | 402.39 | 0 | 13.83 | 0 | 0 | 0 |
|
|
13.68 | 0 | 0 | 3.56 | 0 | 0 | 0 | 0 | |
|
|
0 | 195.32 | 0 | 0 | 0 | 18.34 | 0.06 | 0.51 | |
A partir de los valores modales de la Tabla 2, en primer lugar calculamos las respuestas máximas probables dadas por la expresión (1) y el término cruzado de la expresión (2), ante las componentes sísmicas actuando por separado. Los valores de las respuestas y la raíz cuadrada del término cruzado (que tiene la misma unidad de las respuestas) se muestran en la Tabla 3, junto con las razones de respuesta (expresión (5); cuando![]() , debemos usar
, debemos usar ![]() y
y ![]() ). Luego calculamos las respuestas críticas
). Luego calculamos las respuestas críticas ![]() , de acuerdo con la regla CQC3 (expresión (4a) ), las cuales se presentan junto con sus ángulos críticos
, de acuerdo con la regla CQC3 (expresión (4a) ), las cuales se presentan junto con sus ángulos críticos ![]() asociados (expresión (4b) ). Para su aplicación utilizamos
asociados (expresión (4b) ). Para su aplicación utilizamos ![]() , correspondiente a los modos de mayor participación.
, correspondiente a los modos de mayor participación.
TABLA 3. Respuestas máximas probables
| RESPUESTA | Componentes separadas | Razones de respuesta | Valores críticos. Componentes simultáneas | |||||
|
|
| |||||||
|
|
|
|
|
β |
|
|
| |
|
Fuerza axial en columna (kN) | 111.42 | 177.49 | 110.38 | 182.59 | 0.628 | 1.029 | 64.04º | 271.96 |
| Fuerza cortante X en columna (kN) | 303.17 | 5.85 | 32.96 | 102.14 | 0.019 | 0.337 | 0.68º | 319.95 |
| Momento flector X en tope de columna (mkN) | 4.64 | 441.55 | 35.56 | 121.43 | 0.011 | 0.275 | 89.63º | 457.96 |
| Fuerza cortante vertical en viga (kN) | 100.75 | 7.92 | 21.94 | 129.72 | 0.079 | 1.288 | 2.73º | 164.38 |
| Momento flector Y en extremo de viga (mkN) | 402.70 | 14.15 | 58.78 | 196.21 | 0.035 | 0.487 | 1.22º | 448.11 |
Los valores de la Tabla 2 se calcularon mediante el programa de computación SAP2000 [Computers and Structures, 1999]. Para obtener los términos cruzados, y a partir de ellos la respuesta crítica (Tabla 3), se requiere de un cálculo suplementario que no es provisto por el programa. Conviene anotar que si en lugar de utilizar el valor constante ![]() calculáramos la respuesta crítica "exacta" considerando los espectros exactos (
calculáramos la respuesta crítica "exacta" considerando los espectros exactos (![]() variable) [Anastassiadis et al., 1998; López y Torres, 1997] obtendríamos resultados semejantes. Por ejemplo para el caso de la fuerza axial en la columna ese cálculo conduce a
variable) [Anastassiadis et al., 1998; López y Torres, 1997] obtendríamos resultados semejantes. Por ejemplo para el caso de la fuerza axial en la columna ese cálculo conduce a ![]() para un ángulo crítico
para un ángulo crítico ![]() . Como se puede comprobar, estos dos valores son muy cercanos a los dados por la regla CQC3 en la Tabla 3.
. Como se puede comprobar, estos dos valores son muy cercanos a los dados por la regla CQC3 en la Tabla 3.
Observemos que la fuerza axial en la columna es bastante sensible a la dirección de las componentes sísmicas horizontales, estando el ángulo crítico en una posición intermedia entre los ejes X y Y; ésto se debe a que las respuestas ![]() y
y ![]() tienen valores semejantes y el término cruzado
tienen valores semejantes y el término cruzado ![]() es relativamente grande. Por el contrario para las otras respuestas estudiadas es predominante la acción en una dirección principal, y en consecuencia el ángulo crítico casi coincide con los ejes X o Y. En cuanto a la importancia de la respuesta a la componente vertical hemos obtenido una gama de valores
es relativamente grande. Por el contrario para las otras respuestas estudiadas es predominante la acción en una dirección principal, y en consecuencia el ángulo crítico casi coincide con los ejes X o Y. En cuanto a la importancia de la respuesta a la componente vertical hemos obtenido una gama de valores ![]() que van desde 0.275 a 1.288, configurando una variedad de casos, desde ser poco influyente a ser dominante.
que van desde 0.275 a 1.288, configurando una variedad de casos, desde ser poco influyente a ser dominante.
Calculamos ahora los valores de ![]() para cada regla normativa, aplicando las expresiones (6) a (9) con los valores de
para cada regla normativa, aplicando las expresiones (6) a (9) con los valores de ![]() ,
, ![]() y
y ![]() . Se presentan en la Tabla 4 junto con el cociente
. Se presentan en la Tabla 4 junto con el cociente ![]() , el cual nos indica el grado de precisión de la estimación de cada regla de combinación. Podemos comprobar que los valores obtenidos de
, el cual nos indica el grado de precisión de la estimación de cada regla de combinación. Podemos comprobar que los valores obtenidos de ![]() están comprendidos entre los valores de
están comprendidos entre los valores de ![]() y
y ![]() establecidos en la Sección 5, interpolando adecuadamente en las Figuras (3),(4),(5),(6). Notemos que para las respuestas estudiadas: a) la regla de la RCSC da resultados casi exactos; b) la regla del 30% deriva en pequeñas subestimaciones o algo mayores sobreestimaciones, las cuales se producen cuando
establecidos en la Sección 5, interpolando adecuadamente en las Figuras (3),(4),(5),(6). Notemos que para las respuestas estudiadas: a) la regla de la RCSC da resultados casi exactos; b) la regla del 30% deriva en pequeñas subestimaciones o algo mayores sobreestimaciones, las cuales se producen cuando ![]() es cercano a 0.3, tal como se observó en la Figura 4; c) la regla del 40 % es siempre conservadora; y d) la regla del IBC#1 es conservadora para valores pequeños de
es cercano a 0.3, tal como se observó en la Figura 4; c) la regla del 40 % es siempre conservadora; y d) la regla del IBC#1 es conservadora para valores pequeños de ![]() , pero puede conducir a subestimaciones importantes cuando
, pero puede conducir a subestimaciones importantes cuando ![]() es superior a 1. En todo caso, en esta estructura la particular correlación entre las respuestas a las componentes sísmicas conduce a que las estimaciones de las reglas estén más cerca de sus valores mínimos posibles que de los máximos posibles.
es superior a 1. En todo caso, en esta estructura la particular correlación entre las respuestas a las componentes sísmicas conduce a que las estimaciones de las reglas estén más cerca de sus valores mínimos posibles que de los máximos posibles.
TABLA 4. Respuestas estimadas y su relación con la respuesta crítica.
| RESPUESTA | R E G L A N O R M A T I V A | |||||||
| SRSS | 30% | 40% | IBC#1 | |||||
|
|
|
|
|
|
|
|
| |
|
Fuerza axial en columna (kN) | 277.95 | 1.020 | 269.26 | 0.990 | 298.15 | 1.096 | 264.34 | 0.972 |
| Fuerza cortante X en columna (kN) | 319.96 | 1.000 | 335.56 | 1.049 | 346.36 | 1.083 | 333.87 | 1.044 |
| Momento flector X en tope de columna (mkN) | 457.97 | 1.000 | 479.37 | 1.047 | 491.98 | 1.074 | 478.00 | 1.044 |
| Fuerza cortante vertical en viga (kN) | 164.44 | 1.000 | 162.32 | 0.987 | 173.19 | 1.054 | 139.98 | 0.852 |
| Momento flector Y en extremo de viga (mkN) | 448.19 | 1.000 | 465.81 | 1.039 | 486.85 | 1.086 | 461.82 | 1.031 |
7. CONCLUSIONES
Se evaluaron varias reglas normativas utilizadas para combinar las respuestas a tres componentes sísmicas, dentro del marco del método de análisis espectral. Se consideró el caso usual de que una componente principal es vertical, mientras que las dos componentes horizontales principales se supuso que pueden tener cualquier orientación en el plano. Se tomó en cuenta la posible diferencia de intensidad espectral ![]() entre las dos componentes horizontales principales.
entre las dos componentes horizontales principales.
Las respuestas ![]() estimadas por las reglas normativas se compararon con la respuesta crítica
estimadas por las reglas normativas se compararon con la respuesta crítica ![]() calculada más exactamente mediante la regla CQC3, la cual provee la máxima respuesta para todos los ángulos de incidencia posibles y una intensidad espectral
calculada más exactamente mediante la regla CQC3, la cual provee la máxima respuesta para todos los ángulos de incidencia posibles y una intensidad espectral ![]() dada. Se estudiaron las cotas máxima y mínima de la relación
dada. Se estudiaron las cotas máxima y mínima de la relación ![]() considerando todos los valores posibles de la relación entre las respuestas a componentes horizontales ortogonales, para los diferentes casos de intensidad espectral y los diversos grados de respuesta a la componente vertical (
considerando todos los valores posibles de la relación entre las respuestas a componentes horizontales ortogonales, para los diferentes casos de intensidad espectral y los diversos grados de respuesta a la componente vertical (![]() ). Los resultados presentados son válidos para cualquier sistema estructural y cualesquiera espectros de respuesta.
). Los resultados presentados son válidos para cualquier sistema estructural y cualesquiera espectros de respuesta.
Se desarrollaron expresiones analíticas para los extremos superior e inferior de la relación ![]() , para cada regla normativa estudiada, válidas para toda la variación posible de grados de respuesta a la componente vertical, pero particularizadas a una intensidad espectral
, para cada regla normativa estudiada, válidas para toda la variación posible de grados de respuesta a la componente vertical, pero particularizadas a una intensidad espectral ![]() fija. Por otro lado, se presentaron gráficamente resultados que muestran la variación del cociente
fija. Por otro lado, se presentaron gráficamente resultados que muestran la variación del cociente ![]() en función de la relación β entre las respuestas a componentes horizontales ortogonales y del grado de respuesta a la componente vertical
en función de la relación β entre las respuestas a componentes horizontales ortogonales y del grado de respuesta a la componente vertical ![]() para diversas intensidades espectrales
para diversas intensidades espectrales ![]() representativas.
representativas.
Para valores de la intensidad espectral ![]() comprendidos entre 0.5 y 0.8, encontramos que las respuestas estimadas por la regla de la RCSC están entre 1 y 1.26 veces la respuesta crítica, las estimadas por la regla del 30% entre 0.92 y 1.20, las estimadas por la regla del 40% entre 0.99 y 1.32 y las estimadas por la regla IBC#1 entre 0.30 y 1.30 veces dicha respuesta.
comprendidos entre 0.5 y 0.8, encontramos que las respuestas estimadas por la regla de la RCSC están entre 1 y 1.26 veces la respuesta crítica, las estimadas por la regla del 30% entre 0.92 y 1.20, las estimadas por la regla del 40% entre 0.99 y 1.32 y las estimadas por la regla IBC#1 entre 0.30 y 1.30 veces dicha respuesta.
Con respecto a la ausencia de respuesta a la componente vertical, el efecto de su presencia en la relación ![]() es el de: a) disminuirla para la regla de la RCSC; b) aumentarla o disminuirla para las reglas del 30% y del 40%; c) aumentarla ligeramente para la regla IBC#1 cuando dicha respuesta es pequeña, pero disminuirla enormemente cuando la misma es significativa.
es el de: a) disminuirla para la regla de la RCSC; b) aumentarla o disminuirla para las reglas del 30% y del 40%; c) aumentarla ligeramente para la regla IBC#1 cuando dicha respuesta es pequeña, pero disminuirla enormemente cuando la misma es significativa.
Nótese que las reglas de la RCSC y del 40% son conservadoras, la regla del 30 % está en una situación intermedia entre conservadora y liberal, mientras que la regla IBC#1 puede ser extraordinariamente poco conservadora. Las situaciones de subestimación de esta regla resultan algo compensadas mediante las combinaciones de diseño normativas, debido a la adición de las solicitaciones gravitacionales a las solicitaciones sísmicas; una evaluación del grado de precisión de las solicitaciones combinadas requiere estudios adicionales.
El análisis de un ejemplo con una estructura sencilla corroboró los resultados teóricos respecto al rango de estimaciones, con cierta cercanía a los valores mínimos debido a la particular correlación entre las respuestas a las componentes sísmicas separadas.
8.
REFERENCIAS1. ASCE, American Society of Civil Engineers, ASCE Working Group on Seismic Analysis of Safety Related Nuclear Structures. Seismic Analysis of Safety Related Nuclear Structures and Commentary. NY, 1986. [ Links ]
2. Anastassiadis K, Avramidis IE y Panetsos PK. Earthquake resistant design of structures under three-component orthotropic seismic excitation. Proceedings of the 11th European Conference on Earthquake Engineering T10, France, 1998. [ Links ]
3. CEN, Comité Europeo de Normalización. Eurocódigo 8: Disposiciones para el proyecto de estructuras sismorresistentes. Bruselas, Bélgica, 1998. [ Links ]
4. Chopra AK. Dynamics of Structures: Theory and Applications to Earthquake Engineering (2nd edn). Prentice Hall: Saddle River, NY, 2001. [ Links ]
5. Computers and Structures, Inc. SAP2000 Structural Analysis Program. Berkeley, California, 1999. [ Links ]
6. COVENIN, Comisión Venezolana de Normas Industriales. Edificaciones Sismorresistentes, COVENIN 1756. Caracas, 2001. [ Links ]
7. Hernández JJ y López OA. Response to three-component seismic motion of arbitrary direction. Earthquake Engineering and Structural Dynamics 2002; 31:55 - 77. (2002 a). [ Links ]
8. Hernández JJ y López OA. Revision of code combination rules for response to three components of seismic motion. Proceedings of the 7th U.S. National Conference on Earthquake Engineering , Boston, 2002. (2002 b). [ Links ]
9. Hernández JJ y López OA. Evaluation of combination rules for three-component seismic analysis. Earthquake Engineering and Structural Dynamics 2003, (propuesto para publicación). [ Links ]
10. ICBO, International Conference of Building Officials. 1997 Uniform Building Code, Structural Engineering Design Provisions, vol. 2, Whittier, CA, 1997. [ Links ]
11. ICC, International Code Council, Inc. 2000 International Building Code. Birmingham, AL, 2000. [ Links ]
12. López OA, Chopra AK y Hernández JJ. Critical response of structures to multicomponent earthquake excitation. Earthquake Engineering and Structural Dynamics 2000; 29:1759 - 1778. [ Links ]
13. López OA, Chopra AK y Hernández JJ. Evaluation of combination rules for maximum response calculation in multicomponent seismic analysis. Earthquake Engineering and Structural Dynamics 2001; 30:1379 - 1398. [ Links ]
14. López OA y Hernández JJ. Generalización del criterio CQC3 para incluir tres componentes sísmicas en cualquier dirección. Revista Técnica de la Facultad de Ingeniería, Universidad del Zulia, Maracaibo, Venezuela, vol. 24, Nº 2, Agosto 2001. (2001 a). [ Links ]
15. López OA y Hernández JJ. Criterios para combinar respuestas ante dos componentes sísmicas. Revista Técnica de la Facultad de Ingeniería, Universidad del Zulia, Maracaibo, Venezuela, vol. 24, Nº 3, Diciembre 2001. (2001 b). [ Links ]
16. López OA y Hernández JJ. Response spectra for two horizontal seismic components and application of the CQC3-rule. Proceedings of the 7th U.S. National Conference on Earthquake Engineering , Boston, 2002. [ Links ]
17. López OA, Hernández JJ y Raven EC. Espectros de respuesta de las componentes horizontales principales del movimiento sísmico. VI Congreso Internacional de Métodos Numéricos en Ingeniería y Ciencias Aplicadas, CIMENICS 2002, AD08, Caracas, 2002. [ Links ]
18. López OA y Torres R. The critical angle of seismic incidence and the maximum structural response. Earthquake Engineering and Structural Dynamics 1997; 26:881 - 894. [ Links ]
19. Menun C y Der Kiureghian A. A replacement for the 30%, 40% and SRSS rules for multicomponent seismic analysis. Earthquake Spectra 1998; 14:153 - 156. [ Links ]
20. Newmark NM. Seismic design criteria for structures and facilities, trans-Alaska pipeline system. Proceedings of the U.S. National Conference on Earthquake Engineering, EERI, 1975, 94 - 103. [ Links ]
21. Nutt RV. ATC–32: Provisional recommendations for the seismic design of bridges. The Fourth Caltrans Seismic Workshop, California Department of Transportation, Sacramento, CA, 1996. [ Links ]
22. Penzien J y Watabe M. Characteristics of 3-dimensional earthquake ground motion. Earthquake Engineering and Structural Dynamics 1975; 3:365 - 374. [ Links ]
23. Rosenblueth E y Contreras H. Approximate design for multicomponent earthquakes. Journal of Engineering Mechanics, ASCE, 1977; 103:895 - 911. [ Links ]
24. Smeby W y Der Kiureghian A. Modal combination rules for multicomponent earthquake excitation. Earthquake Engineering and Structural Dynamics 1985; 13:1 - 12. [ Links ]
9. RECONOCIMIENTO
Los autores manifiestan su agradecimiento al financiamiento parcial otorgado por el Consejo Nacional de Investigaciones Científicas y Tecnológicas, CONICIT, Venezuela, bajo el Proyecto Nº S1-2000000606.