Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Boletín Técnico
versión impresa ISSN 0376-723X
IMME v.46 n.3 Caracas dic. 2008
Metodología para incorporar propiedades de tejido óseo no isotrópico a un modelo de elementos finitos.
Thalía San Antonio1,2, M. Ciaccia1,2, Carmen Müller-Karger1, Euro Casanova1
1 Grupo de Biomecánica, Universidad Simón Bolívar, Caracas, Venezuela.
2 Centro de Investigaciones en Mecánica (CIMEC), Facultad de Ingeniería, Universidad de Carabobo, Valencia, Venezuela.
Resumen
La mayoría de los modelos de elementos finitos encontrados en la literatura asumen que el tejido óseo tiene un comportamiento isotrópico. Para simularlo con mayor exactitud, se plantea utilizar materiales transversalmente isotrópicos.
En este estudio se comprueba la sensibilidad del modelo a las direcciones de las propiedades del material, la respuesta del modelo con tres materiales distintos, y la influencia de la dirección de la carga.
Los resultados muestran que los sistemas de referencia locales convergen a las direcciones de los esfuerzos principales sin necesidad de iterar e independientemente de su posición inicial. El parámetro más sensible a la variación de la orientación de las propiedades es la deformación, y este comportamiento es independiente de la dirección de la carga.
Palabras Claves: modelo óseo, tejido óseo, material transversalmente isotrópico, MEF.
Methodology to incorporate non-isotropic bone properties in a finite element model.
ABSTRACT
Most of the finite element models found in the literature assumes that the mechanical behavior of the bone tissue is isotropic. In order to produce more accurate models, this study proposes the incorporation of transversally isotropic material properties.
An analysis of the models sensibility to the orientation of the materials properties, using three different material types and three load cases is presented.
The results show that the local reference systems converge to the principal stress directions in one step, and this behavior is independent of its initial orientation. The strain is the more sensitive parameter to the variation of the orientation of the materials properties, and this behavior is independent of the direction of the load.
Keywords: bone model, bone tissue, transversally isotropic material, FEM.
Recibido: 25/08/08 Revisado: 14/11/08 Aceptado: 18/11/08
1. Introducción
Los sistemas biológicos, por estar vivos, están cambiando constantemente, siendo ésta la principal dificultad para su simulación. En particular, los huesos son estructuras altamente adaptadas a las funciones que realizan a través de complejas geometrías y materiales que se caracterizan por ser heterogéneos, anisotrópicos, no lineales y viscoelásticos.
En los años setenta, algunos investigadores comenzaron a utilizar el método del elemento finito (MEF) para analizar la conducta mecánica de tejidos óseos. Desde entonces, este método ha llegado a ser el instrumento favorito para investigar la conducta mecánica de huesos bajo condiciones fisiológicas o patológicas. Las aplicaciones de los modelos óseos son muchas, entre ellas se destacan el diseño de dispositivos ortopédicos, análisis de éxito o fracaso de implantes, predicción de carga de fractura, seguimientos a estudios clínicos y estudio de remodelado óseo, entre otros.
Hay varios estudios que describen y establecen procedimientos para desarrollar modelos óseos utilizando MEF (Les et al., 1997; Viceconti et al., 1998; Keyak y Rossi, 2000; Perillo Marcone et al., 2003), estos estudios enfatizan la importancia de tomar en cuenta la mayor cantidad posible de factores que influyen en la conducta estructural del tejido óseo, como son la geometría, las condiciones de borde, la heterogeneidad, las propiedades del material, etc.
Con respecto a las propiedades mecánicas de los huesos, casi todos los modelos recientes encontrados en la literatura, consideran al hueso como heterogéneo e isotrópico. Pocos modelos tratan de aproximar la anisotropía propia de los tejidos óseos en las simulaciones, ésto es llevado a cabo mediante una de las siguientes técnicas: como producto de la simulación del proceso de remodelado óseo (Rakotomanana et al., 1996; Fernandes et al., 1999; Doblaré y García, 2001; Wirtz et al., 2003), utilizando modelos de micro-MEF basados en micro tomografías con el propósito de reconstruir minuciosamente la arquitectura de hueso trabecular (Van Rietbergen et al., 1998; Van Rietbergen, 2001), o alineando las propiedades del material con las direcciones de los esfuerzos principales en modelos de dos dimensiones (Miller et al., 2002).
Otro aspecto importante con relación al comportamiento de los huesos es la sensibilidad que aparentemente poseen algunas células óseas a los estímulos mecánicos como el flujo de fluidos, las deformaciones y el daño, entre otros, los cuales convierten a éstos en señales químicas capaces de regular los mecanismos de remodelado óseo. Existen diversos estudios que intentan determinar que tipo de estímulo mecánico son capaces de captar estas células (El Haj et al., 1990; Bonewald, 2002; Burger y Klein Nulend, 2003; McNamara y Prendergast, 2007).
El parámetro más estudiado ha sido la deformación, ya en 1976 Cowin y Hegedus desarrollaron una teoría de adaptación del tejido óseo basada es este estímulo que al ser aplicada a modelos de elementos finitos (EF) ha producido resultados apegados a los experimentales (Huiskes et al., 2000). Actualmente se sigue manejando la hipótesis de que la variación de la deformación es un parámetro importante en la inducción del remodelado óseo, el cual es el proceso básico para el análisis del comportamiento a largo plazo de las endoprótesis (Papathanasopoulou et al., 2004; Decking et al., 2006; McNamara y Prendergast, 2007; Dubois et al., 2007).
Esta investigación tiene por objeto establecer criterios que permitan la aplicación de propiedades no isotrópicas a modelos de EF en tres dimensiones con miras a analizar estructuras óseas. Se desarrolla una metodología que permite alinear las propiedades del material del modelo con los esfuerzos principales para cada elemento de la malla y poder así analizar la influencia que tiene implementar esta orientación de las propiedades del material en el comportamiento mecánico del modelo.
Se plantea inicialmente analizar la sensibilidad del modelo a la orientación de las propiedades del material y luego analizar la respuesta del modelo al cambiar las características del material. Para ello se utilizarán un material isotrópico, uno transversalmente isotrópico con una dirección arbitraria común a todos los elementos, y por último uno transversalmente isotrópico con las propiedades orientadas en las direcciones de los esfuerzos principales para cada elemento. Finalmente se verificará si la dirección de la aplicación de la carga tiene influencia en la respuesta general del modelo.
2. METODOLOGÍa
Con la finalidad de cuantificar la influencia de la asignación de propiedades no isotrópicas a modelos de elementos finitos, se plantea determinar la sensibilidad de éstos a la variación del ángulo que forman los sistemas de referencia de cada elemento del modelo respecto a su posición inicial. Adicionalmente se verificará el comportamiento del modelo al variar: el tipo de material, la posición inicial de los sistemas de referencia y la dirección de aplicación de la carga.
2.1 Formulación del modelo de elementos finitos
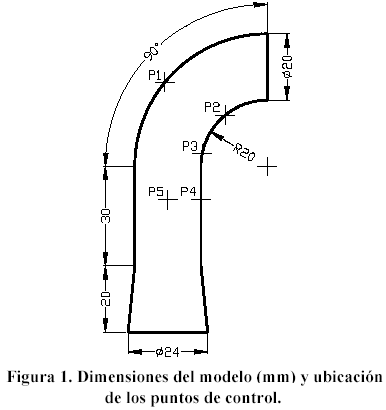
Con el propósito de poder realizar cálculos analíticos que permitan la validación del modelo de EF, es necesaria la utilización de una geometría sencilla. Para ello se creó un bastón con las dimensiones que se presentan en la figura 1, éste tiene una parte curva que permite la aparición de un momento flector al aplicar estados de cargas simples, y una parte recta que se amplía en la base para evitar la concentración de esfuerzos producto de la vinculación. Los modelos en forma de bastón, así como de geometrías cilíndricas, han sido empleados ampliamente en las simulaciones de huesos largos (Comín et al., 1999; McNamara y Prendergast, 2007).
La figura 1 también muestra la ubicación de los puntos de control, numerados de P1 a P5, que serán utilizados en los análisis y validaciones. Estos puntos se seleccionaron de forma que P1, P2 y P3 están ubicados en la parte curva, en zonas donde la magnitud del esfuerzo y la deformación son bajos, medios y altos respectivamente. Los puntos P4 y P5 están a la misma altura y ubicados aproximadamente en el borde y la línea media de la zona recta del modelo. Todos los puntos se encuentran en el plano de simetría, y están alejados del extremo fijo y de la zona de aplicación de la carga.
En esta investigación los análisis de EF se realizan con el programa ANSYS®, utilizando el elemento llamado SOLID92 el cual es un tetraedro de 10 nodos con 3 grados de libertad de desplazamiento por nodo. Este elemento permite una aproximación cuadrática del desplazamiento por lo que es adecuado para modelar geometrías irregulares. Aunque la geometría del modelo utilizado en este estudio es simple, la selección de este elemento obedece a que la motivación de este trabajo es desarrollar una metodología que pueda ser aplicada posteriormente a modelos de huesos reales, los cuales sí poseen geometrías irregulares.
Cada elemento tiene un sistema de referencia local, inicialmente alineado con el sistema de referencia global, al cual se le pueden asociar propiedades de materiales ortotrópicos. Estas propiedades están fijas al sistema de referencia del elemento de forma que al girar éste giran también las propiedades del material.
Con la finalidad de seleccionar una malla adecuada para los análisis de esta investigación se crearon distintas mallas fijando el tamaño máximo de la arista del elemento (ver tabla 1). Los parámetros de convergencia utilizados son la deformación y el esfuerzo equivalentes máximos del modelo, ambos parámetros son calculados por ANSYS® utilizando el criterio de von Mises. Para el análisis de convergencia se utilizó un modelo con material transversalmente isotrópico, con el plano isotrópico perpendicular a la dirección longitudinal del modelo.
Tabla 1. Mallas utilizadas en el análisis de convergencia.
| Mallas | 1 | 2 | 3 | 4 | 5 | 6 |
| Tamaño elemento [mm] | 5,0 | 2,5 | 2,0 | 1,6 | 1,4 | 1,2 |
| Número de elementos | 718 | 4.917 | 10.321 | 19.446 | 30.523 | 49.044 |
| Número de nodos | 1.489 | 8.277 | 16.456 | 30.258 | 46.381 | 73.063 |
2.2 Condiciones de borde
Dado que la geometría y las condiciones de contorno del problema son simétricas (ver figura 2), se modeló solo la mitad del bastón, utilizando como condición de simetría la restricción del desplazamiento en el eje Z de los nodos ubicados en el plano de simetría (plano XY). Además, se restringieron todos los grados de libertad de los nodos del extremo inferior y se aplicaron sucesivamente los tres casos de carga mostrados en la tabla 2 en los nodos ubicados en la sección semicircular del extremo superior (ver figura 2).
Tabla 2. Casos de cargas aplicadas al modelo.
| Carga | Componente | Magnitud [N] |
| 1 | Fx | 0 |
| Fy | -500 | |
| 2 | Fx | -500 |
| Fy | 0 | |
| 3 | Fx | -250√2 |
| Fy | -250√2 |
2.3 Asignación de propiedades mecánicas
Si bien el hueso cortical humano es un material ortotrópico, estudios experimentales como el de Dong y Guo, 2004, demuestran que asumir que este tipo de tejido tiene un comportamiento transversalmente isotrópico es una buena aproximación, ya que las propiedades en el plano transversal a la dirección del mayor módulo de elasticidad son muy similares.
En este estudio se realizarán análisis utilizando tres tipos de materiales con el fin de verificar la influencia de este parámetro en el comportamiento mecánico del modelo. Los modelos son homogéneos con material: isotrópico (Iso), transversalmente isotrópico (T Iso), y transversalmente isotrópico orientado utilizando las direcciones de los esfuerzos principales (T Iso EP). Este último se obtiene a partir de tres orientaciones iniciales distintas, las cuales se describirán detalladamente en la sección 2.5.
Para el material Iso todos los elementos del modelo tienen las mismas propiedades, módulos de elasticidad y Poisson, en todas las direcciones (E = 17 GPa y n = 0,3). El material T Iso tiene un plano p con propiedades isotrópicas, módulos de elasticidad y Poisson (Ep, np), y en la dirección normal al plano isotrópico tiene propiedades distintas, módulos de elasticidad, corte y Poisson (E3, G3p, n3p). En este trabajo se fijará el valor de E3 igual al del material isotrópico y utilizando correlaciones experimentales, presentadas por Dong y Guo, 2004, para hueso cortical humano, se obtendrán el resto de las propiedades (ver tabla 3). El material T Iso EP tiene las mismas propiedades que el T Iso pero con E3 orientado en la dirección del esfuerzo principal con mayor valor absoluto en cada elemento del modelo.
2.4 Metodología para orientar los sistemas de referencia de los elementos con las direcciones de los esfuerzos principales
La metodología para alinear los sistemas de referencia locales, y por tanto las propiedades del material, con los esfuerzos principales y así generar un modelo de EF no isotrópico con miras a analizar estructuras óseas, se basa en dos hipótesis:
-
El esfuerzo mecánico es responsable de determinar la arquitectura del hueso, como fue indicado en el siglo XIX, por el cirujano Julius Wolff (Forwood y Turner, 1995).
-
El tejido óseo se considera ortotrópico, como se ha reportado de pruebas experimentales de probetas de este material (Reilly y Burstein, 1975; Van Buskirk y Ashman, 1980; Ashman et al., 1984).
Esta metodología se inicia resolviendo el modelo con las propiedades del material orientadas en una dirección inicial arbitraria y calculando para cada elemento las direcciones de los esfuerzos principales, resolviendo el problema de autovalores:
[se -lI]j = 0 (1)
Donde se es el tensor de esfuerzos del elemento, l es el esfuerzo principal (autovalor), j es la dirección principal de ese esfuerzo (autovector), e I es una matriz identidad 3x3. Al resolver el problema de autovalores se obtienen tres esfuerzos (s1, s2, s3) y tres direcciones principales (jI, jII, jIII). Estas últimas se pueden arreglar según la ecuación (2):
 (2)
(2)
Donde xi yi y zi son los ángulos que forma la dirección i-ésima con los ejes del sistema de referencia local. Estos ángulos son los que se utilizan para alinear los sistemas de referencia de cada elemento.
Para introducir esta información en ANSYS®, es necesario proporcionar los ángulos de Euler (g, a, b) que transformen el sistema de referencia actual al sistema de referencia nuevo. Los ángulos de Euler se obtienen al igualar la matriz de rotación RE de la ecuación (3) con la matriz de direcciones principales F, de la ecuación (2).
 (3)
(3)
Donde sq = sen (q), cq = cos (q) y q toma los valores a, b, g.
Resolviendo RE = F, los ángulos de Euler se obtienen con las ecuaciones:
 (4)
(4)
Dado que se varía la orientación del sistema de referencia de los elementos y por consiguiente se cambia la orientación de las propiedades del material, ocurre una alteración en el estado de esfuerzos de cada elemento, lo que afecta nuevamente las direcciones de los esfuerzos principales, por lo tanto, este procedimiento deberá ser iterativo. Sin embargo, dado que las condiciones de borde no varían en cada iteración, se espera que la variación en el estado de esfuerzos de cada elemento sea pequeña y la convergencia sea rápida.
Los parámetros que se utilizarán para establecer la convergencia serán la deformación y el esfuerzo equivalentes máximos del modelo.
2.5 Análisis del modelo
El procedimiento que se empleará para determinar la influencia en las deformaciones y los esfuerzos equivalentes al implementar materiales no isotrópicos en el modelo de EF se describe en 4 pasos:
Paso 1. Determinar la sensibilidad del modelo a la orientación de las propiedades del material. Esto se realizará monitoreando la respuesta del modelo al incrementar gradualmente (pasos de 10°) el ángulo α, del sistema de referencia del elemento (Ep, Ep, E3) alrededor del eje Z del sistema de referencia global, entre 0° y 180°, girando así el plano isotrópico (ver figura 3).
Paso 2. Realizar una comparación del comportamiento mecánico del modelo de EF utilizando los tres modelos de material (Iso, T Iso, T Iso EP).
Paso 3. Verificar la influencia de la posición inicial de los sistemas de referencia locales en su posición final al ser alineados con las direcciones de los esfuerzos principales. Se establecen tres posiciones iniciales al alinear E3 con los ejes Y, X, y Z; para facilitar posteriores referencias a estas posiciones se les asignan los nombres de E3oy, E3ox y E3oz, respectivamente.
Paso 4. Determinar la sensibilidad del modelo a la dirección de la carga resolviendo el problema con los materiales del paso 2 y utilizando las cargas descritas en la tabla 2.
3. Resultados y discusión
3.1 Selección de la malla
Como resultado del análisis de convergencia se seleccionó la malla 3 (10.321 elementos y 16.456 nodos) para implementar la metodología propuesta.
3.2 Análisis cualitativo de la sensibilidad del modelo a la orientación arbitraria de las propiedades del material
La figura 4 presenta las relaciones entre la deformación y el esfuerzo equivalentes, y la orientación del plano isotrópico para cada punto de control. Las curvas graficadas muestran variaciones importantes, aunque de forma suave y continua, en las magnitudes de las deformaciones y los esfuerzos a medida que se cambia la orientación de las propiedades del material. Como característica común a todas las curvas se destaca que los valores máximos y mínimos ocurren en ángulos distintos para cada punto de control, confirmando que los estados de esfuerzo y de deformación son funciones de la ubicación espacial del punto analizado. También es importante resaltar que los puntos de cada curva en 0º y en 180º coinciden en el valor y la pendiente, poniendo en evidencia el carácter periódico de las curvas.
3.3 Respuesta del modelo al cambio del tipo de material y a la alineación de las propiedades del material con las direcciones de los esfuerzos principales
El efecto que producen los cambios del material y de orientación de las propiedades del material en la deformación y el esfuerzo equivalentes se expone en las figuras 5 y 6. La primera permite realizar una comparación cualitativa de los valores de deformación y esfuerzo entre los materiales Iso, T Iso y T Iso EP, así como confirmar que el punto 3 está en la zona de máximo esfuerzo. Con la figura 6 se puede efectuar una comparación cuantitativa, ya que muestra las diferencias porcentuales de la deformación y el esfuerzo correspondientes a los materiales Iso y T Iso EP con los correspondientes al material T Iso.
Al efectuarse el cambio de material Iso a T Iso se producen rangos de diferencias porcentuales similares para las deformaciones y los esfuerzos (13% en ambos parámetros), pero inspeccionando los valores por punto se aprecia que los cambios son mayores para la deformación que para el esfuerzo, llegando al 12% en la deformación del punto 1 y al 7,1% en el esfuerzo del punto 5. En la zona de máximo esfuerzo (punto 3) estos valores son del 3,7% y 5,4% respectivamente.
El cambio de material T Iso a T Iso EP produce variaciones mucho mayores en la deformación, no así en el esfuerzo, siendo los rangos del 46% y 7,8% respectivamente. La variación máxima en la deformación ocurre en el punto 4, con 52%, mientras que la del esfuerzo ocurre en el punto 5, con 4,6%. En la zona de máximo esfuerzo (punto 3) estos valores son del 45% y 1,1% respectivamente.
De las cifras presentadas se puede deducir, en primer lugar, que la deformación equivalente es un parámetro más sensible a las alteraciones de las características del material que el esfuerzo el cual, en general, es mínimamente influenciado por dichos cambios. En segundo lugar, se obtienen variaciones mayores en la deformación alineando las propiedades del material transversalmente isotrópico con la dirección de los esfuerzos principales (T Iso a T Iso EP) que cambiando el material de isotrópico a transversalmente isotrópico (Iso a T Iso).
3.4 Influencia de la orientación inicial de las propiedades del material transversalmente isotrópico (T Iso).
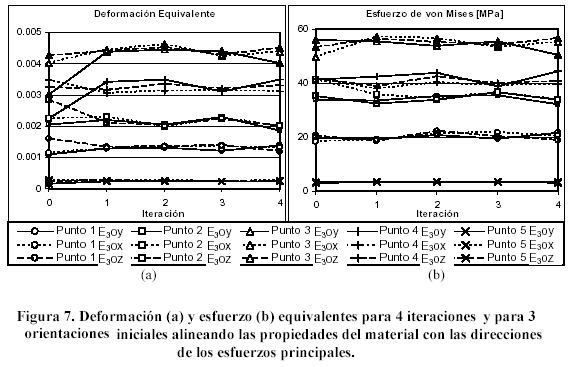
En la figura 7 se muestran los resultados correspondientes a las iteraciones para la verificación de la influencia de la posición inicial de los sistemas de referencia locales en su posición final al ser alineados con las direcciones de los esfuerzos principales. Los resultados que se muestran en la iteración 0 corresponden al modelo con los sistemas de referencia con la orientación inicial, y a partir de la iteración 1 los resultados corresponden a modelos con los sistemas de referencia alineados con las direcciones de los esfuerzos principales. Para cada punto de control se muestran tres curvas, correspondientes a las orientaciones iniciales E3oy, E3ox, E3oz de los sistemas de referencia locales, tal como se describió en la metodología. Se realizaron 6 iteraciones, pero debido al comportamiento monótono de las curvas y para economizar espacio, se muestran solamente las primeras 4 iteraciones.
Del análisis de la figura 7 se desprenden dos resultados interesantes. En primer lugar, todas las curvas muestran convergencia desde la iteración 1, ya que posteriormente se mantienen constantes u oscilan alrededor de un valor medio. Esto es importante porque cada iteración realizada supone la solución del modelo de EF, de manera que resolver el modelo solo 2 veces significa invertir menos recursos computacionales y tiempo. Para cada curva se calculó el rango de oscilación alrededor del valor medio, obteniéndose una variación máxima del 6,5% tanto para la deformación equivalente como para el esfuerzo equivalente. Esta variación se considera aceptable para fines de la convergencia.
El segundo resultado a destacar es que independientemente de la orientación inicial del sistema de referencia del elemento, la deformación y el esfuerzo convergen a valores muy similares desde la iteración 1. Además de los valores, las direcciones de los esfuerzos principales también coinciden, como puede observarse en la figura 8. Las imágenes de esta figura muestran los sistemas de referencia de los elementos ubicados en el plano de simetría del bastón luego de la primera iteración, habiendo partido en cada caso de una orientación inicial diferente. El hecho de que las deformaciones, esfuerzos y direcciones sean independientes de la orientación inicial del sistema de referencia de los elementos es un indicativo de que el modelo de EF está correctamente formulado y elaborado, y que no es necesario tener un cuidado especial en la orientación inicial del objeto de estudio. Este último resultado es importante con miras a la aplicación de estos procedimientos a modelos de huesos reales, en los que definir una orientación inicial específica puede ser complicado.
3.5 Respuesta del modelo a la variación de la dirección de la carga
Con la finalidad de precisar si las tendencias mostradas por la deformación y el esfuerzo equivalentes están relacionadas con la dirección de la carga utilizada en el modelo, se efectuaron nuevamente todos los cálculos empleando dos cargas adicionales que tienen la misma magnitud que la original pero con distintas direcciones, según se expuso en la metodología. Los resultados de las figuras 9, 10 y 11 muestran que efectivamente el cambio de dirección de la carga influye en las magnitudes y direcciones de las deformaciones y los esfuerzos equivalentes, como es de esperarse, pero a la vez confirman las observaciones hechas en la sección 3.3: mayor sensibilidad de las deformaciones equivalentes a los cambios de material, mayor variación de la deformación al orientar las propiedades del material T Iso en dirección de los esfuerzos principales, e incremento de las deformaciones al cambiar el material Iso por los materiales T Iso o T Iso EP.
3.6 Validación de los resultados del modelo con resultados analíticos
Para validar el modelo de EF se calculó analíticamente el esfuerzo equivalente de von Mises y las direcciones de los esfuerzos principales en los puntos de control seleccionados para el estudio. Puesto que dichos puntos se encuentran en el plano de simetría del bastón, se tiene un estado plano de esfuerzos, facilitando la tarea. En los puntos P1, P2 y P3 se utilizó la teoría de vigas curvas para el cálculo de esfuerzos por flexión, incluyéndose además los esfuerzos por carga axial y corte. En los puntos P4 y P5 se utilizó la teoría de vigas rectas para el cálculo de esfuerzos por flexión, incluyéndose además el esfuerzo por carga axial. Los cálculos se realizaron para el caso de carga 1 y el modelo isotrópico de material. En la tabla 4 se puede comprobar que existe una adecuada correspondencia entre los resultados analíticos y numéricos, confirmando la validez del modelo de EF.
Tabla 4. Comparación de resultados analíticos y numéricos.
| Puntos | Analíticos | Numéricos | ||
| Seqv [MPa] | θ [º] | Seqv [MPa] | θ [º] | |
| P1 | 21,1 | 34,2 | 20,8 | 38,3 |
| P2 | 34,6 | 54,7 | 34,7 | 51,2 |
| P3 | 52,9 | 12,8 | 53,2 | 10,7 |
| P4 | 41,4 | 0,0 | 41,6 | 1,12 |
| P5 | 3,18 | 0,0 | 3,20 | 2,15 |
θ: ángulo que forman los esfuerzos principales con los ejes de referencia.
Seqv: esfuerzo equivalente de von Mises.
4. Conclusiones
Se logró incorporar y manipular exitosamente las propiedades de un material transversalmente isotrópico en un modelo de elementos finitos. La versión isotrópica del modelo fue validada analíticamente.
La alineación de las propiedades del material con las direcciones de los esfuerzos principales es un proceso que no requiere iteraciones, y además no es sensible a la orientación inicial de las propiedades del material. Estos resultados permitirán realizar estudios en modelos óseos, efectuando dicho proceso en un solo paso, y con el conocimiento de que la diferencia entre la orientación inicial y la final de los sistemas de referencia no tiene consecuencias en la respuesta del modelo.
La deformación es el parámetro más sensible a los cambios del modelo de material, y estas variaciones son mayores al modificar la dirección de las propiedades (T Iso a T Iso EP) que al cambiar el modelo de material (Iso a T Iso). En virtud de que la deformación es considerada un estímulo mecánico importante en el proceso de remodelado óseo, estos resultados apoyan la importancia de utilizar modelos de material no isotrópicos.
El cambiar la dirección de la carga, si bien influye en la dirección de los esfuerzos principales y por tanto en la dirección de las propiedades del material, no tiene influencia en las tendencias mostradas por la deformación respecto a los cambios del material.
5. Reconocimientos
Este proyecto fue financiado de forma parcial por el FONACIT (proyecto N° 2005000172), DID – USB y CDCH – UC.
6. REFERENCIAS
1. Ashman R. B., Cowin S. C., van Buskirk W. C., Rice J.C. A continuous wave technique for measurement of elastic properties of cortical bone. 1984. Journal of Biomechanics, 17: 349-361. [ Links ]
2. Bonewald L.F. Osteocytes: a proposed multifunctional bone cell. 2002. Journal of Musculoskeletal and Neuronal Interaction, 2(3): 239–241. [ Links ]
3. Burger E. H., Klein-Nulend J., Smit T.H. Strain-derived canalicular fluid flow regulates osteoclast activity in a remodelling osteon a proposal. 2003. Journal of Biomechanics, 36(10): 1453–1459. [ Links ]
4. Comín M., Peris J. L., Prat, J. M., Dejoz J. R., Vera P. M., Hoyos J.V. Biomecánica de la fractura ósea y técnicas de reparación. instituto de biomecánica de Valencia. Pp. 88. Isbn:84-923974-5-4. Depósito legal> V-1481-1999. [ Links ]
5. Cowin S. C., Hegedus D.H. Bone remodelling I: theory of adaptive elasticity. 1976. Journal of Elasticity, 6 (3): 313–326. [ Links ]
6. Decking R., Puhl W., Simon U., Claes L.E. Changes in strain distribution of loaded proximal femora caused by different types of cementless femoral stems. 2006. Clinical Biomechanics, 21: 495–501. [ Links ]
7. Doblaré M., García J.M. Application of an anisotropic bone-remodeling model based on a damage-repair theory to the analysis of the proximal femur before and after total hip replacement. 2001. Journal of Biomechanics, 34: 1157–1170. [ Links ]
8. Dong X. N., Guo X. E. The dependence of transversely isotropic elasticity of human femoral cortical bone on porosity. 2004. Journal of Biomechanics, 37(8): 1281-7. [ Links ]
9. Dubois G., Daas M., Bonnet A. S., Lipinski P. Biomechanical study of a prosthetic solution based on an angled abutment: Case of upper lateral incisor. 2007. Medical Engineering & Physics 29: 989–998. [ Links ]
10. El Haj A. J., Minter S. L., Rawlinson S. C., Suswillo R., Lanyon L.E. Cellular responses to mechanical loading in vitro. 1990. Journal of Bone and Mineral Research, 5(9): 923–932. [ Links ]
11. Fernandes P., Rodrigues H., Jacobs C. R. A model of bone adaptation using a global optimization criterion based on the trajectorial theory of Wolf. 1999. Computer Methods in Biomechanics and Biomedical Engineering, 2: 125–138. [ Links ]
12. Forwood M. R., Turner C.H. Skeletal adaptations to mechanical usage. 1995. Bone, 17: 197s-205s. [ Links ]
13. Huiskes R., Ruimerman R., van Lenthe G. H., Janssen J.D. Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. 2000. Nature, 405: 704–706. [ Links ]
14. Keyak J. H., Rossi S.A. Prediction of femoral fracture load using finite element models: an examination of stress and strain based failure theories. 2000. Journal of Biomechanics, 33(2): 209–214. [ Links ]
15. Les C. M., Keyak J. H., Stover S. M., Taylor K.T. Development and validation of a series of three-dimensional finite element models of the equine metacarpus. 1997. Journal of Biomechanics, 30: 737–742. [ Links ]
16. McNamara L. M., Prendergast P.J. Bone remodelling algorithms incorporating both strain and microdamage stimuli. 2007. Journal of Biomechanics, 40: 1381–1391. [ Links ]
17. Miller Z., Fuchs M. B., Arcan M. Trabecular bone adaptation with an orthotropic material model. 2002. Journal of Biomechanics, 35: 247–256. [ Links ]
18. Papathanasopoulou V. A., Fotiadis D. I., Massalas C.V. A theoretical analysis of surface remodeling in long bones. 2004. International Journal of Engineering Science, 42: 395–409. [ Links ]
19. Perillo-Marcone A., Alonso-Vazquez A., Taylor M. Assessment of the effect of mesh density on the material property discretisation within QCT based FE models: a practical example using the implanted proximal tibia. 2003. Computer Methods in Biomechanics and Biomedical Engineering, 6: 17–26. [ Links ]
20. Reilly D. T., Burstein A.H. The elastic and ultimate properties of compact bone tissue. 1975. Journal of Biomechanics, 8: 393-401. [ Links ]
21. Rakotomanana L. R., Terrier A., Leyvraz P.F. Anisotropic bone adaptation models: comparison and application of orthopaedic implants. 1996. Computer Methods in Biomechanics and Biomedical Engineering, 95-104. [ Links ]
22. Van Buskirk W.C., Ashman R.B. The elastic moduli of bone. 1981. Mechanical Properties of Bone, American Society of Mechanical Engineers, 131-143. [ Links ]
23. Viceconti M., Bellingeri L., Cristofolini L., Toni A. A comparative study on different methods of automatic mesh generation of human femurs. 1998. Medical Engineering & Physics, 20: 1–10. [ Links ]
24. Van Rietbergen B., Majumbar S., Pistoia W., Newitt D. C., Kothari M., Laib A., Rüegsegger P. Assessment of cancellous bone mechanical properties form micro-FE models based on micro-CT, pQCT and MR images. 1998. Technology and Health Care, 6: 413-420. [ Links ]
25. Van Rietbergen B. Micro-FE analysis of bone: state of the art, 2001, Bioengineering Conference, ASME, BED-Vol 50. [ Links ]
26. Wirtz D. C., Pandorf T., Portheine F., Radermacher K., Schiffers N., Prescher A., Weichert D., Niethard F.U. Concept and development of an orthotropic FE model of the proximal femur. 2003. Journal of Biomechanics, 36: 289–293. [ Links ]