Técnicas de procesamiento de la señal ECGAR aplicadas en el prototipo DIGICARDIAC

Techniques HRECG signal processing applied at DIGICARDIAC prototype

Nelson Dugarte J^1,2, Antonio Alvarez², Edinson Dugarte¹, Gabriel Álvarez²

¹ Grupo de Ingeniería Biomédica de la ULA (GIBULA). Avenida Don Tulio, Facultad de Ingeniería, Postgrado en Ingeniería Biomédica de la Facultad de Ingeniería. Mérida, Estado Mérida. Venezuela.

² Instituto Regional de Bioingeniería (IRB) de la Universidad Tecnológica Nacional (UTN). Mendoza, República Argentina.

Mail: ndj0227@gmail.com, antonioalvarezabril@yahoo.com.ar, edinson0909@gmail.com, gabo_121_7@hotmail.com.

Resumen.

Este artículo reporta el desarrollo de la etapa de procesamiento de la señal electrocardiográfica implementada en el prototipo DIGICARDIAC. El prototipo DIGICARDIAC es un instrumento de uso médico que permite la adquisición simultánea de las doce derivaciones del electrocardiograma (ECG) estándar, con características de alta resolución (ECGAR). El software desarrollado, pretende agrupar algunos de los criterios expuestos por los investigadores e implementar algunas técnicas novedosas, en la detección del latido cardiaco y la medición de los intervalos QT y ST en la señal ECGAR adquirida con el sistema. En las pruebas de funcionamiento se comprobó la eficiencia del algoritmo. Los errores obtenidos en la detección del complejo QRS son inferiores al 0,1 % y en la medición del intervalo QT se obtuvo un error promedio del 1,89 % en las señales ECG de los pacientes control.

Palabras claves: Algoritmo de procesamiento, Prototipo Digicardiac, Electrocardiograma de alta resolución (ECGAR), Análisis de la señal electrocardiográfica, Medición de intervalos del latido cardiaco.

Abstract.

This paper reports the development stage of the electrocardiographic signal processing implemented at the prototype DIGICARDIAC. The DIGICARDIAC prototype is a medical instrument that allows the simultaneous acquisition of the twelve-lead electrocardiogram (ECG) standard, which features high resolution (HRECG). The software developed, aims to bring together some of the criteria set up by the researchers and implement some new techniques, in heartbeat detection and measurement of QT and ST intervals in the HRECG signal acquired with the system. The algorithm  efficient  was proved through tests of perfomance. The errors obtained in QRS complex detection are lower than 0,1% and measuring QT interval averaging 1.89% error in the ECG signals of the control patients was obtained.

Key words: Processing algorithm, Digicardiac prototype, High resolution electrocardiogram, Electrocardiographic signal analysis, Intervals measurement of heartbeat.

Recibido: 30 de octubre de 2015 Aprobado: 02 de marzo de 2016

INTRODUCCIÓN

Las enfermedades cardiovasculares constituyen en la actualidad una de las principales causas de muerte (1). La ciencia moderna permite el estudio de las patologías cardiacas con técnicas cada vez más eficientes. La evaluación electrocardiográfica permite el estudio del trabajo cardiaco de forma no invasiva. Este tipo de examen consiste en adquirir y valorar las señales eléctricas que se originan en el corazón del paciente (2).

El electrocardiograma o ECG (3), consiste en la captación de las señales eléctricas originadas por la actividad de biopotenciales en el corazón. La señal captada presenta características diferentes en función del ángulo en que se coloquen los electrodos sobre el cuerpo. Se han estandarizado 12 derivaciones que conforman la representación gráfica de la señal cardiaca desde todos los ángulos (2) (3). Las derivaciones estándar son: I, II, III, aVR, aVL, aVF, V1, V2, V3, V4, V5, V6.

El instrumento que se utiliza para adquirir la señal cardiaca se denomina electrocardiógrafo. Los electrocardiógrafos comerciales normalmente adquieren una derivación a la vez. La presentación gráfica del ECG se realiza en una tira de papel con formato cuadriculado estándar, en la mayoría de los casos trazada con una velocidad de 25 milímetros por segundo (mm/s) y con una resolución de amplitud de 10 milímetros por milivoltios (mm/mV).

Estudios modernos presentan las relaciones entre las enfermedades cardiovasculares y los valores de tiempo de los diferentes elementos que conforman la señal ECG (3) (4). La Fig. 1, presenta el registro correspondiente a un latido cardiaco, donde se identifican algunos de los intervalos que la componen.

El intervalo QT del Electrocardiograma es un indicador de la repolarización ventricular. Las relaciones en los cambios del QT, son utilizadas para evaluar el riesgo de arritmias y muerte súbita. Las alteraciones en este intervalo se pueden presentar como alargamientos o acortamientos del tiempo (5). Las relaciones entre el ST y la isquemia, los cambios del QT como respuesta a los medicamentos, las alteraciones del complejo QRS en función de la cardiopatía y otros índices, sugieren el tratamiento o la intervención del paciente en función de los criterios del médico especialista (3) (5).

El ECG convencional, es adquirido para visualizar señales con frecuencias por debajo de 120 Hz. Los electrocardiógrafos modernos normalmente digitalizan a 500 muestras por segundo (mps) con 8 bits de resolución (3). Esta resolución permite obtener una forma de onda con definición suficiente para la visualización humana, pero está comprobado que muchos detalles pueden pasar desapercibidos al análisis del experto, (4) (5). Para una mayor definición se utiliza el electrocardiograma de alta resolución (ECGAR) (6). El ECGAR consiste en adquirir la señal cardiaca en un rango ampliado del ancho de banda y con mayor resolución que el ECG convencional.

Estudios realizados desde el año 2009, en el Grupo de Ingeniería Biomédica (GIBULA) de la Universidad de Los Andes (ULA) en la República Bolivariana de Venezuela, en conjunto con el Instituto Regional de Bioingeniería (IRB) de la Universidad Tecnológica Nacional (UTN) en la República Argentina, han generado una serie de productos de innovación tecnológica en cuanto al hardware de adquisición del ECGAR de 12 derivaciones (6) (7) y al software de manipulación (8) y análisis de la señal, enmarcados dentro del proyecto denominado DIGICARDIAC. Estos trabajos de investigación y desarrollo científico están orientados a la implementación amigable y eficiente de un sistema de electrocardiografía de alta definición en busca de índices cuantificables que permitan a los médicos especialistas diagnosticar patologías cardiacas en su fase temprana (9).

Este artículo reporta uno de los algoritmos desarrollados en el marco del proyecto DIGICARDIAC, que pretende implementar técnicas de análisis de bajo costo computacional para medir con relativa precisión los principales intervalos que componen el latido cardiaco.

METODOLOGÍA

El sistema DIGICARDIAC se diseñó para ser manejado desde un entorno de Historia Médica Electrónica (HME) (8). El software de procesamiento se ejecuta a cuando el especialista acciona el botón “Analizar”, desde el expediente de HME.

El procesamiento implementado, pretende agrupar algunos de los criterios expuestos por los investigadores, en cuanto a la detección del latido cardiaco y medición de los intervalos QT y ST, con el propósito de analizar la señal ECGAR adquirida. El diagrama de la Fig. 2, describe la secuencia de los algoritmos.

Cada recuadro de subproceso, en la Fig. 2, corresponde a un algoritmo específico que se encarga de una etapa independiente. Todo el software de procesamiento se desarrolló en Linux bajo la plataforma de software libre de Ubuntu, utilizando la herramienta de análisis denominada Octave. El procesamiento se realiza analizando una derivación a la vez, pero es aplicable a cualquiera de las derivaciones.

Detección del latido cardiaco

La detección del latido cardiaco consiste en ubicar los intervalos de tiempo donde ocurren los complejos QRS en el electrocardiograma. El procesamiento consiste en aplicar algunos criterios expuestos por Pan y Tompkins (10), en combinación con algunas técnicas descritas por Dotsinsky y Stoyanov (11), agregando algunos cambios estructurales a la secuencia del algoritmo con el propósito de mejorar su eficiencia. El algoritmo propuesto consiste en convertir los complejos QRS en picos bien definidos mientras se descarta el resto de los componentes del ECG, luego se aplica una discriminación basada en umbrales de amplitud y tiempo para descartar los falsos complejos QRS.

El procesamiento se inicia con un filtro paso alto de tipo recursivo (12), con frecuencia de corte de 0,65 Hz. Este filtro tiene la función de eliminar corrimientos de línea de base y ruidos de baja frecuencia. Está definido por la ecuación 1, donde X conforma la señal de entrada, Y los datos de salida, C1 y C2 los coeficientes del filtro.

Y(i) = C1[X(i) - X(i-1)] + C2[Y(i-1)]                [1]

Las ecuaciones 2 y 3 permiten calcular los coeficientes C1 y C2 a partir de la frecuencia de corte Fc y del periodo de muestreo T.

El paso siguiente en el algoritmo consiste en procesar la señal con un filtro  paso bajo con una frecuencia de corte de 35 Hz. El filtro implementado está definido por la ecuación 4, donde X conforma los datos de la señal de entrada, Y los datos de salida y N representa los coeficientes del filtro. La Fc = 35 Hz se logra con una ventana de N = 26.

Seguidamente, la señal se deriva para magnificar los cambios de amplitud del complejo QRS. Con la ecuación 5, se obtiene una aproximación a la derivada de la señal (10), donde X representa la señal de entrada y Y es la señal derivada.

Y(i) = 2X(i) + X(i-1) - X(i-3) - 2X(i-4)            [5]

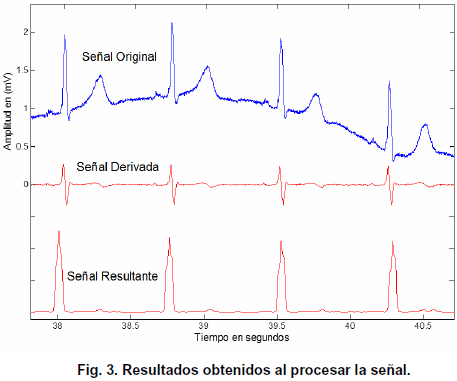
El paso siguiente en el algoritmo es aplicar un filtro rectificador, el cual consiste en elevar al cuadrado la señal derivada. Esto se realiza con el propósito de obtener solo picos positivos. Luego, la señal se somete a un filtro paso bajo idéntico al descrito por la ecuación 4, pero con una ventana de 60 muestras. Se utiliza una ventana de 60 muestras para que la frecuencia de corte sea de 15 Hz, lo cual es suficientemente baja para generar la integración de los picos obtenidos en un único pulso de gran amplitud, pero sin alterar la duración del espacio que ocupa el complejo QRS. La Fig. 3, muestra tres segundos de la señal original en la parte superior, en el medio de la imagen se presenta la aproximación a la derivada que se obtiene como resultado de aplicar la ecuación 5 y en la parte inferior se encuentra el resultado definitivo, que se obtiene al rectificar y luego filtrar paso bajo la señal que se procesa.

El retardo causado por los filtros se elimina introduciendo el factor de corrección temporal apropiado. Cabe destacar que no importa la morfología de la señal original, aun cuando los complejos QRS sean negativos o deformes, la señal resultante siempre genera un pulso positivo definido en el intervalo QRS correspondiente al latido.

La etapa siguiente en el algoritmo, consiste en detectar los pulsos. Esto se realiza evaluando los cambios de amplitud con respecto al tiempo, que se registran en la señal. La detección de un pulso es seguido por la ubicación del punto de mayor amplitud. Esto se hace para someter el pulso encontrado a criterios de evaluación de amplitud y tiempo que permitan verificar si se trata de un complejo QRS verdadero (10) (11).

El primer criterio de evaluación se establece por comparaciones de amplitud, definido por un umbral adaptativo. El umbral adaptativo se obtiene al promediar el valor de los últimos 6 picos R aceptados como verdaderos. La discriminación por amplitud se realiza considerando que un pico R es verdadero si su amplitud está en un rango de ± 20% del umbral adaptativo.

El segundo criterio de evaluación se establece en función del tiempo. Se basa en que el tiempo de los intervalos RR no puede cambiar en más de 30% en intervalos consecutivos (10) (13). El periodo RR se evalúa considerando como referencia al promedio de los últimos 6 RR aceptados como verdaderos. Al terminar la evaluación de todos los pulsos, se reubican los puntos encontrados sobre los picos R de la señal original.

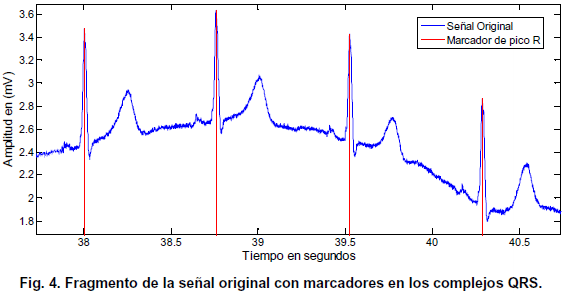
La gráfica de la Fig. 4, presenta un fragmento de 3 segundos de la señal adquirida, con líneas marcadoras que señalan la ubicación de los picos R en cada uno de los complejos QRS detectados y evaluados como verdaderos.

Detección de los puntos Q y S

La detección de los puntos Q y S se realiza debido a la necesidad de medir algunos intervalos de tiempo que son parámetros de importancia médica, como los intervalos QT, ST y la duración del complejo QRS. Para la detección de estos puntos, el procesamiento utiliza la señal resultante con el procedimiento descrito en la sección anterior, ejemplo de la cual se presenta en la parte inferior de la Fig. 3.

El algoritmo para la detección de los puntos Q y S, se ejecuta en un lazo repetitivo que evalúa todos los pulsos generados por los complejos QRS verdaderos a partir de la señal original. Esto se debe a que el ancho de cada pulso, ocupa el intervalo del complejo QRS al que corresponde. Por consiguiente, el inicio del pulso identifica al punto Q y el final del pulso equivale al punto S, en cada latido.

La detección de los puntos Q y S se basa en la estimación del punto más pronunciado en la curva inicial y final del pulso, respectivamente. Los investigadores en la materia han implementado muchas técnicas para detectar el inicio o el final de un pulso, con diferentes resultados. Una de las aplicaciones más eficientes consiste en la técnica del trapecio implementada por Seisdedos y col. (13). Esta técnica fue empleada para detectar el final de la onda T, pero es aplicable a cualquier pulso. La Fig. 5, muestra un ejemplo de aplicación del método del trapecio para detectar el final del pulso.

El método consiste en localizar el valor máximo del área de la figura trapezoidal que se forma sobre la curva. Los puntos demarcados en la zona de evaluación se identifican por (Xm,Ym), (Xr,Ym), (Xr,Yi), (Xi,Yi). Donde los valores X representan el desplazamiento en el tiempo de las muestras y los valores Y representan la amplitud de la señal, dado por el valor de la muestra en ese instante de tiempo. El área del trapecio se calcula con la ecuación 6.

El valor de amplitud Ym se mantiene constante mientras que el valor de Yi cambia en función de Xi. El procesamiento consiste en calcular el valor del área del trapecio para cada punto posible en el desplazamiento de “Pe” sobre la curva.

El valor de Ym se determina por el 30% de amplitud del pulso o pico R. Xm corresponde al tiempo en que ocurre Ym. Xr se determina en un 15% del valor de RR a partir del punto Xm. El punto Pe identificado por Xi y Yi, se toma como el factor de evaluación que determina los cambios en el área del trapecio. Yi se evalúa en todas las muestras del intervalo que va desde 0,1R hasta amplitud mínima dentro del intervalo definido por Xm y Xr. Xi adquiere el valor correspondiente de cada Yi. El punto (Xi,Yi) donde se obtiene el valor máximo del área del trapecio señala el punto más pronunciado de la curva y por ende se marca como punto S.

El paso siguiente en el algoritmo, se realiza con el propósito de encontrar el punto Q. Consiste en fijar la zona de evaluación en el área anterior al inicio del pulso. Sobre la zona de evaluación se establecen los cuatro puntos que determinan los vértices del trapecio, idéntico al de la Fig. 5, pero con la figura geométrica trapezoidal formada en la parte anterior al pulso.

A continuación, el algoritmo ubica el pulso siguiente, correspondiente a un nuevo complejo QRS en la señal y se repite todo el proceso para detectar los nuevos puntos Q y S. El procedimiento se repite hasta el final del registro. La Fig. 6, presenta un fragmento de 3 segundos de la señal original, con líneas marcadoras que señalan los puntos Q y los puntos S ubicados con el procesamiento.

Los filtros paso alto pueden lograr una buena corrección de la línea de base, pero también implica la perdida de componentes de baja frecuencia y deformación de la morfología de la onda original. La pérdida de componentes esenciales no puede ser admitida en los análisis de las señales de alta resolución. Por consiguiente, se implementó una técnica idéntica a la propuesta por Laguna y Sornmo (14).

Esta técnica consiste en generar una señal que solo representa el corrimiento de la línea de base a partir de la señal original. Seguidamente se realiza una operación matemática de sustracción entre la señal original y el vector generado.

El procesamiento se inicia marcando puntos a 0,02 segundos antes de cada punto Q, los cuales, para efecto de cálculo, se identifican como puntos PQ. Esta acción se realiza porque se considera que la señal entre el final de la onda P y el inicio del complejo QRS debe estar sobre la línea de base.

El funcionamiento de esta etapa del software se inicia tomando los primeros 6 puntos PQ marcados en la señal original, para generar por interpolación una curva que pase por ellos. Para esto se genera una ecuación polinómica que describa el comportamiento de los puntos marcados. La ecuación 7 representa el polinomio generado en este algoritmo, donde n es el grado y X contiene los valores de amplitud correspondientes a los puntos PQ seleccionados.

P(x) = a₁Xⁿ + a₂X^n-1 +...a_nX + a_n+1       [7]

Se utilizó n = 6, porque el trabajo empírico definió que la ecuación polinómica de grado 6 es la más eficiente para describir la señal en el intervalo.

En el paso siguiente se evalúa la ecuación polinómica encontrada en igual número de muestras que la señal original, dentro el intervalo correspondiente a PQ = 3 y PQ = 4. Se tomó el intervalo intermedio entre los puntos PQ seleccionados, porque se considera la fracción de la curva más representativa de la línea de base. El resto de los intervalos definidos por los 6 puntos PQ, solo se utilizan para describir el comportamiento de la curva por extrapolación.

El paso siguiente del algoritmo, se descarta el punto PQ = 1 y se toman los 6 puntos siguientes, desde PQ = 2 hasta PQ = 7, para una nueva estimación. Seguidamente se repite el procedimiento para encontrar por interpolación una nueva ecuación polinómica para calcular los valores de la línea de base en el intervalo entre PQ = 4 y PQ = 5. Este ciclo se repite hasta completar la evaluación de todos los intervalos marcados por los puntos PQ. Los valores obtenidos en cada ciclo de evaluación son concatenados en un vector de resultados, que describe el comportamiento de la línea de base en toda la señal analizada.

Al concluir el ciclo repetitivo, se procede a realizar la operación matemática de substracción entre el vector original y el obtenido. El resultado genera un nuevo vector donde se elimina el corrimiento de línea de base sin alterar los valores de amplitud o la morfología de la señal original. La Fig. 8, muestra en la parte superior, un fragmento de 10s de una señal adquirida con algunas alteraciones de la línea de base. En la parte inferior de la figura, se presenta el mismo segmento pero con la señal corregida.

La onda T conforma la última parte de la señal correspondiente a un latido cardiaco. El final de la onda T se define por la mayor protuberancia de la curvatura sobre el eje isoeléctrico al final de la señal (2) (3) (15). La Fig. 1, demarca el final de la onda T y a los espacios de tiempo correspondientes al intervalo QT y al segmento ST.

La dificultad que se presenta radica en la baja frecuencia en esta parte de la señal y a las diferentes morfologías que puede presentar. Las formas irregulares de ondas T dificultan la detección porque alteran el resultado que se espera del procesamiento (13) (16). La Fig. 9, presenta dos casos de onda T irregulares, el primero con una morfología alterada y el segundo con una onda T bifásica.

Para solventar el problema en la detección del final de la onda T, se desarrolló una técnica basada en la aplicación combinada de algunas técnicas de procesamiento digital de señales reportadas en la literatura.

El algoritmo desarrollado para la detección del final de la onda T, se divide en tres etapas. La primera parte del procesamiento, se basa en la técnica propuesta por Zong y Saeed (17). Esta técnica consiste en generar una señal donde se captan las ondas T y se elimina el resto de los componentes de la señal electrocardiográfica. La segunda parte del procesamiento, aplica una técnica similar al pre-procesamiento utilizado por Pan y Tompkins (10), pero utilizado para generar un pulso único que se define sobre el espacio de tiempo de cada onda T. La última parte del procesamiento consiste en aplicar el método de los trapecios, descrito por Seisdedos y col. (13), para ubicar con precisión el final del pulso obtenido, correspondiente al final de la onda T.

La señal electrocardiográfica a procesar, es la obtenida con el procedimiento de corrección de la línea de base y con la estimación de los puntos Q, R y S, descritos en la sección anterior, ver Fig. 8. El primer paso en el algoritmo, se procede a marcar los intervalos de tiempo que solo contienen la onda T de cada latido en el registro. Cada intervalo se define entre 0,15*RR y 0,6*RR segundos después de cada pico R. Se tomaron estos puntos en el tiempo porque se considera que cubre el intervalo que debe contener la onda T, aún en los casos con síndrome de QT largo. Los umbrales temporales se establecen con respecto al intervalo RR, para que la selección de los puntos se realice de forma automática en cada registro.

En el paso siguiente, el algoritmo reemplaza por líneas rectas todos los componentes que no estén contenidos dentro de los intervalos que contienen las ondas T. Seguidamente se eleva al cuadrado todo el registro, para rectificar los posibles componentes negativos de las señales irregulares.

A continuación se aplica un filtro promediador equivalente al descrito por la ecuación 4, pero con una ventana de 60 muestras. Se utiliza una ventana de 60 muestras para que la frecuencia de corte sea de 15 Hz. Esta frecuencia de corte es suficientemente baja para integrar los picos que se forman cuando se procesan ondas con morfologías irregulares y de esta manera obtener un pulso único por cada onda T.

La Fig. 10 presenta una fracción de 1,5 segundos del registro original en comparación con la señal obtenida. El resultado logrado presenta una clara definición sobre la onda T mientras que se atenúan el resto de los componentes.

La tercera etapa del algoritmo, consiste en detectar el punto más pronunciado en el codo final de los pulsos obtenidos. Este procedimiento evalúa el final de cada pulso generado en el procesamiento, aplicando el método de los trapecios, descrito en la sección anterior, ver Fig. 5.

Después de evaluar todos los pulsos del vector, se introduce el factor de corrección que permite eliminar el desplazamiento en el tiempo causado por la aplicación de los filtros. El último paso de este algoritmo consiste en realizar la correspondencia de los marcadores encontrados con la señal original.

No importa que la morfología de las ondas T sea irregular o invertida, el procesamiento siempre genera una forma de onda positiva y con una clara definición del codo final. La Fig. 11, muestra una sección de 4 segundos de señal adquirida de un paciente enfermo, que presenta onda T invertida. Adicionalmente se grafican las marcas que ubican el final de las ondas T, obtenidos automáticamente con el procesamiento.

Los valores de los intervalos QT y ST pueden ser ajustados mediante las ecuaciones de corrección con referencia al ritmo cardiaco. Algunos investigadores han desarrollado diversas ecuaciones de corrección (18). La más utilizada actualmente es la fórmula de Bazett, mostrada en la ecuación 8. Donde RR corresponde al promedio de intervalos RR válidos.

RESULTADOS

La evaluación del software se realizó en el Grupo de Ingeniería Biomédica de la Universidad de los Andes (GIBULA) en la ciudad de Mérida, Venezuela y fue certificada en el Instituto Regional de Bioingeniería (IRB) de la Universidad Tecnológica Nacional (UTN) en la República de Argentina. Las pruebas se realizaron analizando 329 registros de la base de datos marcada para QT y con certificación internacional de Physionet, la cual se encuentra con acceso disponible en Internet (19).

Certificación en la etapa para la detección de los complejos QRS

Debido a que la base de datos Physionet no posee marcadores indicativos de los QRS, las pruebas en esta etapa se realizaron verificando manualmente los latidos detectados en cada registro. Las pruebas se realizaron analizando 20 registros de pacientes sanos y 30 registros de pacientes enfermos. Los resultados presentaron un error promedio de 0,095 % con desviación estándar de 3,15.

El resultado comparativo con el desarrollo de otros autores demuestra la eficiencia del sistema. Como ejemplo se puede citar el trabajo presentado por Pan y Topkins (10) en 1985, en el cual obtienen un margen de error de 0,675 %. En la publicación de Dotsinsky y Stoyanov (11), presentan un error de 0,38 % en cuanto a la especificidad y de 0,96 % en cuanto a la sensibilidad. También se presentan trabajos con niveles de error en la detección muy bajos, pero que involucran procesamientos de alto costo computacional, como detección empleando máquinas de soporte vectorial o análisis utilizando transformada wavelets.

Certificación en la medición de los intervalos QT

El análisis se clasificó sobre dos grupos de registros de la base de datos de Physionet, un grupo de pacientes control y un grupo de pacientes enfermos. El número de pacientes control tomados de la base de datos fue de 51. La muestra de registros analizados de estos pacientes fue de 73. El error diferencial se calculó utilizando la ecuación 9.

Error Diferencial = QTanotado - QTmedido         [9]

Donde el “QTanotado” corresponde al valor dado en la base de datos y el “QTmedido” es el valor obtenido con la aplicación del software desarrollado. La estimación del error porcentual se obtiene a partir del error diferencial, tomando como 100 % el valor anotado por Physionet. El error porcentual se puede calcular con la aplicación de la ecuación 10.

La Tabla 1, muestra una parte de los resultados obtenidos al analizar los archivos de los pacientes control, en contraste con los valores anotados en la base de datos. El valor de “QT medido” corresponde al promedio de todos los intervalos QT en el archivo analizado. La columna siguiente muestra la desviación estándar que presenta la dispersión de las mediciones de QT con respecto al promedio en el mismo archivo. Las dos columnas finales presentan los valores de error obtenidos con la aplicación de las ecuaciones 9 y 10, respectivamente.

Al analizar los resultados de todos los registros de pacientes control se obtuvo un error diferencial promedio de 0,43 ms, con desviación estándar de 9,25. El error porcentual promedio fue de 1,89 % con desviación estándar de 1,48.

El número de pacientes enfermos tomados de la base de datos fue de 113. Los registros en estos pacientes presentan patologías como infarto al miocardio, cardiomiopatía por insuficiencia cardiaca, bloqueo de rama, hipertrofia del miocardio, enfermedad cardiaca valvular, miocarditis y otras. La muestra de registros analizados de estos pacientes fue de 256.

Los errores diferencial y porcentual se calcularon con la aplicación de las ecuaciones 9 y 10 respectivamente. La Tabla 2, muestra una parte de los resultados obtenidos al analizar los archivos de los pacientes enfermos, en contraste con los valores anotados en la base de datos.

Al analizar los resultados los registros de pacientes enfermos se obtuvo un error diferencial promedio de -10,32 ms, con desviación estándar de 22,93. El error porcentual promedio fue de 5,09 % con desviación estándar de 4,91.

Los resultados obtenidos con el procesamiento descrito son comparativamente buenos en relación con los obtenidos por otros investigadores. Como ejemplo se puede citar el procesamiento de Starc y Schlegel (20), publicado en 2006, con el cual obtiene un error promedio de 2%. El procesamiento publicado por Seisdedos et al (13), presenta un error de 2,9 % aplicando el método del trapecio y de 4,9 % aplicando el método de triangulación. De la misma forma que detectando los QRS, también se han publicado métodos con errores muy bajos pero que involucran altos costos de procesamiento. También se debe tomar en cuenta que el procesamiento desarrollado permite detectar el final de la onda T aún en los casos en que la señal está deforme o es invertida, cosa que no es aplicable en muchos de los trabajos revisados.

Certificación en la medición del intervalo ST

Debido a que la base de datos Physionet no posee marcadores indicativos del intervalo ST, no se lograron realizar pruebas independientes para esta sección, sin embargo, dado que la detección del punto S se realiza en condiciones idénticas a la detección del punto Q, se considera que los errores esperados sean los mismos que en la medición de los intervalos QT.

CONCLUSIONES

La medición de los intervalos contentivos entre los diferentes puntos del latido del corazón representa una forma específica de evaluar el trabajo cardiaco. Con una medición precisa se minimizan los errores cometidos por la evaluación de los expertos y por consiguiente se mejora el diagnostico. La incorporación de la etapa de procesamiento al instrumento DIGICARDIAC constituye una herramienta de uso práctico que expande la capacidad del instrumento.

La mayoría de las técnicas de análisis de señales implementadas son tomadas de la experiencia de otros investigadores, la innovación se destaca en la interrelación de estas técnicas aplicadas con el propósito de generar un algoritmo robusto y que mejore los índices de errores de la literatura consultada.

Cabe destacar que las técnicas implementadas son de bajo costo de procesamiento. Esto permite que el procesamiento completo se ejecute en muy poco tiempo, aproximadamente 30 segundos en analizar un registro con 300 complejos QRS. Lo que hace pensar en la posibilidad de implementar este software en tiempo real.

AGRADECIMIENTOS

Se agradece a la Universidad de Los Andes y a sus instituciones como el Grupo de Ingeniería Biomédica (GIBULA), por el apoyo prestado. Se agradece al Instituto Regional de Bioingeniería (IRB) de la Universidad Tecnológica Nacional de la República Argentina por su colaboración en la certificación del instrumento. También se agradece a FONACIT, a CENDITEL y al CDCHT, por permitir que este proyecto sea factible.

REFERENCIAS:

1) Pan American Health Organization (PAHO). Índice de mortalidad; 2007. Disponible en: www.paho.org. (Consultado Septiembre, 2010).        [ Links ]

2) González J. Tutorial de Electrocardiograma. España: Publicaciones del Servicio de Cardiología UCC, Complejo Hospitalario Universitario de Santiago de Compostela; 2008.        [ Links ]

3) Ganong W. Fisiología Médica, Manual Moderno. 17 ed. México, D.F.: McGraw- Hill; 1999.        [ Links ]

4) Centro de información cardiovascular. Anatomía del corazón; 2007. Disponible en: http://www.texasheartinstitute.org/. (Consultado Junio, 2009).        [ Links ]

5) Lanjewar P, Pathak V, Lokhandwala Y. Issues in QT interval measurement. Indian Pacing and Electrophysiology Journal. 2004; 4 (1): 156-161.        [ Links ]

6) Dugarte N, Medina R, Rojas R. Desarrollo del Prototipo de un Sistema de Adquisición de Datos para la Digitalización de la Señal Electrocardiográfica de Alta Resolución. Rev. Inst. Nac. Hig. "Rafael Rangel”. 2012; 43 (2): 28-38.        [ Links ]

7) Dugarte N, Medina R, Rojas R, Dugarte E. Bioamplificador Multicanal para la Adquisición de la Señal ECGAR, del Prototipo DIGICARDIAC. Rev. Inst. Nac. Hig. "Rafael Rangel”. 2014; 45.        [ Links ]

8) Dugarte N, Medina R, Rojas R. Open Source Cardiology Electronic Health Record Development for DIGICARDIAC Implementation. 11th International Symposium on Medical Information Processing and Analysis (SIPAIM 2015). November 2015; Cuenca, Ecuador.        [ Links ]

9) Dugarte N, Medina R, Rojas R, Álvarez A. Certificación del Sistema ECGAR para su Aplicación en Centros de Salud. 4to Congreso Iberoamericano de Estudiantes de Ingeniería Eléctrica “IV CIBELEC 2010”. Art. IB-01. Mayo 2010; Mérida, Venezuela.        [ Links ]

10) Pan J, Topkins W. A Real Time QRS Detection Algorithm. IEEE Transactions on Biomedical Engineering. 1985; 32 (3): 230-236.        [ Links ]

11) Dotsinsky I, Stoyanov T. Ventricular beat detection in single channel electrocardiograms. BioMedical Engineering OnLine. 2004; doi: 10.1186/1475- 925X-3-3.        [ Links ]

12) Cuadros J. Procesamiento avanzado de la señal electrocardiográfica de pacientes chagásicos. Tesis de Maestría del Grupo de Ingeniería Biomédica. Mérida, Venezuela: Facultad de Ingeniería Eléctrica, Universidad de Los Andes; 2012.        [ Links ]

13) Seisdedos C, Neto J, Miranda M, Moreno E, Oliveira R. Detección del final de la onda T en el ECG mediante áreas de trapecios. 21º Congreso Brasilero de Ingeniería Biomédica CBEB. Brasil; 2008: 1703-1706.        [ Links ]

14) Laguna P, Sornmo L. Biomedical Signal Processing in Cardiac & Neurological Applications - Solutions Manual. España: Academic Press, Elsevier; 2005.        [ Links ]

15) Portillo M. Electrocardiografía: Técnica de interpretación Básica. Mérida, España: Hospital del S.E.S; 2011.        [ Links ]

16) Lanjewar P, Pathak V, Lokhandwala Y. Issues in QT interval measurement. Indian Pacing and Electrophysiology Journal. 2004; 4 (1): 156-161.        [ Links ]

17) Zong W, Saeed M, Heldt T. A QT Interval Detection Algorithm Based on ECG Curve Length Transform. Computers in Cardiology Journal. 2006; 17 (20): 377- 380.        [ Links ]

18) Lanza G. Fórmulas para el QT corregido y consideraciones clínicas. Gaceta Médica de Caracas. 2008; 116 (3): 224-234.        [ Links ]

19) Hans K, Bousseljot R, Kreiseler D, Schmitz L. The ptb diagnostic ecg database; 2011. Disponible en: http://www.physionet.org/physiobank/database/ptbdb/. (Consultado Mayo, 2013).        [ Links ]

20) Starc V, Schlegel T. Real-time multichannel system for beat-to-beat QT interval variability. Journal of Electrocardiology. 2006; 39: 358–367.        [ Links ]