El método de investigación de Arquímedes de Siracusa: Intuición, mecánica y exhaución

Archimedes of Syracuse’s Investigative Method: Intuition, Mechanics and Exhaustion

Ángel Molina

Universidad del Zulia Maracaibo - Venezuela

Resumen

El presente estudio pretende determinar el esquema básico del método de investigación de Arquímedes de Siracusa, así como las implicaciones históricas y científicas del mismo. Se evaluarán para ello los dos procedimientos fundamentales de dicho método: la aplicación de un novedoso método heurístico de naturaleza mecánica y la posterior confirmación de sus resultados mediante el método de exhaución.

Palabras clave: Arquímedes, método heurístico, demostración, exhaución, cálculo infinitesimal.

Abstract

In this paper the basic scheme of Archimedes of Syracuse’s investigative method is presented, as well as its historical and scientific implications. For this purpose the two fundamental procedures of such method will be evaluated: the application of an innovative heuristic method of mechanical nature, and the further proof of such results through the exhaustion method.

Key words: Archimedes, heuristic method, proof, exhaustion, infinitesimal calculus.

Recibido: 09-12-07 Aceptado: 18-04-08

I. Introducción

Nacido hacia el año 287 a. C., en la colonia griega de Siracusa, Arquímedes tiene un puesto privilegiado dentro de la historia de la ciencia, como destacado matemático, físico e ingeniero. Se le suele ubicar, junto con Newton y Gauss, como uno de los tres matemáticos más grandes de la historia. Su fama le ha hecho protagonista de numerosas anécdotas y leyendas, registradas por famosos historiadores antiguos como Plutarco y Polibio. Su muerte acontece en el año 212 a. C. en su ciudad natal, luego de que su contribución a la defensa de la misma, con sus ingeniosos artefactos, fuera insuficiente: Siracusa fue tomada por el cónsul romano Marcelo en un ataque sorpresa, después de una ceremonia religiosa dedicada a la diosa Artemisa. La versión más recurrente de la muerte de Arquímedes, presenta al genio ensimismado en la resolución de un problema geométrico, ignorando las órdenes de un soldado romano, lo cual provocó la ira de éste, quien con su espada quitó la vida al célebre matemático.

Veamos la versión que nos ofrece Plutarco con relación a este episodio y a la consternación que provocó en Marcelo:

“Mas lo que principalmente afligió a Marcelo fue lo que ocurrió con Arquímedes: hallábase éste casualmente entregado al examen de cierta figura matemática, y, fijos en ella su ánimo y su vista, no sintió la invasión de los Romanos ni la toma de la ciudad. Presentósele repentinamente un soldado, dándole orden de que le siguiese a casa de Marcelo; pero él no quiso antes de resolver el problema y llevarlo hasta la demostración; con lo que, irritado el soldado, desenvainó la espada y le dio muerte. Otros dicen que ya el Romano se le presentó con la espada desnuda en actitud de matarle, y que al verle le rogó y suplicó que se esperara un poco, para no dejar imperfecto y oscuro lo que estaba investigando; de lo que el soldado no hizo caso y le pasó con la espada. Todavía hay cerca de esto otra relación, diciéndose que Arquímedes llevaba a Marcelo algunos instrumentos matemáticos, como cuadrantes, esferas y ángulos, con los que manifestaba a la vista la magnitud del Sol, y que dando con él los soldados, como creyesen que dentro llevaba oro, le mataron. Como quiera, lo que no puede dudarse es que Marcelo lo sintió mucho, que al soldado que le mató de su propia mano le mandó retirarse de su presencia como abominable, y que habiendo hecho buscar a sus deudos los trató con el mayor aprecio y distinción.”¹

Bastando los datos biográficos previos para conocer un poco del autor y su contexto, adentrémonos en el tema principal de nuestro trabajo, esto es, los elementos metodológicos del proceder investigativo de Arquímedes.

El método de investigación del científico siracusano generó gran curiosidad entre los matemáticos y pensadores con el correr de los siglos, sobre todo en el Renacimiento, surgiendo muchas especulaciones al respecto. Sólo en 1906 son disipadas en buena medida las dudas con relación a dicho método, cuando es descubierto por el filólogo e historiador danés Johan Ludvig Heiberg, en un palimpsesto de Estambul, un nuevo texto de Arquímedes, denominado Del método relativo a los teoremas mecánicos, para Eratóstenes.²

Este texto, como su título deja entrever, contiene una propuesta de investigación, inédita para su época: inclusión de consideraciones mecánicas en el razonamiento de un problema geométrico y en su argumentación; inclusión que nos permite anticipar un resultado plausible, verosímil. Tal resultado es demostrado posteriormente con todo el rigor que amerita para ser aceptado plenamente como verdadero. Así se dirige Arquímedes a Eratóstenes en el preámbulo de dicho tratado:

“Reconociendo, como digo, tu celo y tu excelente dominio en materia de filosofía, amén de que sabes apreciar, llegado el caso, la investigación de ciertas cuestiones matemáticas, he creído oportuno confiarte por escrito, y explicar en este mismo libro, las características propias de un método según el cual te será posible abordar la cuestión de ciertas cuestiones matemáticas por medio de la mecánica. Algo que, por lo demás, estoy convencido, no es en absoluto menos útil en orden a la demostración de los teoremas mismos. Pues algunos de los primeros que se me hicieron patentes por la mecánica, recibieron luego demostración por geometría, habida cuenta de que la investigación por ese método queda lejos de una demostración; como que es más fácil construir la demostración después de haber adquirido por ese método cierto conocimiento de los problemas, que buscarla sin la menor idea al respecto.”³

En consonancia con esto, examinaremos los dos pasos o estadios fundamentales del método de Arquímedes, la evaluación mecánica preliminar del problema y la demostración por convergencia o exhaución.

II. El método heurístico de evaluación mecánica

Luego del preámbulo a su escrito, el autor enumera una serie de teoremas, en su mayoría demostrados en su obra Sobre el equilibrio de los planos⁴, mediante los cuales presenta la noción de centro de gravedad, con la cual trabajará al abordar los diversos casos a lo largo del tratado. Tales teoremas servirán de base teórica, constituyendo los presupuestos mecánicos sobre los cuales se desarrollará toda la labor posterior.

Se parte, en los problemas de determinación de áreas o volúmenes, de comparaciones con otras áreas o volúmenes previamente conocidos, cotejándose en el procedimiento y respectivo diagrama éstos con relación a aquéllos.

A modo de ejemplo, podemos describir de manera muy general la resolución del primero de los problemas, consistente en determinar el área de un segmento parabólico. En el mismo, se compara el área que se pretende hallar, con la de un triángulo inscrito en ella, de igual base. A su vez, se traza un triángulo rectángulo que contiene a las dos figuras anteriores. Posteriormente, se trazan una serie de rectas en las figuras con la intención de generar un escenario en el cual se vayan evidenciando propiedades geométricas y de proporción, asentadas en los Elementos de Euclides, y propiedades mecánicas y geométricas ya demostradas en obras anteriores del propio Arquímedes. El procedimiento se expresa gráficamente de la siguiente forma⁵:

Así, se consideran rectas trazadas como palancas, y puntos de intersección como baricentros (centros de gravedad) o fulcros (momentos): “Imaginemos que es una palanca cuyo punto medio es K” o “el punto K es el centro de gravedad de la suma de ambos pesos”, refiriéndose esta última aseveración a los pesos de los segmentos TH y M⁶. Finalmente, en función de algunos teoremas de obras previas del siracusano, como Sobre el equilibrio de los planos y Sobre la cuadratura de la parábola, así como de otros fijados en los Elementos de Euclides, y tras varias operaciones que no vienen al caso, el autor concluye que el área del segmento parabólico es cuatro tercios del triángulo inscrito.

Lo más interesante y novedoso de este método heurístico de evaluación mecánica se revela con la consideración por parte del autor de “las figuras planas como constituidas por el conjunto de todas las rectas en ellas trazadas paralelamente a una cierta dirección, y a las figuras sólidas como «llenas» de sus secciones planas paralelas a una determinada posición”⁷. Esta suposición o, más bien, intuición, carente de rigor demostrativo, es la base del cálculo integral, el cual vendría a ser ideado y desarrollado muy posteriormente por Newton y Leibniz en la segunda mitad del siglo XVII.

Sin embargo, es preciso recalcar que las intuiciones que sustentan el cálculo integral, coincidentes en buena medida con las que sustentan el método mecánico arquimedeo, se generaron independientemente de la propuesta del siracusano. Recordemos que la obra donde expone Arquímedes el método mecánico —Del método relativo a los teoremas mecánicos, para Eratóstenes— es redescubierto apenas en 1906. Por otra parte, el método de exhaución y la eficiencia con la cual es utilizado por Arquímedes sí sirvió de inspiración para grandes matemáticos a partir del Renacimiento, influyendo en una de las grandes aportaciones de la Modernidad: el cálculo diferencial e integral.

Con relación a la visión arquimedea de las formas geométricas, podemos apreciar, en el caso previamente descrito del segmento parabólico, cómo se entienden, en un momento del procedimiento, las figuras, en tanto planas, como compuestas de rectas paralelas:

“Ahora bien, como las rectas trazadas en el triángulo ZA constituyen el propio triángulo ZA y los segmentos tomados en la sección del mismo modo que O componen el segmento AB, por ende el triángulo ZA, manteniéndose en su sitio, equilibrará respecto del punto K al segmento de la sección colocado con su centro de gravedad en Q de manera que el centro de gravedad de la suma de ambos sea el punto K”⁸

Para ponderar adecuadamente el nivel de novedad y rebeldía intelectual de Arquímedes, es preciso tener en consideración el hecho de que en su época se consideraba inviolable el estatus de “prioridad metódica” de la geometría, así como su “autonomía teórica”, atentando contra ambas la introducción de las consideraciones estáticas ya citadas⁹. Y es que lo común era que de la matemática pura se descendiera a sus aplicaciones en otras esferas del conocimiento de índole menos teórica y más práctica, siendo la mecánica una de éstas. Y esto las veces que se llevaba a cabo tal descendimiento: vale recordar que el prejuicio platónico, aún presente en la ciencia alejandrina, de perseguir el conocimiento de las Ideas matemáticas y metafísicas, adquiría en ocasiones un carácter de radical exclusividad, desdeñándose las aplicaciones concretas del conocimiento adquirido. El acto de Arquímedes de fisicalizar la geometría podía perfectamente ser considerado una heterodoxia imperdonable en la tradición matemática griega.

Asimismo, debe tenerse en cuenta que la mecánica no tenía el estatus de ciencia en aquel tiempo, sólo representaba un conocimiento técnico. Rodolfo Mondolfo señala, respecto al infortunado impacto del Método de Arquímedes en la antigüedad: “Puede agregarse que probablemente la mayoría de los intelectuales de la antigüedad no reconocieron la fecundidad del Método relativo a los teoremas mecánicos por menospreciar todo lo que tenía relación con lo mecánico y el trabajo manual”¹⁰.

Sin embargo, la escala jerárquica de las ciencias y los dogmas imperantes en la época del matemático de Siracusa no representaron un impedimento para utilizar su propuesta metodológica, apuntando firme e ingeniosamente hacia el desarrollo del conocimiento científico. Por eso dice E. T. Bell: “Este es uno de sus títulos de mente moderna: utilizó todas y cada una de las cosas que se sugirió a sí mismo como arma para atacar sus problemas”¹¹. No en vano es considerado, tal como se adelantó en una nota previa, el legítimo fundador de la mecánica como disciplina científica.

Pese a lo previamente expuesto, es preciso señalar que Arquímedes respetó en buena medida los procedimientos aceptados por la comunidad científica de su tiempo, razón por la cual no se limitó en la generación de sus teoremas al método mecánico. No en vano le llamamos heurístico. Este método vendría a pertenecer, respetando el contexto alejandrino, a lo que se denomina, en términos epistemológicos modernos, contexto de descubrimiento. Esto es, la fase creativa e informal del método científico, en la cual se inventa la hipótesis.

Para que cualquier descubrimiento que hiciese Arquímedes fuera aceptado plenamente como verdad científica por sus colegas, era imprescindible algún método de demostración rigurosamente geométrico. En el científico de Siracusa dicho método vendría a ser el método de convergencia o exhaución. Éste correspondería, continuando la categorización epistemológica previa, al contexto de justificación; es decir, la fase de demostración de la hipótesis asumida, procedimiento que permite validar la misma.

Esta distinción entre contexto de descubrimiento y contexto de justificación es obra del filósofo alemán neopositivista Hans Reichenbach¹². Independientemente de que estemos a favor o en contra de la misma, ésta funciona excelentemente bien para apreciar con claridad los dos estadios en el método científico del siracusano.

En consonancia con las ideas expuestas, relativas a los niveles de respeto e irrespeto de Arquímedes por las convenciones metodológicas de la época, debemos aclarar que es un problema aún discutido. No en vano, autores como Sergio Toledo Prats generan agudas preguntas como la siguiente: “¿Ahora bien, necesitaba Arquímedes probar mediante la geometría lo que ya había probado mediante la mecánica para asegurarse de la certeza de sus resultados o sólo para que fueran aceptados?”¹³. El autor se inclina por la primera opción, recalcando la prioridad metódica de la geometría sobre la mecánica que hemos apuntado previamente.

Consideramos que la misma es una respuesta responsable, apegada al contexto en el cual vivió el siracusano. A su vez, afirmamos que aceptar dicha conclusión no se traduce necesariamente en restarle originalidad y genialidad a este científico: la propuesta mecánica no pierde validez e innovación por el hecho de que no sea suficiente por sí misma para generar un resultado científicamente seguro. Sólo nos basta prestar atención a las ya citadas palabras de Arquímedes al presentar su propuesta metodológica: ésta proporciona un resultado muy plausible y allana el camino para la posterior demostración. Más adelante, cuando expongamos las implicaciones del método de exhaución de Arquímedes, volveremos a tratar el punto del respeto al contexto histórico.

El método de exhaución

Insistimos: el método heurístico previo no basta para cimentar un teorema: hace falta una demostración geométrica, la cual ostenta el rigor necesario para ello. El método de demostración recurrente en Arquímedes es el llamado de exhaución¹⁴. Este consiste, en términos generales, en una aproximación entre figuras geométricas conocidas, inscritas y circunscritas, sobre otra por conocer, de manera que la diferencia entre unas y otras sea tan indeterminadamente pequeña que se consideren equivalentes. En tal procedimiento interviene un razonamiento lógico que garantiza la verdad de la aserción geométrica: la reducción al absurdo. Así, la negación de la equivalencia entre las áreas ocasiona una contradicción lógica insoluble, lo cual nos obliga, en aras de mantener el procedimiento lógicamente coherente, a aceptarla como verdadera.

El método previamente expuesto tiene una interesante historia. Suele apreciarse el germen o noción primigenia del mismo en el sofista Antifón (480-411 a.C.). Éste, como muchos otros pensadores griegos, pretendió resolver el famoso problema de la cuadratura del círculo. El mismo, que consistía en construir un cuadrado de área idéntica a un círculo, supuso una dificultad insoluble para la geometría de aquel entonces.

Buena parte de la dificultad tiene relación con la irracionalidad del valor de la relación entre la circunferencia del círculo y su diámetro, conocida como p. Recordemos que un número irracional es una fracción decimal con dígitos que no se repiten consecutivamente después de la coma y que se prolongan infinitamente. Así, p es 3,14159..., hasta el infinito. Más adelante veremos la importancia que tiene Arquímedes en la estimación de este valor. Otros ejemplos de números irracionales son algunas raíces cuadradas, como Ö2 o Ö3. La imprecisión de p dificultó a los griegos el tratamiento del círculo, más aún, el intento de igualar su área con la de un cuadrado. Sólo en 1882 se demuestra la imposibilidad de la resolución de dicho problema con el uso exclusivo de una regla y un compás, por obra del matemático alemán Ferdinand Lindemann¹⁵.

Para la resolución del comentado problema, Antifón propuso la inscripción de un triángulo equilátero sobre el cual se trazan triángulos isósceles. A su vez, sobre los lados de tales triángulos se forman nuevos triángulos, originando este proceso continuado una sucesión de polígonos de creciente número de lados, aproximándose proporcionalmente al área del círculo, con el fin de agotar la diferencia entre ellos:

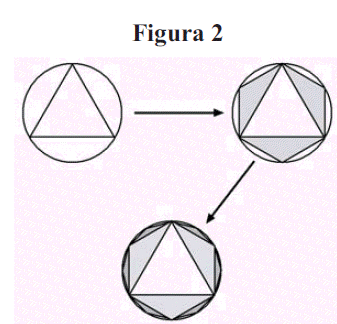
Se procede finalmente a equiparar el área del polígono de varios lados con la de un cuadrado, en función de su condición de polígonos regulares. Más tarde, Brisón de Heracles no sólo inscribió polígonos en el círculo para tales fines, sino que también los circunscribió¹⁶:

Sin embargo, suele haber consenso entre los historiadores de la matemática en atribuir concretamente a Eudoxo de Cnido (408-355 a. C.), matemático contemporáneo a Platón, la invención del comentado método. Así dice, por ejemplo, Florian Cajori, refiriéndose al célebre matemático: “Él hace un frecuente y diestro uso del método de exhaución, del cual fue con toda probabilidad el inventor”¹⁷. Es este matemático quien le proporciona carácter demostrativo al procedimiento que previamente era de índole meramente intuitiva, lo cual logra con la inclusión de la reducción al absurdo, razonamiento lógico explicado anteriormente.

Es pertinente resaltar la importancia metodológica que tuvo el método de exhaución en el tratamiento de problemas geométricos en la Grecia Clásica y en Alejandría. El mismo resuelve en buena medida las dificultades inherentes a la comprensión del concepto de infinito y sus consecuencias en el tratamiento de las figuras geométricas, ya que permite una evaluación finita y rigurosa de problemas que en cierto sentido involucran aspectos asociados con la infinitud. Dicho concepto, sobre todo luego de las famosas paradojas de Zenón de Elea (490-430 a. C.), constituyó un verdadero problema para los sabios de la antigüedad.

Recordemos brevemente las paradojas y sus implicaciones, principalmente en la geometría. La finalidad de ellas es demostrar la imposibilidad lógica del movimiento en función de la concepción del espacio y el tiempo en Grecia, la cual consideraba a éstos como infinitamente divisibles. Tales paradojas son la del estadio, la de Aquiles y la tortuga, la de la flecha disparada y la de las filas en movimiento¹⁸. Explicar brevemente la más célebre de ellas –Aquiles y la tortuga– bastará para evidenciar los problemas que acarrean las paradojas en conjunto.

La paradoja nos dice que, en una hipotética carrera, el veloz Aquiles jamás podrá alcanzar a la lenta tortuga si esta última sale con alguna ventaja respecto a aquél, ya que cuando Aquiles llegue a un punto, digamos A, en el cual estuvo la tortuga breves instantes antes, la misma estará en otro punto B, más avanzado, y así sucesivamente ad infinitum, aunque Aquiles llegue a estar detrás de la tortuga por una ínfima diferencia. Si no se quiere caer en tales paradojas, es preciso negar la infinitud en el espacio y en el tiempo.

La geometría, como rama de la matemática encargada de las figuras, las cuales están en un espacio determinado, se ve afectada por las implicaciones de los cuestionamientos de Zenón. Todo procedimiento matemático que incluyera algún tipo de procedimiento asociado a la infinitud carecía de rigor y veracidad. La infinitud no era explicable de manera diáfana por los griegos, razón por la cual procuraron mantenerse en el cómodo ámbito finito de los problemas matemáticos. Burton dice respecto a este punto:

“Zenón fue en parte responsable del curso posterior del pensamiento matemático griego. En el fondo, sus famosas paradojas estuvieron relacionadas a la aplicación de procesos infinitos en geometría. Debido a la incapacidad de los geómetras griegos de responderle claramente, ellos proscribieron de las matemáticas el uso de métodos que envolvieran el concepto de infinito e hicieron un “horror del infinito”, parte de la tradición matemática griega”¹⁹.

Es en tales circunstancias donde se evidencia el valor que cobra el método de exhaución. Si el agotamiento de la diferencia entre las áreas que entran en juego se admite cuando el valor de dicha diferencia es ínfima, inferior a cualquier magnitud previamente dada, ¿no nos encontramos en un modo enmascarado de infinitud?, ¿Acaso no sería equivalente, al menos en términos prácticos, hablar de un valor infinitamente pequeño y por lo tanto insignificante? Consideramos válido afirmar que, a través de dicho método, se hace una aproximación cautelosa a la infinitud. Aproximación que no pasa de ello, de mera aproximación. Haciendo referencia al método de exhaución y a su inventor, dice Bell: “Eudoxo demostró que no necesitamos aceptar la ‘existencia’ de ‘cantidades infinitamente pequeñas’. Para los propósitos de un matemático es suficiente poder alcanzar una magnitud tan pequeña como queramos por la división continuada de una magnitud dada”²⁰.

Quizá el lector se pregunte, en función de lo previamente expuesto, qué relación tiene Arquímedes con el método de exhaución. Retomemos entonces al matemático de Siracusa, en quien no sólo es recurrente el uso de tal método, sino que hace un uso más refinado que su inventor Eudoxo, especialmente como complemento riguroso del método heurístico mecánico que ocupa un lugar previo en su proceso de investigación. Por otra parte, no es precisamente en su recurrencia que tal método adquiere protagonismo dentro del proceder científico del siracusano: es en la potencia que tiene en manos de Arquímedes donde tal método exhibe su capital importancia. Como dice Cajori: “Con Euclides y sus predecesores, el método de exhaución sólo era el medio de probar proposiciones que debieron haber sido vistas y creídas antes de ser probadas. Pero en manos de Arquímedes se volvió un instrumento de descubrimiento”²¹.

Luis Vega clasifica dos tipos de exhaución en Arquímedes: aproximación y acotación de equivalencia. A su vez, expone de la siguiente manera la acotación de equivalencia, principal tipo de exhaución presente en el trabajo de Arquímedes:

“La compresión, o acotación de equivalencia, puede considerar, a su vez, diferencias o razones en orden decreciente. En ambos casos se parte de inscripciones y circunscripciones sucesivas de figuras regulares dentro y fuera, respectivamente, de la figura cuya área o volumen se desea establecer. Cuando se consideran diferencias, el área o volumen de las figuras inscritas o circunscritas crece o decrece regularmente hasta que la diferencia entre ellos y el área o volumen buscados sea menor que cualquier magnitud previa dada. En el otro caso se consideran razones entre polígonos de forma similar”²².

La aproximación se encuentra menos presente en la obra del matemático, aunque su fundamento es el mismo. Consiste en la inscripción de figuras geométricas de manera sucesiva dentro del área que se desea determinar, convergiendo la sumatoria de las mismas a dicha área.²³

No hay mejor manera de comprender el funcionamiento de un procedimiento que con un ejemplo en el cual se aplique, y uno de los mejores para este caso se nos presenta en el resultado de Arquímedes de uso más cotidiano: la estimación precisa del valor de la relación entre la circunferencia de un círculo y el diámetro del mismo, mejor conocida como p.

Este aporte se encuentra en su obra Sobre la medida del círculo²⁴. La misma se compone de tres proposiciones, siendo la última de ellas la expresión definitiva de la estimación del valor de p; dicha proposición representa el resultado de las dos proposiciones previas y sus correspondientes demostraciones. Explicaremos en términos muy generales el proceso que llevó a cabo el célebre matemático para la determinación de este valor.²⁵

Como se podría anticipar en función de las descripciones previas del método, se procede a inscribir y circunscribir en un círculo de diámetro 1, polígonos regulares, los cuales en principio serán hexágonos. La explicación de la elección de dichas figuras nos la da Burton: “De todos los polígonos regulares, el hexágono es el que se puede inscribir más fácilmente”²⁶. Veamos el procedimiento de inscripción y circunscripción:

Así, tales polígonos van aumentando progresivamente su cantidad de lados mediante continuas bisecciones de arcos, llegando a tener 16 veces la cantidad de lados que los hexágonos primigenios, esto es, 6 x 16 = 96. De esta manera los perímetros de los polígonos, uno inscrito y otro circunscrito, que por abstracción algebraica se consideran de n lados, se aproximan en gran medida a la circunferencia, tienden a ella. Tendencia que se considera equivalencia: las tres figuras tienen un valor común, el de la circunferencia, ya que los polígonos en cierto modo comprimen a la misma, igualándose con ella.

Finalmente, se recurre a una reducción al absurdo, evidenciando las contradicciones lógicas de suponer las dos conclusiones posibles distintas a la igualación, esto es, que el área de la figura corresponde a la magnitud de la figura circunscrita o inscrita, mayor o menor a la que se pretende demostrar.

Todo este proceso da origen, como previamente se anticipó, a la proposición 3, que es la siguiente: “la circunferencia de un círculo excede tres veces su diámetro, con una parte que es menor que 1/7 pero mayor que 10/70 del diámetro”²⁷; lo que es equivalente: 3 10/71< p < 3 1/7; en números decimales: 3,14084507...< p< 3,14285714...

Es pertinente señalar cómo se evidencia, una vez más, la oposición de Arquímedes a los dogmas científicos de su tiempo. Y es que en la evaluación de un problema estrictamente geométrico, hace uso de los números, pertenecientes al campo de la aritmética. Este aspecto provocó que el matemático siracusano fuera blanco de crítica incluso por matemáticos de la época moderna, de línea ortodoxa.²⁸

Se hace casi inevitable la asociación de este método con el del cálculo infinitesimal y su noción de límite. Y es que el empleado por Arquímedes constituye un precedente, un paso previo a lo cual vendría a ser el novedoso procedimiento infinitesimal de la Edad Moderna. Así, por ejemplo, nos dice Karl Fink, acerca del método de exhaución: “Éste y muchos otros resultados fueron obtenidos por Arquímedes mediante el método de exhaución, el cual usualmente entre los antiguos tomó el lugar de la integración moderna”²⁹. En el mismo orden de ideas, señala Cajori: “En nuestros días, materias de este tipo se vuelven sencillas con el uso del cálculo infinitesimal. En su lugar, los antiguos utilizaron el método de exhaución”³⁰.

Asimismo, es una opinión comúnmente aceptada que Arquímedes estuvo muy cerca de una investigación del tipo infinitesimal, al punto que algunos, como E. T. Bell, –a nuestro modo de ver, imprudentemente, sin evaluarlo en su debido contexto– considera que “anticipándose a Newton y Leibniz en más de 2000 años inventó el Cálculo integral”³¹. Y es que ya se ha dicho que los matemáticos antiguos procuraban permanecer dentro de los ámbitos de la finitud, ya fuera por recelo al infinito o por precisión científica. Por lo tanto, estamos plenamente de acuerdo con Burton cuando, explicando el uso del método de exhaución en su aplicación para el cálculo del valor de p, asevera:

“Aunque se tienda a considerar al círculo como el límite de los polígonos inscritos (o circunscritos), como el número de lados incrementados indefinidamente, no es un paso directo al límite. Los matemáticos griegos nunca pensaron el proceso como continuado por un número infinito de pasos; ellos sólo consideraron llevarlo a cabo en escenarios finitos hasta un grado de precisión deseado”³².

Por otra parte, existe una limitante de distinta índole: el sistema de simbolización matemática griega era muy dificultoso, imperfecto para tratar con operaciones de tipo infinitesimal, pese a que el propio Arquímedes realiza avances enormes desde el punto de vista aritmético con su obra El Arenario.³³

En la misma, Arquímedes propone un novedoso sistema de numeración que permite contar el número de granos de arena que podría dar cabida la Tierra, la esfera celeste, y aún más. Con el mismo, le permite al limitado sistema de numeración griego trabajar con números muy grandes, ascendiendo a los niveles de infinitud de la serie de los números naturales de modo similar a nuestro sistema de numeración³⁴. Sin embargo, la intención de dicho sistema es precisamente finitizar las cantidades enormes, permitir establecer con exactitud números muy grandes. Su carácter de infinitud, así como en el caso de nuestro sistema numérico, radica en la posibilidad de continuar contabilizando números en escala ascendente ad infinitum, de manera recurrente. A diferencia de este logro aritmético, en el ámbito de la infinitud espacial o geométrica no se puede advertir un resultado tan sólido.

En este sentido, el campo de la geometría carecía de métodos unívocos y plenamente satisfactorios para el tratamiento de magnitudes infinitesimales. Los antiguos generaron y comprendieron el concepto de infinito, pero sólo los modernos estuvieron preparados para hacer uso de él, para manipularlo plenamente. En este orden de ideas, señala Cajori:

“Euclides, Arquímedes, y Apolonio llevaron a la geometría a un alto estado de perfección tanto como quizás pudo ser llevada sin introducir primero algún método más general y más poderoso que el antiguo método de exhaución. Fue necesario un simbolismo más conciso, una geometría cartesiana y un cálculo infinitesimal. La mente griega no estaba adaptada para la invención de métodos generales.”³⁵

Conclusiones

A modo de síntesis, podemos aseverar que el método de Arquímedes pasa por dos estadios: 1) el método heurístico mecánico, no riguroso, el cual se sostiene sobre postulados geométricos euclidianos y postulados propios de índole mecánica; y 2) el método de exhaución, que posee rigor demostrativo por incluir una reducción al absurdo, procedimiento lógico utilizado en aquel entonces para evidenciar la verdad de una conclusión matemática dada. En ambos casos el matemático siracusano se aproxima a procedimientos infinitesimales, similares al futuro cálculo diferencial e integral, anticipando unos 19 siglos las nociones –y sólo ellas– que servirían de inspiración a los genuinos descubridores de tales procedimientos.

Asimismo, Arquímedes representa un ejemplo de la capacidad inventiva e innovadora del espíritu científico. Obviando los elementos negativos de la tradición científica alejandrina, propuso y perfeccionó, con la autoridad y originalidad que le caracterizaban, métodos para el desarrollo de la ciencia de su tiempo. Autoridad que posee el que se reconoce como genio y como correcto en su proceder. ¿Y cuál mejor ámbito que el científico, con sus requisitos de coherencia lógica y verificabilidad, para garantizar la correspondencia con la realidad de las aseveraciones probablemente en principio sólo intuidas, y la aplicación satisfactoria de los resultados conseguidos?

Referencias

1. ARQUÍMEDES: El método, Alianza Editorial, Madrid, 1986.        [ Links ]

2. ARQUÍMEDES: Tratados I EUTOCIO: Comentarios, Gredos, Madrid, 2005.         [ Links ]

3. ARMSTRONG, A: Introducción a la Filosofía Antigua, EUDEBA, Buenos Aires, 1993.        [ Links ]

4. BELL, Eric: Men of mathematics, Fireside, New York, 1965.        [ Links ]

5. BURTON, David: The History of Mathematics: An Introduction, McGraw-Hill, E.U.A., 2005.        [ Links ]

6. CAJORI, Florian: History of Mathematics, Macmillan, Boston, 1894, edición electrónica, disponible en: http://ia301112.us.archive.org/3/items/historyofmathema001062mbp/ historyofmathema001062mbp.pdf, p. 26-28 (última consulta: 18-02-08)        [ Links ]

7. CAJORI, F.: A History of mathematics, Chelsea Publications, New York, 1991.        [ Links ]

8. FINK, Kart: A brief history of mathematics, Chicago, 1900, p. 200, edición electrónica, disponible en: http://www.archive.org/details/ABriefHistoryOfMathematics (última consulta: 18-02-08).        [ Links ]

9. GIBSON, Ian, (ed.), Protagonistas de la civilización: Arquímedes, Editorial Debate, Madrid, 1983.        [ Links ]

10. HEATH, Thomas: The Works of Archimedes, Dover Publications, Mineola, 2002. Hay edición electrónica disponible en: http://www.archive.org/details/worksofarchimede029517mbp (última consulta: 18-02-08).        [ Links ]

11. HEIBERG, E.: Archimedis opera omnia cum commentariis Eutocii, Teubner, Leipzig, 1881.        [ Links ]

12. KIRK, A. y RAVEN, M.: Los filósofos presocráticos, Gredos, Madrid, 1979.        [ Links ]

13. MONDOLFO, Rodolfo: El infinito en el pensamiento de la antigüedad clásica, Eudeba, Buenos Aires, 1971.        [ Links ]

14. PLUTARCO: Vidas Paralelas, Tomo II, edición electrónica disponible en: http//www.librosclasicos.org/ buscador/search.php?kw=plutarco, p. 373-374 (última consulta 12-01-07).        [ Links ]

15. Plutarco, Vidas paralelas, ed. de A. Ranz Romanillos, Vergara, Barcelona, 1968.        [ Links ]

16. VEGA, Luis: “Introducción” a Arquímedes: El método, Alianza Editorial, Madrid, 1986.        [ Links ]

17. REICHENBACH, Hans: Experience and Prediction, University of Chicago Press, Chicago, 1938.        [ Links ]

18. TOLEDO PRATS, Sergio: “El significado filosófico de las matemáticas en la cultura griega” en: MONTESINOS SIRERA, José (ed.): Symposium Arquímedes, Fundación Canaria Orotava de Historia de la Ciencia y Max Plack Institute for the History of Science, edición electrónica, disponible en: www.mpiwg-berlin.mpg.de/Preprints/P239.PDF (última consulta 18-02-08).        [ Links ]

19. VEGA REÑÓN, Luis: “Eudoxo de Cnido” en http://divulgamat.ehu.es/weborriak/historia/MateOspetsuak/Eudoxo.asp (última consulta: 18-02-08).        [ Links ]

Notas

1 PLUTARCO: Vidas Paralelas, Tomo II, edición electrónica disponible en: http//www.librosclasicos.org/ buscador/search.php?kw=plutarco, p. 373-374 (última consulta 12-01-07), también en: Plutarco: Vidas paralelas, ed. de A. Ranz Romanillos, Vergara, Barcelona, 1968.

2 Heiberg había publicado los textos de Arquímedes conservados hasta la fecha en Archimedis opera omnia cum commentariis Eutocii, Teubner, Leipzig, 1881. Luego de su descubrimiento del nuevo escrito, lo incluye en dicha compilación y publica entre 1910 y 1915 una nueva edición de la misma. Esta edición bilingüe (griego y latín), ha sido desde sus inicios de carácter canónico para el estudio riguroso de la obra del matemático de Siracusa.

3 ARQUÍMEDES: El método, Alianza Editorial, Madrid, 1986, p. 35, traducción de María Luisa Puertas y Luis Vega. Cursivas nuestras. En adelante, esta obra será citada como Método.

4 Esta obra trata problemas físicos, pero en el ámbito de las figuras planas. En la misma se utiliza el concepto de centro de gravedad sin definirlo; y estudia, entre otras cosas, las leyes del equilibrio de la palanca. Vale acotar que dicha obra, conjuntamente con otra obra del siracusano, De los cuerpos flotantes, sienta los fundamentos de la mecánica como disciplina científica. Hay edición de ambas obras en inglés, formando parte de la compilación de las obras conocidas hasta ese entonces, por parte de Sir Thomas Little Heath, partiendo en buena medida de la citada edición de Heiberg. Véase: HEATH, Thomas: The Works of Archimedes, Dover Publications, Mineola, 2002. Hay edición electrónica disponible en: http://www.archive.org/details/worksofarchimede029517mbp (última consulta: 18-02-07). Véase respecto al contenido de esta nota: GIBSON, Ian (ed.): Protagonistas de la civilización: Arquímedes, Editorial Debate, Madrid, 1983, pp. 44-46.

5 Figura extraída de Método, p. 40.

6 Método, p. 41.

7 GIBSON, I.: Ob. cit., p. 64.

8 Método, pp. 41-42.

9 VEGA, Luis: “Introducción” a Método, p. 30. Esta Introducción nos parece altamente recomendable.

10 MONDOLFO, Rodolfo: El infinito en el pensamiento de la antigüedad clásica, Eudeba, Buenos Aires, 1971, p. 195. En este sentido, recalcando el desprecio que sentía la tradición griega con respecto a todo lo que tuviera relación con lo práctico, nos dice Armstrong: “los trabajadores manuales convierten a un hombre en banáusico [vulgar] es decir, en una persona inferior y vulgar desprovista de la virtud necesaria para ser un ciudadano”: ARMSTRONG, A.: Introducción a la Filosofía Antigua, EUDEBA, Buenos Aires, 1993, p. 183.

11 BELL, Eric: Men of Mathematics, Fireside, New York, 1965, p. 31, traducción nuestra.

12 Véase: REICHENBACH, Hans: Experience and Prediction, University of Chicago Press, Chicago, 1938.

13 TOLEDO PRATS, Sergio: “El significado filosófico de las matemáticas en la cultura griega” en: MONTESINOS SIRERA, José (ed.): Symposium Arquímedes, Fundación Canaria Orotava de Historia de la Ciencia y Max Plack Institute for the History of Science, edición electrónica, disponible en: www.mpiwg-berlin.mpg.de/Preprints /P239.PDF (última consulta 18-02-07).

14 El término que hemos seleccionado para la denominación de este método, “exhaución”, no es del agrado de algunos estudiosos del tema, quizás por la similitud con el “exhaustion” inglés. Algunos, como Luis Vega Reñón, prefieren referirse al método como de “convergencia”; véase: “Eudoxo de Cnido” en http://divulgamat.ehu.es/weborriak/historia/ MateOspetsuak/Eudoxo.asp (última consulta: 18-02-07). Rodolfo Mondolfo, en su obra citada en este estudio, se refiere al mismo como “método exhaustivo”. Sin embargo, el término que decidimos escoger es de amplia utilización y análogo a las citadas alternativas.

15 1852-1939. Fue el tutor de la Tesis Doctoral de David Hilbert.

16 Acerca de este punto véase: CAJORI, Florian: History of Mathematics, Macmillan, Boston, 1894, edición electrónica, disponible en: http://ia301112.us.archive. org/3/ items/historyofmathema001062mbp/historyofmathema001062mbp.pdf, pp. 26-28 (última consulta: 18-02-07), también en: CAJORI, F.: A History of Mathematics, Chelsea Publications, New York, 1991.

17 Ibid, p. 33, traducción nuestra.

18 Para una descripción y explicación de cada una de las paradojas, véase: KIRK, A. y RAVEN, M.: Los filósofos presocráticos, Gredos, Madrid, 1979, pp. 408-415.

19 BURTON, David: The History of Mathematics: An Introduction, McGraw-Hill, E.U.A., 2005, p. 104, traducción nuestra.

20 BELL, E.: Ob. cit., p. 27, traducción nuestra.

21 CAJORI, F.: Ob. cit., p. 42, traducción nuestra. Es interesante la expresión de Cajori al referirse al método de exhaución: “instrumento de descubrimiento”. Esto puede parecer contradictorio con lo que hemos expuesto hasta el momento, ya que se ha aseverado que la carga inventiva le pertenece fundamentalmente al método mecánico y no al de exhaución. La contradicción tiene una explicación sencilla: la obra de Cajori fue publicada en 1894, fecha en la cual, como se ha explicitado, se desconocía la existencia de Del método relativo a los teoremas mecánicos, para Eratóstenes.

22 VEGA, L.: Ob. cit., p. 27.

23 Ibid, p. 28.

24 Hay edición en español de esta obra: ARQUÍMEDES: Tratados I. EUTOCIO: Comentarios, Gredos, Madrid, 2005. En dicha publicación también están incluidos otros dos escritos de Arquímedes: Sobre la esfera y el cilindro y Sobre conoides y esfenoides.

25 Con relación a este punto véase: BURTON, D.: Ob. cit., pp. 200-206.

26 Ibid, p. 203.

27 CAJORI, F.: Ob. cit., pp. 41-42, traducción nuestra.

28 Con respecto a este punto véase: GIBSON, I.: Ob. cit., p. 57.

29 FINK, Karl: A Brief History of Mathematics, Chicago, 1900, p. 200, edición electrónica, disponible en: http://www.archive.org/details/ABriefHistoryOfMathematics (última consulta: 18-02-07).

30 CAJORI, F.: Ob. cit., p. 42, traducción nuestra.

31 BELL, E.: Ob. cit., p. 32, traducción y cursivas nuestras.

32 BURTON, D.: Ob. cit., p. 203, traducción nuestra.

33 Véase: HEATH, T.: Ob. cit., p. 411.

34 Acerca de esta obra, véase: MONDOLFO, R.: Ob. cit., pp. 163-166

35 CAJORI, F.: Ob. cit., p. 50, traducción nuestra.