Gradiente de presión de flujo de gas y líquido en tuberías horizontales considerando El Efecto de las Propiedades de Mezcla

M. HAOULO, J. SOTO, F. GARCÍA*

Escuela de Ingeniería Mecánica, Universidad Central de Venezuela, Apartado 48222

Los Chaguaramos 1041-A, Caracas, Venezuela. *garciaga@ucv.ve

RESUMEN
En este trabajo se evalúa el efecto de la densidad y de la viscosidad dinámica de la mezcla en la determinación del gradiente de presión longitudinal de flujo bifásico de gas y de líquido en tuberías horizontales considerando un fluido pseudo homogéneo. Se evalúan 18 ecuaciones de viscosidad de mezcla y 4 ecuaciones de densidad de mezcla presentadas en la literatura especializada.
La combinación de estas ecuaciones de propiedades de mezcla generan 72 modelos, cuya única diferencia es la forma de calcular las propiedades de mezcla. La evaluación del desempeño de los diferentes modelos para determinar el gradiente de presión, se realiza comparando los resultados obtenido por cada modelo con 93 datos experimentales que incluyen los patrones de flujo intermitente, anular, burbuja dispersa y estratificado ondulado. En la evaluación del desempeño frente a todos los puntos de la base de datos experimentales, la combinación que agrupa a las ecuaciones de viscosidad y densidad de mezcla presentadas por Beattie y Whalley (1982), obtiene el mejor desempeño con un error absoluto promedio de 19.3%. El peor desempeño lo presenta
la combinación formada por la ecuación de viscosidad de mezcla de Hatschek (1928) y la ecuación de densidad de mezcla de Dukler et al. (1964) con un error absoluto promedio de 288.8%. Adicionalmente, se evalúa el desempeño de las 72 combinaciones clasificando los datos experimentales por patrón de flujo.
Palabras claves: Gradiente de presión, modelo homogéneo, flujo bifásico, viscosidad de mezcla, densidad de mezcla.

PRESSURE GRADIENT OF GAS AND LIQUID FLOW IN HORIZONTAL PIPES CONSIDERING MIXTURE PROPERTIES

ABSTRACT
In this work the effect of the density and the dynamic viscosity of the mixture is evaluated to determine the longitudinal pressure gradient of two-phase gas-liquid flow in horizontal pipes considering a pseudo homogenous fluid. Eighteen mixture viscosity equations, and 4 mixture density equations present in the specialized literature are evaluated. The combination of these equations for mixture properties generate 72 models whose only difference is in the form of evaluating the mixture properties. The performance evaluation of the different models in order to determine the pressure gradient is carried out comparing the results obtained by each model with 93 experimental data sets that include the flow patterns: intermittent, annular, stratified wavy and dispersed
bubble. In the performance evaluation, the combination that contains the equations of mixture viscosity and mixture density presented by Beattie and Whalley (1982) performs best with an average absolute error of 19.3%. The combination of the mixture viscosity equation of Herschel (1928) with the mixture density equation of Dukler et al. (1964) presents the worst performance with an average absolute error of 288.8%. Additionally, the performance of the 72 combinations is evaluated classifying the experimental data by flow pattern.
Keywords: Pressure gradient, homogeneous model, two-phase flow, mixture viscosity, mixture density.

Recibido: abril de 2005 Recibido en forma final revisado: diciembre de 2005

INTRODUCCIÓN
El estudio del flujo simultáneo de gas y de líquido a través de un conducto, es una de las combinaciones de flujo bifásico más complejas que existen. Esto se debe principalmente a la gran variedad de configuraciones relacionadas con la distribución espacial de ambas fases en la tubería y a que la fase gaseosa es compresible. Estas configuraciones espaciales se conocen como patrones de flujo.El flujo de gas y de líquido es encontrado frecuentemente en la industria petrolera, química, nuclear, en plantas termoeléctricas, etc. En la industria petrolera, este tipo de flujo a lo largo del sistema de producción puede ser cualquier combinación de una fase de gas natural, una fase líquida de hidrocarburo y una fase de agua. El reto de las investigaciones y desarrollos en la industria petrolera es optimizar el diseño y funcionamiento de los diferentes componentes del sistema de producción para reducir de manera significativa los costos asociados a la construcción y operación de los mismos. Se han desarrollado modelos de flujo para sistemas bifásicos que son independientes del patrón de flujo existente. Una de las características de estos modelos es que ignoran la compleja configuración del flujo y tratan a éste como un fluido pseudo homogéneo. En estos modelos no se considera la distribución espacial de las fases y se aplican las herramientas desarrolladas para flujo monofásico a una pseudo fase homogénea cuya velocidad y propiedades físicas son un promedio entre ambas fases. Las soluciones obtenidas a través de este tipo de modelos requieren esfuerzos numéricos menores y son ampliamente utilizados en los simuladores de yacimiento. El efecto de las propiedades de mezcla en el modelo homogéneo no está claramente establecido. Resultados
reportados por García et al. (2003) muestran diferencias significativas en la predicción del gradiente de presión entre modelos homogéneos cuya única diferencia es la forma de evaluar la viscosidad de mezcla. Por ejemplo, los modelos de McAdams et al. (1942) y de Cicchitti et al. (1960), presentan errores porcentuales absolutos promedios de 38% y 275%, respectivamente, al comparar los valores de gradiente de presión calculados con los experimentales. Haoulo y García (2004), observaron un marcado efecto de la densidad de mezcla en el gradiente de presión debido a los cambios de energía cinética y adicionalmente evaluaron el efecto de la viscosidad del líquido en el gradiente de presión total. Sin embargo, no evaluaron el efecto de las propiedades de mezcla en el gradiente de presión total.
El problema confrontado en este estudio es evaluar el efecto de la densidad y de la viscosidad de la mezcla en el gradiente de presión longitudinal de flujo de gas y de líquido en tuberías horizontales considerando un fluido pseudo homogéneo.
MODELO DE WALLIS (1969)
El modelo homogéneo más conocido es el denominado modelo de flujo homogéneo de Wallis (1969). Las
ecuaciones básicas de conservación de masa y de momentum en régimen permanente del modelo homogéneo para flujo unidimensional isotérmico en tuberías son:

donde M U y M ρ son la velocidad promedio y la densidad de la mezcla, respectivamente, A , P y θ son el área de la sección transversal, el perímetro y el ángulo de inclinación de la tubería, respectivamente, es el gradiente de presión en la dirección del flujo, W τ es el esfuerzo de corte en la pared de la tubería y es la aceleración de gravedad.

Generalmente la ecuación (2) se presenta como una ecuación explícita en términos del gradiente de presión:

la Ecuación (6) varía en función de la definición de densidad de la mezcla utilizada.
El tercer componente ( )G dz dp / es debido a los cambios de energía potencial como consecuencia de los cambios de pendiente en la tubería. En el caso de tubería horizontal el gradiente de presión debido a los cambios de energía potencial es cero y por esta razón no se considera en este en flujos con una alta fracción volumétrica de líquido, este puede ser el término predominante.

PROPIEDADES DE LA MEZCLA
El modelo de la viscosidad de mezcla implica el estudio de la reología del fluido y su posible dependencia del patrón de flujo, el cual en ocasiones es bastante complejo y ello explica los diferentes intentos para formular una ecuación idealizada que aproxime el comportamiento reológico del sistema. La viscosidad de la fase por separado para flujo isotérmico se puede considerar constante. Una de las formas de generar un modelo para evaluar la viscosidad de la mezcla, es establecer una relación entre la viscosidad de ambas fases constituyentes del flujo bifásico. Esta relación en general es un promedio ponderado entre ambas viscosidades. Debido a la diferencia notable entre la viscosidad del líquido y la viscosidad del gas, generalmente se establecen los modelos en términos de la fracción volumétrica del líquido sin deslizamiento l_L , la fracción del flujo másico x . En la Tabla (1), se representan las ecuaciones más utilizadas para evaluar la viscosidad de la mezcla m_M , donde r_L  y r_G  son las densidades del líquido del gas, respectivamente; m_L  y m_G son las viscosidades del líquido y del gas, respectivamente;y m_L m_G son los flujos másicos de gas y de líquido, respectivamente.

La densidad de mezcla resulta de un modelo donde se genera una relacion entre las densidades de las fases que forman la mezcla. Generalmente la densidad del liquido tiene una mayor incidencia en la densidad total. En la Tabla (2), se presentan las ecuaciones de densidad de mezcla M ƒÏ utilizadas en este estudio.
Algunas ecuaciones utilizadas para evaluar las propiedades de mezcla requieren conocer la fraccion volumetrica de liquido con deslizamiento . En este estudio la fraccion volumetrica de liquido con deslizamiento se evalua con el ajuste de la correlacion de Eaton et al. (1967) propuesto por Garcia (2004).
Para determinar el gradiente de presion longitudinal para flujo bifasico mediante el modelo homogeneo desarrollado, se utilizan las diferentes ecuaciones para la evaluacion de la viscosidad y la densidad de mezcla presentadas anteriormente para generar 72 combinaciones.
El proceso de identificacion de las diferentes combinaciones, se desarrolla asignando a las cuatro correlaciones de densidad de mezcla, un codigo de identificacion (C.I.), tal como se indica en la Tabla (3).
Por ejemplo, la combinacion de la correlacion de la viscosidad de mezcla (ViscM) de Dukler et al. (1964) con
la combinacion de la ecuacion de la densidad de mezcla (DenM) de Oliemans (1976), se representa de esta manera Dukler-d4, indicando primero la ecuacion de viscosidad utilizada y luego la de densidad de mezcla. Otro ejemplo, la ecuacion de la ViscM de Oliemans (1976) combinada con la ecuación de DenM usada por Ouyang (1998) se identifica como Oliemans-d2.
BASE DE DATOS EXPERIMENTALES
Se desarrolla y procesa una base de datos para flujo de gas y de líquido en tuberías horizontales, utilizando como fuente los datos experimentales para flujo bifásico isotérmico de aire y de agua en tuberías horizontales reportados por Johnson et al. (1952), Johnson (1955) y Reid et al. (1957).
Se procesaron 93 conjuntos de datos experimentales que se emplean en el estudio comparativo para evaluar el
desempeño del modelo homogéneo, utilizando las 72 combinaciones de ecuaciones de mezcla. En la Tabla (4)
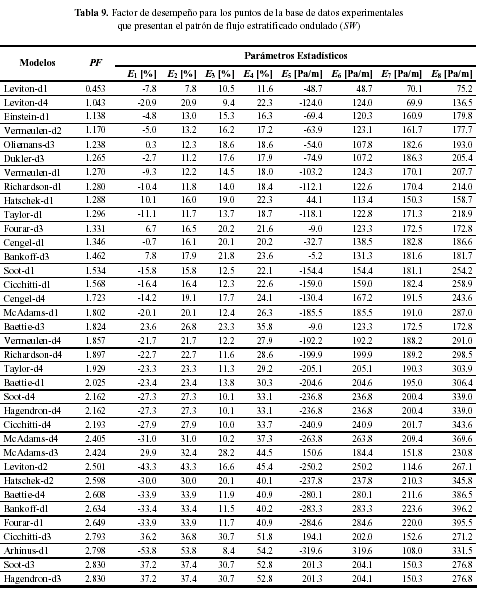
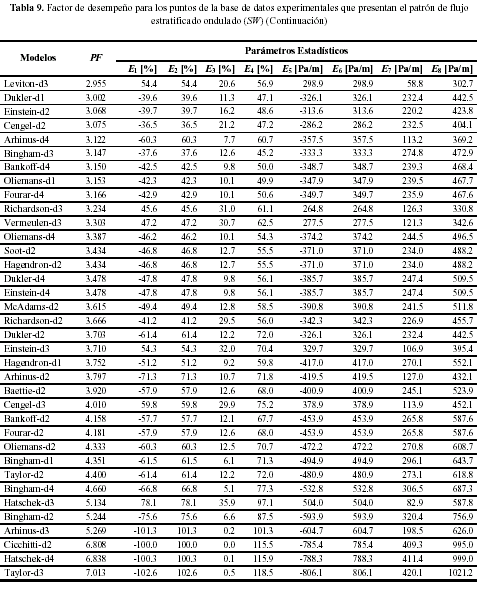
donde se indica el resumen de la base de datos utilizada. En la base de datos experimentales existen 62 puntos que presentan un patrón de flujo tapón (Slug Flow: SL ), 15 puntos que presentan un patrón de flujo anular (Annular Flow: AN ), 12 puntos que presentan un patrón de flujo burbuja dispersa (Dispersed Bubble Flow: DB) y 4 puntos presentan un patrón de flujo estratificado ondulado Stratified Wavy Flow: SW ). Aunque en la base de datos existen puntos experimentales correspondientes al tipo de flujo estratificado ondulado, esto representan menos del 4.5% de la base de datos. Esto implica, que los resultados cuantitativos del análisis del desempeño del modelo por tipo de flujo para este patrón son poco concluyentes. Sin embargo, la evaluación del desempeño de los 72 modelos para flujo Estratificado Ondulado se incluye para ser utilizadas de manera cualitativa.

EVALUACIÓN DEL DESEMPEÑO DEL MODELO HOMOGÉNEO PARA DIFERENTES COMBINACIONES DE VISCOSIDAD Y DENSIDAD DE MEZCLA
Los resultados en la determinación del gradiente de presión total de los 72 modelos, formados a partir de las
combinaciones de las propiedades de mezcla, se compara con la base de datos experimentales reportados por Johnson et al. (1952), Johnson (1955) y Reid et al. (1957).
La evaluación de la capacidad de predicción del gradiente de presión de los diferentes modelos se realiza utilizando un factor de desempeño (Performance Factor: PF ), el cual fue propuesto por García (2003). Este es una modificación del factor de desempeño recomendado por Ansari et al. (1994) y García et al. (2003), definido por:

donde E₁ es el error porcentual promedio, E₂ es el error porcentual absoluto promedio, E₃  es la desviación estándar del error porcentual promedio, E₄  es la desviación estándar del valor calculado menos el valor experimental dividido entre el valor experimental ó la raíz cuadrada del promedio del error porcentual al cuadrado, E₅  es el error promedio,  E₆ es el error absoluto promedio,  E₇ es la desviación estándar del error promedio y 8 E es la desviación estándar del valor calculado menos el valor experimental ó la raíz cuadrada del promedio del error al cuadrado, los cuales están definidos por:

El error porcentual promedio es una medida de la concordancia entre los valores calculados y experimentales,
este índica en promedio el grado de sobrepredicción (valores positivos) ó subpredicción de los valores calculados con respecto a los experimentales. Similarmente, el error porcentual absoluto promedio 2 E es una medida de la
concordancia entre los valores calculados y experimentales. Sin embargo, los errores positivos y negativos no se cancelan entre sí. Por esta razón, el error porcentual absoluto promedio es considerado un parámetro clave para evaluar la capacidad de predicción de modelos y correlaciones. La estándar del error porcentual promedio 3 E indica el grado de dispersión de los errores con respeto al promedio.
La raíz cuadrada del promedio del error porcentual al cuadrado,  E₄ indica el grado de dispersión entre los valores

calculados y los valores experimentales. Los parámetros estadísticos  E₅ ,  E₆ ,  E₇ y  E₈ son similares a E₁ , E₂ ,  E₃ y E₄ pero están basados en el error absoluto i e . Los valores mínimo y máximo posibles para el factor de desempeño son 0 y 8, correspondientes al mejor y peor desempeño, respectivamente.

El proceso de evaluación del desempeño se realiza inicialmente para todos los puntos de la base de datos

experimentales, independientemente del patrón de flujo presente. Luego se realiza el estudio para cada patrón de

flujo por separado. Los resultados de la evaluación del desempeño de los 72 modelos contra toda la base de datos, se presentan en la Tabla (5).

En la Tabla (5), se observa que la combinación de Beattied1 obtiene el mejor desempeño con un factor de desempeño de 0.09 y un error absoluto promedio de 19.3%. El peor desempeño lo obtiene la combinación de Hatschek-d3 con un factor de desempeño de 8 y un error porcentual absoluto promedio de 288.8 %. En las Tablas (6)-(9), se presentan los resultados de la evaluación de los modelos en estudio para cada patrón de
flujo. Para flujo tapón, la combinación de Beattie-d1 obtiene el mejor desempeño con un factor de desempeño de 0.09 y un

 

error absoluto promedio igual a 14.7 %. En flujo burbuja dispersa la combinación de Einstein-d1 presenta el mejor
desempeño con un factor de desempeño de 0.27 y un error absoluto promedio de 7.5%. Las combinaciones de Fourard1 y Leviton-d1 obtienen los mejores desempeños para flujo anular y estratificado ondulado, con factores de desempeño y errores absolutos promedios de 0.18 ( E₂ = 27.5 %  ) y 0.45
( E ₂ = 7.8 %  ), respectivamente.
El peor desempeño para flujo tapón y flujo anular, lo obtiene la combinación de Hatschek-d3 con un PF de 8 y un error absoluto promedio de 214.2% y un PF de 8 y un error absoluto promedio de 887.1, respectivamente. La
combinación de Taylor-d3 obtiene el peor desempeño para flujo burbuja y flujo estratificado, con un PF de 7.12 y un error absoluto promedio de 106.7 % y un PF de 7.01 y un error absoluto promedio de 102.3 %, respectivamente.

SUMARIO Y CONCLUSIONES
La evaluación del factor de desempeño de los 72 modelos para el cálculo del gradiente de presión total, formados a partir de las combinaciones de las propiedades de mezcla frente a la base de datos experimentales reportados por Johnson et al. (1952), Johnson (1955) y Reid et al. (1957), depende en gran parte del patrón de flujo presente. En la evaluación del desempeño en la determinación del gradiente de presión de los 72 modelos contra toda la base de datos, la combinación de Beattie-d1 obtiene el mejor desempeño con un factor de desempeño (PF) de 0.09 (E ₂ =  19.3%  ). El peor desempeño lo presenta la combinación de Hatschek-d3 con un PF de 8 (E ₂ = 288.8   % ). Al evaluar el factor de desempeño para los datos experimentales que presentan el patrón de flujo tapón, la combinación de Beattie-d1 también obtiene el mejor desempeño con un PF de 0.09 (  E₂ =14.7%   ). La
combinación de Hatschek-d3 de manera similar presenta el peor desempeño con un factor de desempeño de 8
(  E₂ =214.2%    ). Esto era de esperarse debido a que el 66,7% de los datos experimentales corresponden a flujo tapón. Para los puntos experimentales correspondientes al patrón de flujo burbuja dispersa, la combinación de Einstein-d1 tiene el mejor desempeño con un factor de desempeño de 0.27 ( E₂ =  7.5 %  ) y la combinación de Taylor-d3 obtiene el peor desempeño con un factor de desempeño de 7.12 (  E₂ = 106 .9 % ). Es interesante destacar que la ecuación de Einstein solo considera la viscosidad de la fase continua (fase líquida) para evaluar la viscosidad de la mezcla la cual es mayor que la viscosidad de la fase continua.

Para flujo anular, la combinación de Fourar-d1 obtiene el mejor desempeño con un factor de desempeño de 0.18

( E ₂=27.5%  ). El peor desempeño lo presenta la combinación de Hatschek-d3 con un factor de desempeño

de 8 (E ₂ = 887.1%  ). El mejor desempeño para los puntos con patrón de flujo estratificado ondulado lo presenta la combinación de Leviton-d1 con un factor de desempeño de 0.45 ( E ₂ = 7.8%  ). El peor desempeño lo presenta la combinación de Taylor-d3 con un factor de desempeño de 7.01 (E 2 = 102.6 % ). Sin embargo, es importante resaltar que los datos experimentales con este tipo de patrón de flujo solo representan el 4.3% del total de experimentos.

En los casos estudiados, para todos los patrones de flujo a excepción de burbuja dispersa, la ecuación de densidad de mezcla que permite obtener los mejores desempeños es la presentada por Beattie y Whalley (1982). Esta ecuación define a la densidad de la mezcla como un promedio ponderado de la densidad por la fracción volumétrica sin deslizamiento de cada una de las fases. Por otra parte, en aquellos modelos que consideran únicamente la viscosidad de la fase líquida para la definición de la viscosidad de la mezcla, combinados con la definición de densidad de la mezcla propuesta por Dukler et al. (1964) (d3), presentan los peores desempeños con errores absolutos mayores al 170%.

La diferencia tan significativa en el desempeño de los modelos de viscosidades de mezcla presentados por Beattie

y Whalley (1982) (E ₂ = 19.3%  .  ) y Hatschek (1928) ( E 2 = 106.9 % ). ambos combinados con la ecuación de densidad de mezcla presentada por Beattie y Whalley (1982) era ser debido a que la ecuación de viscosidad de mezcla de Hatschek (1928) es determinada únicamente a partir de la viscosidad de la fase líquida.

En flujo anular y estratificado, el efecto de la velocidad relativa entre las fase puede ser significativo. Sin embargo, los resultados de este estudio muestran que el incluir este efecto a través de la fracción volumétrica de líquido con deslizamiento en la definición de la densidad de mezcla permitiría determinar el gradiente de presión longitudinal en tuberías horizontales con un relativo buen grado de precisión. No obstante, esto requiere mayores estudios en los cuales se utilice una base de datos con un amplio intervalo de operación.

AGRADECIMIENTOS
Los autores del presente trabajo agradecen al CDCHUCV por el apoyo económico otorgado a través de
los proyectos de investigación No 08.15.5340.2003, No 08.15.5195.2005 y 08.00.5653.2004 y la ayuda
institucional 08.00.5652.2004.

REFERENCIAS

1. ARRHENIUS, S., (1887), On the Internal Friction of Solutions in Water. Zeitschrift für Physikalische Chemie
(Leipzig) 1, 285-298.

2. BANKOFF, S.G., (1960), A Variable-Density, Single-Fluid Model for Two-Phase Flow with Particular Reference
To Steam-Water Flow, Trans. ASME, 8.

3. BEATTIE, D., WHALLEY, P.D., (1982), A Simple Two-Phase Frictional Pressure Drop Calculation Method, Int.
J. Multiphase Flow 8(1), 83-87.

4. BINGHAM, E. C., (1906), Viscosity and Fluidity, American Chemical Journal (35) 3. 195-217.        [ Links ]

5. Brinkman, H. C., (1952), The Viscosity of Concentrated Suspensions and Solutions. Journal of Chemical
Physics (20) 4, 571.

6. Cengel, J. A., (1967), Viscosity of Liquid-Liquid Dispersions in Laminar and Turbulent Flow, Ph. D, Thesis,
Oregon State Univ. Abst. No. 67-11805.

7. CICCHITTI, A, LOMBARDI, C., SILVESTRI, M., SOLDAINI, G., ZAVATTAREUI, R., (1960), Two-Phase Cooling
Experiments-Pressure Drop, Heat Transfer and Burnout Measurements, Energi Nucl. 7(6), 407-425.

8. DUKLER, A.E., WICKS III, M., CLEVELAND, R., (1964), Frictional Pressure Drop in Two-Phase Flow: B. An
Approach through Similarity Analysis, AIChE Journal 10, 44-51.

9. EATON, B., ANDREWS, D., KNOWLES, C., SILBERBERG, I., BROWN, K., (1967), The Prediction of Flow Patterns, Liquid Holdup and Pressure Losses Occurring During Continuous Two-Phase Flow in Horizontal Pipelines.
Trans. AIME, 815.

10. EINSTEIN, A., (1909), A New Definition of Molecular Dimensions. Annalen der Physik (4) 19. 289-306.        [ Links ]

11. FOURAR, M., BORIES S., (1995), Experimental Study of Air- Water Two-Phase Flow through a Fracture (Narrow
Channel) 1995. Int.J. of Multiphase Flow21 (4), 621- 637.

12. GARCÍA, F., (2003), Factor de Fricción para Flujo Bifásico de Gas y de Líquido en Tuberías Horizontales para
Régimen Laminar y Turbulento. Proyecto de Tesis Doctoral, Facultad de Ingeniería, Universidad Central de Venezuela.

13. GARCÍA, F., (2004), Factor de Fricción para Flujo Bifásico de Gas y de Líquido en Tuberías Horizontales para
Régimen Laminar y Turbulento. Tesis Doctoral, Facultad de Ingeniería, Universidad Central de Venezuela.

14.  GARCÍA, F., GARCÍA, R., PADRINO, J. C., MATA, C., TRALLERO, J., JOSEPH, D., (2003), Power Law and Composite Power Law Friction Factor Correlations for Laminar and Turbulent gas-Liquid Flow in Horizontal
Pipelines, Int. Journal of Multiphase Flow 29. 1605- 1924.

15. HATSCHEK, E., (1928), The Viscosity of Liquids. London: Bell & Sons Ltd.        [ Links ]

16. HAOULO M., GARCÍA F., (2004), Efecto de La Viscosidad y de La Densidad de Mezcla en El Gradiente de Presión
de Flujo de Gas-Líquido en Tuberías Horizontales.Memorias del V Congreso Nacional de ingeniería Mecánica. Mérida -Venezuela. 301-306,

17. HOOGENDOORN, C., (1959), Gas-Liquid Flow in Horizontal Pipes, Chem. Eng. Sci. 9. 205-217,        [ Links ]

18. JOHNSON, H., (1955), Heat Transfer and Pressure Drop for Viscous-Turbulent Flow of Oil-Air Mixtures in a
Horizontal Pipe, Trans. ASME 77, 1257-1264.

19. JOHNSON, H., ABOU-SABE, A., (1952), Heat Transfer and Pressure Drop for Turbulent Flow of Air-Water Mixtures in a Horizontal Pipe, Trans. ASME. 74, 977- 987,        [ Links ]

20. MCADAMS, W., WOODS, W., HEROMAN, L., 1942, Vaporization Inside Horizontal Tubes, Trans. ASME 64, 193.        [ Links ]

21. OGLESBY, K., 1979, An Experimental Study on the Effects of Oil Viscosity Mixture Velocity and Water Fraction on Horizontal Oil-Water Flow1979. TEGM The University of Tulsa OLIEMANS, R., 1976, Two Phase Flow in gas-Transmission Pipelines. ASME paper 76-Pet-25, presented at Pet. Div. ASME meeting, Mexico.        [ Links ]

22. OUYANG, L., 1998, Single Phase and Multiphase Fluid Flow in Horizontal Wells. PhD Dissertation Thesis.
Department of Petroleum Engineering. School of Earth Sciences. Stanford University. Stanford, CA.,
248.

23. REID, R., REYNOLDS, A., DIGLIO, A., SPIEWAK, I., KLIPSTEIN, D., (1957), Two-Phase Pressure Drops in Large- Diameter Pipes, AIChE J. 3(3), 321-324.        [ Links ]

24. RICHARDSON, E. G., (1933), On the Viscosity of Emulsions. Kolloid Zeitschrift (65) 1, 32-37         [ Links ]

25. SOOT, P. M., (1971), A Study of Tow-Phase Liquid-Liquid Flow in Pipes, Ph. D. Thesis, Oregon Statte University, Abst. No. 71-2479        [ Links ]

26. TAYLOR, G. I., (1932), The Viscosity of Fluid Containing Small Drops of Anther Fluid. Proceeding of the
Royal Society of London (138A), 41-48

27. VERMEULEN, T., WILLIAMS, G. M. AND LANGLOIS, G. E., (1955), Interfacial Area in Liquid-Liquid and Gas-Liquid Agitation, Chm. Eng. Progress (51) Feb. 2, 85F- 94F        [ Links ]

28. WALLIS, G., (1969), One Dimensional Two-Phase Flow, McGraw-Hill.        [ Links ]