Simulación de grietas cortas originadas por fatiga de bajo ciclaje en aceros 2¼Cr 1Mo

O. BORNIA* J.B. VOGT** J. B. LEÓN*

*Universidad Central de Venezuela. Escuela de Ingeniería Metalúrgica y Ciencia de los Materiales.

**Université des Sciences et Technologies de Lille. Laboratoire de Métallurgie Physique et Génie des Matériaux, URM CNRS 8517.

RESUMEN

Los Aceros 2.25Cr 1Mo han sido estudiados en Fatiga Oligocíclica (LCF) a elevadas temperaturas en una investigación previa1. Esta fatiga de bajo ciclaje caracterizada por un estado de agrietamiento múltiple donde la mecánica de fractura convencional no reproduce la cinética de crecimiento de grietas cortas, resulta un reto en el área de simulación. Una modificación realizada a la ecuación de cinética propuesta por Lankford¹⁰ y una adaptación al fenómeno de LCF en la ecuación de Tomkins⁹ permiten reproducir el fenómeno a elevadas temperaturas en este tipo de aceros antes de que una grieta macroscópica induzca el fallo en el material. En este trabajo se simula computacionalmente la fatiga de bajo ciclaje basado en las nociones del daño y el estudio estadístico de poblaciones de grietas utilizando como plataforma el lenguaje computacional JAVA (TM) 2SDK, V 1.4.2-001. El simulador reproduce el agrietamiento múltiple en este tipo de aceros atendiendo a condiciones pseudoaleatorias, generando una aproximación del 90% a los resultados experimentales.

Palabras clave: Low Cycle Fatigue, aceros 2.25Cr1Mo, Lenguaje computacional JAVA

LOW CYCLE FATIGUE (LCF) SHORT CRACK SIMULATION OF 2.25Cr 1Mo STEELS

ABSTRACT

The 2.25Cr 1Mo Steels have been studied in Low Cycle Fatigue (LCF) to high temperatures in a previous paper. Low Cycle Fatigue is characterized by a multiple cracking stage where conventional fracture mechanics do not reproduce kinetic short crack growth, thus providing a challenge in the area of simulation. A modification made to the kinetic equation proposed by Lankford¹⁰ and a LCF adaptation on Tomkins⁹ equation, allows us to reproduce the phenomenon to high temperatures in this type of steel before the macroscopic crack induces the failure of the material. In this work, the Low Cycle Fatigue is simulated based on damage knowledge and the statistical record of crack populations using the computational language JAVA (TM) 2SDK, V 1.4.2-001 as a platform. The simulator reproduces the multiple typical cracking in this type of steel under pseudo-random conditions, generating an approximation of 90 % to the experimental results.

Keywords: Low Cycle Fatigue, 2.25 Cr1Mo steels, computational language JAVA.

Recibido: marzo de 2005   Revisado: marzo de 2006

INTRODUCCIÓN

Los Aceros 2.25Cr-1Mo son ampliamente utilizados en la industria de generación de energía debido a sus buenas propiedades a altas temperaturas. Estos aceros presentan una microestructura bifásica compuesta por granos de Ferrita y Bainita, los cuales son variables de mucha importancia Debido a que la respuesta cíclica del material ante la aplicación de cargas depende significativamente de la relación entre las fracciones volumétricas de estas fases.

El daño físico producido por Fatiga Oligocíclica (LCF) se manifiesta en la mayoría de los casos por un agrietamiento múltiple, con una densidad de grietas superficiales que puede legar a cientos por mm² dependiendo del nivel de esfuerzo/ eformación aplicado⁵ así como de la microestructura del material. Sobre probetas desprovistas de entalla, las grietas pueden nuclear y crecer durante una fracción importante de la vida a fatiga que puede ascender a 80% de ésta, antes de que una grieta macroscópica induzca el fallo luego de que una de entre ellas comience a propagar en volumen6. Ello muestra que el crecimiento de grietas cortas resulta muy importante para el estudio del fenómeno.

Sobre probetas desprovistas de entalla, las grietas pueden nuclear y crecer durante una fracción importante de la vida a fatiga que puede ascender a 80% de ésta, antes de que una grieta macroscópica induzca el fallo luego de que una de entre ellas comience a propagar en volumen⁶. Ello muestra que el crecimiento de grietas cortas resulta muy importante para el estudio del fenómeno.

El crecimiento de las grietas cortas sigue la dirección del plano de deslizamiento en el grano en el que la nucleación tuvo lugar (por ende la orientación de los granos que conforman la estructura del material juega un rol importante en esta etapa de crecimiento)¹⁰.

La superficie de propagación por su parte, encuentra gran cantidad de discontinuidades por concepto de barreras estructurales, éstas, están constituidas en el material generalmente por los límites de grano. Las grietas son detenidas parcial o permanentemente en estos límites. Esto se debe a la naturaleza de los granos adyacentes así como a la diferencia de orientación entre los mismos. Cuando el arresto es parcial, para continuar la propagación, se requiere de una energía extra que puede ser suministrada por la acumulación de deformación en la punta de la grieta.

Investigaciones en aceros 2.25Cr-1Mo^1,8,12 muestran la influencia que ejercen los límites de grano como barreras estructurales a la propagación de grietas cortas.

En Fatiga Oligocíclica, el crecimiento de microgrietas puede ser acelerado por la acción de una atmósfera oxidante. El comportamiento de la capa de óxido formada como producto de la interacción con el medio a temperaturas elevadas, depende del tipo de esfuerzo al cual es sometido el material.

En la región del umbral de fatiga las tasas de crecimiento de estas grietas cortas son muy lentas, y la influencia de la microestructura y el medio son muy importantes en la propagación de las mismas. Se ha demostrado que en esta región, la cinética de crecimiento de grietas no obedece a as mismas leyes que describen el crecimiento de grietas argas⁸.

PROCEDIMIENTO EXPERIMENTAL

En vista de la importancia de los límites de grano al crecimiento de grietas en la etapa I de crecimiento se realizó un estudio de las grietas producidas en el acero 2.25Cr 1Mo con fracciones volumétricas de 35% (V35) y 85% (V85) de ferrita, ensayados a LCF a una temperatura de 565°C en una investigación precedente1. Los ensayos se realizaron a fractura y de manera interrumpida a 25%, 50% y 75% de la vida del material, los ensayos además fueron realizados en vacío y al aire.

Dicho estudio fue fundamentalmente realizado en Microscopía óptica, y soportado en las investigaciones previas realizadas a estos aceros^1,2,3,4. Éste consistió en un registro estadístico de las grietas, basado en el método de análisis propuesto por J. Stolarz7; el cual atendió principalmente al número de barreras microestructurales superadas en función del porcentaje de vida del material sobre las secciones planas de probetas ensayadas producto del corte longitudinal a través del eje de revolución de lasección útil de las mismas.

Una vez analizado el estudio del daño físico generado sobreel acero por el fenómeno de Fatiga Oligocíclica, y haciendo basamento en las teorías propuestas acerca de la cinética que involucra la propagación de grietas^{8,9,10,13,14,15,16,17} se procedió a establecer las variables y condiciones a ser tomadas en cuenta para la creación de un simulador computarizado que permitiera la visualización del fenómeno.

ESTUDIO ESTADÍSTICO DE POBLACIONES DE GRIETAS

Del estudio de un gran número de grietas en el acero, se puede observar la importancia de los límites de grano como barreras al proceso de propagación de las mismas, esto se evidencia en el alto porcentaje de grietas tipo I o inferiores a un tamaño de grano (figura 1) durante el 75 % de la vida del material (figura 2).

 Figura 1. Clasificación de Grietas en función de las Barreras Microestructurales18.

Figura 2. Evolución de la Densidad de Grietas del Acero V35 en Ensayos realizados en Aire «et = 1.2%

SIMULACIÓN DEL DAÑO FÍSICO POR FATIGA OLIGOCÍCLICA

La simulación numérica fue realizada bajo el lenguaje de programación JAVA (TM) 2SDK, Standard Edition, V 1.4.2-001. Sobre este programa  ayudarán a reproducir la evolución de poblaciones de grietas cortas observadas en la sección longitudinal de las probetas. Los criterios en torno a la generación y propagación de las grietas involucran estadística y probabilística.

La malla es una representación ampliada de una sección de la superficie de la probeta estudiada, la cual simula la microestructura del acero. Los granos son asumidos como hexágonos regulares, donde cada uno de ellos presenta una orientación propia.

Las grietas son clasificadas en función del criterio de barreras estructurales, empleado por T. Thorpe¹⁸ (figura 1). Éstas son generadas de forma aleatoria desde la superficie de la probeta, descartando la nucleación en el seno del material por las dimensiones de la región representada; la propagación de las grietas fue establecida según la etapa de crecimiento de las mismas (cinética en Etapa I y II) así como por la barrera estructural que se oponía al avance de las grietas, el medio de ensayo y el nivel de deformación impuesto.

El fenómeno de interacción entre grietas no es considerado en el simulador por dos razones fundamentales: bajo porcentaje de casos de coalescencia que fueron registrados en el estudio de las secciones longitudinales de las probetas sometidas a Fatiga Oligocíclica en caliente; y la complejidad computacional que involucra.

PRINCIPIOS DEL MODELO NUMÉRICO

La Malla

La microestructura de ambos aceros V35 y V85 es asumida compuesta por granos equiaxiales. A partir de ello, computacionalmente los granos se suponen hexagonales isomorfos en su geometría con un tamaño de 40 pixels equivalente al tamaño de grano medio de cada estructura, 80.75μm y 44.50μm correspondientemente; este tamaño de grano medio fue calculado a partir de la relación [1].

Ambas fases son representadas en un área de 207.846,096 pixels², lo que corresponde a secciones de 0.8483 mm² (V 35) y 0.2566 mm² (V 85).

A los granos se les asignó un color, lo cual, permitió la diferenciación entre las dos fases presentes en el acero. El color gris claro fue asignado para identificar la fase Ferrita y el color gris oscuro fue asignado para representar la fase Bainita (figura 3 a). La fracción volumétrica de cada acero fue estimada para la representación computacional y distribuida de manera aleatoria en la superficie de la sección, conservando la relación entre las fases. De forma estocástica a cada grano le es asignada una orientación, la sección angular (figura 3 b) entre la que fluctúa ésta se encuentra ente -55° y 55° con respecto a la perpendicular al eje de aplicación de esfuerzos¹⁹. Los granos correspondientes a la superficie de la probeta presentan características diferentes al resto de los granos del material en la representación.

Figura 3. Esquema de Sección de la Malla, en la que se refleja la morfología de grano y la orientación (a). Sección ángular para la asignación de orientación del grano (b).

Generación de Grietas

El agrietamiento se representa de manera aleatoria sobre los granos que conforman la superficie de la malla. Los dos tipos de grano muestran la isma probabilidad de inicio de grietas atendiendo a los resultados experimentales obtenidos y sustentados en los trabajos de otros investigadores^1,2,7.

La orientación del grano, es el parámetro que determina la generación de grietas: para que una grieta pueda nuclear la orientación de grano inicialmente, debe atender a valores dentro de secciones angulares definidas (± 5°) cercanos a los ángulos reportados por la teoría (45° y 90°). Las secciones angulares iniciales correspondían a -40° -50°; - 5° 5° y 40° 50° (figura 4a). Para representar la nucleación de nuevas grietas durante el avance del ciclaje se calculó el número de grietas equivalente al área computacional a medida que la vida del material se reducía. Para lograr este cometido, las secciones angulares eran ampliadas en 10° (figura 4b), de esta manera se logró reproducir el fenómeno de agrietamiento múltiple.

Figura 4. Esquema de Secciones angulares consideradas en los granos del material: a) Secciones angulares Iniciales. (b) Ampliación de secciones angulares.

La nucleación en el grano se produce de manera aleatoria en la longitud de la arista (0-5) para granos de 6 aristas y en la longitud de la arista (0-3) para granos de 4 aristas (figura 5). El tiempo inicial de nucleación es también aleatorio respondiendo a un intervalo de tiempo entre 0 y 500 seg. (registro computacional que se hace equivalente al tiempo real de nucleación de grietas).

Figura 5. Representación de los tipos de grano en la superficie del material en función del número de aristas que los constituyen.

DESCRIPCIÓN DE LA CINÉTICA DE CRECIMIENTO PROPUESTA

Una vez que la grieta ha nucleado, la propagación de la misma responde a los criterios impuestos en las etapas de crecimiento.

Etapa I

Para reproducir el crecimiento de grietas nucleadas en la superficie, al seno del material, se dispuso de la ecuación de Lankford modificada[1]¹².

Esta expresión revela un comportamiento mas cercano a la realidad en el crecimiento de grietas cortas, esto si se toman en cuenta los resultados de investigadores en el área respecto al decremento de la velocidad frente a la presencia de los límites de grano como barreras microestructurales al paso de las grietas. La figura 6 muestra el comportamiento de esta ecuación modificada frente a la expresión original de Lankford.

Figura 6. Cinética de Crecimiento en Etapa I. Según la ecuación de Lankford modificada

Etapa II

Debido a la naturaleza del corte en las probetas, en el estudio es difícil estimar el cambio en la dirección de propagación que define el nuevo modo de crecimiento de las grietas o etapa II, no obstante, se logró establecer una longitudpromedio para el cambio de dirección en dos tamaños de
grano, esto soportado por investigaciones precedentes en el acero¹.

Una vez que la grieta ha alcanzado dos tamaños de grano, la ecuación de Lankford modificada no reproduce la cinética de crecimiento del material. Es en este momento cuando la etapa II de crecimiento se pone de manifiesto y los efectos de la microestructura y la orientación son casi imperceptibles.

En base a esto, la ecuación de Tomkins⁹ [3] fue empleada para representar esta etapa de crecimiento.

Tomkins señala que la tasa de crecimiento de grietas es proporcional al tamaño de la grieta por una constante que depende del nivel de esfuerzo y deformación aplicados, â puede ser aproximado, a través de relación [4].

Donde («σ/2)_m se asume como la amplitud de esfuerzo media en la zona de estabilización del material en el curso del ciclaje y «ó_max se asume como la amplitud de deformación máxima registrada en el ensayo. El comportamiento de esta ecuación se ilustra para cada acero en las figuras 7 y 8.

Figura 7. Cinética de crecimiento en Etapa II, (ec. Tomkins) Acero V85.

Figura 8. Cinética de crecimiento en Etapa II, (ec.Tomkins) Acero V35.

CÁLCULO DE DENSIDAD DE POBLACIONES DE GRIETAS

Con el fin de generar un resultado comparable a los valores experimentales, el simulador realiza el cálculo de densidad de poblaciones de grietas. Éstas fueron cuantificadas según la clasificación de barreras estructurales; y tomando en cuenta el área relativa de la malla, se calculó el número de grietas por unidad de superficie. [5].

Donde D es la densidad de grietas, N es el número de grietas en el área considerada y A_M es el área de la malla generada en mm2.

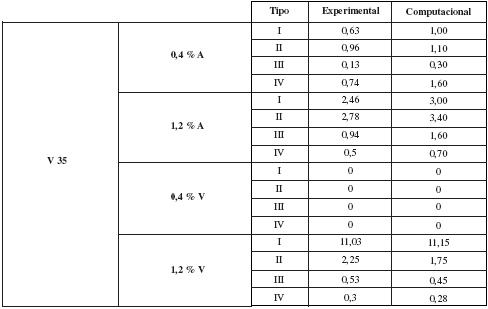
La densidad de grietas es reflejada en gráficos de barra para todas las condiciones bajo las cuales fueron evaluados ambos aceros. Cada una de estas condiciones, impuestas al material, fue ejecutada 10 veces para obtener resultados representativos. Las figuras 9 y 10 muestran algunos de los registros computacionales realizados. De igual forma las tabla 1 y 2 enmarcan los resultados obtenidos por el simulador computacional.

Figura 9. Densidad de Grietas. Acero V35 1.2% Vacío

Figura 10. Densidad de Grietas. Acero V85 1.2% Aire

Tabla 1. Densidad de Grietas (Acero V 85

Tabla 2. Densidad de Grietas (Acero V 35)

CONCLUSIONES

El simulador computacional reproduce el agrietamiento múltiple característico del fenómeno de LCF en el acero 2.25Cr 1Mo. Los resultados computacionales muestran que las ecuaciones de Lankford (modificada) y Tomkins reproducen en buena medida la cinética de crecimiento degrietas en el materialestudiado, reflejando una aproximación del 90% a los resultados experimentales.

REFERENCIAS

1. LEÓN, J. (2001). Analyse de Comportement en Fatigue Oligocyclique a Chaud D’aciers 10 CD 9.10: Influence de la Microstructure et de L’environnement. These de Doctorat en Sciences des Matériaux, Université des Sciences et Technologies de Lille, Laboratorie de Métallurgie Physique.        [ Links ]

2. ARGILLIER, S. (1998). Analyse des Mécanismes de Plasticité Cyclique a Chaud d’aciers de Type 10CD910: Détermination d’un indicateur D’endommagement de Fatigue. Université des Sciences et Technologies de Lille, Laboratorie de Métallurgie Physique.        [ Links ]

3. VOGT, J. ARGILLER, S. MASSOUD, J. PRUNIER, V. (2000) Fatigue Damage Evaluation of a Power Plant Component from Analysis of the Dislocation Structures. Enginnering Failure Analysis. Vol 7. pp. 301-310.        [ Links ]

4. VOGT, J. ARGUILLER, S. LEÓN, J. MASSOUD, J. PRUNIER, V. (1999). Mechanisms of Cyclic Plasticity of a Ferrite Bainite 2 ¼ Cr 1 Mo Steel After Long-term Service at High Temperature. ISIJ International. Vol 39. N° 11. pp. 1198-1203.        [ Links ]

5. TVERGAARD, V. WEI, Y. HUTCHINSON, J. (2001). Edge Cracks in Plastically Deforming Surface Grains. Eur. Journal Mechanics A/Solids N 20, pp. 731-738.        [ Links ]

6. BAFFIE, N. GARONES, A. MATEO, A. ANGLADA, M. STOLARZ, J. (1999). Influence of Interfaces on LCF Short Crack Propagation in the Bulk in Single Phase and in Duplex Stainless Steel. Fatigue’99., pp. 1-6.        [ Links ]

7. STOLARZ, J. (2000). Obstacles Structuraux a L’endommagement par Fatigue des Alliages Polyphasés. Habilitation a Diriger des Recherches,Spécilité Pysiques. Université des Sciences et Technologies de Lille.        [ Links ]

8. HUSSAIN, K. TAUQUIR, A. HASHMI, F. KHAN, A. (1994). Short Fatigue Crack Growth Behavior in Ferritic-Bainitic Steel. Metallurgical and Material Transaction A, Vol 25 A, pp. 2421-.2425.        [ Links ]

9. TOMKINS, B. (1981). Fatigue: Mechanisms. Creep and Fatigue in High Temperatures Alloys. Editado por Bressers, J. Applied Science Publishers, Londres, pp 73-143.        [ Links ]

10. FAN, J. MCDOWELL, D. HORSTEMEYER, M. GALL, K. (2001). Computacional Micromechanics Análisis of Cyclic Crack-tip Behavior for  Microstructurally Small Cracks n Dual Phase Al-Si Alloys. Engineering Fracture Mechanics, N 68, pp. 1687-1706.        [ Links ]

11. MILLER, K. Short Fatigue Cracks. Editado por Moura, C. Guerra, L. Advances in Fatigue Science and Technology. Nato ASI Series. Vol 159., England, pp. 3-21.        [ Links ]

12. BORNIA, O, LEÓN, J. B. (2004). Simulación Numérica del Daño Físico a Fatiga en Caliente en un Acero ASTM A155. Tesis de Grado, Universidad Central de Venezuela.        [ Links ]

13. PÓLAK, J. (2001). The Growth of Short Cracks and Life Prediction. VII Summer School of Fracture Mechanic, seria Mechanika, Polonia, pp. 298-316.        [ Links ]

14. YATES, J. MILLER, K. Non-Propagating Fatigue Cracks: The True Fatigue Limit. Editado por Moura, C. Guerra, L. Advances in Fatigue Science and Technology. Nato ASI Series. Vol 159. England, pp. 253-265.        [ Links ]

15. COFFIN, L. JR. (1972). The Effect of High Vacuum on the Low Cycle Fatigue Law. Metallurgical Transaction, Vol 3, pp. 1777-1788.        [ Links ]

16. COFFIN, L. Damage Evaluation and Life Extension of Structural Components. Editado por Moura, C. Guerra, L. Advances in Fatigue Science and Technology. Nato ASI Series. Vol 159. England, pp. 727-730.        [ Links ]

17. GOSWAMI, T. (1996). Prediction of Low Cycle Fatigue Lives of Low Alloy Steels. ISIJ International, Vol 36, N 3, pp.354-360.        [ Links ]

18. THORPE, T. SMITH, G. (1981). Elevated Temperature, Low Cycle Fatigue of AISI 316 Stainless Steel. Editado por: Francois, D. Advances in fracture Research. Vol 5. 5th International Conference on Fracture. Francia, pp.2413-2421.        [ Links ]

19. BATAILLE, A. (1992). Modelisation Numerique de L’endommagement Physique en Fatigue: Cas de L’acier 316L et D’un Acier Ferrito-Perlitique. These de Doctorat en Sciences des Matériaux, Université.A        [ Links ]

20. AZERY Z., PLUVINAGE G. (1994). Utilisation d’un Modèle Probabiliste pour L’évaluation des Différentes Stades de Croissance de Fissures et de L’endommagement en Fatigue Oligocyclique à Chaud. Matériaux et Techniques N° 8-9, pp. 33-38.        [ Links ]

21.  POLAK, J. OBRTLIK, K, VASEK, A. (1997). Short Crack Growth Kinetics and Fatigue Life of Materials. Materials Science and Engineering A234-236, pp. 970-973.        [ Links ]

22.  HUSSAIN K., DE LOS RIOS E. R., NAVARRO A. (1993). A Two-Stage Micromechanics Model For Short Fatigue Cracks. Engineering Fracture Mechanics Vol 44, N°3, pp. 425-436.        [ Links ]

23.  STOLARZ, J. (1998). Stereological Analysis of Fatigue Short Crack Propagation Zircaloy-4. Low Cycle Fatigue and Elasto-Plastic Bahaviour of Materials K-T Rie and P. D. Portella (Editors), Elsiever Science, pp. 535 –540.        [ Links ]

24.  BATAILLE, A., MAGNIN T. (1994). Surface Damaging Accumulation In Low Cycle Fatigue : Physical Analisis and Numerical Modelling. Acta Metall. Mater Vol 42, N° 11, pp. 3817-3825.        [ Links ]

25.  HUSSAIN K. (1997). Short Fatigue Crack Behaviour and Analytical Models: A Review. Engineering Fracture Mechanics Vol 58, N°4, pp. 327-354.        [ Links ]