Conductividad térmica en metales, semiconductores, dieléctricos y materiales amorfos.

FREDDY FERNÁNDEZ-ROJAS¹,  CARLOS J. FERNÁNDEZ-ROJAS¹,  KEYFFER J. SALAS P.¹,  VÍCTOR J. GARCÍA¹, ERNESTO E. MARINERO²

¹ Universidad de los Andes, Facultad de Ciencias, Departamento de Física, Grupo de Física de la Materia Condensada. La Hechicera, Mérida 5101 Venezuela. e-mail: freddyf@ula.ve

²  San Jose Research Center 3403 Yerba Buena Road San Jose CA 95135.

RESUMEN

Se estudia la física de la conductividad térmica y sus aspectos más importantes en una variedad de materiales. La conductividad térmica es influenciada por diferentes mecanismos de dispersión de fonones o electrones, los cuales limitan el transporte de energía térmica en el sólido. La conductividad térmica a una temperatura cercana al 80% de la temperatura de fundición es elevada en metales (~300 W/mK) y en semiconductores (~22 W/mK); es baja en dieléctricos (~6 W/mK) y es muy baja en materiales amorfos (~1,5 W/mK). En particular, en materiales amorfos la muy baja conductividad térmica es consecuencia del desorden atómico y de la ocurrencia de procesos de dispersión asociados a la existencia de potenciales de pozo doble asimétricos y a la presencia de modos vibracionales localizados. El propósito de este estudio es revisar las teorías existentes para explicar la conductividad térmica en sólidos y así identificar aspectos o procesos físicos relevantes en el régimen de muy altas temperaturas y antes de la temperatura de fundición, que nos permita articular las conclusiones en un referencial que nos sirva de guía para la especificación y preparación de materiales que puedan ser usados en la elaboración de la nueva generación de barreras térmicas. Nuestro interés se restringe al estudio de la conductividad térmica en sólidos dieléctricos a muy altas temperaturas, en donde hemos encontrado que la contribución de los fonones con un camino libre medio del orden de las dimensiones de las constantes de la red es muy importante y en algunos casos también se logra identificar una contribución relevante por parte de los electrones y/o fonones localizados (fractones localizados).

Palabras clave: Conductividad térmica, Fonones, Electrones, Fractones, Fonones localizados, Barreras térmicas.

Thermal conductivity in metals, semiconductors, dielectrics and amorphous materials.

ABSTRACT

We studied the physics underlying thermal conductivity and the most important thermal properties in a myriad of materials. Thermal conductivity is determined by different phonons or electron scattering mechanisms that limit the transport of thermal energy inside the solid. For the sake of the analysis, thermal conductivity close to 80% of melting point in metals is elevated (~300 W/mK) and low in semiconductors (~22 W/mK); is lower in dielectrics (~6 W/mK) and is very low in amorphous materials (~1,5 W/mK). The very low thermal conductivity in amorphous materials is a consequence of the atomic disorder, the occurrence of scattering processes associated with the existence of asymmetric double-well potential and localized vibrational modes. The purpose of this study is to review existing theories explaining the thermal conductivity of solids and so identify issues or relevant physical processes with regard to conditions of very high temperature and near to the melting point that could be important when studying thermal conductivity. This would allow us to place the findings in a framework that could guide the functionalization and preparation of materials that can be used in the elaboration of the new generation of thermal barrier coatings. Our interest is restricted to the study of thermal conductivity at very high temperatures in dielectric solids, where we found that the contribution of phonons with a free path of the order of an interatomic spacing is very important and in some cases we also found relevant the contribution of electrons and/or localized phonons (fractons).

Keywords: Thermal conductivity, Phonons, Electrons, Fractons, Localized phonons, Thermal barriers coating.

Recibido: noviembre de 2007   Recibido en forma final revisado: abril de 2008

INTRODUCCIÓN

La teoría cinética elemental de los gases conduce a la siguiente ecuación para la conductividad térmica, k = (1/3) C_V^SP vl, donde v es la velocidad promedio de los portadores de energía térmica, l es el camino libre medio de dichas partículas (distancia promedio recorrida entre colisiones sucesivas) y C_V^SP es el calor específico a volumen constante. En un sólido existen diferentes portadores de energía térmica, siendo los electrones y fonones o paquetes de ondas elásticas los más representativos. Hay algunos casos en los cuales las ondas electromagnéticas (radiación térmica), ondas de spin y otras son consideradas como portadores de energía térmica, lo que nos permite generalizar la expresión anterior a: , el subíndice i denota el tipo de portador y la sumatoria está dada sobre un           conjunto  de portadores.

La conductividad térmica es afectada por una variedad de mecanismos de dispersión de los portadores de energía térmica. La frecuencia de ocurrencia de eventos de dispersión determina en buena medida la conductividad térmica. El camino libre medio de los portadores es limitado por la naturaleza del elemento dispersante, tales como: impurezas, imperfecciones de la red, interacción fonónfonón, interacción electrón-fonón, etc.

Basado en las teorías propuestas por Debye (1914); Peierls (1929); Klemens (1951), para explicar la conductividad térmica de los sólidos cristalinos Callaway (1959) desarrolló un modelo fenomenológico que facilita el cálculo de la conductividad térmica de la red a bajas temperaturas. Para ello consideró los siguientes mecanismos de dispersión:

a) Impurezas (isótopos)

b) Proceso normal de tres fonones

c) Procesos «umklapp»

d) Dispersión por la frontera de la muestra

En el modelo de Callaway (1959), no existe distinción entre un fonón longitudinal y un fonón transversal, el tiempo de relajación para procesos normal y umklapp es equivalente (t_N^-1 t_U^-1) y proporcional a ω²T³, expresión sólo válida para fonones longitudinales de baja frecuencia. Un modelo más completo de la conductividad térmica fue propuesto por Holland (1963), este modelo considera además de las contribuciones señaladas por Callaway (1959) la contribución de fonones longitudinales y transversales (diferentes fonones polarizados).

No fue sino hasta comienzos del siglo XXI cuando Srivastava (2001) partiendo del modelo de Callaway (1959) y Holland l (1963) conceptualizó un modelo, suficientemente general como para explicar la conductividad térmica en sólidos cristalinos en todo el rango de temperaturas desde 0 K hasta aproximadamente la temperatura de fundición. En este modelo se expresa la conductividad térmica como una función de la dinámica de los fonones, la cual es influenciada por los diferentes mecanismos de dispersión que se manifiestan entre fonones durante el transporte de energía térmica. El modelo propuesto por Srivastava (2001) usa conceptos propios de la física estadística y toma en consideración cuatro elementos esénciales: a) la relación de dispersión de los fonones ω = ω (qs), la cual relaciona la frecuencia de vibración ω y el vector de onda; q b) el tiempo de relajación, t (qs) = l (qs)/ ns (qs) el cual incluye el camino libre medio para los fonones en todos sus posibles modos o mecanismos de interacción y a diferente temperatura; c) la estadística de Bose-Eintein y d) un método numérico confiable para ejecutar la suma de la expresión.

El propósito de este estudio es revisar las teorías existentes para explicar la conductividad térmica en sólidos y así identificar aspectos o procesos físicos relevantes en el régimen de muy altas temperaturas y antes de la temperatura de fundición, que nos permita articular las conclusiones en un referencial que nos sirva de guía para la especificación y preparación de materiales que puedan ser usados en la elaboración de la nueva generación de barreras térmicas.

CONDUCTIVIDAD TÉRMICA EN SÓLIDOS

En un sólido varios portadores de energía contribuyen a la conductividad térmica, estos son fonones, electrones, fractones, fotones, par electrón-hueco, y electrones y huecos. Si consideramos que cada portador contribuye en forma independiente a la conductividad térmica, la expresión más general de la conductividad térmica para los sólidos se define entonces como la sumatoria de todas las contribuciones:

  (1)

donde:

  (2)

  (3)

  (4)

El primer término del lado derecho de la ecuación (4) representa la contribución de los portadores de carga llamado a veces término polar y el segundo término representa la contribución del par electrón-hueco o termino bipolar:

  (5)

  (6)

  (7)

En las ecuaciones de la (2) a la (7); ħ es la constante de Planck dividida por 2p, V representa el volumen del cristal, T es la temperatura, k_B es la constante de Boltzmann, ω (qs) es la frecuencia, sc(q) = Ñω(qs). es la velocidad de grupo del paquete de ondas elásticas, (qs) es el número promedio de fonones en el q -ésimo modo, dada por la función distribución de Bose-Einstein, t(qs), t_e, t_fractón son el tiempo de relajación efectivo para fonones con vector de onda q e índice de polarización s, y el tiempo de relajación de electrones y fractones, respectivamente; m es la masa del electrón, n_e es la velocidad del electrón, N es el número de electrones, r es la resistividad eléctrica, e carga del electron, b tasa de movilidad del par electronhueco, E_G es la brecha de energia entre la banda de valencia y la banda de conduccion y,  D_a (T) es la constante de difusion asociada a el movimiento o viajes cortos «áhopping» «salto» de los fractones o modos localizados, C_a (T) es el calor especifico a volumen constante del fracton en el modo a y R (ω_a ) es la distancia entre la posicion espacial de los estados inicial y final del fracton, s_R es la constante de Stefan-Boltzmann, n es el indice de refraccion y l_foton es el camino libre medio del foton.

El principal problema que se presenta al estudiar la conductividad termica es determinar el comportamiento del camino libre medio de los portadores de energia termica, debido a los diferentes mecanismos de dispersion que pueden ocurrir en el solido. A continuacion, identificamos los mecanismos de dispersion que consideramos mas relevantes.

Existen varios mecanismos de dispersion que limitan el valor del camino libre medio l del portador. No trataremos todos ellos con detalles, pero incluiremos los mas frecuentes en el proceso de conduccion de energia termica en la tabla 1.

Los tiempos de relajacion se combinan usando el promedio geometrico para dar un valor efectivo total t de los diferentes procesos de dispersion:

(8)

CONDUCTIVIDAD TERMICA EN METALES

 La conductividad termica en metales es modelada considerando que las contribuciones mas importantes son debidas a los electrones libres (ecuacion 3) y a los fonones (ecuacion 2). En general, la energia termica es transportada en mayor cantidad por electrones y en menor cantidad por fonones, aunque a altas temperaturas se hace mas relevante la contribucion debida a los fonones.

Existen varios mecanismos de dispersion de electrones y fonones que limitan el valor del camino libre medio de los portadores de energia termica en los metales; a continuacion, trataremos los mecanismos de dispersion mas relevantes, para ello dividiremos la grafica de k vs T. en cuatro regiones, dependiendo del patron de variacion de la conductividad con la temperatura.

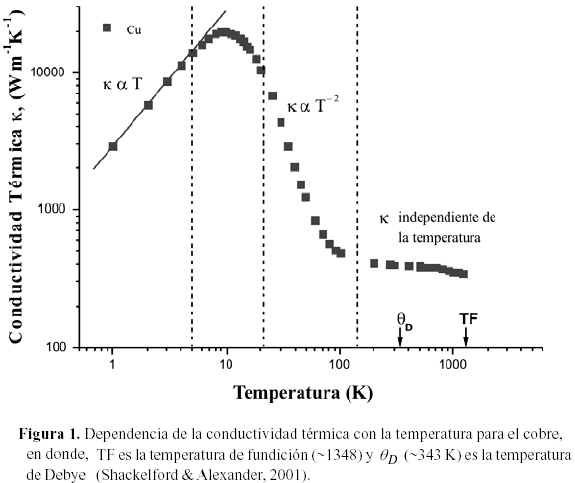
La figura 1 muestra la conductividad termica como funcion de la temperatura de un metal puro, en este caso particular la del cobre. La grafica esta dividida en cuatro regiones con la intencion de identificar y mostrar los diferentes mecanismos de dispersion en todo el rango de temperatura desde 0 K hasta la temperatura de fundicion. En la region I, con temperaturas entre 0 y 5 K, domina la dispersion de electrones por impurezas, defectos de la red y frontera o dimensiones del metal. El camino libre medio de los electrones es inversamente proporcional a la concentracion de impurezas, es decir, l_e µ 1/n_i y la conductividad se incrementa en proporcion a la temperatura (k µ T). La region II, donde la conductividad termica alcanza un maximo, es influenciada por el efecto del tamano de los granos, dislocaciones y la anarmonicidad en la red. Esta region define una transicion entre la region I y la region III.

En la region III, la influencia de las anarmonicidades de la red son significativas, lo que conduce a una disminucion de la conductividad termica, en este caso, la concentracion de fonones se incrementa con la temperatura elevada al cubo ( n_fonones µ T³) y l_fonon µ T^-3, asi la conductividad termica se hace proporcional al inverso de la temperatura elevada al cuadrado ( ( k µ T^-2) . Finalmente en la region IV, la concentracion de fonones se incrementa con la temperatura ( n_fonones µ T), el camino libre medio del fonon es inversamente proporcional a la temperatura ( l_fonón µ T^-1) y la conductividad termica se hace independiente de la temperatura. Asi, en la region IV el comportamiento de la conductividad termica es debido a electrones y fonones cuyo camino libre medio es del orden del espaciamiento interatomico (Auerbach y Allen, 1984).

En la figura 2, se puede observar la dependencia de la conductividad termica en funcion de la temperatura normalizada con respecto al punto de fundicion para varios metales, desde metales con un punto de fundicion elevado como el W, Ta y Zr, hasta metales con un menor punto de fundicion (Cu, Ag, Al, Au).

La conductividad termica en cada metal, tiene un maximo en la region intermedia a bajas temperaturas. Cuanto mas pura es la muestra mayor y mejor definido es este maximo, de acuerdo a la figura 2.

Por debajo de este maximo la conductividad es proporcional a la temperatura y esta dependencia lineal se puede observar en la figura 2. La conductividad termica en semiconductores y dielectricos es mas complicada que la de los metales porque, ademas de que los procesos de dispersion de electrones dependen significativamente de la temperatura (a altas temperaturas en dielectricos), como en el caso de un metal, el numero real de portadores de energia termica varia con la temperatura. Hemos visto que en los metales, la dispersion de electrones libres ocurre por la interaccion con los fonones y atomos de impurezas. En los semiconductores y dielectricos ocurren estos dos tipos de interaccion, pero su dependencia con la temperatura es diferente. A continuacion, se discute el comportamiento de la conductividad termica en semiconductores y dielectricos.

CONDUCTIVIDAD TERMICA EN SEMICONDUCTORES Y DIELECTRICOS

Los fonones son los principales contribuyentes a la conductividad termica en los solidos no metalicos. Es importante conocer la relacion de dispersion (ω = ω (qs)) que relaciona la frecuencia de vibracion ω y el vector de onda q, y el camino libre medio del fonon, el cual puede ser obtenido resolviendo la ecuacion de transporte de Boltzmann (Srivastava, 1990).

A medida que la temperatura en el solido cambia, el espectro de vibraciones de la red cambia: a bajas temperaturas dominan modos vibracionales de baja frecuencia (longitud de onda larga) y la conductividad termica depende del tamano y forma del cristal, si se incrementa la temperatura dominan modos de alta frecuencia (longitud de onda corta) y la conductividad aumenta hasta alcanzar un maximo, a temperatura por arriba de este maximo la conductividad termica es limitada por la interaccion fonon-fonon. Cerca del maximo, k es afectado por las imperfecciones e impurezas en el solido. Finalmente a muy altas temperaturas se hace independiente de la temperatura y su magnitud se reduce a un valor pequeno (Clarke, 2003; Fernandez et al. 2006). En semiconductores a muy altas temperaturas (temperaturas mucho mas elevadas que la temperatura de Debye, T >> q_D), la contribucion a la conductividad por parte de los electrones resulta ser importante (~40% ) (Glassbrenner & Slack, 1964; Fulkerson et al. 1968). En semiconductores la conductividad termica total resulta de sumar la contribucion de los fonones, (ecuacion (2)), la contribucion de los electrones, (ecuacion (4)), y la contribucion de la radiacion termica (Parrot, 1975; Kelly et al. 2006), (ecuacion 1), en el caso de dielectricos corresponde a las ecuaciones (2) y (7).

En la figura 3, se muestra la conductividad termica en funcion de la temperatura para un semiconductor tipico, como el silicio. Tambien se resaltan las cuatro regiones caracteristicas de diferentes regimenes de conductividad termica, que a su vez y a diferencia de los metales, son caracterizados por diferentes mecanismos de dispersion, los cuales se muestran en la tabla 1.

En la region I, la conductividad termica es determinada por las dimensiones fisicas del material, el tamano del grano y el espaciamiento entre dislocaciones. En la region II se reducen las contribuciones por efecto del tamano de los granos, dislocaciones y por falta de armonia (anarmonia) en la red. El pico en la region II usualmente ocurre a una temperatura ~ q_D /20. A temperaturas por encima de este pico, en la region III, la falta de armonia (anarmonia) de los fonones comienza a ser significativa disminuyendo la conductividad termica de forma tal que ¥ê se hace proporcional al inverso de ( k µ T^-1). Finalmente, en la region IV el comportamiento de la conductividad termica es debido a fonones cuyo camino libre medio es del orden de un espaciamiento interatomico y la conductividad se hace independiente de la temperatura (Fernandez et al. 2006).

En la figura 4, se observa la dependencia de la conductividad térmica en función de la temperatura normalizada con respecto a la temperatura de fundición para varios semiconductores.

En semiconductores y dieléctricos la principal contribución a la conductividad térmica es debido a fonones. A altas temperaturas se observa que la conductividad disminuye debido a la interacción fonón-fonón y procesos de múltiples fonones. La figura 5 muestra la dependencia de la conductividad térmica en función de la temperatura normalizada con respecto al punto de fundición para el diamante y varias muestras policristalinas de óxidos.

Mientras que los materiales cristalinos y, en menor medida, los semicristalinos presentan un patrón regular y repetitivo de átomos o iones formado de estructuras tridimensionales periódicas, los materiales amorfos no tienen orden de largo alcance o estructura cristalina, es decir, no tienen un ordenamiento periódico.

Nuestra preocupación principal es describir y explicar algunas propiedades importantes de los sólidos amorfos, actualmente el interés en este campo es la búsqueda de nuevos materiales para la elaboración de barreras térmicas. A continuación se discute el comportamiento de la conductividad térmica en estos materiales.

CONDUCTIVIDAD TÉRMICA EN SÓLIDOS AMORFOS

En los sólidos amorfos en general, la conductividad térmica tiene un valor muy pequeño a temperatura ambiente, cuando se compara con otros materiales y se reduce aún más al disminuir la temperatura. Esta baja conductividad es consecuencia del desorden atómico, que es responsable del camino libre medio tan pequeño, l , de los fonones. La diferencia en la conductividad térmica en un sólido amorfo y en su fase cristalina se resume en tres características principales: i) a temperaturas entre 0 y 3 K, la conductividad termica es proporcional al cuadrado de la temperatura (k µ T²), ii) los solidos amorfos no exhiben un pico en la curva k  vs., el cual es caracteristico de todos los solidos cristalinos, asi, para los amorfos la conductividad se hace constante entre 3 y 15 K y iii) por arriba de 15 K, hay un incremento de la conductividad con el aumento de la temperatura (Jagannathan et al. 1989; Srivastava, 1990). Estas tres caracteristicas son mostradas por las regiones I, II, III en la figura 6.

En la region I o temperatura por debajo del «plateau »(< 3 K), dominan fonones de baja energia, la fuente principal de dispersion de fonones en este rango de temperatura se debe a la presencia de estados de tunelamiento. La dispersion resonante ocurre entre dos niveles de baja energia del potencial de pozo doble asimetrico. El camino libre medio de los fonones en cada evento de dispersion varia con la temperatura de acuerdo a la siguiente expresion, l µ coth ( ħw/ 2 k_BT), para fonones de bajas frecuencias, el camino libre medio es proporcional a la temperatura (l µ T) y la conductividad termica es proporcional a T². En la region II a temperaturas entre 3 y 15 K, la conductividad se hace constante. Orbach et al. (1986) sugieren un modelo para explicar este comportamiento basado en las interacciones anarmonicas entre fractones (longitud de onda corta) y fonones (longitud de onda larga). El modelo de Orbach introduce la idea de fonones propagandose a baja frecuencia ( ħw< k_BT) y fractones localizados espacialmente a alta frecuencia con temperatura T » ħw_c / k_B, donde; w_c  es la frecuencia umbral de separacion entre un fonon y un fracton. Los fractones no portan energia termica debido a que representan modos vibracionales localizados. Por lo tanto, los fonones de muy corto camino libre medio ( l_fonon ) son el unico medio de transporte de energia termica. Considerando que el camino libre medio del fonon es independiente de la temperatura, la conductividad termica se hace constante (Alexander et al. 1986). En esta region el principal proceso de dispersion del fonon es la interaccion entre fractones y fonones del tipo:

A temperaturas por arriba del «plateau» o region III, la conduccion de energia termica es debido a fonones inducidos y mecanismos de salto ¡ìhopping¡í del fracton, conduciendo a una conductividad termica que se incrementa con la temperatura. Las interacciones anarmonicas en esta region son del tipo:

La conservacion de la energia puede ser satisfecha considerando w_fonón << wf_racton. En la region III, el inverso del tiempo de vida del fracton (mecanismo de salto «hopping») se incrementa linealmente con la temperatura t^-1_fracton  µ T  y el calor especifico (C_a (T)) a temperaturas por arriba de la region de ¡ìplateau¡í es constante. Asi, la conductividad termica representada por la ecuacion (5) es proporcional a T.

Considerando el mecanismo de salto del fracton como un mecanismo extra para la conduccion de energia termica, podemos expresar a temperaturas por arriba de la region de «plateau», a la conductividad termica como proporcional a la temperatura (k_fracton µ T).

La figura 7 muestra la conductividad térmica en función de la temperatura normalizada con respecto al punto de fundición para algunos sólidos amorfos.

De lo anteriormente expuesto surge una estrecha relación entre los principales procesos físicos que se manifiestan en los materiales estudiados a muy altas temperaturas. A continuación se menciona este comportamiento y se analiza la conductividad térmica a muy altas temperaturas para varios sólidos, en especial, para dieléctricos y amorfos.

INTERPRETACION DE RESULTADOS EXPERIMENTALES A ALTAS TEMPERATURAS

En la region de altas temperaturas (T > q_D) y antes de la temperatura de fundicion, los principales portadores que contribuyen a la conductividad termica son; fonones y electrones (interaccion electron-fonon) en metales; fonones, electrones (par electron-hueco, electrones, huecos) y fotones en semiconductores y para el caso de dielectricos, los fonones (procesos de tres, cuatro y mas fonones), la radiacion termica y posiblemente los electrones en un muy bajo porcentaje. Fractones y fonones en solidos amorfos.

En la figura 8 se observa que la conductividad termica a una temperatura cercana al 80% de la temperatura de fundicion es elevada en metales (~300 W/mK) y en semiconductores (~22 W/mK); es baja en dielectricos (~6 W/mK) y es muy baja en materiales amorfos (~1,5 W/mK).

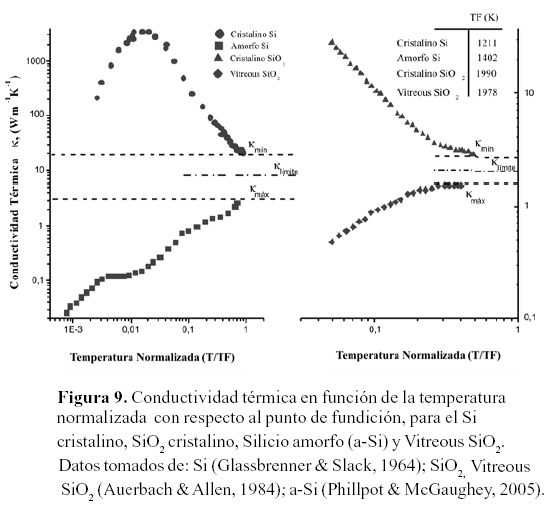
La figura 9 muestra que el valor de la conductividad termica a muy altas temperaturas en solidos dielectricos y materiales amorfos parece «converger» o se aproxima a un valor limite, en el caso de los dieléctricos hablamos de un valor mínimo de conductividad térmica antes del punto de fundición y en el caso de los materiales amorfos se habla de un valor máximo para la conductividad antes del punto de fundición. Este valor límite de la conductividad térmica a muy altas temperaturas es intrínsico al material y debe ser muy similar al valor de la conductividad térmica del sólido en su fase líquida.

Aunque los materiales amorfos muestran una conductividad térmica a temperatura ambiente mucho menor que la de los sólidos cristalinos (~1 W/mK), (figura 8), los datos sugieren que la diferencia en conductividad térmica entre un material amorfo y un dielectrico no es relevante a temperaturas muy por encima de la temperatura de Debye (Clarke y Phillpot, 2005), lo que nos conduce a pensar que los diferentes procesos fisicos (presencia de modos vibracionales localizados) que se manifiestan en los materiales amorfos pueden ser relevantes en la comprension del valor minimo de conductividad termica de solidos cristalinos dielectricos registrado a muy altas temperaturas (figura 9). Esta observacion nos presenta la posibilidad del uso de materiales amorfos en la elaboracion de barreras termicas. Considerando que: 1) los solidos amorfos muestran estabilidad a temperaturas elevadas (Majundar y Jana, 2001); 2) el muy bajo valor de  k a T >> q_D  debido a procesos de transporte de energia termica no convencionales, tales como el salto de fonones localizados.

CONCLUSIONES

La conductividad termica a una temperatura cercana al 80% de la temperatura de fundicion es elevada en metales (~300 W/mK) y en semiconductores (~22 W/mK); es baja en dielectricos (~6 W/mK) y es muy baja en materiales amorfos (~1,5 W/mK).

En metales puros la contribucion mas dominante es la de los electrones, siendo equivalente a unas veinte veces la contribucion de los fonones. La conductividad termica se hace constante a temperaturas por debajo de la temperatura de Debye y la contribucion de fonones es importante a altas temperaturas.

Para metales la conductividad termica comienza a ser constante a una temperatura entre 2 y 5% del punto de fusion (efecto de los fonones), mientras que para semiconductores y dielectricos la conductividad se hace constante entre un 60 y 80% del punto de fusion (efecto de los electrones y otros portadores, como fonones localizados).

En semiconductores la contribucion de electrones a bajas temperaturas es de un 3% y a muy altas temperaturas corresponde aproximadamente a un 60% (Glassbrenner y Slack, 1964).

En dielectricos domina la contribucion por fonones, la conductividad termica se hace constante a muy altas temperatura. Los procesos de interaccion fonon-fonon de alto orden que pueden ocurrir incluyen procesos de tres, cuatro y mas fonones, los procesos de tres fonones y mas, contribuyen a la dependencia de k con T^-1 siendo significativa la contribucion de los procesos donde participan tres fonones, los procesos de cuatro fonones y mas, los cuales juegan un rol relevante cuando la temperatura alcanza valores muy altos (T >> q_D ) y la conductividad termica alcanza su valor minimo, sin embargo, se espera que exista contribucion de otros portadores tales como electrones libres a muy altas temperaturas y antes de la temperatura de fundicion, cuya naturaleza desconocemos y una contribucion por mecanismos de salto ¡ìhopping¡í de modos vibracionales localizados. Es importante mencionar que el transporte de energia termica por radiacion es relevante a muy altas temperaturas.

Procesos fisicos como los modos vibracionales localizados que se manifiestan en los materiales amorfos pueden jugar un rol muy importante en los materiales dielectricos a muy altas temperaturas y antes de la temperatura de fundición, ya que en ambos casos sus conductividades térmicas tienden a «converger» a un valor límite y la relación entre el valor máximo de la conductividad térmica en materiales amorfos y el valor mínimo de la conductividad en materiales cristalinos, podría servir para explicar en parte el valor de la mínima conductividad térmica a muy altas temperaturas para los sólidos cristalinos dieléctricos.

REFERENCIAS

1. AUERBACH, A. & ALLEN, P. B. (1984). Physical Review B, 29 (6); 2884-2890.        [ Links ]

2. ALEXANDER, S., ENTIN-WOHLMAN, O., ORBACH, R. (1986). Physical Review B, 34 (4); 2726-2734.        [ Links ]

3. CALLAWAY, J. (1959). Physical Review, 113 (4); 1046-1051.         [ Links ]

4. CLARKE, D.R. (2003). Surface and Coatings Technology, 163 (164); 67-74.        [ Links ]

5. CLARKE, D.R. & PHILLPOT, S.R. (2005). Materials Today, 22-29.        [ Links ]

6. DEBYE, P. (1914). Vortrage uber die kinetische theorie dermaterie und der elektrizitat, Teubner, Berlin.        [ Links ]

7. FERNÁNDEZ, F., RONDÓN, E., SANCHEZ, F., SALAS, K., GARCÍA, V., MAURO, J. (2006). Revista de la Facultad de Ingeniería (UCV, Caracas), 21 (2); 21-27.        [ Links ]

8. FULKERSON, W., MOORE, J.P., WILLIAMS, R.K., GRAVES, R. S., MCELROY, D. L. (1968). Physical Review, 167 (3); 765-782.        [ Links ]

9. GLASSBRENNER, C.J., & SLACK, G.A. (1964). Physical Review, 134 (4A); A1058-A1069.        [ Links ]

10. HOLLAND, M.G. (1963). Physical Review, 132 (6); 2461-2471.        [ Links ]

11. JAGANNATHAN, A., ORBACH, R., ENTIN-WOHLMAN, O. (1989). Physical Review B, 39 (18); 13465-13477.        [ Links ]

12. JAMES, F. S., & WILLIAM, A. (2001). Materials Science and Engineering Handbook. Third Edition. Crs Press.        [ Links ]

13. KLEMENS, P.G. (1951). Proc. R. Soc. A208; 108.         [ Links ]

14. MAJUNDAR, A. & JANA, S. (2001). Bull. Mater. Sci, 24 (1); 69-77.        [ Links ]

15. MATTHEW, J.K., WOLFE, D.E., SINGH, J. (2006). Applied Ceramic Technology, 3 (2); 81-93.        [ Links ]

16. OLSON, J. R., & POHL, R. O. (1993). Physical Review B, 47 (22); 14850-14856.        [ Links ]

17. OLSON, J.R., POHL, R.O., VANDERSANDE, J.W., ZOLTAN, A., ANTHONY, T.R., BANHOLZER, W.F. (1993). Physical Review B, 47 (22); 14850-14856.        [ Links ]

18. OMINI, M., & SPARAVIGNA, A. (2000). Physical Review B, 61(10); 6677-6688.        [ Links ]

19. PARROT, J.E., & STUCKES, A.D. (1975). Thermal Conductivity of Solids. London: Pion Ltd.        [ Links ]

20. PHILLPOT, S.R., & MCGAUGHEY, J.H. (2005). Materialstoday; 18-20.        [ Links ]

21. PIERLS, R. (1929). Ann. der Phys, 3; 1055.        [ Links ]

22. SRIVASTAVA, G. P. & VERMA, G.S. (1974). Physical Review B, 10 (1); 219-225.        [ Links ]

23. SPAVIERI, G., CABREA, F., MARCANO, G., ROMERO, H. (1980). Physical Review B, 21 (4); 1610-1616.        [ Links ]

24. SLACK, G.A. (1972). Physical Review B, 6 (10); 3791-3800.        [ Links ]

25. SRIVASTAVA, G.P. (2001). Materials Research Society Bulletin, 26 (6); 445-450.        [ Links ]

26. SRIVASTAVA, G.P. (1990). The Physics of Phonons. Bristol: Adam Hilger.        [ Links ]

27. ZELLER, R. C., & POHL, R.O. (1971). Physical Review B, 4 (6); 2029-2041.        [ Links ]

28. ZIMAN, J.M. (1960). Electrons and Phonons (First Edition ed.). Clarendon: Oxford.        [ Links ]