El comercio de canicas: Herramienta de apoyo para la enseñanza-aprendizaje práctico de la programación lineal

Jorge Pérez¹, Patricia Jaramillo², Luis Moreno²

¹Universidad de Antioquia. Grupo de Investigación Gestión de la Calidad. Departamento Ingeniería Industrial. Medellín – Colombia. e-mail: ejipr056@udea.edu.co

²Universidad Nacional de Colombia. Escuela de Sistema. Medellín – Colombia. e-mail: pjaramillo@unal.edu.co; lfmoreno@unal.edu.co

RESUMEN

Este artículo ofrece una lúdica denominada “El Comercio de Canicas”, diseñada para complementar la clase magistral de programación lineal (PL) con elementos prácticos que permitan incorporar principios constructivistas, aprendizaje colaborativo y basado en problemas, en los procesos de enseñanza-aprendizaje de: modelación, resolución y análisis de sensibilidad, y a su vez, vincularlos con el contenido de otras asignaturas. Desde el punto de vista académico se llena un vacío de conocimiento en el ámbito específico para el que fue desarrollado, y además, a nivel general subyace información útil para docentes, estudiantes e investigadores, como: ideas para trabajos futuros y elementos metodológicos que sirven de guía para estudiar y generar otras herramientas de apoyo a cursos magistrales. A nivel práctico, dado su diseño, simplicidad y accesibilidad a los materiales que se requieren, puede ser desplegada tal cual en cursos de PL de cualquier institución educativa. A modo de validación, la lúdica es desplegada exitosamente en uno de los cursos de PL de la Universidad de Antioquia (Colombia), exponiéndose en este artículo aspectos que más gustan, lecciones aprendidas y oportunidades de mejora.

Palabras clave: Lúdica, Programación lineal, Enseñanza de la investigación de operaciones, Aprendizaje basado en problemas, Aprendizaje colaborativo.

“Marbles marketplace”: Support tool for the teaching-learning experience of linear programming

ABSTRACT

This paper proposes a game called “Marbles Marketplace”, designed to complement theoretical classes of linear programming (LP) with practical elements that allow us to incorporate constructivist principles and collaborative learning based on problems on the teaching-learning process of modeling , resolution and sensitivity analysis, and in turn, to link them with topics from other courses. From the academic point of view, a gap in knowledge is filled in the specific field for which the article was developed, and besides, at a general level, there is information for faculty, students and researchers, such as: ideas for future work and methodological elements that serve as a guide to study and generate other tools to support theoretical courses. On a practical level, given its design, simplicity and accessibility of the materials needed, the game can be deployed as it is on PL courses of any educational institution. As a way of validation, the game is successfully deployed in one of the PL courses at the University of Antioquia (Colombia); in this article we show aspects that participants seemed to like the most, the lessons learned and opportunities for improvement.

Keywords: Game, Linear programming, Teaching operations research, Problem-based learning, Collaborative learning.

Recibido: septiembre de 2009   Recibido en forma final revisado: febrero de 2010

INTRODUCCIÓN

La enseñanza de la programación lineal (PL), específicamente la modelación matemática, la resolución y el análisis de sensibilidad, son temas que pueden dificultar la asimilación en estudiantes que construyen su propio aprendizaje a partir de la búsqueda de satisfacción de sus propias necesidades y de la generación de experiencias individuales con el entorno.

Hoy día, en el contexto educativo, es creciente la necesidad de vincular contenidos desarrollados en los cursos con situaciones propias de fenómenos reales, que evidencien la practicidad de lo aprendido en el ámbito en el que se desempeña o se desempeñará el estudiante.

Todo lo anterior, con la firme intención de disminuir causas de deserción y de incrementar motivación, compromiso, utilidad y comprensión del estudiante en torno a los conocimientos que, como coproductor de su propia formación, se desea adquiera, desarrolle y evidencie.

En los últimos años, el uso de actividades lúdicas, como herramientas para incorporar los anteriores elementos pedagógicos en las sesiones magistrales, vienen incrementándose. Por ejemplo, en firmas consultoras de talla mundial, responsables de capacitar y de entrenar personal operativo de las empresas, puesto que, dados los escenarios laborales (agotamiento, personal adulto, entorno bajo presión, necesidades específicas en temas como calidad y productividad, entre otros), empleando sesiones magistrales, rápidamente desaparecerían del mercado.

Igualmente, en el ámbito académico colombiano esta corriente viene en auge, con eventos como los de la comunidad GEIO, orientados a la enseñanza de la Investigación de Operaciones haciendo uso de actividades lúdicas, que impactan el desarrollo procedimental del estudiante.

Las tecnologías de información y comunicación (TIC’s), la necesidad de vincular la teoría con la práctica, y de titulados competentes en torno a: pensamiento sistémico, orientación al logro, creatividad, trabajo en equipo, resolución de problemas, flexibilidad y adaptabilidad al contexto social, entre otros, son algunas de las razones que han propiciado el desplazamiento del “protagonismo” del profesor hacia el alumno, ameritando la transformación de los procesos de enseñanza-aprendizaje.

La evolución de dicho proceso destaca la importancia de generar ambientes de trabajo lúdico, colaborativo y basado en casos problema, propios de la cotidianidad, donde el estudiante parta de sus modelos mentales, interactúe con el entorno social, experimente en la realidad, reciba retroalimentación considerando varias perspectivas y genere esquemas mentales más cercanos a la “mejor” solución al progreso del ámbito en el cual se desenvuelve.

Centrando el enfoque en Ingeniería, específicamente en la enseñanza-aprendizaje de PL, vincular elementos que propicien integración entre sus contenidos, de estos con otros cursos, y a su vez, faciliten incorporar las citadas alternativas de aprendizaje, es un campo de conocimiento en infancia desde el punto de vista aplicado, cuyos aportes se hacen necesarios para la comunidad académica y empresarial.

El conocimiento adquirido por los autores, permite sistematizar el problema objeto estudio, en la siguiente pregunta de investigación:

¿Qué actividad emplear en cursos de PL, para que en la enseñanza de modelación matemática, resolución y análisis de sensibilidad, se incorporen escenarios colaborativos donde los estudiantes vivencien un problema que les despierte interés, realicen experimentaciones en la realidad y evidencien practicidad de conceptos teóricos previamente introducidos?

Desde el punto de vista académico el presente trabajo llena un vacío de conocimiento en el ámbito específico para el que fue desarrollado y además, a nivel general proporciona información útil para docentes, estudiantes e investigadores, entre la que cabe mencionar: elementos metodológicos que sirven de guía para estudiar y generar nuevas herramientas de apoyo al desarrollo procedimental en cursos magistrales, así como ideas para trabajos futuros. A nivel práctico, dado su diseño, simplicidad y accesibilidad a los materiales que se requieren, puede ser desplegado tal cual en cursos de PL de cualquier institución educativa.

El segundo apartado de este artículo ofrece un marco teórico que facilita la comprensión de las demás secciones. Luego, se describe con detalle la herramienta lúdica para apoyar la enseñanza-aprendizaje práctica de PL, la cual ha sido denominada por los autores como “El Comercio de canicas”. Seguido, se presentan evidencias de despliegue de esta herramienta en uno de los cursos de PL de la Universidad de Antioquia, destacando lo que más gusta, lecciones aprendidas y oportunidades de mejora. Finalmente, se exponen las conclusiones del estudio realizado y las referencias que lo sustentan teóricamente.

MARCO TEÓRICO

Teorías de aprendizaje

La enseñanza-aprendizaje que subyace en “El Comercio de canicas” se apoya en teorías sobre:

Constructivismo: la síntesis de esta teoría, es el asocio del aprendizaje con la creación de significados a partir de experiencias (Bednar, 1991). Es decir, la mente filtra lo que llega del mundo para producir su propia y única realidad (Jonassen, 1991). En el contexto de interés, se parte de que los estudiantes actúan como coproductores de su propia formación, construyendo aprendizaje a partir de la búsqueda

de satisfacción de sus propias necesidades, surgidas debido de experiencias e interacciones individuales.

Aprendizaje colaborativo: apoyados en John (1998) y enfocados en el ámbito de interés; esta teoría posibilita, bajo un ambiente de respeto y mediante análisis grupal de casos, que se comparta autoridad con los estudiantes, se les invita a la ayuda mutua y a participar en diálogos abiertos y significativos. Además, se intercambian opiniones, se comparte conocimiento, se soportan críticas, se compromete el pensamiento reflexivo y creativo, y se buscan consensos para el logro de objetivos, que redunden en altos niveles de aprendizaje.

Aprendizaje basado en problemas: haciendo alusión al estudiante, se le enfrenta a situaciones debidamente planeadas y estructuradas, típicas de su entorno, lo cual constituye un punto de partida para adquirir e integrar nuevos conocimientos (Barrows, 1986). Allí, siguiendo el ciclo de la exploración (Branda, 2001), se le induce a reflexionar sobre ¿qué problemas encuentra?, ¿cuáles son sus causas? y ¿cómo pueden mejorarse?

Con el ánimo de incorporar los anteriores elementos en la enseñanza-aprendizaje de PL, generando espacios donde los estudiantes interactúen y pongan en práctica sus conocimientos; es de suma utilidad la actividad lúdica, dado que permite la vinculación de: emociones, toma de decisiones, habilidades comunicativas, pensamiento creativo y entornos simulados de trabajo, constituyéndose en una importante fuente de vivencia y aprendizaje (Ortega, 2003a; 2003b).

Programación lineal (PL)

PL es una de las herramientas de la Investigación de Operaciones (IO), y ésta última remonta sus orígenes a Inglaterra y Estados Unidos durante la Segunda Guerra Mundial, con aplicación a las operaciones militares (Arreola & Arreola, 2003). El uso de la IO cobra cada vez mayor rigor en las decisiones empresariales a nivel público, privado, industrial y de servicios (Quirós, 1990; Vallada et al. 2005; Epstein et al. 2001; Waring & Wainwright, 2002; Pérez et al. 2006). En ella, empleando elementos que van desde la programación matemática hasta simulación computacional, que buscan maximizar el beneficio en una o más funciones de interés, restringidas comúnmente de manera compleja.

Entrando en materia, los problemas de PL poseen “n” variables de decisión, “n” restricciones de no negatividad, “m” restricciones tecnológicas y una sola función objetivo, siendo estas tres últimas de tipo lineal (Larrañeta, 1987). Entre los problemas más comunes abordados por medio de esta herramienta se encuentran: mezclas, programación de producción, dietas, inversiones, transporte, recorte de piezas y programación de turnos.

Para aplicar PL es necesario seguir las etapas de la IO, a saber: definición del problema, construcción del modelo, resolución, validación e implementación de la solución (Taha, 2004). Para resolver problemas de PL existen diversos métodos, siendo los más utilizados: gráfico, algebraico, Simplex (desarrollado por Dantzig (1991)) y punto interior. Con los avances en software hoy día se cuenta con innumerables herramientas, entre ellas: Gams, Solver de Excel, Lingo y el WinQsb.

Al modelo original de PL se le denomina primal, y a éste le corresponde un problema dual (Hiller & Lieberman, 1997), cuyas variables de decisión se enfocan en el valor unitario de los recursos del modelo primal, y que junto con el análisis de sensibilidad, son fundamentales, entre otros, para la toma de decisiones en procesos de compra, venta o alquiler de recursos o expansión de operaciones. Para ello, se apoyan en el significado de los precios sombra y en los intervalos en que estos pueden oscilar sin generar cambios en las variables de la base óptima del problema o en la factibilidad del mismo.

PL, si bien amerita el supuesto de comportamientos lineales en los sistemas objeto de estudio, lo cual en casos no se da, es una base fundamental para el desarrollo de habilidades y destrezas para construir, en lenguaje matemático, representaciones abstractas de una situación real, comprenderla, resolverla, analizarla y buscar mejorar su comportamiento, recurriendo posteriormente, cuando amerite, a elementos de mayores niveles, dependiendo de la complejidad del sistema de interés.

DESCRIPCIÓN DE LA LÚDICA

Caso “canicas innovadoras” (CI)

La empresa CI tiene dos nuevos productos (grande, pequeño) elaborados en dos plantas distintas. Actualmente desconoce ¿qué cantidades insertar en los mercados “A” y “B”, separados geográficamente, de modo que obtenga la mayor utilidad posible?

Para insertar los productos en dichos mercados, la empresa primero debe transportarlos, lo cual le consume combustible. En cada planta se tiene un camión que recorre 5cm por cada mililitro de combustible. En cada viaje, dichos camiones sólo pueden transportar una canica grande o dos pequeñas, y al mes, se dispone de 500 ml de combustible. Los camiones no hacen recorridos entre plantas, puesto que se considera sumamente costoso.

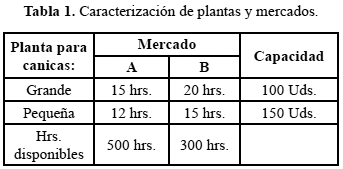
Una vez el producto está en el mercado objetivo, inician actividades publicitarias que demandan horas de promotores de venta. En la tabla 1 se muestran las horas de promoción que demanda cada tipo de canica en cada mercado, junto con las horas disponibles para promocionar y la capacidad de producción de las dos plantas.

Por cada canica grande que tenga éxito en el mercado “A” se obtiene $2.500 de utilidad, y en el mercado “B” de $2.000; en tanto que por cada canica pequeña que tenga éxito en el mercado “A” la utilidad es de $1.500 y en “B” de $1.800.

Caso “canicas de excelencia” (CE)

La empresa CE, una firma extranjera, está interesada en comprar y/o alquilar los recursos que posee canicas innovadoras y desea formular una propuesta para ofertar. Para ello, integró un equipo de profesionales de los procesos de gerencia, mercadeo, producción y mejoramiento. A esta empresa le interesa tanto la compra de capacidad de producción de canicas grandes y pequeñas, pero con la posibilidad de llevarlas al mercado (alquiler de horas de promotores y compra de combustible), colocando en ello su marca posicionada.

A las 9:40 am (la hora depende del momento de despliegue) se llevará a cabo la negociación en el restaurante del hotel PL en Medellín. Si a dicha hora en punto, una de las partes no se encuentra, recibe una multa de 10 puntos menos en la negociación (nota de la lúdica).

Como puede verse, esta empresa corresponde al caso Dual de la primera, y por tanto, toda la información de CI es de interés para CE.

Equipos de trabajo

Se forman equipos, aproximadamente de cuatro integrantes, pero garantizando que la cantidad de ellos sea un número par. En un primer momento de la lúdica los estudiantes actúan como promotores de canicas en los diferentes mercados, y en una segunda etapa, adquieren funciones de: gerencia, producción, mercadeo y mejoramiento. Dichos equipos, a su vez, pertenecen a dos grandes grupos, uno de ellos asume el caso de CI y el otro, de CE.

Materiales

Por cada equipo de trabajo se requiere lo expuesto en la tabla 2.

El facilitador, además de preparar los anteriores materiales para cada uno de los equipos, requiere cinta de enmascarar y una plantilla en cartulina (cartón paja, entre otros.), similar a la figura 1, cuyas esquinas representan las ubicaciones de las plantas y de los mercados objetivo. Esto con el propósito de estandarizar la distribución geográfica de dichos elementos para cada equipo.

La cinta que indica “Grande” representa la ubicación de la planta de producción de canicas de ese tamaño y allí, se posiciona la canica de mayor tamaño. En las demás, se ubican las tres canicas de menor tamaño. Dos de ellas representan los mercados objetivo (el tamaño en estas zonas es para dificultar el éxito en el lanzamiento), y la otra, la planta de producción de canicas “pequeñas”. Las distancias específicas se dejan a criterio del facilitador, a fin de que el estudiante, con uso de la regla, también realice mediciones para responder al caso.

Distribución del área de trabajo

La distribución del lugar donde se despliega la lúdica se presenta en la figura 2, para el caso de cuatro equipos de trabajo.

Saberes específicos

Elementos de otros cursos. A fin de obtener una estimación del posible éxito a lograr con el ingreso de cada tipo de canica en los mercados de interés, ambas empresas (CI y CE) diseñan el experimento expuesto en la figura 3.

Bajo este diseño, la variable asociada al resultado de cada experimento, puede representarse como eventos Bernoulli (Freund et al. 2000), así:

Y_ijkl: es el l-ésimo resultado de que la canica tipo i sea insertada en el mercado j, siendo ofertada por el promotor k, con Y_ijkl = 1 (se obtuvo éxito) y Y_ijkl = 0 (fracaso). Se obtiene éxito cuando el estudiante, al lanzar una de las canicas desde la ubicación de la planta de producción, ésta golpee la canica ubicada en el mercado objetivo; en caso contrario, se considera fracaso.

Sea p_ij la probabilidad de que la canica tipo i tenga éxito en el mercado j. La estimación de este parámetro está dada por la ecuación (1).

donde:

W_ij corresponde al total de éxitos que obtuvo la canica tipo i en el mercado j y N es el total de pruebas de esa canica en dicho mercado (8 veces según el experimento).

La tabla 3 ofrece la matriz de datos para el registro de los experimentos aleatorizados por medio del programa informático Statgraphics 5.1.

Elementos de PL y su vinculación con otros saberes. La función objetivo para el caso de CI, enfocada en maximizar utilidades, puede representarse como en la ecuación (2), recurriendo a la utilidad esperada en función de la probabilidad de éxito de las canicas y la cantidad a insertar en los mercados.

donde:

X_ij representa el número de canicas tipo i que serán insertadas en el mercado j y, u_ij la utilidad unitaria por cada canica i que ingresa con éxito al mercado j.

Mapa mental. En la figura 4 se presenta un esquema del caso CI, que a su vez, es de interés para los equipos de CE.

Procedimiento de despliegue. En la tabla 4 se presenta la guía de despliegue de la actividad, resaltando que es flexible con base en criterio del facilitador.

DESPLIEGUE

Evidencias de implementación

La lúdica fue corrida por primera vez en el curso de PL, del Departamento de Ingeniería Industrial, impartido en el semestre 2009-01, donde participan estudiantes de dicha carrera y también de Ingeniería de Sistemas. En el despliegue se contó con 32 estudiantes, conformándose ocho equipos de trabajo, cuatro de ellos con el caso de “CI” y los restantes, son de “CE”. En la figura 5 se recopilan fotografías que evidencian la realización de dicha actividad.

Lo que más gusta

El despliegue de la lúdica en los estudiantes del curso de PL de 2009-1, arrojó, bajo la opinión de los mismos, una serie de incidentes críticos, cuyas causas vale la pena estandarizar para asegurar que sus buenos efectos se repitan. En la tabla 5 se socializan los incidentes críticos más relevantes.

Lecciones aprendidas

En palabras de los estudiantes:

“Para realizar una buena negociación, no se trata de querer engañar a las personas con las que se negocia, …”. “Negociar bien no es ganar demasiado, es ganar y abrir la posibilidad para seguir ganando en el futuro”. “PL nos brinda elementos importantes para tomar decisiones dentro de una organización”. “Mediante el análisis de un modelo de PL, podemos tomar decisiones que nos den seguridad en una negociación de compra de recursos”. “Mediante una simulación nos podemos acercar de cierta forma a una situación real”. “Se puede estimular la negociación empresarial a través de estas lúdicas”.

Por mejorar

Del mismo modo, es fundamental tener presente lo que menos agrado generó en los estudiantes, a fin de analizar sus causas y eliminarlas, para que sus efectos no se repitan. A continuación, lo más mencionado de manera textual: “La limitación del tiempo de clase”. “Sugerimos aplicarla con más tiempo, ya que la negociación final se hace rápidamente y no se analiza como uno quisiera”. “Algunos equipos tuvieron estimaciones distintas de las probabilidades de éxito, lo que dificulta a la hora de tomar decisiones en la negociación”. “La programación del tiempo (la lúdica) en tres horas sería excelente”. “Que se haga en dos sesiones de clase y en una locación más apta para la actividad”. “Permitir cinco minutos para practicar lanzamientos, de manera que los resultados de la experimentación sean más uniformes y que no exista tanta influencia en la toma de datos, al tener integrantes que quizá posean más experiencia que otros al lanzar canicas”.

CONCLUSIONES

Se ha diseñado una lúdica de fácil replicación hasta en clases con numerosos estudiantes de cualquier institución educativa, la cual puede desplegarse con recursos fácilmente accesibles a docentes y estudiantes. Igualmente, permite incorporar en los procesos de enseñanza-aprendizaje de PL, específicamente para modelación, resolución y análisis de sensibilidad, elementos prácticos que propicien un aprendizaje basado en problemas y construcción de conocimiento a partir de necesidades reales de los estudiantes. Todo ello, además, bajo un ambiente colaborativo donde se intercambian opiniones, se estimula el pensamiento crítico, reflexivo y la inteligencia emocional, se fomenta el trabajo en equipo, el liderazgo y se muestra la asociación con saberes de la inferencia estadística y del diseño experimental.

Para el mejoramiento de la lúdica, escuchando la voz de los estudiantes y mediante observación del despliegue, se propone realizarla en tres horas, puesto que las dos de una clase típica llevan a una negociación final acelerada, imposibilitando que se reflexione y se aplique, con tranquilidad emocional, la planeación realizada, al tiempo que se adquiera conocimiento a partir de la importante vivencia que ello deja.

Con el fin de que la variabilidad sea mínima entre los equipos, respecto a las estimaciones de las probabilidades de éxito, al final de las experimentaciones de cada equipo, pueden integrarse los datos para obtener una sola estimación, bien sea para cada grupo de empresas (Innovadoras – Excelencia) o para la clase en conjunto. Finalmente, otorgar unos minutos antes de las experimentaciones, para que los estudiantes practiquen lanzamiento de canicas, a modo de recordar sus posibles anteriores vivencias y/o de nivelar aquellos más nuevos en ello.

Para que el estudiante interactúe con el medio, siendo coproductor de su propia formación y actuando el docente como un facilitador, se propone complementar la actividad magistral con el uso de actividades que permitan “aprender mientras se juega”, al igual que propiciar integración de contenidos entre asignaturas, fomentar trabajo en equipo, exponer al estudiante a problemas reales que le resulten de interés y desarrollar la inteligencia emocional.

Si bien el Comercio de Canicas ha sido diseñado para contenidos de PL, sirve de base para que, por medio de su adaptación, se fortalezca el desarrollo procedimental del estudiante en cursos asociados con diseño de experimentos, teoría de la probabilidad, inferencia estadística, administración, estrategias de negociación, trabajo en equipo, entre otros.

AGRADECIMIENTOS

Los autores agradecen a los estudiantes de los programas curriculares: ingeniería industrial e ingeniería de sistemas, del curso Programación Lineal de la Facultad de Ingeniería, Universidad de Antioquia, grupo 01 del semestre 2009-1; por la participación en el despliegue de este trabajo y por los excelentes aportes al mejoramiento del mismo.

REFERENCIAS

1. Arreola, J., Arreola, A. (2003). Programación lineal: una introducción a la toma de decisiones cuantitativa. Thomson Ed. México, pp. 1-10.        [ Links ]

2. Barrows, H. (1986). A taxonomy of problem based learning methods. Medical Education, 20, pp. 481-486.        [ Links ]

3. Bednar, A., Cunningham, D., Duffy, T., Perry, J. (1991). Theory into practice: how do we link? En G. Anglin (Ed.) Instructional Technology: Past, Present and Future. Denver, CO: Libraries Unlimited, pp. 88-101.        [ Links ]

4. Branda, L. (2001). Aprendizaje basado en problemas, centrado en el estudiante, orientado a la comunidad. En: Aportes para un cambio curricular en Argentina. Jornadas de Cambio Curricular de la Facultad de Medicina de la Universidad de Buenos Aires. Buenos Aires: Organización Panamericana de la Salud, pp. 79-101.        [ Links ]

5. Dantzig, G. (1991). Linear programming. History of Mathematical Programming (Lenstra, J., Rinnooy, K. and Schrijver, A.). North-Holland, pp. 19-31.        [ Links ]

6. Epstein, R., Henríquez, R., Catalán, J., Weintraub, G., Martínez, C. (2001). Programación entera mejora el proceso de licitación de raciones alimenticias. Revista Ingeniería de Sistemas. V. XV, Nº 1, Junio, pp. 13-30.        [ Links ]

7. Freund, J., Miller, I., Miller, M. (2000). Estadística matemática con aplicaciones. Prentice Hall. Ed. 6, p. 624.        [ Links ]

8. Hiller, F., Lieberman, G. (1997). Introducción a la Investigación de Operaciones. MacGraw-Hill, p. 998.        [ Links ]

9. John, D. (1998). Cooperation in the classroom. lnteraction Book Company, Seventh Edition, pp. 1-2.        [ Links ]

10. Jonassen, D. (1991). Objectivism vs. constructivism: do we need a new philosophical paradigm? Educational Technolgy Research and Development. ETR&D. Springer Boston. Vol. 9, N° 3, pp. 5-14.        [ Links ]

11. Larrañeta, J. (1987). Programación lineal y grafos. Universidad de Sevilla. Ed. 2. Series Ingeniería. N° 1. España, pp. 10-11.        [ Links ]

12. Ortega, R. (2003a). Play, activity and thought: reflections on Piaget’s and Vygotsky theories. En D Lytle (Eds.), Play and culture studies, pp. 99-115.        [ Links ]

13. Ortega, R. (2003b). El juego: la experiencia de aprender jugando. En JL Gallego y E Fernández (Eds.), Enciclopedia de educación infantil, I. pp. 765-787.        [ Links ]

14. Pérez, J., Parra, C., Torres, D. (2006). Modelación y simulación computacional de un proceso productivo de una pequeña empresa usando dinámica de sistemas. Universidad del Norte. Revista Ingeniería y Desarrollo. Nº. 20, pp. 151-171.        [ Links ]

15. Quirós, R. (1990). Optimización del proceso de aserrío en madera de cortas dimensiones en el Pacífico Seco, Costa Rica. Tesis (Mag Sc). Turrialba (Costa Rica), p. 129.        [ Links ]

16. Taha, H. (2004). Investigación de operaciones. 7ª Edición. Pearson Educación. México, p. 8.        [ Links ]

17. Vallada, E., Maroto, C., Ruiz, R., Segura, B. (2005). Análisis de la programación de la producción en el sector cerámico español. Boletín de la sociedad española de cerámica y vidrio. V. 44, Nº 1, pp. 39-44.        [ Links ]

18. Waring, T., Wainwright, D. (2002). Comunicating the complexity of computer integrated operations: an innovative use of process modelling in a North East Hospital Trust. International Journal of Operations & Production Management, 22 (4), pp. 394-411.        [ Links ]