Propuesta de modelo multisegmento del pie para el análisis de marcha

Lucia Marino^1,2, Yomar González², César González^2,3, Marcel Rupcich²

1 Escuela de Ingeniería Mecánica, Universidad de Carabobo, Valencia, Venezuela. email: lmartino@uc.edu.ve

2 Instituto Nacional de Bioingeniería, Universidad Central de Venezuela, Caracas, Venezuela. email: marcelrupcich@gmail.com

3 Hospital Clínico Universitario, Universidad Central de Venezuela, Caracas, Venezuela. email: cesar.gonzalez@inabio.edu.ve

RESUMEN

El motivo de este trabajo fue desarrollar y evaluar un protocolo para el estudio de la cinemática del pie, modelándolo como un objeto multisegmento. En el mismo, la geometría del pie es dividida en dos partes, el retropié (calcáneo y astrágalo) y el antepié (metatarsos). Esta segmentación supone el manejo de información adicional a la suministrada por el modelo unisegmento (en el que el pie es un solo objeto). El nuevo modelo permitirá al especialista en marcha, diagnosticar con mayor precisión ciertas patologías durante un análisis de miembros inferiores. El protocolo desarrollado no afecta el procedimiento estándar para el análisis de marcha, lo cual es otra ventaja desde un punto de vista operativo, el mismo fue calibrado e implementado durante estudios de marcha convencionales en estrecha colaboración con el Laboratorio de Marcha del Hospital Ortopédico Infantil de Caracas (Venezuela), considerando la interacción entre los segmentos en estudio (tibia, retropié y antepié). Los movimientos que se van a representar entre los segmentos son: supinación y pronación, rotación interna y externa, flexión dorsal y plantar, abducción y aducción, e inversión y eversión. Los análisis de resultados basados en las gráficas representativas del movimiento son prometedores y abren las posibilidades para futuras líneas de investigación en el área.

Palabras clave: Pie multisegmento, Modelado del pie, Análisis de marcha, Retropié, Antepié.

Proposal of multisegment foot model for gait analysis

ABSTRACT

A new protocol for gait analysis based on multi-segment model of foot was developed. The geometry of the foot is divided in two segments, the rearfoot and forefoot, instead of the standard one-segment model used in gait analysis systems. This model will provide additional information for clinical diagnosis within lower extremities pathologies. This protocol was implemented in the Orthopedic Children Hospital (Caracas-Venezuela) and does not affect the standard procedure, despite additional kinematic parameters to be included. The results are very promising, based on graphic representation of the kinematic parameters during gait motion.

Keywords: Foot multisegment, Foot model, Gait analysis, Rearfoot, Forefoot.

Recibido: febrero 2013 Recibido en forma final revisado: octubre 2013

INTRODUCCIÓN

En los últimos años se ha estudiado al pie en el proceso de la marcha de diversas formas, entre las cuales está el considerarlo como un cuerpo rígido unisegmento (Kadaba et al. 1990), modelo base del VICON®, con lo que se calcula la flexión dorsal-plantar del tobillo y el ángulo de progresión del pie (que se refiere al ángulo medido en el plano transverso de la proyección del segmento del pie en el suelo, con respecto a la línea de progresión del laboratorio); aspecto alejado de la realidad, puesto que el pie está constituido por 27 huesos, con sus respectivas articulaciones y grados de libertad, lo que hace que sea un miembro del cuerpo humano que presenta una serie de movimientos relativos entre sus partes, por lo que al realizar este tipo de aproximaciones y simplificaciones, redunda en dejar de estudiar algunos de sus movimientos.

Estudios recientes dividen al pie en múltiples segmentos. Entre estos se tiene que Pohl et al. (2007), dividen al pie en dos segmentos, retropié y antepié, para examinar en qué difiere la relación entre la pierna, el retropié y el antepié mientras se camina o se corre a diferentes velocidades; Stebbins et al. (2004) consideran un modelo previo propuesto por otro investigador, para detectar si es repetible y confiable entre sesiones en distintos días usando a los mismos individuos sanos, y así detectar la variabilidad en la ubicación de los marcadores de dicho modelo; en su trabajo, Hunt et al. (2001) comparan la magnitud y patrones de movimiento de los segmentos retropié y antepié con respecto a la pierna y la fuerza reacción del suelo en adultos normales durante la fase de apoyo de la marcha, encontrando que el ángulo es mayor entre el retropié y la pierna, que entre el antepié y la pierna, así como el mayor movimiento ocurre al inicio y final de la fase de apoyo, donde las fuerzas son máximas; Simon et al. (2006), desarrollan y evalúan un método para la medición de la cinemática del pie que pueda ser usado clínicamente en niños con patologías en el mismo; para ello, dividieron al pie en tres segmentos y usaron 10 marcadores reflectantes. Este método resultó viable para la práctica médica. Leardini et al. (2007), proponen un nuevo protocolo para rastrear una cantidad grande de segmentos (cuatro en este estudio) durante la fase de apoyo con la mínima cantidad marcadores posible, particularmente enfocados en el plano coronal, como resultado se obtuvo que la información obtenida es consistente con los datos clínicos y ayudó a comprender la dinámica del pie durante esta fase; McNitt-Gray et al. (2004) en su estudio dividen al pie en 6 segmentos y aplican diversos modos de contacto del pie con el suelo para determinar las fuerzas y momentos de reacción. Todos estos estudios calculan, en los diferentes planos, los ángulos que representan los movimientos entre los segmentos (flexión/extensión, rotación in/externa, entre otros). Sobre la base de estos modelos, se propone en esta investigación un modelo multisegmento del pie, así como la ubicación de los marcadores reflectantes, el cual busca mejorar su descripción funcional.

Esta investigación tiene como objetivo desarrollar un protocolo de modelado del pie que sea fácil de implementar en pacientes, que se complemente y que no entorpezca el protocolo actual de estudio de marcha utilizado en el Laboratorio de Marcha del Hospital Ortopédico Infantil de Caracas, el mismo es preliminar puesto que pretende evaluar si es factible esta propuesta de ubicación de marcadores que definan los segmentos del pie.

El tener representado de forma gráfica las curvas de movimiento de los segmentos de los miembros inferiores, permite al médico plantear el o los procedimientos quirúrgicos y/o tratamientos que se deben seguir para corregir la patología o las consecuencias de la misma, así como también efectuar comparaciones entre un pre y postoperatorio, y, finalmente, disminuir la subjetividad en la apreciación e interpretación visual del examen médico.

FUNDAMENTOS TEÓRICOS

El pie, según Gage (2004), es la plataforma sobre la cual el cuerpo del bípedo se apoya y balancea, e inicia el caminar, saltar y correr. Para que el tobillo y el pie funcionen adecuadamente, la rodilla y el pie deben estar apropiadamente alineados al plano de progresión (plano de marcha). El pie es requerido para funcionar como una plataforma estable, y para eso el tobillo necesita de un adecuado rango de movimiento, y de la potencia de generación/absorción de los músculos. En el impacto, y durante la respuesta a la carga, el pie está relativamente en valgo, y su función es la de absorber el impacto. En cambio, al final de la fase de apoyo, las rotaciones del tobillo y del retropié, actúan para darle al pie un relativo varo que permite usarlo como brazo de palanca para la flexión plantar del tobillo. Cabe destacar que el 50% de la potencia requerida proviene de lo anterior descrito, y el otro 50% proviene de los músculos que actúan alrededor de la cadera.

Biomecánica del pie

El movimiento que realiza el pie en su conjunto, se corresponde con movimientos combinados que tienen lugar en los tres planos del espacio, y en los que se encuentran implicados 55 articulaciones, es decir, no son movimientos puros (Núñez-Samper & Llano, 2006).

En la Tabla 1 se indican los movimientos del pie según el plano y eje de realización. En el pie, los movimientos que se producen en los planos coronal y transversal cambian con respecto al resto del cuerpo, debido a que la pierna y el pie presentan un ángulo entre si de 90º, por lo que en el plano coronal del pie se describen los movimientos de rotación, en el plano transversal tienen lugar los movimientos de abducción (separación) y aducción (aproximación), y en el plano sagital no se modifica. En la Figura 1 se pueden observar los movimientos mencionados en la Tabla 1. Una vez conocido el comportamiento del objeto en estudio, se puede a definir los segmentos a utilizar.

Definición de los ángulos de las articulaciones anatómicas

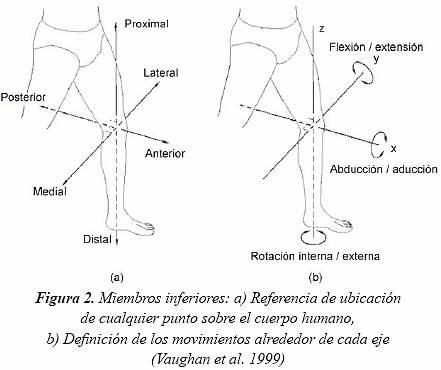
Para definir los ángulos de las articulaciones, se utilizan las propuestas de Grood & Suntay (1983) y de Tupling & Pierrynowski (1987), en las cuales cada articulación tiene un segmento proximal y uno distal de referencia, por ejemplo para la articulación de la cadera se toma la pelvis y el fémur. En el cuerpo humano se estableció un marco de referencia espacial para ubicar las partes del mismo entre ellos (Vaughan et al. 1999), y con ellos facilitar la descripción de cualquier punto (Figura 2a).

Los ángulos de las articulaciones (Figura 2b) se definen como la rotación del segmento distal en relación con el segmento proximal. Las rotaciones se pueden definir como sigue:

• Flexión / extensión: tienen lugar alrededor del eje mediolateral del segmento proximal, eje Y.

• Rotación interna /externa: tienen lugar alrededor del eje longitudinal del segmento distal, eje Z.

• Abducción / aducción: tienen lugar alrededor del eje perpendicular a los dos anteriores, eje X.

MATERIALES Y MÉTODOS

Recursos materiales

El desarrollo del protocolo requirió del uso de los equipos VICON® Motion System 460 de la Oxford Metrics Group, que consta de: 6 cámaras de captura de movimiento (rayos infrarrojos) a 60 ciclos, una estación de datos “datastation” (CPU), una barra y una escuadra de calibración, 22 marcadores reflectantes de 14 mm. de diámetro, además de una placa de fuerza formada por tres paneles ubicados en el piso del laboratorio que miden aproximadamente cada una 0,5 m x 0,5 m, que con el uso de la barra de calibración se delimita un volumen de control de 1,10 m x 1,10 m x 4,0 m. (alto, ancho, largo), que es el volumen efectivo para las cámaras de rayos infrarrojos, un dispositivo denominado KAD (Knee Alignment Device) que se usa para definir los ejes de flexo/extensión de la rodilla durante la estática, además consta de los programas Workstation®, Bodybuilder®, Polygon® que el sistema VICON® proporciona para la recolección y procesamiento de los datos obtenidos; y de cámaras de video para grabar el recorrido del paciente en los planos coronal y sagital. Estos recursos se encuentran disponibles en el Laboratorio de Marcha del Hospital Ortopédico Infantil de Caracas, en la Figura 3 se muestra la distribución de los equipos en el mismo.

En el sistema VICON®, las cámaras de rayos infrarrojos emiten señales que se dirigen al centro del espacio (volumen) destinado para el estudio, inciden sobre los marcadores reflectantes, ubicados sobre el individuo (en puntos anatómicos), que se encuentra realizando su recorrido de estudio, caminando sobre una pista, en la cual están empotradas las placas de fuerza ubicadas en el piso, luego estas señales rebotan hacia las cámaras de infrarrojos, las cuales regresan al equipo convertidor de señales, permitiendo que esta información pueda ser procesada por el técnico del laboratorio (con el uso de los programas antes mencionados), para luego ser presentado a través de gráficos que el especialista en marcha interpretará para emitir un diagnóstico.

El VICON® system utiliza tres archivos para procesar y calcular los parámetros establecidos, estos archivos se pueden modificar para adaptarse al modelo que se necesite. Los mismos son: el sistema de marcadores (marker set), los parámetros del modelo (model param) y el modelo (model). En el marker set se indican los nombres de los marcadores y la secuencia de enlace de estos, que representan cada segmento, para ello se utilizan como mínimo tres marcadores los cuales formarán un plano por segmento. En el model param se establecen los parámetros y las variables que por defecto debe tomar el programa, también recibe los parámetros que se introducen al inicio del procesamiento de los datos, es decir, las medidas antropométricas del paciente. En el model es donde se indican las rutinas utilizadas para calcular los centros de rotación y otros cálculos, para luego obtener los ángulos de movimientos de cada segmento definido; así como la salida de los datos obtenidos.

Como se mencionó, para definir un segmento se colocan como mínimo tres marcadores (lo que forma un plano). Estos tres marcadores son, a su vez, los componentes de dos ejes (eje1 y eje2) que se utilizan para definir el vector normal al plano (calculado con el producto vectorial que va del eje1 al eje2), que es el vector que representa al segmento, y es utilizado para calcular los ángulos de movimiento en los diversos planos de proyección. Estos ejes se definen de tal manera que el vector normal tenga dirección proximal (hacia arriba). Es importante aclarar que los ángulos a calcular son con respecto a la línea vertical de la pierna, por lo que es muy conveniente que el vector normal de cada segmento, en lo posible, tengan la misma dirección.

Una vez definidos los vectores para el segmento, el vector segmento se calcula a partir de la expresión (1).

En donde:

Punto I, Punto origen del vector segmento.

PFV1, Punto final del vector 1.

PIV1, Punto inicio del vector 1.

PFV2, Punto final del vector 2.

PIV2,Punto inicio del vector 2 y finalmente “token”, Indica el sentido (regla de la mano derecha) y la dirección que tomará el vector obtenido, para cada instante de la marcha, así como el orden de ejecución de los cálculos de los ángulos por plano.

Definidos los segmentos de trabajo, se procede a realizar los cálculos de los ángulos intersegmentos, basados en el sistema de ángulos Cardan o ángulos de Euler (Orin et al. 1979; Pandy & Berme, 1988; Winter, 2005). (Figura 4).

Para calcular los ángulos, se debe establecer un segmento móvil y uno fijo (el segmento fijo es el más distal de los segmentos involucrados), además de tomar en cuenta el sentido de los vectores para calcular los ángulos correctos. El ángulo se mide para los segmentos en este estudio, con respecto a la vertical del segmento móvil. La instrucción en el archivo del modelo es:

Estudio de la marcha

En el estudio de la marcha se determinan la cinemática y la cinética de la misma, dicho estudio tiene dos partes, la estática y la dinámica. En la estática, como su nombre lo indica, el sujeto está de pie sin moverse (aproximadamente en el centro del volumen de control en la mitad de la placa de fuerza), con el propósito de establecer los valores iniciales y calcular los centros de rotación de las articulaciones; en la dinámica, el sujeto se desplaza de un punto a otro establecido, con la misma se obtienen las coordenadas de todos los marcadores durante ese desplazamiento; en ambos casos los datos se consiguen luego de procesar las señales capturadas con las cámaras de infrarrojo.

De la cinemática se obtienen las coordenadas de los puntos que conforman los segmentos para luego calcular los ángulos entre ellos, y en la cinética se obtienen la potencia y momentos de los segmentos.

Ciclo de la marcha

Un ciclo de marcha o zancada, unidad básica de medida de la marcha, comienza cuando el pie entra en contacto con el suelo y termina con el siguiente contacto con el suelo del mismo pie. El período de tiempo entre contactos de pie se normaliza en tiempo y se porcentualiza, y se dice que entre el contacto inicial y final del miembro en estudio hay 100% de ciclo de marcha, por lo que se representa en porcentaje de 0 a 100 %. El ciclo de marcha consta de dos fases principales, la fase de apoyo y la fase de balanceo.

La fase de apoyo normal (60% del ciclo) comienza con el “contacto inicial” del talón y finaliza con el despegue de los dedos, momento en el cual se inicia la fase de balanceo. Los eventos y períodos (o subfases) en los cuales se subdivide la fase de apoyo son: contacto inicial, respuesta a la carga, apoyo medio, apoyo final y prebalanceo.

La fase de balanceo (40% del ciclo) se define como el período transcurrido desde el despegue hasta cuando el pie toca el suelo de nuevo. Cada uno de estos eventos ocurre secuencialmente, en porcentajes específicos del ciclo de marcha. La fase de balanceo se subdivide en: balanceo inicial, balanceo medio y balanceo final.

En la cinemática, el eje de la ordenada representa el rango angular del movimiento del segmento y la abscisa el porcentaje del ciclo de marcha donde ocurre el evento; y en la cinética, la ordenada representa la potencia o el momento, según sea el caso.

MODELO PROPUESTO

En el estudio de la marcha, el cuerpo puede representarse como un mecanismo de barras articuladas y definir así los segmentos involucrados. Debido a la complejidad de los movimientos articulares, se suelen emplear modelos sencillos para su estudio.

Para definir el modelo que se va a desarrollar se hizo un estudio de los modelos desarrollados por los siguientes autores: Kirtley (2004), Pohl et al. (2007) y Rattanaprasert et al. (1999) que dividieron al pie en dos segmentos; Carson et al. (2001), Myers et al. (2004), Moseley et al. (1996) y Stebbins et al. (2006) en tres segmentos; Leardini et al. (1999; 2007) y Simon et al. (2006) en cuatro segmentos; y, por último, Buczek et al. (2006) y MacWilliams et al. (2003) dividieron al pie en 8 segmentos; tomando en cuenta las características de cada investigación se establecieron las ventajas y desventajas de sus modelos, para luego, basados en los criterios establecidos para nuestro modelo (fácil de implementar y que no estorbe el protocolo estándar actual), se definió el numero de segmentos a utilizar, así como el numero de marcadores.

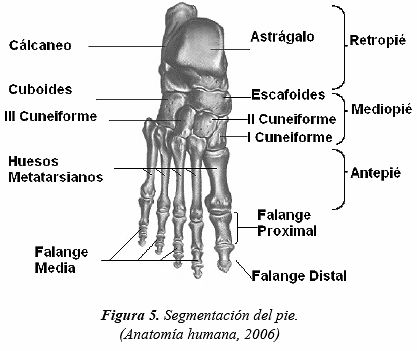
En el modelo propuesto se divide al pie en dos segmentos: el retropié y el antepié. El primero está constituido por el calcáneo y el astrágalo, y el segundo por los metatarsos (Figura 5). El resto de los segmentos que se pueden definir no se consideran para este estudio, debido a que se necesita un modelo simple; el mediopié (los cuneiformes, el cuboides y el escafoides) se toma como elemento de transmisión de movimiento entre los otros dos segmentos del pie (Carson et al. 2001).

Para identificar los segmentos se colocan marcadores reflectantes, sobre puntos anatómicos del pie, fáciles de ubicar e identificar por el asistente del laboratorio (fisioterapeuta), tal que se minimicen los efectos del movimiento de la piel y de la elasticidad de los cartílagos, tendones y otros elementos blandos que lo forman.

La denominación empleada, para los nuevos marcadores, da continuidad a la utilizada por el sistema actual del Laboratorio de Marcha del Hospital Ortopédico Infantil de Caracas.

La Tabla 2 muestra el nombre y ubicación de cada marcador utilizado en la zona de estudio. Los marcadores en el modelo actual del pie unisegmento, son tres: ANK, HEE y TOE (VICON® 2002), y los propuestos para el modelo son LCA, MCA, P5M y D5M, como se muestran en la Figura 6. Esta configuración se repite en ambos pies, por lo que se le agrega el prefijo L “Left” (izquierdo) y R “Right” (derecho). En la estática, el retropié lo forman los marcadores HEE, MCA y LCA, y el antepié, los marcadores P5M, D5M y TOE. En la dinámica en lugar del marcador MCA, se utiliza un marcador virtual MRC para definir el retropié, cuya configuración y función se explica mas adelante, esto porque MCA era tropezado al caminar. Para la dinámica se utiliza un segmento auxiliar en el retropié (HEE, LCA y ANK), porque el programa en los recorridos no permite segmentos sin conexión o concatenación. El centro de rotación del tobillo se calcula con el modelo unisegmento actual.

No se colocan mas marcadores para definir los segmentos, porque estos estarían ubicados tan cerca, unos de otros, que se pueden solapar en la captura durante el recorrido, perdiendo información de sus coordenadas, lo que no permite realizar los cálculos correspondientes.

Definición de los segmentos

Tibia

Ubicación de marcadores

Está definida como en el modelo utilizado en el estudio de la marcha por los marcadores KNEE ubicado en el lado lateral de la rodilla a nivel del epicóndilo lateral del fémur, TIB ubicado en el punto medio de la pierna del lado lateral, y ANK que se coloca a nivel del maléolo externo, se colocan procurando que todos estén alineados.

Retropié

Ubicación de marcadores

El calcáneo define al retropié. Para los cálculos lo representan los marcadores HEE, LCA y MRC. HEE se coloca sobre el calcáneo de tal manera que esté alineado con TOE (antepié), LCA colocado en el lado externo del pie sobre la apófisis lateral de la tuberosidad, y MRC es un marcador virtual que su definición se expresa mas adelante.

Definición de los vectores

El eje 1 va de HEE a LCA, y el eje 2 va de HEE a MRC.

Antepié

Ubicación de marcadores

Compuesto por los cinco metatarsos que se asumen como un cuerpo rígido o un solo segmento. Se representa con los marcadores TOE, D5M y P5M. TOE se ubica distal entre el 2do y 3er metatarso, D5M colocado lateral a la cabeza del 5to metatarso, y P5M se sitúa lateral sobre la tuberosidad del 5to metatarso.

Definición de los vectores

El eje 1 se define uniendo los marcadores TOE y D5M, y el eje 2 con P5M y D5M.

Movimiento entre los segmentos

A continuación se definen los movimientos entre los segmentos involucrados en este estudio, según el plano de ejecución.

Retropié relativo a la Tibia:

• Flexión Dorsal/Plantar: alrededor del eje transverso de la tibia.

• Inversión/Eversión: alrededor del eje longitudinal del retropié.

• Rotación Interna/Externa: alrededor del eje perpendicular a los dos anteriores.

Antepié relativo al Retropié:

• Flexión Dorsal/Plantar: alrededor del eje transverso del retropié.

• Supinación/Pronación: alrededor del eje longitudinal del antepié.

• Abducción/Aducción: alrededor del eje perpendicular a los dos anteriores.

Antepié relativo a la Tibia:

• Flexión Dorsal/Plantar: alrededor del eje transverso de la tibia.

• Supinación/Pronación: alrededor del eje longitudinal del antepié.

• Abducción/Aducción: alrededor del eje perpendicular a los dos anteriores.

Sujetos de la investigación

Los sujetos utilizados en esta investigación son individuos sanos. Dos hombres con un promedio de edad de 23 años, estatura de 1,75 m, peso 80 kg, y una mujer de 40 años, estatura 1,68 m, peso 74 kg, con un tamaño del pie entre 23 y 30 cm. de largo.

Recolección y procesamiento de los datos

Las cámaras 4, 5 y 6 (Figura 4) se colocaron a una altura mayor con respecto a las otras tres, con el fin de que los rayos infrarrojos incidieran con más precisión en el volumen de control y por ende sobre los marcadores. Esta nueva configuración permitió que el número de marcadores que se sobreponían y el tiempo de pérdida visual de los mismos disminuyera, lo que redundó en un ahorro del tiempo de proceso de la data.

Una vez realizados los recorridos de marcha, uno de los archivos obtenidos tiene extensión “c3d”, en los cuales se almacenan las coordenadas tridimensionales de los marcadores. Luego se procesa la información obtenida usando los programas del VICON® 460, en el cual el técnico une los marcadores establecidos mediante líneas (como se estableció en el marker set), formando una figura geométrica (triángulo) para cada segmento, en la Figura 7 se puede observar el modelo propuesto sobre el actual.

Método de procesamiento de datos

Una vez seleccionada la ubicación de los marcadores a utilizar en el modelo y definidos los segmentos de trabajo, se realiza el estudio de marcha con 10 recorridos (trials) por individuo, de los cuales se seleccionan los que mayor y mejor información proporcionen; es decir, los que posean recorridos con pocos tramos de perdida de posición de marcadores, para luego procesarlos y proceder a realizar los cálculos de los ángulos intersegmentos.

Descripción del ensayo

La tibia viene definida por el modelo estándar del sistema VICON®. En el caso del antepié están colocados los tres marcadores para definir el segmento; pero en el retropié para la dinámica, se utiliza un tercer marcador MRC (Figura 8), que es un marcador virtual (VICON®, 2002), que se crea con la combinación de algunos componentes de los otros dos marcadores, se tiene que los marcadores HEE y LCA tienen coordenadas (x1,y1,z1) y (x2,y2,z2) respectivamente, y el marcador virtual MRC tendrá las coordenadas (x2,y1,z2) como se muestra en la Figura 9, con lo que se evita el uso de un marcador medial en el calcáneo que estorbaría el paso del paciente, y si es tropezado daría un error de lectura o se desprendería, lo que implica comenzar desde el principio el estudio.

Luego de procesar los datos de los sujetos se obtienen las coordenadas de los marcadores, y como ya se mencionó se calculan los ángulos en los diversos recorridos.

Definición de los vectores segmento

A continuación se presenta la definición de los vectores para cada segmento, recordando que L indica izquierdo y R derecho, basándonos en la ecuación (1), se tiene:

{*Antepié formado por los marcadores reales P5M, D5M, TOE*}

LAntepié = [LD5M, LD5M-LP5M, LTOE-LD5M, xzy]

RAntepié = [RD5M, RD5M-RP5M, RD5M-RTOE, xzy]

{*Retropié formado por los marcadores reales HEE y LCA; y el marcador virtual MRC *}

LMRC = {1(LLCA),2(LHEE),3(LLCA)} {*Creación del marcador virtual, pie derecho*}

RMRC = {1(RLCA),2(RHEE),3(RLCA)} {*Creación del marcador virtual, pie izquierdo*}

LRetropié = [LLCA,LLCA-LMRC,LLCA-LHEE,yxz]

RRetropié = [RLCA,RMRC-RLCA,RLCA-RHEE,yxz]

A continuación se muestran las expresiones del cálculo de los ángulos, utilizando la ecuación (2):

{*Mov. Relativo 1: Retropié >> Tibia)*}

LRT1 = <LRetropie,LTibia,yxz>(-1)(-3)

RRT1 = -<RRetropie,RTibia,yxz>(-3)

{* Mov. Relativo 2: Retropié >> Antepié *}

LAR1 = <LRetropie,LAntepie,yxz>(-1)(-2)

RAR1 = -<RRetropie,RAntepie,yxz>

{*Mov. Relativo 3: Antepié >> Tibia*}

LAT1 = <LAntepie,LTibia,yxz>

RAT1 = -<RAntepie,RTibia,yxz>

El término token, al final de la expresión de la ecuación (2), indica que primero se calcula el ángulo de flexión dorsal /flexión plantar (plano sagital) alrededor del eje y, luego el de abducción/aducción (plano frontal) alrededor del eje x, y por último la rotación interna/externa (plano transverso) alrededor del eje z, para cada instante de la marcha, basado en el sistema de ángulos de Euler o Cardan, por lo que se obtienen 9 gráficas, tres para cada combinación de segmentos en estudio. Los valores entre paréntesis, después de los vectores-segmento, son ajustes en las rotaciones.

RESULTADOS

Una vez procesados los datos se muestran, en forma gráfica, los resultados de la cinemática y cinética de los segmentos. En cada gráfica se representan los valores de los individuos estudiados y el promedio de los mismos, esto para hacer comparaciones preliminares con otros autores (Simon et al. 2006 y Stebbins et al. 2006) que utilizan las cámaras de infrarrojo cercanas al pie. En primera estancia, las gráficas obtenidas por el modelo propuesto presentan una tendencia unívoca a la mostrada por estos autores en los segmentos en estudio. Los resultados se consideran aceptables para efectos de comparación preliminar. Sin embargo, la rigurosidad de evaluación del modelo amerita una muestra mayor para ser implementado como parte del análisis de marcha de cualquier laboratorio de marcha. Por ahora, la tendencia en los valores es suficiente indicativo para efectos de validación, basados en la disponibilidad y distribución de los equipos dentro del Laboratorio de Marcha.

Movimientos relativos en individuos sin patologías

Las gráficas obtenidas para cada segmento, se muestran en las Figuras 10, 11 y 12 respectivamente, para los planos sagital, frontal y transverso, en ellas se puede observar el movimiento en cada uno de los planos en los que se proyecta el movimiento del pie de cada par de segmentos del estudio. La curva que se muestra representa el valor promedio del valor del ángulo de movimiento entre segmentos en individuos sin patologías.

Se observa que la forma de la curva de la amplitud angular de los segmentos retropié y antepié con respecto a la tibia (Figuras 10a y 12a), y del retropié y antepié (Figura 11a), en el plano sagital es muy similar.

En las gráficas (Figuras 10a y 12a) también se observa como el retropié y el antepié se acercan y se alejan de la tibia, como consecuencia del apoyo y despegue del pie, esto para poder impulsarse y continuar con la marcha. Cuando el pie está en el comienzo de la fase de balanceo, tiene una ligera rotación debido a que está en el aire y sin más restricción que la del complejo tibioastragalino.

Movimiento del retropié-tibia: en el plano sagital (Figura 10a) se presenta un valor máximo de flexión dorsal, que ocurre al momento de la elevación del talón (50% del ciclo de marcha). El valor máximo de la flexión plantar sucede cercano al 60% del ciclo de la marcha, que es cuando comienza la fase de balanceo.

En el plano frontal (Figura 10b) el valor máximo ocurre cercano al 95% de la marcha, ya que es el momento antes de apoyar el talón, por lo que el pie busca una angulación que permita un apoyo estable. Cercano al 55% del ciclo de la marcha, se tiene un incremento de la inversión porque para ese instante el pie está tomando el impulso para balancearse y crear la estabilidad del paso.

En el plano transverso (Figura 10c) el máximo valor de rotación interna se ubica cercano al comienzo de la fase de balanceo (60% ciclo de marcha), entre el despegue del pie y el balanceo inicial, que es cuando el pie despega del suelo y se mueve, como se mencionó anteriormente, sin mas restricción que la del complejo calcáneo-astrágalo; también presenta una rotación externa cerca del balanceo medio, debido a que el pie está preparándose para el contacto del talón, lo que conduce a la estabilidad del contacto y del paso.

Movimiento relativo entre el retropié y el antepié: en el plano sagital (Figura 11a) se tiene la flexión dorsal en dos fases de la marcha, en el apoyo medio (30-40%) y cercano al balanceo medio (80-90%). La flexión plantar ocurre cercano al 60% del ciclo de la marcha, que es cuando comienza el balanceo, luego tiende a la flexión dorsal hasta llegar al nuevo contacto de talón con la superficie. En el plano frontal (Figura 11b) se comienza el apoyo del talón con una ligera supinación que decrece hasta el apoyo medio, para luego comenzar a incrementarse (supinarse) hasta el inicio del despegue del pie, cercano al 60% del ciclo de la marcha. Luego de esto decrece (prona) para mantenerse hasta el balanceo medio en donde comienza de nuevo a incrementarse hasta el nuevo apoyo del talón.

En el plano transverso (Figura 11c) se tienen dos valores picos de abducción muy similares en su valor, en el apoyo medio y el valor máximo en el balanceo medio. El máximo valor de aducción ocurre al momento del despegue del pie (60%).

El movimiento entre los segmentos definidos para el pie no son tan disímiles, ya que estos no poseen una articulación interna como la que se encuentra en la cadera o rodilla, sino que se comporta como un sistema locomotor, es decir, el primero (tibia) arrastra a los otros segmentos (retropié y antepié).

Movimiento del antepié-tibia: en el plano sagital (Figura 12a) se observa un punto máximo de flexión dorsal cercano al 50% de la marcha, que es el momento entre la elevación del talón y el despegue del pie, en el cual el antepié se acerca mas a la pierna, y así dar el impulso para despegar el pie y separar del piso el retropié; y un máximo de flexión plantar entre el despegue del pie y el balanceo inicial (65% del ciclo de marcha),ya que el pie está elevándose del piso y por la fuerza de gravedad es atraído hacia abajo, aumentando el ángulo entre el retropié y la tibia, y como consecuencia entre el antepié y la tibia; luego el pie se acerca a la tibia para poder apoyarse en el suelo con estabilidad.

En el plano frontal (Figura 12b) existen dos momentos en los que se puede observar la supinación del pie, al momento del despegue del mismo (terminando la fase de apoyo) y al momento del balanceo medio antes del apoyo del talón. Cuando la pierna tiende a estar vertical se tienen los valores máximos de pronación, que ocurren al momento del apoyo plantar (20%) y en el balanceo medio (75%).

En el plano transverso (Figura 12c) se pueden observar dos valores máximos de abducción en la elevación del talón (40-50%) y en el contacto del talón (100%), ya que el pie normalmente está ligeramente abducido para dar estabilidad al cuerpo al estar de pie. La máxima aducción se observa en el balanceo inicial (70%) como consecuencia del impulso para el despegue del pie.

Momentos y potencias de individuos sin patologías

Las gráficas de las Figuras 13, 14 y 15 representan respectivamente los componentes de la fuerza reacción del suelo, los momentos y la potencia promedio en el tobillo durante la marcha.

Con respecto a la cinética del pie se pueden generar las siguientes interpretaciones: las gráficas de la Figura 13 muestran las componentes de la fuerza de reacción del suelo en el tobillo, durante la fase de apoyo del pie, como respuesta a la pisada, a las fuerzas internas (musculares) y al peso del cuerpo; para luego en el balanceo estabilizarse debido a que solo actúan las fuerzas internas del miembro inferior. En las mismas se muestra la variación de valor de la fuerza en cada instante en que el pie se está apoyando sobre la placa. La componente en el eje x de la fuerza (Fx) (Figura 13a), indica que el pie viene con un impulso de la fase de balanceo, que luego disminuye para poder desacelerar al pie, apoyarse sobre el piso y dar estabilidad tanto al pie como al cuerpo. En el eje y, la fuerza Fy (Figura 13b) es la que hace que el pie tienda a abducir/aducir en el plano transverso, en cambio la componente en el eje z (Fz) (Figura 13c), es la que refleja mejor la respuesta al peso del cuerpo y a la fuerza de gravedad; recordando que todas estas fuerzas (Fx,Fy,Fz) son las componentes de una fuerza resultante (Fr) denominada fuerza reacción del suelo, que es la fuerza de respuesta de la placa a la pisada. Se puede observar en las gráficas, que durante la fase de apoyo (entre 0 y 65%) los valores varían fuertemente, oscilando para Fx entre -80N y 420N, para Fy entre 180N y 245N, y para Fz entre 0 y 900N, lo que involucra un gradiente de aproximadamente 500N, 65N y 900N respectivamente; por el contrario, en la fase de balanceo (entre 65 y 100%) la situación es muy diferente registrándose un valor cuasi contaste cercano a 220N para Fx y Fy, y de 0N para Fz.

Las gráficas de la Figura 14 muestran el momento en el tobillo en los tres planos. Nótese que el mayor valor del momento se muestra en el plano sagital, que es donde ocurre el movimiento principal que caracteriza al tobillo, la flexión dorsal/plantar del pie, en donde el pie actúa como palanca, impulsando la pierna para que se desplace hacia adelante y permita el avance del miembro inferior, y con ello la marcha. El valor máximo se produce en el instante del despegue del talón (aproximadamente en el 45% del ciclo de marcha) que es cuando todo el peso del cuerpo se aplica en el antepié, siendo este punto más lejano del centro de rotación.

En la gráfica de la Figura 15 se muestra la potencia en el tobillo, cuyo máximo valor se observa en el despegue del talón, aproximadamente 55% del ciclo de marcha, ya que el antepié genera potencia para poder levantar el pie, producir el despegue, y lograr el desplazamiento del resto del cuerpo hacia adelante. Sin este proceso de absorción y generación de potencia por parte de los músculos y demás tejidos involucrados en la marcha, no se podría levantar el pie y permitir la marcha. El valor de la cinética, se comparó con la forma de las curvas que contiene el programa VICON® por defecto en su base de datos.

Comparación entre el modelo diseñado y los modelos de otros autores

Primeramente se comparó la gráfica que el modelo actual presenta con respecto al modelo propuesto, ésta es la flexión dorsal/plantar del tobillo. En la misma están involucrados el retropié y la tibia, que a pesar de que en el modelo propuesto no están directamente conectados, muestran un comportamiento similar, lo que quiere decir, que el modelo del retropié es bastante aceptable. En la figura 16 se puede observar que la curva obtenida posee una forma muy similar a la actual, el punto de cambio de la flexión plantar hacia la flexión dorsal, ocurre entre el 60 y 70% del ciclo, donde comienza el balanceo. Luego se realizó una tabla para comparar los valores máximos y mínimos, y sus respectivos puntos de ocurrencia, de cada curva representativa de los movimientos entre los segmentos estudiados, tanto para el modelo propuesto como para los valores disponibles en la literatura técnica provenientes de cuatro autores Hunt et al. (2001), Myers et al. (2004), Simon et al. (2006) y Stebbins et al. (2006), debe mencionarse que cada autor estudia los segmentos de su interés y puede que no coincidan con los de este estudio.

En la Tabla 3 puede notarse la buena concordancia al comparar los resultados de Myers et al. (2004), Simon et al. (2006) y Hunt et al. (2001) con los de esta investigación. El modelo desarrollado se aproxima más al modelo de Stebbins et al. (2006), que al de los autores Hunt et al. (2001), Myers et al. (2004) y Simon et al. (2006), ya que los mismos ubican los marcadores de los segmentos en posiciones diferentes y utilizan un número mayor de segmentos.

Stebbins et al. (2006) realizó un conjunto de mediciones similares en cantidad y ubicación de marcadores, a las realizadas en esta investigación. La concordancia de los resultados entre Stebbins et al. (2006) y el presente trabajo es similar a la encontrada con otros autores. Sin embargo, pueden notarse diferencias sustanciales en algunos valores en los movimientos de aducción e inversión. Esto puede explicarse debido a que el estudio de Stebbins et al. (2006), fue realizado solo a nivel de las piernas, lo que implica que las cámaras de infrarrojo se encuentran más cercanas al objeto de estudio, con menos interferencia y posibilidad de solape de la data de los marcadores, que es diferente a la utilizada en esta investigación, en donde las cámaras se mantuvieron en la misma posición de un análisis de marcha estándar, de manera de captar en su totalidad a los miembros inferiores, sin afectar el normal desenvolvimiento del estudio, ya que de implementarse, sería para pacientes con dificultades de marcha, que necesitan que el estudio se realice en el menor tiempo posible.

La diferencia con los otros autores puede deberse al número menor de individuos usados en este estudio, pero recalco, el valor de este modelo ya se explicó anteriormente.

CONCLUSIONES

Las gráficas obtenidas por el modelo propuesto presentan una forma similar a la mostrada por otros autores en los segmentos en estudio, razón por la cual se puede aseverar que el modelo propuesto es aceptable con la configuración del laboratorio, por supuesto se debe realizar un número mayor de estudios, basados en normas estadísticas, para implementarlo como parte del análisis de marcha de cualquier laboratorio de marcha.
El modelo propuesto es versátil y no invasivo, porque no perturba el normal desenvolvimiento del examen durante el análisis de marcha; además de usar una cantidad de marcadores que no molesta al individuo. El modelo propuesto no es invasivo.

El hecho de usar marcadores del lado externo del pie, evita que el individuo los tropiece, desajustando su posición o despegándolo de su sitio. Cabe recordar que si se despega un marcador, el estudio comienza de nuevo, desde la calibración inicial.

El conocer el movimiento de los distintos segmentos en que se divide el pie, le permite al especialista en marcha identificar algunas patologías (hemiparesia, diplejia, entre otras) del mismo.

Las curvas reflejan el comportamiento de los segmentos del pie establecidos para este modelo.

Al estar colocados los marcadores sobre puntos anatómicos, fáciles de situar, no amerita el uso de otros estudios como el de rayos X para ubicarlos, asegurando de esta manera que los segmentos queden bien definidos, sin importar la deformidad que presente el pie.

Los ángulos entre los segmentos se calculan mejor utilizando los ejes locales.

La representación gráfica del movimiento del segmento, permite cuantificar el ángulo real de movimiento del mismo.

Las curvas obtenidas se aproximan a las curvas presentadas por otros autores para los segmentos en estudio, discrepando en algunos valores, debido al número de marcadores utilizados y a la configuración del estudio.

RECOMENDACIONES

Cuando el pie se encuentra en posición de supinación, se pueden colocar los marcadores LCA, P5M y D5M unos milímetros por encima del punto anatómico establecido para evitar que se despegue el marcador o dé una lectura errónea de su ubicación durante la marcha.

Tomar en cuenta el segmento del mediopié para futuros modelos.

Es vital aplicar este modelo, sobre la base de los protocolos médicos y estadísticos, a una cantidad representativa de individuos. De esta manera se puede implementar y tomarlo como una referencia de marcha normal más detallada dentro de las gráficas.

Realizar un programa para el procesamiento de datos de marcha, que sea independiente de cualquier programa comercial que se utilice para dicho estudio, para de ese modo poder utilizar los datos registrados por otros investigadores.

Conocer el valor de los momentos en cada segmento, permitirá mejorar el diseño en los aditamentos como las férulas, entre otros.

Agradecimientos

A Mark Cornejo y Diego Gómez, pasantes del INABIO; y al Dr. Carlos Prato, Gerardo Palmieri y Danirida Urbano del Laboratorio de Marcha del Hospital Ortopédico Infantil de Caracas por su apoyo a esta investigación, y al Dr. Marcel Rupcich por haber generado esta idea.

REFERENCIAS BIBLIOGRÁFICAS

1. Anatomía humana. (2006). [Página web en línea]. Disponible en: http://www.anatomiahumana.ucv.cl, Consulta diciembre, 2006.        [ Links ]

2. Buczek, F., Walker, M., Rainbow, M., Cooney, K., Sanders, J. (2006). Impact of mediolateral segmentation on a multi-segment foot model, Gait & Posture, 23 (4); pp. 519-522.

3. Carson, M., Harrington, M. E., Thompson, N., O’connor, J. J., Theologis, T. N. (2001). Kinematic analysis of a multi-segment foot model for research and clinical applications: a repeatability analysis, Journal of Biomechanics, 34; pp. 1299–1307.

4. Gage, J. (2004). The treatment of gait problems in cerebral palsy, MacKeith Press, Londres, Inglaterra.

5. Grood, E. & Suntay, W. (1983). A joint coordinate system for the clinical description of three-dimensional motions: application to the knee”. Journal of Biomedical Engineering, 105; pp. 136-144.

6. Hunt, A, Smith, R., Torode, M., Keenan, A. (2001). Inter segment foot motion and ground reaction forces over the stance phase of walking. Clinical Biomechanics, 16, pp. 592-600.

7. Kadaba, M. P., Ramakrishnan, H. K., Wootten, M. E. (1990). Measurement of lower extremity kinematics during level walking. Journal of Orthopaedic Research, 8; pp. 383-392.

8. Kirtley, C. (2004). 3D foot kinematics from plantar pressure data. CGA Teach-in 2004, The Catholic University of America, Washington DC, USA.

9. Leardini, A., Benedetti, M. G., Catani, F., Simoncini, L., Giannini, S. (1999). An anatomically based protocol for the description of foot segment kinematics during gait. Clinical Biomechanics, 14; pp. 528-536.

10. Leardini, A., Benedetti, M. G., Berti, L., Bettinelli, D., Nativo, R., Giannini, S. (2007). Rear-foot, mid-foot and fore-foot motion during the stance phase of gait. Gait & Posture, 25 (3); pp. 453-462.

11. Macwilliams, B. A., Cowley, M., Nicholson, D. E. (2003). Foot kinematics and kinetics during adolescent gait. Gait and Posture, 17, pp. 214-224.

12. Martino, L. (2009). Diseño e implementación de un modelo computacional para el pie. Trabajo de grado de maestría no publicado. Universidad de Carabobo, Venezuela.

13. Mcnitt-Gray, J. L., Requejo, P. S., Flashner, H. (2004). An experimental based approach for modeling foot-surface interaction, J. Orthopaedics & Sports Physical Therapy, 34 (9), A10.

14. Moseley,, L., Smith, R., Hunt, A., Gant, R. (1996). Three-dimensional kinematics of the rearfoot during the stance phase of walking in normal young adult males, Clinical Biomechanics, 11(1), pp. 39-45.

15. Myers, K. A, Wang, M., Marks, R. M., Harris, G. F. (2004). Validation of a multisegment foot and ankle kinematic model for pediatric gait, IEEE Transactions on neural systems and rehabilitation engineering, 12 (1); pp. 122-130.

16. Núñez-Samper, M. & Llanos, L. F. (2006). Biomecánica, medicina y cirugía del pie. Editorial Elsevier-Masson, 2da Edición, Barcelona, España.

17. Orin, D. E., Mcghee, R. B., Vukobratovic, M., Hartoch, G. (1979). Kinematic and kinetic analysis of open-chain linkages utilizing Newton-Euler methods. Mathematical Biosciences, 43; pp. 107-130.

18. Pandy, M. G. & Berme, N. (1988). Model for the understanding of the ankle and knee during double support. Modeling and Control Issues in Biomechanical Systems, ASME Winter Annual Meeting, Chicago; pp. 89-102.

19. Podo-ortosis (2007). [Página web en línea]. Disponible en: http://www.podoortosis.com. Consulta marzo, 2007.

20. Pohl, M. B., Messenger, N., Buckley, J. G. (2007). Forefoot, rearfoot and shank coupling: Effect of variations in speed and mode of gait. Gait & Posture, 25 (2); pp. 295-302.

21. Rattanaprasert, U., Smith, R., Sullivan, M., Gilleard, W. (1999). Three-dimensional kinematics of the forefoot, rearfoot, and leg without the function of tibialis posterior in comparison with normals during stance phase of walking. Clinical Biomechanics, 14; pp. 14-23.

22. Simon, J., Doederlein, L., Mcintosh, A. S., Metaxiotis, D., Bock, H. G., Wolf, S. I. (2006). The Heidelberg foot measurement method: Development, description and assessment. Gait & Posture, 23 (4);pp. 411-424.

23. Stebbins, J. A., Harrington, M. E., Thompson, N., Theologis, T. N. (2004). Advances in the measurement of foot kinematics in children. J. Orthopaedics & Sports Physical Therapy, 34 (9), A11.

24. Stebbins, J., Harrington, M., Thompson, N., Zavatsky, A., Theologis, T. (2006). Repeatability of model for measuring multi-segment foot kinematics in children. Gait and Posture, 23 (4); pp. 401-410.

25. Tupling, S. &Pierrynowski, M. (1987). Use of cardan angles to locate rigid bodies in three-dimensional space. Journal of Medical and Biological Engineering and Computing, 25; pp. 527-532.

26. Vaughan, C., Davis, B., O’connor, J. (1999). Dynamics of Human Gait. Kiboho Publishers, South Africa.

27. VICON® (2002). Manual Bodybuilder for Biomechanics. Version 460, Oxford Metrics Ltd.

28. Winter, D. (2005). Biomechanics and motor control of human movement. 3era Edición, Editorial John Wiley and Sons, New Jersey, USA.