A história da matemática como recurso didático para o ensino da teoria dos números e a aprendizagem da matemática no ensino básico

Claudia Lisete Oliveira Groenwald, Lisandra de Oliveira Sauer, Rosvita Fuelber Franke

Claudia Lisete Oliveira Groenwald:  Doutora  em Ciências da Educação pela Universidade Pontifícia de Salamanca – Espanha. Professora Titular da Faculdade de Matemática da Universidade Luterana do Brasil - ULBRA - Canoas/RS. claudiag@ulbra.br

Lisandra de Oliveira Sauer:  Mestre em Matemática pela Universidade Federal do Rio Grande do Sul. Professora Adjunta da Faculdade de Matemática da Universidade Luterana do Brasil. Canoas/RS. sauer@portoweb.com.br

Rosvita Fuelber Franke:  Mestre em Matemática pela Universidade Federal do Rio Grande do Sul. Professora Adjunta da Faculdade de Matemática da Universidade Luterana do Brasil. Canoas/RS.

Resumo

Este trabalho trata da importância didática da História da Matemática no processo de ensino e aprendizagem e apresenta três exemplos da utilização da Teoria dos Números relacionada à História da Matemática e à resolução de problemas.

Palavras Chave: História da Matemática, Teoria dos Números, Resolução de Problemas.

Abstract

This work deals with the didatic importance of the History of Mathematics in the teaching learning process. It also presents three examples of usage of the Number Theory related to the History of Mathematics and resolution of problems.

Key-words: History of Mathematics, Number Theory, Resolution of problems.

Recibido: 22/06/2005  Aceptado: 25/10/2005

 Introdução

O enorme desenvolvimento da Matemática nas últimas décadas não impediu que crescessem as dificuldades em ensinar os conteúdos matemáticos. Um dos problemas apresentados pelos alunos está em aplicar os conceitos de aritmética, nos tópicos de divisibilidade, máximo divisor comum e congruência com números inteiros.

Entre os obstáculos encontrados pelos professores de Matemática na transposição didática dos conceitos citados, e que são importantes para o desenvolvimento do pensamento aritmético, podemos destacar a falta de modelos, pois cada problema se resolve de um modo, além disso, é muito raro encontrar atividades didáticas aplicáveis no Ensino Básico.

Para Lins e Gimenez (1997) a aritmética escolar propõe um sentido integrador que permite resolver problemas diversos, assim as técnicas e regras deveriam servir para solucionar problemas.

As atividades didáticas envolvendo a  resolução de problemas podem ser desenvolvidas de forma a estimular nos alunos o interesse pela Matemática, aprimorando o raciocínio lógico e ampliando a compreensão dos conceitos básicos para o refinamento do pensamento aritmético, fazendo com que os mesmos desenvolvam a capacidade de manipular conceitos e propriedades de forma clara e objetiva.

Com o objetivo de estudar os conceitos elementares da Teoria dos Números, analisando o processo de ensino e aprendizagem de tópicos importantes que devem ser desenvolvidos no Ensino Básico,  foram investigados os seguintes itens: Números Inteiros, Divisibilidade, Máximo Divisor Comum e Congruência de Números Inteiros.

A metodologia de ensino escolhida para o desenvolvimento das atividades com a Teoria dos Números foi a utilização da história como recurso didático associado a resolução de problemas.

A História da Matemática como recurso didático

A História da Matemática pode ser um potente auxiliar no processo de ensino e aprendizagem, com a finalidade de manifestar de forma peculiar as idéias matemáticas, situar temporalmente e espacialmente as grandes idéias e problemas, junto com suas motivações e precedentes históricos e ainda enxergar os problemas do passado, bem como encontrar soluções para problemas abertos.

Mendes (2001) afirma que o conhecimento provém de diferentes grupos sócio-culturais que se organizaram e se desenvolveram intelectualmente de acordo com suas necessidades, interesses e condições de sobrevivência, levados pela mobilidade característica da sociedade humana e que a informação histórica pode contribuir  para a disseminação desse conhecimento.

A História da Matemática é considerada um tema importante na formação do aluno. Ela proporciona ao estudante a noção exata dessa ciência em construção, com erros e acertos e sem verdades universais, contrariando a idéia positivista de uma ciência universal e com verdades absolutas. A História da Matemática tem este grande valor, de poder contextualizar o saber, mostrar que seus conceitos são frutos de uma época histórica, dentro de um contexto social e político.

Para Valdés (2002), “Se estabelecermos um laço entre o aluno, a época e o personagem relacionado com os conceitos estudados, se conhecerem as motivações e dúvidas que tiveram os sábios da época, então ele poderá compreender como foi descoberto e justificado um problema, um corpo de conceitos, etc..”

Essa visão da Matemática faz com que ela seja vista pelo estudante como um saber significativo, que foi e é construído pelo homem para responder suas dúvidas na leitura do mundo, permitindo ao aluno apropriar-se desse saber, o que lhe propiciará uma melhor leitura do contexto global. 

Segundo Ozámiz (1993) a história da Matemática, como recurso didático, visa atingir os seguintes objetivos:

• mostrar que o processo do descobrimento matemático é algo vivo e em desenvolvimento;

• aceitar o significado dos objetos matemáticos em seu triplo significado: institucional, pessoal e temporal;

• estabelecer distinções entre uma prova, uma argumentação e uma demonstração dos conceitos matemáticos, bem como saber dosá-las de maneira equilibrada no currículo escolar;

• destacar a importância da aplicação de “provas” para os alunos, porém provas que contribuam ao conhecimento e não somente para testar “decorebas”.

Klein apud Tahan (1984) afirma que: “O professor que ensina a Matemática desligada de sua parte histórica, comete verdadeiro atentado contra a ciência e contra a cultura em geral”. É nesse sentido que tem crescido cada vez mais o interesse pela História da Matemática em relação ao ensino, não somente como uma ferramenta didática, mas também como campo de investigação.

Um certo conhecimento de História da Matemática, deveria ser parte indispensável da bagagem de conhecimentos de qualquer matemático em geral e do professor de todos os níveis. Isso, não somente com a intenção de utilizá-la como um instrumento em seu ensino, mas principalmente por que a História pode proporcionar uma visão verdadeiramente humana da Matemática, o que é difícil de se imaginar, pois a imagem que os alunos possuem dessa disciplina está totalmente desvinculada da realidade (Guzmán, 1993).

Uma visão mais profunda da História permite ao professor evoluir em seu trabalho educativo, pois lhe possibilita visualizar melhor o futuro, ou seja, de enxergar antes o que pode acontecer, as dúvidas que podem surgir. Além disso, permite que ele descubra as dificuldades do passado, comprovando os caminhos da invenção, com a percepção da ambigüidade e confusões iniciais.

Valdés (2002) nos chama a atenção para: “O valor do conhecimento histórico não consiste em ter uma bateria de histórias e anedotas curiosas para entreter os alunos, a história pode e deve ser utilizada, para entender e fazer compreender uma idéia mais difícil e complexa de modo mais adequado.”

Para Nobre (1999) a utilização da História da Matemática no contexto didático não deve se restringir à sua utilização como elemento de motivação ao desenvolvimento do conteúdo, pois sua amplitude extrapola o campo da motivação.

Baseados nesses princípios, justificamos a utilização da História como um recurso metodológico capaz de auxiliar no processo de construção do conhecimento.

Teoria dos Números no decorrer da história

A Teoria dos Números é a ciência que tem por objetivo principal estudar as propriedades e relações entre os Números Inteiros. Essa teoria aparece como ferramenta em diversas áreas da Matemática, tais como: Probabilidade, Álgebra, Sistemas Dinâmicos, etc., servindo de alicerce para resultados significativos.

É na Grécia que inicialmente identificamos a Teoria dos Números tal como a entendemos hoje. Foram os pitagóricos que estudaram as relações entre números do ponto de vista do que hoje denominamos Teoria dos Números (Figura 1).

Figura 1. Relações entre os números segundo os pitagóricos

A Aritmética era o estudo das propriedades fundamentais dos Números Inteiros, domínio dos matemáticos e filósofos da época. A Logística era a arte de calcular com Números Inteiros, domínio dos comerciantes e profissionais da época e é o que chamamos de Aritmética nos dias de hoje.

Entre os problemas da Teoria dos Números abordados pelos gregos antigos estão:

• cálculo do máximo divisor comum entre dois números;

• a determinação dos números primos menores que um inteiro dado;

• a demonstração de que há uma infinidade de números primos.

Entre os principais estudiosos dessa teoria podemos citar Euclides de Alexandria (330 -275 a.C), geômetra grego, professor de Matemática a convite do então imperador da parte egípcia da Grécia Antiga: Ptolomeu I. Ele organizou a obra monumental “Os Elementos”, composta de 13 livros. Os livros VII, VIII e IX estão dedicados à Teoria dos Números. Os conceitos numéricos estão expressos em uma linguagem geométrica. Euclides se refere a um número como um segmento, utilizando expressões do tipo “mede A” ou “está medido por” no lugar de é “divisor de” ou é “múltiplo de”.

Vários outros matemáticos gregos estudaram problemas da Teoria dos Números. Desses o mais importante foi sem dúvida Diofanto. Sua Aritmética, escrita por volta de 250 d.C., trata principalmente da solução de equações indeterminadas com coeficientes inteiros.

Embora a Matemática tenha sido intensamente estudada por outros autores gregos, e, posteriormente, por árabes, indianos e europeus, a Teoria dos Números caiu em esquecimento até o século XVII.

Bachet, em 1612, publicou o texto original em grego da Aritmética de Diofanto, incluindo uma tradução latina, que era a língua usada pelos eruditos europeus da época.

Entre 1621 e 1636, o francês Pierre de Fermat, magistrado da corte de Toulouse, adquiriu uma cópia desse livro. Fermat leu o texto de Diofanto, anotando na margem as idéias que lhe ocorriam. Isso marcou o início de seu  interesse pela Teoria dos Números, que posteriormente, expressou uma torrente de resultados importantes.

Fermat nasceu em 1601, e era um magistrado por profissão, não um  matemático. Na verdade,  poucas pessoas exerciam a Matemática como profissão naquela época. A comunicação entre os matemáticos também era precária, não havia revistas especializadas. A comunicação era conduzida, principalmente, através de cartas e por algumas pessoas que serviam de “centros difusores” dos novos resultados. A primeira revista dedicada à Matemática só foi criada em 1794.

O mais famoso divulgador dos resultados obtidos na Matemática  foi o frade francês Marin Mersenne. Muito amigo de alguns dos maiores matemáticos da época, como Descartes, Pascal e o próprio Fermat, Mersenne logo comunicava a toda a “República de Letras” as novidades matemáticas que chegavam ao seu conhecimento.

Foi na forma de cartas enviadas a Mersenne e a outros matemáticos contemporâneos que boa parte da obra de Fermat ficou conhecida. Depois de sua  morte, em 1665, coube a Samuel Fermat,  seu filho, coletar e publicar a obra de seu pai, dispersa em cartas e anotações. Ele começou com a publicação da Aritmética de Diofanto, incluindo todas as anotações feitas por Fermat à margem da sua cópia. Dessas anotações,  a mais famosa é o chamado Último Teorema de Fermat: Não existe solução não nula, para a equação, onde e x, y e z números inteiros. Esse resultado só foi provado em 1995 pelo inglês Andrew Wiles, mais de 300 anos após ser enunciado por Fermat.

O sucessor de Fermat foi o suíço Leonhard Euler, que nasceu em 1707, quarenta e dois anos após o falecimento de Fermat. Euler publicou uma obra matemática imensa, tendo contribuído para quase todas as áreas da Matemática pura e aplicada existentes no século XVIII. Ele não foi professor de nenhuma universidade, mas esteve ligado a academias científicas na Alemanha e na Rússia. Essas academias eram, na verdade, instituições de pesquisa, cujas atas publicavam, primordialmente, as contribuições científicas de seus membros.

O interesse de Euler pela Teoria dos Números teve início em sua correspondência com Christian Goldbach, foi através dele que Euler chegou à obra de Fermat. Em sua primeira carta a Euler, em 1729, Goldbach acrescenta o seguinte Post scriptum: Você conhece a observação de Fermat de que todos os números são primos? Ele disse que não sabia prová-la; nem ninguém conseguiu fazê-la, que eu tenha conhecimento.

Euler reagiu com ceticismo e não demonstrou muito interesse, mas Goldbach não desistiu e voltou a abordar o assunto. Em 1730, Euler começou, finalmente, a ler a obra de Fermat. Nos anos seguintes ele provaria e estenderia grande parte dos resultados enunciados por Fermat, resolvendo, inclusive, a questão proposta por Goldbach.

Através de seus trabalhos Euler popularizou a Teoria dos Números, como Fermat não havia conseguido.

Podemos destacar, dos estudos de Goldbach, a famosa conjectura que afirma: “Todo número par maior que 2 pode ser decomposto na soma de dois números primos”. Esse resultado não foi provado até os dias de hoje.

Porém o desenvolvimento sistemático da Teoria dos Números somente iniciou com a obra Disquisitiones arithmeticae, do alemão C. F. Gauss, publicada em 1801.

Objetivos

A investigação teve como objetivo geral desenvolver atividades didáticas envolvendo a Teoria dos Números, analisando o processo de ensino e aprendizagem de conceitos importantes que devem ser desenvolvidos no Ensino Básico,  permitindo aos estudantes o refinamento do pensamento aritmético.

Os objetivos específicos foram: investigar a importância didática da História da Matemática na Teoria dos Números no processo de ensino e aprendizagem da Matemática; pesquisar atividades e recursos que permitam ao aluno conjeturar, comparar e estabelecer estratégias mentais na resolução de situações problemas de outras áreas do conhecimento relacionando-os à Teoria dos Números.

Metodologia da pesquisa

Optou-se pela abordagem qualitativa, entendendo que nessa perspectiva é possível uma análise mais detalhada da situação pesquisada, possibilitando conhecer e entender as circunstâncias particulares em que o objeto do estudo se insere.

Esse trabalho foi desenvolvido em duas etapas: estudo aprofundado dos conceitos da Teoria dos Números desenvolvidos no Ensino básico e implementação de um experimento de ensino.

A primeira etapa, para atender aos objetivos propostos, se constituiu em um estudo detalhado da Teoria dos Números e de como desenvolver atividades didáticas, utilizando a história como recurso didático associado a resolução de problemas. Essa fase foi desenvolvida com reuniões semanais para discussão do trabalho a ser desenvolvido com todo o grupo de pesquisa e com a realização de seminários trimestrais para apresentação do material pesquisado a comunidade acadêmica do curso de  Matemática, da Universidade Luterana do Brasil, buscando levantar a discussão para o assunto pesquisado.

Na segunda fase foi aplicado um experimento de ensino, com as atividades pesquisadas na primeira fase. O experimento de ensino buscou criar um espaço de discussão, onde os alunos trabalhando em pequenos grupos, pudessem refletir e buscar soluções para os problemas apresentados e o professor, através da análise das conjecturas levantadas pelos alunos, os auxiliasse a alcançarem sucesso no desenvolvimento do trabalho proposto.

Os participantes, dessa etapa, foram 12 alunos do início do curso de Licenciatura em Matemática da Universidade Luterana do Brasil, do município de Canoas do estado do Rio Grande do Sul. A aplicação do experimento de ensino foi realizada em cinco terças feiras dos meses de setembro e outubro de 2004, com duração de 4 horas aulas, em cada dia.

Os dados foram coletados através da observação participativa, registrando os eventos. Posteriormente os dados foram descritos e analisados conforme as categorias, relativas aos alunos que participaram do experimento didático: motivação para a realização das atividades; conhecimento teórico necessário e capacidade de relaciona-los; capacidade de trabalho em grupo; análise das possibilidades de utilização das atividades, quando professores, no Ensino Básico.

Exemplos da utilização da Teoria dos Números no processo de ensino e aprendizagem da Matemática

Associar a História da Matemática à metodologia resolução de problemas é um forte aliado para desenvolver, no estudante, a capacidade de lidar com situações novas de forma criativa e independente.

Com o objetivo de que a Teoria dos Números ganhe espaço nos currículos escolares do Ensino Básico apresentaremos três aplicações de sua utilização, que foram desenvolvidas no experimento de ensino com alunos de licenciatura em Matemática.

Máximo Divisor Comum entre dois números (mdc)

Como já comentamos, o universo de Euclides era geométrico. Ele descreveu em um dos volumes dos Elementos o conhecido Algoritmo de Euclides, ou algoritmo das divisões sucessivas, para determinação do máximo divisor comum (mdc) entre números inteiros.

O algoritmo das divisões sucessivas afirma que: considerando a e b inteiros, tais que e, existem e são únicos os inteirose, tais que, onde.

Se, então, ou seja, a é múltiplo de b. Logo,. Se, então.  Daí, para b eexisteme, tais que,  onde.

Se, então b =, ou seja, b é múltiplo de . Logo, o. Se, repetimos o processo até encontrarmos um resto, tal qu.

Logo, o mdc (a,b) =.

Esse algoritmo pode ser sintetizado no seguinte dispositivo:

 

Figura 2. mdc entre a e b

A seguir, apresentaremos uma aplicação geométrica desse dispositivo, através do exemplo do cálculo do mdc entre os números inteiros 6 e 9.

Começamos construindo um retângulo com lados medindo 9u.c. e 6u.c. e traçamos quadrados, tantos quanto possíveis, medindo 6u.c. (Figura 3) cada lado, contidos no retângulo inicial.

Figura 3. retângulo de lados 9 e 6

Obtemos um quadrado de lado 6u.c. e um retângulo de lados 3u.c. e 6u.c., isto é:      

      

Como o resto não é zero, repetimos o processo para 6 e 3, agora construíndo um retângulo de lados 6u.c. e 3u.c (figura 4).

 

Figura 4. retângulo de lados 6 e 3

Obtemos dois quadrados com lados 3u.c., ou seja,. Como o resto é 0, então o, logo o.Podemos comparar o processo da obtenção geométrica do mdc com o processo aritmético.

Pelo algoritmo de Euclides temos: 9=6.1+3 e 6 = 3.2 + 0, logo o mdc (9,6) é 3.

Congruência com Números Inteiros

A congruência de Números Inteiros é uma poderosa ferramenta para resolvermos problemas relacionados à divisão em quaisquer níveis.

Podemos definir a congruência módulo m, como: dados a e b números inteiros e m um número inteiro positivo fixo, dizemos que a é congruente a b módulo m se, e somente se m divide a diferença a – b, ou seja, a – b é múltiplo de m.

            Notação:        a=b(mod m)   .

            Podemos exemplificar com:.

No Ensino Básico podemos nos referir à congruência como restos da divisão de a e b por m.

Podemos apresentar como exemplo de atividade para alunos de 11 anos,  o seguinte problema: “Uma camponesa levava uma cesta de ovos. Ao perguntar-lhe quantos ovos levava, respondeu: “São menos de 100. Se os divido de 2 em 2, sobra 1; se os divido de 3 em 3 me sobram 2; dividindo de 4 em 4 me sobram 3; de 5 em 5 sobram 4.” Quantos ovos ela levava?”

A solução teórica do problema pode ser realizada pela análise das congruências. Porém, como se trata de alunos de 11 anos, a solução deve ser realizada com o enfoque da divisibilidade dos números inteiros.

Organizando uma tabela de números de 1 a 100, podemos eliminar os números que não satisfazem as condições.

Primeiro, o número não é divisível por 2, logo, podemos eliminar todos os números pares.

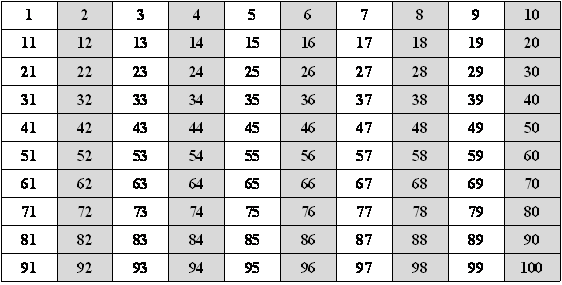
            Segundo, o número desejado não é divisível por 3, logo, eliminamos os múltiplos de 3.

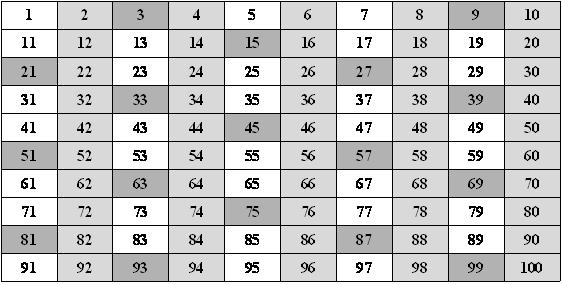
            Terceiro, o número procurado não é múltiplo de 5, logo, eliminamos os múltiplos de 5.

Os números restantes são os que ao serem divididos por 5 deixam resto 1, 2, 3 e 4. Então, eliminamos todos os números que não deixam resto 4 ao serem divididos por 5.

Logo nos sobram os números: 19, 29, 49, 59, 79, 89.

Analisando as condições, eliminamos os números 19 e 79 porque ao serem divididos por 3 não deixam resto 2, após eliminamos os números 29, 49 e 89 porque ao serem divididos por 4 não deixam resto 3. Logo, o número restante é o 59 e este é o número procurado.

Esse tipo de raciocínio possibilita ao estudante aprimorar sua compreensão sobre divisibilidade, o que nos leva a recomendar a utilização desse tipo de problemas no Ensino Fundamental.

Leitor de Mentes

Outra atividade didática, para os alunos do Ensino Básico, que se utiliza dos conceitos de congruência para sua compreensão é o Leitor de Mentes.

1. Pense em um número de dois dígitos, (como exemplo, utilizaremos o 95)

2. Subtraia deste número a soma dos dígitos do número pensado, (95-14=81)

3. Olhe na tabela abaixo o símbolo correspondente ao número encontrado.

Concentre-se no símbolo e clique no quadrado mágico:

Ao clicar no quadrado, aparecerá o símbolo que o aluno visualizou. No exemplo, que é o número 81, aparecerá o símbolo ©.

A explicação para essa atividade está baseada na congruência módulo 9, vejamos:

Exemplo: 95 dividido por 9 tem resto 5;

9+5=14 e 14 dividido por 9 tem resto 5;

A diferença 95-14=81 é divisível por 9.

Considerando um número ab de dois algarismos, que pode ser representado por 10a +b. Se resto da divisão de ab por 9 é r, temos: ab  = 9q + r e 10a + b = 9q + r.

Então 9a + a + b = 9q + r; o que implica em a + b = 9 (q – a) + r

Assim ab ≡ r (mod 9) e a + b ≡r (mod 9) e portanto ab – (a + b) ≡ 0 (mod 9).

Logo, o resultado sempre é divisível por 9 e, analisando a tabela com os símbolos, podemos observar que todos os múltiplos de 9, possuem o mesmo símbolo.

Conclusão

O experimento de ensino foi avaliado, pelo grupo de pesquisa, como muito positivo nos seus resultados. Os alunos estiveram, durante o trabalho de grupo, motivados e interessados na realização das atividades e 70% dos 12 alunos investigados afirmaram que perceberam progresso no estudo de disciplinas do curso nas quais estavam matriculados, durante a implementação do experimento.

Os alunos demonstraram desenvoltura no trabalho em grupo, propiciando um clima de discussão e troca de idéias, bem como, um ambiente favorável ao levantamento de dúvidas em todas as atividades propostas, o que é fundamental para a aplicação de uma metodologia que busca a resolução de problemas.

Observou-se que os alunos participantes do experimento encontraram dificuldades para justificar as atividades propostas, e não identificaram os conceitos aplicados, os alunos não conseguiram relacionar a teoria com a prática e, como conseqüência, a solução não foi encontrada.

Os alunos demonstraram não ter conhecimento de atividades desse tipo e nem da importância do trabalho com os conceitos referidos para o desenvolvimento do pensamento aritmético e do quanto esse conhecimento auxilia os alunos na compreensão de outros conceitos, principalmente na resolução de problemas. Os doze alunos afirmaram que reconhecem a importância das mesmas e mostraram–se receptivos a aplicação de uma metodologia de trabalho em sala de aula, como as desenvolvidas no experimento didático.

Também o uso da história da Matemática, além de ser um forte motivador, auxilia a compreensão da construção dos conceitos e dá suporte para a organização de aulas mais significativas para os alunos. Todos os participantes do experimento de ensino declararam que não estão preparados para utilizar a história na preparação de aulas, o que nos mostra a importância de investigar situações didáticas com o tema proposto.

Concordamos com Lins e Gimenez (1997) que afirmam que um bom trabalho aritmético, para a prática do professor é: reconhecer a necessidade de uma mudança curricular que sirva para desenvolver um sentido numérico; integrar diversos tipos de raciocínios na produção de conjecturas; assumir o papel dos distintos cálculos, que não se reduzam a obtenção de resultados, e contribuam para aprimorar processos como planificar, desenvolver estratégias diferentes, selecionar as mais adequadas; fomentar uma avaliação que contemple a regulação e o controle constante do processo de ensino proposto.

Assim, entendemos que os cursos de Licenciatura em Matemática devem primar por desenvolver um espaço para a discussão, reflexão e estudo dos conceitos aritméticos que privilegiem o desenvolvimento de estratégias para a prática docente, incentivando o estudo da história da Matemática como recurso didático.

 Referências

1. Alencar Filho, E. (!992). Teoria Elementar dos Números. São Paulo: Nobel.        [ Links ]

2. Chemale, E.; Kruse, F. (1999). Curiosidades Matemáticas. Novo Hamburgo: FEEVALE.        [ Links ]

3. Guzmán, M. de; Pérez, D. (1993). Enseñanza de las Ciencias y la Matemática. Madrid: Popular.        [ Links ]

4. Lins, Rômulo Campos; Gimenez, J. (1997). Perspectivas em aritmética e álgebra para o século XXI. São Paulo: PAPIRUS.        [ Links ]

5. Mendes, I.. (2000). História no ensino da Matemática. Departamento de Matemática da Universidade de Aveiro. Portugal.        [ Links ]

6. Mendes, I. (2001). Ensino da Matemática por atividades: Uma aliança entre o construtivismo e a história da Matemática. Natal: UFRN, 2001. Tese de doutorado, Universidade Federal do Rio Grande do Norte, Centro de Ciências Sociais e Aplicadas.        [ Links ]

7. Mendes, I. (2001). O uso da História no Ensino da Matemática. UEPA, Belém do Pará.        [ Links ]

8. Nobre, S. A. (s/f). Pesquisa em História da Matemática e suas relações com a Educação Matemática. In: Pesquisa em Educação Matemática: Concepções e Perspectivas.        [ Links ]

9. Oliveira, Z. C. (1995). Uma Interpretação geométrica do MDC. Revista do Professor de Matemática nº 29, 3º quadrimestre.        [ Links ]

10. Oliveira Santos, J. de. (1998). Introdução à Teoria dos Números. IMPA. Rio de Janeiro: CNPq.        [ Links ]

11. Ozámiz, Miguel de Guzmán; Pérez, D. (1993). Enseñanza de las ciencias y la matemática: tendencias e innovaciones. Madrid: IBER cima.        [ Links ]

12. Tahan, M. (1984). O homem que calculava. São Paulo: Círculo do livro.        [ Links ]

13. Valdés, J. E. Nápoles. (2002). La Historia como elemento unificador en lá Educación Matemática. Argentina. (texto digitado).        [ Links ]

14. Vásquez, M. S.; Acosta, Mario González; García, Andrés Sánchez; Astudillo, Maria Teresa González. (1989). Divisibilidad. Madrid: Síntesis.          [ Links ]