Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Paradígma
versión impresa ISSN 1011-2251
Paradígma vol.34 no.2 Maracay dic. 2013
Idoneidad epistémica del significado de la derivada en el curriculo de bachillerato
Luis R. Pino-Fan; Walter F. Castro; Juan D. Godino; Vicenç Font
Universidad de Granada, España. lrpino@ugr.es, luispino23@gmail.com
Universidad de Antioquia, Colombia. wfcastro82@gmail.com
Universidad de Granada, España. jgodino@ugr.es
Universitat de Barcelona, España.
vfont@ub.eduRESUMEN
En este trabajo presentamos una síntesis de la reconstrucción del significado global de la derivada que hemos realizado con la ayuda de algunas herramientas teóricas del enfoque ontosemiótico del conocimiento y la instrucción matemática. Así mismo, caracterizamos el significado pretendido en el currículo de Bachillerato a partir de las prácticas matemáticas propuestas tanto en el Plan de Estudios como en los libros de texto de dicho nivel. La comparación de ambos significados (global y curricular) permite valorar la idoneidad epistémica del significado curricular. La metodología de análisis didáctico aplicada para el caso de la derivada en el currículo (Plan de Estudios y libros de texto) mexicano, se puede aplicar a otros contenidos y contextos. La información aportada puede ser útil para el profesor de matemáticas de bachillerato ya que revelamos algunos sesgos en los significados de la derivada privilegiados por el currículo que podrían ser evitados para mejorar la enseñanza de la derivada.
Palabras Clave: derivada, significado global, currículo de matemáticas, conocimiento del profesor, enfoque ontosemiótico.
Epistemic suitability of the derivative meaning in the high school curriculum
ABSTRACT
In this paper we report a synthesis of a reconstruction of the derivative holistic meaning carry out using some theoretical notions of the onto-semiotic approach. We characterize the intended high school curricular meaning about the derivative, based on the mathematical practices proposed in both the core curriculum and in the textbooks. The comparison between the global and curricular meanings allows assessing the epistemic suitability of curricular meaning, intended for the high school curriculum. The methodology of the didactical analysis, applied to the case of the derivative in the Mexican curriculum and textbook can be extended to other contents and contexts. The information provided may be useful for high school mathematics teacher because we reveal some biases in the meanings of the derivative privileged by the curriculum that could be avoided to improve the teaching of the derivative.
Key Words: derivative, holistic meaning, mathematics curriculum, teacher knowledge, onto-semiotic approach.
Recibido: 17/07/2013 Aceptado: 16/10/2013
Antecedentes
El descubrimiento del Cálculo
1 es uno de los grandes logros intelectuales de la civilización, pues ha servido por más de tres siglos como una herramienta cuantitativa para la investigación de problemas científicos. El cálculo es fundamental para áreas de las matemáticas tales como la probabilidad, la topología, la teoría de grupos y aspectos del álgebra, la geometría y la teoría de números. Sin él, la tecnología moderna y la física podrían ser difíciles de imaginar (Kleiner, 2002).Sin embargo, la enseñanza del cálculo es conocida por ser una fuente de serios problemas, tanto para los estudiantes como para los profesores (Hitt, 2003), de cara a la comprensión de sus ideas fundamentales. La derivada es uno de los conceptos fundamentales para el estudio del cálculo, aunque un tratamiento excesivamente algebraico del concepto, sin la utilización de otro tipo de representaciones para su enseñanza, puede contribuir al surgimiento de dificultades de cara a su comprensión. Artigue (1995), señala que aunque se puede enseñar a los estudiantes a efectuar de forma más o menos mecánica algunos cálculos de derivadas y a resolver algunos problemas estándares, se encuentran grandes dificultades para que logren alcanzar una comprensión satisfactoria de los conceptos y métodos de pensamiento que conforman el núcleo de este campo de las matemáticas.
Así mismo, Artigue (1998) señala que las investigaciones didácticas evidencian que es difícil para los estudiantes entrar en el campo conceptual del Análisis, cuando éste no se reduce a su parte algebrizada, sino que pretende el desarrollo de los modos de pensamiento y de las técnicas que hoy en día están fundamentadas en él. De esta forma, algunos estudiantes son capaces de resolver ejercicios con la aplicación de las reglas de derivación, no obstante, manifiestan dificultades cuando se les pide usar la derivada, y sus diversos significados, en situaciones no procedimentales.
Algunas investigaciones referentes al significado de la derivada, se han centrado en describir las características de los significados construidos por los estudiantes, mostrando la existencia de conflictos e inconsistencias respecto de los significados formales presentados en los libros de texto (Ferrini-Mundy y Graham, 1994; Sánchez-Matamoros, García y Llinares, 2006). No obstante, diversas investigaciones (Inglada y Font, 2003; Badillo, Font y Azcárate, 2005) evidencian que el origen de los conflictos cognitivos de los estudiantes sobre el significado de la derivada, puede estar asociado a la presentación de la derivada en los libros de texto; por ejemplo, el conflicto causado por la introducción implícita de la función derivada en la definición de la derivada en un punto al usar la notación incremental ![]() como primera notación para definir la derivada en un punto. Estos conflictos e inconsistencias también se observan en algunos profesores como señalan diferentes investigaciones. Por ejemplo, Badillo, Azcárate y Font (2011) documentan la confusión, o la no diferenciación, entre los macroobjetos f(a) y f(x) por algunos profesores, y la relacionan con su complejidad semiótica.
como primera notación para definir la derivada en un punto. Estos conflictos e inconsistencias también se observan en algunos profesores como señalan diferentes investigaciones. Por ejemplo, Badillo, Azcárate y Font (2011) documentan la confusión, o la no diferenciación, entre los macroobjetos f(a) y f(x) por algunos profesores, y la relacionan con su complejidad semiótica.
Uno de los objetivos de este artículo es caracterizar el significado pretendido en el currículo de bachillerato a partir de las prácticas matemáticas propuestas tanto en el Plan de Estudios como en los libros de texto de dicho nivel. Teniendo en cuenta el significado global de la derivada reconstruido en Pino-Fan, Godino y Font (2011), y cuya síntesis se presenta en la primera parte de este documento, se realiza una comparación entre el significado global de la derivada y el significado pretendido en el currículo de matemáticas del nivel Bachillerato. Dicha comparación nos permite finalmente, emitir juicios de valoración de la idoneidad epistémica del significado curricular de la derivada en el nivel bachillerato, información que consideramos de utilidad para el profesor de matemáticas que debe interpretar y concretar tanto las directrices curriculares como los libros de texto para diseñar sus actuaciones en el aula.
Nociones teóricas y metodológicas
Para el logro de los objetivos planteados en este trabajo, hemos adoptado el modelo teórico conocido como
Enfoque Onto-Semiótico (EOS) del conocimiento y la instrucción matemática desarrollado en diversos trabajos por Godino y colaboradores (Godino y Batanero, 1994; Godino, Batanero y Font, 2007). Dicho marco teórico incluye un modelo epistemológico de las matemáticas, sobre bases antropológicas y socioculturales; un modelo cognitivo, sobre bases semióticas de índole pragmatista, y un modelo instruccional coherente con los anteriores.Concretamente utilizamos la noción de
configuración epistémica (Figura 1), la cual nos permite analizar y describir sistemáticamente los objetos matemáticos primarios (situaciones/problemas, elementos lingüísticos, conceptos/definiciones, proposiciones/propiedades, procedimientos y argumentos) que intervienen en las prácticas matemáticas sobre la derivada propuestas en el currículo de matemáticas del nivel bachillerato (Font, Godino y Gallardo, 2013). Es importante aclarar que para el análisis de las prácticas matemáticas sobre la derivada (y los significados de la derivada que estas conllevan) propuestas en el currículo de bachillerato, consideramos tanto el Plan de Estudios de cálculo diferencial como los libros de texto utilizados en dicho nivel.El análisis de dichos libros de texto se hace debido a la importancia que estos adquieren para los profesores en la implementación de clases. La dependencia que los profesores establecen con los libros de texto, ha sido indagada por Nathan y Koedinger (2000), quienes manifiestan, "Es razonable suponer que el uso de los libros de texto en la estructuración diaria de las lecciones de clase, tareas semanales y la secuencia curricular anual, lleva a los profesores a internalizar la imagen de las matemáticas que implícitamente transmiten" (p. 228).
Por su parte, el trabajo de Cooney (1985), reveló que los libros de texto son la influencia primaria para las concepciones curriculares de los maestros, así como para su estilo de presentación en la clase. Adicionalmente, Love y Pimm (1996) señalan, "El libro es todavía, en gran medida, la tecnología más extendida y usada en las clases de matemáticas. Debido a su ubicuidad el libro de texto ha moldeado nuestra noción de la matemática y como debe enseñarse" (p. 402).
Así, el análisis conjunto del Plan de Estudios y de los libros de texto, nos permite estudiar tanto el tratamiento que se le da a la derivada como los significados pretendidos en el currículo de matemáticas de bachillerato.
Finalmente, para contrastar los significados curriculares con el significado global de la derivada, así como para el estudio de la adecuación de los primeros respecto del segundo, utilizamos la noción de
idoneidad epistémica. Esta se refiere al grado de representatividad de los significados institucionales pretendidos (o implementados) respecto de un significado de referencia.La noción de idoneidad didáctica, sus dimensiones, criterios, y descomposición operativa, han sido introducidos en el EOS (Godino, Bencomo, Font y Wilhelmi, 2006) como herramientas que permiten el paso de una didáctica descriptiva–explicativa a una didáctica normativa, esto es, una didáctica que se orienta hacia la intervención efectiva en el aula. La idoneidad didáctica de un proceso de instrucción se define como la articulación coherente y sistémica de las seis componentes siguientes (Godino, Batanero y Font, 2007): idoneidad epistémica, cognitiva, interaccional, mediacional, afectiva y ecológica. El proceso de diseño instruccional requiere que el maestro defina el tema, determine la audiencia, adapte la instrucción al desarrollo cognitivo de los estudiantes, proponga y desarrolle los objetivos, las estrategias de evaluación, de valoración y revisión del proceso. El proceso de instrucción debe ser idóneo, es decir debe cumplir diversas condiciones para que el mismo cumpla tanto con los objetivos curriculares como con el desarrollo de competencias matemáticas por los estudiantes. Es por tanto deseable que los significados de la derivada implementados o pretendidos tanto en los libros de texto como en el Plan de Estudio de cálculo diferencial de bachillerato, representen idóneamente los significados de referencia.
En síntesis, la metodología aplicada en esta investigación ha consistido en las siguientes tres fases: 1) La determinación de un significado global de referencia para la derivada mediante una revisión de tipo histórico-documental desde la matemática griega hasta el siglo XX; 2) La determinación del significado pretendido para la derivada en el currículo de bachillerato de México (a partir del Plan de Estudios y de libros de texto); y 3) la aplicación de los criterios de idoneidad epistémica para valorar dicho currículo y guiar su mejora.
Significado holístico de la derivada
La noción de configuración epistémica (CE) nos permitió reconstruir el
significado holístico2 mediante la identificación de los significados parciales de la derivada, a partir de los informes de investigación y documentos históricos sobre el Cálculo (Pino-Fan, Godino y Font, 2011). Para una institución de enseñanza concreta, el significado de referencia será una parte del significado holístico del objeto matemático.Para determinar el significado holístico de la derivada, se realizó una revisión histórico-documental desde la matemática griega hasta el siglo XX, en la que se efectuó un análisis de los objetos matemáticos primarios intervinientes en los distintos problemas que fueron abordados en distintas épocas y que culminaron con el surgimiento de dicha noción. A partir de esta revisión, se identificaron nueve configuraciones epistémicas asociadas a los distintos problemas, a saber: 1)
tangente en la matemática griega (CE1); 2) variación en la edad media (CE2); 3) métodos algebraicos para hallar tangentes (CE3); 4) concepciones cinemáticas para el trazado de tangentes (CE4); 5) ideas intuitivas de límite para el cálculo de máximos y mínimos (CE5); 6) métodos infinitesimales en el cálculo de tangentes (CE6); 7) cálculo de fluxiones (CE7); 8) cálculo de diferencias (CE8) y, 9) derivada como límite (CE9). Estas configuraciones pueden relacionarse como se muestra en la Figura 2.Las
configuraciones epistémicas se componen de los objetos matemáticos primarios y sus relaciones, que intervienen y emergen de los sistemas de prácticas matemáticas en distintos contextos de uso. Un objeto matemático, como la derivada, puede tener varias configuraciones epistémicas las cuales a su vez llevan asociadas un significado parcial distinto para dicho objeto matemático (Font y Godino, 2006). El significado es aquí entendido en términos sistémico-pragmáticos, esto es, como el sistemas de prácticas que se ponen en juego para resolver un determinado tipo de situaciones-problemas.Los sistemas de prácticas en los cuales se activan las configuraciones CE1 a la CE6, se denominan primarios. Las configuraciones activadas en dichos sistemas primarios tienen un carácter extensivo en tanto que se resuelven ciertos tipos de situaciones-problema con métodos y procedimientos particulares.
Las configuraciones CE1, CE3 y CE6 pueden considerarse similares, puesto que activan significados parciales semejantes para la derivada. Por esta razón se pueden agrupar para dar origen a un sistema de prácticas más genérico, en el que se abordan situaciones-problema sobre tangentes, denominado Tangentes.
Análogamente, las configuraciones CE2 y CE4 pueden agruparse en un nuevo sistema de prácticas más general, con su respectiva configuración asociada, la cual denominamos Variación, Velocidades. La configuración CE5 la hemos denominado Máximos y Mínimos.
Posteriormente Newton, con base en la configuración subyacente al sistema de prácticas Variación-Velocidades, desarrolla un nuevo sistema de prácticas de la derivada como fluxión, en la cual se activa una configuración más general (CE7) en la que los nuevos procedimientos, lenguajes, conceptos, definiciones, proposiciones y argumentos, se aplican para resolver situaciones-problema característicos de los sistemas de prácticas Tangentes, Máximos y Mínimos, y Variación-Velocidades.
Del mismo modo Leibniz, con base en la configuración asociada al sistema de prácticas Tangentes, desarrolla un nuevo sistema de prácticas de la derivada como cociente de diferenciales en el que se activa una configuración más general (CE8). Esta configuración se utiliza para la resolución de situaciones-problema característicos de los sistemas de prácticas sobre Tangentes y sobre Máximos y Mínimos.
Finalmente, matemáticos tales como Euler, Cauchy, Bolzano, Taylor, Lagrange y Weierstrass, quienes sucedieron a Newton y Leibniz, tomaron como base sus desarrollos (CE7 y CE8) para generar un nuevo sistema de prácticas de carácter formal para la derivada como límite del cociente de incrementos. A este sistema de prácticas se le asocia una configuración (CE9) que constituye la formalización de la derivada. Los objetos matemáticos primarios que componen CE9 se aplican para la resolución de problemas propios de los sistemas de prácticas designados con los términos Tangentes, Variación-Velocidades y Máximos y Mínimos.
La consideración conjunta de los elementos y sus relaciones, ilustrados en el esquema de la Figura 2, conforma primordialmente, el
significado holístico de la derivada. No obstante, el significado global de la derivada quedaría incompleto si no se consideran las distintas generalizaciones que históricamente ha experimentado dicho objeto matemático tales como derivada parcial, direccional, de Carathéodory, de Fréchet, de Gâteaux, entre otras.Criterios de idoneidad epistémica para el estudio de la derivada
A partir de la reconstrucción del significado global de la derivada, y de las investigaciones que se han realizado en el campo de la didáctica de las matemáticas sobre aspectos de la enseñanza y aprendizaje de la derivada, es posible proponer criterios que permitan analizar y caracterizar los significados de la derivada pretendidos en el currículo de bachillerato. A partir de dicha caracterización es posible emitir juicios de valoración sobre la idoneidad epistémica de los significados de la derivada en el currículo de dicho nivel.
A continuación describimos cuatro criterios que proponemos para el análisis de la idoneidad epistémica de los significados curriculares de la derivada. No obstante cabe señalar que dichos criterios son generales y pueden ser utilizados para el análisis de la idoneidad epistémica de un tópico matemático cualquiera. Para cada uno de los cuatro criterios "genéricos", proponemos subcriterios que están relacionados con el tópico matemático en estudio.
I. Representatividad de los campos de problemas propuestos.
La elección de tareas matemáticas que pongan en juego los objetos y significados matemáticos es crucial para promover aprendizajes significativos. Para Freudenthal: "[La matemática como una actividad humana] es una actividad de resolución de problemas, de buscar problemas, pero es también una actividad de organización de una disciplina " (Freudenthal, 1971, pp.413-414).
Los significados de un objetos matemático están ligados a los sistemas de prácticas realizadas para resolver un determinado tipo de problemas, estos problemas deben ser representativos del campo correspondiente, a fin de que los significados que se propongan a los estudiantes sean representativos del significado global del objeto en cuestión.
Para el caso de la derivada, los campos de problemas (CP) que identificamos a partir del estudio histórico se pueden resumir en los siguientes:
a) CP1: cálculo de tangentes
b) CP2: cálculo de tasas instantáneas de cambio.
c) CP3: cálculo de tasas instantáneas de variación.
d) CP4: aplicación de la derivada para el cálculo de máximos y mínimos, análisis de gráficas de funciones, etc.
Un último campo de problemas surge a partir de cómo los libros abordan algunos "problemas" sobre cálculo de derivadas de funciones, en los que basta aplicar algunas reglas o proposiciones para su resolución. Esto trasciende el componente algebraizado del Cálculo. Así el quinto campo de problemas que consideraremos es:
CP5: Cálculo de derivadas a partir de reglas y teoremas de derivación.e)
II. Tipo de representaciones activadas en el planteamiento y solución de las tareas.
Durante el proceso de análisis de la idoneidad epistémica es necesario considerar los distintos lenguajes utilizados para referir a los diferentes tipos de objetos matemáticos, así como los tratamientos y conversiones entre los mismos. De acuerdo con Font (1999), existen tres subprocesos, relacionados con los elementos lingüísticos, que intervienen en el cálculo de la función derivada:
f (x);a) Traducciones y conversiones entre las distintas formas de representar
b) El paso de una representación de f (x)
a una forma de representación de f(x); yc) Traducciones y conversiones entre las distintas formas de representar f(x)
.Así, consideraremos los diferentes tipos de representaciones activadas en estos tres subprocesos: descripción verbal, gráfica, fórmula (simbólica) y tabular; esto tanto para la función como para su derivada.
III. Representatividad de los elementos regulativos y argumentativos
A partir de los elementos lingüísticos identificados con el criterio anterior, se hace posible la identificación de definiciones, proposiciones, procedimientos y argumentos propuestos tanto en los Planes de Estudio como en libros de texto de bachillerato sobre derivadas. Estos elementos deberán de ser representativos de los elementos correspondientes en los diversos significados parciales que componen el significado holístico de la derivada.
IV. Conocimientos previos a la introducción de la derivada
Este criterio se refiere a la enumeración, presentación y relación entre los conocimientos previos a la presentación de la derivada, que se formulan tanto en los libros de texto como en el Plan de Estudios de cálculo diferencial. En este sentido, para el análisis de este tercer criterio, enumeramos los conocimientos centrales previos, tal como aparecen tanto en los libros texto como en los Planes de Estudio de cálculo diferencial. La valoración de la pertinencia se hace con base en el análisis epistémico-histórico del objeto en estudio, la derivada, y en el uso posterior que los autores de los textos dan a estos conocimientos previos presentados.
V. Representatividad de los significados institucionales pretendidos (o implementados) respecto del significado global de referencia.
Una de las tareas que son propias del maestro es el diseño instruccional, en la cual se involucran diversos aspectos tales como los epistémicos (contenidos), los cognitivos o los instruccionales. El conjunto de contenidos matemáticos que se proponen en el Plan de Estudios y en los textos, corresponden a una elección por parte de la institución: el currículo pretendido. Esos contenidos matemáticos y los significados conferidos a estos en los textos representan a los significados institucionales de referencia.
Para que la instrucción sea epistémicamente idónea, este conjunto de objetos y significados institucionales de referencia deben representar al significado global de la derivada. El énfasis en determinados significados y objetos matemáticos, y el desconocimiento de otros puede resultar en un cubrimiento epistémico parcializado que puede afectar la idoneidad del proceso de instrucción.
Es importante señalar que, aunque el significado de un objeto matemático está en función del campo de problemas en el que se utiliza, en el ámbito institucional muchas veces se utiliza un objeto matemático en un sentido distinto al campo de problemas en el que se activa. Por ejemplo, algunos libros de texto introducen la derivada utilizando problemas sobre velocidades pero aplicando la derivada en su acepción de tasa instantánea de variación (límite del cociente de incrementos).
Los cinco criterios de idoneidad epistémica mencionados se operativizan en el siguiente apartado en el que, además de describir las configuraciones de objetos y procesos subyacentes a los sistemas de prácticas de los Planes de Estudio y los libros de texto, realizamos el análisis de la idoneidad epistémica de los significados curriculares sobre la derivada (Tablas IV y V).
Significado epistémico de la derivada en el currículo de bachillerato
Entre las cuestiones que surgen cuando se ha logrado la construcción del significado global de referencia de la derivada, destacamos las siguientes:
● ¿Cuáles son los significados de la derivada que actualmente se pretende en el currículo de matemáticas de bachillerato?
● ¿Cuál es el significado de la derivada propuesto en los Planes de Estudio de cálculo diferencial de nivel bachillerato?
● ¿Cómo se organizan tales significados en los libros de texto?
● ¿Los significados pretendidos tanto en los libros como en los Planes de Estudio de cálculo diferencial, son representativos del significado global de la derivada?
Para responder a estas cuestiones, tomaremos como ejemplo el currículo de matemáticas del sistema de bachillerato de México y analizaremos los significados pretendidos en dicha propuesta curricular. Así mismo, revisamos una muestra de libros de texto de cálculo diferencial de dicho nivel educativo. El análisis conjunto del Plan de Estudios de cálculo diferencial y de los libros de texto, permite indagar cómo se aborda la derivada en el currículo de bachillerato mexicano.
La derivada en el Plan de Estudios de bachillerato en México
Hasta hace poco, el bachillerato o la Educación Media Superior (EMS) en México, estaba conformada por alrededor de 25 subsistemas con estructuras y formas de organización diversas, que operaban de manera independiente, sin correspondencia con un panorama general articulado, con poca comunicación y complementación entre ellos. Sin embargo, en la actualidad, la Secretaría de Educación Pública (SEP)3, atendiendo a esta desestructuración ha implementado una Reforma Integral de la Educación Media Superior cuya propuesta está centrada en tres principios básicos: 1) Reconocimiento universal de todas las modalidades y subsistemas del bachillerato; 2) Pertinencia y relevancia de los Planes de Estudio; y 3) Tránsito entre subsistemas y escuelas.
Sin embargo, aún persisten subsistemas como los bachilleratos asociados a Universidades Autónomas o los bachilleratos estatales, que "sobreviven" intactos a dicha Reforma. A continuación analizamos el currículo tanto para el bachillerato propuesto por la Reforma Integral de la Educación Media Superior (SEP, 2010) como el currículo para bachillerato asociado a la Universidad Autónoma de Yucatán (UADY, s.f.). El análisis se hará sobre los significados de la derivada pretendidos en dichas propuestas curriculares.
En relación con el "cálculo diferencial", la Reforma Integral propone: 1) "analizar cualitativa y cuantitativamente la razón de cambio instantáneo y promedio, lo que permitirá dar soluciones a problemas del contexto real del estudiante al facilitarle la formulación de modelos matemáticos de problemas financieros, económicos, químicos, ecológicos, físicos y geométricos"; 2) "la resolución de problemas de optimización". Para esto, se distribuye en cuatro bloques los contenidos u objetos de aprendizaje de la asignatura cálculo diferencial (Tabla I).
TABLA I. DISTRIBUCIÓN DE LOS CONTENIDOS DE APRENDIZAJE DE CÁLCULO DIFERENCIAL SEGÚN LA REFORMA INTEGRAL
| Bloque 1 | Argumentas el estudio del cálculo mediante el análisis de su evolución, sus modelos matemáticos y su relación con hechos reales | |
|
| Propósito | Este bloque pretende que los estudiantes se ubiquen y conozcan los antecedentes históricos de esta rama de las matemáticas y cómo su nacimiento ha contribuido a los avances de la humanidad |
| Contenidos específicos | · Evolución del Cálculo · Modelos matemáticos: un acercamiento a máximos y mínimos | |
| Bloque 2 | Resuelves problemas de límites en situaciones de carácter económico, administrativo, natural y social | |
|
| Propósito | Este bloque busca que los estudiantes resuelvan problemas sobre límites en diversas ciencias, mediante el análisis de tablas, gráficas y aplicación de las propiedades de los límites. |
| Contenidos específicos | · Los límites: su interpretación en una tabla y en una gráfica, y su aplicación en funciones algebraicas. · El cálculo de límites en funciones algebraicas y trascendentes. | |
| Bloque 3 | Calculas, interpretas y analizas razones de cambio en fenómenos naturales, sociales, económicos, administrativos, en la agricultura, en la ganadería y en la industria | |
|
| Propósito | En este bloque se estudia la razón de cambio promedio e instantánea, el cambio de posición de un objeto en el tiempo y la interpretación geométrica de la derivada. |
| Contenidos específicos | · La variación de un fenómeno a través del tiempo. · La velocidad, la rapidez y la aceleración de un móvil en un periodo de tiempo. | |
| Bloque 4 | Calculas e interpretas máximos y mínimos sobre los fenómenos que han cambiado en el tiempo de la producción, producción industrial o agropecuaria | |
|
| Propósito | En este bloque se trabaja la obtención de máximos y mínimos absolutos y relativos y cómo ellos influyen en el éxito o fracaso de las producciones empresariales, industriales, agrícolas y en el comportamiento de los fenómenos naturales. |
| Contenidos específicos | · Producciones, máximos y mínimos. · Variaciones en las producciones, máximos y mínimos relativos. | |
El Bloque 1 motiva el estudio del cálculo diferencial " mediante el análisis de su evolución, sus modelos matemáticos y su relación con hechos reales", (SEP, 2010, p.11). Luego se introduce el concepto de límite (Bloque 2), para posteriormente definir la derivada como razón de cambio (Bloque 3). Finalmente en el Bloque 4 se estudian situaciones interdisciplinares que involucran el cálculo de máximos y mínimos.
Los problemas son contextualizados (agricultura, economía, industria, administración, etc.) para introducir nuevos objetos de aprendizaje o aplicar los objetos de aprendizaje ya introducidos.
Entre los elementos lingüísticos destacan las diversas representaciones para los límites y funciones (tabular, gráfica y simbólica) y para la derivada (verbal, gráfico y simbólico).
Respecto a los conceptos/definiciones, la propuesta curricular resalta algunos, tales como los de función (algebraica y trascendente), límite, derivada (como razón de cambio), razón de cambio promedio e instantánea, velocidad, rapidez, aceleración y máximos y mínimos.
Entre las proposiciones se consideran las propiedades y reglas para el cálculo de límites; no se mencionan las propiedades y reglas para el cálculo de razones de cambio. El cálculo de: límites, razones de cambio, máximos y mínimos y la aplicación de estos cálculos a la resolución de problemas contextualizados, son algunos de los procedimientos que se proponen en esta propuesta curricular.
Los propósitos establecidos por esta reforma, se inician con la justificación del estudio del cálculo, y la resolución de problemas extra matemáticos, de carácter aplicativo, mediante el uso de los conceptos de límite y derivada. Utiliza para ello la derivada en su acepción de cambio promedio instantáneo, cambio de posición y la interpretación de la derivada, hasta la "obtención" de máximos y mínimos.
Por su parte, la propuesta curricular del bachillerato de la Universidad Autónoma de Yucatán (UADY, Tabla II), tiene como propósito: "Aplicar el concepto de la función derivada de funciones algebraicas y trascendentes, a través de estrategias que incentiven la reflexión y análisis, en la resolución de problemas de la vida cotidiana para desarrollar el razonamiento lógico y analítico de los alumnos" (UADY, s.f., p. 4).
Es posible observar en la Tabla II, que la propuesta curricular del bachillerato asociado a la Universidad Autónoma de Yucatán introduce el concepto de límite y sus propiedades (Unidad 1), posteriormente define la derivada como pendiente de la recta tangente y provee los teoremas y reglas de derivación (Unidad 2), finalmente la Unidad 3 se orienta a la aplicación de la derivada para el cálculo de extremos y razones de cambio, y para analizar las gráficas de funciones.
En cuanto a los elementos lingüísticos se aprecia la preponderancia del lenguaje simbólico (definición - de límite) y gráfico (interpretaciones geométricas para el límite y para la derivada, así como la graficación de funciones). Entre los conceptos centrales se encuentran: función (algebraica y trascendente), límite (indeterminados, unilaterales, al infinito, infinitos); continuidad, derivada (como pendiente de la recta tangente), regla de la cadena, derivadas de orden superior, etc.
Respecto a las proposiciones, se consideran los teoremas sobre límites, las fórmulas de derivación, los criterios de la primera y segunda derivada para la determinación de extremos, el teorema del valor extremo, criterios para determinar concavidades y crecimiento o decrecimiento en las funciones.
Entre los procedimientos que se prevén se encuentran el cálculo de límites y su aplicación a la determinación de la continuidad de funciones, el cálculo de derivadas mediante el uso de las reglas de derivación, y el cálculo de tangentes, normales, razones de cambio y máximos y mínimos.
Si bien se mencionan "problemas de la vida real", no queda claro si dichos problemas se proponen para: introducir objetos matemáticos nuevos, ejemplificar la inclusión de nuevos objetos matemáticos o la aplicación de objetos matemáticos previamente introducidos.
Es posible observar en las Tablas I y II, que ambas propuestas curriculares se asemejan en la organización de los temas de estudio; introducen primeramente el concepto de límite para posteriormente usarlo para definir al objeto derivada.
Sin embargo, ambas propuestas destacan significados distintos para la derivada. Por ejemplo, la propuesta de la Reforma Integral (Tabla I), acentúa la derivada interpretada como razón de cambio (Bloque 3) y propone prácticas matemáticas en las que la derivada se interpreta como un máximo o un mínimo (Bloques 1 y 4). En esta propuesta curricular la interpretación de la derivada como la pendiente de la recta tangente a una curva, parece tener un papel secundario, puesto que aunque se contempla el estudio de la interpretación geométrica de la derivada (Tabla I, Bloque 3), no se hacen explícitos contenidos específicos que acentúen dicha interpretación de la derivada.
Por su parte, en la propuesta curricular de la UADY, se resalta la interpretación geométrica de la derivada (Tabla II, Unidad II). Se define la función derivada mediante el concepto de límite, se dan las reglas de derivación, se utiliza la derivada para encontrar máximos y mínimos, y se estudian las razones de cambio.
ABLA II. DISTRIBUCIÓN DE LOS CONTENIDOS DE APRENDIZAJE DE CÁLCULO DIFERENCIAL SEGÚN LA UADY| Unidad 1 | Límites y continuidad | |
|
| Propósito | Manejar el concepto de límite de una función algebraica a través de su interpretación intuitiva y geométrica, para su cálculo y posterior aplicación en la continuidad y la derivada de una función. |
| Contenidos específicos | · Concepto intuitivo de límite de una función · Definición formal de límite de una función (épsilon-delta) · Teoremas sobre límites de funciones · Límites aparentemente indeterminados · Límites unilaterales · Límites al infinito · Límites infinitos · Concepto de función continua · Continuidad de una función en un punto · Continuidad de una función en un intervalo | |
| Unidad 2 | La función derivada | |
|
| Propósito | Conocer el concepto derivada y ejecutar su cálculo a través de su interpretación geométrica y de las fórmulas básicas de derivación, para desarrollar el razonamiento lógico y analítico de los alumnos en la solución de los problemas. |
| Contenidos específicos | · Motivación: Pendiente de la tangente a una curva en un punto · Obtención de las ecuaciones de las rectas tangente y normal a una curva en un punto · Definición de la derivada de una función · Fórmulas de derivación · Derivación de funciones algebraicas · Derivación de funciones compuestas, regla de la cadena · Derivación de funciones trascendentes · Derivación implícita · Derivadas de orden superior | |
| Unidad 3 | Aplicaciones de la derivada | |
|
| Propósito | Aplicar los conceptos de derivadas de funciones algebraicas y trascendentes, a través de estrategias que incentiven la reflexión y análisis, en la resolución de problemas de la vida cotidiana para desarrollar el razonamiento lógico y analítico. |
| Contenidos específicos | · Tangentes y normales a la curva · Graficación de las funciones ü Teorema del valor extremo ü Funciones crecientes y decrecientes ü Criterio de la primera derivada para valores extremos relativos ü Concavidad y puntos de inflexión ü Criterio de la segunda derivada para valores extremos relativos · Problemas de máximos y mínimos · Razón de cambio | |
Para nuestro estudio se analizaron una muestra de libros de texto (Tabla III) sugeridos en las propuestas curriculares, del nivel bachillerato. Sin embargo, por motivos de espacio, presentamos el análisis detallado de dos de ellos (libros 1 y 7). Nos centramos en el análisis de las prácticas matemáticas propuestas en dichos libros de texto, en los capítulos dedicados al estudio de la derivada.
ABLA III. LIBROS DE TEXTO SUGERIDOS EN LA PROPUESTA CURRICULAR DE BACHILLERATO| Libros de bachillerato | |
| 1 | Martínez de G., Mayra et al. (2009). Cálculo diferencial e integral. México: Santillana |
| 2 | Stewart, H., et al. (2010). Introducción al cálculo. México: Thompson |
| 3 | Thomas, G. (2006). Cálculo. Una variable. México: Pearson Educación. |
| 4 | Purcell, E., Varberg, D., y Rigdon, S. (2007). Cálculo diferencial e integral. México: Pearson Educación. |
| 5 | Simmons, G.F. (2002). Cálculo y Geometría analítica. Madrid: McGraw-Hill. |
| 6 | Ayres, F., y Mendelson, E. (1991). Cálculo diferencial e integral. España: McGraw-Hill. |
| 7 | Quijano, M. y Navarrete, C. (2003). Cálculo diferencial. México: UADY. |
| 8 | Salazar, L., Bahena, H., y Vega, F. (2007). Cálculo Diferencial. México: Grupo Editorial Patria. |
Para efectuar el análisis se utiliza la noción de configuración epistémica (Godino y Font, 2006) la cual permite identificar y describir sistemáticamente los objetos matemáticos primarios (problemas, elementos lingüísticos, conceptos, proposiciones, procedimientos y argumentos) que se ponen en juego en la solución de las prácticas matemáticas propuestas.
Configuraciones epistémicas asociadas a las prácticas propuestas en los libros de texto de bachillerato
Libro 1
Este libro contempla dos unidades didácticas para el estudio de la derivada. La primera se orienta a la presentación y definición del objeto, y la segunda se orienta a la aplicación del mismo. Se abordan cuatro tipos de situaciones/problemas: 1) problemas introductorios contextualizados que ayudan a definir conceptos y propiedades; 2) problemas (resueltos) que refuerzan y ejemplifican el uso de los conceptos y propiedades introducidos; 3) problemas contextualizados y no contextualizados para la aplicación de los objetos matemáticos introducidos; y 4) demostraciones de algunos teoremas para derivar funciones.
Se introducen conceptos/definiciones tales como los de velocidad, velocidad promedio, velocidad instantánea, la derivada en un punto como velocidad instantánea y como pendiente de la recta tangente en un punto, función derivada definida como el límite del cociente de incrementos y derivadas de orden superior. Los conceptos de función, límites y continuidad de una función, son considerados conocimientos previos.
Entre las propiedades/proposiciones que se introducen, podemos señalar los teoremas para derivación de funciones, criterios para identificar la derivabilidad de funciones, criterios para el análisis de gráficas de funciones (crecimiento o decrecimiento, extremos, concavidades, ), regla de la cadena, teorema del valor medio para la derivada, teorema de Fermat y teorema de Rolle.
Tanto los
conceptos como las proposiciones se entrelazan en los procedimientos los cuales consisten básicamente en el cálculo de velocidades promedio, tiempos y distancias a partir de la relación v=d/t y su interpretación como pendiente de la rectas secantes; cálculo de la derivada de funciones en puntos específicos, cálculo de la derivada de funciones mediante las reglas para derivar, graficación de la función derivada, cálculo de la derivada de segundo orden, derivación de funciones compuestas, análisis de gráficas de funciones con base en los criterios de derivadas, cálculo de máximos y mínimos, cálculo de tangentes y normales, y demostración de teoremas para derivar funciones. Dichos procedimientos, a su vez, dan cuenta de elementos lingüísticos: lenguaje verbal (natural), simbólico y gráfico. Se nota la ausencia de lenguaje tabular.Como
argumentos podemos señalar las justificaciones dadas a la inclusión de conceptos/definiciones o proposiciones, ejemplificación y explicaciones de técnicas a seguir, y del uso de conceptos/definiciones y proposiciones. Además en la resolución de los distintos problemas se hace necesario argumentaciones deductivas y gráfico-visuales.Una de las características importantes de este texto es el uso de situaciones/problema particulares para definir o presentar conceptos, propiedades o reglas. En cuanto al significado institucional pretendido, predomina la derivada como velocidad instantánea y como pendiente de la recta tangente. Sin embargo, dichas acepciones de la derivada se logran a partir de la definición de la derivada como tasa instantánea de variación (límite del cociente de incrementos).
Libro 7
El libro de Quijano y Navarrete (2003) consta de tres unidades. La primera dedicada al estudio de los límites y continuidades de funciones. La segunda unidad se dedica al estudio de la función derivada y la tercera a las aplicaciones de la derivada. A lo largo de dichas unidades se abordan cuatro tipos de
situaciones/problemas: 1) problemas contextualizados para introducir o definir conceptos y propiedades; 2) problemas (resueltos) no contextualizados que refuerzan y ejemplifican el uso de conceptos y propiedades introducidos; 3) problemas contextualizados y no contextualizados para la aplicación de los objetos matemáticos introducidos; y 4) demostraciones de algunos teoremas para derivar funciones. Así mismo, el libro hace uso de elementos lingüísticos tales como el lenguaje natural (verbal) con el cual se introducen los nuevos conceptos, reglas y propiedades. Se distingue el predominio del lenguaje simbólico el cual se intenta vincular con los elementos gráficos para la presentación de algunas definiciones y proposiciones.Por su parte, los
procedimientos dan cuenta del uso predominante de los lenguajes simbólico y gráfico para el cálculo de: 1) derivadas mediante su definición como límite del cociente de incrementos y las reglas para derivar; 2) tangentes, normales, máximos y mínimos, puntos de inflexión; 3) uso de la derivada en el análisis de gráficas de funciones; y 4) uso de la definición de la derivada como límite del cociente de incrementos para demostrar algunos teoremas de derivación de funciones.Respecto a los
conceptos/definiciones, se consideran como previos los de función, límites y continuidad. Como emergentes podemos mencionar los de velocidad promedio, velocidad instantánea, la derivada en un punto como razón instantánea de cambio, la función derivada definida como el límite del cociente de incrementos, derivadas de orden superior y derivación implícita.Las
proposiciones introducidas a lo largo de las tres unidades dedicadas al estudio de la derivada son los teoremas o reglas para la derivación de funciones, criterios para identificar la derivabilidad de funciones, criterios para el análisis de gráficas de funciones (crecimiento o decrecimiento, extremos, concavidades, ) y regla de la cadena. En cuanto a los argumentos destacan las justificaciones dadas a la inclusión de conceptos y proposiciones, la ejemplificación y explicaciones de las técnicas a seguir y del uso de conceptos y proposiciones. Además en la resolución de los problemas se requiere el uso de argumentaciones deductivas y gráfico-visuales.En este libro, se observa un predominio del uso de la derivada como razón instantánea de cambio. No obstante dicho significado se alcanza a partir de la definición de la derivada como tasa instantánea de variación. Otros significados, tal como la derivada en un punto como pendiente de la recta tangente, son considerados como aplicaciones, y su estudio se realiza en la unidad tres.
Finalmente el libro de Quijano y Navarrete (2003), propone introducir conceptos, definiciones, reglas generales y proposiciones a partir de ejemplos concretos o situaciones particulares que justifican su inclusión, lo cual no siempre se logra. Las Tablas IV y V presentan un resumen del análisis de la idoneidad de los significados pretendidos en los libros 1 y 7.
Tabla V. Significados parciales de la derivada identificados en los libros 1 y 7
| Significados parciales | Campos de problemas | ||||
| CP1 | CP2 | CP3 | CP4 | CP5 | |
| CE1: Trazado de tangentes en la matemática Griega |
|
|
|
|
|
| CE2: Problemas sobre variación en la edad media |
|
|
|
|
|
| CE3: Cálculo de subtangentes y tangentes con el álgebra |
|
|
|
|
|
| CE4: Trazado de tangentes mediante consideraciones cinemáticas |
|
|
|
|
|
| CE5: Cálculo de máximos y mínimos mediante la idea intuitiva de límite |
|
|
|
|
|
| CE6: Cálculo de tangentes y subtangentes mediante métodos infinitesimales |
|
|
|
|
|
| CE7: Cálculo de fluxiones |
|
|
|
|
|
| CE8: Cálculo de diferencias |
|
|
|
|
|
| CE9: Derivada como límite | 1,7 | 1,7 | 1,7 | 1,7 | 1,7 |
La Tabla IV muestra el tipo de problemas contemplados en los libros de texto así como las representaciones que se activan tanto en su planteamiento como en su solución. Así, por ejemplo, la celda sombreada en gris que contiene el código
1,7, indica que en los libros 1 y 7 se contemplan problemas sobre el cálculo de tangentes en los que se requiere que el estudiante obtenga, a partir de la expresión simbólica de la función, una expresión simbólica para la derivada de dicha función.De esta forma, se aprecia como las entradas en la Tabla IV están distribuidas en tan sólo algunas casillas. Si bien es cierto que los libros estudiados proponen varios sistemas de representación también lo es que el vínculo entre ellos, la función y su derivada están escasamente usados en ambos textos. Se reconoce la dificultad de diseñar actividades matemáticas que, en conjunto, utilicen todas las posibles relaciones exhibidas en la tabla; el énfasis en tan sólo algunas puede afectar la atribución de significados, olvidando algunos y reforzando otros. Reconocer tales énfasis es importante en tanto que:
● La institución escolar puede proponer un cubrimiento más completo de significados y de formas de representación.
● El maestro puede tomar conciencia de la distribución no homogénea de significados y diseñar actividades matemáticas que resalten algunos vínculos.
● Los estudiantes tendrán acceso a una oferta más amplia de significados, modos de representación y vínculos entre ellos que puede ayudar a configurar una visión un poco más holística del tema bajo estudio.
Por su parte, en la Tabla V, se aprecia el énfasis en el significado parcial de la "derivada como límite" (Figura 2) en cinco campos de problemas: CP1, CP2, CP3, CP4 y CP5. Tal énfasis no es sorprendente en tanto que en la sección 3 se indicó cómo las configuraciones primarias han dado paso a la configuración CE9, que es mayoritariamente usada en los cursos de Cálculo. El significado de la derivada manifestado en esta última configuración se fundamenta en el uso del límite del cociente de incrementos.
Es necesario aclarar que la Tabla V propone cruzar los significados parciales para la derivada con los campos de problemas, y en modo alguno se afirma, por ejemplo, que en la matemática griega o medieval surjan significados asociados al cálculo de derivadas a partir de reglas.
Significado de la derivada pretendido en el currículo de bachillerato
El análisis de la dupla <Plan de Estudios, Libros de Texto>, de cálculo diferencial, ha permitido identificar el significado de la derivada pretendido actualmente en el currículo de bachillerato mexicano. Por un lado, la organización que se hace en los Planes de Estudio de los temas planificados para la enseñanza del cálculo diferencial, evidencia que independientemente del contexto o de los sistemas de prácticas con los que se introduce la derivada, el objeto límite juega en la actualidad un papel fundamental para su introducción y definición en el bachillerato. Como vimos en la sección 5.1, la propuesta de la Reforma Integral (Tabla I), acentúa la interpretación de la derivada como razón de cambio, mientras que la propuesta curricular de la UADY (Tabla II), resalta su interpretación geométrica. Sin embargo, ambas propuestas recurren a la noción de límite, para definir local y globalmente la derivada.
Así mismo, tanto el Plan de Estudios de cálculo diferencial propuesto por la UADY como el propuesto por la Reforma Integral, sugieren una serie de textos que, en teoría, se adaptan a los propósitos educativos institucionales. Hemos analizado para este estudio, una muestra de 8 libros de texto de cálculo diferencial (4 por cada Plan de Estudios), de los cuales se ha presentado el análisis detallado de dos de ellos (uno de cada Plan de Estudios). Como se pudo apreciar en el apartado
5.2.1, tanto los libros 1 y 7, como los otros seis (Tabla III), consideran como conocimientos previos a la introducción de la derivada: funciones, continuidad y, fundamentalmente, la noción de límite.
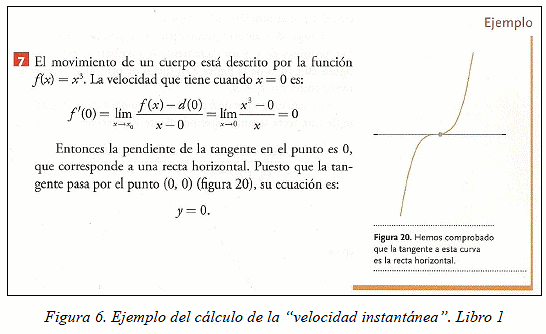
En el análisis se pudo observar que las situaciones/problemas (Figura 6), conceptos/definiciones (Figuras 3 y 5), proposiciones (Figura 4), procedimientos y argumentos que se activan en los textos, independientemente del contexto de uso de la derivada, siempre aludían a un mismo significado:
la derivada como límite del cociente de incrementos (Tabla V). Esto se puede distinguir, por ejemplo, en la primera definición que plantea el libro 7 a partir de una situación sobre velocidades (Figura 3).El análisis realizado de los Planes de Estudio y los libros de texto de cálculo diferencial de nivel bachillerato, revela que en la actualidad el significado de la derivada pretendido en el currículo de bachillerato mexicano es:
la derivada como límite del cociente de incrementos (Figura 7). El análisis nos ha permitido contrastar el significado de la derivada pretendido en el currículo de bachillerato (Figura 7) frente al significado holístico de la derivada (Figura 2). Se evidencia que pese a las recomendaciones realizadas desde el campo de investigación en didáctica del cálculo, la configuración que se activa para la resolución de problemas sobre derivadas en el proceso de enseñanza de dicho objeto es la CE9 (Figura 2). Hay que señalar que, como se vio en la sección 3, la configuración CE9 surge por la necesidad de fundamentar con rigor, o bien, de manera formal, el cálculo diferencial establecido sobre los trabajos de Newton y Leibniz. Tal formalización no representa una necesidad primordial para los estudiantes que se enfrentan por primera vez con las nociones del cálculo diferencial.Los ejemplos, ejercicios y problemas propuestos en los textos, requieren mayoritariamente de la activación de representaciones simbólicas y gráficas. Usualmente se parte o bien de la expresión simbólica de la función y =
f(x) para dar la expresión simbólica y/o gráfica de la primera y segunda derivada, o bien, a partir de la representación gráfica y tabular de la función se piden representaciones simbólicas o descripciones verbales para la primera y segunda derivada (Tabla IV). La exploración de vínculos entre las tres funciones: función, primera derivada y segunda derivada en otros contextos (numérico y gráfico), y con otros ordenes de gestión de las representaciones (a partir de la primera derivada dar información sobre la función de la cual fue obtenida o sobre la segunda derivada, etc.) no son numerosos.Orton (1983) señala que una aproximación inicial "informal" a los conceptos del cálculo, debe involucrar exploraciones numéricas y gráficas. Por su parte Font (1999) considera que las diferentes representaciones de los objetos matemáticos y las traducciones entre ellas son un elemento fundamental para la comprensión y, por tanto, para la enseñanza y aprendizaje de la derivada. De esta manera, se aborda el cálculo de la función derivada como un proceso en el que intervienen tres subprocesos, en cada uno de los cuales se pueden utilizar diferentes representaciones (descripciones verbales, simbólicas, gráficas y tabulares). Lo anterior permite la ampliación del "abanico" de técnicas de cálculo de la función derivada, lo cual a su vez favorece trascender el simple cálculo de la derivada mediante límites o mediante el uso de reglas de derivación.
Reflexiones finales
El estudio de la idoneidad epistémica de los significados sobre la derivada que se pretenden en el currículo de bachillerato, es de sumo interés, puesto que una "adecuación pobre" del significado holístico en la enseñanza, podría obstaculizar tanto la correcta comprensión del objeto por parte de los estudiantes como por parte de los profesores en formación inicial. Sierpinska (1990) señala que, "Comprender el concepto será concebido como el acto de captar su significado. Este acto será probablemente un acto de generalización y síntesis de significados relacionados con elementos particulares de la estructura del objeto (la estructura es la red de sentidos de las sentencias consideradas). Estos significados particulares tienen que ser captados en actos de comprensión" (p. 27). El criterio de "representatividad" es uno que favorece valorar la calidad matemática de la instrucción y debería ser considerado cuando se planean actividades matemáticas. Parece claro que la elección de tareas matemáticas que pongan en juego los objetos y significados matemáticos es crucial para promover aprendizajes significativos.
Como señalan Godino y Batanero (1994), los significados logrados (aprendidos) por los estudiantes dependen fundamentalmente de los significados institucionales, concretamente, de los significados pretendidos asociados a los sistemas de prácticas planificados para un proceso particular de instrucción, así como de los significados efectivamente implementados en dicha instrucción y de los evaluados.
Además, el profesor, como parte de la institución escolar, debe recurrir, para la elección de los significados pretendidos, a los significados de referencia. "En una institución de enseñanza concreta este significado de referencia será una parte del significado holístico del objeto matemático. La determinación de dicho significado global [u holístico] requiere realizar un estudio histórico-epistemológico sobre el origen y evolución del objeto en cuestión, así como tener en cuenta la diversidad de contextos [sistemas de prácticas] de uso donde se pone en juego dicho objeto" (Godino y Font, 2007, p. 2).
En este sentido diversos investigadores (Tall, 2009; Doorman y van Maanen, 2008) sugieren que la enseñanza de la derivada debería considerar otros métodos que conserven los vínculos con la historia del cálculo diferencial, lo que favorecería que los estudiantes desarrollen el pensamiento matemático, comprendan el significado holístico de un objeto matemático y, en particular, daría sentido a la simbología de Leibniz que prevalece en la actualidad.
En el presente trabajo de investigación, hemos propuesto criterios o pautas para determinar la idoneidad de los significados de la derivada pretendidos en el currículo de bachillerato. Nuestra hipótesis es que si las instituciones educativas, apoyadas en los desarrollos de las investigaciones en el campo de la Matemática Educativa, logran diseñar un currículo idóneo respecto a los significados de los objetos matemáticos, ello facilitaría que los profesores de matemáticas logren diseñar e implementar procesos de instrucción idóneos.
Cabe señalar que hemos asumido el currículo como la fusión de dos aspectos clave en la enseñanza, por un lado el Plan de Estudios, de cálculo diferencial en nuestro caso, y por otro los libros de texto que son esenciales para la planeación de los procesos de instrucción. El análisis que hemos realizado evidencia que el enfoque moderno del cálculo diferencial se basa fundamentalmente en el concepto de límite. Así, se hace necesario efectuar investigaciones curriculares que centren su atención en la adecuación de los significados pretendidos respecto del significado holístico de la derivada (Pino-Fan, Godino y Font, 2011), y en general, de cualquier tema particular.
Así mismo, se hacen necesarias investigaciones que indaguen sobre cuestiones tales como,
- ¿Cuál es la diferencia entre el significado pretendido en el currículo de bachillerato y el pretendido en el currículo de los futuros profesores de bachillerato?
- ¿Cómo contribuye el significado pretendido en el currículo de los futuros profesores de bachillerato a que los futuros profesores gestionen de forma eficaz el significado de la derivada en sus estudiantes?
Es de interés indagar los conocimientos didáctico-matemáticos de los futuros profesores sobre el objeto derivada, en particular aquellos conocimientos relacionados con las formas de vinculación o asociación que los futuros profesores establecen entre los diversos significados de dicho objeto matemático.
Reconocimientos
Trabajo realizado en el marco de los proyectos de investigación sobre formación de profesores, EDU2012-31869 (Universidad de Granada) y EDU2012-32644 (Universidad de Barcelona).
Notas
1 Usaremos la palabra
Cálculo para referirnos al Cálculo Infinitesimal (diferencial e integral).2 El lector puede encontrar un análisis más detallado y completo sobre los significados parciales de la derivada en Pino-Fan, Godino y Font (2011).
3 La Secretaría de Educación Pública (SEP) es el organismo de gobierno encargado de regular las políticas que rigen el Sistema Educativo en México. La SEP a través de la Subsecretaría de Educación Media Superior creó la Reforma Integral de la Educación Media Superior (RIEMS) con la cual se organiza y estructura el currículo del nivel medio superior.
Referencias
1. Artigue, M. (1995). La enseñanza de los principios del cálculo: Problemas epistemológicos, cognitivos y didácticos. en M. Artigue, R. Douady y P. Gómez (Eds.), Ingeniería didáctica en educación matemática (pp. 97-140). México, Grupo Editorial Iberoamérica, [ Links ]
2. Artigue, M. (1998). Enseñanza y aprendizaje del análisis elemental: ¿Qué se puede aprender de las investigaciones didácticas y los cambios curriculares? Revista Latinoamericana de Investigación en Matemática Educativa, 1(1), pp. 40-55.
3. Badillo, E., Azcárate, C., y Font, V. (2011). Análisis de los niveles de comprensión de los objetos f (a) y f (x) de profesores de matemáticas. Enseñanza de las Ciencias, 29(2), 191–206.
4. Badillo, E., Font, V., y Azcárate, C. (2005). Conflictos semióticos relacionados con el uso de la notación incremental y diferencial en libros de física y de matemática del bachillerato. Enseñanza de las Ciencias, Número Extra, VII Congreso.
5. Ball, D., Thames, M. H., y Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal for Research in Mathematics Education, 59(5), pp. 389-407.
6. Cooney, T. J. (1985). A beginning teacher's view of problem solving. Journal of Research in Mathematics Education, 16, pp. 324-336.
7. Nathan, M. J., y Koedinger, K. R. (2000). An investigation of teacher beliefs of students´algebra development. Cognition and Instruction, 18(2), pp. 209-237.
8. Doorman, M., y van Maanen, J. (2008). A historical perspective on teaching and learning calculus. Australian Senior Mathematics Journal, 22(2), pp. 4-11.
9. Ferrini-Mundy, J., y Graham, K. (1994). Research in calculus learning. Understanding limits, derivates and integrals. En E. Dubinsky, y J. Kaput (Eds.), Research issues in undergraduate mathematics learning (pp. 31-45). Washington, DC: Mathematical Association of America.
10. Font, V. (1999). Procediments per obtener expressions simbòliques a partir de gràfiques. Aplicacions a la derivada. Tesis doctoral, Universitat de Barcelona.
11. Font, V., Godino, J. D., y Gallardo, J. (2013). The emergence of objects from mathematical practices. Educational Studies in Mathematics. 82, 97–124.
12. Freudenthal, H. (1971). Geometry between the devil and the deep sea. Educational Studies in Mathematics, 3 (3/4), pp. 413-435.
13. Godino, J. D., y Font, V. (2006). La noción de configuración epistémica como herramienta de análisis de textos matemáticos: Su uso en la formación de profesores. Educação Matematica Pesquisa, 8(1), pp. 67-98.
14. Godino, J. D., y Font, V. (2007). Algunos desarrollos de la teoría de los significados semióticos. Recuperado el 24 de marzo de 2013, de http://www.ugr.es/~jgodino/indice_eos.htm
15. Godino, J. D., y Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14(3), pp. 325-355.
16. Godino, J. D., Batanero, C., y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM, The International Journal on Mathematics Education, 39(1), pp. 127-135.
17. Godino, J. D., Bencomo, D., Font, V., y Wilhelmi, M. (2007). Análisis y valoración de la idoneidad didáctica de procesos de estudio de las matemáticas. Paradigma, 27(2), pp. 221-252.
18. Hitt, F. (2003). Dificultades en el aprendizaje del cálculo.
Décimo Primer Encuentro de Profesores de Matemáticas del Nivel Medio Superior. Universidad Michoacana de San Nicolás de Hidalgo, Morelia, México. Recuperado el 8 de mayo de 2010 de http://www.matedu.cinvestav.mx/librosfernandohitt/Doc-6.doc19. Inglada, N., y Font, V. (2003). Significados institucionales y personales de la derivada. Conflictos semióticos relacionados con la notación incremental.
XIX Jornadas del SI-IDM. Córdoba 2003, 1-18.20. Love, E., y Pimm, D. (1996). This is so: A text on texts. En A. Bishop, K. Clements, C. Keitel, J. Kilpatrick, y C. Laborde (Eds.),
International handbook of mathematics education (pp. 371–409). Dordrecht: Kluwer.21. Nathan, M. J., y Koedinger, K. R. (2000). An investigation of teacher beliefs of students´ algebra development.
Cognition and Instruction, 18(2), pp. 209-237.22. Kleiner, I. (2002). History of the infinitely small and the infinitely large in calculus.
Educational Studies in Mathematics, 48, pp. 137-174.23. Orton, A. (1983). Students understanding of differentiation.
Educational Studies in Mathematics, 14, pp. 235-250.24. Pino-Fan, L., Godino, J.D., y Font, V. (2011). Faceta epistémica del conocimiento didáctico-matemático sobre la derivada.
Educação Matematica Pesquisa, 13(1), pp. 141-178.25. Sánchez - Matamoros, G., García, M., y Llinares, S. (2006). El desarrollo del esquema de derivada.
Enseñanza de las Ciencias, 24, pp. 85 – 98.26. Secretaría de Educación Pública (SEP). (2010).
Programa de Estudio de Cálculo Diferencial. Recuperado el 7 de junio de 2011, de http://www.dgb.sep.gob.mx/informacion_academica/programasdeestudio.html27. Sierpinka, A. (1990). Some remarks on understanding in mathematics.
For the Learning of Mathematics, 10(3), pp. 24-36.28. Tall, D. (2009). Dynamic mathematics and the blending of knowledge structures in the calculus.
Mathematics Education, 41, pp. 481-492.29. Universidad Autónoma de Yucatán (UADY). (s.f.).
Programa de Curso y Unidad de Cálculo I. Recuperado el 24 demarzo de 2013, de http://www.prepa1.uady.mx/planedu.php