Determinación del tipo de régimen de lluvia anual en estaciones pluviométricas venezolanas, según análisis de Fourier y el análisis de grupo*

Rain Annual Rate Regime of a set of Venezuelan Rainfall Stations, Based on Fourier Analysis, and the Analysis of Group

Andrés Blanco, Jesús Barboza, Jorge Rodríguez

Andrés E. Blanco T. Licenciado en Geografía (2000) Especialista en Análisis de Datos en Ciencia Sociales (escolaridad completa) Profesor Instructor por Concurso (2007) Escuela de Geografía UCV. Área de Investigación: Climatología Básica y Aplicada. Modelos Lineales, Univariados y Multivartiados; Series de Tiempo. Correo electrónico: andeloblant@yahoo.com.

Jesús L. Barboza. Licenciado en Geografía (2000). Profesor Instructor Escuela de Geografía UCV. Área de Investigación: Climatología Básica y Aplicada. Modelos Lineales, Univariados y Multivartiados; Series de Tiempo. Correo electrónico: jlubarbo@yahoo.com.

Jorge Armando Rodríguez Gómez. Licenciado en Geografía, Mención Cartografía (1968, UCV). Ingeniero Civil, Mención Estructuras (1983, USM). Magíster Scientiarum en Geografía (1986, UCV) Especialista en Planificación e Ingeniería de los Recursos Hidráulicos (1991, USB). Profesor Titular (2000) Escuela de Geografía UCV. Docencia en Matemáticas (USB). Maestría en Estadística (escolaridad completa) Especialista en Análisis de Datos en Ciencia Sociales (2004, UCV). Área de Investigación: Climatología Básica y Aplicada. Modelos Lineales, Univariados y Multivartiados; Series de Tiempo. Correo electrónico: jarpine@yahoo.es.

RESUMEN

Para describir el régimen climático de precipitación intra-anual, generalmente se identifican los lapsos de valores mayores y menores a la media aritmética de los 12 valores mensuales, así como los montos pluviales extremos. Este trabajo tiene como finalidad configurar la variación de la lluvia en el año aplicando el Análisis de Fourier a los registros climáticos correspondientes al lapso 1961-1990, a 15 estaciones pluviométricas distribuidas en el territorio nacional, para, posteriormente, agruparlas en conjuntos internamente homogéneos pero externamente heterogéneos utilizando la técnica de agrupación automática (Cluster Análisis). La obtención de los coeficientes de Fourier, generó una matriz de 15 casos por 6 valores asociados a las curvas armónicas de tres ciclos, valores correspondientes a las amplitudes y ángulos de fases de dichas funciones periódicas, y explican más del 90% de la variabilidad mensual de la lluvia, así se obtuvieron siete grupos: (1) Barcelona, Ciudad Bolívar, Maturín, San Fernando de Apure, con un régimen pluvial unimodal y máximo en julio–agosto; (2) Barquisimento, Santa Elena de Uairén, con máximo en junio y otro secundario en octubre; (3) Colonia Tovar, Maracaibo, Maracay, Mene Grande con máximos en septiembre-octubre y otro máximo secundario en mayo-junio; (4) Coro, Maiquetía con un régimen de lluvia que se incrementa desde febrero y marzo hasta fines de año; (5) Mérida con régimen bimodal con máximos en Mayo y Octubre con mínimo secundario en julio; (6) Puerto Ayacucho con régimen pluvial unimodal con máximo en junio y extremo mínimo por encima de los 30 mm y (7) San Antonio del Táchira tiene un régimen bimodal con máximos en abril y octubre y mínimo secundario que comprende los meses de Julio y Agosto. Al comparar los resultados de agrupación con los pluviogramas se constató que su representación mediante los coeficientes de Fourier fue adecuada, concluyéndose que puede sugerirse como una opción para incluir la condición de variabilidad pluvial anual.

PALABRAS CLAVE: Lluvia, clima, régimen, análisis de Fourier, análisis de agrupamiento, Venezuela.

ABSTRACT

To describe the climate regime of intra-annual precipitation, generally identified lapses greater and less than the arithmetic mean of the 12 monthly values and extreme rainfall amounts. This paper aims to set the variation of rainfall in the year by applying Fourier analysis to the climate record, covering the period 1961-1990, 15 rainfall stations distributed over the national territory, and then combined into groups internally homogeneous but externally heterogeneous using automatic clustering technique (Cluster Analysis). Obtaining the Fourier coefficients by multiple regression, generated a matrix of 15 cases for 6 values associated with three cycles of harmonic curves, which at least explained in more 90% of the variability of monthly rainfall. In this way were seven groups, namely: (1) Barcelona, Ciudad Bolívar, Maturín, San Fernando de Apure, which are characterized by a unimodal rainfall regime with a peak in july-August (2) Barquisimento, Santa Elena de Uairén, with maximum in june and october secondary, (3) Colonia Tovar, Maracaibo, Maracay, Mene Grande peaks in september-october and another secondary maximum in may-june (4) Coro, Maiquetía with a rain which increased from february and march until the end of the year (5) Merida presents a bimodal peaks in may and in october with minimal side july (6) Puerto Ayacucho with unimodal rainfall regime with maximum in june and far above the minimum of 30 mm and (7) San Antonio del Tachira has a bimodal peaks in april and october and lower secondary which covers the months of july and august. Comparing these results with the automatic grouping respective pluviogramas was found that the representation by means of Fourier coefficients was properly concluded that it may be suggested as a choice to include the status of annual rainfall variability.

KEYWORDS: Rain, Climate, Regime, Fourier Analysis, Cluster Analysis, Venezuela.

* Recibido: 21-03-2009.

Aceptado: 15-10-2009.

PRESENTACIÓN

La determinación del régimen pluvial anual consiste en identificar la estacionalidad de la lluvia, al señalar los máximos y mínimos relativos así como la ubicación y duración de los lapsos lluviosos y no lluviosos. Por ejemplo, una estrategia a seguir es aplicar los criterios del sistema de clasificación climática de Köeppen, el cual considera hasta, distintivamente, tres regímenes: (1) con máximo o máximos en posición astronómica alta de sol (régimen w); (2) con máximo o máximos en posición astronómica baja de sol (régimen s) y (3) sin diferencia significativa de períodos pluviales (régimen f);. de este modo, el régimen pluvial de la estación La Carlota (Distrito Capital) es de carácter unimodal con máximo en el mes de junio, mientras que la estación Observatorio Cagigal es unimodal con máximo en el mes de octubre.

Tal información no es adecuada para incorporarla a una base geográfica de datos por ser incompleta, ya que no aclara acerca de lo acontecido en la pluviosidad en el resto del año. Ello plantea la disyuntiva de incluir, al menos, los doce datos climáticos de la lluvia o bien realizar parámetros, mediante algún procedimiento, tal comportamiento pluvial anual con una menor cantidad de índices, de modo que tal síntesis no implique una pérdida significativa de la información original.

En otro orden de ideas, la literatura matemático-estadística plantea que el Análisis Fourier, tanto de procesos periódicos o no, es pertinente para desagregar los componentes que determinan una curva compleja en el dominio del tiempo. La descomposición de la curva original en sus componentes, llamados armónicos, permite, simultáneamente, estimar la contribución de los distintos regímenes que intervienen en la curva original y, así mismo, indexar numéricamente cada armónico mediante los coeficientes binómicos Fourier o bien con los coeficientes polares Fourier.

El Análisis Fourier permite desagregar los componentes (armónicos) que determinan una curva compleja, con los cuales se estima la contribución de los distintos subregímenes que intervienen en la curva original e indexar cada armónico mediante sus coeficientes Fourier. En ese orden de ideas, Kyrkyla y Hameed. (1989), en Estados Unidos de América, y Rodríguez (2003), en la región norte de Venezuela, separan matemáticamente los componentes estacionales que contribuyen con la configuración de la curva intra-anual pluviométrica de un conjunto de sitios de medición con distribución espacial irregular. Ahora bien, dado que la curva pluvial climática tiene 12 valores (uno por cada mes), se pueden generar, máximo, 11 coeficientes Fourier (ó 5 armónicos). Pero, según criterio del investigador, es factible reducir el número de armónicos a 3 ó menos, lográndose una solución más parsimoniosa que la información pluvial original.

En consecuencia, si la curva pluvial original tiene 12 valores, es posible generar, hasta un máximo, de 11 coeficientes Fourier, apreciándose que la reducción de valores solamente es de una unidad.

Sin embargo, es posible cuantificar la contribución a la varianza muestral total de cada armónico, y determinar de modo aproximado, si esa contribución es estadísticamente significativa. Por lo tanto, es factible que el número de armónicos significativos sean tres o menos, reduciéndose así el número de coeficientes a seis, un 50% de la información pluvial original.

A tal efecto, este estudio se planteó, a partir de una base de datos climáticos mensuales pluviales, provenientes de un conjunto de estaciones venezolanas, cuatro objetivos, a saber:

1. Obtener los coeficientes Fourier de los seis armónicos, matemáticamente posibles, de cada serie de 12 valores pluviales.

2. Seleccionar el número de armónicos que acumulen una cantidad importante de la varianza explicada de la información original, para obtener un modelo con un número menor de coeficientes armónicos.

3. Determinar el número de grupos, según la homogeneidad de los coeficientes armónicos, que constituyen el conjunto de estaciones seleccionadas.

4. Comprobar la validez de los resultados obtenidos, comparándolos con los gráficos pluviales de las series mensuales de orden climático.

METODOLOGÍA EMPLEADA

Base de datos

Se hizo una base de datos constituida por una matriz de 15 x 12, correspondientes a 15 estaciones pluviométricas del territorio nacional y a las medias aritméticas de las 12 lluvias mensuales, promedio correspondiente al lapso de 30 años de registro (1961-1990); en el cuadro 1, se compilan los respectivos montos mensuales en mm.

En el cuadro 1, puede estimarse que el rango de las coordenadas georreferenciales es, latitudinalmente, del orden de los 800 km, mientras que longitudinalmente es del orden de los 1300 km, lo que supone una amplia cobertura territorial. En cuanto a la altitud, se extiende desde los 3 m (MIQ) hasta los 1.790 m (COL). Así mismo, los datos compilados de la lluvia mensual se extienden desde 1 mm (SFA) hasta 408 mm (PAY).

METODOLOGÍA

El estudio cubrió las etapas que se indican en el siguiente diagrama.

DEFINICIÓN Y REPRESENTACIÓN DE LOS COEFICIENTES FOURIER

De acuerdo con Quinet (1982; p.159), los trabajos de Fourier (1791-1867) han mostrado que ciertas funciones periódicas pueden ser representadas como la suma de una serie de funciones trigonométricas que algebráicamente se expresan como:

Donde:

f(x) es una función univariable de x

A₀, A_n, B_n son los Coeficientes Fourier

cos nx: la función trigonométrica coseno aplicada

sobre el ángulo nx

sen nx: la función trigonométrica seno aplicada en el ángulo nx

En la ecuación (1.3) se manifiesta que f(x) es equivalente o se puede representar por la siguiente suma algebraica:

Por lo tanto, nuestro objetivo, para buscar el equivalente trigonométrico de f(x), es la estimación de los ángulos sobre los cuales se aplican las funciones trigonométricas seno y coseno (x, 2x,…), así como la estimación de todos los pares infinitos coeficientes A_n y B_n, así como el coeficente A₀.

Ahora bien, si solamente se utiliza £ un número finito de sumandos, la representación de f(x) sería:

En la ecuación (3.3) se expresa que f(x) se representará, aproximadamente, por una serie Fourier con k pares de sumandos senocosenoidales más el término A₀.

Si f(x) es periódica en el intervalo [-À, À], los coeficientes Fourier pueden estimarse, si x es continua, mediante las fórmulas:

Si f(x) es una serie de tiempo, se tendría que f(x) se sustituye por f(t) y, por ende:

Donde T es el período de recurrencia de f(t) y la nueva variable w₀ es igual a 2 À / T; 2 À es el período fundamental de las funciones trigonométricas seno y coseno, mientras que T representa el período fundamental o básico de la serie de tiempo f(t). La constante w₀ es denominada velocidad angular de la serie f (t) y nos da la cantidad de arco, en radianes, por cada unidad de tiempo. Todo ello significa que las unidades finales de los coeficientes Fourier son las mismas de f(t).

Es frecuente que, en la práctica, sólo se tenga una información limitada y discreta de N valores t, determinando ello que, el operador integral sea reemplazado por el operador lineal suma o sumatoria £, resultando el siguiente grupo de fórmulas:

Apréciese que el coeficiente A₀ es la media aritmética del fenómeno temporal f(t). ´t es el intervalo de separación entre cada valor de t y si el intervalo ´t es unitario, se tendría, finalmente, que los coeficientes A_n y B_n se obtendrían de la forma siguiente:

Por lo tanto, la representación en series de Fourier de la serie de tiempo f(t) quedará como:

ESTIMACIÓN DE LOS COEFICIENTES FOURIER DE LAS SERIES PLUVIALES

De acuerdo con Rodríguez (1994) hay distintas maneras de estimar los coeficientes Fourier. Una de ellas es el algoritmo mínimo-cuadrático de la regresión lineal múltiple que se fundamenta en que a los 12 datos climáticos de la lluvia mensual, para cada una de las 15 estaciones climáticas, se les ajustará un hiperplano, el cual se origina de la siguiente ecuación matricial: Y = +ε = X +ε, donde Y es un vector columna, de orden 12 x 1, de los datos compilados de la lluvia mensual de un lugar específico; = X es el vector columna de los datos estimados por el modelo lineal; μ es el error debido al ajuste del modelo a los datos; X es una matriz, de orden 12 x 11, contiene valores trigonométricos seno-cosenoidales y es el vector de los 11 posibles coeficientes regresores, correspondientes a los coeficientes Fourier.

La solución mínimo cuadrática a las incógnitas de los coeficientes Fourier se obtiene con la formulación matricial:

= (X^T X)^-1 X^T Y

11x1 11x11 11x12 12x1

Por ejemplo, para la estación San Fernando de Apure, se tiene la siguiente sucesión temporal de lluvia mensual (en mm)

Estos datos se compilarán en el vector columna Y, de orden 12 x 1. Así mismo, la matriz X, de orden 12 x 11, tendría el siguiente contenido:

El número de columnas se corresponde con el número de coeficientes Fourier a estimar, los cuales se compilan a continuación.

El coeficiente Ao es la media aritmética de los doce valores mensuales de lluvia, generándose la aproximación de los mismos mediante las series Fourier:

Sustituyendo por los valores calculados:

Apartando a las series Fourier, se tiene:

Una determinación análoga se realizó para el resto de los catorce lugares, originándose la siguiente matriz de coeficientes Fourier:

Ahora bien, se puede demostrar que la varianza de cada función armónica o Fourier puede estimarse mediante la fórmula

Donde:

V [f_K (t)]= varianza explicada por el k-ésimo armónico de la función f(t)

A²_K = cuadrado del coeficiente cosenoidal Fourier del k-ésimo armónico de f (t)

B²_K = cuadrado del coeficiente senoidal Fourier del k-ésimo armónico de f (t)

Luego, se llega a la siguiente simplificación,

Por lo tanto, la varianza total de la función f(t) es igual a:

Con base en la fórmula (14.3) se calculó la varianza aportada por cada armónico, resultado que se llevó al cuadro siguiente.

Bajo las columnas con los encabezamientos V₁, V₂ ,.., V₅ se han egistrado las varianzas aportadas por cada armónico para cada lugar. a columna suma totaliza la varianza aportada por la serie Fourier espectiva, mientras que en la columna V pluvial se ha inscrito la varianza luvial muestral, anotándose, finalmente, en columna la Residuo, la iferencia entre la columna V pluvial y la columna suma, donde se aprecia ue las series Fourier no están representando el 100% de la varianza uestral dado que, teóricamente, ello se conseguiría con infinitas series ourier.

Seguidamente, se determinó la varianza acumulada por los cinco rmónicos con el propósito de delimitar cuántos armónicos, y por ende, uántos coeficientes Fourier, se utilizarían para la parametrización pluvial anual. He aquí un cuadro que es el resultado de los cálculos mencionados.

La intención es obtener una cantidad de parámetros que sea menor al número de meses del año (12) para que la solución sea parsimoniosa. Se ha resaltado que los tres primeros armónicos explican al menos el 92% de la variación total de la pluviosidad mensual, lo cual se consideró como una representación Fourier pertinente para la función pluvial f(t).

Para evaluar el grado de aproximación que se logra representando a f (t) con los 3 primeros armónicos, se presentan, a modo de ejemplo, los gráficos de la serie pluvial original de San Fernando de Apure y su representación Fourier, modelo trigonométrico que explica el 99,83% de la varianza total.

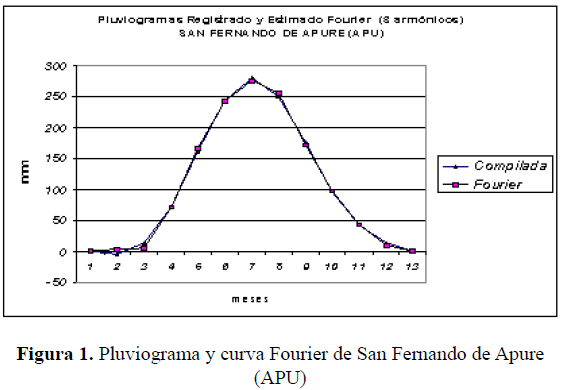
Apréciese que la serie Fourier de la sucesión pluvial reproduce bastante bien la gráfica original, concluyéndose que los 6 parámetros Fourier serían suficientes para analizar el régimen pluvial en el año.

Cada función armónica f_K(t) = A_K cosk w₀t + B_K senk w₀t puede transformarse en una función trigonométrica cosenoidal o senoidal única. Por ejemplo, se cumplirá que (H. P. Hsu; 1973; 5; J. Quinet; 1982; 159):

C_K cos (k w₀t - F_K) representación polar de la suma k-ésima de Fourier

C_Ka amplitud del k-ésimo armónico

_Ka º ángulo de fase, cosenoidal, del k-ésimo armónico.

Por ejemplo, para f₁ (t), cuando T = 12 meses, es

Donde:

C₁ = amplitud –máximo valor de f₁ (t)— del primer armónico

W₀ = 2 À / T = 2 À rad / 12 meses = 0,524 rad / mes a 30 ° / mes

W₀= frecuencia fundamental

₁ = ángulo de fase cosenoidal del primer armónico

₁ = arc tg (B₁ / A₁)

En el caso de la estación San Fernando de Apure se tiene que

Por lo tanto,

En cuanto al ángulo de fase cosenoidal (AFC₁ = ₁), se obtiene

En consecuencia,

Para f₁ (t), ello significa que su máximo valor C₁ se halla a una distancia angular de 215,05º.

En virtud de que la forma polar f_k(t) = C_k cos(kw₀t - F_k) es más adecuada que la forma binómica f_k(t) = A_k coskw₀t + B_k senkw₀t porque incluye 2 de las características asociadas al comportamiento pluvial en el régimen anual (máximo valor y localización de éste), se decidió elaborar una base de datos de 15 x 6 valores, donde, ahora, los seis valores se corresponden con las amplitudes y ángulos de fase cosenoidales de los tres primeros armónicos.

Pero, debido a que la amplitud y el ángulo de fase se expresan en unidades distintas, se creó una matriz estandarizada de datos, que se anexa de inmediato, que hiciera posible la interpretación de los resultados del análisis multivariable de agrupamiento que se aplicaría subsiguientemente.

DETERMINACIÓN DE LOS GRUPOS DE ESTACIONES PLUVIOMÉTRICAS CON IGUAL RÉGIMEN PLUVIAL ANUAL

Como se comentó en el ítem anterior, se sustituyó la base de quince estaciones con sus doce valores pluviales mensuales (15 x 12 = 180 datos) por una nueva base de datos constituidas por los coeficientes Fourier estandarizados de los primeros 3 componentes armónicos, los cuales explican, al menos, el 92% de la variación total de la pluviosidad mensual de cada lugar; tal varianza explicada se consideró, tanto numérica como climáticamente, que formaban una representación Fourier pertinente para la función pluvial f(t) respectiva.

Seguidamente, se indagó acerca de cuántos regímenes pluviales distintos estaban definidos por los quince casos seleccionados. Para obtener la solución a tal propuesta se aplicó la siguiente estrategia:

1. Aplicación del algoritmo del promedio ponderado (Average Linkage, en inglés) con distancia euclidiana con el propósito de evaluar qué cantidad de grupos es la adecuada. El promedio ponderado (PP) es un algoritmo aglomerativo, jerárquico, combinatorial, compatible y espacialmente invariante (véase, Propuesta de una Metodología de Clasificación Climática Mediante la aplicación de Técnicas Multivariables a Indicadores Geográficos-Ambientales; Marzo 2005; 208-223). El programa estadístico posee un coeficiente llamado ÍNDICE DE SIMILITUD que orienta al usuario acerca del número conveniente de grupos, el cual se complementa con el respectivo dendrograma. En ese orden de ideas, se seleccionaron siete grupos.

2. Corrida del algoritmo promedio ponderado, con distancia euclidiana, requiriéndosele que formara siete grupos, los cuales quedaron constituidos de la forma siguiente:

El cuadro señala, por ejemplo, que las estaciones CORO (COR) y MAIQUETÍA (MIQ) tienen un régimen pluvial semejante, según la base estandarizada de Fourier, de modo que constituyen el grupo cuatro.

3. A fin de validar la solución que genera el procedimiento semiautomático anterior, se aplicaron otros algoritmos del programa estadístico, los cuales se consideró no eran satisfactorios en relación con el promedio ponderado (PP). El dendrograma (figura 2) donde se muestran estos siete grupos. La línea continua gruesa señala, de modo aproximado, los siete grupos formados.

4. Las 6 variables estandarizadas de las amplitudes y ángulos de fase cosenoidales forman un sistema cartesiano oblicuo, lo que impide que la distancia euclidiana sea la verdadera distancia de los casos en el espacio no métrico de las variables citadas. En consecuencia, se ortogonalizó el espacio R6 de las variables mediante la técnica multivariable de Componentes Principales (ACP) y luego se aplicó el algoritmo PP, resultando una solución no pertinente cuando se utilizó como validación la gráfica pluvial de los datos originales de los quince sitios.

5. Finalmente, se decidió que el algoritmo PP con distancia euclidiana era el apropiado, aunque la distancia entre los casos podía estar sobre o subestimada por una cantidad que depende del signo y magnitud de la correlación o ángulo entre las variables.

RESULTADOS

Para comprobar lo pertinente de la agrupación homogénea de regímenes pluviales realizados mediante la metodología aplicada se presentan los distintos pluviogramas para cada grupo especificado.

El programa MINITAB versión 13.2 produce una serie de estadísticas de las características de los grupos formados, índices que se reproducen parcialmente.

En la columna 4 se compila la Distancia Promedio de los casos respecto al centroide del grupo (DPC), índice que permite cuantificar la homogeneidad interna del grupo. De esta manera, se puede elaborar el cuadro 10.

En este cuadro se muestra que los grupos más homogéneos son los grupos 5, 6 y 7, con un solo caso (Mérida, Puerto Ayacucho y San Antonio del Táchira, respectivamente), mientras que el menos homogéneo es el grupo 1 (Barcelona, Ciudad Bolívar, Maturín y San Fernando de Apure), ello significa que, en el grupo 1 es donde hay menos semejanza en las amplitudes y ángulos de fase cosenoidales estandarizados y por tanto, según nuestra hipótesis, en los regímenes pluviales.

Si se desea £ escoger el caso más representativo en los grupos múltiples, MINITAB estima la distancia de cada estación con respecto al centroide del grupo; de ahí que el caso con menor distancia al centroide puede escogerse como el representante del grupo. En ese orden de ideas, se obtuvieron los siguientes resultados:

Ciudad Bolívar (CBO) tiene la menor distancia al centroide del grupo 1 (véase columna 3) lugar que tiene el siguiente pluviograma. Se trata de una curva unimodal con máximo pluvial en julio. Colonia Tovar (COL) tiene la menor distancia al centroide del grupo 3 (véase columna 3), sitio que tiene el siguiente pluviograma. Se trata de una curva unimodal pero con leve descenso antes de alcanzar su máximo pluvial en octubre. Dado que la distancia centroidal de los casos es la misma, es indistinto escoger el caso representativo. Por ejemplo, en Barquisimeto (BRQ) se aprecia una curva unimodal con un mínimo local secundario pluvial en septiembre. La estación Coro (COR), exhibe una curva sin estacionalidad anual pero con mínimo local secundario en agosto. Gráficamente se tiene:

CONCLUSIONES

La reducción de los doce montos pluviales, de un grupo seleccionado de quince lugares, a seis coeficientes estandarizados de amplitudes y ángulos de fase cosenoidales de las series Fourier, con aplicación a posteriori de un procedimiento de agrupación automático supervisado, ha resultado ser apropiado en cuanto a que ha permitido definir hasta 7 grupos de regímenes pluviales; estos regímenes se distinguen por su estacionalidad anual (unimodal, bimodal, no estacional), así como por la localización y magnitud de los valores pluviales máximos y mínimos.

Esos resultados sugieren que la parametrización con las series Fourier es una opción válida para caracterizar el régimen anual de la lluvia (así como de cualquier otro elemento climático) e incorporarlos a una base de datos, tanto por su enfoque reduccionista como por la posibilidad de obtener una mayor discriminación del patrón de la distribución espacial que la lograda por los procedimientos climáticos convencionales.

REFERENCIAS BIBLIOGRÁFICAS

1. Cañada, A. (2002). Series de Fourier y aplicaciones: Un tratado elemental con notas históricas y ejercicios resueltos. Ediciones Pirámide.        [ Links ]

2. Howell, K.B. (2001). Principles of Fourier Analysis. Chapman & Hall/CRC.        [ Links ]

3. Hsu, H. P. (1973). Análisis de Fourier. Fondo Educativo Interamericana. EEUU.        [ Links ]

4. Kyrkyla, K. I. y Hameed, S. (1989). Harmonic analysis of the seasonal cycle in precipitation over the United Status: a comparison between observations and a general circulation model. Journal of Climatology, 2 (12), 1463-1475.        [ Links ]

5. Quine, J. T. (1982). Curso de matemática superior. Editorial Paraninfo. España.        [ Links ]

6. Programa estadístico MINITAB versión 13.2.        [ Links ]

7. Rodríguez G., J. (1994). Conceptos básicos el análisis armónico. Trabajo de ascenso a la categoría de asociado. UCV-Caracas.        [ Links ]

8. Rodríguez G., J. (2003). Distribución de las fechas del inicio de la temporada lluviosa mediante análisis armónico de la región centro norte de Venezuela. Estudios Geográficos, LXIV (251), (335-346). Instituto de Economía y Geografía. Madrid, España. Publicación trimestral.        [ Links ]

9. Rodríguez G., J. (2005). Propuesta de una metodología de una clasificación climática Trabajo de Especialización en Análisis de Datos en Ciencias Sociales. UCV-Caracas.        [ Links ]