Cuantificación del perfil del viento hasta 100 m de altura desde la superficie y su incidencia en la climatología eólica

Quantification of the Profile Wind up 100m from Surface and its Incidence in Air Climatology.

José Manuel Guevara Díaz

José Manuel Guevara D. Egresado de la Universidad Central de Venezuela como Licenciado en Geografía, obtiene maestría en la Universidad de Boston y posteriormente, doctorado en la UCV. Profesor Titular. Durante su labor educativa universitaria de pregrado ha dictado los cursos de Meteorología, Climatología, Geografía Física, Geografía de Venezuela, Geografía Regional y trabajo de Campo. A nivel de postgrado, Climatología Urbana y Problemas Climáticos de Venezuela. Su obra escrita es diversa con artículos publicados en revistas nacionales y extranjeras y en libros como: Meteorología; La Geografía Regional, la Región y la Regionalización; Métodos de estimación y ajuste de datos climáticos, Geografía de las regiones Central y Capital de Venezuela y su más reciente, Historia de la Escuela de Geografía de la UCV.

RESUMEN

Se discuten las formulaciones que permiten la representación de la variación del viento con la altura o perfil del viento, y se enfatiza sobre su correcta interpretación, dado que se aprecia cierta confusión en el uso de las fórmulas según las condiciones de estabilidad atmosféricas y la altura sobre el suelo, así como en la determinación de la altura de desplazamiento, d la altura de rugosidad, Z₀, y la velocidad del viento de fricción, u*. Por otra parte, en la interacción del perfil del viento con la geografía, se debe recordar que en Europa, muy urbanizada, sin embargo, actualmente, entre un 20% y 30% de la energía eólica producida proviene de zonas donde los bosques afectan el flujo del viento, y allí, como en otra zonas, el conocimiento de los parámetros d y Zo, son altamente necesarios para evitar la sobreestimación de la velocidad del viento en zonas cubierta de vegetación o en zonas industriales. Se concluye que los modelos exponencial y logarítmico, y los modelos basados en la teoría de la similitud de Monin-Obukhov (MOST) son las formulaciones utilizadas más frecuentemente en los problemas aplicados del viento en la climatología eólica relacionadas con la producción de energía limpia y con los modelos de dispersión de contaminantes. Los casos explicado en Montoya et al (2004) en la caracterización de la turbulencia y estabilidad atmosférica en Bogotá, el de Venora (2009) aplicado en la estación Horns Rev en el Mar del Norte, el de Gualtiere (2011) en Italia y las comparaciones de las estaciones de Owez y Horn Rev por Sathet et al. (2012) son ejemplos aplicados que ilustran la tendencia de la climatología del viento en la capa superficial y en la capa límite atmosférica.

Palabras clave: Perfil del viento, cizallamiento, modelo exponencial, modelo logarítmico, Monin- Obukhov

ABSTRACT

The formulations that allow represents of the variation of the wind with the height or profile of the wind, and are discussed and emphasizes on their correct interpretation, since it is appraised certain confusion in the use of the formulas according to the atmospheric conditions of stability and the height on the ground, as well as in the determination of the height of displacement, d the height of , rugosidad, Z₀, and the wind speed of friction, or *. On the other hand, in the interaction of the profile 0 of the wind with geography, is due to remember that in and Europe, very urbanized, nevertheless, at the moment, between a 20% and 30% of the produced Aeolian energy it comes from zones where the forests affect the flow of the wind, and there, like in another one zones, the knowledge of the parameters d and Zo, are highly necessary to avoid the overestimation of the wind speed in zones covered with vegetation or industrial zones. One concludes that the models exponential and logarithmic, and the models based on the theory of the similarity of Monin-Obukhov (MOST) are the used formulations more frequent mind in the applied problems of the wind in the Aeolian climatology related to the production of clean energy and the models of dispersion of polluting agents. The cases explained in Montoya et al. (2004) in the characterization of the turbulence and the atmospheric stability in Bogota, the one of Venora (2009) applies in the station Horns Rev in the North Sea, the one of Gualtiere (2011) in Italy and the comparisons of the stations of Owez and Horn Rev by Sathet ET to (2012) are applied examples that illustrate the tendency of the climatology of the wind in the layer superficial and in the atmospheric boundary layer.

Key words: Profile of the wind, shear, exponential model, logarithmic model, Monin-Obukhov

Introducción

Por el título de este artículo, la porción de la atmosfera que interesa en la discusión de los perfiles de la velocidad del viento, es la parte inferior de la capa límite (Atmospheric Boundary Layer, ABL) la cual es denominada capa atmosférica superficial (Atmospheric Surface Layer, ASL) de altura variable con máxima entre 60 y 100 metros sobre la superficie del suelo, agua o hielo. En esta capa superficial de la atmosfera, existe una alta interacción de flujo de calor, humedad y de momento entre la atmosfera y la superficie, los cuales son estudiados dentro del campo específico de la micrometeorología y microclimatología. Es en esta capa, donde los modelos de perfil vertical del viento tienen su validez. Modelos más complejos, aplicables a toda la capa limite o gran porción de ella, han sido propuestos por Sathe et al. (2010); Tambke et al. (2004); Sathe et al. (2010) y Peña et al. (2009) y serán mencionados al final de este trabajo.

En la capa atmosférica superficial, se conoce por mucho tiempo, que la velocidad del viento tiende a incrementarse a medida que se asciende y que la superficie terrestre ejerce una acción de fricción o de retardo sobre la velocidad el viento. La representación de este comportamiento de la velocidad del viento con la altura, es lo que se conoce como el perfil vertical del viento o simplemente el perfil del viento y es expresado mediante fórmulas matemáticas, unas empíricas, como los modelos exponencial y logarítmico del viento y otras, con fundamentos teóricos, como la basada en la teoría de similitud de Monin-Obukhov (1954). Mejor conocida internacionalmente por la abreviación de MOST.

En los perfiles del viento, lógicamente, las superficies más irregulares o rugosas, tendrán mayor influencia sobre la velocidad del viento que las superficies más lisas, como las aguas estancadas o la superficie de un aeropuerto.

Las figuras (1a y 1b) representan perfiles típicos del viento por los modelos exponencial y logarítmico hasta la altura de 100 metros, correspondientes al viento medio de la isla La Orchila, Venezuela, periodo 1951-1980, según datos de Las Fuerza Aérea de Venezuela. (s/f), para el exponente de rugosidad α, = 0,1546 del modelo logarítmico y de la altura de rugosidad, Zo = 0,0024 m, del modelo exponencial.

En estas figuras (1a y 1b), si se continuara ploteando las velocidades del viento con la altura, se irían apartando del ascenso logarítmico o exponencial y los modelos dejarían de ser válidos. A elevaciones superiores, cercano a los 1000 m, la influencia de la superficie es considera nula y el viento se comportará como un viento geostrófico, es decir, que no lo afecta la fuerza de fricción que ejerce la superficie de la tierra, y por ello, estos vientos fluyen paralelos a las isobaras y a gran velocidad.

Fórmula exponencial del perfil vertical del viento

De seguida se discuten las diferentes fórmulas o modelos de mayor utilización para representar el perfil vertical del viento, esencialmente útiles para la condición de equilibrio atmosférico neutro. Para revisar este concepto y lo relacionado con las otras clases de equilibrio atmosférico, véase Guevara (2008).

Donde:

V_z : Velocidad del viento a estimar a una altura Z sobre el nivel del suelo

V_ref , velocidad de referencia, velocidad del viento observada a una altura preestablecida, denominada altura de referencia, Z_ref , generalmente 10 m o 2 m, aunque puede ser otra.

α, exponente de rugosidad (wind shear exponent). Varía entre 0,0 a 0,40, según el tipo de rugosidad del terreno: agua, 0,13; grama, 0,14 a 0,16; cultivos y arbustos, 0,20; bosques, 0,25 y zonas urbanas, 0,40.

En la aplicación de las fórmulas exponencial (1a,1b,1c,1d) y logarítmica (2a y 2b), se requiere conocer al menos una observación de la velocidad y dirección del viento sobre un punto durante un periodo de un año y buen conocimiento de la geografía física de la zona donde estén emplazados los anemómetros de copa, o bien los sensores sónicos como el Sodar o el lumínicos como el Lidar, que también son empleados modernamente para determinar la velocidad del viento, mediante el sonido y la luz, respectivamente, Wagner et al. (2008).

Cuando la información de la velocidad del viento es para un momento dado, se pueden aplicar las fórmulas, pero solo serán válida para ese instante y por consiguiente, sus resultados nada estables, pero ilustrativos del perfil del viento de la zona, en ese momento, tal como lo es un sondeo meteorológico de un día.

Si se aplica logaritmo neperiano en (1a) o a (1b), se escribirán como en (1c) y (1d) y se le conoce como la fórmula de Archibald (WMO: World Meteorological Organitazion, 1960), pero no se trata del modelo logarítmico que se vera más adelante.

Donde: Ln, logaritmo neperiano.

V_z ; V_ref , α, Z y Z_ref , previamente identificados

Se debe destacar que el coeficiente de rugosidad α, no es una constante como se pudiese creer, sino que depende de Z₀, (1e); de la velocidad del viento y de las alturas correspondientes, (1g). Hsu (1982) realizó observaciones de vientos a 10 m y 33 m durante un año en las costas de las islas Vírgenes y determino los coeficientes, α, para diferentes condiciones atmosféricas, a los cuales recomienda para cualquier zona costera tropical.

Entonces, al conocerse la altura de rugosidad, Z₀, α, se calcula por (1e), según CICES, 2003; y si se conocen las velocidades (V_ref  y Vz) a las alturas (Z_ref  y Z), sobre un mismo punto, por (1g), según fórmula de Panofsky y Dutton (1984):

Z₀, Altura o parámetro de rugosidad, en metros.

La altura de rugosidad, Z₀, como concepto es sencillo, y es la altura desde el suelo donde la velocidad del viento es teóricamente cero y varía desde 0,0001 m en superficie acuáticas tranquila, hasta más de 2 metros. Esta altura no es la altura de la superficie continua que forman los obstáculos rugosos, como árboles, bosques, colinas, cerros, edificaciones, etc., pero está asociada con ellos, como se verá más adelante.

Por otra parte, el modelo exponencial, sigue en vigencia, y es el empleado por la NASA Surface Meteorological and Solar Energy (2012), para estimación de la velocidad del viento a la altura de 50 m, aunque lo denominan incorrectamente, “Ripe law”, como si este conocido experto, Paul Ripe, fuese el autor del modelo.

DeMarrais (1959) pensaba que el modelo exponencial era válido hasta unos 300 metros y realiza estudio de perfiles del viento en Brookhaven National Laboratory, USA con énfasis en la estimación del exponente del modelo exponencial, al cual prefiere. Mientras que Sedefian (1980) y Hsu (1982) opinan que el modelo exponencial, puede ser aplicable a toda la capa limite (Atmospheric Boundary Layer, ABL), es decir, más allá de la capa superficial, apartándose de lo aceptado científicamente en este aspecto de no aplicarlo a más de 100 o 120 metros de altura.

Fórmula logarítmica del perfil del viento

Mientras en (1a) se trata de una fórmula exponencial, ahora, en (2 a y 2b) es logarítmica, con resultados muy parecidos.

La identificación de los componentes de las formulaciones (2a y 2b) es la misma que en (1a y 1c), solo es nuevo el término Z₀, la altura o longitud de rugosidad en metros, la cual expresa la rugosidad de la superficie, entendida según Wieringa et al. (2001), como la capacidad que tiene una superficie para convertir la energía del viento que fluye sobre ella, en movimiento turbulento. En el cuadro 1, la clasificación de la rugosidad de Davenport revisada por Wieringa et al. (2001), es lo último en rugosidad y es la empleada por instituciones como la WMO, ASCE y el Handbook de Stull.

La fórmula (2c) despejada de (1e) relaciona el exponente de rugosidad α con la altura de rugosidad, Z₀:

Ejemplos de altos valores de rugosidad: 1,8 en Mann et al (2007) en una zona boscosa de Dinamarca; 2, en un bosque de 15 metros de altura al norte de escocia. Como regla general, la rugosidad de los bosques es una fracción de su altura media, h, la consideraba en 0,08h. También es muy utilizado el Tabla de rugosidad, según el paisaje, utilizado por ADIE (2000), Dinamarca del Atlas Eólico Europeo, WAsP.

Estimación gráfica de Z₀:

Otra forma de estimar el valor de la rugosidad, Z₀, es desde un gráfico del perfil del viento semilogarítmico, al prolongar la recta de la velocidad del viento, hasta tocar el eje Y, donde el viento es teóricamente igual a cero, ya que Z₀, es el intercepto de la recta.

El modelo logarítmico (2a y 2b) al igual que el exponencial, opera adecuadamente en condición de estabilidad atmosférica neutra, es decir, cuando la superficie del suelo no difiere significativamente de la temperatura del aire (Gradiente adiabático seco igual al altotérmico) y no hay los movimientos convectivos característicos de la atmósfera inestable.

La página web <The Swiss wind data ch/tool/profile.php> contiene el Wind Profile Calculator, el cual estima y grafica el perfil del viento con base en el modelo logarítmico estándar (fórmula 2), y para lo cual requiere información sobre la rugosidad de la superficie, Z₀, y velocidad del viento a una altura de referencia.

Fórmulas logarítmicas descritas por la teoría de similitud de Monin-Obukhov (MOST) validos hasta unos 100 metros de altura

Al considerar conceptos teóricos como la velocidad de fricción, u_*, la altura de rugosidad, Z₀, y la constante de von Karman, se tiene la fórmula que Geiger (1971) denominó modelo de Prandtl (3a) y Foken (2006) lo reconoce por su existencia en 1925. Otros como Webb (1965), simplemente la denominan perfil logarítmico, pero diferente al modelo ya considerado.

El modelo de Prandtl (3a) está íntimamente relacionado con la teoría de similitud desarrollada posteriormente por Monin y Obukhov (1954) puesto que este modelo es una de las base de su teoría:

Donde: V_z, velocidad del viento en m/s a estimar en la altura Z, en m y en condiciones de estabilidad neutra

Z₀, altura de rugosidad en m (o rugosidad aerodinámica).

k, constante adimensional de von Karman, 0,4.

u_*, velocidad de fricción (wind shear velocity, velocidad dinámica) en m/s. Altos valores de u* indican alta turbulencia.

Quien más acertadamente describe los modelos de perfil del viento es Baldocchi (2010) cuando afirma que “el perfil del viento es una función logarítmica de la relación entre la altura y la rugosidad de la superficie y es proporcional a la transferencia de movimiento cuantificada por la velocidad de fricción.”

Si se conoce una velocidad del viento a una altura, Z, el perfil se calcula en función de V_z y Z₀, ya que u_* se estima por:

Las fórmulas (3b2), (3b3) (3b4) y (3b5) permiten estimar la velocidad de fricción u_* :

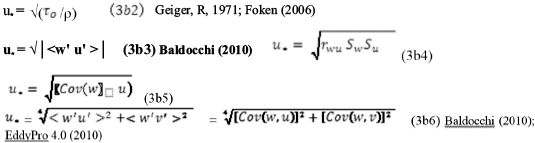
Donde: τ₀, esfuerzo tangencial del viento en la superficie, [N/m²] o[kg/ms²]; ρ, densidad del aire en o [kg/m³]; <w`u`>, media de los productos de las anomalías de la componente vertical del viento, w` y la anomalía de la componente horizontal del viento, u`, es decir, <w`u`> es la covarianza entre w y u; w, componente vertical del viento, u, componente meridional del viento; u_*, la raíz de la cov(w, u); v es la componente lateral del viento; r_wu, el coeficiente de correlación entre w y u; S_w, S_u, desviación estándar de w y de u, respectivamente. Los demás parámetros fueron identificados anteriormente. Las anomalías se representan con el signo (') y la covarianza por < >

La fórmula (3a) es válida solo en atmósfera neutra, similar a la (3c) si ψ_m = 0. Para atmósfera estable o inestable, se le agrega a (3a) la función de estabilidad atmosférica, o factor de corrección representada por: [ψ_m(z/L)] siguiendo la teoría de Monin-Obukhov (1954)

La fórmula 3c, es denominada fórmula con “corrección diabática”, por Sathe et al. (2011) y se refieren a la corrección que aporta el término [ψ_m(z/L)] para que la velocidad del viento a estimar en la altura, sea la correcta según que la atmósfera sea, estable o inestable.

Para condiciones de atmósfera estable: ψ_m = -5 (3c1), pero, Venora (2009), Sathe et al. (2010), Peña et al. (2009), prefieren -4,7, mientras en el “calculador de L” (APTI, 2001) emplean -6. Cualquiera de estos valores por ser muy cercanos entre sí, cuantifican adecuadamente el perfil del viento.

En atmosfera inestable en 3c:

Siendo x función de (z/L): x = [1-16(z/L)]^0,25  (3c3)

Siendo L, la longitud o altura de Monin Obukhov, a estimar mediante la fórmula (3c4 o 3c5):

O bien:

Donde, u_* velocidad de fricción del viento, m/s, la cual es un una expresión de la turbulencia del aire. u_* se define como la raíz cuadrada de la covarianza entre las componentes vertical (w) y meridional(u) del viento:

u* = raíz(Cov(w, u)).

k, constante de von Karman, 0,4; g, fuerza de gravedad, 9,81 m/s²; T_o, Temperatura del aire, en K; Q, flujo de calor sensible en W/m² ; C_p, calor especifico a presión constante, J/kg.K; ρ, densidad del aire, kg/m³; T_o, temperatura potencial en K; (Q/C_p ρ) o <w`θ`>, flujo de calor cinético de la superficie en [K(m/s)]. Cuando este flujo se escribe <w`θ`>, significa la covarianza entre la componente vertical del viento y la temperatura potencial, Cov (w, θ).

El calculador de la longitud de Monin-Obukhov, está disponible online en APTI (2000) para estimar el valor de L en cualquier condición de estabilidad, así como la velocidad del viento solo en condiciones de atmósfera estable. Allí se define a L como “la altura en la cual la turbulencia atmosférica es generada más por la flotabilidad que por el cizallamiento del viento” (wind shear).

Si por ejemplo, en una atmósfera estable, la velocidad de fricción es 0,6 m/s; la rugosidad de la superficie del sitio, 0,024 m: la temperatura virtual del aire, 301 k y el flujo de calor -0,03 [K(m/s)], el resultado de L por el calculador, es L=552,86 m y el viento a la altura de 30 metros, 11,2 m/s. Resultado que coincide con la formula 3c:

En verdad, no es sencillo entender que un valor con la dimensión en metros, como el concepto de longitud de Monin-Obukhov, L, sea captado fácilmente como integrante de una fórmula del perfil del viento. ¿Cómo debe interpretarse esa longitud o altura? La longitud de Monin- Obukhov, L, en metros, expresa la combinación de diferentes procesos de la turbulencia atmosférica que se llevan a cabo en la parte más baja de la atmósfera (la cual no excede de 100 metros de altura), por ello, Monin y Obukhov (1954) le asignan el significado físico de “altura del substrato de la turbulencia dinámica”.

Mediante anemómetros ultrasónicos, instrumentos fundamentales del método Eddy covariance, se mide continuamente el viento en diferentes niveles, así como se miden los flujos de calor sensible [ρC_p<T`w`>]; de calor latente [Lv <q`w`>] y de momento [ρ <w`u`>] y con estos flujos, se estima el valor de L. Bañuelos et al. (2011), por ejemplo, reporta que con mediciones horarias a 2 y 10 metros de altura realizadas en Bogotá en 3 días consecutivos y para nivel de rugosidad de 0,01 m, graficaron velocidades del viento y velocidades de fricción. Así, a 10 m la velocidad fue 3,8 m/s y la velocidad de fricción, de 0,22 m/s.

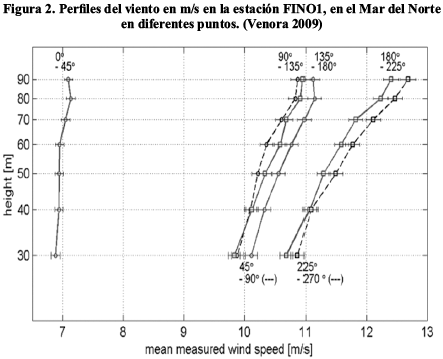
En las investigaciones del perfil del viento, además del clásico gráfico con las escalas de la altura en metros y la escala de la velocidad del viento en m/s, se emplean escalas diversas como el cociente de dos velocidades a dos alturas diferentes, (V₂/V₁) en el eje Y, con el parámetro estabilidad atmosférica (z/L) en el eje X; escala Ln Z en eje Y, con la velocidad, V en m/s en escala X; o escala (Ln Z- ψ) versus V en m/s, en eje X. Véase Venora (2009) p.59 con ejemplos de perfil del viento en dos localidades a escalas con (V₂/V₁) y (10/L). En esos perfiles del viento empleando el modelo logarítmico por la teoría de Monin-Obukhov en zonas sobre el mar del Norte, Tambke, et al. (2004) encontraron mayor incremento de la velocidad del viento con la altura que lo esperado por el modelo, es decir, se desviaban del perfil del viento sobre tierra y tal desviación sin una clara explicación, pero la influencia de las olas, la variación de la rugosidad y las condiciones no estacionarias en la cual son realizadas las observaciones, pudiesen causar ese desvío. La figura 2 muestra seis perfiles verticales del viento en la estación FINO1, para comparar con estimaciones por los modelos de perfil vertical del viento y con el calculador APTI (2000). Así, conociendo que la rugosidad, Zo = 0,0002 m; la longitud de Monin-Obukhov medida, L = 40 m, y la velocidad de fricción medida, u*= 0,26 m/s, en el cuarto perfil vertical, se lee directamente en el gráfico una velocidad de 10,2 m/s. El valor estimado de la velocidad mediante el modelo logarítmico descrito por la teoría de similitud de Monin-Obukhov, en atmósfera estable (con ψ_m= -5, es 10,2 m/s; y mediante el calculador (con ψ_m= -6 y flujo de calor cinético (Q/Cp ρ) de -0.034 [K m/s]) es 10,7 m/s.

Influencia de la altura de desplazamiento, (d), y la altura de rugosidad, Z₀ en el perfil del viento

Cuando la velocidad del viento y su perfil vertical se requieren en superficies continuas como un bosque, una superficie de cultivo bajo, una superficie de gramíneas altas, de arbustos compactos, zonas urbanas, etc., todos los modelos del perfil del viento en la capa atmosférica superficial, deberán ser modificados al restar la altura del desplazamiento, d, de la altura, Z, (donde se estimará la velocidad de viento) para quedar (z-d), en lugar de z. Pero, ¿Qué es ese desplazamiento y que significado físico tiene para que se incluya en los modelos de perfil del viento en las condiciones señaladas? Físicamente, la altura de desplazamiento (o simplemente el desplazamiento) se refiere a “la altura sobre el suelo donde se considera totalmente absorbido el flujo de momento”, WMO, (2010) y Thom, (1981), citado por Baldocchi, (2010). Por ello, su denominación más completa es “desplazamiento del plano cero para el flujo de momento” (zero plane displacement for moment) como lo emplean Hicks et al. (1975), entendiendo por “momento”la expresión ρ Cov(w,u), es decir, al producto de la densidad del aire, ρ, por la covarianza de la componente vertical del viento, w, y la componente, u, zonal (o este-oeste) del viento. Entonces, aceptando que la altura de desplazamiento comprende desde el nivel del suelo hasta un nivel por debajo del dosel del bosque, (o de la altura media de una ciudad), inmediatamente después de la altura de desplazamiento, le sigue la altura de rugosidad, Zo. Por ello, es un error decir que en la altura de desplazamiento se inicia el perfil del viento que fluye sobre un bosque o sobre una ciudad, ya que ese origen por definición, se encuentra a la altura de la rugosidad, Zo, ubicada inmediatamente después de d, en todo caso, sería a la altura (d+Zo) tal como se muestra en la figura 3 de Scarabino (2005), donde se aprecia claramente, que la línea punteada que representa el perfil del viento, empieza en la parte superior de Zo, por debajo del dosel del bosque, (hc, canopy top) en lugar de la línea curva de la derecha.

Por todo esto se enfatiza que Zo cuando existe desplazamiento, es una capa, un grosor desde la altura de desplazamiento, y no una altura desde el suelo.

La altura de desplazamiento, d, se determina experimentalmente mediante el método Eddy covariance o Eddy correlation que posee sensores compuestos por anemómetros ultrasónicos, analizadores de gases, medidores de flujo, etc., y ubicados a diferentes niveles del bosque. Los cálculos se realizan mediante calculadores como el LICOR Eddy Pro. Por ejemplo, la altura media por mediciones en un bosque de pino joven al sur de Australia, durante el mes de octubre de 1972, fue de 12,4 m, el desplazamiento, 10 m sobre el suelo, y la rugosidad, Zo, de 0,32 m por encima del desplazamiento. Como se aprecia, la altura de desplazamiento no es la altura del bosque, h, pero está en función de esa altura. En este caso, la relación d/h = (10/12,4) = 0,81, es decir, d = 0,81h, valor que está en el rango señalado por Jarvert, et al (1976) citados por Tachman (1981) de 0,61h a 0,90h.

Si se desea la velocidad del viento a la altura de 36 m del suelo y el desplazamiento es de 10 m del suelo, en las fórmulas de perfil del viento, la altura sobre el suelo será, Z=36 m, y (Z- d) = (36- 10) =26 m, por encima de la altura de desplazamiento. Inmediatamente después de la altura de desplazamiento, está la altura de la rugosidad, Zo, donde teóricamente el viento es nulo y, finalmente, la altura media del bosque. Como consecuencia de lo discutido previamente, el modelo exponencial (1 b) queda modificado, en (1bd):

La fórmula (1e) para calcular el exponente alfa, queda modificada en (1ed)

La fórmula 1f en (1fd)

El modelo logarítmico (2 a) queda modificado, en (2ad):

El modelo logarítmico (3 a) queda modificado en (3ad) y el 3c en (3cd):

Donde: d, altura de desplazamiento (o superficie desplazada). Se aplica cuando el viento es medido sobre una superficie homogénea como cultivos, edificaciones, bosque, etc., por sobre la cual fluye el viento. Los demás términos, ya fueron identificados anteriormente. Si no hay desplazamiento, d=0.

¿Pero, qué ocurre con la rugosidad de la superficie, Zo, en las fórmulas con desplazamiento?

Si recordamos que el concepto de altura de rugosidad, Zo, es altura en metros sobre el suelo donde teóricamente la velocidad del viento se hace nula, que no hay viento perceptible de ser medido por los sensores, esa altura de la rugosidad en la superficie boscosa, urbana, etc., como se dijo anteriormente, está inmediatamente después de la altura de desplazamiento, d, por consiguiente, Z₀ , estará a una altura de (d+Zo) desde el suelo.

En general, para el tipo de terrenos de interés para la energía eólica, d, suele valer cero. Sin embargo, en Europa, entre 20% y 30% de la energía eólica producida proviene de zonas donde los bosques afectan el flujo del viento, Mann et al. (2007). Así, por ejemplo, en estudios detallados del perfil del viento sobre un bosque de 25 metros de altura media, en Lille Bogeskov, Dinamarca, Mann et al. (2007) realizaron mediciones del viento con anemómetros de copa en torre a diferentes alturas sobre el suelo: 37 m, 41 m, 48 m, y 57 m; con sensores LIDAR a 24 m y con anemómetros sónicos a 43 m y 57 m. La altura de rugosidad encontrada fue de 1,8 m, es decir, a esa altura el viento posee teóricamente velocidad cero.

La información de esta investigación permite complementar la correcta interpretación de los modelos de perfil vertical cuando existe una superficie boscosa homogénea, al plantearse preguntar por la velocidad del viento a 57 metros del suelo, conociendo que a 37 m del suelo la velocidad era de 4,3 m/s; la altura media del bosque, 25 m, la rugosidad de 1,8 m y una altura de desplazamiento de 20,6 m. La respuesta se logra mediante la aplicación de la fórmula 1bd, donde el desplazamiento, 20,6 aparece restando de ambas alturas:

Entonces, el viento a 57 m del suelo, o mejor a la “altura efectiva” de 36,4 metros desde la superficie boscosa, se estima en 5,64 m/s, y el exponente de rugosidad α, que se desconocía, fue estimado para el bosque en 0,34, mediante la fórmula (1ed).

Luego de conocer la velocidad sobre el dosel del bosque, se aplicó la fórmula (1fd) que emplea las velocidades con las alturas correspondientes, y el exponente, coincidió en 0,34.

De los resultados numéricos anteriores y de su correcta interpretación, se concluye que al considerar una superficie boscosa sobre la cual se determina el perfil del viento, todos los parámetros se verán afectados por la altura de la superficie de desplazamiento. En este sentido, se debe prestar atención a la nota que mantiene la NASA (2012) en Surface Meteorology and Solar Energy, donde alerta que los datos del viento a 50 metros que publica en su página web, y que son obtenidos de sensores desde satélites meteorológicos, se refieren a 50 metros sobre el suelo y no desde las superficies de los cultivos o altura efectiva. ¿Exactamente que significa tal aclaratoria? Que esas velocidades del viento están a 50 m sobre la superficie del suelo, como si no tuviese vegetación, pero como sí la tiene, y se conoce el tipo y su altura, esa altura se debe considerar en los perfiles verticales del viento.

La misma aclaratoria es válida para los datos de las relaciones de velocidades de 10 m y 50 metros (V₁₀/V₅₀), para 17 tipos de vegetación.

El perfil del viento y las condiciones de estabilidad atmosférica

El modelo logarítmico del perfil del viento con corrección por estabilidad atmosférica (3c, 3cd) expresa que el valor de la velocidad del viento está influida por la estabilidad atmosférica del momento y en caso de valores promedios, por la estabilidad predominante. La figura 4 de Gardiner (2004) contiene las formas de los perfiles del viento en cada situación atmosférica: neutra, estable e inestable, y en porción inferior derecho, las comparaciones de las tres condiciones, donde se aprecia con claridad que en atmósfera estable la velocidad del viento en la altura se incrementa mucho más que en atmósfera estable e inestable.

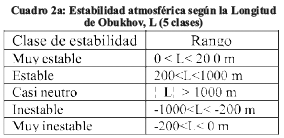
Se debe enfatizar que el índice empleado para expresar la estabilidad atmosférica, no es el clásico del gradiente altotérmico versus gradiente adiabático, sino la longitud L de Monin-Obukhov (o simplemente L de Obukhov) y el cual ha sido tabulado en categorías de 5 y de siete clases, cuadros (2a y 2b):

En la representación del perfil del viento, sin embargo, lo que más se emplea es la escala (z/L), es decir, su inverso multiplicado por z, por ejemplo para la Z=40, se tiene (z/L) del cuadro 2c:

Modelos del perfil del viento basado en la teoría de la altura de mezcla

Como un complemento al estudio del perfil del viento en la capa atmosférica superficial, se mencionan los modelos del perfil del viento basado en la teoría de la altura de mezcla, y los cuales han resultados exitosos en alturas por encima de la capa atmosférica superficial hasta unos 300 metros sobre el suelo.

Peña et al. (2009) agrupa estos modelos según la condiciones atmosférica:

a) En atmósfera neutra

b) En atmósfera estable

c) En atmósfera inestable

Los términos no identificados en los modelos:

Z, altura, m, donde se estima la velocidad del viento

Zi, altura, m, de la capa límite, (Atmospheric Boundary Layer, ABL)

λ, altura de mezcla, m, en la atmosfera libre, es una escala de longitud.

λ= 0,00027Vg/f

Vg, viento geostrófico, m/s; f, parámetro de coriolis

Ψ_m, factor de estabilidad atmosférica en los modelos de atmosfera estable e inestable.

Ψ_m en atmósfera estable, cualquiera de los siguientes valores: -4,7; -5; -6

Ψ_m en atmosfera inestable, Ψ_m = 2Ln[(1+x)/2]+Ln[(1+x²)/2]-atan(x)+(π/2); siendo x= [1-16(z/L)]^0.25

Para ilustrar el uso de los modelos basados en la teoría de la altura de mezcla, y con la información en el cuadro 3 se estimó la velocidad del viento a 40 m, según la condición de estabilidad atmosférica. El resultado, en la última columna:

Algunas aplicaciones de la velocidad del viento en aspectos relacionados con la geografía

a) En estimación de la velocidad del viento en estudios de la ETo

Una de las actividades humanas más geográficas, es la agricultura y su dependencia real de los factores y elementos climáticos y meteorológicos, es mundialmente reconocida. Entre los esfuerzos por una agricultura más eficiente, están los estudios de evapotranspiración, teóricos y experimentales, donde se incluyen las fórmulas que estiman la evapotranspiración de superficie húmeda cubierta de vegetación, y muy especialmente la de Penman, y la de Penman-Monteith- FAO98, (FAO, 1998) las cuales estiman la evapotranspiración de referencia, ETo. Esas fórmulas requieren de la velocidad del viento en m/s a 2 metros sobre una superficie cubierta de grama, pero, cuando no hay esta información, se recurre a su estimación a partir de observaciones a otras alturas. La fórmula que recomienda la FAO, 1998 es empleada en Guevara Díaz (2006):

La fórmula (4), aunque correcta, posee tres constantes que deben aceptarse sin conocer su origen. Resulta más claro crear una fórmula a partir del modelo logarítmico, sabiendo que la altura sobre el suelo siempre será de 2 metros y la rugosidad de la superficie cubierta de grama, también será fija, 0,0024 m, o bien, a partir del modelo exponencial, conociendo que el exponente alfa para superficie cubierta de grama es 0,14 a 0,15, obtenidos al comparar observaciones del viento a 10 m y 100 m de alturas. Con la información anterior, se llega a la fórmula (5a) y (5b), más sencillas y mucho más prácticas, que la (4) para estimar la velocidad del viento a 2 metros de altura, V₂, requerido en los estudios de la evapotranspiración de referencia, ETo.

Donde: V₂, es la velocidad del viento a 2 m sobre la superficie del suelo cubierta de grama con altura de rugosidad de 0,0024 m en (5ª) y exponente alfa de 0,15 en (5b); Vz, la velocidad del viento en m/s a la altura, Z.

Si se requiriere la velocidad a 2 m para estimar la ETo en una zona agrícola donde el viento a 10 m de altura es 5,6 m/s, la velocidad del viento a las condiciones exigidas será de: 4,2 m/s por (4); y 4,5 m/s, por (5a) y 4,4 por (5b)

b) En el cálculo del potencial del viento

La energía cinética del viento es convertida en potencia en aparatos diseñados para tal fin, denominados aereogeneradores o turbinas, los cuales se ubican a la altura entre 50 y 60 metros del suelo.

La potencia, P, del viento, depende de la densidad del aire y del cubo de la velocidad del viento, fórmulas (6a) en potencia, W, y (6b), en densidad de potencia, W/m².

Donde: ρ, densidad del aire en kg/m³. En problemas de energía eólica, la densidad empleada es del aire seco, a presión atmosférica al nivel del mar (1013,25 hPa) y temperatura de 15ºC. En estas condiciones, ρ =1,225 kg/m³

V, velocidad del viento, m/s

A, área del rotor del aereogenerador, en m²

La velocidad mínima del viento para generación de electricidad, a nivel de 10 m sobre el suelo debe estar entre 4 m/s y 6 m/s, por ello, se requiere de al menos un año de observaciones, mediante los anemómetros tradicionales o bien mediante los anemómetros sónicos o tipo laser, que en estas actividades son preferidos, aunque mucho más costosos.

c) En instalación de granjas eólicas

El conocimiento del régimen del viento es esencial y previo para la explotación del recurso eólico tal como se realiza en todas partes del mundo. En Venezuela González-Longart, et al. (2006), señalan las zonas con mejores opciones para explotar este recurso y proponen localizar una granja eólica en la localidad de La Vecindad, 1 km de Santa Ana, en la isla de Margarita, con 11 turbinas de viento Modelo E-70, 2000 kW, 22 MW de capacidad y que pudiesen generar 2000 kW. Mencionan detalles técnicos y de costos, pero no sobre el impacto ambiental, que es un aspecto que siempre se debe considerar, especialmente sobre la generación de ruido molesto.

d) En los modelos de dispersión de los contaminantes en la atmósfera

La concentración de contaminantes en la atmosfera es inversamente proporcional a la velocidad del viento. La atmosfera, especialmente la urbana, recibe impurezas de diferentes fuentes: vegetal, industrial, vehiculares, etc., que elimina mediante sus movimientos horizontales (el viento) y los verticales (convección, turbulencia). El viento es más efectivo como proceso limpiador del aire, cuando la atmosfera se encuentra en equilibrio estable, puesto que los movimientos convectivos están ausentes, como en los casos extremos de las inversiones térmicas. Si en estas condiciones, no hay viento, se está en la peor situación de contaminación. Mientras que en la condición inestable, la atmosfera se puede limpiar sin viento, ya que los movimientos ascendentes, actúan de manera eficaz elevando los contaminantes hacia las capas superiores y de allí, quedan bajo la acción de vientos de velocidades mayores que lo alejan de la zona contaminada.

Todas estas condiciones son incluidas en los modelos de dispersión, donde la variable fundamental es la velocidad del viento y su dirección, en combinación con las condiciones de estabilidad atmosférica. Existen numerosos modelos de dispersión, pero, la agencia Environmental Protection Agency (EPA) (2005), recomienda el modelo de dispersión gausiano, denominado AERMOD.

En la erosión eólica potencial, P

La erosión eólica potencial, P, es el arrastre y trasporte desde un material seco expuesto al viento y se calcula a partir de la velocidad de fricción del viento sobre la superficie erodable (EPA, 2006). La expresión (7a) permite estimar P en [g/m²]:

P = 58 (u_* - u_t* )² +25(u_* - u_t*) en [g/m²]   (7a) (EPA, 2006)

Donde: u_t*, la velocidad de fricción umbral, m/s, ( u* a la cual empieza la erosión). Depende del tamaño de las partículas. Sobre la arena, u_t* es (0,2 a 0,6).

u_* la velocidad de fricción, m/s: Se estima por: u* = 0,053 u₁₀ (8b)

Si u* es igual o menor que el umbral, P=0 y no hay erosión eólica. u* es una medida de la tensión del viento, (wind shear stress)

u₁₀, Velocidad del viento más alta a 10 m de altura en un lapso de 3 días. Si la altura es diferente, se convierte a 10 m, por modelo logarítmico: (u_z/u_ref ) Ln(Z/LnZ₀)/Ln(Z_ref/LnZ₀).

Por ejemplo, si la velocidad de fricción a 10 metros de altura, u_* = 0.25 m/s y la velocidad de fricción umbral es 0,03 m/s, la erosión potencial de ese viento sobre una superficie seca erodable es 5,55 g/m², calculada directamente por:

P = 58 (0.25 – 0.03)² +25(0.25-0.03 =5,55 [g/m²]

La estimación de la erosión potencial del viento se hace más compleja como en el caso de una zona cubierta con polvo de carbón, donde se sabía que en los tres días sucesivos: 10; 11 y 12 de marzo de 2012, las velocidades a 5 m de altura fueron: 8,3 m/s; 7,2 m/s y 11,4 m/s. La velocidad de fricción umbral y la rugosidad, Zo, del material (Tabla 13.252 en EPA 2006) eran respectivamente 0,54 m/s y 0,005 m.

Antes de aplicar la fórmula (7a) se escoge la velocidad del viento, que fue 11,4 m/s, por ser la más alta en el lapso de los 3 días considerados. Al ajustarlo a la altura de10 m, fue 12,5 m/s:

uref= 11,4 *Ln(10/0.005)/Ln(5/0.005) = 12,5 m/s

La velocidad de fricción por la fórmula (7a): u_* = 0.053V₁₀ = 0.053*12,5 = 0,66 m/s

Y la erosión potencial del viento, 8,56 g/m²:

P = 58 (0.77 -0.545)² +25(0.77 - 0.545) =8,56 [g/m²]

Conclusiones y recomendaciones

-Lo que se denomina el perfil del viento es el gráfico de la variación de la velocidad del viento con la altura, y términos como “cizallamiento del viento” o “wind shear profile” en inglés, son utilizados para significar lo mismo. Aunque cizallamiento del viento esta más asociado, con los cambios bruscos de la velocidad o la dirección del viento en sentido horizontal como vertical, así como con los graves accidentes en la aviación durante el despeje y aterrizaje.

-Los modelos para calcular el perfil del viento de mayor uso son el exponencial, el logarítmico, el logarítmico “sin corrección diabática” y el logarítmico “con corrección diabática”, estos dos últimos descritos por la teoría de similitud de Monin-Obukhov y los cuales son los preferidos en las investigaciones y aplicaciones en problemas de energía eólica y en modelos de contaminación del aire. Los modelos con base a la altura de mezcla, son más complejos y requieren información e instrumentación más especializada y costosa. Estos modelos son los indicados para estimar la velocidad del viento hasta alturas de unos 300 metros.

- En la aplicación de los modelos del perfil del viento, es incorrecto denominar al modelo exponencial como “ Ripe power law”, puesto que Paul Ripe no fue el autor del modelo, aunque sí un experto en la materia.

-En los gráficos del perfil del viento, es tradicional colocar la variable dependiente, la velocidad del viento en el eje X, en lugar del uso general del eje Y. Pero, ambos son apropiados. En los modelos logarítmicos, basados en la teoría de Monin-Obukhov, se emplean, además de las escalas de altura en metros y velocidad del viento en m/s, la de cocientes de velocidades a dos alturas, (V /V ) con el parámetro de estabilidad (z/L) y Ln Z con V en m/s. 2 1

-La velocidad media mínima del viento para que sea aprovechada como un recurso, se estima entre 4 m/s a 6 m/s, a 10 m sobre el suelo y con dirección persistente. Por debajo de 4 m/s, sigue siendo útil para otros propósitos, como los bioclimáticos relacionado con el bienestar y confort humano.

-La distribución estadística que mejor describe el comportamiento de la velocidad del viento sigue siendo la distribución de Weibull, la cual tiene dos parámetro: de forma o asimetría, alfa, y de escala, k. Con ella se obtiene la probabilidad de ocurrencia de un viento a una velocidad y dirección dadas.

-No hay diferencia estadísticamente significativa en el uso de los modelos, si en el exponencial se conoce bien el exponente alfa, y en el modelo logarítmico, se conoce bien la rugosidad, Zo. El modelo logarítmico “con corrección diabática”, basado en la teoría de similitud de Monin-Obukhov, es más realista, pero requiere de la velocidad de fricción y parámetros relacionados con la turbulencia y estabilidad atmosférica, que solo es posible obtener en sitios donde se dispone de mediciones especializadas, como en los parques eólicos con anemómetros sónicos tridimensionales.

-Aplicando la teoría de similitud de Monin-Obukhov, si un sitio presenta condiciones semejantes en su geografía y climatología, se podría aplicar los parámetros de otro sitio de similar condiciones para el cálculo de sus perfiles de viento.

-Se recomienda para estimar el perfil del viento mediante el modelo logarítmico estándar, el calculador WAsP (disponible en referencia ADIE, 2000) y el Wind Profile Calculator en la página web <The Swiss wind data ch/tool/profile.php>. Solo requieren introducir la velocidad del viento a una altura dada y la rugosidad Zo de la superficie.

- Se recomienda consultar la fuente de datos de vientos mensuales en m/s (a 10 m sobre la superficie en cualquier lugar, en la página web NASA Surface Meteorology and Solar Energy: <http://eosweb.larc.nasa.gov/sse/> para lo cual se entra en Meteorology and Solar Energy-data Table. Solo se requiere entrar con la latitud y longitud del lugar. Además, tiene datos de temperatura del aire, humedad relativa, radiación solar diaria y presión atmosférica.

-Se debe tener presente la información de ADIE (2000) para entender lo relacionado con la conversión de energía eólica en potencia eléctrica: un aerogenerador típico de 600 kW posee diámetro del rotor de 43 m, área del rotor de 1500 m² y cada cilindro con masa de 1,9 toneladas. La altura de la turbina en zonas despejadas y sin vegetación arbórea, es entre 50 a 60 m y en un radio de 100 m, debe tener 9 m sobre cualquier obstáculo. En caso de establecer una “granja eólica” las turbinas deben orientarse según la dirección predominante del viento y separadas unos 300 m (7 diámetros del rotor), conocer la variación del viento diario, su direcciones, las condiciones de estabilidad atmosférica, la cantidad de partículas en el aire, además del perfil vertical del viento.

Referencias bibliográficas

1. ADIE. Asociación Danesa de la Industria Eólica. (Danish Wind Industry Association). (2000). Manual de Referencia sobre energía eólica. Documento en línea. Disponible en: http://www.windpower.org/es/stat/unitsw.htm [Consultado: 12-junio -2012].        [ Links ]

2. APTI (2000). Monin-Obukhov lenght and windspeed profile calculator. [Consultado: 12-8-2012]. Documento en línea. Disponible en: http://www.shodor.org/os411/courses        [ Links ]

3. BALDOCCHI, DENNIS (2010). ESPM 129 Biometeorology Plant-Ecosystem-Atmosphere Iteractions. University of California, Berkely. Department of Environmental Science, Policy and Management. Documento en línea. Disponible en: http://nature.berkeley.edu/biometlab/espm129/ [Consultado: 20-8-2012].        [ Links ]

4. BUSINGER, J; A WYNGAARD; J IZUMI AND Y BRADLEY (1971). Flux-profile relationships in the atmospheric surface layer. Journal of the Atmospheric Sciences. 28:181–189.        [ Links ]

5. BAÑUELOS, F; ÁNGELES CAMACHO; SERRANO, J y MUCIÑO, D. (2008). Análisis y Validación de metodología usada para la obtención de perfiles de velocidad de viento. Universidad Nacional Autónoma de México, México. Documento en línea. Disponible en: <http://www.scribd.com/doc/11545563/Analisis-de-perfiles-verticales-de-viento> [Consultado: 14-junio -2012]        [ Links ]

6. CICES (2003). Zonas potencialmente productoras de energía eléctrica en Baja California. Reporte final. Centro de Investigaciones Científicas y de Educación Superior. Gobierno de Baja California, México.        [ Links ]

7. DEMARRAIS, GERARD (1959). Winds peed Profiles at Brookhaven National Laboratory, Journal of Meteorology, Vol 16, pp. 181-190.        [ Links ]

8. ENVIRONMENTAL PROTECTION AGENCY (EPA).(2005). Part III 40 CFR. Part 51. Revision to the Guideline on Air Quality Models: Adoption of a Preferred General Purpose (Flat and Complex Terrain) Dispersion Model and Other Revisions; Final Rule. Federal Register / Vol. 70, No. 216 / November 9, 2005 / Rules and Regulations. Documento en línea. Disponible en: http://www.epa.gov/scram001/guidance/guide/appw_05.pdf [Consultado: 16 julio 2012]        [ Links ]

9. ENVIRONMENTAL PROTECTION AGENCY (EPA) (2006). Industrial wind erosion. Documento en Línea. Disponible en: http://www.sciencedirect.com/science/article/pii/S0301421508001092        [ Links ]

10. FUERZA AÉREA DE VENEZUELA (s/f). Promedios climatológicos de Venezuela. Periodo 1951-80. Grupo Logístico de Meteorología. Maracay.        [ Links ]

11. FOKEN, T (2006). 50 Years of the Monin-Obukhov Smilarity Theory. Boundary-Layer Meteorology, Vol. 119, N. 3, pp. 431-447.        [ Links ]

12. GEIGER, RUDOLF. (1961). The Climate near the ground. Friedrich Vieweg and Son. Brunswick, Germany. Third Printing, 1971, USA        [ Links ]

13. GONZÁLEZ-LONGART FRANCISCO; RUBÉN TERÁN, JUAN MÉNDEZ, ARTURO HERNÁNDEZ, FREDNIDES GUILLEN (2006). Evaluación del Recurso Eólico en Venezuela: Parte I. I Congreso de Petrolero Energético Asme-Unefa, 26-28 Oct, Pto. Cabello.        [ Links ]

14. GONZÁLEZ-LONGART, F; J. MÉNDEZ, R. VILLASANA, C. PERAZA (s/f). Preliminary Evaluation of Wind Energy Utilization on Margarita Island, Venezuela. Documento en línea. Disponible en: http://www.giaelec.org.ve/Articulos/A2006-04.pdf [Consultado: 10-julio -2012]        [ Links ]

15. GARDINER, BARRY (2004). Airflow over forest and forest gaps. Paper presented at the 'Wind flow and Trees' workshop organised by the British Wind Energy Association 17/3/2004 Glasgow, UK. Documento en línea. Disponible en: http://www.bwea.com/planning/trees.html [Consultado:15/9/2012]        [ Links ]

16. GUALTIERI, GIOVANNI, Y SAURO SECCI. (2011). Wind shear coefficients, roughness length and energy yield over coastal locations in Southern Italy. Renewable Energy. 36 pp1081-1094.        [ Links ]

17. GUEVARA DÍAZ, J.M. (2006). La fórmula de Penman–MonteithFAO1998 para determinar la evapotraspiración de referencia, ETo. Terra Nueva Etapa Vol 23 No.31. IGDR, Universidad Central de Venezuela.        [ Links ]

18. GUEVARA DÍAZ, J.M. (2008). Problemas fundamentales en Meteorología. UCV. Fondo Editorial de la FH y E, Caracas.        [ Links ]

19. HICKS, B; P HYSON AND J. MOORE (1975). A study of Eddy fluxes over a forest. Journal of Applied Meteorology. Vol. 14.        [ Links ]

20. HSU, S (1982). Determination of the power law wind profile exponent on a tropical cost. Journal of Applied Meteorology.Vol. 21        [ Links ]

21. LICOR (2012). Programa EddyPro, 4.0. Documento en línea. Disponible en: <www.Licor.com the eddy covariance method>        [ Links ]

22. MANN, JAKOB, EBBA DELLWIK, FERHAT BINGÖL AND OLE RATHMANN. (2007). Laser measurements of flow over a forest. Wind Energy Dept., Risø National Laboratory, DTU, DK-4000 Roskilde, Denmark. Journal of Physics: Conference Series 75.        [ Links ]

23. MARRERO S, MARÍA. (2011). Parámetros de rugosidad representativos de terrenos naturales. Tesis de Máster en Geofísica y Meteorología, Universidad de Granada. España. Documento en línea. Disponible en: <http://www.ugr.es/~andyk/Theses/TesinaMaria.pdf> [Consultado: 12-julio -2012]        [ Links ]

24. MONIN, A AND OBUKHOV, A (1954). Basic laws of turbulent mixing in the ground layer of the atmosphere. Trud. Geofiz. Inst. Akad. Nauk. SSSR, No. 24, 151, pp. 163–187. Traducción del Ruso en 1959, por American Meteorological Society y disponible en Defense Technical Information Center. Documento en línea. Disponible en: <http://handle.dtic.mil/100.2/AD672723>        [ Links ]

25. MONTOYA, GERARDO; WILLIAM CEPEDA Y JESÚS ESLAVA (2004). Características de la turbulencia y de la estabilidad atmosférica en Bogotá. Rev. Acad. Colomb. Cienc. 28 (108): 327-335.        [ Links ]

26. MUÑOZ, D Y B CANADILLAS (2012). Forecasting de diabatic offshore wind profile at Fino 1 with wrf mesoscale model. Dewi Magazin. No. 40.        [ Links ]

27. NASA (2012). NASA Surface Meteorology and Solar Energy. Documento en línea. Disponible en: <http://eosweb.larc.nasa.gov/sse/> [Consultado: 1-julio -2012]        [ Links ]

28. PEÑA, ALFREDO; SVEN-ERIK GRYNING; CHARLOTTE B HASAGER; AND MICHAEL COURTNEY (2009). Extending the wind profile much higher than the surface layer. Risø National Laboratory for sustainable Energy, DTU.        [ Links ]

29. PEÑA, ALFREDO; SVEN-ERIK GRYNING AND CHARLOTTE BAY HASAGER (2010). Comparing mixing-length models of the diabatic wind profile over homogeneous terrain. Documento en línea. Disponible en: <http://windenergyresearch.org/wp-content/uploads.pdf> [Consultado:11-agosto -2012]        [ Links ]

30. PETERSEN, ERIK L; NIELS G. MORTENSEN; LARS LANDBERG; JRGEN HJSTRUP AND HELMUT P. FRANK (1997). Wind Power Meteorology. Part II, Siting and Models, Ris National Laboratory, Roskilde, Denmark.        [ Links ]

31. SATHE AMEYA; SVEN-ERIK GRYNING AND ALFREDO PEÑA (2012). Comparison of the atmospheric stability and wind profiles at two wind farm sites over a long marine fetch in the North Sea. Wind Energy, Vol. 14. Published online 10 February 2011 in Wiley Online Library.        [ Links ]

32. SATHE AMEYA; SVEN-ERIK GRYNING AND ALFREDO PEÑA (2010). Atmospheric stability and wind profiles at two wind farm sites in the North Sea. Dutch wind Worksshops, octubre 2010.        [ Links ]

33. SEDEFIAN, LEON. (1980). On the vertical extrapolation of mean wind power density. J. Appl. Meteor. 19, pp. 488-499.        [ Links ]

34. Scarabino, Ana (2005). Características de la turbulencia atmosférica en un bosque de coníferas. Tesis para el título de Doctora en Ingeniería en la Universidad de Nacional de la Plata Facultad de Ingeniería, Departamento Aeronáutica.        [ Links ]

35. SUTTON, O. (1951). Atmospheric turbulence and diffusion. Compendium of Meteorology, AMS. Baltimore        [ Links ]

36. TAMBKE, JENS; JOHN A.T. BYE; JÖRG-OLAF WOLFF; SASKIA TAUTZ; BERNHARD LANGE; MATTHIAS LANGE Y ULRICH FOCKEN. (2004). Modelling Offshore Wind Profiles using Inertially Coupled Wave Boundary Layers. Documento en línea. Disponible en: http://2004ewec.info/files/23_1400_jenstambke_01.pdf        [ Links ]

37. VENORA, ANDREA (2009). Monin-Obukhov Similarity Theory Applied to Offshore Wind Dat, Validation of Models to Estimate the Offshore Wind Speed Profile in the North Sea. Master Thesis en Delft University, Denmark. Documento en línea. Disponible en: <http://www.lr.tudelft.nl/fileadmin/Faculteit/LR/Organisatie/Afdelingen_en_Leerstoelen/ Afdeling_AEWE/Wind_Energy/Education/ Masters_Projects/Finished_Master_projects/doc/Andrea_Venora_r.pdf>        [ Links ]

38. WAGNER, ROZENN, HANS JØRGENSEN, UWE PAULSEN, TORBEN LARSEN, IOANNIS ANTONIOU, LEO THESBJERG. (2008). Remote sensing used for power curves. IOP Conf. Series: Earth and Environmental Science. Documento en línea. Disponible en: http://iopscience.iop.org/1755-1315/1/1/012059/pdf/1755-1315_1_1_012059.pdf Consultado: 2-julio -2012]        [ Links ]

39. WEBB, E (1965). Aerial microclimate. En Agricultural Meteorology. Meterological Monograph, No. 28, Vol. 6. AMS, Boston.        [ Links ]

40. WIERINGA, JON; ALAN DAVENPORT, SUE GRIMMOND AND TIM OKE (2001). New revision of Davenport roughness classification. Presented at the 3rd European an African Conference on Wind Engeneering. July 2001. Eindhoven Netherlands. Documento en línea. Disponible en: http://www.kcl.ac.uk/ip/suegrimmond/publishedpapers/DavenportRoughness2.pdf [Consultado: 9-8-2012]        [ Links ]

41. WORLD METEOROLOGICAL ORGANIZATION (WMO). (1960). Guide to Climatological Pratices. Geneva, Switzerland.        [ Links ]

42. WORLD METEROROLOGICAL ORGANIZATION (WMO). (2010). Updated in 2012. Guide to Agricultural Meteorological Practices. No. 134. Geneva 2, Switzerland. Documento en línea. Disponible en: <http://www.wmo.int/pages/prog/wcp/agm/gamp/documents/WMO_No134_en.pdf>        [ Links ]