Grafos bipartitos balanceados hamiltoniano y conjuntos independientes balanceados

Hamilltonian balanced bipartite graphs and balanced independent sets

Daniel Brito

Universidad de Oriente, Núcleo de Sucre, Escuela de Ciencias, Departamento de Matemáticas, Cumaná, Venezuela. E-mail: danieljosb@gmail.com

RESUMEN

Sea G un grafo bipartito balanceado de orden 2n, es decir, un grafo con una bipartición en dos conjuntos de vértices independientes cada uno de ellos con n vértices, y mínimo grado, es decir, el menor número de lados incidentes a un vértice, al menos cuatro. Si para cada conjunto independiente balanceado de cuatro vértices, es decir, un conjunto independiente conteniendo dos vértices de cada lado de la bipartición, su número de vecinos es al menos n + 1, entonces G es hamiltoniano.

Palabras clave: Unión de vecindades.

ABSTRACT

Let G be a balanced bipartite graph of order 2n, i.e. a graph with a bipartition into two independent vertex sets of the same cardinality n, and minimum degree, i.e. at least number of edges incidents on a vertex, the least four. If for every balanced independent set of four vertices, i.e. an independent set containing two vertices from each side of the bipartition, the number of neighbors is at least n + 1, then G is Hamiltonian.

Key words: Neighborhood union.

Recibido: enero 2013. Aprobado: enero 2013. Versión final: febrero 2013

INTRODUCCIÓN

Se usa Behzad et al. (1981) para terminologías y notaciones no definidas aquí.

El problema hamiltoniano nace en 1857 cuando el matemático William Rowan Hamilton, nacido en Dublín en 1805, inventa y presenta su Juego Icosiano, The Icosian Game, y posteriormente una variante del anterior con los nombres de Dodecaedro del viajero, Un viaje alrededor del mundo, en los que aparecen un grafo formado por doce caras pentágonos regulares, veinte vértices y treinta aristas. El juego se puede plantear técnicamente así: se trata de encontrar en el dodecaedro un camino que, partiendo de un vértice cualquiera, vuelva a ese mismo vértice después de pasar, a través de sus aristas, por todos los demás vértices una sola vez. Tal recorrido, en la teoría de grafos, se llama ciclo y, en honor de su descubridor, ciclo hamiltoniano. Si el recorrido se hace sin que el vértice inicial y vértice final coincidan, es decir, que no haya ciclo cerrado, recibe el nombre de camino hamiltoniano. Cuando un grafo posee un ciclo hamiltoniano, se denomina grafo hamiltoniano o de Hamilton. La caracterización de los grafos hamiltonianos sigue siendo un problema abierto y en consecuencia el problema de determinar cuando un grafo es hamiltoniano es un problema NP-completo, es decir no existe un algoritmo que lo resuelva en tiempo polinomial, lo que se tiene son condiciones sobre algunos parámetros, por ejemplo el grado de un vértice, es decir el número de lados incides a dicho vértice, que garantizan cuando un grafo es hamiltoniano. El primero en dar una condición sobre los grados de dos vértices independientes, es decir que no forman un lado, en función del número de vértices en grafos fue Ore (1960) y en grafos bipartitos balanceados Moon y Moser (1963).

Las investigaciones de ciertos problemas extremales envolviendo condición de unión de vecindades para conjuntos independientes balanceados de cardinalidad cuatro en grafos bipartitos balanceados fueron iniciadas por Amar et al. (1998).

CAMINOS EN LA SOLUCIONES POSIBLES

El primer resultado en grafos bipartitos balanceado usando la condición de unión de vecindades para conjuntos independientes balanceados de cardinalidad cuatro, garantizando el grafo es conexo, es decir existe un camino entre cada par de vértices del grafo, el cual es una condición que se requiere para buscar si un grafo es ó no es hamiltoniano, fue el siguiente:

Si un grafo bipartito balanceado con mínimo grado al menos dos tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo es conexo.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 2. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)|≥ n + 1, entonces G es conexo.

Bajando el mínimo grado y el número de vecinos en uno con respecto al primer resultado se garantiza que el grafo tiene un matching perfecto, es decir un conjunto de lados independientes que saturan los vértices del grafo, es el siguiente:

Si un grafo bipartito balanceado con mínimo grado al menos uno tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo tiene un matching perfecto.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 1. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)|≥ n + 1, entonces G tiene un matching perfecto.

Buscando nuevas técnicas de demostración en grafos se define un dumbbell, el cual consiste de dos ciclos unidos por un camino y es mostrado en la siguiente figura:

Se dice que un dummbell generador es maximal si el camino que une los dos ciclos es el más grande entre todos los dummbells generadores y se prueba el siguiente resultado:

Si un grafo bipartito balanceado tiene un dummbell generador maximal con un conjunto de cuatro vértices tal que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno y el grafo no es hamiltoniano, entonces el conjunto de cuatro vértices es independiente y el grafo contiene un subgrafo generador formado por un ciclo y un lado aislado. Si el número de vecinos de cada conjunto de cuatro vértices independiente es al menos la mitad del total de los vértices del grafo más tres, entonces el grafo es hamiltoniano.

Es decir

Sea G un grafo bipartito balanceado y D un dummbell generador maximal de G con S= {a₁, b₁, a₂, b₂}. Si |N(S)| ≥ n+1 y G no es hamiltoniano, entonces S es independiente y G contiene un subgrafo generador formado por un ciclo y un lado aislado. Si |N(S)| ≥ n + 3, entonces G es hamiltoniano.

Subiendo el mínimo grado en uno con respecto al primer resultado se garantiza que el grafo tiene ó un ciclo que recorre todos los vértices del grafo ó un ciclo que recorre todos los vértices menos dos vértices del grafo y un lado aislado y el resultado es el siguiente:

Si un grafo bipartito balanceado con mínimo grado al menos tres tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo ó es hamiltoniano ó contiene un subgrafo generador formado por un ciclo y un lado aislado.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 3. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)|≥ n + 1, entonces G es ó hamiltoniano ó contiene un subgrafo generador consistiendo de un ciclo y un lado aislado.

Como una consecuencia inmediata del resultado anterior se garantiza un camino hamiltoniano es decir que el grafo es traceable y el resultado es el siguiente:

Si un grafo bipartito balanceado con mínimo grado al menos tres tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo es traceable.

Es decir Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 3. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)|≥ n + 1, entonces G es traceable.

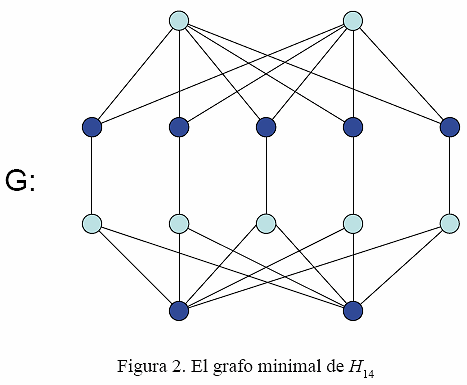
Todo grafo hamiltoniano tiene un dos factor, es decir un subgrafo generador donde todos sus vértices son de grado dos, pero lo contrario no siempre es cierto, es decir no todo grafo que contenga un dos factor es hamiltoniano. Manteniendo las condiciones del resultado anterior el grafo tiene un dos factor o pertenece a una clase de grafos denotadas por Η₁₄, donde Η₁₄ es la clase de grafos obtenido del grafo dibujado en la Figura 2, donde alguno o todos los cuatro lados posibles entre los vértices de la parte superior y los vértices de la parte inferior pueden estar presente

El resultado es el siguiente. Si un grafo bipartito balanceado con mínimo grado al menos tres tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo tiene un dos factor ó pertenece a Η₁₄.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 3. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)|≥ n + 1, entonces G tiene un 2-factor ó G pertenece a Η₁₄.

Subiendo en dos el número de vecinos con respecto al resultado anterior se garantiza que el grafo es hamiltoniano y el resultado es el siguiente:

Si un grafo bipartito balanceado con mínimo grado al menos tres tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas tres, entonces el grafo es hamiltoniano.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 3. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)| ≥ n +3, entonces G es hamiltoniano.

Amar et al. (1998) dejan la siguiente conjetura:

Si un grafo bipartito balanceado con mínimo grado al menos tres tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo es hamiltoniano ó pertenece a Η₁₄.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 3. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)|≥ n + 1, entonces G es hamiltoniano ó G pertenece a Η₁₄.

Tratando de resolver la conjetura planteada por Amar et al. (1998), aumentando el mínimo grado en uno, Brito y Lárez (2007) obtienen el resultado siguiente:

Si un grafo bipartito balanceado con mínimo grado al menos cuatro tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo es hamiltoniano.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 4. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)| ≥ n + 1, entonces G es hamiltoniano.

Este resultado es el mejor posible en primer lugar el mínimo grado no puede ser bajado a tres ya que el grafo Η₁₄ tiene mínimo grado tres y satisface la condición del número de vecinos, de cualquier conjunto independiente de cardinalidad cuatro, es al menos n + 1 y el grafo no es hamiltoniano. En segundo lugar la condición del número de vecinos, de cualquier conjunto independiente de cardinalidad cuatro no puede bajarse a n, como se puede observar en el grafo siguiente:

En la Figura 3 el orden del grafo G = 2n = 2.8, mínimo grado 4 y para cualquier conjunto independiente de cuatro vértices su numero de vecinos es n = 8 y el grafo G no es hamiltoniano.

Lo que no se publicó fueron las consecuencias de este último resultado, los cuales son:

Si un grafo bipartito balanceado con mínimo grado al menos cuatro tal que para cada conjunto independiente balanceado de cardinalidad cuatro se tiene que su número de vecinos es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo es traceable.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 4. Si para cada conjunto independiente balanceado, S, con |S|= 4 se tiene |N(S)| ≥ n + 1, entonces G es traceable.

Si un grafo bipartito balanceado con mínimo grado al menos cuatro tal que para cada conjunto independiente balanceado de cardinalidad cuatro vértices se tiene que la suma de sus grados es al menos la mitad del total de los vértices del grafo mas uno, entonces el grafo es hamiltoniano.

Es decir

Sea G un grafo bipartito balanceado de orden 2n y mínimo grado δ (G) ≥ 4. Si para cada cuatro vértices independientes la suma de sus grados es al menos n + 1, entonces G es hamiltoniano.

AGRADECIMIENTO

El autor agradece al Dr. Leonardo De Sousa por su valioso aporte en la revisión crítica del manuscrito.

REFERENCIAS BIBLIOGRÁFICAS

1. Amar D, Brandt S, Brito D, Ordaz O. 1998. Neighborhood conditions for balanced independent sets in bipartite graphs. Discrete Math. 181:31-36.         [ Links ]

2. Behzad M, Chartrand G, Lesniak-Foster L. 1981. Graphs and Digraphs, Wadsworth Int. Group, USA.

3. Brito D, Lárez G. 2007. Neighborhood conditions for balanced bipartite graphs to be Hamiltonian. Int. J. Pure Applied Math. 34: 509-512.

4. Moon J, Moser L. 1963. On Hamiltomiam bipartite graphs. Israel J. Math. 1:163-165.

5. Ore O. 1960. A note on Hamilton circuits. Amer. Math. Monthly. 67:55.