El convertidor matricial en aplicaciones de conversión CA-CA trifásicas: métodos escalares y vectoriales de control.

Lara, Jorge; Guzmán, Víctor; Cabello, Alexis; Giménez, María Isabel; Restrepo, José

El MSc. Jorge Lara es Profesor Agregado en el Dpto. de Ingeniería de Sistemas de la UNEXPO, Vicerrectorado Caracas, Venezuela. teléfono 0212-4712355., correo electrónico jlara@unexpo.edu.ve.

.El MSc. Alexis Cabello es Profesor asistente en el mismo Departamento y teléfono, correo electrónico alexiscabello@cantv.net.

 Los Doctores Víctor Guzmán, María Isabel Giménez y José Restrepo son Profesores Titulares en el Dpto. de Ingeniería Electrónica y Circuitos de la Universidad Simón Bolívar, teléfonos y correos electrónicos 0212-9063676, Caracas, Venezuela vguzman@usb.ve , 0212-9063677, Caracas, Venezuela.  magimenez@usb.ve, y 0212-9064005 - ext. 111. Caracas, Venezuela.  restrepo@usb.ve.  respectivamente.

Resumen: Este trabajo muestra las características de operación de un convertidor matricial (CM) empleado en conversión CA-CA trifásica, operado con control escalar y con control vectorial del voltaje de salida. La conversión directa CA-CA por medio de convertidores matriciales permite modular la tensión, frecuencia y fase del sistema eléctrico trifásico a objeto de controlar el comportamiento de la carga, y permitir la regeneración de energía de la carga a la alimentación principal. Con un control adecuado, esta configuración puede ser más versátil que el sistema tradicional de conversión CA-CA indirecta, formado por la conexión en cascada de un conversor AC-DC, usualmente no controlado, y un conversor DC-AC tipo inversor trifásico. Los convertidores matriciales son complejos debido a que su matriz de conmutación usa dieciocho interruptores unidireccionales y cada conmutación es crítica. En este trabajo se consideran cuatro métodos de control escalar y un método de control vectorial. Los algoritmos de control se prueban mediante simulación digital en una PC en Matlab y a continuación se aplican experimentalmente, utilizando plataforma de desarrollo basada en el procesador digital de señales AD-21364 de Analog Devices.

Palabras Clave: Convertidor Matricial/ Método Escalar/ Método Vectorial.

THE MATRIX CONVERTER IN AC-AC THREE-PHASE CONVERSION APPLICATIONS: SCALAR AND VECTOR CONTROL METHODS

Abstract: This paper offers the operational characteristics of the matrix converter (MC) used in AC-AC conversion operated with a scalar control and with a vector control of the outlet voltage. Direct AC-AC conversion using matrix converters allows for the modulation of the tension, frequency and phase of the three-phase electric system in order to control the behavior of the load and account for the regeneration of power of the load to the main supply. With an adequate control this configuration may be more versatile than the traditional indirect AC-AC conversion system formed by the cascade connection of a usually uncontrolled AC-AC converter and a three-phase DC-AC inverter-type converter. The matrix converters are complex since their commutation matrix uses eighteen unidirectional switches, and each commutation is critical. This work considers four scalar control methods and one vector control method. The control algorithms are tested through digital simulation in a PC in Matlab and then are experimentally applied using a development platform based on the AD-21364 signal digital processor of Analog Devices.

Keywords: Matrix Converter/ Scalar Method/ Vector Method.

 Manuscrito finalizado en Caracas, Venezuela, el 2007/08/10, recibido el 2007/10/17, en su forma final (aceptado) el 2007/12/07.

I.- INTRODUCCIÓN.

La conversión CA-CA trifásica ha quedado rezagada en aplicaciones de electrónica industrial, debido por una parte a limitaciones técnicas, ya que requiere configuraciones electrónicas complejas, lo que llevó al estancamiento teórico de sus principios, y por otra parte al vertiginoso desarrollo del inversor trifásico en las aplicaciones industriales [1]. El estudio moderno de la conversión CA-CA trifásica se inicia con los trabajos de Alesina y Venturini en 1980 sobre convertidores matriciales [2], los cuales dieron un paso alentador para la aplicación de los convertidores matriciales en aplicaciones industriales, ya que a partir de un desarrollo matemático riguroso, se demostró que es posible obtener un transformador electrónico ideal, es decir, un transformador que a partir de una señal de entrada polifásica alterna de magnitud, frecuencia y fase fijas, es capaz de producir a su salida una señal polifásica alterna de frecuencia, fase y amplitud variables, controlables en forma 22 independiente. Esta idea revolucionaria atrajo el interés para realizar accionamientos de carga de corriente alterna directamente de la red eléctrica alterna, sin pasar por una etapa DC intermedia. Sin embargo, la complejidad del sistema de conmutación, consecuencia del alto número de dispositivos electrónicos requeridos, y el continuado interés en el inversor trifásico, colocaron a un lado al convertidor matricial. Para la década de los 90 del siglo pasado, un grupo de trabajos teóricos, apoyados en la capacidad de cómputo de los simuladores digitales, alentaron a un pequeño grupo de investigadores a dedicarse al área, aumentando el interés en los CM [3]. Un aspecto importante de este renovado atractivo se resaltó con el calificativo de “conversor todo silicio” (All Silicon Converter) dado al CM, en contraposición a la estructura tradicional conversora en cascada AC-DC-AC, que requiere de componentes pasivos en el lazo DC entre el rectificador AC-DC de entrada y el inversor DC-AC de salida. Los avances prosiguieron con los trabajos de Neft y Schauder, con el diseño de un convertidor matricial de 30 HP [4] y los esfuerzos de Eupec para integrar en un módulo electrónico de potencia todos los componentes de conmutación requeridos en un convertidor matricial [5]. En Abril de 2002 la revista Transactions of Industrial Electronics de la IEEE dedica todo el ejemplar 49 a los convertidores matriciales. Los últimos avances en materia de los CM los constituyen los trabajos efectuados por Borojevic y Casadei [6][7], que orientaron el uso de los CM en el campo del espacio geométrico de vectores espaciales. La interpretación de los resultados de estas técnicas vectoriales es compleja, dado que al efectuar la transformación vectorial se generan múltiples vectores de salida, cada uno con una dirección determinada, pero con magnitudes variables, pudiendo producir hasta veintisiete combinaciones. Los principios de la técnica de control vectorial se utilizan para facilitar el diseño de accionamientos de máquinas rotativas en el dominio del lugar geométrico de los vectores espaciales, lo cual da lugar a diversas técnicas de control basadas en el control vectorial, VSC, tales como el control directo de par, el control directo de potencia, y cualquier otra que permita interpretar fácilmente los fenómenos físicos en el campo vectorial. En la actualidad el desarrollo de los CM se ha orientado a la modulación por vectores espaciales porque presentan grandes ventajas en aplicaciones de accionamiento y control electrónico, mejoran la ganancia de tensión y proporcionan un enfoque compacto. El convertidor matricial puede usarse, entre otras aplicaciones, en la interconexión eléctrica de subsistemas eléctricos, en vehículos eléctricos basados en alternadores CA o híbridos, en vehículos de combate de tracción eléctrica, donde las baterías y/o condensadores sean un factor crítico, en sistemas de regulación hidroeléctricos, termoeléctricos, y sobre todo en generadores eólicos, en los cuales es imprescindible entregar a la línea una señal de tensión, frecuencia y fase perfectamente estables, aunque se produzcan variaciones importantes en la salida entregada por el aero-generador.

El trabajo considera dos clases de métodos de control:

• Métodos de Control Escalar.

Basados en una matriz de conmutación accionada en el tiempo, las técnicas consideradas son:

a.- La “matriz de baja frecuencia”, propuesta por Alesina y Venturini.

b.- La inyección de tercera armónica, propuesta por Alesina y Venturini.

c.- El método de Roy.

d.- El “Bus DC Ficticio”.

• Método de Control Vectorial:

Correspondiente a la modulación de vectores espaciales. Los vectores espaciales se obtienen de las veintisiete posibles maneras de conectar el sistema trifásico de entrada hacia la carga; de estos, seis se descartan, ya que no forman un vector de orientación fija, tres combinaciones corresponden con el vector nulo y las dieciocho restantes se usan para modular el vector espacial deseado, tanto en magnitud como en su velocidad angular. La ganancia con este método alcanza hasta 115,6%.

Los resultados muestran la factibilidad del convertidor matricial y su versatilidad en aplicaciones de control. La distorsión armónica disminuye a mayor ganancia y las conmutaciones se realizan sobre una envolvente sinusoidal.

II.- DESARROLLO

1.Principio de operación de los Convertidores Matriciales.

Los convertidores matriciales de entrada y salida trifásica están basados en una matriz de conmutación formada por nueve interruptores bi-direccionales, como se muestra en la Figura 1. Esta matriz de conmutación 3x3 permite conectar cualquiera de las tres líneas de entrada con cualquiera de las tres líneas de salida, asegurando la circulación bi-direccional de la corriente en todas las líneas. Dado el estado actual de la tecnología de semiconductores, la implementación real de esta topología requiere del uso de dieciocho dispositivos semiconductores unidireccionales completamente controlados en encendido y apagado, usualmente del tipo IGBT.

 

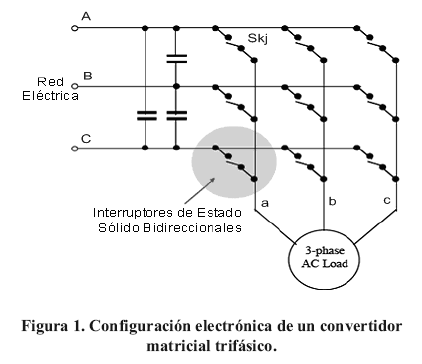
La regla básica de operación de los conmutadores en la matriz viene dada por (1):

Por razones de seguridad no todos los estados teóricamente posibles en la matriz son aplicables en la práctica. Para evitar cortocircuitos en la fuente trifásica durante la operación, sólo son aceptables aquellas combinaciones que cumplen con la condición:

La Tabla I muestra los veintisiete estados de la matriz de conmutación que pueden ser aceptados de acuerdo a la restricción de la ecuación (2); en la tabla los estados se agrupan por el tipo de salida que producen durante el intervalo de aplicación (variable, constante y nula), y cada estado se identifica con un número asociado al vector que producen.

2. Métodos de Control Escalar.

2.1. Matriz de baja frecuencia de Alesina-Venturini (AV).

Los voltajes de entrada y salida referidos al neutro se pueden expresar como vectores de la siguiente forma:

Dada la matriz de conmutación entre la fuente de voltaje y la carga, se obtiene una expresión como:

Donde T es la matriz de transferencia instantánea.

La expresión vectorial para la corriente de entrada y salida viene dada por:

Siendo T^T la matriz transpuesta de T.

Dado el conjunto de ecuaciones (3) a (6), se formula la hipótesis de existencia de una matriz de transferencia instantánea T, que produzca una señal de salida cuya magnitud, frecuencia y fase sean manipulables por un controlador de acuerdo a:

Si se considera b = 0 para simplificar el análisis, y se representa el voltaje de una fase como:

Entonces los coeficientes K1, K2, K3, conforman la matriz de transferencia deseada para una fase:

Dado que la ecuación de secuencia cero viene dada por:

se pueden modificar los coeficientes K como k +1, sin alterar la ecuación:

El producto matricial queda:

Sí w_m=w_o-w_i, al sustituir en (12) el voltaje de salida a partir de la ganancia q resulta:

Y al efectuar una serie de manipulaciones algebraicas se encuentra una matriz con la siguiente característica:

Al aplicar el mismo procedimiento para las otras dos fases, se tiene por analogía la matriz de transferencia completa:

 Las matrices M1 y M2 se conocen como matrices de transferencia de baja frecuencia, pero se utilizan muy poco en la práctica. Su uso es posible mediante un interesante artificio de modulación en alta frecuencia para obtener el valor promedio que permita la representación de cada término de la matriz por muestreo [1], logrando así la solución deseada. La ecuación (17) permite para estimar los tiempos de conmutación de cada interruptor durante cada ciclo de muestreo:

Esto conduce a la matriz de conmutación directa de Alesina- Venturini, cuya desventaja es que el valor máximo de la ganacia es de 50%, esto es, que la tensión máxima de salida es, en el mejor de los casos, igual a la mitad de la tensión de entrada.

2.2.- Inyección de tercera armónica por Alesina Venturini.

A fin de mejorar la ganacia del caso anterior, Alesina y Venturini proponen el empleo del voltaje de modo común para inyectar un conjunto de armónicas de tercer orden en la señal de entrada y salida. La siguiente matriz representa la solución propuesta de manera análoga al estudio anterior[5].

Y modificándola para efectos prácticos por la matriz de conmutación para la secuencia de muestreo de cada término, se tiene:

Esta nueva matriz de conmutación produce una ganacia máxima de 86,0%, sin modificar la topología del convertidor.

 2.3.- Técnica de Roy.

Otro método interesante fue propuesto por Roy y April [6], en base a la modulación por ancho de pulso, siguiendo la referencia de salida y ajustando el aporte de cada fase de voltaje de acuerdo a su signo. Es decir, dados los siguientes voltajes de entrada instantáneos:

a la salida de convertidor matricial, el valor instantáneo del voltaje de salida se puede expresar por la ecuación (23):

donde K-L-M son variables que pueden ser asignadas a A, B o C de acuerdo con la siguiente reglas:

Regla 1: A la fase que tenga una polaridad distinta a las otras dos, se le asigna la letra “M”.

Regla 2: Las otras dos fases se asignan de la siguiente forma: la letra “K” a la que posea el menor valor absoluto y la “M” a la fase restante.

En este método se obtiene una ganancia de sólo 50%, producto de los instantes de conmutación natural del sistema trifásico.

2.4.- Bus DC Ficticio.

El control escalar por “Bus DC Ficticio”, también conocido como función de transferencia inversa, requiere de un convertidor matricial modificado como se muestra en la Figura 2. Se observa que la nueva estructura contiene por separado un rectificador y un inversor completamente controlados, conectados mediante un bus DC sin condensador de filtro, por lo tanto las tensiones en la carga se toman directamente de la red trifasica.

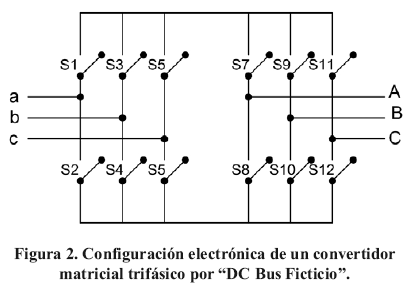
El retificador controlado actúa con un multiplicador del voltaje de entrada mediante una matriz A y el inversor permite la modulación hacia la carga por medio de una matriz B, es decir

Donde la matriz A se conoce como “Bus DC Ficticio” y está representada por:

Mientras que B viene dada por:

Entonces:

De allí que la tensión de salida es:

El valor máximo de K_A está dado cuando en el bus DC se obtiene el máximo positivo o negativo del voltaje de entrada, es decir K_A = 2√3/π. Por otra parte K_B representa el indice de modulación que puede alcanzar 2/π, por lo tanto la máxima ganancia viene dada de sustituir K_A y K_B en la ecuación (29), por lo tanto q=6√3/π² = 105,3%; esto es, la tensión instantánea de salida puede ser ligeramente mayor que la entrada.

3.- Método de Control Vectorial.

3.1- Técnica de Modulación por Vectores Espaciales.

La salida de los convertidores matriciales puede representarse mediante un conjunto de vectores espaciales correspondientes a los veintisiete modos de conexión en el convertidor matricial, clasificados en tres grupos como se muestra en la Tabla I. Para el análisis vectorial no se considera el primer grupo, puesto que sus integrantes son vectores giratorios, y la técnica de control vectorial requiere de vectores de dirección fija. El segundo grupo está formado por dieciocho vectores espaciales de dirección fija, cuya amplitud varía con el tiempo; en términos de variables circuitales, las magnitudes de los vectores de voltaje, V_o, y de corriente, Io, en la matriz de conmutación varían, respectivamente, de acuerdo al voltaje y a la corriente de línea instantáneos. Los vectores espaciales de orientación fija dividen el plano geométrico en seis zonas, como se muestra en la Figura 3. La modulación de los vectores espaciales en los convertidores matriciales se define por cuatro vectores, por medio de la transformación a vectores espaciales [6][7]:

Donde v y v_o son, respectivamente, los vectores espaciales de voltaje de entrada y salida, mientras que i_i e i_o son, respectivamente, los vectores espaciales de corriente de entrada y salida.

Los esquemas de control basados en la modulación de vectores espaciales (SVM por sus siglas en inglés) se aplican en los convertidores matriciales partiendo del principio de modulación por ancho de pulso: la amplitud deseada del vector de salida se logra combinando los períodos de activación de los vectores adyacentes asociados al sector del vector de salida deseado. La aplicación práctica de los principios de la modulación de los vectores espaciales en los convertidores matriciales fue desarrollada por Huber y Borojevic [6]. En este trabajo se trata la configuración de transferencia directa, usando el método clásico de modulación PWM de los vectores espaciales. La Figura 4 muestra el vector de referencia de voltaje V_o^* en el plano geométrico de los vectores espaciales del convertidor matricial. Para obtener el vector V_o^* es necesario sintetizar los vectores adyacentes V_α^*  y V_β^*  durante intervalos de tiempo definidos por d_α y d_β respectivemente. Si el voltaje de salida del convertidor matricial se considera constante durante un instante T_s, el voltaje de referencia puede expresarse como la suma del producto de los vectores adyacentes por sus respectivos intervalos activos:

La duración de la aplicación de los vectores activos adyacentes determina la dirección de V_o^*, mientras que la duración de la aplicación del vector cero corrige la amplitud de V_o^* hasta lograr el valor deseado. Los ciclos de trabajo de activación de los vectores adyadentes son:

Debido a que para cada acción de control se tienen hasta seis vectores adyacentes utilizables para sintetizar la salida deseada, en la selección de los vectores a usar existe una libertad relativa, por lo que se pueden definir diversos criterios de selección de los vectores. Los criterios inciden en aspectos particulares de la operación del CM. Por ejemplo, se puede seleccionar aquel vector de voltaje cuyo correspondiente en corriente permita ajustar el factor de potencia, o aquél de mayor amplitud en el correspondiente cuadrante, entre otras opciones. La ganancia en este caso viene dada por el factor de la transformación vectorial q= 2/√3=115.4%

4. Resultados de la Simulación Digital de las Técnicas de Control en los Convertidores Matriciales.

4.1. Resultados del Método Escalar de Alesina-Venturini.

La Figura 5 muestra las tensiones y corrientes obtenidas en un CM con carga RL de R=0,70 Ω, L=0,0019 H, para una ganancia q=0,3, una frecuencia de salida, f_o=30 Hz, y una frecuencia de conmutación F_c=10 kHz.

El voltaje V_AN es la tensión instantánea de salida en la fase A y V_an es la señal de tensión deseada en la carga para la componente fundamental de la fase A, valor de referencia que se carga en el algoritmo de control. Se puede observar que la corriente I_an presenta un rizado producto de las conmutaciones de las tensiones aplicada a la carga.

4.2. Resultados del Método Escalar de Alesina-Venturini con inyección tercera armónica.

La Figura 6 muestra el voltaje de salida por el método AV modificado, mediante el voltaje de modo común por inyección de tercera armónica usando la carga y parámetros de operación anterior.

Al igual que el caso anterior, V_an es la señal de referencia de la tensión de salida deseada, valor que se carga en el algoritmo de la matriz; nótese que este voltaje en modo común tiende a ser mínimo en los punto de conmutación natural y a aumentar en los valores máximos del sistema trifásico. En este caso la ganancia del convertidor aumenta hasta q=0,86.

4.3. Método de Roy.

Los resultados del método de Roy son muy similares a los obtenidos en AV “matriz de baja frecuencia”; sólo hay diferencia en el transitorio de inicio.

La Figura 7 muestra el resultado para la misma condición de carga, frecuencia de salida y frecuencia de conmutación del caso anterior, pero con una ganancia de voltaje q=0,3, además de un corrimiento de la fase del voltaje de referencia V_an de retraso de π/3; esto trae como consecuencia que la corriente I_an este adelantada con respecto al voltaje real de entrada, demostrando la capacidad del convertidor para controlar el factor de potencia del sistema.

2.4.4. Técnica “Bus DC Ficticio” ó función de transferencia inversa:

La Figura 8 muestra el resultado obtenido por el método de control escalar para la configuración “Bus DC Ficticio” para la misma condición de carga, frecuencia de salida y frecuencia de conmutación del caso anterior, con q=1, y un corrimiento de la fase del voltaje de referencia V_an en adelanto de π/3.

La tensión en una fase de salida se corresponde con la diferencia de potencial de dos fases de entrada, aumentando la tensión máxima instantánea a 1,732 p.u., mejorando la magnitud de la ganancia a 105,3%. Se puede observar que el aspecto de la salida de tensión es similar al que presenta la modulación de la tensión del bus DC de un inversor trifásico convencional; además, como consecuencia de la estrategia de modulación empleada, se producen algunos picos de voltaje contrario a la polaridad de la referencia debido a la carga inductiva y la secuencia de disparo.

4.5. Método vectorial por modulación de vectores espaciales para un convertidor matricial:

La Figura 9 muestra las corrientes y tensiones de las tres fases, para una carga RL con R=0,707 Ω, L=0,0019 H, una frecuencia de conmutación fo=10 kHz, cuando el vector de referencia gira a 60 Hz, con una ganancia de q=1.

En el control por modulación de vectores espaciales se tiene una referencia que es un vector de magnitud y velocidad angular dadas. Este vector de referencia debe seguirse a partir de la modulación de los vectores adyacentes correspondientes a la posición del vector de referencia. La magnitud y la frecuencia del voltaje de salida en cada fase son las mismas y dependen de la transformación de coordenadas del vector espacial de referencia. Se puede observar que debido a la naturaleza inductiva de la carga la corriente presenta menos distorsión.

III. CONCLUSIONES

1. Los algoritmos empleados son producto de enfoques matemáticos sencillos en base a los cuales se generan las secuencias de conmutación para accionar los dispositivos de control de potencia que forman la matriz de conmutación de dieciocho interruptores.

2. Las tensiones de salida son el producto de una modulación de la envolvente del sistema trifásico de voltaje de entrada y que se puede controlar de forma independiente los voltajes, las fases y la frecuencia sobre la carga.

3. Las corrientes producidas son sinusoidales con rizado armónico, y es factible el control del factor de potencia introduciendo un defasaje arbitrario entre la referencia de tensión y la tensión de línea de entrada.

4. Los métodos escalares manejan los interruptores de acuerdo al valor instantáneo de las tensiones de entrada siguiendo una ley de formación expresada mediante ecuaciones matemáticas.

5. En las técnicas de la matriz de baja frecuencia ó AV y en la de Roy existe la limitante de que la ganancia máxima de tensión es de 50%, ésto es, la amplitud de la salida sólo puede llegar a ser igual a la mitad de la amplitud de la entrada.

6. La técnica AV de inyección de terceras armónicas mejora la ganancia hasta 86 %, a expensas de causar mayor distorsión en la corriente, mientras que la técnica de “Bus DC Ficticio” ó función de transferencia inversa permite elevar la ganancia a 105,3%, pero requiere aumentar el número de conmutadores a doce, formando dos puentes H tal como en las configuraciones convencionales completamente controladas.

7. El método vectorial busca posicionar un vector espacial de acuerdo a una combinación de interruptores, por lo tanto se recurre a la modulación por vectores espaciales de voltaje.

8. Esta técnica tiene la ventaja que el control sobre la carga se realiza en el dominio vectorial sin necesidad de emplear transformación de coordenadas.

9. Los resultados obtenidos muestran una ganancia del vector de voltaje de salida de 115,4%.

10. La técnica de modulación por vectores espaciales en convertidores matriciales sirve de base para el desarrollo de control vectorial en el campo de accionamiento de motores.

IV.- REFERENCIAS

1. Alesina, A.; and  Venturini, M.G.B., "Solid-State Power Conversion: A Fourier Analysis Approach to Generalized Transformer Synthesis", IEEE Transactions on Circuits and Systems Vol. Cas-28 No. 4, April 1981, pp 319-330.         [ Links ]

2. Alesina, A.; and  Venturini, M.G.B., "Analysis and Design of Optimum-Amplitude Nine-Switch Direct AC-AC Converters", IEEE Transactions on Power Electronics Vol. 4.No. 1., January 1989, pp. 101-112.         [ Links ]

3. Wheeler, P.W. et al. “Matrix Converters: A Technology Review”, IEEE Transactions on Industrial Electronics, Vol. 49, No. 2, April 2002, pp 276-288.        [ Links ]

4. Neft, C. L.; and  Schauder, C. D., “Theory and design of a 30-HP Matrix Converter,” IEEE Trans. Ind. Applicat., vol. 28, no. 3, pp. 546-551, May/June 1992.         [ Links ]

5. Munzer, M., ” EconoMac - the First All In One IGBT Module for Matrix Converters “, Drives and Control Conference, Section 3, London, 2001.         [ Links ]

6. Huber, L.; and  Borojevic, D., “Space vector modulated three phase to three phase Matrix Converter with input power factor correction,” IEEE Trans. Ind. Applicat., vol. 31, no. 6, pp. 1234-1246, November/December 1995.         [ Links ]

7. Casadei, D.; et al. "Matrix Converter Modulation Strategies: A New General Approach Based on Space Vector Representation of the Switch States", IEEE Transactions on Industrial Electronics, Vol. 49, No. 2, April 2002, pp 370-381.         [ Links ]

8. Roy, G.; and  April, G. E., "Cycloconverter Operation Under a New Scalar Control Algorithm", Conf. Rec. IEEE PESC, 1989, pp. 368-375.        [ Links ]