linro.pzo@gmail.com, ronaldfries@gmail.com

Palabras clave: Gravitación / Newton / Einstein / Teoría General de la Relatividad / Lorentz / Coriolis / Energía

Keywords: Gravitation / Newton / Einstein / Theory of General Relativity / Lorentz / Coriolis / Energy.

(Recibido mayo 2012, Aceptado agosto 2012)

Esta pregunta es muy válida en relación de las dos teorías reconocidas de la gravedad. Es generalmente conocido que el efecto gravitatorio, y su causa, representa uno de los mayores enigmas de la Física Teórica en general. En este sentido, la Física Teórica está buscando un camino que permite resolver este enigma de manera científica y matemática. La pregunta es: ¿por dónde empezar a buscar esta solución?

Se podría empezar con la búsqueda de errores y contradicciones en las teorías existentes. En general se acepta que las teorías existentes de la gravitación, como tal, no pueden describirla ni explicarla. Describen sus efectos, pero la causa, la esencia, de la gravedad sigue siendo un misterio.

Las teorías científicas nacen, en parte, por la necesidad de cubrir huecos que las teorías precedentes no lograban. Es un hecho que a medida que se hacen nuevos descubrimientos las teorías van fortaleciéndose, lo hacen hasta que llegando a un punto, esos mismos descubrimientos empiezan a resquebrajarlas. Entonces aparece una teoría superior que integra el conocimiento anterior y que explica los hechos sin contradicciones aparentes. Las fallas que tenían las teorías precursoras desaparecen en la nueva. La nueva teoría es tan poderosa que servirá durante un tiempo para explicar los nuevos descubrimientos que todavía no se han producido. Este es el ánimo de nuestra nueva teoría:

y kappa escrito como:

Ley de de Coulomb

Debido a esta relación, la física teórica habla de un campo gravito magnético.

Y así siguen dos contradicciones.

La analogía matemática es evidente en ambas leyes, pero también ¿lo son en el sentido análogo físico?

Ambos valores son claramente desiguales.

Es matemática y físicamente imposible integrar ambos valores sin violar de manera masiva las reglas. Y debido a que todos los físicos y matemáticos saben que es imposible, ¿se define G con y₀?

Se escribe que Einstein no utilizó el valor de y₀ (y seguramente nunca lo habría hecho…). Por supuesto, tanto él como nadie más lo usa. También es imposible para nadie, porque no hay ninguna posibilidad para especificar un valor numérico o tamaño para y₀.

Él es puro producto de la imaginación, y si no existe la posibilidad de integrar en una ecuación valores numéricos, nunca llegaremos a un resultado solucionándola.

Esta contradicción se deduce de la lingüística: gravito magnético. Suponiendo que es en realidad un campo gravito magnético, sigue la pregunta de ¿por qué no está aquí la constante del campo magnético (μ0 = 12,56637x10^-7N/A²) sino la de la electricidad?

La respuesta está en la analogía ya mencionada, debido a que la interacción resulta entre dos cargas opuestas, una positiva y la otra negativa. De manera similar Newton postula una interacción entre las masas m y M (planetas).

¿La realidad esta de tal forma?

Entonces, de acuerdo con la ley de Coulomb, las masas que interactúan también deben tener cargas opuestas. Sólo hay dos cargas diferentes (positiva y negativa), pero un gran número de planetas y ¿tendrían que tener un 50% de carga positiva o negativa?

Si esto fuera así, la vida no existiría en la forma real del Universo. Las cargas opuestas se aniquilarían entre sí y el Universo, con la suma de todas sus energías, ¡sería sólo radiación!

¡Exactamente este es uno de los hallazgos de la física en absoluto!

El hecho es que la Tierra tiene un campo magnético. Este campo magnético proviene del viento solar y se puede deformar, más o menos, dependiendo de su tamaño.

Esto es fácilmente comprensible y demostrable cuando se comparan las líneas de un campo magnético con las de un campo gravitatorio. Un campo magnético, como se sabe, se extiende del polo positivo al polo negativo. El polo norte de la Tierra es el polo positivo, ya que la Tierra gira de oeste a este, y la dirección de rotación se ve desde el Polo Norte a la izquierda, es decir positiva. Visto desde el polo sur, la dirección es negativa. De esta manera las líneas corren, ligeramente desplazadas, desde el Polo Norte al Polo Sur.

Las líneas de campo de un campo gravitatorio se definen por la aceleración real y efectiva de la gravedad, por lo tanto, en cada punto de la superficie de la Tierra en 89,9 °, sólo casi perpendicular a ella.

En la vista no se reflejan únicamente el orden simétrico de las líneas del campo norte y sur con su curvatura radial, sino también y con precisión el tamaño espacial de un campo gravitatorio, como Einstein lo señaló, en su Teoría General de la Relatividad, que es limitado.

Nota: En la vista presentada no hay relación ninguna con el tamaño real del campo gravitatorio (dibujo de principio).

Esto afecta ahora a la parte izquierda de su ecuación de la energía. Además de la curvatura radial, el campo gravitatorio tiene una torsión (axial) dependiente de la velocidad de rotación. Su valor numérico es definido por el tensor energía-impulso (Tμυ) a la derecha del signo igual.

Einstein empieza la descripción geométrica del campo gravitacional con bases ciertas (axiomáticas). Para describir esto, la geometría euclidiana no es suficiente. A la izquierda del signo igual de su ecuación de la energía son el tensor de Ricci (Ruv) y el tensor métrico (guv función de distancia). Juntos forman el llamado tensor de Einstein. Es generalmente conocido que la representación matemática de estos tensores es sólo posible sobre la base de la geometría esférica (exceso esférico). Igualmente se sabe que pi no es aplicable y no se utiliza en la geometría esférica porque conduce a resultados incorrectos. David Hilbert - uno de los mejores matemáticos del mundo de su tiempo (!) - estaba al lado de Einstein y participo activamente en el desarrollo de las ecuaciones de la TGR. Ellos sabían muy bien, al igual que todos los físicos y matemáticos actualmente, que pi no es aplicable en el exceso esférico. ¿Sin embargo, Einstein introduce el número pi como una constante absoluta en su propia teoría? ¿Quién puede explicar correctamente como los dos podrían cometer un error tan flagrante?

Personalmente, no puedo aceptar tal cosa.

Esto lleva a la pregunta de: ¿cómo es posible que durante casi 100 años lo consideramos correcto, lo aprendemos y lo enseñamos? ¿Lo escribió Einstein esto realmente así?

Las ecuaciones en el guión original, escritas manualmente por Einstein, eran altamente no linearizadas y se linearizaron y retardizaron ulteriormente.

¿Por qué?

Incluso ecuaciones no linearizadas se resuelven! ¿Por qué razón las ecuaciones originales se modificaron?

La diferencia fundamental radica en la sustitución de la variable X (Ji) en el original con el tamaño K (kappa) en la forma actual de la ecuación. El problema, en la época y ahora, reside que en el Universo no hay y no puede haber constante, ¡a excepción de la velocidad de la luz c!

del campo gravitatorio y g es la aceleración de la gravedad (diferente para cada planeta). Debido a que todas estas variables son relativas y no hay ninguna constante, Einstein llamo esta teoría: la teoría de la relatividad y no ¡la teoría de las constantes!

Por supuesto, primero se debe calcular el valor numérico específico antes de integrarlo en la formula. Por lo tanto, la ecuación básica se basa en 10 ecuaciones acopladas, con la que estos valores se calculan. Estas ecuaciones existen en forma linearizadas y retardizadas, esto es también conocido. Hasta la fecha, no existe un físico o un matemático en el mundo que haya tenido éxito para resolver numéricamente estas ecuaciones obteniendo resultados con cifras verificables. Eso no será posible en el futuro porque con X (Ji) surgen otras ecuaciones.

Considerando ahora las consecuencias de la visión de Einstein - la relatividad de la constante gravitacional - para toda la física, cada persona normalmente inteligente podría entender el terror de Drude y Planck cuando entendieron lo que representaba X. Si hay evidencia de que la constante de gravitación no es constante, colapsan todas las teorías existentes, es también válido para hoy como para la época de Einstein. La constante gravitacional G es una cantidad fundamental en todo el modelo de pensamiento de la física teórica. No hay en la cosmología, casi ningún proceso, o parte de proceso, que puede representarse sin esta constante y sin embargo el la gravedad, como tal, ¿sigue siendo, un misterio?

¿Eso quiere decir que tenemos que desmentir las teorías de Einstein y asumir que son en realidad una tontería, como muchos críticos pretenden a nivel internacional?

Es cierto que las modificaciones, a su sentido original, surgen probablemente debido a un conflicto de intereses.

Por ahora, si dejamos de un lado la constante kappa y utilizamos X como en el original de Einstein, obtenemos un sistema completamente diferente de ecuaciones que no tiene nada que ver con lo conocido, ni siquiera remotamente. Sin embargo, este sistema de ecuaciones proporciona cifras claras al 100% con resultados numéricos precisos.

Esta es, otra vez, para confirmar que todas las declaraciones de Einstein están correctas. Lo mismo se aplica a la constante fundamental de la gravedad, cuya relatividad puede ser demostrada de manera matemática. Este valor es conocido hasta hoy como un valor de medición y nadie puede calcularlo en absoluto. Tomando las declaraciones de Einstein, esto nos da la posibilidad de desarrollar formulas muy sencillas que nos conducen, entre otras cosas, a soluciones para calcular la constante de gravitación:

Más abajo tenemos el factor de corrección para la ubicación de Zúrich (Suiza), donde hay el experimento de última generación y de alta precisión para la medición de G. Este factor de corrección se refiere a la latitud del lugar. Para cada conjunto de valores, hay una prueba matemática precisa. La unidad de la constante gravitacional se omitió deliberadamente, porque objetivamente no se conoce. Las justificaciones o derivaciones de la misma son muy diversas, y necesitan la comprensión de los fundamentos para entenderlas. La explicación de los detalles se podría publicar en un artículo separado hacer por razones de espacio. Lo importante es, sin duda, apoyar la declaración de Einstein que afirma que las leyes de la física son las mismas en todos los sistemas inerciales. ¡Iguales son también todas las ecuaciones inerciales! El 19’410 m/s de la velocidad orbital solar vale para todos los planetas. Si insertamos los tamaños específicos de cada planeta en las ecuaciones, obtendremos en cada uno la constante gravitacional ecuatorial.

La segundo raíz de la relación de la fracción es el valor numérico de la constante de gravitación en el ecuador y en el nivel del mar (NN). El valor de 19’410 m/s es la velocidad orbital del Sol y de su sistema planetario medido por la astronomía por medio de la distancia definida hasta las estrellas fijas. 9,789’515’119 m/s2 es la gravedad exacta de la Tierra en el ecuador al nivel del mar (NN) que no es se puede calcular con tanta precisión con la teoría de Newton.

Constante calculada según esta descripción:

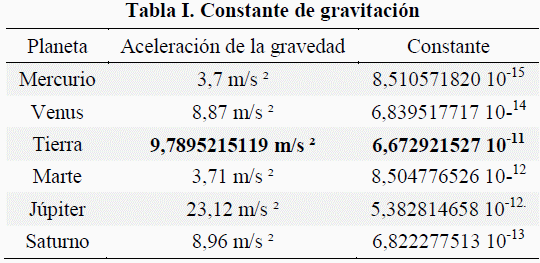
Cada lector notara que sólo la Tierra tiene la mayor constante de gravitación, a pesar de que no es ni el más grande ni el más pequeño de los planetas del sistema solar. Hay otra vez una excelente explicación matemática. La Tierra es el único planeta del sistema solar cuya órbita en relación con los datos relativos a la magnitud de su campo gravitacional dan como resultado 1:

Para explicar los detalles debemos, otra vez por razones de espacio, referirnos a futuros artículos. Es importante demostrar que se confirma, una vez más, la evidencia de Einstein del tamaño espacialmente limitado de un campo gravitatorio.

Como uno de los primeros y más citados ejemplos para la confirmación de la exactitud de su teoría de la relatividad general, es la ecuación de Einstein para probar los 43 segundos de arco incomprendidos de la rotación perihelica de Mercurio.

Lo que significan los símbolos individuales es conocido y no necesita ninguna explicación adicional. La ecuación da el ángulo de rotación, y sólo por la multiplicación de los radianes y los resultados de 3’600 se obtienen los 43 segundos de arco.

Matemáticamente, esta ecuación debe ser considerada como correcta. La pregunta es si esto se aplica también a la interpretación correcta de la causa física de la rotación del perihelio.

¡Es evidente que Einstein inserta aquí, en el numerador de la fracción, Pi y G que son dos constantes presuntamente absolutas, que en realidad no son constantes! Sin embargo, no está describiendo las propiedades de un campo gravitatorio, sino la resultante de la interacción entre los campos gravitacionales.

Aunque el pensamiento de Einstein es correcto, contiene un error lógico de análisis fácilmente explicable. Einstein señala de forma absolutamente correcta, que las leyes de la física son las mismas en todos los sistemas inerciales, ¡entonces esta ecuación debe ser aplicable a todos los otros planetas!. Exactamente esto es imposible y los resultados lo demuestran.

Cualquiera que conozca la literatura sabe que el cálculo del perihelio de los planetas se diferencia en las teorías de Einstein de las de Newton. Ambos métodos de cálculo dan resultados diferentes y por lo tanto no son exactos. Tenemos una sola naturaleza, un Universo, una gravedad, y por lo tanto cada planeta tiene su propia rotación perihelica. ¡No hay ninguna rotación del perihelio que se adapta a las teorías de Newton o de Einstein! Ella resulta de la geometría real y del movimiento, si esto no es exactamente conocido o comprendido, se producirán errores en las representaciones matemáticas.

El error en la explicación de la geometría de movimiento de los planetas se radica en el hecho de que el perihelio del planeta no es lo único: la rotación total de los planetas está compuesta por el perihelio y el periastro, los dos se superponen. Con Mercurio y el Sol, el centro de gravedad común - el periastro – se sitúa dentro del Sol y sólo a unos pocos kilómetros de su centro geométrico. Por lo tanto hay conexión directa con la excentricidad, que no tenemos con la rotación del perihelio. La ecuación antes citada de Einstein describe con exactitud la rotación del perihelio. Sólo porque el periastro es tan cerca del centro geométrico del Sol, visualmente las dos rotaciones parecen una misma cosa. Debido a que no lo tomamos en cuenta, no diferenciamos rotaciones del perihelio y del periastro, obtenemos resultados matemáticos imposibles.

En consecuencia, la tarea es de desarrollar ecuaciones que toman en cuenta estas diferencias y que se basa en las declaraciones originales de Einstein. Esto es posible. Una constante gravitatoria o la masa de los valores numéricos no son necesarias para esto porque no están relacionados con la geometría del movimiento.

Lo hicimos y aquí pueden ver los resultados en la siguiente Tabla:

El resultado es exactamente lo contrario! Tanto la rotación del periastro como la del perihelio, al aumentar la distancia con el Sol se ponen siempre más grandes. Esto no puede ser de otra manera, en la parte externa los períodos orbitales se ponen siempre más largos con velocidad constante del Sol. Ahora tenemos que poner especialmente atención en la columna 6. La precesión geodésica de todos los planetas está dada por:

ΔF es el perihelio (columna 4), T es el período sideral (columna 5) y r es el radio orbital (columna 1). Todos estos valores están generalmente disponibles en los atlas de astronomía. Ahora comparamos los valores de la precesión geodésica (columna 6) con la tercera Ley de Kepler. La analogía con su declaración es flagrante y sería posible añadir una cuarta ley a las tres leyes de Kepler. La evidencia de que las ecuaciones son correctas se proporciona con ella.

Cada planeta tiene, debido a sus propios movimientos espaciales, su propio valor de Pi.