Estudio de la eficiencia eléctrica en los hornos de arco eléctrico sumergido de sidor en función de la pérdida de calor a través de su refractario de trabajo y la longitud de arco.

Jesús Rendón F. ¹, Francisco Rojas H. ¹, Ervis Díaz N. ², Adra Rodríguez C. ¹

¹ UNEXPO, Puerto Ordaz- Venezuela,

² CVG SIDOR

Resumen:

Este trabajo presenta un estudio sobre la eficiencia eléctrica de los hornos de arco eléctrico sumergido de la Acería de Planchones de SIDOR en función de la altura de sus electrodos y de las pérdidas de calor a través sus refractarios de trabajo, mediante el uso de simulaciones con el Método de Elementos Finitos. Las simulaciones eléctricas y térmicas mostraron que operar con longitudes de arco superiores a 0,25 m implica uso de excesos de energía en el interior del horno y que disminuir la conductividad térmica en el refractario de trabajo desde su valor usado actualmente de 5,1 hasta 2,5 W/m°K representaría un ahorro de energía de aproximadamente 2,46 GWh, que equivale al gasto energético de 140 casas a razón de 1500 kWh mensual. Además, que la cantidad de energía calórica que fluye a través de los refractarios hacia afuera del horno es apenas el 0,65 por ciento, 3,92 KWh/ton, de la energía total entregada al mismo (601,63 KWh/Ton), pero que es alta respecto al valor de 2,65 KWh/ton reportado por otro autor. Los valores de la temperaturas obtenidas por la simulación fueron validadas con mediciones de temperaturas realizadas con un pirómetro.

Palabras claves: Horno de arco eléctrico sumergido, eficiencia eléctrica, refractarios, SIDOR, simulaciones termoeléctricas.

Study of electrical efficiency in the electric arc furnace submerged sidor depending on heat loss through their refractory work and the length of arc.

Abstract:

This paper presents a study on the electrical efficiency of submerged electric arc furnace in the steelworks SIDOR, depending on the height of their electrodes and the loss of heat through their refractory, by using simulations with The Finite Element Method. Electrical and thermal simulations showed that operation with arc lengths greater than 0.25 m involves an excessive use of energy inside to the oven and that to reduce the thermal conductivity in the refractory from its value currently used 5.1 up to 2.5 w/m°K would represent an energy saving of approximately 2.46 GWh, which is equivalent to the energy consumption of 140 homes at a rate of 1500 kWh per month. In addition, the amount of heater energy that flows through the refractory to the outside of the oven would just 0.65 per cent, 3.92 KWh/ton, of the total energy supplied (601.63 KWh/Ton), but which is high compared to the value of 2.65 KWh/ton reported by another author. The values of the temperatures obtained by the simulation were validated with measurements of temperature with a pyrometer.

Key words: Submerged electric arc furnace Electrical efficiency, Refractory, SIDOR, Thermoelectric simulations.

Recibido (17/10/16), aceptado (12/12/16)

I. INTRODUCCIÓN

Venezuela no escapa de la crisis energética mundial, particularmente la de energía eléctrica, la cual se usa en inmensas cantidades en los grandes procesos industriales, por ejemplo los que usan para producir acero y aluminio. La reciente restricción en el consumo de energía eléctrica impuesta por el estado a los grandes consumidores en nuestro país, como es el caso de la Siderúrgica del Orinoco Alfredo Maneiro SIDOR, causó una merma en su producción de acero.

SIDOR es un complejo siderúrgico el cual ubica a Venezuela en cuarto lugar como productor de acero integrado de América Latina y el principal de la región Andina, ha logrado colocar su nivel de producción en torno a los 4 millones de toneladas de acero líquido por año. Utiliza para la fabricación de acero, metodologías de Reducción Directa y Hornos de Arco Eléctrico Sumergido, este último abreviado como HAES.

La política actual del país busca el uso eficiente de la energía eléctrica. En ese sentido, SIDOR está haciendo investigaciones con el objetivo de disminuir y optimizar su consumo de energía eléctrica en todas sus áreas, enfocándose principalmente en el área de Acería de Planchones donde se encuentran cuatro HAES para producir acero, los cuales consumen 130 MVA cada uno, representando éstos junto con los de la planta de Acería de Palanquillas aproximadamente el 64,5 por ciento de la energía eléctrica de todo el complejo industrial como se puede observar en la Figura 1.

En consecuencia, surge la necesidad realizar un estudio que permita comparar el comportamiento termoeléctrico del HAES al variar la longitud del arco eléctrico (distancia entre la punta del electrodo y la superficie superior del acero líquido) y las conductividades térmicas de los refractarios (representando dos tipos de refractarios) para determinar cuáles son las mejores configuraciones que implican disminuciones en las pérdidas de flujo de calor hacia afuera de los HAES, lo que equivale a mejorar la eficiencia eléctrica de éstos.

En una investigación de marzo de 2010 realizada por Magnesita Refractarios a SIDOR denominada "Proyecto de Reducción de la Energía Eléctrica en los hornos de SIDOR" [1] se hace un estudio sobre los cambios de los perfiles térmicos el interior de los HAES en función del uso de un nuevo refractario. La investigación determinó los perfiles por medio del Método de Elementos Finitos (MEF), con el programa ANSYS en dos dimensiones y como resultado se presenta a la empresa SIDOR una propuesta de ahorro energético significativo por tonelada de acero producido.

En esta nueva investigación, que toma como referencia comparativa el estudio anterior, se hace un estudio en tres dimensiones con el MEF, nuevamente con el programa ANSYS, para realizar comparaciones entre los perfiles de las distribución de temperatura s y de potencial eléctrico en el interior de los HAES en función de dos variables de los hornos: las conductividades térmicas de los refractarios, específicamente la que se corresponde con los refractarios usado actualmente por SIDOR y el propuesto por Magnesita Refractarios; y la longitud del arco eléctrico. Especialmente, se estudia el calor que se pierde a través de las dos paredes refractarias mencionadas; así como también, la importancia que tiene la longitud del arco eléctrico, permitiendo estudiar la relación entre altura de los electrodos con el mejor aprovechamiento de la energía eléctrica suministrada a través de ellos.

II. METODOLOGÍA

2.1 Modelo computacional del HAES

La Figura 2 muestra un corte longitudinal del modelo computacional en 3D que representa al HAES, el cual fue elaborado a través del programa de simulación ANSYS debido a su capacidad de realizar cálculos por medio del MEF y su frecuente uso para este tipo de problema [2-5]. A su vez, se aprecia cada uno de los componentes que conforman al horno.

Una vez realizado el modelo, se configura el elemento a utilizar. En este caso de modelado termoeléctrico se utilizó SOLID69 [6], el cual tiene 8 nodos y 2 grados de libertad por cada nodo: temperatura y voltaje, y posteriormente se realizó el mallado de todo el sólido (ver Figura 3).

Se elaboraron tres modelos computacionales del horno variando la distancia entre la superficie superior del acero líquido y la punta inferior de los electrodos (longitud de arco) para unos valores de separación de 0,25 m, 0,35 m y 0,45 m, los cuales son valores usados frecuentemente [7-9].

Por otro lado, en el modelo se varió la conductividad térmica en los refractarios de trabajo. El primer caso (Caso A) implica la condición de operación actual del horno, en donde la conductividad térmica tiene valor de K=5,1 [w/m°K] como lo indica la Tabla 1; para los modelos restantes que involucran el caso B y C, se consideró un valor de K=2,5 [w/m°K] y uno de K=1,5 [w/m°K] respectivamente. Es importante acotar que para este estudio no se variaron las conductividades térmicas de los otros refractarios.

2.1 Propiedades térmicas y eléctricas de los materiales

Las propiedades de los materiales necesarias para el análisis termoeléctrico son la conductividad térmica, la resistividad eléctrica y la densidad propia de cada material. Las utilizadas para representar los refractarios fueron aportadas por la empresa Magnesita Refractario; las que definen las propiedades de los electrodos y las placas de contacto fueron suministradas por [10], las del acero por [11] y las de la escoria están en el mismo orden de magnitud que se menciona en [12-14]. Todas estas propiedades se muestran a continuación en la tabla I.

2.1 Consideraciones de operación del HAES

En la figura 4 se observa el diagrama eléctrico del HAES [10]. El modelo computacional sólo representa el circuito secundario del diagrama (sin incluir la resistencia y la reactancia en el transformador). Es necesario tomar en cuenta que el voltaje de fase del circuito secundario del horno que de acuerdo a la operatividad del mismo y para condiciones estables, es de aproximadamente 600 V. Así como también, el factor de potencia para estas condiciones es de 0,9 para una corriente de fase de 65 kA, datos suministrados por la empresa a través de [15].

El potencial eléctrico asociado es cero en el fondo de la cuba, de esta manera el voltaje de arco se mide respecto al potencial cero mencionado. La convección en la superficie de la cuba en contacto con el aire es de 24 W/ m2K de acuerdo con [16] a una temperatura de 50°C. No se considera el aporte de energía de la lanzas de oxígeno.

2.2 Ecuaciones termoeléctricas

En todos los nodos del modelo del HAES, la distribución de potencial eléctrico la obtiene el programa de elementos finitos ANSYS a partir de la conocida ecuación de continuidad de la carga:

donde [σ(T)] es la matriz de conductividad eléctrica, la cual es dependiente de la temperatura (T).

Los elementos diagonales de la matriz de conductividad son iguales, σ_xx = σ_yy = σ_zz, debido a las condiciones de homogeneidad e isotropía que hemos impuesto en el modelo. Conocido el potencial eléctrico, V, el vector intensidad del campo eléctrico, {E}, se calcula mediante la ecuación de la electrostática:

El vector densidad de corriente, {J}, se obtiene por medio de la ley de Ohm:

Similarmente, el programa calcula la distribución de temperatura T(x, y, z) del HAES por medio de la ecuación para la transferencia de calor:

donde es la velocidad de generación de calor por unidad de volumen causada por efecto Joule y K es la matriz de conductividad térmica, definida por:

Nuevamente los elementos diagonales son iguales debido a las condiciones de homogeneidad e isotropía asumidas. También, todo programa de elementos finitos necesita las condiciones de contorno para resolver este conjunto de ecuaciones diferenciales del problema en particular estudiado. Las condiciones de contornos utilizadas para el modelo son las siguientes:

T (x, y, z) = T     (7)

la cual específica la temperatura constante (T=100ºC) sobre las superficies externas de los porta electrodos; y la condición de flujo de calor dada por

en donde h son los coeficientes peliculares sobre las superficies sometidas a flujo de calor por convección, T_S es la temperatura de la superficie y T_∞ es la temperatura del medio en contacto con la superficie. El potencial eléctrico en un contorno está dada por:

V (x, y_p, z) = V    (9)

la cual especifica V=0 voltios en la cara inferior del volumen que representa al acero. El programa también asume en las interfaces las siguientes condiciones por defecto

E_t1 - E_t2 = 0     (10)

J_n1 - J_n2 = 0     (11)

Los subíndices t y n indican respectivamente las componentes tangenciales y normales a las interfaces. La Ecuación (10) garantiza la condición de equilibrio electrostático del campo eléctrico mientras que la (11) garantiza la continuidad de la componente normal de la corriente.

III. DISCUSIÓN DE RESULTADOS

3.1 Simulación de los perfiles térmicos y eléctricos del horno

A continuación se presentan los resultados obtenidos del software para una longitud de arco de 0,25 m. La Figura 5-a muestra el comportamiento del potencial eléctrico en el baño líquido de escoria, en donde se puede apreciar que decae a medida que se aleja de la zona interna del baño hacia la zona externa del mismo. A su vez, se puede observar que el valor de voltaje alcanzado por el arco eléctrico es de aproximadamente 270 V, el cual se puede comparar con el valor teórico para el voltaje del arco V_a , definido por:

donde ,

V_Cat-Ano es la caída de voltaje ánodo-cátodo @ 40V, cosφ representa el factor de potencia.

Para los valores suministrados por la empresa y con el uso de la Ecuación (12) el voltaje de arco teórico es de aproximadamente 271,76 V, difiriendo en apenas un 0,53% con respecto al simulado, lo cual valida el resultado de la simulación eléctrica, e indica que las resistividades eléctricas usadas en los materiales son correctas, propiedades mostradas en la Tabla I.

Igualmente, se puede observar por medio de la Figura5-b el comportamiento del potencial eléctrico en uno de los electrodos. La diferencia de potencial en todo el electrodo es de 5,385 V de acuerdo a la simulación. Para obtener el valor teórico de la caída de potencial eléctrico en el electrodo, primeramente se hace necesario conocer la resistencia del material, la cual se obtiene con la ecuación:

El electrodo tiene una longitud de 4,8 m, un área de 0,282743 m2 y su resistividad promedio 5,0 μΩm; por lo tanto, su resistencia es de 84,882 μΩ. El potencial eléctrico se calcula muy fácilmente con la conocida ley de Ohm para circuitos,

V = I R    (14)

Para una intensidad de corriente de 64 kA y una resistencia de 84,882 μΩ, entonces, el voltaje en el electrodo es 5,43 V, el cual difiere apenas en un 0,82% con respecto al simulado.

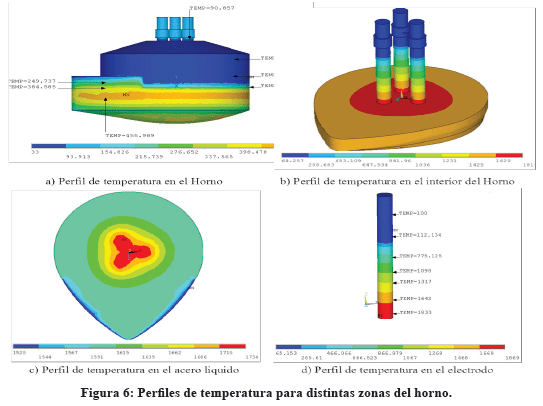
Seguidamente, se presentan los resultados térmicos obtenidos por el software. La Figura 6 muestra cuatro zonas relevantes del horno; la primera (Figura 6-a) es la parte externa de todo el horno; la segunda (Figura 6-b) es la zona interna del horno donde se visualiza el comportamiento térmico que en su mayoría, se produce debido al efecto joule; la tercera zona (Figura 6-c) implica el comportamiento del acero líquido y por último se observa en la Figura 6-d el comportamiento de la temperatura de uno de los electrodos.

La Figura 6-a muestra las mediciones de temperatura arrojadas por la simulación en siete puntos estratégicos del HAES. Estas son comparadas con mediciones reales (realizadas por [15] en el mes de mayo de 2013) para los mismos puntos, mediante un pirómetro y para condiciones estables de operación, justo antes de realizar la colada como se muestra en la Tabla II.

Se logra observar que los valores obtenidos por la simulación se encuentran dentro de lo esperado ya que el porcentaje de error entre el valor simulado y el valor real es menor al 3%.

3.2 Simulaciones termoeléctricas para diferentes longitudes de arco eléctrico

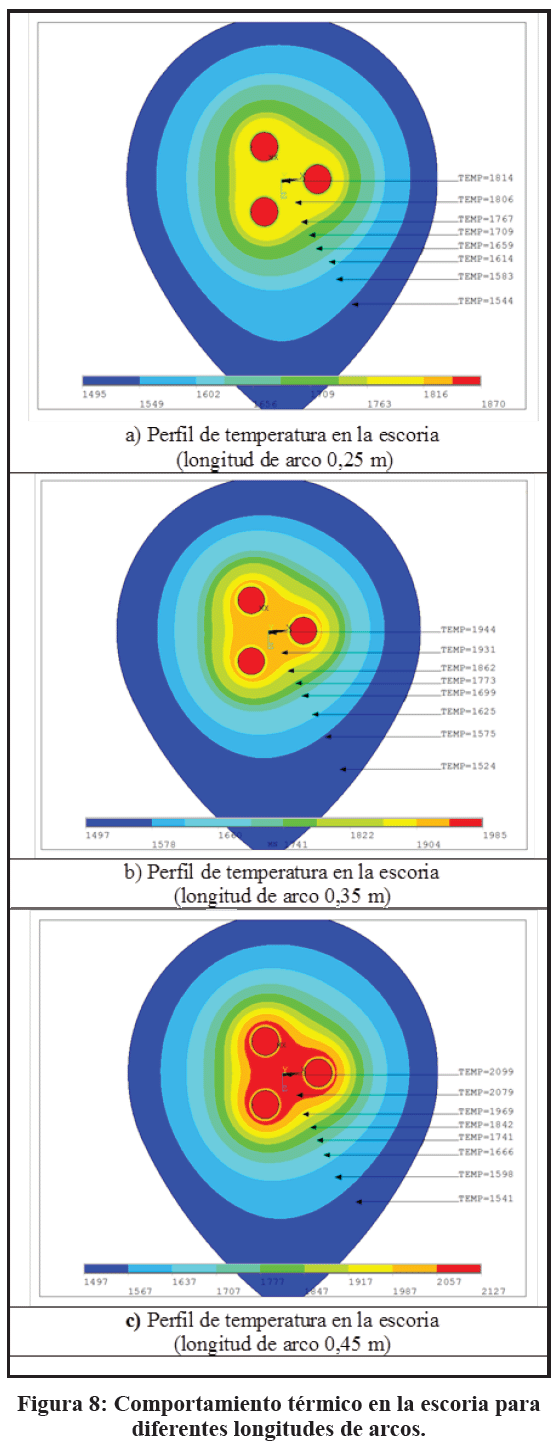
En la Figura 7 se puede apreciar gráficamente como aumenta linealmente el voltaje en el arco eléctrico a medida que se incrementa la longitud de arco. Por otro lado, la Figura 8 muestra los perfiles térmicos para dichas longitudes.

El incremento de la caída del potencial eléctrico con la mayor altura de la longitud del arco implica que la temperatura en la escoria y en el acero líquido aumente debido al efecto joule. Para una longitud de arco de 0,35 m la temperatura máxima, focalizada en el centro de la escoria, aumenta en casi 130°C, con respecto al caso de una longitud de arco de 0,25 m, lo que representa un incremento de 5,51%; y para el caso de 0,45 m, la temperatura aumenta casi 285°C lo que representa un incremento de 15,7%

3.3 Simulaciones para diferentes valores de conductividad térmica de los refractarios

A continuación se muestra en la Figura 9 el resultado obtenido de la simulación para el caso (A) en donde se puede observar el perfil de temperatura a través de la cuba. La temperatura mínima de la simulación para la superficie inferior exterior de la cuba del horno es de aproximadamente 72°C. Para los casos B y C las temperaturas mínimas fueron 50°C y 39°C, respectivamente, en la misma zona mencionada.

Mediante las simulaciones de los tres casos se obtuvo que el gradiente de temperatura a través de la zona refractaria disminuye a medida que va decreciendo su conductividad térmica (K), lo que implica una disminución de las pérdidas de calor a través de la misma.

La Figura 9 muestra el resultado gráfico de las simulaciones para los perfiles de temperatura específicamente en los refractarios de trabajo para los tres casos. Se observa que a medida que disminuye la constante de proporcionalidad (K), la temperatura mínima en los extremos más externos de los refractarios disminuye. Para el caso A dicha temperatura resultó 466°C, para el B 285°C y para el caso C 196°C. En términos porcentuales las disminuciones de temperaturas respecto al caso A equivalen 38,7% y 57,9%.

Los porcentajes de disminución de temperatura son relevantes, ya que implican un ahorro energético debido a las disminuciones de las pérdidas de calor a través del espesor de las paredes de los refractarios de trabajo.

3.3 Cuantificación de las pérdidas de energía del horno durante la fase estable del proceso de aceración.

En la Tabla III se presenta la energía consumida por los refractarios de trabajo al variar la conductividad térmica, en su periodo más estable o de temperatura constante en el metal, obtenidos con las simulaciones térmicas.

En la columna 3 se muestra la transferencia de calor en vatios, que representa la energía calórica que pasaría a través de los refractarios, para los distintos valores de conductividades térmicas, según se muestra en la columna 1. En la columna 5 se indica la energía eléctrica equivalente a la energía calórica de la columna 3 por colada, que corresponde a un tiempo de colada de dos horas. En la columna 6 aparece el consumo de energía por toneladas de acero producido, tomando en cuenta un promedio de 20 coladas diarias aportadas por los 4 hornos. Es importante destacar que la cantidad de energía que se pasa a través de los refractarios de trabajo es apenas el 0,65 por ciento (3,92 KWh/Ton) de la energía eléctrica total (601,63 KWh/Ton) entregada al horno en el caso A. Este porcentaje, es alto respecto al valor de 2,65 KWh/Ton reportado en [10]. Por lo que cambiar la propiedad de la conductividad térmica en el refractario de trabajo a un valor de k=2,5 representaría un ahorro de energía de aproximadamente 2,46 GWh al año para 20 coladas diarias, que equivalen al gasto energético de 140 casas a razón de 1500 kWh mensual. Similarmente, cambiar la propiedad a un valor de k=1,5 implica un ahorro de energía de aproximadamente 3,60 GWh al año.

IV. CONCLUSIONES

Se observó el comportamiento del potencial eléctrico y de temperatura en el horno variando la longitud del arco en 0,25 m, 0,35 m y 0,45 m, lo que determinó que:

• La caída de potencial eléctrico en el arco aumenta linealmente con la longitud del arco debido a que la resistencia eléctrica del baño aumenta con la longitud del arco; lo que implica un incremento de la temperatura en la escoria y el metal debido al incremento de la energía por efecto joule.

• Operar con longitudes de arco superiores a 0,25 m en la etapa más estable de operación implica uso de exceso de energía para producir acero.

Se cuantificaron los ahorros de energías que equivalen a disminuir la conductividad térmica de los refractarios de trabajo desde el valor usado actualmente de 5,1 W/m°K hasta valores inferiores propuestos, obteniéndose lo siguiente:

• hasta K= 2,5, implica un ahorro anual de 2,46 GWh lo que representa un ahorro en el consumo eléctrico de 140 casas, a razón de 1500 kWh mes.

• hasta K= 1.5 se ahorra anualmente 3,60 GWh.

V. REFERENCIAS

1. Magnesita Refractarios. Informe técnico: Proyecto de Reducción de la Energía Eléctrica, Presentado a SIDOR. 2010.         [ Links ]

2. Rodríguez, A. Simulación de la distribución de temperatura producidas por los Hornos de Arco Eléctrico para distintas inclinaciones de los electrodos en un horno de producción de ferromanganeso en FERROVEN. Tutor Académico: Francisco Rojas. Trabajo de grado de Ingeniería Metalúrgica de la de la Universidad Nacional Experimental Politécnica "Antonio José de Sucre", UNEXPO, 2011.         [ Links ]

3. Mc Dougall, I. Finite element modelling of electric currents in AC submerged arc furnaces. XI International Congress of Ferroaloy INFACON. Pretoria, South Africa, 2007.         [ Links ]

4. Arzpeyma, N. Modeling of Electric Arc Furnaces (EAF) with electromagnetic stirring. Master Degree Project School of Industrial Engineering and Management Department of Materials Science and Engineering. Royal Institute of Technology, Stockholm, 2011.         [ Links ]

5. Trejo, E . Simulación de Procesos en Hornos Eléctricos de Arco (HEA). Disponible en http://www.mty.itesm.mx/dia/consorcio/Posters/SimulacionProcesosHornosElectricosArco.pdf. Consultado junio de 2015.         [ Links ]

6. Ansys, Release 8.0, Solid 69, Element Referente, part I.         [ Links ]

7. Sepúlveda, G. Ramírez, M. Espinoza, J. Modelo matemático del efecto térmico generado por quemadores de gas en un horno de arco eléctrico de corriente directa. 2do Foro De Ingeniería E Investigación En Materiales. VOL. 2, 2005, p 265-272.         [ Links ]

8. Melting behavior of simulated DRI in liquid steel. Archives of metallurgy and materials, Volume 53, Issue 2, 2008. Disponible en: http://www.imim.pl/files/archiwum/Vol2_2008/artykuly/Gonzalez.pdf. Consultado junio de 2015.         [ Links ] 

9. Espinoza, J. Ramírez, M. Conejo, A. Mathematical modeling of the melting process in AC electric arc furnaces. 16th IAS Steelmaking Conference, Rosario, Argentina, 2007. p 83-92.         [ Links ]

10. Astigarraga, J. Horno de Arco para fusión de acero. Mcgraw-Hill, Madrid. (1995). p 18, 81, 141.         [ Links ]

11. Daevis, E. J. Conduction and induction heating. Heat engineering, Title II, Series 621.402. Peter Peregrinus Ltd, London, United Kingdom, 1990.         [ Links ]

12. Bezuidenhout, J.J., Eksteen, J.J. and Bradsaw, S.M. Computational fluid dynamic modelling of a three-phase electric smelting furnace        [ Links ]