Kober fractional q-integral operator of the basic analogue of the H-function 

R.K. Saxena¹, R.K. Yadav¹, S.D. Purohit¹ and S.L. Kalla² 

¹Department of Mathematics & Statistics, Jai Narain Vyas University, Jodhpur-342001, INDIA. ²Department of Mathematics and Computer Science, P. O. Box 5969, Safat 13060 KUWAIT. E-mail: kalla@mcs.sci.kuniv.edu.kw; shyamkalla@yahoo.com 

Abstract 

This paper deals with the derivation of the Kober fractional q-integral operator of the basic analogue of the H-function defined by Saxena, Modi and Kalla [Rev. Téc. Ing., Univ. Zulia. 6(1983), 139-143]. Several interesting results involving G_q(.);E_q(.); the basic elementary functions and the basic Bessel functions such as J_v(x; q); Y_v(x; q); K_v(x; q); H_v(x; q), are deduced as the special cases of the main results. 

Key words: Kober fractional q-integral operator, basic integration, basic analogue of Fox’s H-function, basic Bessel functions.

Operador q-integral fraccional Kober de la análoga básica de la función H 

Resumen 

Este trabajo trata de la derivación del operador q-integral fraccional de Kober de la análoga básica de la función H definida por Saxena, Modi y Kalla [Rev. Téc. Ing., Univ. Zulia, 6 (1983), 139-143. Se deducen varios resultados interesantes que involucran G_q (.); E_q (.); las funciones elementales básicas y las funciones de Bessel básicas tales como J_v(x; q); Y_v(x; q); K_v(x; q); H_v(x; q), como casos especiales de los resultados principales. 

Palabras clave: Operador q-integral fraccional Kober, integración básica, análoga básica de la función H de Fox, funciones de Bessel básicas.

Recibido el 23 de Septiembre 2004

En forma revisada el 20 de Junio 2005

1. Introduction 

A basic analogue of the Kober fractional integral operator, as defined by Agarwal [1], is given as:

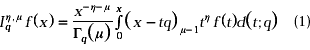
where µ is an arbitrary order of integration with Re(µ)> 0 and h being real or complex. 

Following Agarwal [1] and Al-Salam [2], the basic integration is defined as:

By virtue of the result (2), (1) can be expressed as:

where Re(µ) > 0 and h being real or complex. 

Further, for real or complex a and 0 < |q | < 1, the q-shifted factorial is defined as:

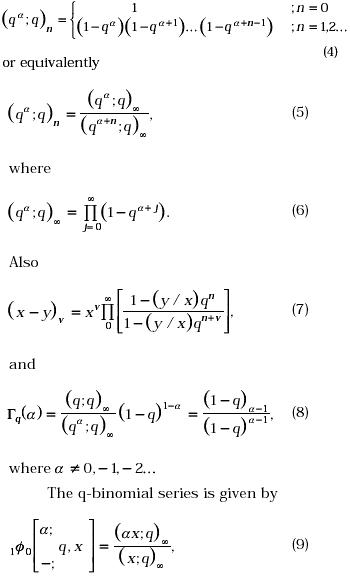
Following Saxena, Modi and Kalla [3], the basic analogue of H-function is defined as:

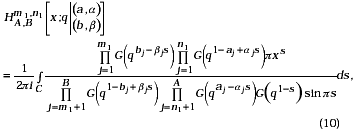
where 0 ≤ m₁ ≤ B, 0 ≤ n₁ ≤ A; a'_i s and b'_j s are all positive integers, the contour C is a line parallel to Re(ws)= 0, with indentations, if necessary, in such a manner that all poles of, G(q^bj-bjs),1≤ j ≤ m₁ are to the right, and those of G(q^1-aj+ajs),1≤ j ≤ n₁, to the left of C. The integral converges if Re[s log(x) - log sin ps] < 0 for large values of |s| on the contour, that is, if |{arg(x) - w₂w₁^-1 log|x|}| < p, where 0 < |q | < 1, log q = -w = -(w₁ + iw₂), w, w₁, w₂ are definite quantities, w₁ and w₂ being real. 

Further, the q-gamma’s used above are given by

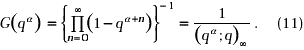
Indeed, it is interesting to observe that 

(q;q)_∞(1-q)^1-aG(q^a) = G_q(a).         (12) 

If we set a_i = b_j = 1,"i and j in equation (10), then it reduces to the basic Meijer’s G-function, namely

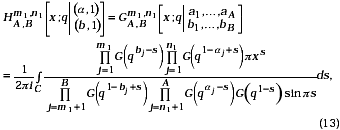
where 0 ≤ m₁ ≤ B, 0 ≤ n₁ ≤ A and Re[s log(x) - log sin ps] < 0. For the shortened notation, the basic analogue of the G-function will be denoted by G_q(.). Further, if we take n₁ = 0; m₁= B in (13), we arrive at the following basic analogue of MacRobert’s E-function

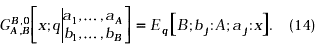
The basic analogues of the Bessel functions J_u(x), Y_u(x), K_u(X), H_u(x); which are expressible in terms of the function G_q(.) cf. Saxena and Kumar [4], are defined as:

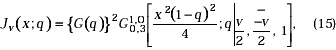
where J_u(x;q) denotes the q-analogue of Bessel function J_u(x).

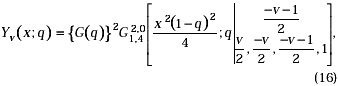
where Y_u(x;q) denotes the q-analogue of the Bessel function Y_u(x).

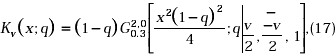
where K_u(X;q) denotes the basic analogue of the Bessel function of the third kind K_u(X).

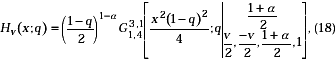
where H_u(x;q) is the basic analogue of the Struve function H_u(x). 

By virtue of the definition (13), the following elementary basic (q-) functions are expressible in terms of the basic analogue of Meijer’s G-function as:

A detailed account of various special functions expressible in terms of Meijer’s G-function [5] or Fox’s H-function can be found in research monographs by Mathai and Saxena [6, 7]. 

The object of this paper is to evaluate Kober fractional basic integral operator of the basic analogue of the H-function and then to deduce certain results involving G_q(.), E_q(.), various basic Bessel and q-elementary functions as applications of the main result. The results obtained in this paper are believed to be a new contribution to the theory of q-fractional calculus and are likely to find certain applications to the solution of the fractional q-integral equations involving various q-hypergeometric functions. In this connection one can refer to the work of Prabhakar and Chakrabarty [8], and Yadav and Purohit [9]. 

2. Main Results 

In this section, we will evaluate the following fractional q-integral operator of Kober type involving basic analogue of the H-function.

Proof: Using (3) and (10) the left hand side of (24) can be expressed as:

On interchanging the order of summation and integration, which is valid under conditions given with (24), we obtain

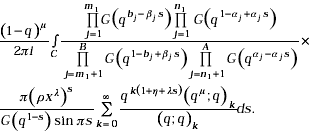
On summing the inner ₁f₀(.) series with the help of equation (9) and then making use of the relation (5), it yields

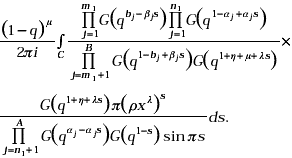
The above expression on being interpreted with the help of (10), yields the right hand side of (24). 

Similarly, we can prove (25). 

3. Applications 

In this section, we will deduce the following eleven results given in tabular form, as applications, of the general result (24). 

The results (26) and (27) follows directly from (24) in view of the definitions (13) and (14) respectively. Where as the results (28)-(31) can be obtained by taking and l = 2 in (24) and make use of the results (15)-(18). Similarly, one can prove the results (32)-(36) by suitably assigning values to the parameters in light of the definitions (19)-(23). It is further interesting to observe that for h= 0, and on employing the relation

one can obtain several special cases, where denotes the Riemann-Liouville fractional q-integral operator, given by

Acknowledgement 

The third author (S. D. Purohit) is grateful to CSIR, Govt. of INDIA, for providing a Junior Research Fellowship No. 9/98(51)2003-EMR-I, to enable him to carry out the present investigations. The authors are also thankful to the referee for his valuable comments and suggestions.

References 

1. Agarwal, R.P.: Certain fractional q-integrals and q-derivatives. Proc. Camb. Phil. Soc. 66 (1969), 365-370.          [ Links ]

2. Al-Salam, W.A.: Some fractional q-integrals and q-derivatives. Proc. Edin. Math. Soc. 15 (1966), 135-140.          [ Links ]

3. Saxena, R.K., Modi, G.C. and Kalla, S.L.: A basic analogue of Fox’s H-function. Rev. Tec. Ing., Univ. Zulia 6 (1983), 139-143.          [ Links ]

4. Saxena, R.K. and Kumar, R.: Recurrence relations for the basic analogue of the H-function. J. Nat. Acad. Math. 8 (1990), 48-54.          [ Links ]

5. Erdélyi, A. and Magnus, W., Oberhettinger, F. and Tricomi, F.G.: Tables of Integral Transforms. Vol-II, McGraw-Hill Book Co. Inc., New York, 1954.          [ Links ]

6. Mathai, A.M. and Saxena, R.K.: Generalized Hypergeometric Functions with Applications in Statistics and Physical Sciences. Lecture Series in Math. No.348, Springer-Verlag, Heidelberg, 1973.          [ Links ]

7. Mathai, A.M. and Saxena, R.K.: The H-function with Applications in Statistics and other Disciplines. John Wiley & Sons. Inc. New York, 1978.          [ Links ]

8. Prabhakar, T.R. and Chakrabarty, M.: A class of basic integral equations with basic hypergeometric function ₁f₁(.) in the kernels. Indian J. Pure. Appl. Math. 7(1976), 1253-1260.          [ Links ]

9. Yadav, R.K. and Purohit, S.D.: Application of Riemann-Liouville fractional q-integral operator to basic hypergeometric functions. Acta Ciencia Indica 30(iii)(2004), 593-600.          [ Links ]

10. Gasper, G. and Rahman, M.: Basic Hypergeometric Series. Cambridge University Press, Cambridge, 1990.        [ Links ]