Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Boletín Técnico
versión impresa ISSN 0376-723X
IMME v.44 n.3 Caracas nov. 2006
Cálculo de la matriz de rigidez por integración analítica de un elemento finito cuadrilátero subparamétrico de ocho nodos
L. Videla1, T. Baloa1, D.V. Griffiths2 y M. Cerrolaza1
1 Instituto de Materiales y Modelos Estructurales, Universidad Central de Venezuela, Apto. Postal 50.361, Caracas 1050-A, Venezuela. (Email: videlal@ucv.ve , baloat@ucv.ve , mcerrola123@cantv.net )
2 Colorado School of Mines, Colorado, USA (Email: d.v.griffiths@mines.edu)
Resumen
En el ejercicio de la ingeniería, el análisis matricial de medios continuos tiene hoy una aplicación más generalizada, como consecuencia del desarrollo computacional, optimizando así los métodos y técnicas utilizadas mediante los Sistemas de Álgebra Computacional (SAC), estos permiten obtener expresiones analíticas en diversas aplicaciones en la Ingeniería así como académicas y en la industria.
Este trabajo presenta la integración analítica aplicada a un elemento cuadrilátero serendipity de 8 nodos y de tipo subparamétrico. El propósito de este trabajo es calcular los términos de la matriz de rigidez para obtener mejoras en los tiempos de cálculo matemáticos en computadora además de aumentar la precisión en los cálculos de la matriz de rigidez para este tipo de elemento.
Para lograr este objetivo se utilizaron programas que utilizan técnicas de matemática simbólica tales como el MAPLE, DERIVE entre otros, estos programas permitieron obtener 6 ecuaciones que calculan todos los términos de la matriz de Rigidez, estas expresiones se manipularon agrupando en constantes los factores de las expresiones de los términos de la matriz de Rigidez, quedando así expresiones algebraicas más sencillas en función de las variables naturales (ε, η). Estas constantes son a su vez función también de las coordenadas cartesianas de los nodos y de los parámetros elásticos del material, módulos de Young y Poisson, esto facilitó la integración analítica para cada término en la matriz, adicionalmente se crearon códigos que permiten calcular todos estos términos utilizando un lenguaje de alto nivel tipo Fortran.
Palabras Claves: Manipulación simbólica en MEF, Integración exacta, Elementos finitos planos de 8 nodos, Matriz de rigidez, Deformación plana.
ANALYTIC INTEGRATION OF THE STIFFNESS MATRIX OF A 8-NODED PLANE CUADRILATERAL SUBPARAMETRIC FINITE ELEMENT
ABSTRACT
Computer Algebra Systems (CAS) are powerful tools to obtain analytical expressions for many engineering applications in both academic and industrial environments.
The explicit (analytical) for of the stiffness matrix of an 8-noded plane-elasticity finite element is obtained and described in this paper. Six basic formulas to generate the stiffness terms were obtained by using MAPLEã. The formulas are function of the cartesian coordinates of the element, as well as a function of the elastic parameters.
Once the formulas were obtained, some algebraic manipulation were done in order to optimize the analytical expressions. The reduction in CPU time by using analytical integration instead of classical Gaussian-numerical integration was very promising, leading to over 50% saving in CPU time. Also, as expected, analytical integration leads to a more accurate results than numerical integration does.
A sensitive analysis was done, showing that analytical integration is useful even in the case of very distorted finite elements.
Key Words: exact integration, symbolic FEM manipulation, stiffness matrix, 8-node element, plane strain
Recibido: 24/05/05 Revisado: 03/10/05 Aceptado: 30/08/06
1. ANTECEDENTES
El resolver problemas en los medios continuos resulta laborioso, tomando el dominio de estudio como un continuo, por esta razón se utilizan técnicas numéricas que discretizan el mismo. Una de estas técnicas es el Método de los Elementos Finitos (M.E.F.) que permite resolver de una manera eficiente y rápida estos problemas. La aproximación utilizada por este método se hace con el diseño de una malla de elementos finitos en la cual se concentra la masa del continuo en unos puntos denominados nodos. La calidad de la respuesta con este método depende en gran medida de la cantidad de elementos finitos que se consideren en la malla a estudiar. Como consecuencia de esto se hace necesario obtener resultados precisos y rápidos. La respuesta en la actualidad ante este problema es la integración numérica (Cuadratura de Gauss) la misma genera errores de precisión al trabajar con elementos finitos muy distorsionados en su geometría. Un ejemplo son los elementos poseen ángulos internos superiores a 120º
En los últimos 20 años los avances computacionales han posibilitado el trabajo de los investigadores en obtener soluciones semi-analíticas y/o analíticas, utilizando generalmente sistemas de álgebra computacional (SAC), tales como: REDUCE, DERIVE, MATHCAD, MATHEMATICA, MACSYMA, MAPLE, entre otros. Los sistemas mencionados tienen en mayor o menor grado posibilidades de manipular grandes y complicadas expresiones matemáticas tales como ecuaciones integro-diferenciales en forma simbólica.
Utilizando la manipulación simbólica se ha logrado obtener grandes avances en la mecánica de análisis de medios continuos. Los lectores de este trabajo pueden referirse a los trabajos de Korncoff(1977), Korncoff and Fenves (1979), Noor and Andersen (1979), Jensen and Niordson (1977), entre otros trabajos.
En aplicaciones de análisis dinámico no lineal, específicamente en placas y conchas estas requieren de mucho tiempo computacional, debido a los numerosos cálculos de matrices de rigidez en forma recursiva, las cuales involucran grandes cantidades de cálculos con integrales. Entre los más destacados investigadores en este campo están Zienkiewicz et al (1971), quien presentó una integración semi-analítica para placas y conchas, reportando en su trabajo una disminución del 50% de tiempo computacional, frente a la integración numérica utilizada en esta clase de problemas. Rengarajan et al (1995), presenta una integración analítica con elementos finitos híbridos para análisis de conchas. En este trabajo no se reporta comparaciones de tiempo de cálculo entre integración numérica y analítica, pero el trabajo con elementos finitos híbridos permite eliminar la aparición de la matriz de transformación de coordenadas (Jacobiano) del denominador de las integrales. Esto no se puede evitar en elementos finitos formulados bajo el método de los desplazamientos el cual es el más ampliamente utilizado. Vlachoutsis (1990), propone la integración analítica para elementos de conchas degeneradas con espesor considerable, el mismo logra descomponer la matriz del Jacobiano en dos términos que representan al comportamiento de las variables en la superficie media de la concha, pero deja de considerar los efectos en la superficie fuera de la superficie media de la concha, este trabajo reporta mejoras de 9% de velocidad de cálculo entre la integración numérica y la integración analítica, adicionalmente reporta que se pierde precisión con la integración analítica al compararla con la integración numérica, ya que esta última considera efectos adicionales necesarios en el análisis de concha.
En el trabajo de Yagawa et al (1990) se discute combinar técnicas de manipulación simbólica para lograr mejoras en los tiempos computacionales de la integración numérica aplicado en elasticidad plana. Este trabajo reporta mejoras en los tiempos de cálculo de 15% en matrices de rigidez. Bardel (1989) trabaja con elementos finitos P-Adaptables, utilizando polinomios con exponentes de alto grado para las funciones de forma típicas para estos elementos finitos el mismo reporto mejoras en los tiempos de cálculo. Mizukami (1986) muestra fórmulas de integración analítica para elementos finitos rectangulares planos de cuatro nodos isoparamétricos y no muestra comparaciones de tiempo entre integración analítica y integración numérica. Kikuchi (1989) utiliza el programa REDUCE para obtener expresiones analíticas de elementos finitos isoparamétricos de cuatro nodos, obteniendo buenas precisiones para elementos distorsionados pero no muestra mejoras en los tiempos de cálculo entre integración numérica e integración analítica, sin embargo el autor justifica que los bajos tiempos de cálculo obtenidos por el REDUCE se deben a que el programa no genera códigos optimizados para programar las operaciones de cálculo computacional. Rathod (1988) presenta fórmulas de integración analítica para elementos finitos de cuatro nodos isoparamétricos. Las mismas fueron obtenidas por métodos de integración básicos.
El trabajo de Griffiths (1994) presenta una metodología general, basada en transformaciones de coordenadas, utilizando relaciones entre los grados de libertad de los nodos del elemento finito obteniendo expresiones semi-analíticas para el cálculo de la matriz de rigidez en un elemento finito plano de cuatro nodos isoparamétrico. La metodología desarrollada por el autor se basa en obtener expresiones semi-analíticas de los términos de la matriz de rigidez, utilizando para ello integración numérica (cuadratura de Gauss-Legendre), logrando así obtener una expresión que genere todos los términos de la matriz de rigidez, el mismo reporta mejoras en los tiempos de cálculo entre la integración numérica e integración semi-analítica. Se recomienda revisar el trabajo donde se discuten y presentan este tipo de integrales (Griffiths 2002). Videla et al (1996) presenta unas fórmulas analíticas de integración para los términos de la matriz de rigidez de un elemento finito plano de cuatro nodos isoparamétrico, reportando mejoras de un 50% en los tiempos de cálculo al comparar la integración numérica con la integración analítica, además de mejorar la precisión en el cálculo de elementos distorsionados. El autor utilizó el programa DERIVE-1989 para obtener las expresiones analíticas de la matriz de rigidez. Las expresiones obtenidas se optimizaron para no realizar cálculos innecesarios en el proceso. Esta metodología obtenida es totalmente analítica diferente a la propuesta por Griffiths (1994). En el trabajo de Lozada et al (2004), presentan fórmulas semi-analítica para obtener los términos de la matriz de rigidez de un elemento finito de ocho nodos superparamétrico, las mismas fueron derivadas de las fórmulas obtenidas por Griffiths (1994) para un elemento finito de cuatro nodos isoparamétrico, obteniendo mejoras de 37% en los tiempos de cálculo al comparar la integración numérica con las fórmulas obtenidas por integración numérica optimizada (semi-analítica).
La respuesta en la actualidad a los problemas de precisión presentados por la integración numérica, utilizada ampliamente en la solución de las ecuaciones integro – diferenciales propias de los métodos numéricos actuales, tales como el Método de Elementos Finitos (MEF) y el Método de Elementos de Contorno (MEC), entre otros son las metodologías analíticas, las cuales pueden ser el futuro, estas técnicas pueden superar sustancialmente en tiempos de cálculo a las metodologías numéricas, además de aumentar la precisión de los cálculos ante elementos muy distorsionados que pueden aparecer por deficiencias en los generadores de malla, se entiende que la solución no es totalmente exacta debido a la discretización de los medios continuos, pero es la mejor aproximación que se puede obtener en el campo de los métodos numéricos.
Este trabajo presenta una metodología general totalmente analítica, aplicable a cualquier tipo de elemento finito e inclusive a cualquier método numérico.
2. FORMULACIÓN E IMPLEMENTACIÓN
Este trabajo presenta el cálculo de la matriz de rigidez por integración analítica de un elemento finito cuadrilátero serendipity de 8 nodos de convergencia subparamétrica, el cual será calculado bajo tensión plana. Este elemento se define con un sistema de coordenadas cartesiana (X,Y) y dos coeficientes que definen sus propiedades elásticas coeficiente de Young (E) y el coeficiente de Poisson (n).
En el proceso de implementación de ésta formulación general, se toma un elemento finito cuadrilátero de 8 nodos con dos grados de libertad por nodo, numerados en sentido anti horario, promediando las coordenadas de los nodos esquina del sistema cartesiano para obtener las coordenadas de los nodos medios del elemento. El estudio con esta clase de elemento finito se justifica, ya que la mayoría de los generadores de malla comerciales producen elementos finitos de lados rectos.

Figura 1. - Elemento general cuadrilátero de 8 nodos
En este trabajo se obtiene una fórmula general que permite calcular los términos de la matriz de rigidez (K) del elemento cuadrilátero mencionado.
Para obtener la fórmula general, se utilizan sistemas de álgebra computacional (SAC), tales como MAPLE y DERIVE, facilitando la obtención por integración analítica de las expresiones que la generan.
En los medios continuos, se utiliza el método de elementos finitos (M.E.F.) para calcular la matriz de rigidez, el cual se basa en el método de los desplazamientos. Esta formulación necesita transformar el elemento finito general definido en el plano Euclidiano (X,Y) a otro normalizado en un plano Gaussiano adimensional (e,h), relacionando ambos planos con una transformación Jacobiana (J).
Las expresiones que se generan con los sistemas de álgebra computacional (SAC) permiten obtener los términos de la matriz de rigidez en el plano adimensional (e,h). Las mismas se agrupan en constantes que a su vez son función también de las coordenadas cartesianas y parámetros elásticos del elemento. Con estas constantes agrupadas, se construyen 6 ecuaciones características que son función de las variables naturales (e,h). Las mismas se integran respecto a éstas variables, las cuales permiten calcular los términos de la matriz de rigidez del elemento finito. Se debe resaltar que éstas 6 ecuaciones características se simplifican en una ecuación general.
Los sistemas de álgebra computacional permiten generar líneas de código en lenguajes de alto nivel, tales como, Fortran, C, Pascal entre otros. Estos lenguajes de programación ayudan a desarrollar rutinas que permiten representar la matriz de rigidez en forma ordenada, comparando la precisión y tiempos de cálculo entre la matriz de rigidez generada por integración analítica contra la matriz de rigidez generada por integración numérica. En el trabajo se presentan códigos desarrollados en el lenguaje de programación Fortran.
Los códigos desarrollados permiten comparar la dispersión de los resultados de los términos de las matrices de rigidez obtenidas por integración numérica (cuadratura de Gauss-Legendre 2 puntos y 3 puntos) con la obtenida por integración analítica, además de comparar los tiempos de cálculo entre las mismas.
Al ubicarse en el plano adimensional (e,h) y tomando la formulación del método de elementos finitos, es necesario utilizar funciones de forma, las cuales definen la geometría y los campos de desplazamientos. Estas son función de las coordenadas adimensionales del elemento, una propiedad fundamental de estas funciones es la de tomar el valor "1" en el nodo en estudio y "0" en los demás nodos. En este trabajo se consideran funciones de forma del tipo Serendípity para un elemento finito de 8 nodos, (1).
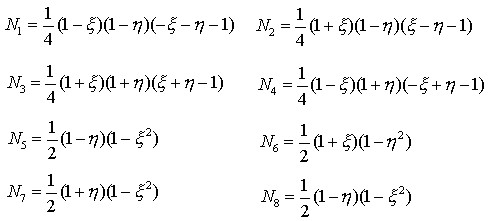 (1)
(1)
Con las funciones de forma presentadas en (1), se procede a la obtención de la regla de correspondencia que relaciona el plano cartesiano, (XY), con el plano adimensional (e,h) en forma biunívoca.
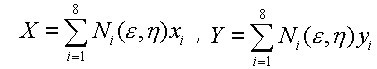 (2)
(2)
Las coordenadas X e Y corresponden a la multiplicación de las funciones de forma por las coordenadas de los nodos ![]() e
e ![]() .
.
Con las expresiones (1) y (2), quedan establecidas las transformaciones de coordenadas y las funciones de forma, además al utilizar la derivación en cadena con respecto a las variables e,h, permite relacionar las funciones de forma con el plano euclidiano:
 (3)
(3)
En forma matricial:
 (4)
(4)
Donde J es la matriz de transformación de las coordenadas cartesianas a las naturales o simplemente el Jacobiano. La matriz del Jacobiano es la que relaciona de manera biunívoca el plano euclidiano con el plano Gaussiano:
 (5)
(5)
Despejando de (4) las derivadas de las funciones de forma en función de las coordenadas cartesianas, genera la matriz de transformación deformación – desplazamiento,(B):
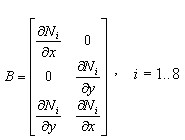 (6)
(6)
Se debe considerar la matriz que representa las propiedades elásticas del material, D que contiene parámetros elásticos, coeficiente de Young (E) y coeficiente de Poisson (n).
 (7)
(7)
La multiplicación de las matrices (6) y (7) de la siguiente manera permiten obtener la matriz de rigidez, K:
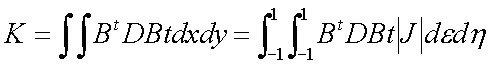 (8)
(8)
Siendo t el parámetro que representa el espesor del elemento, permaneciendo constante en el cálculo.
Por la interacción entre los nodos i y j, considerando 2 grados de libertad, (2 GDL), por nodo, se genera una submatriz de rigidez típica. Esta submatriz de rigidez típica contiene el resultado de las integrales de los productos de las derivadas parciales divididas entre el determinante del Jacobiano de la transformación (9).
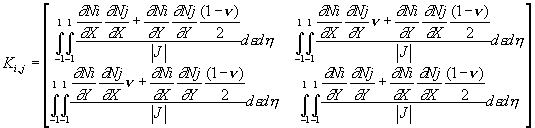 (9)
(9)
Para obtener, los términos de la submatriz de rigidez se generaron procedimientos automatizados en MAPLE 8.0 que permiten obtener las expresiones de cada término que se generan por la interacción entre los nodos del elemento finito, estas expresiones se agrupan en constantes que contienen las coordenadas cartesianas y parámetros elásticos del elemento. Con estas constantes agrupadas se construyen 6 ecuaciones características que son función de las variables naturales e,h, (Figura 2) y dividiendo las mismas entre el determinante del Jacobiano de la transformación, encontrando así las 6 ecuaciones características típicas.
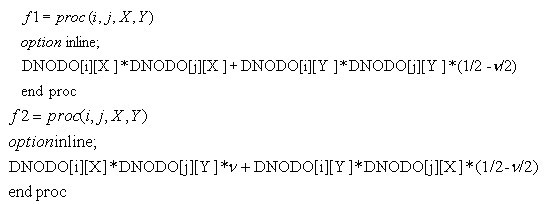
Figura 2. Procedimientos que generan las expresiones del numerador de los términos de la submatriz
Por inspección de los procedimientos f1 y f2 se deduce que al aplicar f2(i,j,X,Y) y f1(i,j,X,Y) se obtienen las expresiones de los cuadrantes del sistema cartesiano I y II respectivamente y para obtener los cuadrantes III y IV se invierten las coordenadas cartesianas de (i,j,X,Y) por (i,j,Y,X), dejando constantes i,j que son los nodos en estudio de la submatriz para determinar los términos.
Ejemplo: Se quiere determinar las expresiones de los términos K1,9, K5,8, Tabla 1.
El término K1,9 corresponde a la interacción del nodo 1 con el nodo 5, situado en el II cuadrante de la submatriz. Para el término K5,8 los nodos que interactúan son el nodo 3 con nodo 4 cambiando los cuadrantes con respecto a los nodos anteriores.
Tabla 1. Ejemplo de obtención de los términos de la matriz de rigidez
| Términos | Función utilizada | Ecuación asociada |
| K1,9 | f1(1,5,X,Y) | 3 |
| K5,8 | f2(3,4,Y,X) | 1 |
A continuación se muestran unas constantes típicas que se obtienen con el uso del programa MAPLE 8.0 al utilizar los procedimientos f1 y f2.

Las constantes mostradas son las típicas generadas de un grupo de 22 de ellas para cada ecuación de las 6 encontradas, se usa el índice (i) para identificar a cual de las 6 ecuaciones características pertenecen dichas constantes.
A continuación se presentan las 6 ecuaciones características encontradas en este trabajo, así como los términos de la matriz de rigidez que generan después de dividir dichas ecuaciones entre el determinante del Jacobiano, (jacob) e integrarlas respecto a las variables naturales (e,h)
Ecua1.-Interacción entre nodos esquinas usando el índice (j) como el que determina los 36 términos de la matriz de rigidez para ésta ecuación.
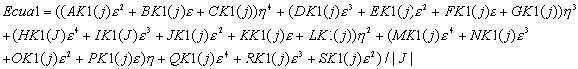
Términos que genera la ecuación 1

Ecua2.-Interacción de nodos esquinas con nodos medios pares, usando el índice (j) como el que determina los 32 términos de la matriz de rigidez para ésta ecuación.
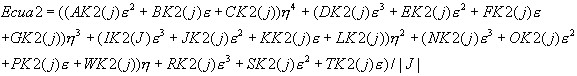
Términos que determina la ecuación 2
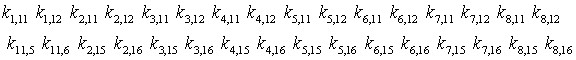
Ecuac3.-Interacción de nodos esquinas con nodos medios impares, usando el índice (j) como el que determina los 32 términos de la matriz de rigidez para ésta ecuación.

Términos que determina la ecuación 3
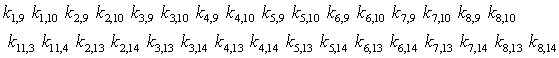
Ecuac4.-Interacción de nodos medios pares, usando el índice (j) como el que determina los 10 términos de la matriz de rigidez para ésta ecuación.
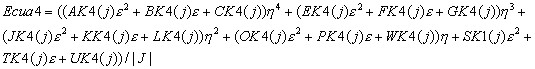
Términos que determina la ecuación 4
![]()
Ecuac5.-Interacción de nodos medios impares, usando el índice (j) como el que determina los 10 términos de la matriz de rigidez para ésta ecuación.
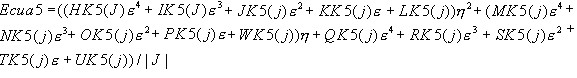
10 términos de la matriz de rigidez para ésta ecuación.
Términos que determina la ecuación 5
![]()
Ecuac6.- Interacción de nodos medios consecutivos, usando el índice (j) como el que determina los 16 términos de la matriz de rigidez para ésta ecuación.
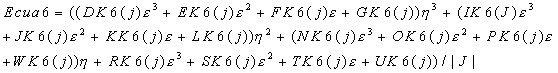
Términos que determina la ecuación 6
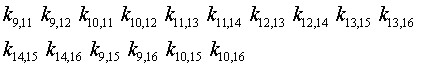
Las 6 ecuaciones características que se formularon generan los 136 términos de la matriz de rigidez, el encontrar cada una de ellas depende del término de la matriz que se quiere encontrar, figura 3.
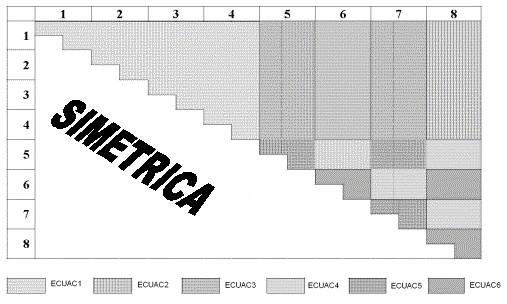
Figura 3. Términos de rigidez calculados en cada ecuación
Las 6 ecuaciones presentadas se simplifican en una sola ecuación característica general, ésta ecuación general serán función de los índices (i) y (j), del determinante del Jacobiano,(jacob), de las variables naturales (e,h) y de las coordenadas cartesianas del elemento,![]() .
.
Donde,
![]() (10)
(10)

Esta ecuación general al integrarla respecto a las variables naturales (e,h) permite calcular todos los términos de la matriz de rigidez K, ésta matriz es función de los índices (i) y (j), del determinante del Jacobiano, (jacob) y de las coordenadas cartesianas del elemento, ![]() :
:
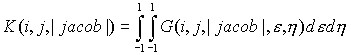 (11)
(11)
A continuación se presenta una fracción del resultado de la matriz de rigidez, K, después de integrar.
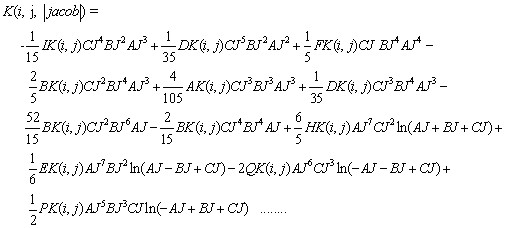
Con las constantes obtenidas para cada ecuación y la ecuación general integrada se desarrollaron unas rutinas programadas en Fortran a las cuales se les sometió a un proceso de optimización, tales como calcular el menor número de veces los logaritmos neperianos y constantes del Jacobiano de grado mayor que uno que aparecen en la pequeña fracción del resultado integrado de la matriz de rigidez, K, logrando reducir el tiempo de cálculo además se optimizaron las líneas de código entre otras optimizaciones que se aplicaron al código.
Durante el proceso de evaluación del tiempo de cálculo con la ecuación general integrada se encontró que el mismo era superior al calculado con las 6 ecuaciones características por separado.
3. PRECISIÓN DE LOS CÁLCULOS Y TIEMPOS
La precisión de los cálculos se medirán en dos formas, una de ellas es usar diferentes puntos de Gauss, (2x2) y (3x3) para la integración numérica, la otra forma es variar la relación de aspecto de los elementos finitos utilizados, hasta obtener elementos muy distorsionados. Por otra parte se compara el tiempo de cálculo computacional simulando diferentes cantidades de elementos finitos.
El porcentaje de error entre la integración analítica y la integración numérica se calcula utilizando la siguiente expresión:

Donde, K_ANAL(ter), es la matriz de rigidez analítica y K_NUM(ter), es la matriz de rigidez numérica, representando el índice (ter) a cada uno de los términos de la matriz de rigidez analítica y numérica.
En la Figura 4 se presenta el modelo de elemento finito a distorsionar, en el cual se varía la relación de aspecto del mismo y en la Tabla 2, se presentan los porcentajes de error entre la matriz de rigidez analítica y la matriz de rigidez numérica, variando la cantidad de puntos de integración, (Cuadratura de Gauss).

Figura 4. Relación de aspecto de un elemento finito cuadrilátero
Tabla 2. Porcentajes de error variando la geometría y los puntos de integración
| Relación de aspecto | 2 Ptos de Gauss | 3 Ptos de Gauss |
|
|
0.53815 | 0.01355 |
|
|
0.87933 | 0.35082 |
|
|
16.12255 | 7.99999 |
En la Tabla 3, se comparan los tiempos de cálculo entre la integración analítica contra la integración numérica variando la cantidad de elementos finitos considerados.
Los tiempos de cálculo computacional se calculan en un mismo computador. Se deduce que en computadores más veloces los tiempos serán menores, pero los porcentajes de ganancia serán los mismos.
Tabla 3. Comparaciones de tiempo entre las matrices numérica y analítica
| Elementos | Numérica (seg) | Analítica (seg) | Tanal / Tnum |
| 1000 | 0.0600 | 0.0310 | 0.5166 |
| 10000 | 0.5808 | 0.2900 | 0.4993 |
| 100000 | 5.7182 | 2.8840 | 0.5043 |
| 1000000 | 56.4111 | 28.1310 | 0.4986 |
En la Tabla 4, se comparan los desplazamientos de dos ejemplos de control calculados con elementos finitos de 8 nodos subparamétrico por integración analítica contra elementos finitos del mismo tipo pero por integración numérica y adicionalmente se comparan con las formulas teóricas usadas en cálculo estructural.
Los dos ejemplos corresponden a una viga en voladizo, sometida a tracción pura  y fuerza de corte
y fuerza de corte 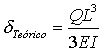 ,
,![]() , E=1000 (kg/cm2), υ=0.0, Figura 5.
, E=1000 (kg/cm2), υ=0.0, Figura 5.

Figura 5. Ejemplos de vigas en tracción pura y en corte
Tabla 4. Comparaciones de desplazamientos
|
|
|
|
|
|
Corte | 1.2552 | 1.0489 | 1.0000 |
| Axial | 0.9976 | 0.9976 | 1.0000 |
En la Figura 6 se presenta una presa de gravedad con carga lateral, discretizada con 72 elementos y 253 nodos y en la Figura 7 se presenta una cuarta parte de una placa simétrica con un hueco central, la cual fue discretizada con 80 elementos y 277 nodos. En ambos casos se toman elementos finitos subparamétricos de 8 nodos.
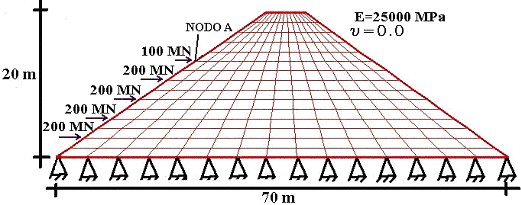
Figura 6. Presa de gravedad modelada con 248 Nodos y 72 Elementos

Figura 7. Placa simétrica con un cuarto de orificio elíptico, modelada con 277 Nodos y 80 Elementos
En la Tabla 5, se presentan los dos ejemplos que comparan los desplazamientos máximos en x e y, además de los esfuerzos en la dirección de X y Y, (σx y σy ). En dicha tabla se comparan los resultados obtenidos con la solución analítica y los obtenidos con la solución numérica de 2, 3, 4 puntos de Gauss, (Integración Numérica). Los parámetros seleccionados se harán en un mismo nodo y un mismo elemento del modelo.
Tabla 5. Comparaciones de desplazamientos en un mismo nodo del modelo y comparaciones de esfuerzos en un mismo punto de tensión y en un mismo elemento del modelo
|
|
| 2° Orden | 3° Orde | 4° Orden | |||
|
|
| Numérica | Analítica | Numérica | Analítica | Numérica | Analítica |
| Presa de Gravedad | |||||||
| Desplazamiento en el nodo A | u | 0.126E-3 | 0.121E-3 | 0.121E-3 | 0.121E-3 | 0.121E-3 | 0.121E-3 |
| v | 0.276E-4 | 0.285E-4 | 0.285E-4 | 0.287E-4 | 0.285E-4 | 0.285E-4 | |
| Esfuerzo | σx | -0.137E+1 | -0.124E+1 | -0.257E+1 | -0.222E+1 | -0.274E+1 | -0.274E+1 |
| σy | 0.174E+1 | 0.196E+1 | 0.191E+1 | 0.211E+1 | 0.219E+1 | 0.219E+1 | |
| Placa con hueco central | |||||||
| Desplazamiento en el nodo B | X | 0.320E-1 | 0.308E-1 | 0.304E-1 | 0.308E-1 | 0.304E-1 | 0.308E-1 |
| Y | -0.786E-2 | -0.805E-2 | -0.804E-2 | -0.805E-2 | -0.804E-2 | -0.805E-2 | |
| Esfuerzo | σx | 0.194E+4 | 0.190E+4 | 0.290E+4 | 0.293E+4 | 0.341E+4 | 0.345E+4 |
| σy | -0.546E+3 | -0.469E+3 | -0.531E+3 | -0.589E+3 | -0.579E+3 | -0.644E+3 | |
4. Conclusiones
- Se obtuvo una ecuación general que permite calcular la totalidad de los términos de la matriz de rigidez de un elemento finito cuadrilátero subparamétrico de 8 nodos, (straight sides ).
- Se generó una rutina que calcula la matriz de rigidez del elemento finito estudiado por integración analítica, ésta fue codificada en el lenguaje de alto nivel tipo fortran.
- Se demostró que la integración analítica de los términos de la matriz de rigidez proporciona mejoras en tiempos de cálculo, siendo estos tiempos hasta de un 50% inferior a los calculados por integración numérica de los términos de la matriz de rigidez.
- Los términos de la matriz de rigidez por integración analítica aumentan la precisión con respecto al cálculo de los términos de la matriz de rigidez por integración numérica.
- Se comprobó que la obtención de los términos de la matriz de rigidez en forma analítica es laborioso y además se obtienen expresiones de gran tamaño las cuales son de difícil manejo al codificarlas en fortran.
- Se encontró que las expresiones analíticas presentan dificultades al compilarse en fortran y que depende exclusivamente de la versión del compilador, siendo de esta manera la versión de compaq fortran v 6.5 la utilizada en este trabajo.
5. LINEAS FUTURAS
▪ Buscar relaciones entre las constantes de los resultados integrados para así reducir tiempos de cálculo en el CPU.
▪ Aplicar la metodología generada para obtener matrices de rigidez por integración analítica a cualquier tipo de elemento finito, (Planos o Espaciales).
6. REFERENCIAS
1. Andersen C.M. and Noor A.K. A computerized symbolic integration technique for development of triangular and quadrilateral composite shallow shell finite element, Rep.NASA TN D-8067, 1975. [ Links ]
2. Bardel N.S. The application of symbolic to computing to the hierarchical finite element method, Int. J. Num. Meth. Eng., 28, 1181 – 1204 (1989). [ Links ]
3. Griffiths D.V. Stiffness Matrix of the Four-Node Quadrilateral Element in Closed Form, International Journal for Numerical Methods in Engineering, Vol 37, 1027-1038, 1994. [ Links ]
4. Griffiths D.V. and Smith I. Programming the finite element method, Wiley, 2002. [ Links ]
5. Jensen J. and Niordson F. Symbolic and algebraic manipulation languages and their application in mechanics, in Perrone & Pilkeg (Eds.),Structural Mechanics Software Series,Univ. Press of Virginia, Charlottesville,1977. [ Links ]
6. Kikuchi M. Application of the symbolic mathematics system to the finite element program, Comput. Mech., 5, 41 – 47 (1989). [ Links ]
7. Korncoff A. R and Fenves S. J. Symbolic generation generation of finite element stiffness matrices, Comput. & Struct., 10,119-124 (1979). [ Links ]
8. Korncoff A.R. Finite element stiffness matrix generation via symbolic manipulation, in C.Wellford (Ed), Proc. Symposium on Application of Comp.Meth. in Eng., Vol.II, 1977, pp.779-785. [ Links ]
9. Lozada I.J, Osorio J.C, Griffiths D.V, Cerrolaza M. Stiffness Matrix Semi-Analytical Integration Of An 8-Noded Plane Elasticity Finite-Element By Using Symbolic Computation, J of Numerical Method in partial differential equation,(accepted, 2004). [ Links ]
10. Mizukami A. Some integration formulas for a four-noded isoparametric element, Comput. Methods Appl. Mech. Eng., 59, 111-121 (1986). [ Links ]
11. Noor A.K. and Andersen C.M. Computerized symbolic manipulation in structural mechanics: Progress and Potential, Comput. & Struct., 10, 95-118 (1979). [ Links ]
12. Rathod H.D. Some analytical integration formulae for a four node isoparametric element, Comput. & Struct., 30(5):1101-1109, 1988. [ Links ]
13. Rengarajan G, Knight N. and Aminpour M. Comparison of symbolic and numerical integration methods for an assumed-stress hybrid shell element, Comm. Num. Meth. Eng.,11,307-316 (1995). [ Links ]
14. Videla L, Ochoa R, Cerrolaza M. Explicit Integration of the Stiffnes Matrix of a Four-Noded-Plane Elasticity Finite Element. Communications In Numerical Methods In Engineering. Vol. 12,731-743,1996. [ Links ]
15. Vlachoutsis S. Explicit integration for three-dimensional degenerate shell finite element, Int. J. Num. Meth. Eng., 29,861-880(1990). [ Links ]
16. Yagawa G, Ye G.W. and Yoshimura S. A numerical integration scheme for finite element method based on symbolic manipulation, Int. J. Num. Meth. Eng., 29,1539-1549 (1990). [ Links ]
17. Zienkiewicz W.C., Taylor R.L. and Too J.M. Reduced integration technique in general analysis of plates and shells, Int. J. Num. Meth. Eng., 3, 275-290 (1971). [ Links ]
















