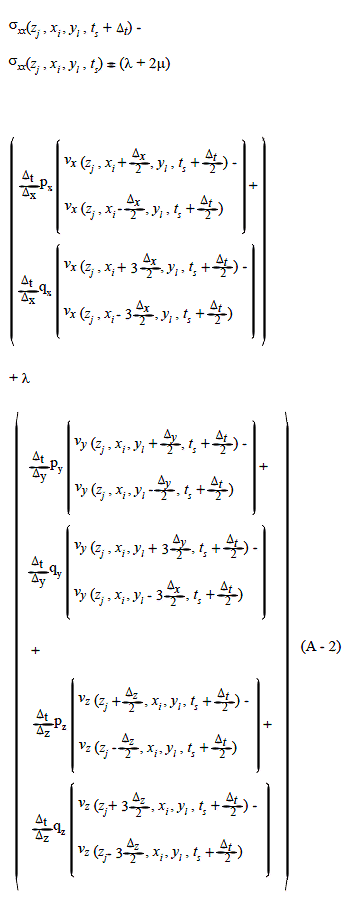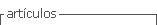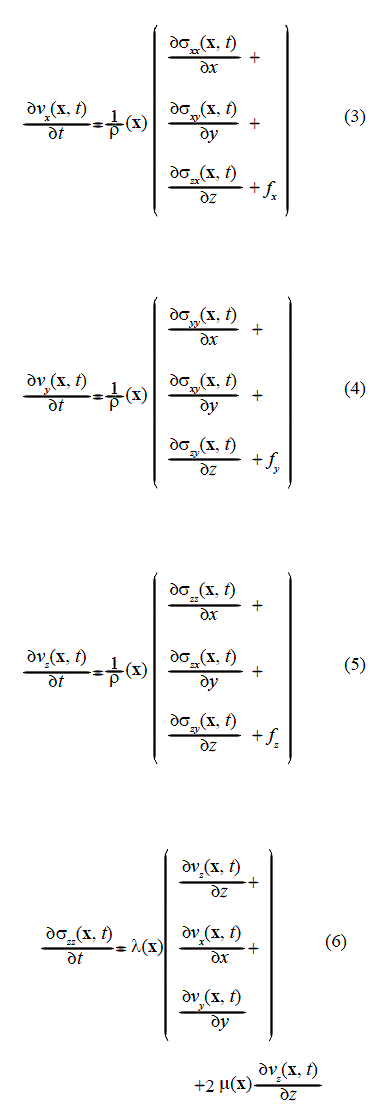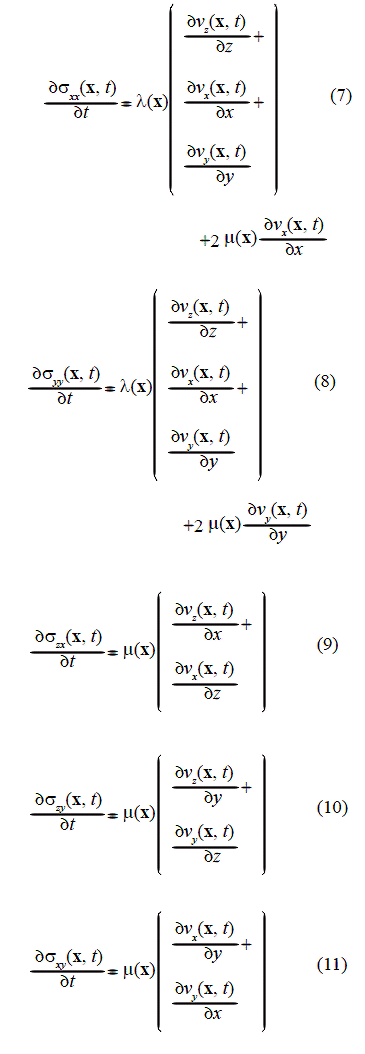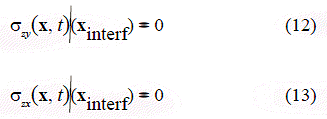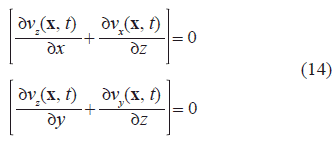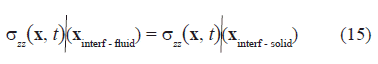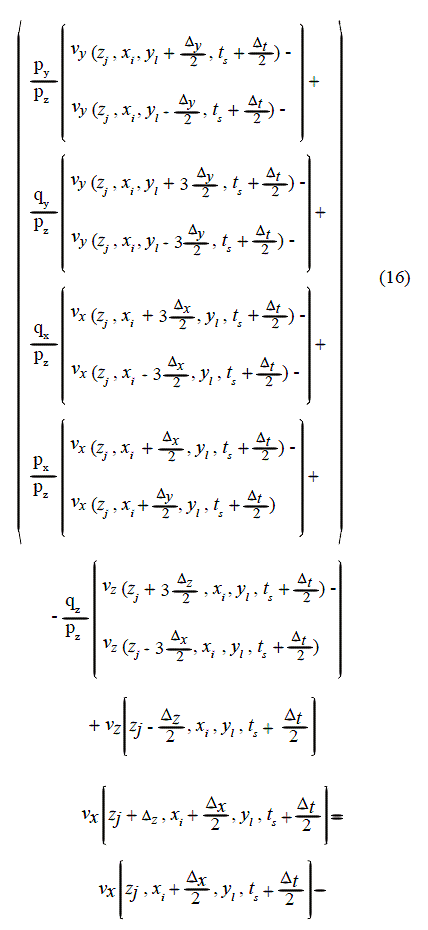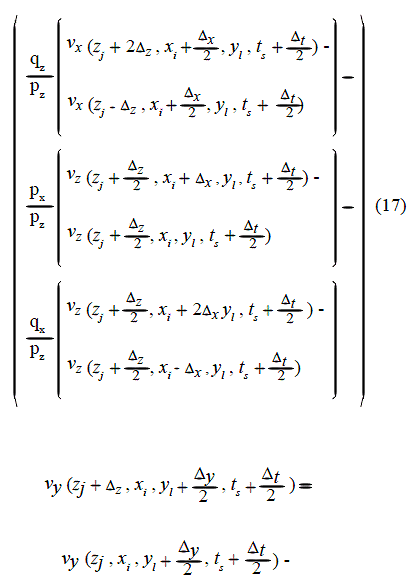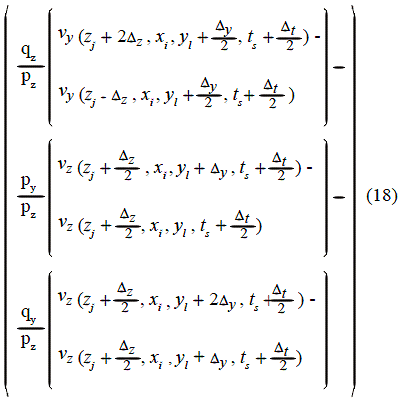Three strategies to solve the wave propagation problem in a 3d fluid-solid interface

Xiomara Contreras¹, Milagrosa Aldana²

¹ Universidad Simón Bolívar. Departamento de Computación y TI. Apartado Postal 89000. Caracas, Venezuela e-mail: xiomara@ldc.usb.ve 

² Universidad Simón Bolívar. Departamento de Ciencias de la Tierra. Apdo. 89000. Caracas, Venezuela e-mail: maldana@usb.ve

ABSTRACT

Two implicit strategies and an explicit approach have been used to solve the problem of a fluid-solid interface in a 3D medium. One of the implicit strategies considers a transitional zone and the other is the traditional one. To solve the boundary conditions at the interface using the explicit strategy, two planes of “fictitious points” were added to the grid. A predictorcorrector approach was considered in this case. A Finite Difference Staggered-Grid method was used to solve the wave propagation problem in all the cases. The results obtained show a marked difference between the three strategies. For the study configuration and the hardware and software conditions of this work, the traditional implicit strategy seems to better model the fluid-solid interface. In this case, the internal interface is not treated by explicit boundary conditions, as it is represented naturally by changes of the elastic parameters and the densities. On the other hand, the reflected wave field shows higher amplitudes than those expected for this problem in the images obtained with both, the explicit strategy and the one that incorporates the transitional zone. Such undesirable effects could be the result of the combination, in the first case, of the small size of the propagation volume considered in this work, the low performance of the boundary condition function applied at the external surfaces of the volume and the predictor-corrector method for the explicit strategy. The first two aspects combined with the presence of the transitional zone could be responsible of the behavior observed for the second implicit strategy

Keywords: Interface, Fluid-solid, Wave propagation, Finite-difference, Staggered-grid.

Tres estrategias para resolver el problema de propagación de ondas en una interfase 3d fluido-sólido

RESUMEN

Dos estrategias de naturaleza implícita y una de tipo explícito son utilizadas para resolver el problema que considera una interfase fluido-sólido en un medio 3D. Una estrategia implícita considera una zona transicional y la otra es la tradicional. Las condiciones de borde en la interfase en la estrategia explícita se resuelven agregando dos planos de “puntos ficticios” a la malla y se aplica una estrategia predictor-corrector. Se usó un método staggered-grid en Diferencias Finitas en todos los casos. Los resultados indican una diferencia marcada entre las tres estrategias. Para el ejemplo estudiado y las condiciones de hardware-software usadas, la estrategia implícita tradicional parece ser la que mejor modela la interfase fluido-sólido. La interfase interna no es tratada de forma explícita ya que los cambios de los parámetros elásticos y las densidades son naturalmente representados. El campo de ondas en las imágenes obtenidas con la estrategia explícita y la que incorpora la zona de transición, muestra intensidades mayores a las esperadas en este tipo de problema. Los efectos indeseables pudieran ser consecuencia de la combinación, en el primer caso, del pequeño tamaño del volumen de propagación considerado en este trabajo, del débil efecto de la función de absorción aplicada en las superficies externas del volumen y del método predictor-corrector para la estrategia explícita. Los dos primeros aspectos, combinados con la presencia de la zona transicional, podrían ser la causa del comportamiento observado con la segunda estrategia implícita.

Palabras clave: Interfase, Fluido-sólido, Propagación de onda, Diferencias finitas, Staggered-grid.

Recibido: julio de 2008 Recibido en forma final revisado: julio de 2009

INTRODUCTION

An elastic medium can be considered as a collection of lithological units, each of them locally homogeneous. Each region has constant petrophysical values such as velocity, density and Lamé parameters. To solve the wave propagation problem, it is desirable that the computational code simulates the internals frontiers automatically or semi-automatically (Kelly et al. 1976). In any acoustic wave problem with fluid-solid interfaces, the case of plane boundaries between both is a canonical problem whose features should be thoroughly understood before analyzing more complicated geometries (de Hoop and van der Hijden, 1983).

In problems as those indicated above it is suitable to use a method that could find the solutions and provide an easy understanding of their behavior. Even more, the obtained solutions should have the expected accuracy. Finite Difference techniques are often used to solve the equations in wave propagation problems. Although very expensive, the finite difference schemes could give a better approach to the physics of the wave propagation problem compared to other approximating schemes (Minkoff, 2002). In fact, finite difference methods allow modeling the wave propagation in media with fairly general spatial variation of elastic properties (van Voosen et al. 2002).

Several authors have treated the propagation problem in heterogeneous media using finite difference (FD) approaches. Alterman and Karal, (1968), considered a finite difference approximation for the equations of elasticity and applied it to the problem of a layered half-space with a buried point source emitting a compressional pulse. Kelly et al. (1976) considered a “homogeneous formulation” of the layered problem; i.e the standard boundary-conditions between media of different elastic properties must be satisfied explicitly. In this formulation, to treat the interface a line of fictitious grid points was incorporated below it. The work is a 2D approach and fluid-solid configurations were not treated. De Hoop and van der Hijden (1983) investigated the acoustic wave motion in a 2D fluid-solid configuration with a plane boundary. They considered a two-dimensional line source emitting an impulsive wave. In their work, expressions for the acoustic pressure of the reflected wave at any point in the fluid and at any time, using the modified Cagniard technique, were obtained. Even more, they reported that there is a marked difference in the time response for the diverse regimes that exist for the wave speed in the fluid in relation to the different wave speeds (compressional, shear, Rayleigh) in the solid (de Hoop and van der Hijden, 1983). Levander (1988) used the 2D Madariaga- Vireux staggered-grid scheme to precisely simulate wave propagation in a mixed acoustic-elastic media. The work included benchmark comparisons of finite-difference and analytical solutions to Lamb`s problem, which were found almost identical (Lamb`s problem results from the application of a point force in a uniform elastic half-space). One of the studied examples was a fluid-elastic configuration with a transitional-zone in the middle. This example was used to verify the stability of the method and acceptable results were reported. Minkoff (2002) developed a parallel code for the wave propagation problem using the velocity-stress staggered-grid formulation. The author treats a numerical example where a layered earth is assumed (velocities and density depend only on depth, z). Particularly, the earth model has eight layers with P-wave velocity, S-wave velocity, and density. The problem of fluid-solid interfaces was not studied. Van Voosen (2002) considered the wave propagation problem in a 2D fluid-solid configuration. He compared a 2D FD treatment with an analytical solution for the wave field reflected at a flat fluid-solid interface. He proposed the use of an imaging method, where the effective media parameters are not involved. Within the fluid, he explicitly set the spatial derivatives of the shear stresses to zero. The solid material properties were used to compute the field variables at the boundary. This method provided good results, particularly for coarse grid spacing at large offsets.

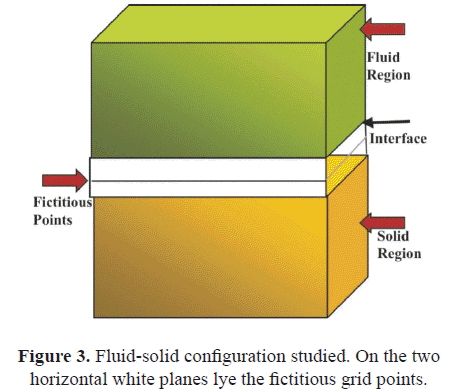
In this work we have considered a heterogeneous propagation medium allocated inside a 3D rectangular volume. A flat and horizontal interface separates the volume into two regions: the first region is a fluid and the second one is solid (Figure 1). This 3D interface, between a fluid and a solid, has not been computationally treated before. To solve the problem, we have used the three-dimensional (3D) isotropic elastic wave equations. The equations have been discretized via staggered finite difference operators (second order in time and fourth order in space). Three strategies to recognize the interface separating both regions into the propagation medium are applied, and all of them have been incorporated automatically or semi-automatically to the simulation program. The computational code was written in Fortran 90.

PROBLEM AND MATHEMATICAL MODEL

Usually in physical applications, the solution of a system of partial differential equations which satisfies certain ¨subsidiary ¨ conditions (e.g. initial and boundary conditions) has to be found. In this case, a system of partial differential equations describes the laws governing the physical system in some region of the space of independent variables (for example the time). The subsidiary conditions give, in a compressed form, the information needed of the history of the system (i.e. initial conditions) and of possible influences that could arise from outside the system (i.e. boundary conditions) (Roubine, 1970).

Let us consider a rectangular bounded volume V with Γ as its external boundary. A flat horizontal interface exists inside V separating two regions with different physical properties. Let [0, T] be a real interval. Ω is a bounded open subset of V ( in fact Ω = Ω_F Ω_S where, Ω_F is a domain (subset of the fluid region) and WS is also a domain (subset of the solid region) (de Hoop and van der Hijden, 1983). We can define the subsets H₁ and H₀ ¹ as (Johnson, 1994):

where:

L2 (Ω) is the space of square integrable functions in Ω. We want to solve the nine equations which were used by Minkoff (2002) to describe the 3-D wave propagation model in volume V described above. These equations show the dependency between stresses, velocities, density values and Lamé parameters (Minkoff, 2002). In this work, from the different kind of sources that are possible according to the mathematical equations proposed by Minkoff, we consider an explosive source. If x is a vector of three coordinates in the Euclidian space; t a temporal variable; r. the medium density;λ and µ the Lamé Parameters; f_z , f_x, f_y the source components; v_x , v_y , v_z the velocities values; σ_zz , σ_xx , σ_yy the normal stresses; σ_zx , σ_zy , σ_xy the shear stresses; and α and β the compressional and the shear velocity, respectively, given by α = we can defined the problem on the space H₀ ¹ (Ω) such as:

For all t, (0 < t < T)

Find v_z , v_x , v_y , σ_zz ,σ_xx , σ_yy ,σ_zx , σ_zy , σ_xy in H₀ ¹ (Ω), which satisfy the following equation system at Ω:

Equations (3) to (11) are the laws that govern the elastic wave propagation event. Such equations involve first order spatial derivatives and second order time derivatives. Equations (3) to (5) allow calculating velocities. Equations (6) to (8) are the expressions for the normal stresses. Equations (9) to (11) are the expressions for the shear stresses. As the initial condition, we suppose that the medium is in equilibrium at t = 0, i. e. stresses and velocities are set to zero everywhere in the medium. The definition of the space of solutions includes the boundary conditions on Γ (which is the external boundary of the rectangular volume). On the fluid-solid interface, the boundary conditions can be specified according to Kelly et al. (1976) as those at a welded interface between two different elastic materials. Boundary conditions require both the stress and the displacement to be continuous.

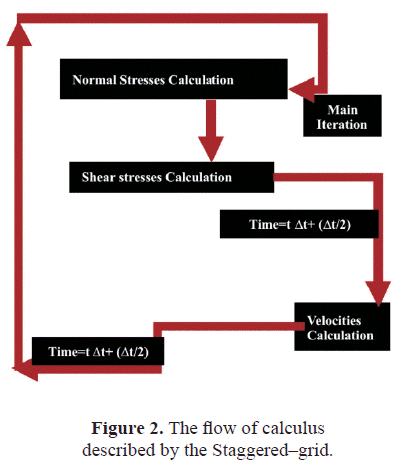
The finite-difference equations and the staggered-grid approach are given in Appendix A (Minkoff, 2002). The grid is staggered in both space and time.

Figure 2 shows a diagram of the staggered-grid method applied in time in the present work. As previously indicated, we solve the numerical and computational problem of a fluid-solid configuration inside a rectangular volume. A flat horizontal interface is considered. The model consists of two layers: the upper layer is a fluid and the lower one is an isotropic solid. The velocities and densities were taken from van Voosen et al. (2002). The fluid density is 1000 kg/ m3, the fluid velocity is 1500 m/s, the solid density is 2500 kg/m3, the P-wave velocity is 3500 m/s, and the S-wave velocity is 2000 m/s.

Absorbing boundaries were considered along all the external sides of the volume. The source is an explosive pulse which emits a 20 Hz wavelet. This source was positioned in the fluid, approximately at the middle between the surface and the interface. The source was placed in the fluid to simulate borehole and marine seismic applications (de Hoop and van der Hijden, 1983). To describe the physical conditions around the interface, we have developed three different numerical approaches.

The traditional implicit form to describe the physical changes occurring across an interface consists in setting, point by point in a data grid, such changes. In this approach, information such as velocities, density values and Lamé parameters have to be memorized at each point of the grid (Kelly et al. 1976). The computational implementation of this approach is a direct task. As previously indicated, we have used two implicit approaches. The first one is the traditional implicit approach. The second implicit strategy incorporates a transitional zone inside the propagation medium. This zone occupies a thin band parallel to the interface. We have not applied any methodology in order to define the P-wave and S-wave velocities values at the transitional zone. Nevertheless such values are closer to and smaller than the velocities values at the solid region. In an analogous way we have assigned the density value at the transitional zone. Although the numerical and physical approaches are more complicated when a transitional zone is included, the computational treatment is similar to the traditional scheme. On the other hand, the explicit strategy requires the inclusion of additional equations to describe the continuity across the interface. These new equations should be incorporated into the computational code. The equations that describe the continuity at the interface, satisfy the following conditions: across the interface, the tangential stresses are zero (see equations (10) and (11)), and the normal stress along z is continuous (Kelly et al. 1976). To perform this numerical approach in a 2D medium, Kelly et al. (1976) introduced one line of ‘fictitious points’. This line was separated a distance Dh from the interface and was placed in the higher velocity zone (Δh is the grid interval in both, x and z axis). To solve our 3D problem, we have added two planes of fictitious points below the interface, i.e. into the medium having the higher P- and S wave velocities (Figure 3). At each time, the velocity values around the interface are calculated using equations (1) to (9) (this can be considered as a predictive calculus). After this, the velocity values are updated using equations (10) to (12) at the fictitious points (this can be considered as a corrective calculus). Therefore, this procedure can be seen as a predictor-corrector strategy.

At each time, the velocity values around the interface are calculated using equations (3) to (11) (this can be considered as a predictive calculus). After this, the velocity values are updated using equations (12) to (14) at the fictitious points (this can be considered as a corrective calculus). Therefore, this procedure can be seen as a predictor-corrector strategy.

Equations (12) and (13) establish the conditions that should be satisfied by the shear stresses:

Replacing the expressions for the stresses from equations (3) to (11) into the equations above, we obtain:

Equation (15) shows the normal stress continuity condition across the interface:

The discretization of equations (12) to (14) leads to equations (16) to (18). In these equations, Δt is the grid step in time; Δz , Δx , Δy are the grid steps for the z-axis, x-axis and y-axis respectively: t_s = sΔt , z_j = jΔ_x , y_l = lΔ_y; zj is the interface position in the grid (aligned with the grid); p_z, p_x , p_y , q_z , q_x , q_y are the coefficients of the fourth-order approximation terms (for example are the Lamé Parameters in both the fluid and solid regions. The lines of fictitious points are z = and z = z_j + Δ_z ,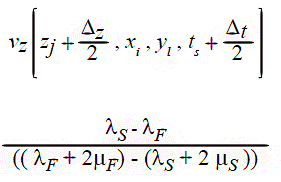

The elastic code was executed on a single node of a PCcluster. The processing environment has the following characteristics: a Dell Power Edge 2400 as Front-End node using OS Linux Red-Hat 6.2, RAM Memory 256 Mb; A 667 MHz Dell Power Edge 1300 Pentium III (dual processor), RAM Memory 256 Mb and OS Linux Red Hat 6.2 at the computing node. Three independent modules were written to execute each of the three strategies (i.e. the two implicit and the explicit one). The stresses and velocities were saved at execution time in the area of the dynamic memory. The 3D stability parameter (Courant factor) was settled equal to 0.494 (Lawrence Livermore National Laboratory (1992)). The time step Δt satisfy the following inequality , where: Δh is the grid space along the three axes, is the higher velocity value of the model and FCourant is the Courant stability factor. The time steps were taken in msec. The distance between the grid points, Δh, along the three axes is 0.035 m.      The interface was located at z=120Δh. The source was positioned at z=50Δh, x=100Δh and y=100Δh for the first implicit strategy and for the other two just x was changed to 125 Δh, as the grid points changed as it is explained below.

This code was executed under identical conditions for the three strategies. In that sense, we have fixed the total number of iterations. We used 500 time steps as the total number of iterations for each execution. The interface was aligned with the 3D horizontal grid in all the cases. The output is a slice of the current 3D space normal-stress solution (z-direction), at different time steps. Snapshots of the wave-field were taken after different time steps. Of particular interest is the behavior of the wave field around the interface.

RESULTS AND DISCUSSION

The scheme we have implemented does not require excessive space to store the spatial variables. Each variable in equations A-1 to A-3 requires only one matrix as its storage device; this matrix is re-written. Adaptations of the code were implemented for each of the three strategies. The implementation of the explicit strategy introduced additional calculus and increased execution time. Regarding the second implicit strategy, an increase in the execution time was observed.

For the first implicit strategy, the physical domain size we have used is 7m x 7m x 7m. The total number of grid points was 200 x 200 x 200. Figures 4 and 5 show the spherical wave field before it has reached the interface. Figures 6 and 7 show the splitting of the wave when it reaches the interface. The evolution observed in these snapshots is that expected for the studied configuration. While the wave is in the fluid medium, it is spherical and no dispersion is observed. The split after arriving at the interface is clearly shown. When the wave field arrives to the bottom of the solid region, it is not spherical due to the variation in the medium parameters when it crosses the boundary surface between the fluid and the solid regions, as is observed in Figure 7.

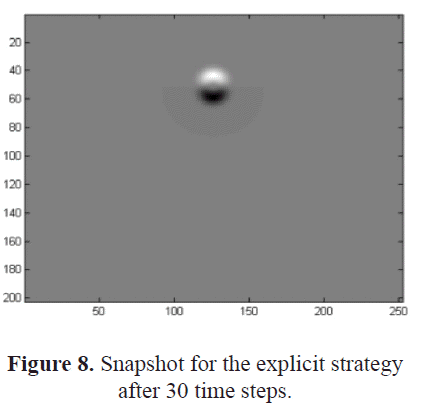
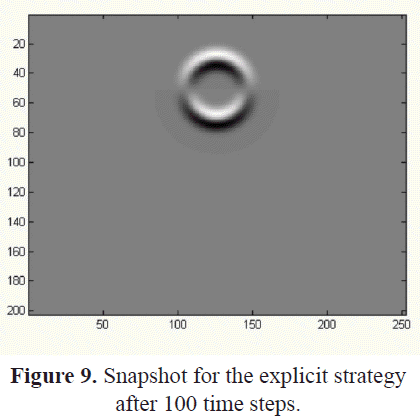
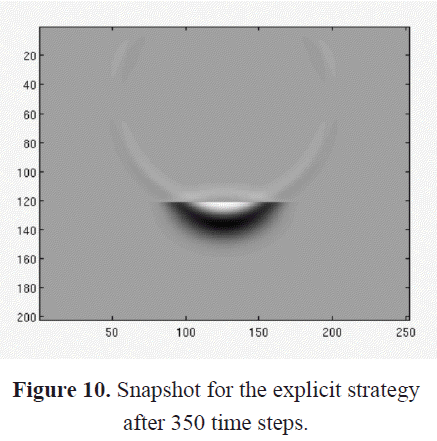
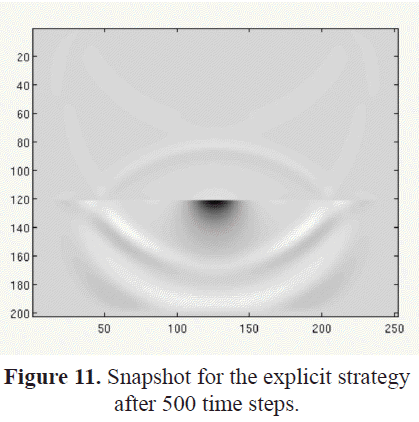
For the explicit strategy, after adding two planes of fictitious points, the physical volume size considered was 7m x 8.75m x 7m. The total number of grid points was 200 x 250 x 200. The results obtained are presented in Figures 8 to 11. Figures 8 and 9 show a spherical wave field. The wave field is inside the fluid region, therefore there is no variation in the medium parameters. Figures 10 and 11 show a non-spherical wave field. This behavior is due to the variation of the medium parameters as the wave field crosses the boundary surface between the fluid and the solid regions. Figure 11 shows a relatively high intensity peak around the middle of the interface. It is also possible to observe reflected waves on the left and right borders of this figure. Probably the combination of the small size of the propagation volume considered in this work, the low performance of the boundary condition function applied at the external surfaces, and the predictor-corrector method used here, contributed to the appearance of the high intensity peak around the middle of the interface. To determine the origin of this peak, new test simulations are required. For example, tests using larger size grids could provide better information about such secondary effects. In that sense, we have considered the migration of the hardware platform and a faster processor to reduce the execution time.

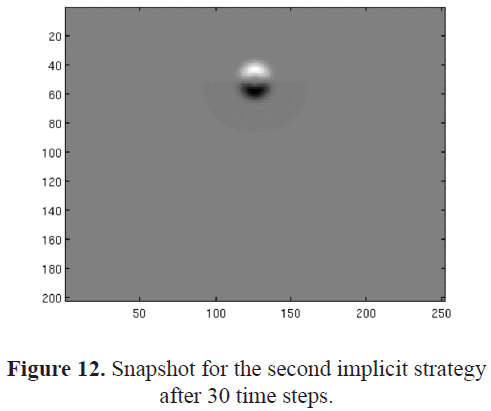
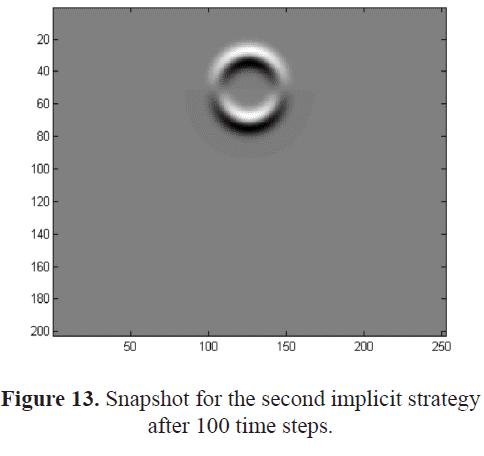
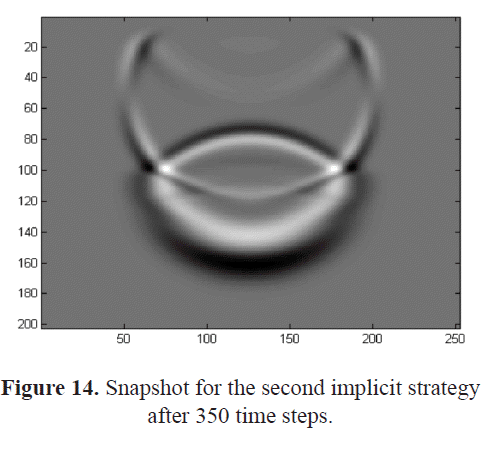
To apply the second implicit strategy we used a transitional zone. The transitional zone, as previously indicated, is a thin band joined to the upper side of the fluid-solid interface. Figures 12 and 13 show a spherical wave field, as the wave is still in the first medium and the parameters have not changed. Figures 14 and 15 show reflections associated to the upper boundary of the volume. Such effects could indicate that the absorbing boundary conditions used to solve the problem are not working in the expected way. It is possible that the small size of the grid used during the simulation intensified such numerical effects. Around the transitional zone, reflected waves of different intensities can be observed. Nevertheless, the intensity of the reflections associated to the interface created after adding the transitional zone is very low. This suggests that the width of the transitional zone we have used is appropriate as no significant additional effect has been introduced. The width of the transitional-zone could be changed. However, thick transitional zones that could turn into small propagation volumes should be avoided. We could not carry out tests using larger grid sizes as they do not fit on a single node at the sequential execution we are performing. Also, memory requirements and execution times increase with larger grid sizes. All these conditions turn into poorer performances: many input/ output operations, increase in the number of mathematical operations, and longer execution times. In order to achieve better results, the migration to another hardware platform, a large memory capacity, and a faster CPU would be recommended. Therefore, additional experimental tests should be performed.

For all the strategies, as was previously indicated, the wave field behavior at the fluid region is the expected one. In that sense, a spherical wave field is observed in figures 4, 5, 8, 9, 12 and 13.

However, as was described above, the results obtained for the studied example indicate a clear difference between the three strategies at the fluid-solid interface. With the hardware and software conditions that we have used, the traditional implicit strategy seems to better model the fluid-solid interface.

Generally, a 3D wave propagation implementation requires, at execution time, larger store space and a faster processor to diminish the execution time that increases due to the intensive calculus and several read-write operations to the main and secondary memories. The simulation code that we have developed stores the data with a double precision format in order to avoid numerical precision errors. Hence nine matrixes are required to store the solutions. In other words, we have 9 x 8 x 106 = 72 x 106 double precision data to process, more or less one MB of data to update at each iteration. In this sense, the hardware platform that we have is not able to deal with the number of data derived when the dimensions of the propagation volume increase; also longer execution times are expected in this case. Nevertheless, it is important to point out that the finite difference approach we have used simplified the physical formulation of the problem we have treated and it was easy to translate on a computational code that is legible and easily modifiable. Finally, a necessary extension of this work should be oriented to generate a parallel simulation code. In this case it is suitable to use semi-automatic tools. Parallel tools and parallel languages that can be used to solve this problem have appeared in recent challenges in computer science (Hayder et al. 1999).

CONCLUSIONS

In this work we have treated the numerical and computational problem of a 3D fluid-solid configuration inside a rectangular volume using three different strategies that apply a staggered-grid finite difference scheme: two of implicit nature and an explicit one. The code was parameterized and adapted using a portable language. The finite difference approach we have used simplified the physical formulation of the problem. Regarding the fluid-solid interface, the traditional implicit strategy seems to better model it. Undesirable effects were observed in the images obtained with the other two strategies. Different reasons could be responsible for this behavior. For the second implicit strategy, the inclusion of a transitional zone combined with the small size of the 3D volume considered in this work and the low performance of the boundary condition function applied at the external surfaces of the volume, could be the reason of the observed effects. The boundary conditions and the volume size, combined with the predictor-corrector strategy developed here, could be the reasons of the artifacts observed for the explicit strategy. However this predictor-corrector approach is suitable as no segmentation was introduced into the code structure. The increase of the memory capacity and the CPU speed could overcome some of these problems.

ACKNOWLEGMENT

The authors would like to thank Emilio Hernández (PHD) and operators working at the Cluster CAR (*Centro de cómputo de Alto Rendimiento*); due to their work it was possible to execute the simulation process we have performed. Particularly, we would like to thank Miguel Landaeta (CAR operator) for all his cooperation regarding the cluster machines maintenance during the experimental phase of this work.

REFERENCES

1. Alterman, Z.S. & Karal, F. C. Jr (1968). Propagation of elastic waves in layered media by finite-difference methods. Bull. Seism. Soc.Am., Vol. 58. p. 367-398.        [ Links ]

2. De Hoop, A. T. & Van Der Hijden, J.H.T. (1983). Generation of acoustic waves by an impulsive line source in a fluid /solid configuration with plane boundary. J. Acoust. Soc. Am. Vol. 74 (1), p. 333-342.        [ Links ]

3. Hayder, M.E., Ierotheou, C., Keyes, D. (1999). Three parallel programming paradigms: Comparisons on an Archetypal PDE Computation. Parallel and Distributed Computing Practices, Vol. 2, 3, p. 267-284.        [ Links ]

4. Johnson, C. (1994). Numerical solution of partial differential equations by the Finite Element method. Cambridge University Press.        [ Links ]

5. Kelly, K. R., Ward, R. W., Treitel, S., Alford, R. M. (1976). Synthetic Seismograms: A Finite Difference approach. Geophysics No.41. p. 2-27.        [ Links ]

6. Lawrence Livermore Laboratory (1992). E3D:2D/3D Elastic Finite Difference wave propagation code. Lawrence Livermore National Laboratory.        [ Links ]

7. Levander, A. (1988). Fourth-order Finite Difference P-SV seismograms. Geophysics Vol. 53(1). p.1425-1436.        [ Links ]

8. Minkoff, S. (2002). Spatial Parallelism of a 3D Finite Difference Velocity-Stress Elastic Wave Propagation Code. SIAM. J. Sci. Comput. Vol. 24(1). p. 1-19.        [ Links ]

9. Roubine, É. (1970). Mathematics Applied to physics. Springer- Verlag Berlin. Heidelberg. New York. Unesco, Paris.        [ Links ]

10. Van Voosen, R., Robertsson, J.O.A., Chapman, CH.H. (2002). Finite-Difference Modeling of wave propagation in a fluid-solid configuration. Geophysics Vol. 67, p. 618-624.        [ Links ]

APPENDIX

The Finite-Difference method and the staggered-grid technique which is referenced at Minkoff (2002) appear below. Staggered-grid storage allows the partial derivatives to be approximated by centered finite differences without doubling the spatial extent of the operators (Minkoff, 2002).