Reconocimiento de patrones con topologías diluidas

Juan Jiménez, Rosa Mujica

Universidad Central de Venezuela, Facultad de Ciencias, Escuela de Física, Laboratorio de Fenómenos no Lineales, Ciudad Universitaria, Los Chaguaramos, Caracas. Venezuela. e-mail: juan@fisica.ciens.ucv.ve; rmujica@fisica.ciens.ucv.ve

RESUMEN

En este trabajo se describe un procedimiento computacional iterativo que permite diluir la topología inicial de las conectividades en redes neurales, conservando las capacidades de almacenamiento y recuperación de éstas. Dicho procedimiento es utilizado para investigar tanto el tiempo de entrenamiento como la robustez de redes muy diluidas en las que, eliminando más del 70% de las conectividades iniciales, se observa un excelente desempeño en el reconocimiento de patrones. Los resultados obtenidos son comparados utilizando topologías diluidas de pequeño mundo y aleatorias.

Palabras clave: Topologías en redes neurales, Memoria asociativa, Red de hopfield, Redes de pequeño mundo, Reconocimiento de patrones.

Pattern recognition with diluted topologies

ABSTRACT

This work describes an iterative computational procedure that allows dilute initial topology of connectivity in neural networks, while preserving these storage and retrieval capacities. This procedure is used to investigate both the training time and robustness of very dilute networks in which, eliminating over 70% of the initial connectivity, there is an excellent performance in pattern recognition. Results are compared using dilute small world and random. topologies.

Keywords: Neural networks topologies, Associative memory, Hopfield neural network, Small-world networks, Pattern recognition.

Recibido: abril de 2009 Recibido en forma final revisado: octubre de 2009

INTRODUCCIÓN

Las redes neurales artificiales son dispositivos utilizados frecuentemente en una gran variedad de problemas de importancia práctica entre los que cabe mencionar: el reconocimiento de patrones (Keysers et al. 2001; Araokar, 2005), la robótica (Janglová, 2004), análisis y predicción de series temporales (Lin et al. 1995; Lee et al. 2001; Liang, 2005) y el diseño de criptosistemas (Socek & Culibrk, 2005; Laskaria et al. 2006), etc.

Inspirados en las redes neurales que se observan en seres vivos, su contraparte artificial consiste, de manera general, en un conjunto de unidades de procesamiento que evolucionan, acopladas entre sí, de acuerdo a una regla dinámica. Dicho con más precisión, el estado S_i ^t+1 de la i-ésima unidad en el instante t+1 viene dado por φ_i (S₁^t, S₂^t,..., S_N^t), en donde N denota el número total de elementos (i=1,…,N), y φ_i la dinámica que sigue la i-ésima unidad. Por su parte, la forma en la que intervienen S₁^t, S₂^t,..., S_N^t en cada función φ_i establece cómo están conectadas las “neuronas” y, por lo tanto, como es el acoplamiento entre cada unidad y el resto de la red.

El principal interés del presente trabajo está, precisamente, en investigar algunos aspectos relacionados con la topología de estas conectividades. En muchas aplicaciones en las que se emplean redes de Hopfield se asume que, antes de llevar a cabo el proceso de aprendizaje, la conectividad de la red es global. Esto se traduce en que cada unidad está, inicialmente, acoplada con todas las demás, y es a través del entrenamiento de la red que eventualmente pueden suprimirse algunas conectividades, modificando así la topología de las mismas.

Tanto en el caso de las redes naturales, como en el de implementación en hardware, la suposición de topologías densamente conectadas resulta costosa, puesto que en este último se requiere una interconexión total entre las compuertas lógicas que componen la red. En los últimos años ha habido un creciente interés en investigar sobre los efectos que tiene el uso de topologías diluidas sobre el desempeño de algunas redes neurales. Específicamente, sobre el efecto de suponer una conectividad inicial diluida correspondiente a redes de pequeño mundo, modulares, aleatorias y regulares, y la comparación entre ellas (McGraw & Menzinger, 2003; Stauffer & Aharony, 2003; Labiouse et al. 2004; Torres, et al. 2004; Davey et al. 2005; Lu et al. 2006; Oshima & Odagaki, 2007).

Naturalmente, el considerar topologías diluidas compromete el desempeño porque, al disminuir el número de conectividades es de esperar que haya un aumento en el tiempo de entrenamiento de la red así como una reducción de la complejidad en las tareas que puede efectuar. De hecho, en los trabajos antes mencionados, el número de patrones almacenados y recuperados es menor al 10% del número de nodos o unidades de procesamiento de la red.

El enfoque presentado aquí no es el de suponer una topología a priori sino, por el contrario, eliminar selectivamente conectividades redundantes mediante un mecanismo iterativo de poda, examinando a posteriori la topología de las conectividades obtenida. Utilizando una red de tipo Hopfield, que es descrita en detalle en la próxima sección, se desarrolla un procedimiento iterativo para eliminar conectividades y éste es aplicado sobre dos tipos de patrones binarios. Los resultados de los experimentos numéricos y la comparación del desempeño de la red con otras redes diluidas están reportados en la sección de resultados. Y finalmente, se presentan las conclusiones.

MEMORIA ASOCIATIVA

Las redes neurales que tomaremos en cuenta son de tipo Hopfield (Hopfield, 1982; Sompolinsky, 1988; Müller & Reinhardt, 1990), de manera que la dinámica viene dada por la regla:

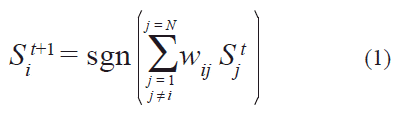
S_i^t = ± 1 denota la actividad del nodo i-ésimo en el instante t, = (w_i1,w_i2,...,w_iN) define su vector de pesos y, tal como indica la ecuación (1), se asume que no hay conexiones de un nodo consigo mismo, mientras que la topología de las conectividades puede no ser simétrica (w_ij ≠ w_ji).

Por lo general, dependiendo del tipo de problema que se quiera tratar, el algoritmo de entrenamiento es diseñado de manera que el proceso de aprendizaje se encarga de ajustar los pesos para que se cumpla la tarea a cabalidad. En el caso particular del reconocimiento de patrones, el entrenamiento conduce a valores de los pesos tales que los patrones de entrenamiento o memorias sean puntos fijos estables de la dinámica, es decir, que si un ejemplo se encuentra cercano a la memoria converge a la misma.

Sin embargo, se quiere hacer énfasis en este estudio que no hace falta ajustar los N(N-1), pesos que definen la red y que corresponden al caso en el que la topología de las conectividades inicial es global, si no por el contrario que se puede suponer, sin afectar el rendimiento de la red, que algunos de ellos son cero, lo que conduce a topologías diluidas.

Específicamente en la fase de entrenamiento se utiliza la regla de aprendizaje del Adatron, un algoritmo propuesto en literatura de mecánica estadística (Anlauf & Biehl, 1989; Cristianini & Shawe-Taylor, 2000), que, además de permitir maximizar el número de patrones que puede almacenar la red y resolver el problema de clasificación binaria en el caso de que los datos sean linealmente separables, es un esquema de aprendizaje adaptativo, rápido y estable (Krauth & Mézard, 1987; Cristianini & Shawe-Taylor, 2000).

La configuración de los pesos sinápticos son ajustados por el algoritmo, tal que dados P patrones memorias:

Los mismos sean puntos fijos estables de la dinámica. Esto es, que se debe satisfacer el conjunto de inecuaciones para cada memoria ν en una unidad de procesamiento, por ejemplo, la i-ésima:

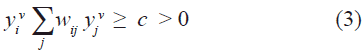
Como los elementos de la diagonal de la matriz de pesos es cero, entonces el conjunto de inecuaciones anteriores se desacopla y cada unidad de procesamiento puede ser tratada independientemente. Si se considera el caso de una sola memoria y se omite el subíndice i, la condición de estabilidad de las memorias se escribe como:

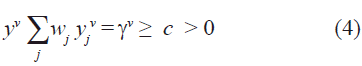
w_j es la j-ésima componente del vector de pesos y γ g^v es el coeficiente de estabilidad o margen funcional para el patrón n-ésimo. La memoria asociativa se entrenará correctamente cuando cada unidad de procesamiento satisfaga la condición de estabilidad. Una medida normalizada de la estabilidad de las unidades de procesamiento, se define como:

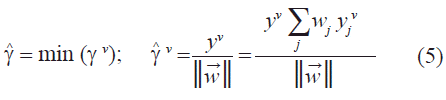
y será el coeficiente de estabilidad. De esta forma, el algoritmo del Adatron alcanza una estabilidad óptima normalizada, es decir, una configuración de pesos sinápticos con un coeficiente de estabilidad máximo para un conjunto de patrones memoria arbitrario. El algoritmo se deriva del problema de minimizar la norma del vector de pesos sujeto a las restricciones de que la condición de estabilidad de los patrones memorias sea igual o mayor a la unidad (Anlauf & Biehl, 1989):

minimizar

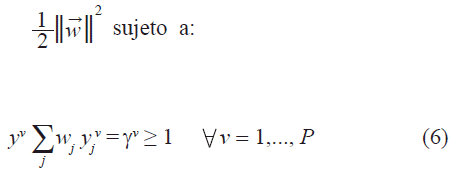
Para este problema de optimización en su formulación dual, la solución tiene la forma:

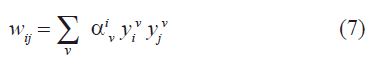
donde: los coeficientes α_i^v son los multiplicadores de Lagrange y pueden ser interpretados como una contribución de la información que cada patrón da a los pesos sinápticos y cuya dinámica de adaptación con la presentación secuencial de los patrones, tiene la forma:

siendo λ un parámetro que influye en la convergencia del proceso de aprendizaje, llamada tasa de aprendizaje. La fase de entrenamiento es completada cuando la mínima condición de estabilidad (4) iguala a la unidad (Anlauf & Biehl, 1989).

Como una medida del desempeño de las redes actuando como memorias asociativas, se examina la estabilidad de los patrones en ausencia de ruido y se analiza la robustez de la red bajo contaminación por ruido.

En ambos casos se evalúa la capacidad de recuperación (CRP) de la red, ésta cuantifica la fracción o porcentaje de patrones que la red es capaz de reconocer, en otras palabras, esta cantidad muestra cuantos de los ejemplos mostrados a la red convergen a los patrones memorias que ella se ha aprendido.

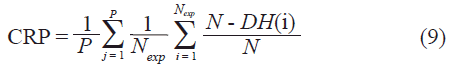
La red es estimulada con un patrón de entrada que al aplicársele la dinámica converge a un patrón que será llamado (S) y que es comparado con la memoria ya almacenada o aprendida por la red (y^j), en este sentido la Distancia Hamming (DH) es la distancia que existe entre el patrón S y la memoria y^j, y se obtiene comparando lugar a lugar ambos patrones y sumando contribuciones si los estados son diferentes, por lo tanto cuando ambos sean iguales la distancia será cero.

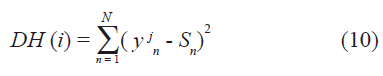
N_exp es el número de experimentos diferentes en los que se calculan las distancias DH(i) y que se realizan para cada patrón memoria en la fase de recuperación.

METODOLOGÍA Y EXPERIMENTOS

El mecanismo de poda consiste en eliminar selectivamente conectividades de la red mediante un procedimiento iterativo que puede ser esquematizado de la siguiente manera:

1. Se escoge un porcentaje p_s de conectividades a suprimir.

2. Se entrena la red completamente conectada.

3. Se ordenan, de acuerdo a valores ascendentes de su módulo, los pesos sinápticos obtenidos en el proceso de aprendizaje.

4. Se elimina el porcentaje de conectividades, que corresponde a pesos sinápticos cuyos valores en módulo sean los menores.

5. Se entrena la red con la nueva topología diluida y, si se recupera el 100% de los patrones memoria, se regresa al paso anterior. En caso contrario finaliza el procedimiento.

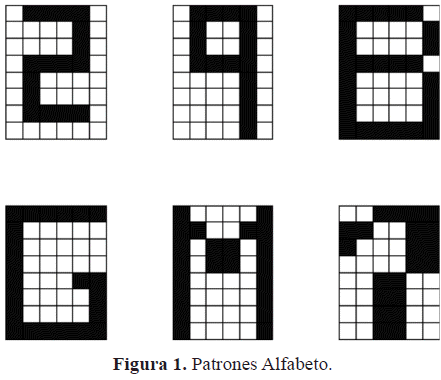
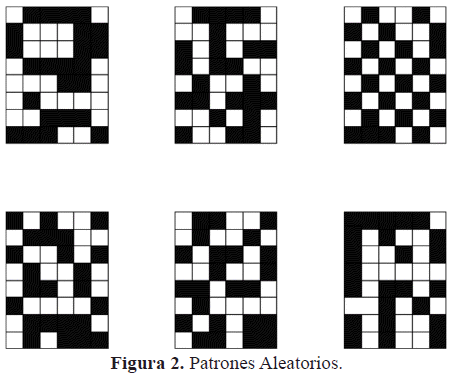
Los resultados corresponden a redes de 48 nodos que almacenan 48 y 24 patrones binarios. El porcentaje de conectividades a suprimir es de p_s = 5% y son considerados dos conjuntos de entrenamiento (figuras 1 y 2): uno denominado Alfabeto, conformado por letras, números y símbolos; y otro denominado Aleatorio, conformado por patrones binarios aleatorios.

Para cada una de las topologías obtenidas mediante el procedimiento descrito se determinan: el tiempo de entrenamiento (te) y de recuperación (tr); el porcentaje de conectividades inactivas (%CI); la capacidad de recuperación (CRP) y la robustez de la red bajo la contaminación de los patrones memoria con ruido.

Los tiempos de entrenamiento y de recuperación son determinados tomando el tiempo real que emplea el computador en realizar cada etapa. El experimento de robustez se realiza con el objetivo de estudiar el desempeño de la red cuando los patrones presentados son contaminados con ruido, en este experimento para todos los patrones que se desean recuperar, se calcula la capacidad de recuperación cuando están contaminados y se grafica la capacidad de recuperación promedio en función del ruido.

La contaminación de los patrones con ruido se realiza de la siguiente manera: para una fracción de ruido específico se visita uno a uno cada lugar del patrón, en cada lugar se genera un número al azar entre 0 y 1, si éste es menor o igual a la fracción de ruido deseado se sortea con probabilidad 0.5 si se cambia o no el lugar del patrón por el estado opuesto, es decir, si el lugar escogido tiene el estado 1, entonces se cambiará por -1 y viceversa.

RESULTADOS

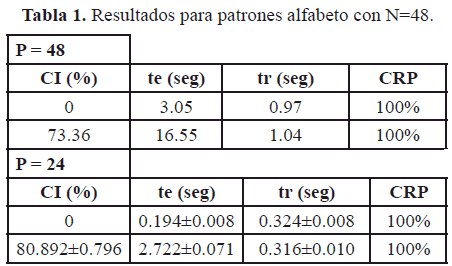
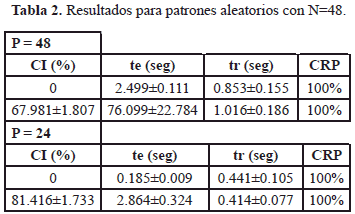
En las tablas 1 y 2, se muestran los resultados para los dos conjuntos de entrenamiento antes mencionados, empleando las topologías obtenidas mediante el mecanismo de poda. Encontrándose primero, que cuando se desea almacenar igual número de patrones que nodos en la red, al emplear el conjunto Alfabeto, el tiempo de entrenamiento es menor en comparación con el obtenido para el conjunto Aleatorio; esto es debido a que los patrones del conjunto Alfabeto son un subconjunto del Aleatorio, y son más fáciles de aprender por la forma en que han sido construidos. Cuando se almacenan 24 patrones no se observa gran diferencia en los tiempos de entrenamiento entre ambos conjuntos. En segundo lugar, aunque los tiempos de entrenamiento se incrementan cuando se pasa de una topología completamente conectada (CI=0%) a una diluida, los tiempos de recuperación no varían mucho.

Hay que resaltar que las cantidades que no presentan desviaciones estándar, son aquellas referidas al conjunto Alfabeto al emplear 48 patrones, debido a que se obtiene una sola topología.

Lo interesante es que las topologías que se obtienen están altamente diluidas y cuando se emplean como redes de memoria asociativa son capaces de almacenar el 100% de los patrones memorias deseados, éste es un excelente resultado cuando se compara con los experimentos realizados en algunos trabajos en donde el número de patrones memorias no excede el 10% del número total de nodos (McGraw & Menzinger, 2003; Stauffer & Aharony, 2003; Labiouse et al. 2004; Torres et al. 2004; Davey et al. 2005; Lu et al. 2006; Oshima & Odagaki, 2007), y sólo emplean patrones aleatorios.

Por otra parte, las redes de pequeño mundo son muy conocidas y han sido empleadas para estudiar algunos fenómenos biológicos, sociales, entre otros (Albert & Barabási, 2002), así como para investigar los efectos de este tipo de topología en redes neurales. El mecanismo de construcción de las redes de pequeño mundo es muy sencillo y fue introducido por Watts y Strogatz en 1998, y consiste en generar una red regular en la cual cada nodo está conectado con sus K primeros vecinos, y luego con una probabilidad de reconexión de conectividades pequeña p; puede obtenerse una topología de pequeño mundo (Watts, 1999). Estas redes presentan dos propiedades importantes, primero, que cualesquiera dos nodos de la red se comunican por un camino de nodos intermedios relativamente pequeño y segundo, que poseen valores altos del coeficiente de agrupamiento, este valor indica que si dos nodos de la red no están conectados directamente entre sí existe una gran probabilidad de que se conecten mediante la intervención de otros nodos.

Con la finalidad de comparar el desempeño de las topologías obtenidas mediante el mecanismo de poda, con otras topologías predeterminadas, se construyeron redes de pequeño mundo y redes aleatorias a partir del mecanismo propuesto por Watts y Strogatz (Watts, 1999), para realizar la tarea de almacenar y recuperar memorias de los dos conjuntos de entrenamiento mencionados anteriormente. Las topologías encontradas en los experimentos de poda no tienen una estructura definida, pero sin embargo se conocen algunos parámetros que las describen, uno de ellos es el número de vecinos por nodo K y también el promedio de estos (K_prom) que es una característica de la red. Es así como se emplea K cercano a K_prom para poder generar las redes de pequeño mundo con una probabilidad de reconexión p = 0.05 y con una probabilidad p = 1.0 para obtener las redes aleatorias y así de esta forma poder realizar una comparación entre dichas redes.

En el caso de las redes de pequeño mundo, en la tabla 3 sólo se muestran los resultados obtenidos para el conjunto de entrenamiento de los patrones alfabeto, ya que para los aleatorios los resultados no son satisfactorios, recordando que el número de vecinos por nodos impuesto para crear la topología es K. Igual se muestra en la tabla 4 los resultados para las redes aleatorias, que en este caso presentan el peor desempeño, las redes empleadas son de N=48 nodos.

En las tablas 3 y 4 no se muestran las desviaciones estándar de las cantidades referidas al porcentaje de conectividades inactivas, ya que al ser fijo el número K, las redes que se construyen siempre tienen el mismo número de conectividades.

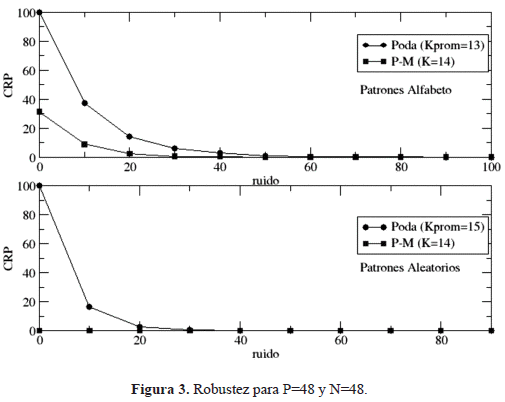
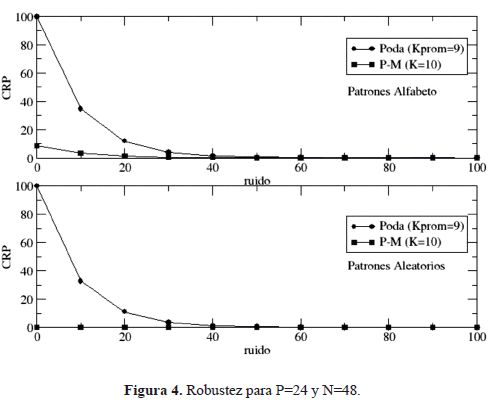
En las figuras 3 y 4 se muestran los experimentos de robustez empleando tanto topologías obtenidas mediante el mecanismo de poda, en la cual se coloca el número de vecinos por nodo promedio Kprom, como las creadas por el esquema de pequeño mundo (P-M) con un número de vecinos K por nodo, esto se realiza para P=N=48 y para P=24. En este experimento, en donde se contaminan los patrones memorias con ruido, se observa que las redes cuyas topologías fueron obtenidas mediante el mecanismo de poda son más robustas que las de pequeño mundo y también que las redes aleatorias, presentan un pobre desempeño.

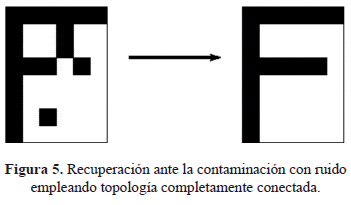
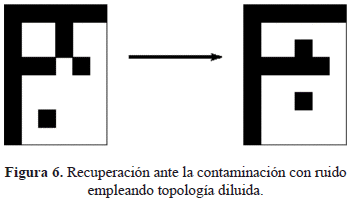
Para finalizar, se muestra un ejemplo en el que se observa una ligera diferencia en la capacidad de recuperación al contaminar con un 10% de ruido los patrones del conjunto alfabeto al considerar los 48 patrones; primero al emplear una topología completamente conectada se obtiene CRP=49.12%, mientras que para la topología diluida mediante la poda se obtiene CRP=48.71%. En la figura 5 se muestra un patrón perturbado y recuperado perfectamente al emplear la topología completamente conectada y en la figura 6 se muestra el mismo patrón con igual perturbación que el anterior y se observa que no converge a la memoria almacenada, sin embargo se puede reconocer muy bien; esto corresponde al caso de emplear la topología diluida.

CONCLUSIONES

En este trabajo se implementó un procedimiento para generar topologías diluidas, que elimina las conectividades entre nodos de la red que son consideradas no importantes. Se consigue un alto grado de dilución con el cual las redes presentan un desempeño perfecto en el reconocimiento de patrones, en ausencia de ruido. Estas redes presentan mejores resultados en cuanto a tiempos de entrenamiento y recuperación, así como mayor robustez que las redes construidas bajo el esquema de pequeño mundo y aleatorias. Se resalta el hecho importante de que las redes generadas por el mecanismo de poda logran recuperar satisfactoriamente los patrones del conjunto aleatorio a diferencia de las otras redes empleadas (pequeño mundo y aleatorias) que no logran hacerlo.

Se ha respondido satisfactoriamente la pregunta inicial, de si se pueden obtener topologías diluidas que presenten buen desempeño en el reconocimiento de patrones. En este aspecto se obtiene una dilución importante, que en el caso considerado más difícil con P=N y patrones aleatorios, la topología se diluye en un 67.981% ± 1.807% con una recuperación del 100% de los patrones memorias presentados a la red. Además, se observa un incremento en el tiempo de entrenamiento al pasar de una topología completamente conectada a una diluida, tal como debería esperarse.

Se ha encontrado una ligera diferencia en cuanto a la capa cidad de recuperación de las redes ante patrones contaminados, cuando se emplean topologías completamente conectadas y diluidas al 24% de conectividades activas, lo cual refleja que el mecanismo de poda produce topologías que compiten muy de cerca con las totalmente conectadas en cuanto a robustez, ya que en ausencia de ruido presentan el mismo desempeño con la gran ventaja de prescindir de un número alto de conectividades. Hay que resaltar el hecho de que emplear topologías diluidas resulta ventajoso, por ejemplo, desde el punto de vista de construcción de dispositivos electrónicos, ya que es importante usar redes cuyas compuertas lógicas no estén densamente interconectadas; así como en otras implementaciones prácticas.

Se observa que el tamaño de las redes empleadas en este trabajo no es grande en comparación con las utilizadas en otros trabajos, sin embargo, nos permite observar el desempeño de las redes para almacenar un alto número de patrones memorias que en nuestro caso es de P=N, lo cual no es considerado en trabajos similares.

Algunos experimentos se han realizado empleando el histograma de conectividades de las redes obtenidas mediante poda, para generar otras topologías con igual grado de dilución y no se consigue la total recuperación de los patrones. Lo que indica que el mecanismo empleado produce topologías que no pueden ser reproducidas al azar. El conocer las propiedades que caracterizan estas topologías encontradas es el trabajo de investigación, con el objetivo de que dado un conjunto de entrenamiento determinado se pueda escoger una topología diluida de antemano que en ausencia de ruido logre almacenar el 100% de los patrones memorias presentados a la red, aun en el caso de considerar un número de patrones elevado.

REFERENCIAS

1.  Albert, R. & Barabási, A. (2002). Statistical mechanics of complex networks. Reviews of modern physics, Volume 74, pp. 47-97.        [ Links ]

2. Anlauf, J. & Biehl, M. (1989). The AdaTron: an Adaptive Perceptron Algorithm. Europhys. Lett. 10 (7), pp. 687- 692.        [ Links ]

3. Araokar, S. (2005). Visual Character Recognition using Artificial Neural Networks. eprint arXiv:cs/0505016.        [ Links ]

4. Cristianini, N. & Shawe-Taylor, J. (2000). An Introduction to Support Vector Machines. Cambridge University Press.        [ Links ]

5. Davey, N., Calcraft, L., Christianson, B., Adams, R. (2005). Associative Memories with Small World Connectivity. Adaptive and Natural Computing Algorithms, 74.        [ Links ]

6. Hopfield, J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. NatL Acad. Sci. USA. Vol. 79, pp. 2554-2558.        [ Links ]

7. Janglová, D. (2004). Neural Networks in Mobile Robot Motion. Inernational Journal of Advanced Robotic Systems, Volume 1 Number 1, pp. 15-22.        [ Links ]

8. Keysers, D., Macherey, W., Dahmen, J., Ney, H. (2001). Learning of Variability for Invariant Statistical Pattern Recognition. Book Series: Lecture Notes in Computer Science. Volume 2167/2001, pp. 263-275.        [ Links ]

9. Krauth, W. & Mézard, M. (1987). Learning algorithms with optimal stability in neural networks. J. Phys. A 20, L745-L752.        [ Links ]

10. Labiouse, C., Salah, A., Starikova, I. (2004). The impact of connectivity on the memory capacity and retrieval dynamics of Hopfield-type networks. Proc. of Santa Fe Comp. Sys. Summer School. 94, p. 262.        [ Links ]

11. Laskaria, E., Meletiou, G., Tasoulis, D., Vrahatis, M. (2006). Studying the performance of artificial neural networks on problems related to cryptography. Nonlinear Analysis: Real World Applications, Volume 7, Issue 5, pp. 937-942.        [ Links ]

12. Lee, C., Lawrence, S., Tsoi, A. (2001). Noisy Time Series Prediction using a Recurrent Neural Network and Grammatical Inference. Machine Learning, Volume 44, Number 1/2, July/August, pp. 161–183.        [ Links ]

13. Liang F. (2005). Bayesian neural networks for nonlinear time series forecasting. Statistics and Computing 15, pp. 13–29.        [ Links ]

14. Lin, F., Hou, X., Gregor, S., Irons, R. (1995). Time Series Forecasting with Neural Networks. Complexity International, Volume 2.        [ Links ]

15. Lu, J., He, J., Cao, J. (2006). Topology influences performance in the associative memory neural networks. Phys. Lett. A 354, pp.335-343.        [ Links ]

16. McGraw, P. & Menzinger, M. (2003). Topology and computational performance of attractor neural networks. Phys. Rev. E 68: 047102.        [ Links ]

17. MÜller, B. & Reinhardt, J. (1990). Neural Networks: An Introduction. Springer-Verlag.        [ Links ]

18. Oshima, H. & Adagaki, T. (2007). Storage capacity and retrieval time for small-world neural networks. Phys. Rev. E, 76, 036114.        [ Links ]

19. Socek, D., Culibrk, D. (2005). On the security of a clipped hopfield neural network-based cryptosystem. Proceedings of the 7th workshop on Multimedia and security table of contents New York, NY, USA, pp. 71 – 76.        [ Links ]

20. Sompolinsky, H. (1988). Statistical mechanics of neural networks. Physics Today, pp. 70-80.        [ Links ]

21. Stauffer, D. & Aharony, A. (2003). Efficient Hopfield pattern recognition on a scale-free neural network. Eur. Phys. J. B, 32(3), pp. 395-399.        [ Links ]

22. Torres, J., Muñoz, M., Marro, J., Garrido, P. (2004). Influence of topology on the performance of a neural network. Neurocomputing, 58-60, pp. 229-234.        [ Links ]

23. Watts, D. (1999). Small World: the dynamics of networks between order and randomness. Princeton University Press.        [ Links ]