SciELO - Scientific Electronic Library Online
 
vol.25 número1Filosofía de la Ciencia en el TractatusUnidad, metodo y matematización de la naturaleza índice de autoresíndice de materiabúsqueda de artículos 		Home Pagelista alfabética de revistas  

Servicios Personalizados

Revista

Articulo

Indicadores

Links relacionados

  • No hay articulos similaresSimilares en SciELO

Compartir

EPISTEME

versión impresa ISSN 0798-4324

EPISTEME v.25 n.1 caracas  2005

 

Franklin Galindo - Kris Martins

Las reglas de Irving Copi y Carl Cohen son una condición necesaria y suficiente de la validez en los silogismos categóricos de forma estándar

Resumen

En la actualidad uno de los libros más usados para dar lógica elemental es el de Irving Copi y Carl Cohen(Introducción a la lógica, 2001), allí se presentan unas reglas para decidir la validez de los silogismos categóricos de forma estándar. Pero en tal texto ni en ninguno que nosotros conozcamos se ofrece una fundamentación de las mismas. Es decir, una demostración de que ellas son realmente una condición necesaria y suficiente de la validez de un silogismo categórico de forma estándar, lo único que hemos leído es su motivación como condición necesaria. El  objetivo de este trabajo es ofrecer una fundamentación de las mismas usando la noción de conjunto (o clase) y la técnica de diagramas de Venn, un concepto y una técnica que están expuestos en los principales textos de lógica elemental, incluyendo el referido anteriormente.

Palabras clave: Silogismo, validez, reglas de Copi-Cohen

Copi and Cohen’s rules as a necessary and sufficient condition of validity in standard categorial syllogisms

Abstract

Currently, one of the most widely used textbooks in elementary logic is the one by Irving Copi and Carl Cohen (Introduction to Logic, 2001). They offer rules for deciding the validity of standard categorical syllogisms. But neither that textbook, nor any other we know of, provides the foundations of these rules; that is to say, the demonstration that they are a necessary and sufficient condition for the validity of a standard categorical syllogism. We have only found motivations for the necessary condition. The main goal of this work is to provide a foundation of these rules using the notion of set as well as Venn diagrams, a concept and a technique exposed in the main textbooks of logic, including the aforementioned.

Keywords: Syllogism, validity, Copi-Cohen’s rules.

Introducción

¿Por qué algunas personas todavía se interesan en la Silogística a pesar de que esta lógica antigua tiene limitaciones expresivas con respecto a las relaciones, y existen lógicas con mucho mayor poder expresivo que la misma en la actualidad, como por ejemplo la lógica de primer orden?

No lo sabemos. Quizá sea por razones filosóficas o históricas, o porque este sistema tiene interesantes propiedades pedagógicas para transmitir los conceptos básicos de la lógica, por ejemplo su simplicidad. O quizá sea por una causa distinta a las mencionadas anteriormente.

En este trabajo intentamos dar respuesta a una pregunta sobre la Silogística que surgió durante la actividad pedagógica. Tal interrogante es la siguiente: ¿Las reglas de Irving Copi y Carl Cohen que se encuentran en su texto, “Introducción a la lógica”(2001), y las cuales usamos para decidir la validez de los silogismos categóricos de forma estándar, son en verdad una condición necesaria y suficiente de tal validez?. Nuestra opinión es que realmente sí los son (como se cree comúnmente), y proponemos una demostración de tal hecho.

Nuestro orden expositivo será el siguiente: En la sección 1 presentamos un resumen de los conceptos básicos de la Silogística y expresamos de una manera más precisa la proposición que afirma la suficiencia y necesariedad de las reglas. Y luego, en la sección 2, demostramos la misma.

1. Desde un punto de vista extensional es usual definir a una proposición categórica como una proposición que afirma o niega la inclusión o exclusión, total o parcial, de una clase (conjunto) en otra. Hay sólo cuatro formas estándar diferentes de proposiciones categóricas: (1) Universal afirmativa: “Todo S es P”, la cual se denota con la letra A. (2) Universal negativa: “Ningún S es P”, la cual se denota con la letra E. (3) Particular afirmativa: “Algún S es P”, la cual se denota con la letra I, y (4) Particular negativa: “Algún S no es P”, la cual se denota con la letra O. Así, los elementos que conforman una proposición categórica son: Cuantificador – Término sujeto - Cópula(Verbo ser) - Término predicado.

Con estas proposiciones categóricas se pueden formular razonamientos, un ejemplo de ello es el silogismo categórico, al cual Irving Copi y Carl Cohen (Introducción a la lógica, 2001) definen como “un argumento deductivo que consiste en tres proposiciones categóricas, que contienen exactamente tres términos, cada uno de los cuales sólo aparece en dos de las proposiciones que lo constituyen”. Nosotros vamos a agregar a esta definición (por consideraciones de simplicidad), el requisito de que los tres términos estén usados exactamente en el mismo sentido en todo el razonamiento.

Decimos que un silogismo categórico está en forma estándar si sus premisas y conclusión están arregladas en un orden específico. Para describir ese orden es útil definir primero cuál es término menor, el término mayor y el término medio de un silogismo categórico. Así como también cuál es su premisa mayor y cuál es su premisa menor. El término menor es el término que aparece como sujeto de la conclusión. El término mayor es el que aparece como predicado de la conclusión. El término medio es el término que aparece en las dos premisas y no aparece en la conclusión. La premisa mayor es la premisa que tiene al término mayor. Y la premisa menor es la premisa que tiene al término menor. Entonces, el orden específico del que se habló anteriormente (la forma estándar del silogismo categórico) consiste en enunciar primero la premisa mayor, luego a la premisa menor y por último a la conclusión.

Premisa mayor

Premisa menor

Conclusión

Un ejemplo de silogismo categórico de forma estándar es:

Ningún venezolano es italiano Todo caraqueño es venezolano Por lo tanto, ningún caraqueño es italiano

Cuya forma lógica sería, usando las variables C, V e I para caraqueño, venezolano e italiano (respectivamente), la siguiente:

 Ningún V es I

Todo C es V

\ Ningún C es I

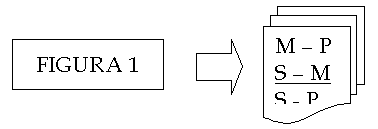
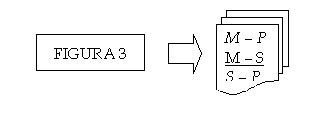
Según la posición que ocupan los términos mayor, medio y menor en las proposiciones que forman un silogismo categórico de forma estándar, se pueden distinguir en total cuatro posibles combinaciones de estos términos. Cada una de las 4 posibles combinaciones forman lo que se llama la figura del silogismo categórico de forma estándar:

 

 

Figura 1

Figura 2

Figura 3

Figura 4

 

 

 

 

 

(Premisa mayor)

M – T

T – M

M – T

T – M

(Premisa menor)

t – M

T – M

M – t

M – t

(Conclusión)

t – T

T – T

t – T

t – T

Se llama modo del silogismo categórico de forma estándar, a la combinación que forman sus tres proposiciones, indicando el tipo y el orden en que se encuentran. Así por ejemplo, un silogismo cuya premisa mayor es de tipo A, la premisa menor de tipo E y la conclusión es de tipo I, su modo correspondiente será: AEI.

Si se combinan todos los modos posibles para cada figura se obtiene un total de 64 formas diferentes, y si se toman en cuenta las cuatro figuras se obtendrán 256 formas posibles distintas de silogismos categóricos de forma estándar en total. Sin embargo, no todas ellas son válidas, es decir, son formas que sin importar el contenido de las proposiciones, impidan que siendo las premisas verdaderas pueda resultar una conclusión falsa. Otra manera de definir validez es la siguiente: La forma de un silogismo categórico de forma estándar es válida si cualquier interpretación que satisfaga sus premisas satisface también su conclusión.

En la tradición escolástica sólo 24 de ellas se consideraban válidas, y para cada una asignaron un nombre medieval, como una forma mnemotécnica para identificarlos con mayor facilidad. Las vocales de cada nombre corresponden al modo del silogismo. Los 19 modos principales son los siguientes:

1ª figura: Barbara, Darii, Celarent, Ferioque.

2ª figura: Camestres, Baroco, Cesare, Festino.

3ª figura: Darapti, Datisi, Felapton, Ferison, Disamis, Bocardo.

4ª figura: Bramantip, Camenes, Fesapo, Fresison, Dimaris.

Los cinco modos restantes (llamados subalternos) son: Barbari y Celaront de la figura 1, Cesaro y Camestrop de la figura 2, y Camenop de la figura 4. En palabras de Manuel Garrido (Lógica Simbólica) estos modos “se caracterizan por ofrecer una conclusión particular, aunque las premisas permitirían que fuese universal”.

Ahora bien, si consideramos el método de las 6 reglas de Copi- Cohen, o el método de Diagramas de Venn para determinar la validez de los silogismos también descrito (entre otros) por Copi-Cohen, se puede observar que de los 24 modos mencionados únicamente 15 resultan válidos. Esto como consecuencia del problema del compromiso existencial. Los modos que por estos dos métodos resultan inválidos son:

·  Darapti y Felapton de la 3ª figura; y

·  Bramantip y Fesapo de la 4ª figura.

·  Todos los subalternos: Barbari, Celaront, Cesaro, Camestrop y Camenop.

 No obstante, si se acepta que no existen clases vacías y se modifica ambos métodos de acuerdo a esto (en el caso de las reglas de Copi-Cohen se elimina la regla 6), se puede demostrar la validez de los 19 modos principales y de los 5 subalternos de acuerdo a la tradición, sin ningún inconveniente.

Las 6 reglas de Copi-Cohen son:

Regla 1:Un silogismo categórico de forma estándar válido debe contener exactamente tres términos, cada uno de los cuales se usa en el mismo sentido en todo el argumento.

Regla 2:En un silogismo categórico de forma estándar válido, el término medio debe estar distribuido por lo menos en una de las premisas.

Regla 3:En un silogismo categórico de forma estándar válido, si cualquier término está distribuido en la conclusión, entonces debe estar distribuido en las premisas.

Regla 4:Ningún silogismo categórico de forma estándar que tiene dos premisas negativas es válido.

Regla 5:Si cualquier premisa de un silogismo categórico de forma estándar es negativa, la conclusión debe ser negativa.

Regla 6:Ningún silogismo categórico de forma estándar con una conclusión particular puede tener dos premisas universales.

Recordemos que una proposición distribuye un término (bien sea el término sujeto o predicado), si éste se refiere a todos los miembros de la clase designada por él, es decir, cuando ese mismo término está tomado en su máxima extensión       dentro de la oración, cuando la proposición hace referencia a todos los individuos designados por ese término. Así las proposiciones universales sólo distribuyen el término sujeto y las proposiciones negativas el predicado.

Nosotros estamos usando una definición de silogismo categórico de forma estándar que incluye a la Regla1, entonces para evaluar un silogismo categórico de forma estándar, carece de utilidad tal regla y la vamos a omitir. Es decir, de ahora en adelante cuando digamos las reglas de Copi-Cohen, nos referimos a las reglas 2,3,4,5 y 6 para trabajar sin compromiso existencial, y 2,3,4 y 5 para trabajar con compromiso existencial.

El objetivo de este artículo es demostrar que las reglas de Copi-Cohen son una condición necesaria y suficiente de la validez de un silogismo categórico de forma estándar, donde un silogismo categórico de forma estándar es válido si su forma lógica correspondiente es válida. Esto lo haremos usando la noción de conjunto (o clase) y la técnica de los diagramas de Venn. Interpretamos lo que vamos a hacer como una fundamentación de tales reglas y que es original, pues no la hemos visto en ningún texto o artículo que conozcamos. Específicamente vamos a probar la siguiente proposición:

Proposición:   Un silogismo categórico de forma estándar es válido si y sólo si satisface las reglas 2-6 de Copi-Cohen.

Es decir, vamos a demostrar que dado un silogismo categórico de forma estándar cualquiera, si él cumple con las reglas, entonces él es válido (condición suficiente de las reglas). Y que si él es válido, entonces cumple con las reglas (condición necesaria de las reglas).

 

2. Prueba de la proposición

Para hacer la prueba de la proposición anterior vamos a fijar un silogismo categórico de forma estándar cualquiera q Y entonces verificaremos que se cumple la equivalencia:

q es válido si y sólo si q satisface las reglas 2-6 de Copi-Cohen,

donde las reglas 2-6 de Copi-Cohen las expresamos así:

Regla 2:El término medio de q está distribuido por lo menos en una de las premisas.

Regla 3:Si un término de q está distribuido en la conclusión, entonces está también distribuido en las premisas.

Regla 4:q no tiene dos premisas negativas.

Regla 5:Si alguna premisa de q es negativa, entonces la conclusión es negativa.

Regla 6:Si las dos premisas de q son universales, entonces su conclusión no es particular (es también universal).

Esto lo haremos en tres pasos:

a)   En primer lugar se procede a determinar mediante los diagramas de Venn cuáles de las 256 formas de silogismos categóricos de forma estándar posibles son válidas y cuales no.

b)   Usando (a) se demostrará que: Si q es válido entonces q cumple con las reglas.

c)    Finalmente, usando otra vez (a), se demostrará que: Si q cumple con las reglas entonces q es válido.

(a)  Análisis de las 256 formas de silogismos categóricos de forma estándar usando Diagramas de Venn:

A continuación se presentan cada una de las 256 formas posibles (64 de cada figura) de silogismos categóricos de forma estándar, con su respectivo Diagrama de Venn. Es pertinente resaltar que los silogismos están presentados en grupos de 4, todos ellos con un mismo diagrama, ya que a pesar de que difieren en la conclusión, tienen exactamente las mismas premisas, y por ende la misma representación gráfica. Sólo en los silogismos que han resultado válidos en este análisis exhaustivo, se ha resaltado su modo y el resultado (que indica válido) con negrilla. Para indicar la existencia de un individuo como lo refieren las proposiciones particulares, se ha usado un cuadradito gris en lugar de la “x”, y las zonas sombreadas en gris sugieren que son zonas vacías donde no existen individuos.

 

 

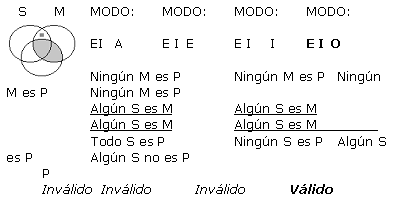
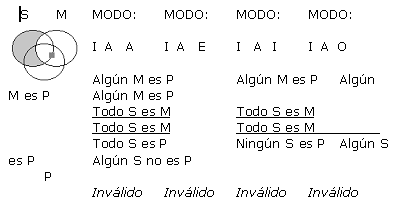
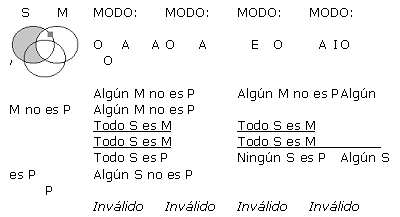
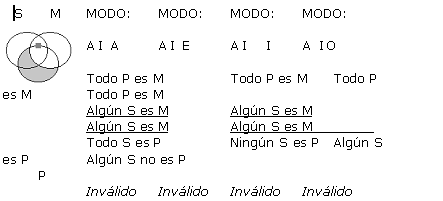
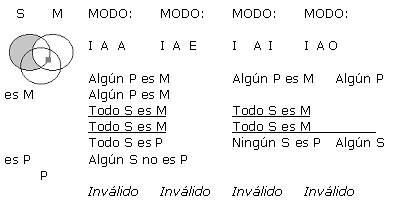
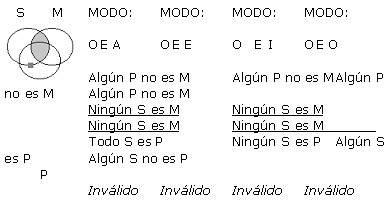
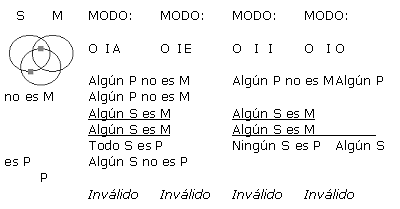
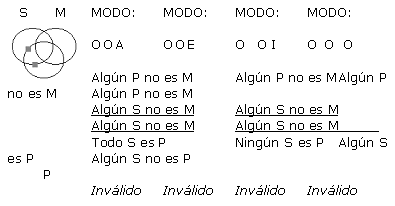
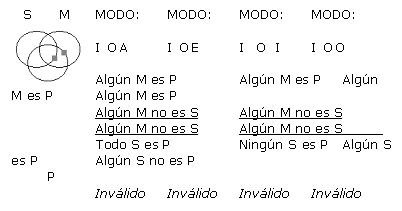
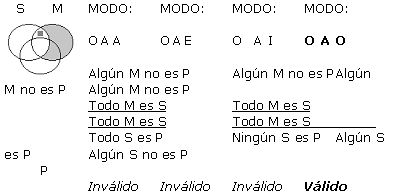
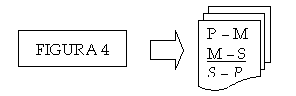
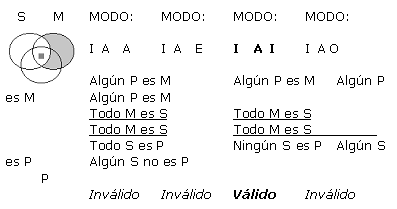
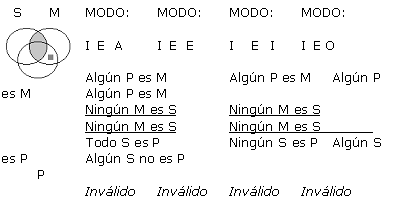
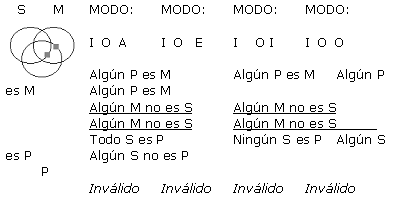
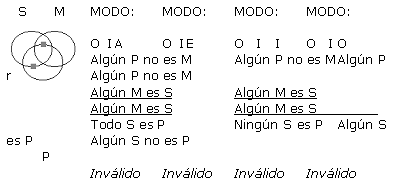
(a)   Supongamos que q es válido. Se probará que q satisface las reglas 2-6 de Copi.

Como q es válido la forma lógica de q tiene sólo 15 modos posibles de ser, según (a):

Figura 1: AAA, AII, EAE, EIO.   Figura 3: AII, EIO, IAI, OAO.

Figura 2: AEE, AOO, EAE, EIO. Figura 4: AEE, EIO, IAI.

 Y cada uno de estos modos satisface las reglas 2-6 de Copi-Cohen, en efecto:

(1) Con respecto a la regla 2, en todos los modos válidos de la figura 1 el término medio queda distribuido siempre en la premisa mayor, ya que las premisas universales distribuyen el sujeto y para la figura 1, el término medio está ubicado en el sujeto de la premisa mayor. De igual manera sucede con los modos Datisi y Ferison de la figura 3; pero en el caso de Disamis y Bocardo, el término medio queda distribuido por las proposiciones universales ubicadas en la premisa menor. En la figura 2, el término medio está ubicado como predicado de las proposiciones y queda distribuido en la premisa menor de los modos Camestres, Baroco, y en la premisa mayor de los modos Cesare y Festino, puesto que estas premisas son negativas. Para la figura 4 el término medio queda distribuido en el sujeto de la premisa menor en los modos Camenes y Dimaris, y en la premisa mayor de Fresison.

(2) La regla 3 se puede verificar en cada uno de los esquemas que se presenta a continuación para todos los modos que no tienen conclusión particular afirmativa (I). Los términos distribuidos se representan en negrilla con color Fucsia, y puede observarse como todos los términos que están distribuidos en la conclusión, también lo están en la premisa donde aparecen.

                                              Barbara                    Celarent                        Ferio

  A Todo M es P            E Ningún M es P                 E Ningún M es P

Figura 1       A Todo S  es M         A Todo S  es M I                  Algún S es M

          A Todo S  es P            E Ningún S  es P  O            Algún  S  no es  P 

Camestres             Baroco                      Cesare                   Festino

Figura 2   A Todo P es M       A Todo P es M       E Ningún P es M         E Ningún P  es M

                E Ningún S  es M     O Algún S no es M   A Todo S es M      I Algún S es M

                E Ningún S es P        O Algún S no es P    E Ningún S es P  O Algún S no es P

 

          Figura 3                                  Figura 4        

       Ferison     Bocardo                         Camenes     Fresison

             E Ningún M es P    O Algún M no es P            A Todo P es M   E Ningún P es M

             I Algún M es S              A Todo M es S                      E Ningún M es S    I Algún M es S      

O Algún S no es P m    O Algún S no es P              E Ningún S es P     O Algún S no es P

(3)En último lugar, ninguno de los 15 modos silogísticos presentados anteriormente tiene dos premisas negativas (regla 4), una premisa negativa sin que la conclusión también lo sea (regla 5), o premisas universales y una conclusión particular (regla 6). Por lo que queda entonces demostrado que q cumple con las reglas de Copi-Cohen, si q es válido.

(c) Supongamos que q cumple las reglas 2-6 de Copi-Cohen. Se probará que q es válido.

(Por absurdo). Si q es inválido, entonces la forma lógica de q tiene 241 modos posibles de ser, como se ha visto en la cláusula (a). Todos estos modos están sistematizados en las cuatro tablas que están después del siguiente párrafo (Ver).

Se puede notar en las tablas que cada modo inválido viola al menos 1 de las reglas 2-6 de Copi-Cohen. Esto contradice la hipótesis y por lo tanto, se concluye que q no puede ser inválido si satisface las reglas 2-6 de Copi-Cohen. Es decir, Si q cumple con las reglas entonces q es válido. Con esto termina la demostración de que las reglas 2-6 de Copi-Cohen son una condición necesaria y suficiente de la validez de los silogismos categóricos de forma estándar.

figura1

Modo

Contradic.

 

Modo

Contradic.

No cumple regla Nº

 

No cumple regla Nº

A

A

A

válido

 

I

A

A

2

A

A

E

3

 

I

A

E

2, 3

A

A

I

6

 

I

A

I

2

 

A

A

O

3, 6

 

I

A

O

2, 3

A

E

A

5

 

I

E

A

5

A

E

E

3

 

I

E

E

3

A

E

I

5, 6

 

I

E

I

5

A

E

O

3, 6

 

I

E

O

3

A

I

A

3

 

I

I

A

2, 3

A

I

E

3

 

I

I

E

2, 3

A

I

I

válido

 

I

I

I

2

A

I

O

3

 

I

I

O

2, 3

A

O

A

3, 5

 

I

O

A

3, 5

A

O

E

3

 

I

O

E

3

A

O

I

5

 

I

O

I

5

A

O

O

3

 

I

O

O

3

E

A

A

5

 

O

A

A

2, 5

E

A

E

válido

 

O

A

E

2, 3

E

A

I

5, 6

 

O

A

I

2, 5

E

A

O

6

 

O

A

O

2

E

E

A

4

 

O

E

A

4

E

E

E

4

 

O

E

E

4

E

E

I

4, 6

 

O

E

I

4

E

E

O

4, 6

 

O

E

O

4

 

figura 2

 

Modo

Contradic.

 

Modo

Contradic.

 

No cumple  regla Nº

 

No cumple regla Nº

 

A

A

A

2

 

I

A

A

2

 

A

A

E

2

 

I

A

E

2, 3

 

A

A

I

2, 6

 

I

A

I

2

 

A

A

O

2, 6

 

I

A

O

2, 3

 

A

E

A

5

 

I

E

A

5

 

A

E

E

válido

 

I

E

E

3

 

A

E

I

5, 6

 

I

E

I

5

 

A

E

O

6

 

I

E

O

3

 

A

I

A

2, 3

 

I

I

A

2, 3

 

A

I

E

2, 3

 

I

I

E

2, 3

 

A

I

I

2

 

I

I

I

2

 

A

I

O

2

 

I

I

O

2, 3

 

A

O

A

3, 5

 

I

O

A

3, 5

 

A

O

E

3

 

I

O

E

3

 

A

O

I

5

 

I

O

I

5

 

A

O

O

válido

 

I

O

O

3

 

E

A

A

5

 

O

A

A

5

 

E

A

E

válido

 

O

A

E

3

 

E

A

I

5, 6

 

O

A

I

5

 

E

A

O

6

 

O

A

O

3

 

E

E

A

4

 

O

E

A

4

 

E

E

E

4

 

O

E

E

3, 4

 

E

E

I

4, 6

 

O

E

I

4

 

 

 

Figura 1

Modo

Contradic.

 

Modo

Contradic.

No cumple regla Nº

 

No cumple regla Nº

E

I

A

3, 5

 

O

I

A

2, 3, 5

E

I

E

3

 

O

I

E

2, 3

E

I

I

5

 

O

I

I

2, 5

E

I

O

válido

 

O

I

O

2

E

O

A

3, 4, 5

 

O

O

A

3, 4

E

O

E

4

 

O

O

E

3, 4

E

O

I

4, 5

 

O

O

I

4

E

O

O

4

 

O

O

O

4

 

Figura 2

Modo

Contradic.

 

Modo

Contradic.

No cumple  regla Nº

 

No cumple regla Nº

E

I

A

3, 5

 

O

I

A

3, 5

E

I

E

3

 

O

I

E

3

E

I

I

5

 

O

I

I

5

E

I

O

válido

 

O

I

O

3

E

O

A

3, 4, 5

 

O

O

A

3, 4

E

O

E

3, 4

 

O

O

E

3, 4

E

O

I

4, 5

 

O

O

I

4

E

O

O

4

 

O

O

O

3, 4

 

Figura 3

Modo

Contradic.

 

Modo

Contradic.

No cumple regla Nº

 

No cumple regla Nº

A

A

A

3

 

I

A

A

3

A

A

E

3

 

I

A

E

3

A

A

I

6

 

I

A

I

Válido

A

A

O

3, 6

 

I

A

O

3

A

E

A

5

 

I

E

A

5

A

E

E

3

 

I

E

E

3

A

E

I

5, 6

 

I

E

I

5

A

E

O

3, 6

 

I

E

O

3

A

I

A

3

 

I

I

A

2, 3

A

I

E

3

 

I

I

E

2, 3

A

I

I

válido

 

I

I

I

2

A

I

O

3

 

I

I

O

2, 3

A

O

A

5

 

I

O

A

2, 5

A

O

E

3

 

I

O

E

2, 3

A

O

I

5

 

I

O

I

2, 5

A

O

O

3

 

I

O

O

2, 3

E

A

A

3, 5

 

O

A

A

3, 5

E

A

E

3

 

O

A

E

3

E

A

I

5, 6

 

O

A

I

5

E

A

O

6

 

O

A

O

Válido

E

E

A

4

 

O

E

A

4

E

E

E

4

 

O

E

E

4

 

Figura 4

Modo

Contradic.

 

Modo

Contradic.

No cumple regla Nº

 

No cumple regla Nº

A

A

A

3

 

I

A

A

3

A

A

E

3

 

I

A

E

3

A

A

I

6

 

I

A

I

válido

A

A

O

6

 

I

A

O

3

A

E

A

5

 

I

E

A

5

A

E

E

válido

 

I

E

E

3

A

E

I

5, 6

 

I

E

I

5

A

E

O

6

 

I

E

O

3

A

I

A

2, 3

 

I

I

A

2, 3

A

I

E

2, 3

 

I

I

E

2, 3

A

I

I

2

 

I

I

I

2

A

I

O

2

 

I

I

O

2, 3

A

O

A

2, 5

 

I

O

A

2, 5

A

O

E

2

 

I

O

E

2, 3

A

O

I

2, 5

 

I

O

I

2, 5

A

O

O

2

 

I

O

O

2, 3

E

A

A

3, 5

 

O

A

A

3, 5

E

A

E

3

 

O

A

E

3

E

A

I

5, 6

 

O

A

I

5

E

A

O

6

 

O

A

O

3

E

E

A

4

 

O

E

A

4

E

E

E

4

 

O

E

E

3, 4

 

Figura 3

Modo

Contradic.

 

Modo

Contradic.

No cumple regla Nº

 

No cumple regla Nº

E

E

I

4, 6

 

O

E

I

4

E

E

O

4, 6

 

O

E

O

4

E

I

A

3, 5

 

O

I

A

2, 3, 5

E

I

E

3

 

O

I

E

2, 3

E

I

I

5

 

O

I

I

2, 5

E

I

O

válido

 

O

I

O

2

E

O

A

4, 5

 

O

O

A

2, 4

E

O

E

4

 

O

O

E

2, 4

E

O

I

4, 5

 

O

O

I

2, 4

E

O

O

4

 

O

O

O

2, 4

 

Figura 4

 

Modo

Contradic.

 

Modo

Contradic.

No cumple regla Nº

 

No cumple regla Nº

E

E

I

4, 6

 

O

E

I

4

E

E

O

4, 6

 

O

E

O

3, 4

E

I

A

3, 5

 

O

I

A

3, 5

E

I

E

3, 5

 

O

I

E

3

E

I

I

5

 

O

I

I

5

E

I

O

válido

 

O

I

O

3

E

O

A

4, 5

 

O

O

A

4

E

O

E

4

 

O

O

E

3, 4

E

O

I

4, 5

 

O

O

I

4

E

O

O

4

 

O

O

O

3, 4

Escuela de Filosofía

Universidad Central de Venezuela

Instituto de Filosofia. apartado 47342. caracas 1041-A. Venezuela