Tecnologias informáticas, constructivismo y pedagogia por projetos: perspectivas de formación inicial de profesores de Matemática

Adriana Richit, Marcus Vinicius Maltempi

Universidade Estadual Paulista – UNESP Rio Claro, SP, Brasil. (adrianarichit@gmail.com) (maltempi@rc.unesp.br)

RESUMEN

Presentamos, en este artículo, parte de los resultados de una investigación que buscó describir y analizar la forma de trabajo con proyectos en geometría analítica, utilizando software de geometría dinámica, con el objetivo de favorecer la formación de futuros profesores de matemáticas. La investigación, de naturaleza cualitativa (Borba y Araújo, 2004; Denzin y Lincoln, 2000 y Goldenberg, 2003), se desarrolló con estudiantes en el primer año de licenciatura en matemáticas de UNESP de Rio Claro, Brasil, con quienes se prepararon actividades didácticas de geometría analítica, utilizando un software de geometría dinámica (Geometricks); actividades éstas que se constituyeron en proyectos temáticos en matemáticas. Los resultados señalan que la combinación de trabajo con proyectos y tecnología fue una estrategia que favoreció la formación docente en relación con los conocimientos específicos de la disciplina y permitió la adquisición de nociones pedagógicas en la utilización de los programas informáticos apoyados con investigación aplicadas a situaciones propias de la práctica docente de los futuros profesores de matemáticas. Los resultados también destacan aspectos del trabajo con proyectos los cuales se ajustan a los preceptos del constructivismo.

Palabras Clave: Tecnologías Informáticas. Constructivismo. Pedagogía de Proyectos

Educação Matemática, construcionismo e pedagogia de projetos: perspectivas à formação inicial de professores

Resumo

Neste artigo apresentamos alguns resultados de uma pesquisa, a qual buscou descrever e analisar como trabalhar com projetos em geometria analítica, usando software de geometria dinâmica, visando a favorecer a formação de futuros professores de Matemática. A pesquisa, de natureza qualitativa (Borba e Araújo, 2004; Denzin e Lincoln, 2000 e Goldenberg, 2003), foi desenvolvida com alunos do primeiro ano da Licenciatura em Matemática da UNESP de Rio Claro, Brasil, os quais se engajaram na elaboração de atividades didáticas de geometria analítica, utilizando um software de geometria dinâmica (Geometricks), atividades estas que se constituíram em projetos temáticos em Matemática. Os dados do estudo sinalizam que a combinação do trabalho com projetos e tecnologia mostrou-se uma estratégia pedagógica favorável à formação inicial docente em Matemática, a apropriação de conhecimentos específicos, a aquisição de noções de uso didático do software e o envolvimento dos licenciandos com situações da prática docente. Ressaltam, também, aspectos do trabalho com projetos que se coadunam aos preceitos do Construcionismo.

Palavras-chave: Tecnologias Informáticas. Construcionismo. Pedagogia de Projetos.

Informatics technologies, constructionism and projects pedagogy: perspectives to Mathematics teachers pre-service education

Abstract

In this paper we present some results of a study by the Graduate Program in Mathematics Education of UNESP at Rio Claro, Brazil. The purpose was to describe and analyze how to work with analytical geometry projects using dynamic geometry software, benefiting the education of future mathematics teachers. The study, of qualitative nature (Borba and Araújo, 2004; Denzin and Lincoln, 2000 and Goldenberg, 2003), was conducted with first year undergraduate students of Mathematics from UNESP, and developed teaching activities of analytic geometry using a dynamic geometry software (Geometricks). These activities composed the thematic projects in mathematics. The data from the study indicated that the combination of projects and technology favored teacher training, mathematic learning, acquisition of pedagogical notions, use of software supported by research and involvement of future mathematics teachers with situations of teaching practice. It also shows aspects of work with projects that are in line with the requirements of Constructionism.

Key words: Informatics Technologies. Constructionism, Pedagogy of Projects.

Recibido: 07/05/2008.   Aceptado: 15/10/2009

Introdução

Posto que as tecnologias da informação e comunicação (TIC) estão presentes no contexto de diversas culturas e realidades sociais, mediando relações interpessoais, redefinindo profissões, modificando as operações comerciais e potencializando os mecanismos de comunicação e transmissão de informações (Lévy, 1998; 1999), sentimo-nos, enquanto professores e pesquisadores, comprometidos com o propósito de incorporarmos esses recursos aos processos educacionais, pois a escola, por constituir-se em espaço formativo, precisa corresponder às demandas coletivas do contexto em que está inserida.

No Brasil, a preocupação com a incorporação de tecnologias na prática educativa tem mobilizado muitos estudos e, com isso, tem se constituído em tema central nas discussões promovidas em eventos na área de educação e educação matemática. Em análise acerca dos temas evidenciados recentemente em eventos como o Encontro Nacional de Educação Matemática (ENEM), Encontro Nacional de Didática e Prática de Ensino (ENDIPE), Congresso Internacional de Ensino de Matemática (CIEM) e Encontro Brasileiro de Estudantes de Pós-Graduação em Educação Matemática (EBRAPEM), apuramos que diversas questões sobre o impacto das mudanças sociais no contexto educacional, incluindo aquelas propiciadas pela evolução das tecnologias (NOTA 1), têm sido debatidas e fomentado experiências/estratégias educativas diferenciadas.

Focando as implicações da presença das tecnologias no contexto educacional Lévy (1998, p.27) diz que “antes mesmo de influir sobre o aluno, o uso dos computadores obriga os professores a repensar o ensino de sua disciplina”. Além disso, segundo Marinho (2002, p.42), mobilizados pela dinamicidade social os agentes escolares tomam consciência de que a “escola está sendo desafiada num processo de reformulação necessária para atender às exigências contemporâneas de uma educação de qualidade. A questão da obrigação da escola de preparar alunos para uma sociedade informatizada está clara para alunos e professores”.

Diante disso consideramos que as transformações sociais e a evolução das tecnologias, juntamente com as reflexões em torno do papel da educação na realidade atual, deflagram mudanças no contexto educacional, incluindo-se modificações curriculares, teóricas e na prática docente, como por exemplo, as estratégias pedagógicas empreendidas em sala de aula (Richit y Maltempi, 2005). Nesse movimento de mudança, estratégias pedagógicas como o trabalho com projetos vêm sendo retomadas e revelando novas dimensões, à medida que tecnologias são articuladas a essas práticas educativas.

Analisando aspectos do trabalho educativo por projetos, discutidos por Hernández y Ventura (1998), Dewey (1959), Hernández (1998) e Sidericoudes (2004), e as dimensões do Construcionismo discutidas por Maltempi (2004) e Valente (1993; 1999), vislumbramos possibilidades de repensar a formação inicial docente em Matemática. Consideramos que a realização de atividades formativas que promovam o desenvolvimento de projetos temáticos, usando recursos que propiciem abordagens diferenciadas do conteúdo matemático, em consonância com os princípios do Construcionismo, é uma estratégia pedagógica que favorece o desenvolvimento de noções de uso pedagógico das tecnologias de forma articulada ao processo de construção do conhecimento específico (matemático) e pedagógico.

Desse entendimento emerge a concepção de formação inicial docente defendida nesse artigo, a qual, para nós, sintetiza o processo que unifica a formação pedagógica (questões relativas à prática de sala de aula, desenvolvimento de estratégias pedagógicas, legislação educacional, fundamentos sociológicos, pedagógicos e psicológicos da educação), específica (conteúdo matemático) e tecnológica (conhecimentos relativos ao uso de tecnologias na abordagem de conteúdos curriculares).

Para embasar a discussão sobre nossa concepção de formação inicial, primeiramente, vamos explicitar o contexto da pesquisa que subsidia as considerações aqui apresentadas.

Contexto do Estudo e Delineamentos Metodológicos

O estudo realizado por Richit (2005), o qual teve o propósito de descrever e analisar como trabalhar com projetos em geometria analítica, usando software de geometria dinâmica, visando a contribuir com a formação de futuros professores de Matemática, baseou-se na metodologia de pesquisa qualitativa, segundo concepção de Denzin e Lincoln (2000), Goldenberg (2003), e Borba e Araujo (2004). Para tanto, os dados foram coletados em uma intervenção pedagógica, pautada no desenvolvimento de projetos temáticos em Matemática, constituída de nove encontros semanais de aproximadamente três horas cada.

A referida pesquisa é de natureza qualitativa, pois buscou uma interpretação detalhada do processo de formação inicial investigado. Para alcançar esse aprofundamento, tal como propõe Goldenberg (2003), foi necessário um contato direto e prolongado da pesquisadora com o contexto e a situação estudada. Ainda, a possibilidade de um estudo favorecer a formulação de novas teorias, segundo Denzin e Lincoln (2000), é característica de investigações de caráter qualitativo, visto que tais estudos não buscam validar teorias já estabelecidas, mas sim contribuir à elaboração de novas teorias a partir do aprofundamento da interpretação e compreensão de uma situação ou fenômeno analisado.

Participaram dos encontros a professora-pesquisadora (primeira autora deste artigo) e seis alunos do primeiro ano da licenciatura em Matemática da UNESP de Rio Claro, em Regime Especial de Recuperação (RER, NOTA 2) na disciplina de geometria analítica. Nesses encontros os participantes, agrupados em duplas, envolveram-se no desenvolvimento de projetos focando conteúdos dessa disciplina, usando um software de geometria dinâmica (Geometricks, NOTA 3), o qual permite a representação de figuras geométricas que podem ser deformadas ou arrastadas, conservando-se as propriedades específicas das mesmas.

Os alunos foram selecionados levando-se em conta o interesse demonstrado pelo trabalho que seria desenvolvido e a disponibilidade de tempo para participar da investigação. Posterior a seleção, os licenciandos divididos em duplas, engajaram-se no desenvolvimento de atividades didáticas, focando conteúdos diversos de geometria analítica, privilegiando o uso do software Geometricks. A criação do ambiente de aprendizagem que pautou o desenvolvimento dos projetos foi norteada pelos princípios do Construcionismo abordados por Papert (1985; 1994), Valente (1999; 2003a; 2003c) e Maltempi (2004; 2005).

Os projetos temáticos elaborados foram apresentados, formalmente, aos colegas engajados na pesquisa em uma sessão destinada à socialização dos trabalhos. Esse encontro contou com a presença de um colega da turma que não estava em RER e do professor de geometria analítica da respectiva instituição no corrente ano, o qual colaborou tecendo comentários sobre as atividades expostas.

Ressaltamos, ainda, que a realização da pesquisa-intervenção, relatada nesse artigo, foi conduzida e desenhada tendo em conta a necessidade de prover aos futuros professores de Matemática uma formação contextualizada. Isto é, partimos do pressuposto que a apropriação do conhecimento específico (matemático) precisa articular-se ao desenvolvimento de noções de uso didático das tecnologias informáticas, por meio do envolvimento dos licenciandos com situações da prática docente, como a elaboração de atividades para o ensino.

Sumarizando, a estratégia pedagógica, que associou o trabalho com projetos ao uso de tecnologias, em consonância com os pressupostos teóricos do Construcionismo, constituiu-se numa forma de entrelaçar o uso das mídias informáticas às experiências educacionais de futuros professores de Matemática. Ademais, tiveram autonomia para pesquisar, construir e reconstruir representações, propor e verificar conjecturas, bem como elaborar projetos envolvendo múltiplos conceitos.

Construcionismo, Projetos e Formação Inicial Docente: Considerações Iniciais

O Construcionismo, iniciado pelo matemático sul-africano Seymour Papert, é uma teoria educacional baseada no Construtivismo que propõe o processo de aprendizagem baseado na interação do aluno com as tecnologias. Nessa interação o aprendiz assume, auxiliado pelo professor, a direção da sua aprendizagem, estabelecendo os procedimentos e as atividades que vão ser realizadas, bem como os recursos e caminhos a serem percorridos.

Essa teoria sugere que ao interagir com as tecnologias o aluno é instigado a investigar, pesquisar e refletir sobre o objeto da sua investigação ou criação. Papert (1994) comenta que a interação do aprendiz com o computador torna-se um meio eficiente de aprendizagem, à medida que o aluno é estimulado a buscar novas informações para satisfazer necessidades pessoais, as quais o levam a uma reorganização cognitiva e, portanto, à construção do conhecimento.

Assim, entendemos que a constituição de um ambiente de aprendizagem propício a investigação matemática, em consonância com essa teoria, implica na reorganização do processo de ensino de modo que o aluno torne-se um agente ativo do processo educativo. Nesse ambiente o professor também precisa atuar como estimulador da investigação e da reflexão e como mediador da interação dos estudantes com as tecnologias, enquanto que as tecnologias são assumidas como fomentadoras à investigação e à produção matemática.

Uma das características do ambiente de aprendizagem construcionista refere-se aos diferentes estilos de realizar uma dada atividade, os quais, segundo Papert (1991), vão dos que planejam tudo antecipadamente aos que improvisam cada procedimento enquanto os realizam – este último, Papert denominou bricolage. Este termo é também usado para designar o conjunto de procedimentos adotados pelo sujeito que, ao não dispor de um recurso adequado para resolver um dado problema, recorre a outro disponível e procura adequá-lo à situação.

Teorizando sobre o papel das tecnologias no processo de construção do conhecimento, Papert (2003) tece considerações sobre a pedagogia do poder das idéias e diz que a aprendizagem pode tornar-se mais interessante se estiver pautada em estratégias de trabalho que se baseiam nas idéias dos sujeitos, como a realização de projetos, por exemplo.

Corroborando a Papert, avaliamos que a realização de atividades baseadas nas idéias dos licenciandos, como o desenvolvimento de projetos, que coadunam a abordagem de conteúdos específicos ao uso de tecnologias, propicia diversas possibilidades de favorecermos a formação inicial docente, pois é uma forma de ampliarmos as experiências formativas de futuros professores acerca do uso didático desses recursos e do conteúdo matemático, ao mesmo tempo em que são confrontados com situações específicas da prática docente.

Por pedagogia de projetos estamos nos referindo à estratégia pedagógica que consiste em “dar forma a uma idéia que está no horizonte, mas que admite modificações, está em diálogo permanente com o contexto, com as circunstâncias e com os indivíduos que, de maneira ou outra, vão contribuir para esse processo (Hernández, 1998, p.22).

Sidericoudes (2004, p.77) comenta que o trabalho pedagógico por projetos é uma prática educativa reconhecida em diferentes períodos do século XX, sob as denominações “métodos de projetos, centros de interesse, trabalho por temas, pesquisa do meio, projetos de trabalho e outros que respondem a visões diferentes e a variações de contexto e conteúdo”.

Ao evidenciar as possibilidades advindas do trabalho educacional por projetos, Hernández e Ventura (1998) avaliam que estes devem favorecer a criação de estratégias de organização dos conhecimentos curriculares, as quais privilegiem o tratamento da informação e a relação entre os conteúdos em torno de problemas ou hipóteses. Tais situações devem propiciar ao aluno “a construção de conhecimentos, a transformação da informação procedente dos diferentes saberes disciplinares em conhecimento próprio” (p.61). Ademais, Dewey (1959) argumenta que o trabalho por projetos precisa ser integrado às atividades de sala de aula e privilegiar as dimensões interesse, interdisciplinaridade, valor intrínseco e duração para que seja uma atividade verdadeiramente educativa.

Diante do exposto e assumindo o trabalho por projetos como sendo uma atividade educacional favorável à criação de ambientes de aprendizagem pautados no Construcionismo, procuramos evidenciar na pesquisa realizada aspectos que explicitassem as possibilidades advindas da incorporação das tecnologias às práticas educativas por projetos na formação inicial docente em Matemática, aspectos esses que serão discutidos a seguir.

Projetos e Tecnologias na Perspectiva do Construcionismo: entrelaçando a formação específica, pedagógica e tecnológica de futuros professores de Matemática

Dentre os aspectos que caracterizaram a intervenção realizada, o qual foi apontado pelos licenciandos como condição favorável à aprendizagem de conceitos de geometria analítica e ao desenvolvimento deles, foi o caráter construcionista da mesma, conforme podemos constatar nos depoimentos que seguem. A estratégia pedagógica adotada no trabalho com os projetos deu-lhes a sensação de autonomia no seu processo de formação, conforme preconizado pelo Construcionismo. Na pesquisa-intervenção investigada, as duplas de estudantes puderam escolher os temas de geometria analítica que seriam desenvolvidos nas atividades, realizar as construções usando procedimentos distintos, bem como estruturar os projetos à sua maneira, sempre com o apoio da professorapesquisadora.

O excerto seguinte expõe a avaliação da estudante P (NOTA 4) acerca da estratégia pedagógica adotada na elaboração dos projetos. Nesse depoimento ela enfatiza a autonomia que lhes foi concedida no desenvolvimento das atividades, princípio esse defendido por Maltempi (2004, 2005), Valente (1993; 1999), Almeida (2003), Papert (1994; 2003) e Richit (2005; 2006) como sendo condição favorável à construção do conhecimento.

PE: Com relação à estratégia adotada na elaboração dos projetos, você achou esta forma de trabalhar positiva? ¿Por quê?

P: Eu gostei, porque a gente se sentiu à vontade para fazer o que queria e abordar o assunto que a gente achava mais interessante. Porque tinha o livro do Paulo Boulos [livro de geometria analítica usado em sala de aula] inteiro e a gente pôde escolher o assunto que a gente quis de verdade, entendeu? Isso é bom porque a gente se motiva mais a fazer o que a gente está fazendo. Porque aí a gente tem mais vontade de fazer. Se você fala pra gente fazer um trabalho sobre cônicas e a gente não gosta de cônicas, por exemplo, eu não vou ter vontade de fazer.. Só que no caso, os que a gente escolheu foram os que a gente queria fazer... Que a gente tinha vontade de desenvolver.

A avaliação dessa estudante, assim como de outros sujeitos da pesquisa, ressalta algumas das dimensões do trabalho com projetos como o interesse e o valor intrínseco, as quais são propostas por Dewey (1959). Identificamos em alguns depoimentos e também nas falas deles durante as interações com a professora-pesquisadora, indicativos de que a dimensão valor intrínseco foi preponderante no desenvolvimento dos projetos, pois cada tema focado ou era o conteúdo preferido da dupla ou o conteúdo que a dupla teve mais dificuldade na disciplina semestral.

Do mesmo modo, a dimensão interesse mostrou-se relevante na pesquisa-intervenção implementada e foi apontada pelos futuros professores como sendo essencial à aprendizagem em geometria analítica, conforme podemos verificar no excerto a seguir.

PE: ¿Você acha que a investigação de temas relacionados à geometria analítica pode ser mais favorável à aprendizagem se esta partir do interesse do aluno?

V: Sim, acho, porque você demonstrando mais interesse relacionado a uma investigação dos temas de geometria analítica que partiu de você ter escolhido, abrange mais as suas expectativas e seu empenho quanto à matéria melhora.

E: Se for de meu interesse estarei fazendo uma coisa que gosto e tudo que você faz quando gosta tem melhores resultados.

Pautando-nos nesses depoimentos e nas observações realizadas na pesquisa-intervenção, inferimos que a aprendizagem por projetos na formação inicial docente, apoiada nos pressupostos do Contrucionismo, pode contribuir para o amadurecimento pessoal dos licenciandos, aspecto este que se reflete na sua postura consciente frente às situações e desafios que se apresentam nesse processo e acerca do seu compromisso com o conteúdo.

PE: Pensando na estratégia que adotamos para elaborar os projetos, na qual você teve liberdade para escolher o assunto que quis ou que você mais gostava. Isso não é ruim? Como fica o restante do conteúdo?

P: Ah! Vendo por esse lado é ruim, porque aí, muitas vezes, a gente deixa de trabalhar algum conteúdo, de fazer outras coisas, mas mesmo assim eu acho legal porque a gente se desenvolve. Tem um monte de desafio no meio disso, porque não está tudo prontinho para a gente. Se estiver tudo pronto, a gente não vai precisar correr atrás das coisas e tal. [...]. Porque na hora de fazer a atividade prática mesmo, é que a gente vai aprender.

A fala da depoente P evidencia a postura consciente dessa estudante no que diz respeito à predominância da dimensão interesse no trabalho com projetos. Segundo essa avaliação, deve haver uma dosagem adequada de interesse combinada com o cumprimento do programa curricular da disciplina, pois essa dimensão favorece o desenvolvimento dos futuros professores, à medida que os remete a novos desafios.

Analogamente, avaliamos que a experiência, mesmo sendo pontual, pode ter contribuído para melhorar a auto-estima dos alunos engajados na investigação, visto que eles tiveram a possibilidade de produzir algo de interesse e domínio público, aspecto este que colaborou para que se sentissem capazes e úteis, além de ter favorecido a inclusão social dos mesmos no âmbito da turma e da instituição. O depoimento abaixo exibe a avaliação dessa mesma estudante sobre tal questão.

PE: Como aluna, você acha que o trabalho que foi desenvolvido aqui pode ter te ajudado em algo mais, além da formação matemática?

P: Pelo fato da gente ter ficado em RER, deu um baque em todo mundo, sabe. Aí a gente foi convidado para fazer esse trabalho aqui, então a gente viu que também era capaz de fazer as coisas, entendeu. A gente aprendeu algumas coisas e agora a gente pode aprofundar, tanto a geometria analítica quanto sobre o Geometricks.

Pontuamos, ainda, como sendo aspecto relevante no trabalho empreendido a atitude de colaboração demonstrada entre os licenciandos, a qual entendemos ser uma atitude essencial ao exercício da profissão docente. Não raro, durante a pesquisa-intervenção, integrantes de duplas distintas discutiam entre si conceitos e propriedades abordadas nos projetos e sobre a forma como as atividades estavam sendo apresentadas, propondo sugestões que pudessem melhorá-las, conforme ilustra o recorte seguinte.

B: ¿O que é que você está fazendo aí? Uma elipse?

L: É.

B: ¿Como você começou essa atividade?

L: Eu tenho a equação aqui [mostra o rascunho] e daí eu achei o valor de c e a [...] e com isso vou construir a elipse no Geometricks.

B: Mas você não tem um problema aqui. Nem enunciado. Nada.

L: Depois eu penso nisso [conversam sobre outros assuntos].

B: Me ajuda então.Vamos começar do início. Vamos escrever o objetivo da atividade. Poderia ser: [..].

Confrontando as peculiaridades do ambiente de aprendizagem promovido à realização da pesquisa com as características do ambiente construcionista discutidas por Maltempi (2004; 2005), Valente (2003a; 2003b; 2003c) e Papert (1991; 1994; 2003), avaliamos que houve convergência entre ambos. Ou seja, as situações vivenciadas pelos licenciandos favoreceram a investigação matemática, a criação, o envolvimento deles com o trabalho proposto, iniciativa à tomada de decisão, a curiosidade, a experimentação. Essas situações abrangem os aspectos interesse e valor intrínseco, discutidos por Dewey (1959), e correspondem às dimensões sintônica e pragmática, respectivamente, norteadoras da criação de ambientes de aprendizagem construcionista segundo Maltempi (2004).

As tecnologias viabilizaram a intervenção proposta, possibilitando aos alunos desenvolverem seus projetos em um prazo razoável, oferecendo feedbacks imediatos de suas ações sobre o conteúdo de geometria analítica. Além disso, à medida que eles elaboravam as atividades didáticas, desenvolvendo-as com os colegas, vivenciavam situações da prática pedagógica nessa disciplina, as quais desencadeavam reflexões sobre formação e prática docente em matemática, bem como sobre o uso didático das tecnologias.

A análise dos projetos (NOTA 5) elaborados pelas duplas fornece indicativos de que a experiência realizada na pesquisa proporcionou o aprofundamento do conhecimento em geometria analítica e do software utilizado na pesquisa, favoreceu o compartilhamento de experiências e a ajuda mútua, contribuindo, destarte, com a formação inicial docente desses futuros professores nas três dimensões sugeridas.

O recorte do projeto desenvolvido pela dupla composta pelos estudantes P e V, apresentado a seguir, ilustra a familiaridade dos mesmos com as funcionalidades do software Geometricks, visto que realizaram as representações sem recorrer à ajuda da professora-pesquisadora e usando procedimentos distintos. Evidencia, ainda, o aprofundamento dado ao conteúdo focado na atividade, visto que a dupla demonstrou preocupação em articular o tema central da questão a outros conceitos e conteúdos matemáticos, principalmente de geometria euclidiana plana.

Posterior a apresentação do enunciado da atividade, os estudantes descreveram os procedimentos utilizados na construção do modelo geométrico ilustrativo da mesma e, também, propuseram dicas e orientações que podem ser consideradas no processo de resolução. Esclarecemos ao leitor que as etapas da representação realizada no software, descritas pela dupla no projeto original, foram omitidas no recorte que segue, pois objetivamos evidenciar o processo analítico proposto como solução.

Para realizar a representação do quadrilátero PQRS a dupla necessitou explorar vários recursos do software, como a opção ponto médio, mediatriz, segmento (po, po), os menus medidas de ângulos e distâncias entre pontos, bem como o recurso construção de fractais, o qual foi usado para colorir a figura, melhorando a visualização dos conceitos e propriedades relacionadas à atividade. Também utilizaram menus específicos na representação de conceitos geométricos fundamentais, tais como pontos, ângulos, semi-retas e retas.

Considerando que as duplas, inclusive a que elaborou a atividade exibida nessa seção, apresentaram boa fluência no manuseio do software e procuraram ampliar as atividades propondo diferentes soluções, inferimos que por meio do trabalho desenvolvido, esses estudantes puderam desenvolver noções de uso didático do Geometricks entrelaçadas a construção do conhecimento em geometria analítica. Além disso, pelo fato da abordagem do conteúdo estar voltada ao contexto da prática docente, consideramos que a experiência favoreceu a formação inicial desses futuros professores, também, na dimensão pedagógica.

Sumarizando, avaliamos que a estratégia pedagógica investigada em Richit (2005; 2006) mostrou-se favorável à formação específica, pedagógica e tecnológica dos sujeitos engajados na pesquisa e, portanto, aponta perspectivas às licenciaturas em Matemática.

O Ensino de Matemática com Tecnologias Informáticas na Visão de Futuros Professores

Olhando para o processo de construção do conhecimento específico (matemático) na formação inicial docente, a partir dos dados gerados na pesquisa, notamos que alguns desses alunos consideram essa dimensão como a mais importante na formação de professores de Matemática, colocando em segundo plano o uso de recursos como as tecnologias informáticas (softwares), calculadoras etc.

PE: Você acha que trabalhar o conteúdo matemático, principalmente de geometria plana e geometria analítica usando um software ajuda você a entender alguns conceitos, a compreender [fui interrompida]

B: É. Vai ajudar, mas só pra visualizar melhor, né, [...] a parte da sala de aula é bem mais importante.

Analogamente, esses licenciandos manifestaram insegurança com relação à possibilidade de usar softwares educativos no ensino de Matemática, mostrando-se muito cautelosos sobre essa questão. Na transcrição subseqüente o depoente V deixa claro que o professor de Matemática precisa, em primeiro lugar, adquirir experiência e segurança com o conteúdo específico e que somente depois deve procurar aprimorar a prática pedagógica, incorporando à mesma as tecnologias.

PE: ¿Você como professor de Matemática tentaria utilizar algum software para dar aula? ¿Como você imagina a sua prática de sala de aula futuramente?

V: Assim, de começo, eu acho que não saberia como usar, porque, eu acho que eu me prenderia a dar a teoria. [...]. Mas eu acho que com o tempo de professor eu aprimoraria [...]. Eu acho no começo eu teria dificuldade de usar software na minha aula por falta de experiência como professor.

Buscando compreender a predominância da valoração da abordagem clássica do conteúdo matemático, manifestada por esses alunos, na qual o ensino do conteúdo curricular baseia-se na apresentação de um determinado conceito e propriedades implícitas, seguido de exemplos e exercícios em sala de aula, constatamos que para esses futuros professores essa forma de proceder é uma prática obrigatória ao professor de Matemática. Esta crença pode ser explicada com base nos resultados de estudos, como de Cury (2001), que mostram que a prática docente é fortemente influenciada pelas experiências vivenciadas ao longo da formação inicial docente, bem como pelas suas vivências sociais, pessoais e escolares. Também, pode ser um reflexo do modelo de formação a que estão submetidos (conhecido no Brasil como 3+1, segundo Moreira e Davi (2005)), no qual maior ênfase é dada à formação matemática e somente no último ano da licenciatura são promovidas reflexões sobre questões pedagógicas e metodológicas da prática docente.

Considerando os aspectos ressaltados por V no depoimento anterior, reforçamos a necessidade da formação inicial docente em Matemática levar em conta a valorização do conhecimento específico, mas que este não seja o fim único desse processo. É preciso que a construção do conhecimento matemático ocorra entrelaçada às experiências formativas do licenciando e ao uso de recursos diversos, como as tecnologias informáticas.

A respeito da formação docente, Valente (1999) avalia que embora um dos objetivos deste processo consista em criar condições para que o professor possa adquirir conhecimentos sobre o conteúdo específico e sobre como o computador pode ser integrado à abordagem desse conteúdo, de modo geral, tal processo não tem acompanhado o desenvolvimento tecnológico, devido à resistência manifestada pelos agentes da comunidade escolar na assimilação e implantação de mudanças, incluindo-se professores, direção e pais.

Partindo das reflexões apresentadas nessa seção e levando em conta as transformações sociais, defendemos que instituições destinadas à formação docente precisam incorporar aos currículos das licenciaturas atividades/disciplinas que favoreçam a investigação das tecnologias, bem como incentivem e ofereçam condições para que os futuros professores adquiram noções de uso pedagógico desses recursos. Tais noções devem subsidiar o processo de incorporação de tecnologias a sua posterior prática.

Visualização, Experimentação e Demonstração com Tecnologias: Implicações à Formação Matemática do Futuro Professor

A visualização e a experimentação, aspectos inerentes à investigação matemática realizada por meio do uso de tecnologias, que são enfatizados por Borba e Villarreal (2005), foram preponderantes no processo de elaboração das atividades didáticas em geometria analítica. Tais aspectos, a nosso ver, foram favorecidos pelo uso do software Geometricks, constituindo-se em momentos propícios à formação matemática dos futuros professores.

Contudo, na visão de alguns licenciandos, o grande mérito dos softwares repousa na possibilidade de ampliarmos a visualização de conceitos e propriedades, restringindo-se a mera aplicação prática do conteúdo, conforme podemos constatar no excerto abaixo.

PE: ¿Você acredita que o uso de softwares no ensino de Matemática pode contribuir com a aprendizagem do aluno? ¿De que forma?

V: Com certeza. Auxiliarão o estudante a ver como foram feitas as atividades, com a simplicidade nas demonstrações e passagens de cada passo da atividade. As atividades com softwares são simples e mostram de forma coerente e fácil as idéias usadas em seus desenhos.

Em contrapartida, outro depoente reforça a importância da visualização na aprendizagem de conceitos matemáticos, no sentido de que este aspecto do ensino de Matemática pode gerar discussões mais ricas à medida que desperta o interesse dos alunos.

Licenciando L: A inserção de exemplos visuais, ou seja, figuras, sempre podem auxiliar no ensino de geometria. A visualização dos conceitos geométricos da geometria analítica, certamente, traria um maior interesse por parte dos alunos [...].

Notamos, também, no decorrer do processo de elaboração das atividades didáticas de geometria analítica, que cada dupla executava uma determinada construção de modo peculiar. Por conseguinte, para uma mesma representação geométrica foram sugeridos procedimentos distintos, assim como, algumas vezes para se obter uma dada figura foi necessário executar várias construções até que os alunos chegassem à forma desejada. E, quando alguma representação não os agradava, excluíam-na e o processo era reiniciado.

Estas situações enfatizam o processo de experimentação concretizado pelos sujeitos para obter uma construção ou elaborar uma atividade, segundo o interesse e necessidades dos mesmos e caracterizam a bricolage. Tais aspectos foram favorecidos pelo fato do ambiente constituído à pesquisa contemplar os princípios do Construcionismo, conforme ressaltam Maltempi (2004), Papert (1994) e Valente (1999), e favorecer a construção do conhecimento matemático, visto que as duplas puderam discutir suas representações, elaborar e verificar conjecturas a respeito das soluções sugeridas às atividades e sistematizá-las a seu modo.

Evidenciando a questão da demonstração matemática no desenvolvimento dos projetos, a qual segundo Lourenço (2002) e Rolkouski (2002) é essencial na construção do conhecimento nessa área, avaliamos que ao potencializar a visualização de conceitos e propriedades, o Geometricks estimulou a demonstração desses conceitos ao mesmo tempo em que estimulou a investigação matemática. Constatamos que a visualização de conceitos e propriedades inerentes às questões elaboradas pelas duplas, incitava-os a validar as conclusões para quaisquer representações que preservassem aquelas propriedades. Com isso, recorriam à axiomas, teoremas e propriedades de geometria plana e analítica e, com isso, desenvolviam demonstrações matemáticas, atribuindo às mesmas relativo “rigor matemático”.

Diante disso, consideramos que o uso do software Geometricks no desenvolvimento dos projetos temáticos em geometria analítica, favoreceu a formação destes licenciandos nas dimensões matemática e tecnológica, visto que fomentou a realização de experimentações, suscitou a investigação matemática e a verificação de conjecturas. O Geometricks ao ser manipulado deixa rastros gráficos e registros simbólicos que estão relacionados à expressão do conhecimento que o aluno possui. Em síntese, ao manipular e construir representações gráficas no software, o aluno tem de expressar as relações entre eles e isso favorece a aprendizagem matemática e suscita a intervenção do professorpesquisador.

Ao buscar outros indicativos da relevância do uso do software à formação matemática dos futuros professores, constatamos que a interface do Geometricks pode ser apontada como facilitadora da interação deles com este recurso e intensificadora da relação licenciando-conteúdo. Esse software é composto de menus que sintetizam muitos conceitos geométricos, de modo que para utilizá-los os estudantes precisaram revisar diversos conteúdos, os quais eram retomados sempre que recorriam a esses menus. Notamos, ainda, que a partir das orientações iniciais dadas pela professora-pesquisadora, as duplas não apresentaram muita dificuldade em expressar as idéias e conceitos envolvidos nas atividades que elaboraram.

Do mesmo modo, avaliamos que devido às características do Geometricks, entre elas a ausência de tabelas que exibam a representação numérica (tabular) de lugares geométricos, foi possível promover maior aprofundamento ao conteúdo de geometria analítica, pois as duplas foram impelidas a explorar visualmente as representações geométricas obtidas para obter as representações algébricas. Isto é, por meio da opção Coordenada (po)/menu Observações, a qual permite que o usuário determine as coordenadas de pontos quaisquer do plano, puderam construir manualmente, usando lápis e papel, tabelas de valores, cujos dados permitiram que chegassem à representação algébrica das cônicas representadas e investigadas nos projetos.

Por outro lado, acreditamos que a análise de algumas propriedades das construções executadas pode ter sido prejudicada, pois os estudantes não puderam estabelecer relações entre a variação numérica das curvas representadas, geralmente expressas por tabelas, com o comportamento gráfico das respectivas representações. Com isso, a representação algébrica de lugares geométricos como parábola e elipse pode ter sido prejudicada.

Com relação às características do Geometricks, destacamos também a necessidade de haver combinação entre vários recursos (lápis, papel, calculadora etc.) para executar uma determinada tarefa, enfatizando mais uma vez a bricolage, discutida por Papert (1985). Do ponto de vista da aprendizagem matemática, este aspecto foi relevante, pois permitiu que os licenciandos fizessem a transição da representação gráfica para a algébrica das cônicas estudadas, a qual, de acordo com Cavalca (1997), tem sido uma das dificuldades evidenciadas por alunos em geral na disciplina de geometria analítica.

A representação de cônicas no Geometricks, por exemplo, dispondo apenas do recurso lugar geométrico, instigou nos alunos a reflexão e a investigação acerca da representação algébrica dada e a sua representação gráfica, de modo que muitos ajustes foram necessários para que se obtivesse a cônica desejada. Este aspecto foi reforçado em um dos encontros, no qual uma dupla estava propondo a representação de uma hipérbole eqüilátera, e como o Geometricks não fornece a equação de lugares geométricos, então, os estudantes precisaram recorrer a definição e efetuar diversas operações matemáticas e ajustes nos procedimentos descritos no software para obter a construção almejada (mais detalhes vide Richit (2005)).

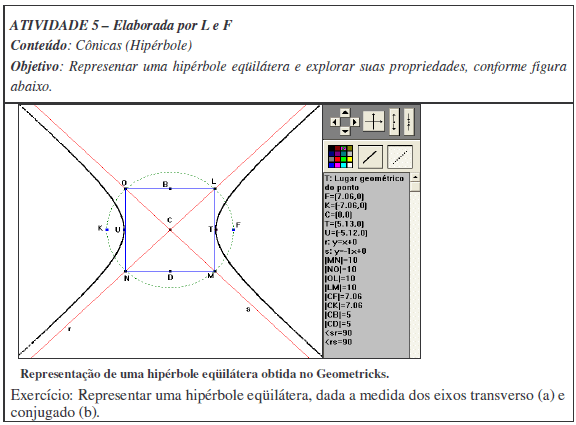
Inicialmente a dupla construiu a hipérbole tomando a = b = 5, conforme definição. Após realizarem a construção do respectivo lugar geométrico, recorreram às propriedades relativas ao conceito de hipérbole eqüilátera para provar que a figura representada classificava-se como tal.

Primeiramente traçaram as assíntotas (retas r e s) da hipérbole de equação (NOTA 6) , visando mostrar que estas retas não interceptavam as curvas da figura representada. Para tanto, usaram as equações r: y = x + 0 e s: y = – x + 0, de modo que o ângulo formado pelas mesmas fosse reto (90°), medida essa exibida na janela de observações do Geometricks e mostrada na figura anterior (< rs=90 e < sr=90).

Como a dimensão em que a hipérbole está sendo considerada é muito pequena, não há como saber se as assíntotas r e s interceptam-na em algum ponto tendendo ao infinito. Então, a dupla recorreu à outra propriedade, que consistiu em traçar uma circunferência com raio (r) igual à distância focal (c) (NOTA 7) da hipérbole dada, isto é r = c = , cujo centro deveria coincidir com o centro da hipérbole (ponto C da figura). Para isso usaram a opção circunferência (centro, raio) do Geometricks, tomando o ponto C por centro e a medida c = como raio. Posterior, marcaram os pontos L, M, N e O de interseção da circunferência com as assíntotas r e s. A partir desses pontos traçaram os segmentos LM, MN, NO e OL, formando o retângulo LMNO, cujos lados MN e NO correspondem às medidas dos eixos transverso e conjugado.

Por último a dupla procurou verificar se o retângulo LMNO era um quadrado. Para isso mostraram, usando a opção distância (ponto, ponto), que MN=NO. Pela figura dada verificamos que eles comprovaram que |MN|=10 e |NO|=10. Logo, o retângulo LMNO é quadrado e, segundo Boulos e Camargo (1987), a hipérbole classifica-se como eqüilátera.

Notamos nessa e noutras atividades elaboradas a preocupação dos licenciandos com o próprio entendimento dos conceitos e propriedades abordados e com a aplicação prática destes, pois procuravam identificar cada conceito enunciado na representação realizada. Ainda, a iniciativa das duplas de solucionar cada uma das atividades produzidas revela que esses estudantes estavam seguros com relação ao conteúdo matemático abordado em seus projetos, indício esse que sinaliza contribuições da estratégia pedagógica implementada na pesquisa-intervenção à formação matemática desses estudantes.

Tecnologias na Formação e Prática Docente em Matemática: possibilidades e desafios às mudanças educacionais

Tomando como premissa a concepção de que o uso de tecnologias deve permear as experiências formativas do futuro professor durante a licenciatura, de modo que este desenvolva noções de uso pedagógico destes recursos, procuramos levantar as compreensões dos licenciandos sobre o uso de tecnologias na formação e prática docente em Matemática, focando as implicações da experiência promovida à formação tecnológica deles.

PE: A estratégia pedagógica desenvolvida com vocês, baseada no desenvolvimento de projetos usando tecnologia informática, pode contribuir para a formação tecnológica de um professor de Matemática?

F: Contribui, [...], mas não pode parar por aí. A gente tem que explorar outras coisas, fazer outras atividades em outras disciplinas. Não podemos parar simplesmente no que foi feito até agora e esquecermos, a gente tem que aprender ainda mais, para que a gente possa formalizar realmente nossas idéias e aquilo que foi aprendido até agora. A gente aprendeu bastante sobre o software e sobre geometria analítica, e eu acho que foi por causa dessa liberdade didática que a gente teve. Mas, até que ponto foi legal para minha formação tecnológica? A curto prazo, se eu fosse dar aula logo, talvez essa liberdade que a gente desfrutou em trabalhar nas atividades, [...] a gente se colocou a várias situações, como travar o computador, por exemplo. Várias coisas que a gente se esforçou, a gente entendeu. Acredito que se eu for dar aula, por ter desfrutado, por ter aprendido a explorar o software, vou estar preparado para enfrentar alguns imprevistos.

As reflexões deste aluno acerca do uso de tecnologias na prática docente sinalizam a necessidade de se colocar o futuro professor, durante a sua formação, em contato com os recursos tecnológicos disponíveis no seu meio, levando em conta as colocações de Ponte et al. (2003), Borba e Penteado (2001) e Papert (2003). Preparando-o, assim, para enfrentar os desafios que possivelmente venham apresentar-se no exercício da profissão docente e, principalmente, estimulando-o a desenvolver habilidades de uso pedagógico destes recursos, contribuindo com a formação dos alunos que estiverem sob a tutela desse licenciando futuramente.

Segundo depoimentos dos sujeitos da pesquisa e das conversas entre eles e a professorapesquisadora, constatamos que mudanças metodológicas na prática não são encaradas com naturalidade, conforme podemos observar no depoimento do estudante E.

E: Como professor, eu quero usar estes recursos, pelo menos em algumas aulas. Mas, primeiro eu daria a teoria e depois aplicaria para o aluno poder ver melhor o que ele está estudando. Para ele ter uma idéia melhor, visualizar, por exemplo, uma cônica. Tem aluno que não consegue visualizar uma cônica (...). Então, no computador ele ia visualizar melhor e isso pode ajudá-lo a aprender aquele conceito ou definição.

PE: E para sua formação? (...) você acha que quando você for dar aula você vai utilizar este software ou um outro? Você acha que seria legal, ou você vai preferir trabalhar sem esses recursos?

B: Ah! É legal usar assim, no caso, por exemplo, eu acho até que é mais importante trabalhar no ensino médio essas idéias, este software.

O depoimento do estudante B revela sua concepção, e possivelmente de outros colegas do Curso, acerca da relevância do uso de softwares no ensino de Matemática. Para esses, a abordagem usual deve prevalecer na prática do professor, reforçando as considerações apresentadas na seção anterior. Ademais, pontuam que a visualização pode ser mais útil na educação básica, sugerindo que os alunos do ensino superior estão mais aptos a trabalhar conceitos matemáticos de forma abstrata e generalizada.

Partindo desses indicativos, depreendemos que para esses futuros professores o papel das tecnologias na prática pedagógica em Matemática abrange os aspectos da visualização e da demonstração, defendidos por Lourenço (2002) e Borba e Villarreal (2005). Porém, complementamos que estes recursos desempenharam, também, papel motivador na intervenção implementada, devido ao valor social que possuem em muitos grupos e contextos culturais, aspecto este discutido por Maltempi (2004). Isso posto, entendemos que a incorporação das tecnologias no contexto escolar pode desencadear movimentos de mudança nos processos educativos, em particular no ensino e aprendizagem em Matemática.

As compreensões desses estudantes sobre o papel da tecnologia no ensino, pelo que pudemos perceber, são influenciadas pelas suas vivências educativas, nas quais há predominância da abordagem clássica do conteúdo curricular. Por outro lado, temos de considerar que essas concepções podem sofrer modificações, à medida que ampliamos nossas experiências com esses recursos e temos a oportunidade de explorar outros modos de uso.

Sob este prisma, ponderamos que a intervenção pode ter modificado as crenças de alguns sujeitos acerca do papel das tecnologias nos processos educacionais em Matemática. Desse modo, enfatizamos a importância e a necessidade de se promoverem reflexões sobre esta questão durante a formação inicial, considerando que a mudança de concepção sobre uso educacional desses recursos é essencial na implementação de novas estratégias de aprendizagem, bem como às mudanças na prática docente.

Pautados nos resultados do estudo de Richit (2005), ressaltamos que a implementação de estratégias pedagógicas, como o trabalho com projetos e tecnologia, ao longo da licenciatura e focando diversas disciplinas do currículo, pode contribuir com o processo de formação inicial docente em Matemática. Por meio dessas, os futuros professores podem aprofundar os conhecimentos sobre as tecnologias utilizadas e dos conteúdos matemáticos focados, devido às diferentes abordagens que são propiciadas pelo uso das mesmas.

Etapas do Trabalho com Projetos e Tecnologias no Âmbito da Pesquisa Desenvolvida

Analisando a estratégia pedagógica que permeou o desenvolvimento dos projetos das duplas, identificamos seis momentos distintos que caracterizam as ações dos licenciandos, etapas essas que são descritas e comentadas na presente seção.

O primeiro momento consistiu em elaborar um plano inicial do projeto. Ou seja, os estudantes precisaram planejar o desenvolvimento dos projetos, delimitando os assuntos que seriam abordados, os procedimentos que seriam utilizados na execução das tarefas, a bibliografia a ser utilizada, bem como a determinação dos objetivos do projeto. Na investigação realizada a escolha do software e da disciplina partiu da professora-pesquisadora, enquanto que as outras escolhas foram definidas pelos alunos.

Enfatizamos, levando em conta as reflexões de Valente (2003a; 2003b; 2003c), Petito (2003) e Maltempi (2004), que esta etapa deve ser realizada em acordo com o professor, pois precisa ser orientada, de modo que o trabalho desenvolvido esteja em consonância com os critérios préestabelecidos pelo docente e com as determinações curriculares.

Da mesma forma, ponderamos que as fontes de consulta (bibliografia usada como material de apoio) podem ser sugeridas pelo docente ou pelos alunos, mas é necessário que sejam previamente examinadas pelo primeiro, pois precisam ser adequadas ao nível dos alunos e as exigências do projeto. Igualmente, ressaltamos que o armazenamento e a organização das informações coletadas durante a pesquisa ou a consulta em materiais de apoio, podem facilitar os trabalhos de comparação e análise dos conceitos e definições que vão ser usadas na elaboração das atividades previstas.

Como segunda etapa destacamos o processo de planejar a construção das representações no software escolhido inicialmente. Esta construção se refere à representação geométrica ou gráfica de um conceito matemático abordado pelos projetistas, a qual é executada usando algum recurso tecnológico ou software adequado àquela disciplina ou aquele conteúdo. Esclarecemos que este recurso pode ser substituído quando não se mostrar apropriado às necessidades e aos objetivos do projeto que está sendo desenvolvido. Do ponto de vista do Construcionismo esta etapa é muito importante, pois cada aluno ou cada dupla pode realizar uma mesma tarefa usando recursos e procedimentos distintos, explicitando os diferentes estilos de executar uma atividade, caracterizando a bricolage.

Este momento, pelo que foi observado na intervenção aqui descrita, abarca várias etapas, como a descrição do enunciado que introduziu cada atividade, a apresentação do objetivo da mesma, a determinação dos procedimentos que seriam usados naquela representação e a realização de pesquisa em sites ou bibliografias pertinentes aos assuntos abordados em cada um dos projetos. No processo de produção das atividades das duplas, os procedimentos adotados para executar as representações geométricas/gráficas foram definidos por experimentação, de acordo com a concepção proposta por Borba e Villarreal (2005).

Dando continuidade ao processo de desenvolver um projeto, evidenciamos o momento de construir as representações geométricas usando a tecnologia selecionada para esta tarefa. Esta se desenvolve na medida em que os alunos realizam a construção das representações geométricas/gráficas associadas aos enunciados elaborados, as quais podem ser incorporadas (ou não) às atividades que estão sendo produzidas, dependendo do objetivo que foi estabelecido. Em alguns casos, os alunos podem acrescentar ao enunciado da atividade, os procedimentos usados na construção e propor uma solução, como verificado nos projetos elaborados. Em outros, o processo de construção e resolução das atividades é realizado pelos alunos como um meio de fomentar investigações matemáticas ou para convencê-los sobre alguma conjectura, podendo não fazer parte do projeto.

A etapa subseqüente à construção das representações geométricas dos conceitos focados nos projetos consiste em sistematizar as atividades elaboradas. Este momento foi relevante no processo que permeou o desenvolvimento dos projetos, pois os licenciandos necessitaram descrever cuidadosamente, usando um editor de texto, cada uma das atividades geradas, revisar os objetivos destas, melhorar ou ampliar as definições apresentadas, seguir normas metodológicas (fonte, margens, formatação etc.), revisar gramática e digitação, acrescentar comentários e conclusões aos projetos e, quando necessário, apresentar os procedimentos usados para realizar uma construção no Geometricks.

Nesta fase, verificamos que as duplas revisitaram o material de apoio, retomando definições, demonstrações e propriedades, visando a ampliá-las ou corrigir possíveis erros. Esta etapa se constituiu numa pesquisa bibliográfica contextualizada. Analogamente, mostraram-se atentos às questões pedagógicas das atividades que estavam produzindo, como a fidedignidade das definições, a clareza dos enunciados propostos e a coerência das soluções.

Considerando a abrangência deste momento, avaliamos que o mesmo é complexo e requer uma intervenção cuidadosa do professor para que os participantes ampliem suas concepções iniciais por meio do confronto de pontos de vista pessoais com concepções já estabelecidas, bem como estejam atentos às exigências estabelecidas àquela tarefa educacional, segundo a abordagem que está sendo assumida. Além disso, o docente precisa auxiliar seus alunos na formalização dos conceitos que estão sendo focados, considerando que a formalização é essencial ao processo de construção do conhecimento em Matemática.

Com base na intervenção realizada, concluímos que este momento exigiu da professorapesquisadora atenção especial a cada uma das duplas, pois foram necessárias reflexões sobre os enunciados propostos, confrontando-os com os objetivos estabelecidos para cada atividade e as definições e propriedades apresentadas nas mesmas, bem como leitura e correção das atividades elaboradas.

O quinto momento do trabalho corresponde à avaliação daquilo que foi desenvolvido. Essa etapa é extremamente importante, uma vez que após receber feedback do professor ou dos colegas, o projetista pode refletir sobre aquilo que produziu, olhando para cada uma das partes e para o projeto como um todo.

A divulgação aos colegas ou à comunidade, daquilo que foi produzido é outra etapa importantíssima na realização de projetos educacionais, pois os alunos recebem feedback de pessoas que não estão diretamente envolvidas no trabalho que realizaram. Tal etapa pode ocorrer diversas vezes ao longo do desenvolvimento do projeto e também no final. O importante é que estas pessoas tenham conhecimento do assunto que está sendo abordado.

Esclarecemos que os momentos do trabalho por projetos aqui categorizados não se verificaram tal como foram descritos nesta seção. No processo de elaboração das atividades alguns licenciandos primeiro executavam uma construção geométrica no software e após várias repetições (experimentações), realizavam a sistematização da atividade que evolveria aquela construção, enquanto que outros planejavam a construção das atividades, em seguida executavam-nas e, finalmente, iniciavam a sistematização.

Frisamos que a sistematização das atividades foi um processo que se repetiu várias vezes. As duplas reescreviam os enunciados e as soluções das atividades, adicionavam comentários e conclusões às mesmas, assim como preocupavam-se com o aspecto estético dos projetos, defendido por Valente(2003b), visando melhorar e ampliar as atividades.

Considerações Finais

Na pesquisa realizada o trabalho com projetos e tecnologias, em sintonia com o Construcionismo, constituiu-se em atividade educacional que concedeu autonomia ao futuro professor para planejar e conduzir determinadas atividades educativas, que favoreceram a construção do conhecimento matemático, o desenvolvimento de noções de uso pedagógico de tecnologias e o enfrentamento com situações da prática docente. Tais atividades, porém, precisam ser planejadas em acordo com o professor, implementadas sob sua orientação, bem como estar em consonância com as exigências curriculares e favorecer a interdisciplinaridade.

Tendo em vista que a pesquisa-intervenção foi desenvolvida com um grupo pequeno de estudantes, sublinhamos que a estratégia pedagógica aqui descrita pode ser implementada com grupos maiores de alunos, inclusive com classes inteiras, pois, tal como ocorreu com os sujeitos da pesquisa realizada, os aprendizes podem, realmente, motivar-se e envolver-se na execução de uma tarefa se esta for de seu interesse. Ainda, ponderamos que atividades com esse caráter permitem que cada aluno construa seu conhecimento de acordo com seu ritmo de trabalho, devido à autonomia que lhe é concedida.

Destacamos, a partir da experiência promovida e da revisão da literatura pertinente ao assunto, que o uso de tecnologias no trabalho com projetos pode auxiliar o futuro professor a perceber a relação existente entre o conhecimento específico adquirido ao longo da licenciatura e as possíveis aplicações destes conceitos em outras situações, além daquelas praticadas em sala de aula. Além de fazê-lo refletir sobre as formas de abordar estes conteúdos na prática pedagógica escolar. Sobre isso, avaliamos que o desenvolvimento de projetos, aliado ao uso de tecnologias, favorece a interdisciplinaridade, a formação de indivíduos criativos e com iniciativa à tomada de decisões, aspectos estes essenciais ao exercício da profissão docente, além de incitar atitudes de companheirismo e colaboração.

Outrossim, por meio da interpretação que fizemos dos dados provenientes da intervenção desenvolvida, pudemos confirmar as colocações de Maltempi (2004; 2005), Valente (1993; 1999; 2003a; 2003b; 2003c) e Papert (1991; 1994; 2003) de que a construção do conhecimento é favorecida em atividades que permitem ao aluno, neste caso licenciando, investigar, refletir, experimentar, expressar suas idéias na realização de uma atividade educativa, ações estas que caracterizam a aprendizagem em ambientes pautados no Construcionismo e evidenciam a sinergia entre o Construcionismo e o trabalho com projetos.

Com isso, sustentamos que as atividades de caráter construcionista, como a que foi implementada nesta pesquisa, podem colaborar na construção do conhecimento matemático, favorecendo a formação do futuro professor de Matemática, preparando-o para utilizar as tecnologias na sua posterior prática docente. Porém, tais mudanças são viabilizadas se o uso desses recursos estiver entrelaçado às experiências formativas na licenciatura. Nesse sentido, entendemos que incentivando a realização de projetos ou atividades abertas, nas quais os licenciandos sejam responsáveis por escolher conteúdos, discutindo-os com seus pares ou professores, assim como investigar distintas formas de resolver um problema, é uma forma de favorecer a formação integral de futuros professores.

Diante disso, avaliamos que o estudo aqui apresentado apontou caminhos para os cursos de formação inicial docente em Matemática, os quais, a nosso ver, precisam favorecer a formação específica, pedagógica e tecnológica. Tais dimensões podem ser privilegiadas entrelaçando as experiências formativas dos licenciandos ao uso de recursos tecnológicos presentes no contexto social e acadêmico desses estudantes.

NOTAS

1. Para evitar repetições excessivas dos termos “tecnologias da informação e comunicação” ou “tecnologias informáticas”, ao longo do texto vamos nos referir as mesmas usando apenas o termo “tecnologias”.

2. Este regime permite aos alunos retidos com notas entre 3,0 e 4,9 em disciplina semestral, que realizem novos exames no semestre seguinte. Cabe ao docente definir dinâmicas de estudo que não sejam aulas convencionais.

3. Software de geometria dinâmica desenvolvido por Viggo Sadolin da The Royal of Educational Studies. Versão Demo disponível em: <http://www.rc.unesp.br/igce/pgem/gpimem.html>.

4. Visando a preservar a identidade dos sujeitos da pesquisa não serão usados os nomes dos mesmos e, para facilitar a distinção das falas ao longo do texto, serão usadas as iniciais dos nomes dos depoentes e a notação PE quando a intervenção referir-se a pesquisadora.

5. Os projetos elaborados pelas duplas estão disponíveis, integralmente, em Richit (2005) e no site <http://www.rc.unesp.br/igce/pgem/gpimem.html>.

6. A equação reduzida da hipérbole, nesse caso, é dada pela expressão: .

7. A distância focal é dada por c² = a² + b². Na questão proposta temos: c² = 5² + 5².

REFERÊNCIAS

1. Almeida, M. E. B. (2003). O computador na escola e a formação de professores. Teoria e Prática da Educação, Edição Especial, 441-455.        [ Links ]

2. Borba, M. C., Araújo, J.L. (Org.), (2004). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica.        [ Links ]

3. Borba, M. C., Penteado, M. G. (2001). Informática e Educação Matemática. (2. ed.). Belo Horizonte: Autêntica, 2001.        [ Links ]

4. Borba, M.C., Villareal, M.E. (2005). Humans-with-Media and the Reorganization of Mathematical Thinking: information and communication technologies, modeling, experimentation and visualization Mathematical. New York, USA: Springer.        [ Links ]

5. Boulos, P., Camargo, I. (1987). Geometria Analítica: um tratamento vetorial. (2. ed.). São Paulo: Pearson Education do Brasil.        [ Links ]

6. Cavalca, A. (1997). Espaço e Representação Gráfica: Visualização e Interpretação. 169 f. Dissertação (Mestrado em Educação Matemática) – Faculdade de Educação, Pontifícia Universidade Católica-PUC, São Paulo.        [ Links ]

7. Cury, H. N. (Org.). (2001). Formação de professores de Matemática: uma visão multifacetada. Porto Alegre: Edipucrs.        [ Links ]

8. Denzin, N.K; Lincoln, Y.S. The Discipline and Practice of Qualitative Research. In: Denzin, N.K; Lincoln, Y.S. Handbook of Qualitative Research. 2nd ed. London: Sage, 2000, p.1-28.        [ Links ]

9. Dewey, J. (1959). Democracia e Educação. (3 ed.). Tradução de Godofredo Rangel e Anísio Teixeira. São Paulo: Companhia Editora Nacional.        [ Links ]

10. Goldenberg, M. (2003). A Arte de Pesquisar: como fazer pesquisa qualitativa em Ciências Sociais. (7 ed.). Rio de Janeiro: Record.        [ Links ]

11. Hernández, F. (1998). Transgressão e mudança na educação: os projetos de trabalho. Tradução de Jussara Haubert Rodrigues. Porto Alegre: ArtMed.        [ Links ]

12. Hernández, F., Ventura, M. (1998). Organização do Currículo por Projetos de Trabalho: o conhecimento é um caleidoscópio. (5 ed.). Porto Alegre: ArtMed.        [ Links ]

13. Lévy, P. (1999). A Inteligência Coletiva: por uma antropologia do ciberespaço. (2 ed.). Tradução de Luiz Paulo Rouanet. São Paulo: Loyola.        [ Links ]

14. Lévy, P. (1998). A Máquina Universo: criação, cognição e cultura informática. Tradução de Bruno Charles Magne. Porto Alegre: ArtMed.        [ Links ]

15. Lourenço, M. L. (2002, set.). A Demonstração com Informática Aplicada a Educação. Boletim de Educação Matemática –BOLEMA, 15(18), 100-111.        [ Links ]

16. Maltempi,, M. V. (2005). Novas tecnologias e construção de conhecimento: reflexões e perspectivas [CD-ROM]. Artigo apresentado no Congresso Ibero-Americano de Educação Matemática–CIBEM, 5. Cidade do Porto.        [ Links ]

17. Maltempi, M. V. (2004) Construcionismo: pano de fundo para pesquisas em informática aplicada à Educação Matemática. In: Bicudo, M.A.V.; Borba, M.C. (Orgs.). Educação Matemática: pesquisa em movimento. (264-282). São Paulo: Cortez.        [ Links ]

18. Marinho, S. P. (2002). Tecnologia, educação contemporânea e desafios do professor. In: Joly, M. C. R. A. (Org.). A Tecnologia no Ensino: implicações para a aprendizagem. (42-62) São Paulo: Casa do Psicólogo.        [ Links ]

19. Moreira, P. C., David, M. M. S. (2005). A formação Matemática do Professor: licenciatura e prática docente escolar. Belo Horizonte: Autêntica.        [ Links ]

20. Papert, S. (2003). Qual é a grande idéia? Passos em direção a uma pedagogia do poder das idéias. Teoria e Prática da Educação, Edição Especial, 369-387.        [ Links ]

21. Papert, S. (1994). A máquina das crianças: repensando a escola na era da informática. Tradução de Sandra Costa. Porto Alegre: Artes Médicas.        [ Links ]

22. Papert,S. (1991). Situating Constructionism. In: HAREL, I.; PAPERT, S. (Eds.). Constructionism, (01-11). Cambridge, MA: MIT Press.        [ Links ]

23. Papert, S. (1985). Logo: Computadores e Educação. São Paulo: Brasiliense.        [ Links ]

24. Petito, S. (2003). Projetos de trabalho em informática: desenvolvendo competências. Campinas: Papirus.        [ Links ]

25. Ponte, J. P.; Oliveira, H.; Varandas, J. M. (2003). O contributo das tecnologias de informação e comunicação para o desenvolvimento do conhecimento e da identidade profissional. In: Fiorentini, D. (Org.). Formação de professores de Matemática: explorando novos caminhos com outros olhares, (159-192). Campinas: Mercado das Letras.        [ Links ]

26. Richit, A. (2005). Projetos em Geometria Analítica Usando Software de Geometria Dinâmica: repensando a Formação Inicial Docente em Matemática. 2005. 215 f. Dissertação (Mestrado em Educação Matemática), Instituto de Geociências e Ciências Exatas, Universidade estadual Paulista, Rio Claro.        [ Links ]

27. Richit, A. (2006). Trabalhando com Projetos e Tecnologias Informáticas no contexto da Geometria Analítica: implicações à Formação Inicial Docente em Matemática segundo a Visão Construcionista [CD-ROM]. Artigo apresentado no Encontro Brasileiro de Estudantes de Pós-Graduação em Educação Matemática – EBRAPEM, 10. Belo Horizonte, MG.        [ Links ]

28. Richit, A. y Maltempi, M. V. (2005, jul/dez). A Formação Profissional Docente e as Mídias Informáticas: Reflexões e Perspectivas. BOLETIM GEPEM - Grupo de Estudos e Pesquisas em Educação Matemática, (47), 91-102.        [ Links ]

29. Rolkouski, E. (2002). Demonstrações em Geometria: uma descrição dos processos de formação utilizados por alunos de Licenciatura em Matemática em ambiente informatizado. 165 f. Dissertação (Mestrado em Educação), Universidade Federal do Paraná, Curitiba.        [ Links ]

30. Sidericoudes, O. (2004). Formação de profissionais-docentes na preparação de jovens para o trabalho com TIC. 166 f. Tese (Doutorado em Educação: Currículo), Pontifícia Universidade Católica de São Paulo, São Paulo.        [ Links ]

31. Valente, J. A. (2003a). Curso de Especialização em Desenvolvimento de Projetos Pedagógicos com o uso das Novas Tecnologias: descrição de fundamentos. In: Valente, J. A.; Prado, M. E.B.B.; Almeida, M.E.B. (Orgs.). Educação a Distância via Internet (23-56). São Paulo: Avercamp.        [ Links ]

32. Valente, J. A. (2003b). Desenvolvendo projetos usando as tecnologias da informação e comunicação: criando oportunidades para a construção do conhecimento. Teoria e Prática da Educação, Edição Especial, 407-422.        [ Links ]

33. Valente, J. A. (2003c). Informatics in Education. Institute of Mathematics and Informatics, Lithuanian Academy of Sciences, 2(1), 122-138.        [ Links ]

34. Valente, J. A. (1999) Análise dos diferentes tipos de software usados na Educação. In: Valente, J. A. (Org.). O Computador na sociedade do conhecimento, (89-99). Campinas: Unicamp/Nied        [ Links ]

35. Valente, J. A. (1993). Por que o computador na educação? In: Valente, J. A. (Org.). Computadores e Conhecimento: repensando a educação, (24-44). Campinas: Unicamp/Nied.        [ Links ]