Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Paradígma
versión impresa ISSN 1011-2251
Paradígma vol.35 no.2 Maracay dic. 2014
Las Demostraciones Geométricas como Instancias de Resolución de Problemas
Jesús Daniel Lárez Villarroel
jesusdlarezv11@hotmail.com; jesusdlarezv11@gmail.com
Universidad Nacional Experimental Rómulo Gallegos, San Juan de los Morros, Venezuela
Jesús Daniel Lárez Villarroel: Lic. Educ. Mención Física y Matemática UCAB. Maestría en Educ. Mención Enseñanza de la Matemática, de la Universidad Nacional Experimental Rómulo Gallegos, donde es profesor adscrito al Área de Agronomía, cátedras: Matemática I y II. Didáctica y aprendizajes.
Resumen
El objetivo de este trabajo es documentar, discutir y analizar la importancia de las demostraciones geométricas como resolución de problemas. Para ello en la sección intitulada, la resolución de problemas, la abordamos como una actividad intelectual sobre la cual se debe sustentar la matemática escolar. En el apartado de las demostraciones geométricas se evidencia como estudiantes de Educación Media tienen la posibilidad de familiarizarse con el proceso formal lógico deductivo, describimos la situación actual en la enseñanza de las demostraciones geométricas, esbozamos un modelo para realizar dichas demostraciones y hacemos hincapié en el valor formativo que esta tarea intelectual tiene para la formación del nuevo republicano.
Palabras Clave: Geometría plana, demostraciones, valores formativos.
Geometrical Demonstrations as Problem Solving Instances
Abstract
The aim of this paper is to document, discuss and analyse the importance of geometrical demonstrations as problem resolution strategy. To do this, under the heading "problem resolution" we approach the intellectual activities on which must be supported school mathematics. In the section of geometrical demonstrations, is evident how students of secondary school have the opportunity to become familiar with the logical deductive formal process, also we describe the current situation in the teaching of geometrical demonstrations, we outline a model for such demonstrations and emphasize the educational value that this intellectual task have on the education of new republicans.
Keywords: plane geometry, mathematics demonstrations, educational values
Recibido: 15/02/2014 Aceptado: 10/09/2014
Introducción
El diseño del Currículo de los Liceos Bolivarianos es el producto del trabajo articulado de varios sectores del quehacer educativo. Pretende formar al y la adolescente y joven con conciencia histórica e identidad venezolana, desarrollando capacidades y habilidades para el pensamiento crítico, cooperativo, reflexivo y liberador (27,28).
Este proceso exige, según el Currículo Bolivariano (2007):
impulsar la construcción de saberes, con la participación permanente de los actores sociales comprometidos con el proceso educativo, para establecer relaciones y solucionar colectivamente conflictos, además de constituir una fuente potencial de aprendizaje que ayuda a reconocer los problemas, superar dificultades, asumir responsabilidades, confrontar el cambio y valorar las diferencias; planteamiento que se corresponde con los aportes teóricos referidos al aprendizaje que garantiza en el individuo la apropiación activa y creadora de la cultura, propiciando el desarrollo de su auto-perfeccionamiento constante, de su autonomía y autodeterminación.
Lo anterior hace que crezca la responsabilidad del docente en diseñar actividades que permitan al estudiante ser, hacer y conocer de forma tal que construyan su conocimiento producto de la interacción crítica con el objeto en un contexto socialmente mediado. Explican García y Mazzarella (2011) que, según los postulados constructivistas, el aprendizaje es una interpretación, a través de la experiencia que tiene el sujeto con el mundo que lo rodea, filtrada por la mente para producir una realidad personal (p.116), y que el mediador debe tomar en cuenta que la interacción sujeto-medio está condicionada por una variedad de factores, entre los que se encuentran los socioculturales.
Eventualmente esto ha llevado a docentes a buscar fórmulas mágicas, que al suponer y pensar que se basan en el constructivismo, les proporcionan cierta garantía que los alumnos aprenden. Sin embargo, es obligatorio que el docente promueva procesos complejos para la construcción del conocimiento, como por ejemplo, el resolver problemas. El tener que resolver problemas exige al estudiante una comprensión que va más allá de actividades como la memorización, la repetición y la realización de tareas rutinarias; debe llevar acabo otras, distintas y más complejas, que incluyen no sólo la reflexión sobre sus conocimientos procedimentales, sino una reflexión sobre sus reflexiones, en un ambiente cooperativo donde discuta con sus pares y docente, ejemplifique, busque contra-ejemplos, argumentos y, por sobre todo, donde pueda equivocarse.
En este ambiente, el docente debe ser un facilitador-mediador del aprendizaje: facilitador porque debe preparar ambientes de aprendizaje que presenten retos para los alumnos; y mediador, al intervenir oportunamente para introducir información o acompañarlos en la solución de algunos problemas que se le presenten al enfrentar los retos planteados, seleccionando fuentes de información y guiándolos hacia el éxito.
En el caso específico de la enseñanza de la matemática, la actividad realizada con el fin de resolver problemas es uno de los pilares de su aprendizaje significativo (Para Halmos, 1980, la resolución de problemas es el corazón de la matemática). Estas situaciones problemáticas se pueden referir al mundo natural y social o bien pueden ser internas a la propia matemática.
Para realizar estas actividades el docente debe presentarles a los alumnos retos, problemas o tareas que requieran de esfuerzo intelectual para resolverlos, ayudar en la construcción de nuevos esquemas de conocimientos al trabajar como facilitador-mediador en las zonas de desarrollo próximo, tanto individuales como colectivas, establecidas en el intercambio de nuevos conocimientos construidos sobre conocimientos previos.
La Resolución de Problemas
La palabra problema proviene del griego πρδβλημα compuesto del prefijo πρδ (delante) y βλημα (lanzamiento), algo que se lanza o arroja hacia delante. Según el diccionario de la Real Academia Española queda definido como aquel conjunto de hechos o circunstancias que dificultan la consecución de algún fin.
Para Campistrous y Rizo (citado por Companioni, 2005, p.6) un problema es toda situación en la que hay un planteamiento inicial y una exigencia que obliga a transformarla y la vía para pasar de la situación o planteamiento inicial a la situación exigida, tiene que ser desconocida. Por su parte Becerra (2005) asume como problema aquello que discrepa, altera u obstaculiza la búsqueda o conocimiento de algo (p.21).
González (2009) lo define como un escenario real o imaginario, que involucra cierto grado de incertidumbre, que para clarificarlo, necesita un manifiesto esfuerzo intelectual por parte de un sujeto. Para Kilpatrick (citado por Pérez y Ramírez, 2011) problema es una definición en la que se debe alcanzar una meta, pero en la cual está bloqueada la ruta directa (p.172).
García y Rentería (2012) establecen que un problema:
es una situación enfrentada por un individuo o un grupo que presenta una oportunidad de poner en juego los esquemas de conocimiento, exige una solución que aún no se tiene para la cual no se conocen medios o caminos evidentes y en la que se deben hallar interrelaciones expresas y tacitas entre un grupo de factores o variables, lo que implica la reflexión cualitativa, el cuestionamiento de la propias ideas, la construcción de nuevas relaciones, esquemas y modelos mentales, es decir la elaboración de nuevas explicaciones que constituyen la solución al problema que significa reorganización cognitiva, involucramiento personal y desarrollo de nuevos conceptos y relaciones generando motivación e interés cognitivo (p. 756).
En resumen, se puede definir un problema como toda situación en la que a un sujeto se le presenta una meta u objetivo, que para poder lograr o cumplir debe ejecutar una serie de acciones que no conoce de antemano.
Lo característico de un problema es la novedad: un objetivo puede constituir un problema para una persona y no serlo para otra. Para aquél que sepa cómo lograrlo, no hay problema alguno en el planteamiento de un objetivo; en cambio, existirá un problema para el que no sepa cómo cumplir una tarea. Lo anterior significa que para que una situación pueda constituir un problema para un individuo en particular, se requieren, según González (2002, Citado por Lárez), dos componentes: (a) un componente objetivo (el objeto matemático a enfrentar) y, (b) un componente subjetivo (la manera como el individuo considere al objeto matemático a enfrentar). El autor denomina elementos subjetivos del problema a los siguientes: (a) un objetivo claramente definido y deseado; (b) cuando el individuo se enfrente al problema, éste debe generarle un desequilibrio cognitivo que obligue al sujeto a coordinar sus experiencias y conocimientos previos y, en algunos casos, su intuición, para lograr un resultado satisfactorio (p.45) y, (c) debe ser capaz de reflexionar acerca de sus ensayos, conjeturas y argumentos con el fin de determinar y probar los más adecuados.
Se tiene entonces que un problema es situacional, novedoso y debe ser tal que requiera, para poder superarlo, de la realización de cierto esfuerzo intelectual.
La Demostración en Geometría
Una demostración, según el Diccionario Larousse (2010, p.323), es un razonamiento que deduce la verdad de una proposición partiendo de axiomas que se han enunciado. Por su parte, Harel y Sowder (citado por Valdivié, 2013) definen demostración como el proceso empleado por un individuo para quitar o eliminar las dudas sobre la verdad de una proposición (p.6).Las proposiciones constan de dos partes: una establece lo que se da o se conoce, llamada dato o hipótesis, y otra que debe probarse, llamada conclusión o tesis. Estas proposiciones reciben el nombre de teoremas.
Para Hemmerling (2003), los teoremas pueden escribirse en cualquiera de las siguientes formas: (a) como una oración compleja, donde la hipótesis es una cláusula que empieza con si o cuando, y la conclusión es una cláusula que empieza con entonces; ejemplo, si dos ángulos son rectos, entonces son congruentes, (b) como una oración declarativa, donde la hipótesis y la conclusión no son tan evidentes; ejemplo, dos ángulos rectos son congruentes.
Debido a que la matemática se apoya principalmente en el razonamiento deductivo, la mayor parte de las proposiciones a demostrar que se presentan son de la forma si p, entonces q. En consecuencia, la demostración de un teorema de esta forma consistirá en demostrar que tal condicional es siempre verdadero.
Para que una tarea geométrica sea realmente una demostración, ésta debe ser novedosa para el sujeto que debe realizarla; es decir, tiene que representar una situación nueva que requiera de un esfuerzo intelectual para poder ejecutarla. No se trata entonces de sólo recordar una serie de axiomas y proposiciones previas ya demostradas, consiste en una tarea que convoca la ejercitación de habilidades cognitivas básicas, como por ejemplo: la lectura comprensiva, el razonamiento, el análisis, la evaluación, entre otras. Las proposiciones que necesiten estas habilidades para ser demostradas pueden ser consideradas como una instancia de problemas.
Efectivamente, al hacer demostraciones geométricas se busca entonces que los alumnos se involucren en una dinámica propia del quehacer matemático. Desarrollar una demostración geométrica, sobre todo en grupo, permite que los estudiantes adquieran una cualidad "matemáticamente potenciadora" porque constituye una experiencia de aprendizaje a través de la cual los estudiantes, en su condición de resolutores, "interactúan con el medio, con la Matemática y con sus compañeros, acción que los ayuda a construir sus conocimientos matemáticos" (Tirapegui, citado por González, 2002, p.13). Por tanto, las demostraciones geométricas en el contexto educativo se asumen como un proceso social, donde los estudiantes reflexionan, dialogan y descubren propiedades, son capaces de comunicarlas y de argumentar su validez, integrándolas así dentro del conjunto de conceptos y relaciones que han ido construyendo a lo largo del proceso de aprendizaje.
Enseñanza de las Demostraciones Geométricas
La geometría es el lugar natural para el desarrollo del razonamiento y de las habilidades para la justificación, ha sido considerada durante mucho tiempo como el lugar del currículo escolar donde los estudiantes aprenden a razonar y a conocer la estructura axiomática de la matemática. Además, las ideas geométricas son útiles para representar y resolver problemas en otras áreas de la matemática y también en situaciones del mundo real.
Esta ciencia puede proveer de importantes herramientas sobre cómo se construyen los conocimientos en matemática, más precisamente cómo se van efectuando los pasos lógicos para desarrollar una demostración. Sin embargo, a pesar de todo esto, puede observarse que la enseñanza de la geometría, en general, presenta serias dificultades. Incluso, se puede señalar, que los contenidos geométricos están presentes en los programas de estudios del área de Matemática, aunque, en muchas ocasiones, ausentes de las clases (Aguilar e Iglesias, 2013, p.152). Lo anterior es reforzado por Sánchez e Iglesias (2012) quienes comprobaron en sus investigaciones que los docentes les restan importancia a los contenidos geométricos privilegiando los contenidos aritméticos y algebraicos, además, los pocos que abordan, no los relacionan entre sí ni con otras áreas de conocimiento. Los autores sostienen que quizás esto se deba a su formación inicial, es decir, a modelajes recibidos tanto en su época de estudiantes de bachillerato como profesional.
En cuanto a las estrategias de enseñanza algunos autores (Lárez 2002, Crespo y Ponteville, 2004), reseñan que más del 63% de los docentes no promueven la solución de problemas como estrategia y tampoco realizan demostraciones geométricas en clases, no reconocen los distintos niveles existentes entre qué es demostrar, qué es saber demostrar y qué es aprender a demostrar. En este sentido, los estudios de Sánchez e Iglesias (2012) evidencian que entre las demandas formativas de los docentes en servicio resaltan la necesidad de herramientas teóricas y metodológicas que recreen construcciones geométricas con regla y compás, la resolución de problemas, la modelización matemática, la formulación de conjeturas y la demostración matemática p.171)
Estos hallazgos demandan atención por ser los docentes los actores encomendados de hacer la transformación didáctica del contenido a enseñar, son los encargados del qué y cómo. Esto requiere de cierta experiencia que permita concebir una actividad de enseñanza adaptada a las preconcepciones, edades e intereses de los estudiantes, con la finalidad de promover la comprensión y adquisición de competencias geométricas.
Por consiguiente, las actividades geométricas que se llevan a cabo en los encuentros de trabajo en aula, quedan a consideración del docente. El profesor no motiva a ciegas el aprendizaje, como mero operario, sino que interpreta y aplica el currículo oficial según unos criterios, entre los que destacan sus concepciones. Carrillo (2000, p.80). Es decir, las actividades dependen de las concepciones que sobre la geometría tengan los profesores. Larios (2002) sostiene que la concepción de la demostración geométrica por parte de los docentes y las personas encargadas de las políticas educativas resulta determinante para la manera de su inclusión en las clases o en el hecho mismo de incluirlas (p.46).
Muchas veces se pretende que los alumnos hagan demostraciones geométricas tras algunos ejemplos (a veces demostraciones fingidas) expuestos por los profesores en los pizarrones. En este proceso no se pide que el alumno construya conjeturas o elabore el enunciado que está siendo tomado en cuenta, sino únicamente que reconstruya el proceso que, previamente, alguien ha realizado (Larios, 2002, p.50). Para que las demostraciones geométricas tengan significado, deben retar intelectualmente hablando al estudiante. Los docentes deben proponer demostraciones, tanto del mundo cotidiano como internas de la propia matemática, que requieran de esfuerzo intelectual, acorde con los esquemas de conocimientos previos de los estudiantes, para que entre las producciones de conjeturas-argumentos y la construcción de la prueba o demostración, exista una moderada continuidad.
Cuando exista alguna complejidad cognitiva tanto de contenido como procedimental, una mediación apropiada por parte del docente es necesaria para solventar aquellos aspectos que generan una ruptura significativa con la cultura de todos los días: la forma de los enunciados, la naturaleza de los razonamientos permitidos, la organización peculiar de las teorías matemáticas, etc.(Boero; citado por Götte, Renzulli y Scaglia, 2010, p.3).
Es aquí donde la perspectiva constructivista del docente debe hacerse presente para rescatar el valor educativo de las demostraciones geométricas. El docente debe elaborar o construir enunciados acorde con la cantidad de información y estrategias que manejan sus estudiantes de forma tal que la nueva exigencia no se convierta en un obstáculo y pierda su objetivo. Hay que crear situaciones de aprendizaje que sirvan de apalancamiento para impulsar significativamente el ingreso hacia una cultura propia del quehacer matemático, novedosa, interesante, retadora, como son las demostraciones.
Un estudiante de bachillerato ya puede apreciar la importancia de argumentar para establecer verdades. A este nivel educativo los estudiantes son capaces de trabajar con enunciados abstractos sobre las relaciones y propiedades de los objetos geométricos y llegar a conclusiones basados en un sistema de deducciones lógicas.
Lo anterior se puede sustentar en la teoría del Desarrollo Cognitivo de Piaget, para el cual los estudiantes de Educación Media se encuentran en el Estadio de las Operaciones Formales. Según Lárez (2002), en esta etapa las operaciones formales son los conceptos de lógica y las matemáticas, así como las reglas de la inferencia que se utilizan en una alta conceptualización y razonamiento, por ejemplo, pensar en contenidos geométricos abstractos difíciles de representar.
Estas potencialidades fueron evidenciadas por Gutiérrez (2001) en un trabajo de investigación que llevo a cabo con estudiantes de Educación Secundaria al hacer demostraciones en un entorno de Cabri. El autor distinguió dos categorías: (a) empíricas, donde los estudiantes sustentan sus demostraciones a través de la verificación de propiedades con ejemplos, y, (b) deductivas, donde el elemento de convicción son argumentos descontextualizados de ejemplos concretos fundamentados en propiedades, abstracciones y deducciones lógicas. Hallazgos parecidos fueron registrados por Laurito y Valdivé (2011) en una investigación que tuvo como propósito estudiar el razonamiento geométrico de los estudiantes en la resolución de problemas de conjetura y demostración, durante el desarrollo de un curso de Geometría con el software Cabri Géomètre II. Los autores manifiestan que el software Cabri Géomètre II tal como fue empleado en la investigación favorece el razonamiento geométrico de los estudiantes cuando resuelven problemas de conjetura y demostración.
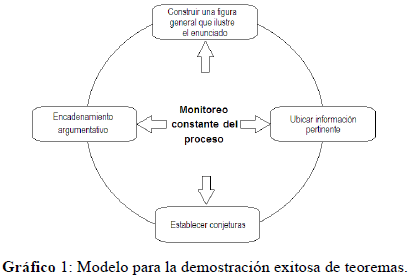
Un Modelo para Abordar las Demostraciones Geométricas
Para el abordaje exitoso de una proposición o teorema, se ha diseñado el siguiente modelo (ver gráfico), el cual consta de cinco fases: (a) Construcción; (b) Información, (c) Conjeturas, (d) Encadenamiento de Argumentos y (e) Evaluación.
La primera fase consiste en construir una figura general que ilustre el teorema a partir de la comprensión de las exigencias que éste plantea. Ella será el punto de partida que permitirá visualizar las propiedades del objeto geométrico y sobre la cual, durante todo el proceso, se realizarán trazos suplementarios que van a facilitar una reorganización visual develando de alguna manera la solución.
Luego de establecer la esencia del teorema y la construcción de una figura general, se requiere ubicar información pertinente y apropiada en función de los esquemas de conocimientos que se poseen sobre resultados anteriores, pasos y razonamientos de tipo procedimental que incluyen a la actividad en cuestión. En esta fase es necesario tomar la decisión sobre qué tipo o estrategia se utilizará para hacer la demostración en base a las normas aceptadas por la comunidad a la que se pertenece.
Las dos primeras fases del ciclo llevan a la producción de conjeturas a través de exploraciones, observaciones, reflexiones, discusiones sobre las afirmaciones que se hacen y una posible sistematización progresiva de éstas. En la fase siguiente, se retoma la anterior para continuar una exploración, pero ya con la finalidad de encontrar argumentos pertinentes para la demostración y se hace el encadenamiento de los mismos. Estos argumentos pueden ser proposiciones establecidas mediante definiciones y postulados aceptados, y teoremas probados con anterioridad. Si el encadenamiento utilizado no es concluyente, es conveniente reconsiderar la comprensión de la estructura lógica del enunciado y por ende, el proceso representacional.
Durante todo el proceso el ejecutor debe ir evaluando con la finalidad de corregir el camino cognitivo seguido contrastando siempre cada paso con el objetivo o meta prevista. Se trata entonces, que el ejecutor procure descubrir los errores causados por una mala ejecución y que asuma conscientemente los resultados logrados. Es sumamente importante el monitoreo permanente, estar vigilante, evitar la impulsividad y asumir una actitud crítica abierta a la retroalimentación externa en caso de procesos colaborativos de demostración.
La Prueba a Dos Columnas
En la segunda etapa de educación primaria cuando los alumnos están aprendiendo a dividir, se les enseña y exige que trabaje con la división larga. Se sabe que en esta forma de dividir el estudiante debe escribir los productos parciales y dejar explicitas las sustracciones. Esta práctica trabaja en paralelo con la adquisición de conocimientos procedimentales por parte del estudiante y con la habilidad del docente para mediar en el aprendizaje del procedimiento y con el conocimiento en juego.
De forma similar que esta manera de dividir permite encontrar un cociente y un resto, la Prueba a Dos Columnas (PDC) cumple con la tarea de proveer una demostración. La PDC es una forma metódica de presentar las demostraciones. Consiste en poner las proposiciones en una columna, y las razones que justifican las proposiciones en otra columna adjunta. Hemmerling (2003) afirma que este modo de presentación permite a uno mismo y a los demás, seguir la línea de razonamiento.
Sekiguchi (Citado por Lee, 2002) describe la forma de PDC como sigue:
Uno traza una línea horizontal y otra vertical desde el punto medio de la primera hacia abajo de tal manera que se forme una letra T, creando así dos columnas bajo la línea horizontal. En la columna de la izquierda, uno escribe una cadena deductiva de enunciados que converjan a la proposición a probar, asignándole un número de orden a cada enunciado. Para cada paso de la deducción, uno debe anotar la razón de la misma en la columna de la derecha bajo el correspondiente número de orden. (p. 78-79)
La Prueba a Dos Columnas es una herramienta que permite estructurar el conocimiento geométrico mediante una serie de pasos encadenados lógicamente hasta llegar a validar, mediante ellos, una proposición dada. Los argumentos geométricos dados siguen una métrica equilibrada: el enunciado que sigue a uno dado debe estar siempre a una razón de distancia. Por consiguiente, Herbst (1999), afirma que la prueba a dos columnas se puede inspeccionar a lo largo de una sucesión de puntos de control (cada renglón de la prueba), y puede ser controlada en lo que atañe al apareamiento adecuado de enunciados y razones (p.3). Su organización gráfica ofrece una forma de razonar en pequeños trozos la cual a su vez permite una reconstrucción ficticia del proceso de conjeturas y argumentos realizados previamente orientada hacia un lector determinado, pues puede leerse fácilmente en una sucesión uniforme de afirmo que, por tal razón.
En consecuencia, se puede decir, que la Prueba a Dos Columnas es una herramienta técnica ya que, en la práctica, permite al estudiante la adquisición de destrezas procedimentales y cognitivas generales que favorecen la adquisición del conocimiento geométrico y al docente, la habilidad para mediar y controlar el proceso de producción. En cuanto a la forma, la prueba presenta de manera escrita la organización lógica de sucesiones tal proposición por tal razón que puede ser seguida por cualquier lector.
Es importante señalar además, que la PDC brinda la oportunidad de adiestrarse en procesos de pensamiento superior, pues, si el ejecutor toma conciencia de su actuación mientras ejecuta las demostraciones y presta atención a las relaciones y asociaciones aplicadas ya sean favorables o no, tiene la posibilidad de transformarlas en una experiencia generalizable y transferible a situaciones objetivas similares. La forma como se emplean las PDC permiten a quien la ejecuta accionar activamente un conjunto de mecanismos para planificar, monitorear su acción a partir de los resultados intermedios que va obteniendo, y revisar y evaluar el resultado de las operaciones realizadas, en pocas palabras, facilita el ejercicio de la metacognición, la cual según González (1996: 18)
constituye un recurso intelectual íntimamente relacionado con el grado de conciencia, destreza, dominio y forma de llevar a cabo el control del proceso de búsqueda de la solución a problemas. Se manifiesta cuando una persona que está intentado resolver un problema, estudia detallada y concienzudamente tanto los elementos de éste como los pasos dados hacia su solución, y es capaz de formularse y responder, entre otras, las siguientes cuestiones: ¿Qué necesito y con qué cuento para resolver el problema? ¿Qué debo hacer cuando estoy resolviendo problemas? Y ¿Qué conozco acerca del proceso de resolución de problemas?
La demostración es una herramienta que puede proveer a los estudiantes experiencias con el rigor y el formalismo matemático. La escuela debe proporcionar a sus alumnos oportunidades de aprender a demostrar, de estudiar demostraciones culturalmente relevantes, y de familiarizarse con el significado de la demostración en la construcción y la validación del conocimiento matemático. Sin embargo, es conveniente que las proposiciones presenten una continuidad posible entre la producción de una conjetura y la construcción de su prueba.
Otra característica especial de este tipo de prueba, es el hecho de limitar qué puede demostrarse, pues apoya una determinada concepción de la geometría. La prueba a dos columnas funciona mejor dentro de una geometría concebida como un estudio descriptivo regido por una lógica general que enfatiza las conexiones lógicas entre propiedades asumidas como hechos y el estudio de figuras construidas y que son siempre construibles, es decir, geometría euclideana.
Hoy en día, frente a la posibilidad de la eliminación práctica de las demostraciones en nuestras aulas escolares, se deben levantar voces que enfaticen el hecho de que la exploración, la conjetura, la representación, y la demostración son aspectos del pensamiento matemático estrechamente conexos entre sí. "Razonamiento y Demostración no deberían considerarse como separables del resto de la actividad matemática. (NCTM, 2005, p. 85, Trad. PH)
Obsérvese el siguiente ejemplo tomado del libro Geometría Elemental de Hemmerling (2003, p.188): la medida de cualquiera de los ángulos externos de un triángulo es igual a la suma de las medidas de los internos no adyacentes a él.
Hipótesis: Ð CBE es un ángulo externo del triángulo ABC.
Tesis: m Ð CBE = m Ð C + m ÐA
Demostración:
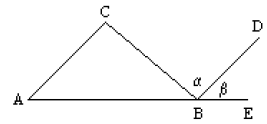
| Proposiciones | Razones |
| 1-.Trazar BD paralela a AC | 1. Teorema demostrado: en un plano que contiene a una recta y a un punto, que no esté en la recta, existe por lo menos una paralela a la recta dada. |
| 2-. m Ð a = m Ð C | 2. Teorema demostrado: si dos rectas se cortan mediante una transversal, los ángulos alternos internos son iguales. |
| 3-. m Ð b = m ÐA | 3. Teorema demostrado: Si dos rectas paralelas se cortan mediante una transversal, los ángulos correspondientes son congruentes. |
| 4-. m Ð CBE = m Ð a + m Ð b | 4. Postulado de la adición de los ángulos. |
| 5-. m Ð CBE = m Ð C + m ÐA | 5. Postulado de sustitución de la igualdad. |
Valores Formativos de las Demostraciones Geométricas
Como se ha comentado, la enseñanza de la geometría y las demostraciones se encuentran actualmente a punto de desaparecer de la práctica cotidiana de las aulas de matemáticas venezolanas, contrario a las consideraciones que tiene en países occidentales como España, Francia y Alemania donde constituye el pilar fundamental de la educación matemática. Aravena y Caamaño (2013) refieren la importancia de la geometría en el proceso de formación de los estudiantes, al ser considerada como una herramienta para comprender, describir e interactuar con el espacio en que vivimos, es quizás la parte más intuitiva, concreta y unida a la realidad de las matemáticas (p.143).
Es sumamente importante reforzar, a fin de robustecer la reflexión, los valores formativos de las demostraciones geométricas. El estudio de las demostraciones geométricas ofrece a sus ejecutores beneficios formativos indispensables para una participación activa y consciente en la sociedad a la cual pertenecen: (a) contribuye a desarrollar operaciones mentales generales; (b) posibilita la mejor utilización del lenguaje al hablar o escribir; (c) incrementa la capacidad de razonamiento; (d) disciplina la voluntad; (e) fomenta la criticidad; y (f) estimula el trabajo colectivo.
Al ejecutar una demostración el ejecutor pone de manifiesto una serie de acciones que contribuyen al desarrollo de operaciones mentales generales tales como comparar, clasificar, abstraer, concretar, analizar, sintetizar, particularizar y generalizar. En cuanto al lenguaje, las demostraciones permiten construir capacidades de argumentación, fundamentación, inferencias, refutación y deducción, además de fomentar el uso preciso de los conceptos para comunicarse con los demás.
La demostración exige al ejecutor poner de manifiesto rasgos de la conducta como es la rigurosidad en sus razonamientos, la exigencia y la reflexividad. Para Bravo, Martínez y Arteaga (2001), al plantear exigencias a los alumnos para evaluar el rendimiento de sus compañeros en las demostraciones, para discutir soluciones verdaderas y falsas, para juzgar propuestas y asumir proposiciones se manifiestan cualidades como la sinceridad, la crítica y la autocrítica (p.22).
Las demostraciones plantean retos, exigen perseverancia, esfuerzo y constancia, es un ejercicio constante de creatividad e inventiva. Bravo, Martínez y Arteaga (2001) señalan que al hacer demostraciones en colectivo, se propicia el compañerismo, la complacencia y la conducta colectiva. Hacer demostraciones en colectivo permite que la interacción entre estudiantes, profesor, teoremas y demás portadores de información, converjan hacia lo que se puede llamar conocimiento objetivo, como consecuencia de la cooperación y la coordinación de los distintos puntos de vistas.
En fin, los valores formativos de las demostraciones se hacen tangibles en el desarrollo de habilidades intelectuales inherentes a la solución de problemas, en la construcción de conocimientos teóricos y procedimentales, en la comunicación efectiva, en la honestidad, la perseverancia, la autoestima, la crítica, la libertad y la autonomía.
Conclusiones
Como se evidenció, los estudiantes de Educación Media tienen la capacidad de realizar demostraciones en geometría, en primera instancia, de forma empírica y al finalizar, de forma deductiva. Las pruebas y procesos argumentativos deben ser exigidos dentro de la programación curricular para que ésta pueda ser considerada de calidad. Hacer demostraciones y en especial en geometría, abre las puertas al resolutor a la esencia de la Matemática: resolver problemas. Las demostraciones novedosas para el estudiante se convierten en un problema pues no conocen de antemano las reglas o estructuras que deben seguir para lograrla.
Para el abordaje de las demostraciones geométricas se ofrece un modelo que consta de cinco fases. Parte de la construcción de una figura que sirve de recurso heurístico para dilucidar estrategias, trazos suplementarios y reglas que permiten develar argumentos pertinentes para hacer el encadenamiento lógico y lograr la demostración demandada. Una vez descrito el modelo se presenta una demostración utilizando la Prueba a Dos Columnas donde se evidencia, además de líneas adicionales sobre el dibujo inicial, la organización de proposiciones y razones que utilizó el resolutor.
Se hace hincapié en que los encuentros presenciales de trabajo en donde la actividad fundamental sea la demostración geométrica en un ambiente cooperativo y reflexivo, formarán en el estudiante un espíritu crítico que le permitirá reconocer los problemas, superar dificultades, discutir con argumentos, entender mejor su entorno, propiciando el desarrollo de su autonomía y pensamiento liberador.
Por lo tanto, la formación del nuevo republicano exige del docente un compromiso mayor, debe ser un acompañante constante en el proceso de construcción del conocimiento por parte del estudiante, facilitándole espacios de discusión, argumentación, reflexión, cooperación que le permita adquirir conocimientos tanto teóricos, procedimentales como actitudinales. Queda en manos entonces de nuestros estimados colegas determinar la inclusión o no de las demostraciones geométricas como instancias de problemas en las aulas de clase de los liceos venezolanos.
Referencias
1. Aguilar R., e Iglesias M.(2013). La geometría de los cuadriláteros en los libros de texto de Educación Primaria. Paradigma, XXXIV(2), 151-173. [ Links ]
2. Avarena M. y Caamaño C. (2013). Niveles de razonamiento geométrico en estudiantes de establecimientos municipalizados de la región del Maule, Talca, Chile. Revista Latinoamericana de Investigación en Matemática Educativa 16(2), 139-178. [ Links ]
3. Becerra, A (2005). Problemática diferenciativa entre pregunta y problema de investigación. Revista de Investigación Nº 58, p 13-47. [ Links ]
4. Bravo M., Martínez J. y Arteaga E. (2001). El valor formativo de las demostraciones. Xixim (Revista en línea), Año 1, número 3, 20-23. Disponible: www.uaq.mx/matemáticas/redm/ (Consulta: 2014, marzo 24). [ Links ]
5. Campanioni M. (2005). Alternativa Didáctica para la Solución De Problemas No Rutinarios En Cuarto Grado. Ponencia presentada en la I Conferencia Internacional de Educación para la Diversidad en el siglo XXI. Camaguey, Noviembre. 2005. [ Links ]
6. Carrillo J. (2000). La formación del profesorado para el aprendizaje de las Matemáticas. UNO, 24, 79-91. [ Links ]
7. Crespo C. y Ponteville C. (2004). Las concepciones de los docentes acerca de las demostraciones. En Díaz, L. (Ed.) Acta Latinoamericana de Matemática Educativa. Vol. 17.Tomo 1. México: Clame. (pp. 39-44)
8. García J. y Rentería E. (2012). La medición de la capacidad de resolución de problemas en las ciencias experimentales. Ciência & Educação, v. 18, n. 4, p. 755-767.
9. García M. y Mazzarella C. (2011). Efecto de una intervención didáctica constructivista sobre el conocimiento y la resolución de problemas relacionados con Herencia Biológica en estudiantes de noveno grado. Revista de Investigación 35(74), 111-138.
10. González F. (1996). Acerca de la Metacognición. Paradigma XIV al XVII, (1-2), 109-135.
11. González J (2009) .Fundamento y práctica de la competencia matemática. Curso CEP Ceuta. 3 y 4 Marzo. Consulta en línea disponible: http://www.cprceuta.es/CPPSXXI/Modulo%204/Archivos/Matematicas/DOC_GONZ_MARI/MODELIZACION%20Y%20RESOLUCION%20DE%20PROBLEMAS/Resoluci%C3%B3n%20de%20problemas.pdf [ Links ]
12. González, F. (1997). Procesos Cognitivos y Metacognitivos que Activan los Estudiantes Universitarios Venezolanos cuando Resuelven Problemas Matemáticos. Tesis Doctoral no publicada, Universidad de Carabobo, Valencia (Venezuela).
13. González F. (1998). Metacognición y Tareas Intelectualmente Exigentes: El caso de la Resolución de Problemas Matemáticos. Zetetiké, 6 (9), 59 – 87. [ Links ]
14. Gonzalez F. (2002). El Decálogo del resolutor exitoso de problemas. Investigación y Postgrado. 17(1), 11-45. [ Links ]
15. Götte M., Renzulli F. y Scaglia S. (2010). El contraejemplo en la producción de conjeturas de propiedades geométricas. Revista de Educación Matemática, Vol. 25, FAMAF, UNC. [ Links ]
16. Gutiérrez Á. (2001). Estrategias de investigación cuando los marcos teóricos existentes no son útiles. Actas del 5° Simposio de la SEIEM. Almería
17. Hemmerling E. (2003). Geometría Elemental (J. Pérez, Trad.). México: Limusa. (Trabajo original publicado en 1971).
18. Herbst P. (1999). On proof, the logic of practice of geometry teaching and the two-column proof format: Some historical considerations. On-line article. Disponible en: http://www.lettredelapreuve.org/OldPreuve/ Newsletter/990102Theme/990102ThemeUK.html. Consulta: 2014, Agosto 14; 09:07) [ Links ]
19. Lárez J (2002). Una Metodología para
20. Larios V. (2002). Demostraciones y conjeturas en la escuela. Xixim (Revista en línea), Año 2, número 3, 45-55. Disponible: www.uaq.mx/matemáticas/redm/ (Consulta: 2014, marzo 20). [ Links ]
21. Laurito F. y Valdivé M. (2011). Razonamiento geométrico en la resolución de problemas de conjeturación y demostración utilizando el software cabri géomètre ii. EDUCARE 15(2), 3-22.
22. Lee, J (2002). Philosophical perspectives on proof in mathematics education. PoME journal 16 [ Links ]
23. MPPE (2007). Curriculo de los Liceos Bolivarianos. Caracas: autor.
24. National Council of Teachers of Mathematics. (1998). Principles and standards for School Mathematics: Discussion Draft Standards 2000. Disponible: http://standards.ntcm.org/. (consulta: 2005, enero 24).
25. Pequeño Larousse Ilustrado (2010). México D.F., México: Larousse [ Links ]
26. Pérez Y. y Ramírez R. (2011). Estrategias de enseñanza de la resolución de problemas matemáticos. Fundamentos teóricos y metodológicos. Revista de Investigación Vol. 35. Nº 73. [ Links ]
27. Sánchez J. e Iglesias M. (2012). El desempeño de los docentes de matemática y sus necesidades formativas. Paradigma, 33(1), 155-173. [ Links ]
28. Valdivé C. (2013). Estrategias implementadas por los matemáticos cuando demuestran: estudio de caso. EDUCARE, 17(2), 4-26. [ Links ]