Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigación y Postgrado
versión impresa ISSN 1316-0087
Investigación y Postgrado v.17 n.1 Caracas abr. 2002
EL DECÁLOGO DEL RESOLVEDOR EXITOSO DE PROBLEMAS
Fredy E. González
(UPEL-IPMAR)
RESUMEN
En la siguiente investigación se reportan diez acciones básicas que un estudiante debe aplicar si desea tener éxito cuando intenta resolver un problema matemático con texto. El Decálogo del Resolvedor Exitoso de Problemas constituye una herramienta heurística, útil para ayudar a los alumnos en la realización de Tareas Intelectualmente Exigentes (TIE). Los "mandamientos" del Decálogo son los siguientes: (1) Conocer las metodologías y técnicas de resolución de problemas; (2) Poseer un esquema secuencial y organizado que pueda orientar la obtención de la solución; (3) Comprender el enunciado del problema; (4) Conocer los diferentes pasos que se deben poner en acción para buscar una solución; (5) Tener en cuenta las condiciones que contextualizan el problema; (6) Hacer una revisión minuciosa de los datos del problema; (7) Estimar la dificultad del problema; (8) Realizar un seguimiento riguroso y minucioso de los diversos factores que intervienen en el problema; (9) Tejer un plan, una estrategia bien definida, que lleve a la solución; (10) Tener en cuenta que no todos los problemas tienen la misma estructura. Se recomienda operacionalizar los "mandamientos" de este Decálogo y hacer estudios que confirmen sus beneficios, así como también su posible ampliación.
Palabras clave: educación matemática; tareas intelectualmente exigentes; metacognición; heurísticas.
THE SUCCESSFUL PROBLEM SOLVER DECALOGUE
ABSTRACT
This research reports ten basic actions which a student must apply if she /he wishes to succeed in trying to solve a mathematics problem with a text. "The successful problem solver Decalogue" is a useful heuristic tool to help students in carrying out Intellectually demanding tasks (IET). The "commandments" of the Decalogue are the following: (1) To know the methodologies and techniques of problem solving. (2) to have an organized and sequential scheme which can guide the achievement of the solution. (3) To understand the problem statement. (4) To know the different steps which must be put into action in order to look for a solution. (5) To consider the context of the problem. (6) To make a careful review of the problem data. (7) To estimate the problem difficulty; (8) To make a strict and careful follow-up of all the factors related to the problem; (9) To devise a plan, a well defined strategy which leads to the solution; (10) To consider that not all the problems have the same structure. It is recommended to set the "commandments" of this Decalogue into practice and to conduct studies which confirm its benefits as well as its possible enhancement.
Keywords: mathematics Education; intellectually demanding tasks (IET); metacognition.
Introducción
La resolución de problemas, concebida como una Tarea Intelectualmente Exigente, TIE, (González, 1998 a), constituye uno de los quehaceres cotidianos básicos del proceso de enseñanza y aprendizaje de la Matemática. Los problemas conforman "el corazón de la Matemática", según lo dice Halmos (1980), de allí que resulte fundamental que los aprendices de esta disciplina desarrollen y fortalezcan su habilidad para resolverlos. El carácter de TIE hace que la búsqueda de solución a algún problema matemático constituya una oportunidad para que los estudiantes desarrollen su "potencia matemática" (NCTM, 1991, citado por Tirapegui, 1997, p. 1)
Efectivamente, cuando el estudiante soluciona un problema auténtico (sobre todo si lo hace en equipo) evalúa ideas, sugiere, escucha, analiza, elabora conjeturas, construye demostraciones o pruebas. En cada una de estas situaciones utiliza diversas modalidades expresivas del lenguaje matemático (dibujos, gráficos, tablas, símbolos), usa calculadoras y/o computadoras (según sea la exigencia o la naturaleza del problema). Todas estas acciones forman parte de lo que se espera que sea capaz un estudiante "matemáticamente poderoso" (Mumme, 1996).
De acuerdo con lo anterior, la resolución de problemas (como instancia específica de las TIE), adquiere una cualidad "matemáticamente potenciadora" (Tirapegui, 1997) porque constituye una experiencia de aprendizaje a través de la cual los estudiantes, en su condición de resolutores, "interactúan con el medio, con la Matemática y con sus compañeros, acción que los ayuda a construir sus conocimientos matemáticos" (Tirapegui, 1997: 1). Por tanto, la resolución de problemas puede ser asumida como una tarea orientada hacia el desarrollo del talento, tal como lo conciben Lorenzo y Martínez (1996), y su realización engloba aspectos cognitivos, afectivo-volitivos y creativos del desempeño personal.
Dentro del contexto conceptual anteriormente esbozado, tuvo lugar el estudio del cual se derivó el Decálogo del Resolvedor Exitoso de Problemas que se expone en este trabajo; el mismo forma parte de una obra mayor llevada a cabo por el autor (González, 1997). Se elaboró utilizando técnicas de Observación Participante, es decir, "una observación sistematizada natural de grupos reales o comunidades en su vida cotidiana, y que fundamentalmente emplea la estrategia empírica y las técnicas de registro cualitativas (Anguera, 1989: 128-143, citado por Gutiérrez y Delgado, 1995: 144), enmarcadas en una investigación cualitativa del tipo Estudio de Caso (Merriam, 1988).
Coordenadas teórico-referenciales
En este estudio se adoptó una Perspectiva Cognoscitivista del Aprendizaje basada en un Modelo del Procesamiento Humano de Información, a partir del cual se construyó una Interpretación Cognitiva del desempeño académico en Matemática. Desde esa perspectiva, el aprendizaje se concibe como un proceso constructivo que requiere de la participación consciente y activa del aprendiz. Dicha participación supone el tratamiento de informaciones provenientes del entorno mediante procesadores ad hoc que conforman su Sistema Cognitivo y cuya operación es supervisada, controlada y regulada por los procesadores del Sistema Metacognitivo. Se asume que la calidad del funcionamiento de este último es responsable de la diferencia en cuanto a ejecución de Tareas Intelectualmente Exigentes que puedan apreciarse en dos personas con igual nivel de desempeño en relación con sus respectivos Sistemas Cognitivos.
Perspectiva cognoscitivista del aprendizaje
Recientemente se ha incrementado la atención al papel del aprendiz como un participante activo en el proceso de enseñanza y aprendizaje. En esta perspectiva se plantea que los efectos de la enseñanza dependen no sólo de los conocimientos previos del aprendiz sino, fundamentalmente, de lo que él hace con dichos conocimientos durante el aprendizaje. El creciente interés por lo que cognitivamente ocurre en el interior del sujeto que aprende, según la opinión de Weinstein y Mayer (1986), es una resultante natural del cambio que está aconteciendo en la Psicología del Aprendizaje, en la que el punto de vista conductista predominante hasta los años 60 y comienzos de los 70, progresivamente, ha sido sustituida por una orientación cognoscitivista según la cual la enseñanza afecta al rendimiento del estudiante a través de sus procesos de pensamiento. El modelo que se propone considera que tales procesos median entre la enseñanza y el rendimiento (Wittrock, 1986), lo cual supone nuevos conceptos, tanto del aprendiz, (visto como un procesador activo de información, que participa de manera consciente en la construcción de su propio conocimiento) como del aprendizaje (conceptualizado como un proceso activo que ocurre dentro del aprendiz y el cual puede ser influenciado por éste). Se asume que el aprendizaje depende tanto de la información que le es presentada al alumno como de la forma cómo éste la procesa. En resumen, el aprendiz es considerado como "un sujeto cognoscente tratante de informaciones, es decir, que activamente busca información del medio ambiente, la recodifica y la almacena para su posterior recuperación y uso" (Izcaray, 1987; p. 123).
Tal interés por los procesos de pensamiento del estudiante se conecta con la idea según la cual la educación no puede consistir sólo en una mera acumulación cuantitativa de conocimientos; por el contrario, entre las metas que las exigencias tecnológicas y científicas de la sociedad contemporánea asignan a la educación, está la de lograr que los ciudadanos sean buenos pensadores; es decir, que no sólo sean solucionadores efectivos de problemas sino que, además, sean reflexivos, que posean un extenso repertorio de herramientas de pensamiento formal e informal y que conozcan cómo y cuándo usarlas; que tengan una buena cantidad de conocimientos acerca de la cognición humana y cómo manejar efectivamente sus propios recursos cognitivos (Nickerson, 1988). Esto último tiene carácter metacognitivo (cfr. González, 1996) y se corresponde con lo expresado por Romberg y Carpenter (1986) quienes sostienen que existe evidencia de que al hacer consciente al estudiante de sus propios procesos de pensamiento, el aprendizaje puede ser incrementado. Tomando en cuenta lo anterior, en el estudio que sirvió de contexto mayor para el trabajo que aquí se reporta, se adoptó un enfoque que se interesa por los procesos internos de funcionamiento intelectual que activa el estudiante en la realización de tareas propias del aprendizaje de la Matemática, particularmente la solución de problemas. Según dicho enfoque, la búsqueda de solución a un problema matemático constituye un complejo conjunto de tareas cognitivas cuyo estudio abarca dos aspectos: (a) los procedimientos (operaciones) matemáticos aplicados en la realización de la tarea, y (b) los procesos de pensamiento que el sujeto (resolutor) activa durante la ejecución de la misma. Luego, si se considera que la solución de problemas es la actividad matemática por excelencia, entonces se está en posibilidad de estudiar el desempeño en Matemática tomando en cuenta los procesos de pensamiento que los estudiantes activan cuando se dedican a solucionar problemas en esta disciplina.
Un modelo del procesamiento humano de información
Los modelos sistémicos de procesamiento humano de información conforman una estructura teórica apropiada para acceder a los estados cognitivos internos del resolutor de problemas. Dichos modelos consideran que el Ser Humano posee dispositivos que le permiten codificar la información proveniente de fuentes externas, almacenarla temporalmente, transformarla, conservarla en dispositivos de almacenamiento a largo plazo, y producir salidas (output) (esta suposición es conocida como "Metáfora del Computador", Lohman, 1989). Vinculada con lo anterior, existe una "Concepción Multialmacén" de la memoria humana (Sierra y Carretero, 1990).
De acuerdo con lo antes mencionado, Kempa (1986) afirma que la resolución de problemas se concibe en términos de un modelo de procesamiento de información "entrada-salida" (input/output), donde la "entrada" representa la percepción del problema por parte del sujeto, y la "salida" su respuesta (o solución). La información es procesada por el "cerebro" del sujeto en el sentido más amplio, lo que implica la utilización de tres tipos diferentes de memoria: (a) a corto plazo, (b) de trabajo, y (c) a largo plazo (sustrato básico de conocimientos).
El mencionado modelo supone, además, la existencia de una serie de procesos de pensamiento que las personas activan cuando operan con la información. Ésta, al ser almacenada en la memoria, manifiesta ciertas características estructurales que, al ser puestas en funcionamiento para interpretar una situación o para resolver un problema, son objeto de elaboraciones y reelaboraciones conforme a unos procedimientos y operaciones peculiares, los cuales dan lugar a dos conjuntos de procesos de control. Uno de ellos dirige las búsquedas en la base de datos (Memoria a Largo Plazo), opera con éstos y difunde la información entre los otros almacenes de información (Memoria a Corto Plazo y Memoria de Trabajo; abarca la colección de esquemas, conceptos, símbolos y reglas que han sido aprendidos en un dominio teórico específico.
El otro conjunto de procesos de control opera como un supervisor del sistema que toma decisiones ejecutivas orientadas a que la búsqueda rinda buenos resultados; supervisa también la localización de datos específicos de información en la Memoria a Largo Plazo, así como la cantidad de esfuerzo requerido para otras operaciones; está constituido por un conjunto de mecanismos ejecutivos que ejercen una especie de supervisión sobre estas unidades y procesos de cognición con el fin de: (a) conservar información acerca de lo que ha sido aprendido; (b) orientar la búsqueda de soluciones; y (c) conocer cuándo se ha alcanzado la solución.
Los procesos pertenecientes al primer conjunto permiten la captación, reelaboración y producción de información propia del dominio de conocimiento del cual se trate; los del segundo conjunto son usados tanto para abordar los problemas propios de la disciplina como para supervisar, controlar y regular el propio proceso de aprendizaje. Estos últimos procesos son los que le permiten a una persona: (a) saber qué es lo que sabe; (b) planificar e invertir más eficientemente el tiempo disponible para la realización de las tareas intelectualmente exigentes (González, 1998 a); y (c) revisar y monitorear su propio pensamiento. Indriago (1988) señala que se ha encontrado que tanto el docente como el proceso instruccional afectan la ejecución académica de un estudiante sólo en la medida en que activan sus propios procesos de pensamiento. Esto quiere decir que el aprendizaje no ocurre automáticamente, sino que se debe principalmente al procesamiento activo de la información por parte de los aprendices.
En el caso específico de las acciones de tipo académico que tienen como meta la adquisición y/o aplicación del conocimiento correspondiente a determinada rama del saber, los dos conjuntos de procesos antes aludidos, según Fuenmayor y Mantilla (1988), cumplen sendas funciones específicas: (a) facilitar el procesamiento de la información que se recibe (procesos cognitivos); y (b) mantener y enriquecer la atención, el esfuerzo y el tiempo que se dedica al aprendizaje (procesos metacognitivos).
Interpretación cognitiva del desempeño académico en matemática
En el campo de la Psicología se ha producido un cambio paradigmático en cuanto a la concepción del aprendizaje (González, 1998 b). En efecto, -afirma Pozo (1990)-, las teorías psicológicas del aprendizaje han ido abandonando progresivamente los modelos según los cuales el conocimiento del sujeto era una simple réplica de la realidad basada en la mera práctica, acercándose a posiciones de acuerdo con las cuales el conocimiento alcanzado por una persona es producto de la interacción entre la información presentada y los conocimientos anteriores que posee. De este modo se tiene que "las teorías psicológicas del aprendizaje se orientan cada vez más al análisis de la interacción entre la información que se ha de aprender y los procesos psicológicos mediante los cuales dicha información es procesada por el sujeto" (Pozo, 1990, p. 201).
De allí que las diferencias en ejecución académica que dos estudiantes con igual conocimiento exhiben frente a un mismo problema podrían ser interpretadas en función de las diferencias que entre ellos haya en cuanto a sus procesos de pensamiento. La competencia en la solución de problemas y en otras tareas académicas que demandan algún esfuerzo intelectual deriva no sólo del conjunto de conocimientos, conceptos y reglas que previamente haya adquirido el estudiante sino, además, de su habilidad para reconocerlos y activarlos cuando sea necesario.
En el marco de esta perspectiva podría intentarse una interpretación cognitiva del bajo rendimiento académico en Matemática registrado en los estudiantes de Educación Superior, el cual podría estar asociado con un funcionamiento metacognitivo deficiente, caracterizado por: (a) la no activación de los procesos cognitivos o procesos intelectuales de orden superior que son demandados por las tareas académicas que le son planteadas (en particular la resolución de problemas); y (b) la falta de conciencia en relación con estos mismos procesos, es decir, que el estudiante no se percate de cómo aborda los problemas y, en consecuencia, no pueda ejercer control ni supervisión alguna sobre dichos procesos.
Por otro lado, concebir el aprender como un proceso de solucionar problemas posibilita un abordaje metacognitivo del aprendizaje, ya que este último podría ser estudiado desde la perspectiva del propio sujeto que aprende, a quien se le considera capaz de observar sus propios procesos cognitivos y de reflexionar sobre ellos (García y La Casa, 1990).
De acuerdo con estos autores, en la resolución de problemas, la metacognición se expresa en la capacidad que tiene el sujeto para observar y reflexionar sobre los procesos de pensamiento que utiliza en la realización de la tarea.
Para Martin y Marchesi (1990), los procesos metacognitivos en la resolución de problemas cumplen una función autorregulatoria, la cual permite a la persona: (a) planificar la estrategia que desarrollará en el proceso de búsqueda de la solución del problema; (b) aplicar la estrategia y controlar su proceso de desarrollo o ejecución; (c) evaluar el desarrollo del plan, es decir, de la estrategia diseñada, a fin de detectar posibles errores cometidos y (d) modificar el curso de la acción cognitiva en función de los resultados de la evaluación.
Planteamiento del problema objeto de este estudio
El enfoque cognitivo del aprendizaje, que concibe la existencia de procesos de pensamiento que median entre la información que recibe el sujeto y su ejecución académica, genera la necesidad de prestar especial atención al funcionamiento cognitivo y metacognitivo del aprendiz, es decir, de qué manera éste procesa la información que se le suministra y, además, a los procesos de control ejecutivo que ejerce sobre su propio modo de abordar las tareas académicas.
El conocimiento de los procesos de pensamiento que una persona activa cuando resuelve problemas sirvió de base para proponer una explicación del desempeño en Matemática de los estudiantes. Este conocimiento toma en cuenta la calidad de su funcionamiento cognitivo y metacognitivo cuando los alumnos se dedican a la solución de problemas matemáticos. Orientado hacia el logro de este propósito y adoptando un enfoque de investigación centrado en el alumno, se planteó un estudio que aspira responder, entre otras, las siguientes interrogantes: (a) ¿Cuáles son las posibilidades de utilización didáctica de la resolución de problemas en el contexto del aula de clases de Matemática?; (b) ¿Se puede explicar el desempeño en Matemática de los estudiantes tomando en cuenta la calidad de su funcionamiento cognitivo y metacognitivo?; (c) ¿Cuáles son los procesos superiores de funcionamiento intelectual que utilizan los estudiantes?, (d) ¿Cuál es su repertorio de herramientas de pensamiento formal, cómo lo usan, qué conocen acerca de la cognición humana? y, (e) ¿Cómo manejan sus propios recursos cognitivos y qué grado de conciencia tienen acerca de ellos? Con este propósito se desarrolló un trabajo de campo, entre cuyos resultados está el Decálogo del ResolvedorExitoso de Problema, descrito en este artículo.
Método
Diseño de la investigación
Por su naturaleza, el diseño de la investigación que aquí se reporta es el que corresponde a un estudio de caso cualitativo. Los estudios de este tipo conducen a descripciones y análisis holísticos e intensivos de unidades sociales específicas; son particularistas, descriptivos y heurísticos, y se apoyan fuertemente sobre el razonamiento inductivo utilizando múltiples fuentes de datos (Merriam, 1988).
Por su orientación disciplinaria, la investigación corresponde a un estudio de caso etnográfico, porque se planteó una descripción intensa y completa de las acciones protagonizadas por un docente y un grupo de alumnos en una situación social determinada (Curso de Resolución de Problemas).
Por la clase de información recabada y por el tratamiento dado a ésta, la investigación aquí reportada puede considerarse como un estudio de caso cualitativo de orientación etnográfico-interpretativa, ya que a partir de descripciones se logró desarrollar una serie de categorías conceptuales que sirvieron de base para construir una teoría de lo acontecido en el aula, en relación con los procesos cognitivos y metacognitivos implicados en la resolución de problemas de Matemática por parte de un grupo de estudiantes universitarios de la Carrera de Formación Docente en esta especialidad.
Además, la presente investigación se concibe como un estudio de caso simple debido a que sus unidades de análisis fueron consideradas todas simultáneamente en un mismo lugar y en un mismo momento: un aula de clase universitaria de Matemática.
Escenario y sujetos del estudio
La institución. El estudio se realizó en el Instituto Pedagógico de Maracay, núcleo de la Universidad Pedagógica Experimental Libertador, cuya misión básica es formar docentes para los niveles de Educación Preescolar, Básica y Media Diversificada y Profesional en las especialidades de Biología, Castellano y Literatura, Ciencias Sociales (Geografía e Historia), Educación Física, Física, Inglés, Matemática y Química. Atiende a una población cercana a los seis mil estudiantes, agrupados por especialidades. La especialidad de Matemática tiene dos menciones: Matemática e Informática. Los alumnos de la especialidad de Matemática, mención Matemática -entre quienes se encuentran los informantes clave de este estudio- obtienen el título de Profesor de Matemática, el cual los habilita para desempeñarse como docentes de esta asignatura a nivel de Educación Media Diversificada y Profesional.
El aula. Las sesiones de trabajo en clase se realizaron en un salón que cuenta con mesas y sillas (sin pupitres) como parte del mobiliario. Éstas fueron dispuestas de manera tal que permitieran organizar grupos de trabajo pequeños y grandes. El salón, además de contar con aire acondicionado, se encuentra relativamente aislado, lo que facilitó el trabajo sin interrupciones.
Los informantes. Los sujetos del estudio que aportaron los datos mediante su interacción con el investigador fueron los alumnos inscritos en la asignatura "Investigación Individual", (Curso de Resolución de Problemas); su tiempo de dedicación a la realización de las tareas propias del curso fue parcial. Los alumnos participantes [Cinco (5) hembras y ocho (8) varones], son cursantes de la especialidad de Matemática, con una edad promedio de 25 años, todos de extracción social humilde, con condiciones de vida características de los niveles socioeconómico medio y bajo; constituyeron un grupo de rendimiento promedio regular, cuya mayoría presentaba índices cercanos a la calificación mínima para graduarse (6 puntos en una escala de 1 al 9); con la excepción de uno de los participantes con un índice académico cercano a nueve (9), lo que le permitió calificar como preparador. El resto de los alumnos podría catalogarse como "normal" (índices oscilantes entre 6 y 7 puntos) .
El índice académico permite afirmar que los participantes poseían diversos grados de experiencia en el conocimiento matemático propio de los cursos universitarios que habían realizado como parte de su formación académica; sin embargo, ello no incidió demasiado en el desempeño de los participantes debido a la naturaleza de la tarea misma: resolver problemas matemáticos con texto, cuyo contenido hacía referencia a conocimientos matemáticos propios de los niveles educativos básico y medio que, se presume, deben ser dominados por una persona que está próxima a graduarse como profesor de Matemática de los mencionados niveles.
Conviene acotar que, además de las características anteriores, como consecuencia de su desempeño como profesores de aula, no graduados, varios de los estudiantes habían tenido la oportunidad de participar en al menos uno de los talleres sobre Resolución de Problemas dictados por el Centro Nacional para el Mejoramiento de la Enseñanza de la Ciencia (CENAMEC) como parte de las actividades vinculadas con el evento denominado "Olimpíadas Matemáticas Venezolanas". Es de hacer notar que en esos talleres el énfasis se orienta hacia los aspectos de contenido matemático y a la modelística empleada, mientras que en el estudio que aquí se reporta interesan, esencialmente, los procesos de pensamiento activados por la persona que resuelve el problema.
Los alumnos desempeñaron un cuádrupe rol: (a) resolvedores de problemas (con miras a mejorar su propia capacidad para resolver problemas); (b) estudiosos del proceso de resolución de problemas (estudiosos de los procesos de pensamiento -cognitivos, metacognitivos y afectivos - que se activan durante la tarea de resolución de problemas); (c) potenciales utilizadores de la resolución de problemas como estrategia didáctica (se partió de la idea de que los profesores de Matemática no usan o usan poco la resolución de problemas como estrategia didáctica debido, en parte, a que ellos mismos no han vivenciado experiencias auténticas, concientizadas sobre la resolución de problemas; (d) Informantes Clave (propietarios de información valiosa que sirvió de base a las expresiones genéricas usadas por el autor para la construcción de las teorías explicativas del desempeño en Matemática, a partir de la actividad resolutora de problemas).
Técnicas e instrumentos
Las técnicas empleadas para la obtención de información fueron: (a) Observación Participante Activa; (b) Entrevistas; (c) Protocolos Verbales del Alumno.
La observación participante activa. El autor del estudio, actuando simultáneamente como investigador y como mediador (facilitador) de los procesos de pensamiento de los alumnos, se mantuvo en interacción con éstos durante todo el trabajo de campo en el cual se desarrollaron 29 sesiones de trabajo presencial. Se acumuló así un total de 70 horas de clase, aproximadamente, durante las cuales se realizaron las actividades propias del curso y, además, se observó el desenvolvimiento de las personas. De esta manera, el investigador logró: (a) involucrarse en la situación objeto de indagación y, al mismo tiempo, observar a los alumnos y a sí mismo; (b) estar atento a muchas de las situaciones que se presentaban en el aula que, para otra persona, podrían haber pasado inadvertidas; (c) tener en mente que las acciones protagonizadas en el aula tenían un propósito que trascendía la actividad misma; (d) poder vivenciar en y por sí mismo los procesos de pensamiento aplicados en la resolución problemas, objeto fundamental del estudio.
Las entrevistas (individual, grupal y colectiva) fueron No Estructuradas, con preguntas no pre-secuencializadas, improvisadas de acuerdo con la dinámica de los intercambios comunicativos que se presentaban entre el investigador (facilitador, entrevistador) y los alumnos quienes pudieron hablar libremente y expresarse en el marco de su propia vivencia como solucionadores de problemas. Las preguntas y respuestas producto del diálogo entrevistador-entrevistados fueron grabadas en cinta magnetofónica y posteriormente transcriptas para su análisis. Las transcripciones fueron elaboradas por personal no vinculado con la investigación, que siguieron las indicaciones del investigador: "respetar las expresiones tal como eran utilizadas por los entrevistados"; esto permitió una versión preliminar. Luego de escuchar la grabación se precisó la versión definitiva de la transcripción.
Pensamiento en voz alta. Esta técnica fue utilizada de la siguiente manera: (a) se les facilitó a los alumnos información relacionada con el sentido de la investigación y se reiteró la necesidad de que verbalizaran todos sus procesos cognitivos; (b) se les indicó que sus verbalizaciones serían grabadas; (c) se insistió en la necesidad de realizar las grabaciones de estas verbalizaciones en el aula de clases, respetando así las condiciones naturales del estudio. Como el investigador fue, al mismo tiempo, el facilitador del curso, su presencia no era extraña a los alumnos; al contrario, resultó ser natural, por ello se piensa que el uso de los grabadores en ningún momento fue visto como intrusivo; (d) se les entregaron los enunciados de los problemas por escrito (guías); (e) se les pidió que pensaran en voz alta, tratando de expresar verbalmente los procesos de pensamiento que se generaron durante la resolución de los problemas; (f) se grabó integralmente en cinta magnetofónica tal verbalización, manteniendo la secuencia temporal del discurso del alumno; (g) el contenido de la grabación fue transcrito y convertido en protocolo verbal para su posterior análisis.
Como resultado de la aplicación de esta técnica se construyeron los protocolos verbales de los alumnos que sirvieron como complemento de las Hojas de Trabajo, es decir, textos manuscritos de los estudiantes en los que se registró el proceso formal de la resolución del problema materializado a través de las ecuaciones, los cálculos y los esquemas gráficos correspondientes.
Los Cuadernos de Notas: (a) son cuadernos donde los participantes debían hacer registros de lo acontecido durante la clase; se aspiraba que el Cuaderno de Notas fuera más allá de un cuaderno de apuntes convencional; se recomendó que en él, los alumnos registraran la siguiente información: ¿cómo se desarrolló la clase?, ¿cuáles fueron los temas tratados?, ¿qué aprendió cada quien?; (b) contienen una mirada del curso desde la perspectiva de los participantes; (c) posibilitaron la reconstrucción de las clases; (d) permitieron las transcripciones de las sesiones de resolución de problemas (en pareja, pequeños grupos, y grupo total) y de las entrevistas que constituyen la fuente básica de información para la realización del estudio. En el Cuaderno de Notas se debían registrar, además, las autorreflexiones que periódicamente se exigían para comparar cómo resolvían problemas antes de iniciar el curso y cómo lo hacían en el momento de estar escribiendo el autobalance.
Procedimiento
Se dispuso de cinco horas académicas (de 45 minutos cada una) durante un período aproximado de 15 semanas para efectuar las observaciones de las diferentes actividades, las cuales incluyeron la resolución de problemas de Matemática por parte de los alumnos. El uso de la Observación Participante, los Cuadernos de Nota, los protocolos, los grabadores y las entrevistas permitió la obtención de la información relevante.
El trabajo de campo fue organizado como un curso sobre la actividad resolutoria de problemas matemáticos con texto en un aula universitaria, durante un período académico (semestre). El docente (investigador) y los alumnos protagonizaron veintinueve (29) encuentros -sesiones presenciales de trabajo o clases- relacionados con la solución de problemas de Matemática. A lo largo del curso se realizaron diferentes actividades, pero la que predominó fue la resolución de problemas, que se desarrolló de la siguiente manera: (a) se enunciaba el problema (planteándolo en alguna de las estas modalidades: narración oral del enunciado o planteamiento escrito); (b) se daba un tiempo prudencial para que cada alumno, individualmente, intentara resolverlo; se dictaban instrucciones para que los alumnos tratasen de llevar un registro del proceso. Transcurrido cierto lapso, se detenía el proceso y se introducían las fases del Modelo de Polya como referencia para organizar el proceso de resolución y ubicar las acciones en cada una de sus diferentes fases; (c) puesta en común (intercambio); (d) reflexión individual.
El profesor presentaba, verbalmente o por escrito, el enunciado de uno o varios problemas (de los denominados "verbales" o "de historia") que tuviesen una alta probabilidad de ser totalmente desconocidos por todos o por la mayoría de los alumnos participantes (esto se lograba extrayendo los enunciados de revistas extranjeras de difícil acceso para los alumnos: Muy interesante (Colombia), Thales (España), Educaçao Matemática (Portugal), Arithmetic Teacher (USA).
Se brindaban instrucciones precisas a los alumnos para que abordaran el problema durante un lapso determinado. Desde este mismo momento se insistió en que el curso no era de Matemática sino de Resolución de Problemas; por ello, se aclaró que lo que se quería, básicamente, era mejorar la habilidad de cada uno de los participantes como resolvedores de problemas. No se trataba de que exhibieran su "fuerza matemática", no se quería estimular un torneo o una competencia de conocimientos, sino propiciar oportunidades para imcrementar la habilidad para resolver problemas. El trabajo podía hacerse individualmente, por parejas, por pequeños grupos o por el grupo total.
Transcurrido cierto lapso (variable según la dificultad que presentase el problema con el cual se estuviera trabajando) se pasaba a la realización de una sesión de trabajo en plenaria. Bajo la dirección del facilitador, los participantes intercambiaban ideas y opiniones en torno a la forma como habían conducido sus esfuerzos para la búsqueda de la solución del problema.
Una vez concluida la "puesta en común" del trabajo individual se proporcionaban indicaciones y asignaciones sobre algún otro problema que sirviera de pretexto para iniciar la próxima clase y para tratar de garantizar la realización independiente de algún trabajo que contribuyera a consolidar lo que se había hecho en clase.
Organización de la información
Una vez terminada la recolección de información: (a) se hizo una lectura global de cada uno de los Cuadernos de Notas y fueron preparadas sendas fichas de clase para los 29 encuentros presenciales, es decir, se elaboraron descripciones que contenían información sobre las actividades realizadas en cada encuentro, las modalidades didácticas utilizadas, los problemas tratados y la intencionalidad del correspondiente encuentro presencial; (b) se elaboraron las transcripciones de los Cuadernos de Notas, las entrevistas y los protocolos de los problemas; (c) se hizo una descripción preliminar de categorías e indicadores; (d) se prepararon los esquemas de clase; (e) se reconstruyó la actividad de aula a partir de las transcripciones de los Cuadernos de Notas.
Después se procedió a elaborar el "Esquema Reconstructivo del Discurso de Aula", en el cual se concibe la actividad presencial como desarrollada en tres fases (apertura, desarrollo y cierre), divididas en episodios. A partir de este esquema se pudo reconstruir la totalidad de las 29 sesiones de trabajo presencial, utilizando los Cuadernos de Notas de los alumnos para efectuar lo que Taylor y Bogdan (1986, p. 125) denominan "control cruzado", con lo cual se logra reconstruir un evento a partir del examen de las perspectivas que, frente al mismo, desarrollan varios (o todos) sus protagonistas.
Las sesiones de trabajo presencial fueron el escenario propicio para recabar la información directa, especialmente las entrevistas. Mientras los grupos trabajaban, se entrevistaba a un alumno o a varios de ellos en grupos pequeños.
El esquema reconstructivo de la actividad de aula permitió visualizar globalmente la secuencia de las acciones presenciales desarrolladas a lo largo del curso. Una versión preliminar de esta reconstrucción fue contrastada revisando las anotaciones consignadas por cada alumno en su respectivo Cuaderno de Notas, con la finalidad de obtener la versión final del curso reconstruido; luego, se utilizó la versión preliminar de las categorías formuladas para "desentrañar" y "descubrir" los temas relevantes.
Unidades de observación
En cuanto al tipo de información a recolectar se establecieron las siguientes unidades de observación: los Cuadernos de Notas, las hojas de trabajo elaboradas durante la actividad de resolución de problemas, las respuestas a las diferentes pruebas (diagnóstico inicial), el contenido de los autobalances, los autorretratos heurísticos, el resumen general del curso, la transcripción de las entrevistas, la transcripción del trabajo de solución de problemas (protocolos), las fichas y los esquemas de clase.
Para estas unidades de observación se definieron como unidades de análisis las anotaciones escritas consignadas por los estudiantes en cada uno de estos documentos. En el caso de las entrevistas, las unidades de análisis se establecieron con base en las transcripciones escritas de los intercambios comunicativos que quedaron grabados en cassettes.
Como unidades de registro se definieron los temas referidos en las Unidades de Análisis por los informantes. Éstos, como ya se ha señalado, ejercieron un cuádruple rol: (a) como resolvedores de problemas, se ubicaron las expresiones que utilizaron para referirse a sí mismos, directamente o en forma impersonal; (b) como estudiosos del proceso de resolución de problemas, se consideraron las expresiones en las que se referían a dicho proceso como algo externo, objetivable y, por ende, susceptible de ser convertido en objeto externo de estudio; (c) como utilizadores de la resolución de problemas como estrategia didáctica, se señalaron las expresiones que emplearon para hacer alusión a las posibilidades didácticas de la resolución de problemas; y, (d) como Informantes Clave, consignaron oralmente (en las entrevistas grabadas), y por escrito (en los Cuadernos de Notas, Hojas de Trabajo y otros documentos que aportaron) la información sobre cuya base se construyó la caracterización de su desempeño en cada uno de los roles que protagonizaron.
Las acciones y los propósitos que caracterizan cada uno de los roles desempeñados por los alumnos se muestran en el Cuadro 1.
¿Cómo se Construyó el Decálogo del Resolvedor Exitoso de Problemas?
Para la construcción del Decálogo del Resolvedor Exitoso de Problemas que se reporta en este artículo, se desarrolló el siguiente procedimiento:
Análisis de Contenido de variados documentos. Éste consistió en una interpretación de diversas producciones escritas elaboradas por los informantes a lo largo del estudio. Se consideraron: (a) las respuestas dadas por los sujetos a las interrogantes formuladas en la Prueba Diagnóstica (Clase No. 1); (b) las expresiones contenidas en los Autorretratos Heurísticos elaborados durante la Fase Final del Estudio (Clase No. 29) y en los cuales los estudiantes compararon las visiones de sí mismo como resolvedores de problemas que tuvieron antes y después del curso y (c) las expresiones extraídas de los registros consignados en los Cuadernos de Notas.
Cuadro 1: Acciones y Propósitos de los Roles del Alumno
| ROLES DEL ALUMNO | ||
| DENOMINACIÓN | ACCIONES | PROPÓSITO |
| Resolvedor de Problemas | | Comprometerse personalmente en la búsqueda de solución a diferentes problemas con el fin de incrementar su pericia en la realización de la actividad resolutoria |
| Estudioso del Proceso de Resolución de Problemas | | Incrementar su conocimiento acerca de las demandas cognitivas implicadas en las diferentes fases del proceso |
| Utilizador de la Resolución de Problemas como estrategia didáctica | Hacer matemática mediante la resolución de problemas | Reconocimiento de las posibilidades didácticas de la resolución de problemas como medio, modelo y finalidad del proceso de enseñanza y aprendizaje de la Matemática. |
| Informante Clave |
| Aportar información de interés para el estudio. |
Autor: González (1997)
"Inmersión Arqueológica" (Foucault, 1991; p. 7) en los Protocolos y Hojas de Trabajo elaboradas por los alumnos. Esta acción analítico-interpretativa consistió en una lectura de las anotaciones que quedaron plasmadas en las hojas de trabajo. En la misma, los alumnos registraron las operaciones de cálculo correspondientes a los diferentes problemas. Además, los protocolos construidos a partir de la transcripción de las grabaciones registraron los intercambios comunicativos orales producidos durante la resolución de problemas en las diferentes modalidades (individual, en pareja, pequeño grupo o grupo total).
El proceso seguido para la Inmersión Arqueológica en los Protocolos se muestra a continuación:
2.1. Se seleccionaron protocolos y hojas de trabajo correspondientes a problemas resueltos individualmente por los participantes durante las diferentes fases en las que fue dividido el Trabajo de Campo.
2.2. Se hizo un análisis por separado de cada uno de estos documentos, teniendo como referencia analítica el Modelo Tetrafásico para la Resolución de Problemas de Polya (1975), según el cual la resolución de un problema puede ser concebido como un proceso divisible en cuatro etapas: comprensión, planificación, ejecución y verificación.
2.3. Cada uno de los protocolos u hojas de trabajo seleccionadas fueron analizados en profundidad, con el propósito de identificar expresiones indicativas del accionar cognitivo, metacognitivo, afectivo y matemático desarrollado por el resolvedor durante el proceso de resolución del problema.
2.4. Se elaboró una Síntesis Integradora que permitió resaltar las características que, como resolvedores de problemas, exhibieron los participantes en el estudio. Dicha síntesis se construyó sobre la base de una comparación de los resultados del análisis de los protocolos y las hojas de trabajo donde los participantes consignaron por escrito gran parte de las incidencias relacionadas con el esfuerzo individual realizado para intentar resolver algunos de los problemas planteados.
El proceso descrito anteriormente sirvió de base para la elaboración de un Decálogo del Resolvedor Exitoso de Problemas, construido a partir de una interpretación que hizo el autor de las expresiones en las que los participantes se referían a los múltiples aspectos vinculados con su actividad resolutoria propia. El Decálogo tiene carácter didáctico y se propone como una herramienta útil cuando se usa la resolución de problemas como estrategia de enseñanza y aprendizaje de la Matemática. Los "mandamientos" del Decálogo se muestran en el Cuadro 2.
Autor: González (1997)
Desarrollo explicativo de los "mandamientos" del Decálogo
- Conocer las metodologías y técnicas de resolución de problemas
"Personalmente estimo, que el conocimiento de las metodologías y técnicas de resolución son elementos fundamentales, que debemos asimilar y poner en práctica, a fin de conformar un cuadro sistemático mental que permita orientar la búsqueda de la solución". (Edgar, Clase No. 1)
Esto se considera de gran importancia para superar dos de las principales dificultades que impiden a los estudiantes resolver problemas con éxito. La primera es el síndrome "no sé cómo entrarle", especie de parálisis cognitiva que inhabilita al resolvedor desde su primer enfrentamiento con el enunciado. La segunda, denominada "Enfoque Algebrizante", es la creencia de que todo problema matemático se puede y debe reducir a ecuaciones. De lo que se trata es de tomar conciencia de que para resolver problemas existen diferentes vías (metodológicas y técnicas). Así, el resolvedor debe apropiarse de un amplio repertorio de Herramientas Heurísticas (Guzmán, 1991) de las cuales debe conocer su alcance, potencial y condiciones de uso.
Sin embargo, antes de aplicar alguna técnica ésta debe ser evaluada en función de: (a) si se adecúa o no a las características del problema; (b) si es fácil o difícil de aplicar (el grado estimado de dificultad está en función de la cantidad y tipo de operaciones matemáticas que han de efectuarse y el nivel de pericia que el resolvedor tenga con respecto a las mismas); y (c) las consecuencias lógicas que se derivan de su aplicación (se trata de estimar el curso que seguirá la actividad resolutoria como consecuencia de adoptar una determinada vía para resolver el problema).
2. Poseer un esquema organizado en secuencias que pueda orientar la obtención de la solución
"Un esquema secuencial y organizado que puede orientar la obtención de una solución a un determinado problema es el modelo de Polya. El mismo contempla la comprensión en sí del problema, un plan de acción, la ejecución de éste plano y la revisión de las etapas antes implementadas" (Edgar, Clase No. 2).
Los procesos metacognitivos se ejercen sobre la actividad resolutoria propia. Por ello es conveniente contar con alguna representación (un modelo) de lo que ocurre en la mente del sujeto resolutor. Aunque no existe procedimiento algorítmico alguno cuya implementación, por sí sola, garantice la solución de cualquier problema, en contextos didácticos sí resulta procedente ofrecer a los estudiantes un modelo que los ayude a formarse una imagen de las incidencias que se generan en su sistema cognitivo cuando enfrentan la realización de Tareas Intelectualmente Exigentes (González, 1998 a), tales como resolver un problema matemático con texto. En este estudio, el modelo ofrecido y trabajado por los alumnos fue el propuesto por Polya (1945), el cual fue concebido, no como una receta a seguir estrictamente, sino como un esquema referencial en cuyo marco se ubicaron las particularidades del accionar cognitivo de los resolvedores y, además, con un vocabulario que facilitó los intercambios comunicativos al momento de realizar la Socialización del Conocimiento Matemático adquirido como consecuencia de concebir a la resolución de problemas como una oportunidad de aprendizaje.
3. Comprender el problema
"Por otra parte, es necesario mantener claridad en la sintaxis del planteamiento (problema) con el fin de interpretar el significado concreto del contenido del problema. (trascendencia de la comprensión del problema)" (Edgar, Clase No. 2).
El enunciado del problema es el soporte básico de sus dos niveles (explícito e implícito); el primero se vincula con los aspectos superficiales del problema, concretados en las oraciones y párrafos que integran el planteamiento; el segundo remite a la estructura profunda del problema, a su significado, el cual está constituido, en este caso, por las relaciones y demás vínculos matemáticos que se pueden establecer entre los diferentes elementos constitutivos del enunciado y que conforman el Modelo Matemático Subyacente (MMS) correspondiente. Si no se accede al nivel MMS no puede decirse que ha habido comprensión del problema. Una vez que el resolvedor se ha apropiado del MMS, debe tenerlo muy presente, pues sobre éste es que se ejecutarán las operaciones y demás acciones matemáticas conducentes a la solución.
A continuación se ilustrará lo expresado en el "mandamiento" 3, con una instancia específica derivada de la interpretación de una de las respuestas dadas por Erlinda en el Autobalance correspondiente a la Clase No. 8.
"En la tarde de hoy el profesor nos pidió que redactáramos cómo éramos antes y ahora resolviendo problemas. Anteriormente yo trataba de ver qué era lo que me pedían primero que todo y qué me daban para encontrarlo, y todo esto lo relacionaba con algunas cosas vistas con anterioridad. Ahora trato de leer bien los problemas más de una vez. Saco mi hipótesis y tesis. Después de esto pienso si existe una via para hacerlo y comienzo a desglosarlo" (Erlinda, Clase No. 8).
"Trataba de ver qué era lo que me pedían primero que todo y qué me daban para encontrarlo", no dice cómo lo hacía; ahora dice "trato de leer bien más de una vez". Al parecer se ha tomado conciencia de la demanda intelectual que plantea el momento inicial del proceso de solución de problemas.
Una de las conductas iniciales del alumno con dificultad para resolver problemas es la impulsividad, actuar irreflexiblemente, sin tomar un tiempo prudencial para familiarizarse con el problema. Aquí se percibe que Erlinda tiene un esquema mental acerca de la estructura de los problemas: éstos piden algo y dan "otro algo" para "encontrar" eso que piden; luego, el accionar de quien pretende resolver el problema debe comenzar por "ver" ese algo que piden en el enunciado y luego identificar lo que dan para encontrarlo. Aquí el proceso cognitivo utilizado viene inmerso en lo que Erlinda señala como "ver" (Pero, ¿cómo "ve"?, no lo expone). Implícitamente se presume que hay un vínculo entre lo que piden y lo que dan para encontrarlo. El descubrimiento de ese vínculo marca el fin de esta fase; luego "todo esto lo relacionaba con algunas cosas vistas en clases con anterioridad". Puede decirse, entonces, que la heurística aplicada está centrada en relacionar con conocimientos previos vistos en clase. Dada la insistencia en la acción de "ver", se podría llamar a éste un "enfoque ocular o visual": captación visual de los elementos del problema y de las relaciones entre ellos.
Al enfrentarse al enunciado del problema "trata de leer bien el problema más de una vez". Es importante explicar este proceso: la captación de la estructura del problema exige la lectura de su enunciado, ésta debe hacerse "bien" ¿qué quiere decir "bien"?; ¿será, acaso, que se habla de lectura comprensiva?; y no basta con una sola vez, se requieren varias lecturas (es decir, leer el enunciado repetidas veces), lo cual es un indicio de que se intenta superar o controlar la impulsividad. Ahora bien, ¿para qué se lee el enunciado?. Erlinda dice "saco mi hipótesis y tesis"; aquí se evidencia la persistencia del esquema "lo que me piden" (Tesis) y "lo que me dan para encontrarlo" (hipótesis). Hallar estos dos elementos y su vinculación parece ser la intencionalidad de la lectura del problema. Luego, se pasa a una segunda fase: "después de esto pienso si existe una vía para hacerlo y comienzo a desglosarlo". Se observa una diferencia con la anterior (relacionar con conocimientos previos, es decir, se aplica un enfoque retrospectivo). Ahora se busca "una vía para hacerlo", es decir, un enfoque prospectivo, se intuye que el proceso de Resolución de Problemas es un "andar hacia adelante". Se percibe una semejanza con la fase polyana de "elaborar un plan"; al encontrar esa vía culmina con la segunda etapa, lo cual da lugar a una tercera: "comienzo a desglosarlo" (¿desarrollar el plan o descomponer el problema?). Se percibe además un abordaje secuencial, lineal y unidireccional: (a) "leo varias veces el enunciado"; (b) "saco hipótesis y tesis"; (c) "encuentro vía"; (d) "desgloso": este desglose puede ser un indicio de aproximación al Modelo Matemático Subyacente (MMS). Esto evidencia que se ha comprendido el enunciado del problema, lo que le permitirá ejecutar las operaciones matemáticas que conducen a su solución.
4. Conocer los diferentes pasos que se deben poner en acción para buscar una solución
"La clase correspondiente, hace alusión al estudio de los diferentes pasos que son recomendables poner en acción, para buscar una solución. Estos pasos no necesariamente tienen una dirección estricta; pueden disponerse de forma tal, que permitan desarrollar la solución en forma práctica y elocuente". (Edgar. Clase No. 6)
Una vez asumido un determinado modelo representativo del proceso a seguir para resolver un problema, debe producirse una apropiación de las demandas cognitivas exigidas por cada una de sus diferentes fases. En el caso específico de este estudio se adoptó el Modelo de Polya, cuyas exigencias, en cada una de sus fases, se muestran en el Cuadro 3.
Cuadro 3. Exigencias Cognitivas de las Fases del Modelo de Polya
| FASE |
| EXIGENCIA COGNITIVA |
| COMPRENSIÓN |
| Captar la Estructura Profunda del Problema. |
| PLANIFICACIÓN |
| Establecer un curso inicial de acción resolutiva. |
| EJECUCIÓN |
| Desplegar acciones derivables del plan de ataque seleccionado, con el propósito de encontrar la solución al problema. |
| VERIFICACIÓN |
| Comparar el Estado Final con el Estado Inicial (Pertinencia y verosimilitud de la solución). Trascender la información (aprender a partir del problema). |
5. Tener en cuenta las condiciones que contextualizan el problema
"Hay que tener en cuenta las condiciones que contextualizan un determinado problema, ya que el mismo, puede ofrecernos datos claves, y estrategias para su respectiva resolución". (Edgar. Clase No. 3).
Esto se refiere a la superación del Fenómeno de la Restricción Figurativa que se manifiesta, en algunos casos, como una imposibilidad de ver más allá de lo que dice el enunciado; en otros, como una dificultad para considerar una figura que forma parte de otra mayor que la incluye y le da sentido y, finalmente, como la tendencia del resolvedor a autoimponerse restricciones no pertinentes, o introducir modificaciones inadecuadas en el enunciado del problema que dificultan su resolución. De lo que se trata aquí es de mantener flexibilidad de pensamiento y considerar el problema desde todos los ángulos posibles.
6. Hacer una revisión minuciosa de los datos del problema
"Por tanto, debe hacerse una revisión minuciosa de los datos del problema". (Edgar. Clase No. 3).
Esto está relacionado con "¿Qué es lo que pide el problema?": un producto específico (v.g. el valor de una incógnita para satisfacer una igualdad); un proceso (v.g. la demostración de una determinada proposición); la identificación de una propiedad a partir de la consideración de ciertos casos específicos. En cada caso, la conciencia que se tiene del Estado-Meta hacia donde se desea llegar, actúa como un mecanismo regulador de la actividad resolutoria y como un criterio que usa el resolvedor para autoevaluarse, según la distancia a la que se encuentre de dicha meta. A continuación se ilustrará esto con una instancia específica.
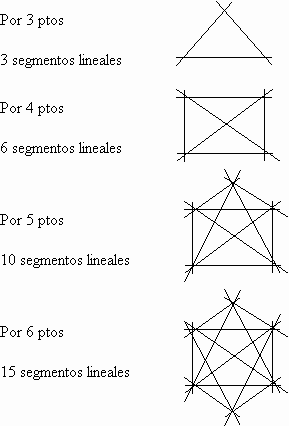
"Esta tarde el profesor comenzó la clase diciendo: "Bueno, vamos a calentar motores trabajando el siguiente problema: ¿Cuántos segmentos de recta diferentes se pueden trazar con n puntos coplanarios distintos?". (Cristóbal. Clase No. 11).
Este planteamiento tenía como finalidad mostrarle a los alumnos que un mismo problema puede tener varias "formas de entrarle". Además, con el problema se demostraría la legitimidad de la aplicación de modelos no algebraicos en la resolución de problemas matemáticos. Asimismo, quedaría establecido que para solucionar dichos problemas hay que comprender el planteamiento.
Este problema permitió, a su vez, trabajar con los diferentes formas de representar la información. Se desarrolló una sesión colectiva de trabajo dirigida por el facilitador. La interpretación del caso se hizo con base en la anotación consignada por Cristóbal. (Clase No. 11).
Descripción de la actividad:
Facilitador: -Bueno vamos a empezar a calentar los motores. Si tenemos dos puntos, ¿cuántos segmentos lineales se pueden trazar?:
La mayoría dijeron una recta, está bien
(Luego preguntó qué estaban utilizando aquí)
Alumnos: -Estamos utilizando estrategia heurística. Esta es una forma de trabajar cualquier problema específico pero también no hay que descartar otras formas de trabajarlo como por ejemplo si le pregunta bueno: (sic)
Facilitador (Fredy): -Determíname el número de segmentos que se puedan trazar teniendo una cantidad de puntos distintos aquí se hace complicada la estrategia utilizada anteriormente, ¿qué se puede hacer?.
(Uno contesta: -por allí bueno, podemos utilizar combinatoria).
(El profesor -Fredy- recalcó: -"ustedes se recuerdan de la fórmula". Unos dijeron: -"bueno la fórmula es: C m,n". Luego Fredy dijo: -"ustedes saben cuál es el orden y la base". Hubo un silencio y nadie decía nada: -"pero bueno m = la base y n es el orden, ¿ustedes no sabían eso?, si eso lo dan en 5to. Año". Después de todo este comentario, se procedió a realizar las operaciones de cálculo combinatorio).

Facilitador: -Otra forma también puede ser formando un cuadro de doble entrada. La diagonal principal se descarta por ser el mismo punto y también se descartan todos los que están por debajo de la diagonal, ya que son los mismos segmentos que se encuentran en la diagonal superior.
El proceso seguido para el desarrollo de esta actividad se describe a continuación: se comenzó con dos puntos, los alumnos trazaron un segmento y contaron uno, luego se dieron tres puntos, los alumnos dibujaron tres segmentos y contaron tres, luego se dieron cuatro, cinco y seis puntos, los alumnos dibujaron seis, diez, quince segmentos y contaron 6, 10, 15, respectivamente. A medida que aumentaba n = No. de puntos dados, se hacía más difícil dibujar (trazar) los segmentos para luego contarlos; se les llamó la atención preguntándoles cómo sería la situación si fuese un valor de n muy grande (por ejemplo 100 puntos). Pensar en esto les hizo caer en cuenta que el procedimiento de dibujar los segmentos para después contarlos no era lo más adecuado, sobre todo, si se piensa que el problema tiene como planteamiento cuántos son los segmentos, no cuáles son. Hasta este momento, los alumnos parecían no haberse dado cuenta del tipo de respuesta que se les estaba solicitando (se pedía un número, una cantidad).
Es importante que los alumnos concienticen estos procesos, porque saber qué clase de respuesta pide un problema puede constituir un criterio para regular y controlar el proceso de resolución, como también, para contrastar con la respuesta encontrada durante la fase de verificación.
Una vez reconocida la dificultad del problema cuando n representa un número muy elevado, emergió la justificación de buscar otras opciones. En este caso, la primera que surgió fue el uso de elementos de teoría combinatoria, concretamente las combinaciones. Luego se planteó la posibilidad de usar un cuadro de doble entrada.
"Pienso que deben medirse las dimensiones del problema para luego instrumentar la vía o técnica más ajustada a las condiciones del planteamiento". (Edgar. Clase No. 3)
Una de las características fundamentales que posee el resolvedor no exitoso es su impulsividad. Esta conducta halla una de sus explicaciones en una subestimación de la dificultad del problema, lo cual, a su vez, está vinculada con una sobreestimación de la capacidad propia. El resultado es el fracaso en el intento por resolver el problema. Se propone un cambio de actitud frente a los problemas: se asume que el esfuerzo por resolverlo constituye una oportunidad para aprender algo nuevo o, en otro caso, reforzar un aprendizaje previamente adquirido. Esta actitud respetuosa ante los problemas se expresa en una consideración previa de su grado de dificultad, información ésta que predispone al resolvedor y lo conduce a mantener un comportamiento razonablemente prudente que, de algún modo, contribuye a mantener en alto su autoconcepto matemático, es decir, la imagen que él tiene de sí mismo en cuanto a su competencia para la realización de los quehaceres propios de la Matemática.
"Debo agregar que en planteamientos de esta naturaleza, se hace necesaria fijar una estrategia concreta y detallada con respecto al proceso, porque ella permite realizar un seguimiento riguroso y minucioso de las diversos factores que intervienen en el problema; más aún cuando el problema tiene numerosos elementos que pueden hacer más compleja la situación". (Edgar. Clase No. 9).
La aseveración anterior tiene que ver con la posesión, por parte del resolvedor, de un elevado nivel de conciencia metacognitiva; los procesos de este orden han de ejercerse sobre la actividad resolutoria propia, a los fines de supervisarla, regularla y controlarla mientras se realiza (metacognición concurrente) y de transformarla en experiencia de aprendizaje una vez concluido el proceso resolutor (metacognición retrospectiva), se haya logrado o no la solución correspondiente.
"Pero debo recordar que la importante es tejer un plan, una estrategia bien definida que nos lleve a la solución y tales planes gozan de formas y variedades estructurales que permiten configurar un sendero accesible orientado hacia la búsqueda de la solución". (Edgar. Clase No. 24).
En alguna medida, el esfuerzo por resolver un problema puede concebirse como una búsqueda disciplinada de saberes, lo cual emparenta esta actividad con el quehacer de un investigador, por ello, la actividad resolutoria es ubicable en un contexto dualmente disciplinado. Por un lado, se ubica el conocimiento propio de la disciplina pertinente al problema y por el otro, los procesos propios de su quehacer (inferir, deducir, inducir, despejar, conjeturar, etc.); por ello, una vez que se haya comprendido el problema, es menester esforzarse por estructurar un plan de ataque, es decir, un conjunto de operaciones que se ejecutarán sobre el MMS con la expectativa de alcanzar la solución.
"Antes del curso consideraba que la resolución de un problema tenía como fin exclusivo, el logro de la solución exacta, debidamente comprobada sobre un soporte axiomático generalmente aceptado. De hecho un problema es una situación coyuntural que amerita uso de razonamientos encadenados para poder despejar la solución implícita. No todos los problemas tienen la misma estructura argumentativa; por lo que se hace necesario establecer ciertas estrategias de variadas perspectivas que puedan orientar el rastreo de la solución en cuestión". (Edgar, Resumen Final del Curso) (Subrayado del investigador).
Lo expuesto se vincula con los diferentes lenguajes que la Matemática puede usar para expresarse. Así que el resolvedor debe tener presente que las ideas y demás asuntos matemáticos son expresables no sólo en términos algebraicos, sino en otras formas igualmente legítimas: gráficos, tablas, ideogramas, esquemas, diagramas sagitales, etc. Inclusive, reconociendo que la Matemática es una modalidad específica del pensamiento humano, en algunos casos los problemas lo que reclaman es el ejercicio de ese pensar; esto puede lograrse a través de acciones que se ejerzan sobre material concreto manipulable (por ejemplo, modelos hechos en cartulina) y procediendo luego a expresar la solución con otra modalidad de lenguaje matemático.
Conclusión
El Decálogo del Resolvedor Exitoso de Problemas hace referencia a un conjunto de expresiones generales de carácter teórico derivadas por su autor a partir de la experiencia desarrollada con un conjunto de estudiantes de docencia en el área de Matemática que participan en un Curso de Resolución de Problemas. Los "mandamientos" del Decálogo son la síntesis de las acciones positivas que, colectivamente, dichos estudiantes exhibieron cuando lograban resolver con éxito alguno de los problemas trabajados durante la realización del curso. Este Decálogo no debe concebirse, en modo alguno, como un recetario. Al contrario, la comprobación de su eficacia está aún pendiente; sin embargo, aun cuando no es concebible una panacea para abordar cualquier tipo de problemas, el Decálogo del Resolvedor Exitoso de Problemas constituye una herramienta heurística útil para ayudar a los alumnos en el enfrentamiento con este tipo de tareas. Se recomienda operacionalizar los "mandamientos" de este Decálogo y hacer estudios que propendan a la confirmación de sus bondades, así como también a su posible ampliación.
Referencias
1. Anguera, M. T. (1989). Metodología de la Observación en las Ciencias Humanas. Madrid: Cátedra. [ Links ]
2. Foucault, M. (1991). Las Palabras y las Cosas: Una arqueología de las ciencias humanas. México: Siglo XXI. [ Links ]
3. Fuenmayor, C. y Mantilla de G., M. (1988). Necesidad de Logro asociada con Estrategias Cognitivas y Motivacionales de Estudio. Memorias EVEMO 2, Sección Necesidad de Logro, pp 31-41. [ Links ]
4. García Madruga, J., La Casa, P. (1990) Procesos Cognitivos Básicos. Años Escolares. En Palacios, J., Marchesi, A. y Coll, C. (Comp.) Desarrollo Psicológico y Educación. Tomo I: Psicología Evolutiva. Madrid: Alianza Editorial, S. A., Capítulo 15, pp 235-250. [ Links ]
5. González F. (1996). Acerca de la Metacognición. Paradigma XIV al XVII, (1-2), 109-135. [ Links ]
6. González, F. (1997). Procesos Cognitivos y Metacognitivos que Activan los Estudiantes Universitarios Venezolanos cuando Resuelven Problemas Matemáticos. Tesis Doctoral no publicada, Universidad de Carabobo, Valencia (Venezuela). [ Links ]
7. González, F. (1998 a). Metacognición y Tareas Intelectualmente Exigentes: El caso de la Resolución de Problemas Matemáticos. Zetetiké, 6 (9), 59 – 87. [ Links ]
8. González, F. (1998 b). Las Ciencias Cognitivas como Contexto para Interpretar las Nuevas Concepciones Acerca del Aprendizaje. Revista EDUCARE (Instituto Pedagógico "Luis Beltrán Prieto Figueroa", Barquisimeto, Venezuela), 2 (ÚNICO); 5-32. [ Links ]
9. Gutiérrez B. L. (1994). La Matemática Escolarizada: ¿La ciencia convertida en dogma?. Un estudio etnográfico realizado en aulas universitarias. Tesis Doctoral no publicada. Universidad Nacional Experimental " Simón Rodríguez". Caracas. [ Links ]
10. Gutiérrez, J. y Delgado, J. M. (1995). Teoría de la Observación. (En). Delgado, J. M. y Gutiérrez, J. (Coords.) (1995). Métodos y Técnicas Cualitativas de Investigación en Ciencias Sociales. Madrid: Editorial Síntesis, S. A.. Capíitulo 6, 141-176.
11. Guzmán, M. De (1991). Para Pensar Mejor. Barcelona (España): Editorial Labor, S. A. [ Links ]
12. Halmos, P. (1980). The Heart of Mathematics. The American Mathematical Monthly, 87 (7), 519-524. [ Links ]
13. Indriago, M. (1988). Modificabilidad de aptitudes específicas y su efecto en el rendimiento académico en matemática de alumnos de noveno grado de ducación básica. Investigación y Postgrado, 3 (1), 61-92. [ Links ]
14. Izcaray, F. (1987). La Psicología Cognoscitiva y el nuevo Paradigma de Investigación en la Comunicación Social. Investigación y Posgrado, 2 (4), 115-139 [ Links ]
15. Kempa, R. F. (1986). Resolución de problemas de Química y Estructura Cognoscitiva. Enseñanza de las Ciencias, 4 (2), 99-110. [ Links ]
16. Lohman, D. (1989). Human Intelligence: An Introduction to Advances in Theory and Research. Review of Educational Research, 59, 4, pp 333-373. [ Links ]
17. Lorenzo, R. y Martínez, M. (1996, Mayo-Agosto). ¿Qué es el Talento?. Educación (Cuba) 88; 10-12. [ Links ]
18. Martin, E., Marchesi, A. (1990). Desarrollo Metacognitivo y Problemas de Aprendizaje. En Marchesis, A., Coll, C., Palacios, J. (Comp.). Desarrollo Psicológico y Educación. Tomo II: Necesidades Educativas Especiales y Aprendizaje Escolar. Madrid: Alianza Editorial, S. A., Capítulo 2, pp 35-47. [ Links ]
19. Merriam, S. (1988). Case Study Research in Eduaction. San Francisco: Jossey-Bass [ Links ]
20. Mumme, J. (1996). Evaluación por Portafolios en Matemáticas. En. Mosquera, J. y Otros (Comps.). Selección de Lecturas en Evaluación del Aprendizaje de la Matemática (Lectura 7; pp. 47-88). Caracas: Ediciones de la Universidad Nacional Abierta. [ Links ]21. Nickerson, R. (1988). On Improving Thinking Through Instruction. Publicación preparada por BBN Laboratories Inc. para Review of Research Education (19 de Febrero de 1988) [ Links ]
22. Polya, G. (1975). Cómo plantear y resolver problemas. México: Editorial Trillas (Primera Edición de 1945) [ Links ]
23. Pozo, J. I. (1990). Estrategias de Aprendizaje. En Palacios, J., Marchesi, A. y Coll, C. (Comp.) Desarrollo Psicológico y Educación. Tomo I: Psicología Evolutiva. Madrid: Alianza Editorial, S. A., Capítulo 12, pp 199-221. [ Links ]
24. Romberg, T. y Carpenter, T. (1986). Research on Teaching and Learning Mathematics: Two Disciplines of Scientific Inquiry. En Wittrock, M. C. (Ed.) Handbook of Research on Teaching (Third Edition). New York: Macmillan Publishing Company. [ Links ]
25. Sierra, B. y Carretero, M. (1990). Aprendizaje, Memoria y Procesamiento de la Información: la Psicología Cognitiva de la instrucción. En C. Coll, J. Palacios y A. Marchesi (Comp). Desarrollo Psicológico y Educación, II, Psicología de la Educación. Madrid: Alianza Editorial, pp 141-158. [ Links ]
26. Taylor, S. J. y Bogdan, R. (1986). Introducción a los métodos cualitativos de investigación: La búsqueda de significados (J. Piatigorsky, trad.). Buenos Aires: Paidós [ Links ]
27. Tirapegui, C. (1997, Mayo). Propuesta de Experiencia de aprendizaje y un modelo de guión didáctico. Ponencia presentada en el II Congreso Venezolano de Educación Matemática (II COVEM), Valencia (Venezuela). [ Links ]
28. Weinstein, C. y Mayer, R. (1986). The Teaching of Learning Strategies. En M. Wittrock (Ed.) Handbook of Research on Teaching. New York: Macmillan Publishing Company. [ Links ]
29. Wittrock, M. (1986). Student'Thought Processes. En M. Wittrock (Ed.) Handbook of Research on Teaching. New York: Macmillan Publishing Company. [ Links ]













