Modelo econométrico para el pronóstico de demanda eléctrica máxima diaria

Acevedo Rueda, Rubén¹ Pimentel, José A.²

1 Despacho Centro Occidente, Edo. Lara – Venezuela,

2 Universidad Centro Occidental Lisandro Alvarado UCLA. Lara – Venezuela,

ruben.acevedo@ucla.edu.ve; japimentel@corpoelec.gob.ve

Resumen: El estado Lara es una región importante en Venezuela y el pronóstico de demanda eléctrica diaria se considera un aspecto clave para la programación de mantenimiento y la aceptación de las intervenciones rutinarias al sistema, ya que las estimaciones de carga son la base de la contingencia y planificación de la operación. Así como los pronósticos de demanda son altamente reconocidos por los autores como una parte fundamental de los procesos de planificación del servicio eléctrico, también sus características de problema multivariable de alta complejidad, su naturaleza no lineal y la necesidad de evaluar la aplicabilidad para cada sistema particular. En este trabajo se presenta un modelo econométrico desarrollado para el pronóstico de carga a corto plazo (PDCP) y su aplicación. Se consideran las variables exógenas, días de semana, días feriados y temperatura son las variables independientes para este modelo. También se considera un pronóstico en dos etapas con el fin de minimizar la influencia de las componentes de las series de tiempo para las estimaciones diarias.

Palabras clave: Pronóstico de demanda a Corto Plazo/ Planificación Operativa/ Modelo Econométrico.

Econometric model for maximum daily electrical load forecast

Abstract: Lara state is an important Venezuelan region and the daily forecast of electricity demand is considered a key issue for maintenance schedules and the acceptance of regular interventions to the system since load estimations are the basis for contingency and operation planning. Just like the demand forecasts are highly recognized by authors as a fundamental part of electrical service planning processes, the characteristics of a highly complex multivariable problem, its non-linear nature and the needs of evaluating the applicability for each particular system, are also realized by authors. This paper presents an econometric model developed for the short-term load forecast (STLF) and its application. Exogenous variables are considered; and weekdays, holidays and temperature are the independent variables for this model. In addition, a two-stage forecast is considered in order to minimize the influence of time series components for daily estimations.

Key words: Short-term load forecast, operation planning, econometric model.

Recibido Noviembre 2013, Aceptado Febrero 2014

I. INTRODUCCIÓN

En la planificación de sistemas de potencia, la primera etapa consiste en formar una base de conocimiento aproximado de la demanda futura. El Pronóstico de Demanda a Corto Plazo (PDCP) es la base para la prestación económica y confiable del servicio eléctrico. La PDCP consiste generalmente en estimaciones de la demanda en lapsos que van desde una hora hasta una semana [1]

La PDCP tiene su aplicación principalmente en los diferentes modelos de planificación operativa y de corto plazo [1] [2]. Las variables económicas y de confiabilidad se consideran para el despacho de carga [3] [4] [5] y algunos autores resaltan la importancia que adquiere la PDCP en este aspecto, especialmente en modelos de mercados de energía abiertos a la libre competencia [1] [6] [7]

Al igual que en México [8], en Venezuela el servicio eléctrico lo presta una sola corporación estatal. La Corporación Eléctrica Nacional, S.A. (CORPOELEC) es responsable de la operación y mantenimiento del sistema eléctrico, mientras que el Centro Nacional de Despacho (CND) es la entidad encargada de la supervisión, coordinación y control de la operación integrada del sistema eléctrico nacional.

El CND cuenta con un Despacho Nacional y ocho Despachos Regionales. El Despacho Centro Occidente (DCO) es responsable del estado Lara. Sus actividades comprenden, entre otras, la consignación de equipos e instalaciones, la aprobación de los permisos de trabajo y los análisis de contingencias, confiabilidad y fallas. La PDCP es la base para estas actividades y un soporte para la toma de decisiones. Como el DCO es una unidad organizativa de reciente creación, los procesos internos se están consolidando y, como parte de esto, se evaluaron diferentes metodologías de PDCP para seleccionar una apropiada para esta región.

Los modelos econométricos y de usuarios finales se utilizan ampliamente en los pronósticos de mediano y largo plazo. Los modelos econométricos combinan la teoría económica y las técnicas estadísticas, estimando las relaciones entre el consumo de energía (variables dependientes) y los factores que influyen sobre su aumento o disminución [4]. Los modelos econométricos se utilizan también para establecer estrategias de mercado teniendo en cuenta las ecuaciones que describen el comportamiento económico y relaciones precio - demanda [9]

En los métodos de regresión se asumen formas funcionales predefinidas que describen las relaciones cuantitativas entre la carga y los factores que la afectan (por ejemplo, el índice de días de la semana y el tiempo). Los coeficientes funcionales se estiman a través de análisis de regresión de los datos históricos [5]

En la evaluación de los diferentes métodos, el DCO decidió desarrollar un modelo econométrico para establecer la relación entre la carga máxima diaria esperada, el tipo de día (día de semana, fin de semana, días laborables o días de fiesta) y la temperatura máxima esperada, variables consideradas como relevantes y además disponibles, a pesar de que los autores reportan que estos modelos han sido aplicados a pronósticos de mediano y largo plazo. El pronóstico se aplica en dos etapas con el objeto de minimizar la influencia de las componentes de las series de tiempo sobre las estimaciones diarias. De esta forma, se modela de un comportamiento estacionario que permite utilizar ese modelo para las estimaciones de máxima carga diaria en valores por unidad, en función de la demanda máxima mensual esperada.

II. DESARROLLO

1. Recopilación y preparación de los datos

La disponibilidad y relevancia de los datos es fundamental para la selección de un método de pronóstico, ya que un conjunto adecuado de variables es la base para la exactitud y confiabilidad que se puede obtener en la estimación.

Algunos trabajos recomiendan considerar el tiempo, la economía, la demografía, los hábito y otras variables [4, 6, 8, 10] mientras que otros autores [7, 11] señalan que las variables y modelos de pronóstico deben seleccionarse y aplicarse para condiciones y casos específicos, en función de la disponibilidad y fiabilidad de los datos, así como el tamaño, la ubicación y el comportamiento del consumo de electricidad de sus clientes.

Los autores están de acuerdo en la marcada influencia de las actividades económicas, días laborables y festivos, sobre el consumo de energía e incluso plantean estudios separado para esos días [8, 12, 13].

2. Selección de las variables

El sistema eléctrico del estado Lara cuenta con 31 subestaciones de 230; 115; 34,5; 24 y 13,8 kV y cerca de 160 MW de generación local instalada, con una capacidad real de 110 MW considerada para estudios técnicos.

Tres de las subestaciones son fuentes primarias (230 kV) de interconexión regional con el sistema nacional. El DCO mantiene una base de datos histórica detallada de la demanda en las barras. La experiencia empírica asocia el comportamiento del consumo de energía se asocia al clima y días de la semana. Las entidades regionales y nacionales de medio ambiente, como el Instituto Nacional de Meteorología e Hidrología (INAMEH) suministra al DCO la información meteorológica y pronósticos de temperatura. Diariamente se realiza un balance energético con los datos de demanda máxima y mínima, que se transmite a las diferentes instancias de CORPOELEC para sus consideraciones técnicas.

Con base en la evaluación de la disponibilidad, pertinencia y calidad de los datos, el DCO identificó la demanda histórica, la temperatura, días de semana y laboralidad como variables independientes para el pronóstico de demanda máxima diaria.

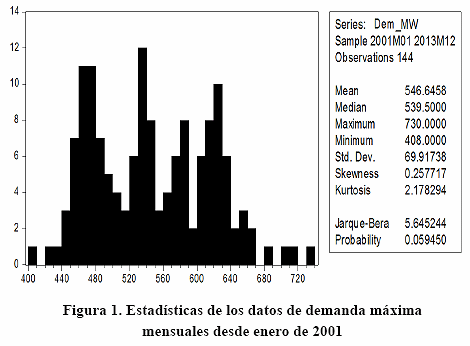
Para el método de PDCP se consideraron datos mensuales desde enero de 2001 con las estadísticas que se muestran en la Figura 1.

Con un total de 144 muestras, la demanda máxima histórica del estado Lara presenta un valor medio de 546,64 MW con 730 MW histórico máximo MW y 408 MW histórico mínimo. Debido a la gran cantidad de data antigua y la mayor relevancia de los datos más recientes, para el modelo econométrico se utilizó el histórico de demanda diaria registrada entre enero de 2010 y septiembre de 2012.

3. Tendencia, ciclo y estacionalidad

La teoría econométrica clásica supone que los datos observados provienen de un proceso estacionario, con medias y varianzas constantes en el tiempo. Los gráficos de series de tiempo económicas, y el registro histórico de las previsiones económicas, revelan la invalidez de tal suposición. La no-estacionariedad parece una característica natural de la vida económica. [10]

Los análisis estructurales de series de tiempo identifican los componentes que describen su comportamiento [9] [14] [15]

- Tendencia: componente variable lenta que muestra el comportamiento a largo plazo

- Estacionalidad: componente periódico de períodos fijos (corto plazo)

- Ciclo: variaciones de mediano plazo (anuales) en torno a la tendencia

- Errores o variaciones irregulares: comportamiento irregular a corto plazo

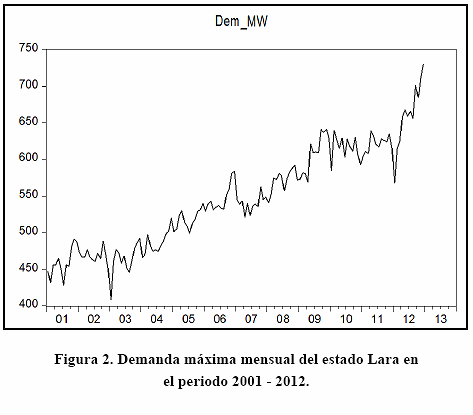
La Figura 2 ilustra un gráfico lineal de series de tiempo de demanda máxima mensual del estado Lara en el periodo 2001 - 2012.

La componente tendencial creciente se puede identificar fácilmente, así como el comportamiento estacional que se presenta de manera repetitiva en los meses de enero y agosto (caída de la demanda), abril-mayo y noviembre-diciembre (picos de demanda). Con un análisis más detallado se podrían identificar los elementos cíclicos y de error, para ser modelados en los pronósticos de mediano y largo plazo.

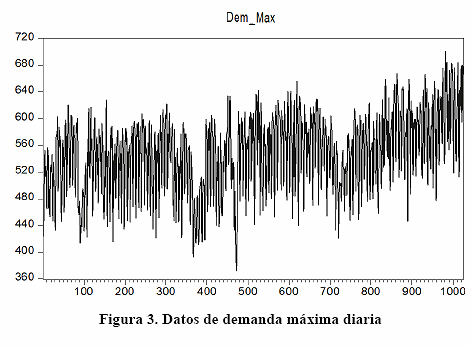
Los datos de demanda diaria, para el pronóstico de corto plazo, también presentan una marcada influencia de esas componentes, como se muestra en la figura 3. Esto hace más complejo modelar su comportamiento en estos lapsos de tiempo.

Los aumentos de la demanda y los cambios en su regularidad hacen más complejo el uso de un método de aproximación al día similar [2]

Con el objeto de modelar un proceso estacionario y aplicar la teoría econométrica clásica se aplicó una conversión por unidad (PU) con los datos de demandas máximas mensuales como valor base, para identificar la relación entre la demanda PU, temperatura y día de la semana.

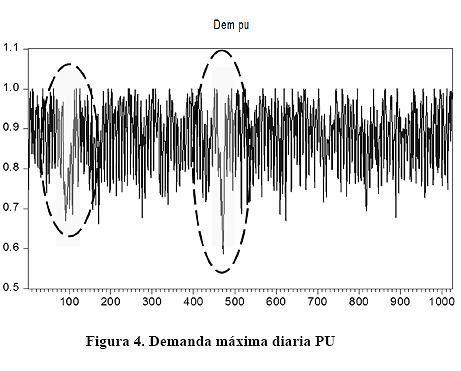
La Figura 4 muestra el conjunto de datos más estacionarios obtenidos con la conversión a valores PU. Esto permite analizar los componentes de series de tiempo por separado para reducir al mínimo su efecto sobre el modelo econométrico.

Sin embargo, un análisis detallado de los datos resultantes permite identificar un comportamiento irregular que se destaca en la Figura 4 y debe ser tratado para un mejor procesamiento.

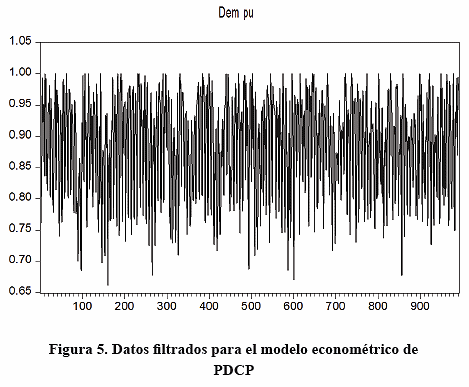
4. Filtrado de datos

Para el desarrollo del modelo econométrico de PDCP se consideran como variables independientes el clima, día de la semana y laboralidad para estimar la demanda en PU para los próximos días. Sin embargo, a pesar de la disponibilidad de data histórica, resulta necesaria una evaluación y filtrado para minimizar los errores en el ajuste del modelo.

En primer lugar, se consideran la falta de datos y los datos evidentemente erróneos. En esos casos se descartan los días con mediciones de demanda erradas y los que no cuentan con registro de datos de temperatura.

Luego, al evaluar visualmente y verificar las fechas, se determina que el comportamiento irregular identificado en la Figura 4 corresponde a la Semana Santa, una temporada no laborable extendida y concurrente. Estas fechas se descartan junto con otras vacaciones extendidas como carnavales, para ser analizadas por separado.

La Figura 5 presenta un conjunto de datos con característica más estacionaria, obtenido como resultado de ese filtro.

5. MÉTODO DE PDCP EN DOS ETAPAS

El método de pronóstico propuesto considera dos etapas, como se muestra en la Figura 6. El modelo econométrico se utiliza para obtener un pronóstico de demanda máxima diaria en PU, que se complementa con el pronóstico mensual obtenido por el método clásico de suavizado exponencial, para obtener finalmente una estimación en MW.

Con el uso de valores PU en el modelo econométrico para el PDCP, se logra minimizar el efecto de las componentes de las series de tiempo, que posteriormente se incorporan al dar el resultado en MW con base en la estimación mensual, realizada con el método clásico de suavización exponencial.

Los coeficientes para las variables independientes en (1) se obtienen aplicando el método de mínimos cuadrados. De esta forma, se obtiene una función lineal para el PDCP en valores PU.

Donde:

DPU: Demanda PU (variable dependiente)

C1: Constante de Estimación (evita que el modelo adopte valor cero)

Dsem: índice de día de semana (0 para fines de semana, 1 cualquier otro día)

feriado: índice de laboralidad (1 para día feriado, 0 para los demás)

TMAX: Temperatura máxima (º C)

C2, C3, C4: Coeficientes

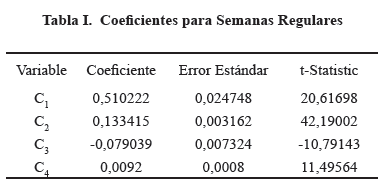
Se utilizaron 992 observaciones de semanas regulares, para obtener los coeficientes como se muestra en la Tabla I.

Entonces, para semanas regulares (1) será:

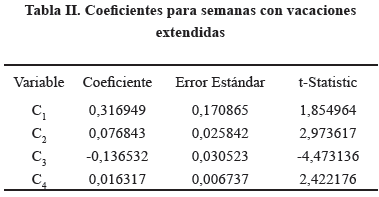
Para obtener los coeficientes aplicables a semanas especiales se utilizó un conjunto de 34 observaciones (vacaciones extendidas) como se muestra en la Tabla II.

Entonces, para semanas con vacaciones extendidas, (1) será:

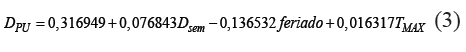
Ambas etapas del método de pronóstico de carga se revisan periódicamente. El pronóstico de demanda máxima mensual utilizado como valor base para la PDCP se revisa diariamente y se corrige si se llega a superar el valor estimado. Los coeficientes del modelo econométrico se revisan y calculan trimestralmente con la data histórica actualizada.

6. ERRORES DE ESTIMACIÓN

Diferentes autores explican que la precisión del pronóstico de demanda depende de particularidades como la complejidad del sistema y los hábitos de las regiones, asumiendo valores entre 1% y 6 % [4] [7] [12]. Además, los pronósticos del clima pueden causar aproximadamente 1% de error en los pronósticos de demanda [15]. Otros autores desarrollan métodos que reportan errores más altos (12-20 %) [6] [11]

En [7] los autores señalan que la precisión en los pronósticos es un aspecto sobreestimado y que en realidad las estimaciones nunca son exactas. Sin embargo, hay rangos aceptables, en función a las características de la empresa que los realiza, que pueden variar entre 2% y 6%.

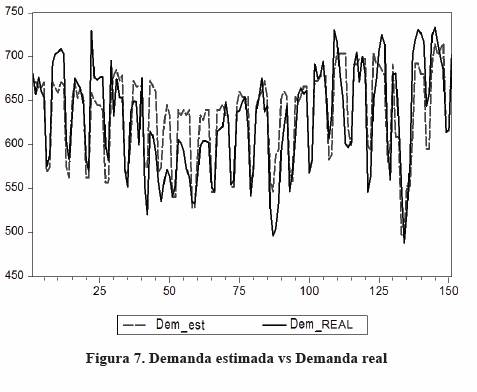
En la Figura 7 se presenta la demanda estimada y la demanda real del sistema eléctrico del Estado Lara para la estimación realizada durante 21 semanas.

El Error Porcentual Promedio Absoluto (MAPE, por sus siglas en inglés) es una medida de la exactitud del pronóstico, que se calcula usando la ecuación (4):

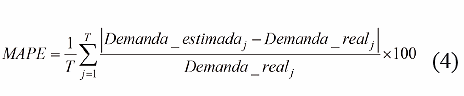
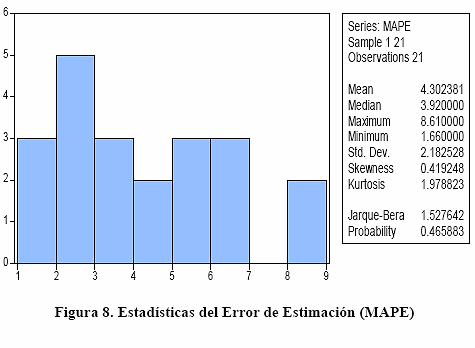
El MAPE semanal se calculó para los datos de las 21 semanas, obteniendo valores entre 1,66 % y 8,61%, como se muestra en la Figura 8.

La precisión obtenida permite al DCO evaluar los programas de operación y mantenimiento, para procesar sus aprobaciones.

III. CONCLUSIONES

1. Los PDCP constituyen un aspecto clave para la planificación y operación, incluso en sistemas eléctricos con régimen económico regulado, donde a pesar de no requerir evaluar estrategias y estrictas consideraciones financieras como en el caso de los mercados eléctricos abiertos, se debe estimar el impacto operativo esperado para las maniobras que se plantean a corto plazo.

2. Aun cuando generalmente los modelos econométricos no son utilizados para PDCP, este método de pronóstico de dos etapas permite modelar un proceso estacionario, para la aplicación del modelo econométrico propuesto, que combinado con el suavizado exponencial de series de tiempo, permite elaborar las estimaciones de demanda máxima diaria.

3. Este método fue desarrollado con base en la disponibilidad y confiabilidad de los datos disponibles y ha sido probado para una región particular (estado Lara), con una precisión bastante aceptable para los propósitos de planificación operativa.

4. El uso de valores PU permite minimizar el efecto de la tendencia y estacionalidad, haciendo posible modelar una relación más ajustada entre las variables independientes y la carga máxima diaria, en forma de ecuación lineal. El comportamiento no lineal causado por las componentes mencionadas, se modela en pronóstico mensual, mediante el suavizado exponencial.

5. El pronóstico de demanda de dos etapas, haciendo uso del modelo econométrico, ofrece un error de estimación (MAPE) aceptable, en comparación con otros métodos más elaborados, expuestos como referencias, cuyos errores varían entre 1% y 20%.

6. La contribución principal de este trabajo es ofrecer un método de pronóstico simple, pero confiable, que ofrece información necesaria para la toma de decisiones y que cualquier nuevo planificador, sin necesidad de conocimientos sofisticados, puede aplicar y actualizar. Los comportamientos irregulares no se consideran en este modelo, pero podrían incluirse en la función como ruido blanco, pero este, así como las estimaciones horarias, son temas para desarrollar en trabajos posteriores.

IV. REFERENCIAS

1. H. Daneshi, A. Daneshi, Real time load forecast in power system, Electric Utility Deregulation and Restructuring and Power Technologies, 2008. DRPT 2008. Third International Conference on, vol., no., April 2008, pp.689-695.        [ Links ]

2. Yang Wang, Qing Xia, Chongqing Kang, Secondary Forecasting Based on Deviation Analysis for Short-Term Load Forecasting, Power Systems, IEEE Transactions on , vol.26, no.2, May 2011, pp.500-507.

3. Zhikun Zhang, Canbing Li, Yijia Cao, Liangxing Tang, Junxiong Li, Bo Wu, Credibility assessment of short-term load forecast in power system, Innovative Smart Grid Technologies - Asia (ISGT Asia), 2012 IEEE , vol., no., May 2012, pp.1-5.

4. P. Campbell, K. Adamson, Methodologies for Load Forecasting, Intelligent Systems, 2006 3rd International IEEE Conference on, Sept. 2006, pp.800-806.
5. Ying Chen, Luh, P.B., Che Guan, Yige Zhao, L.D. Michel, M.A. Coolbeth, P.B. Friedland, S.J. Rourke, Short-Term Load Forecasting: Similar Day-Based Wavelet Neural Networks, Power Systems, IEEE Transactions on , vol.25, no.1, Feb. 2010, pp.322-330.

6. Hongsheng Su; Youpeng Zhang, Short-term load forecasting using H∞ filter and Elman neural network, Control and Automation, 2007. ICCA 2007. IEEE International Conference on , vol., no., May 2007-June 2007, pp.1868-1872.

7. Tao Hong; Pu Wang; H.L. Willis, A Naïve multiple linear regression benchmark for short term load forecasting, Power and Energy Society General Meeting, 2011 IEEE , vol., no., July 2011, pp.1-6.

8. V.H. Otiz, C. Narvaez, Weekdays Load Forecasting in Mexico Using Artif1cial Neural Networks, Transmission & Distribution Conference and Exposition: Latin America, 2006. TDC ‘06. IEEE/PES, vol., no., Aug. 2006, pp.1-6.

9. J.H. Cochrane. Time Series for Macroeconomics and Finance. Graduate School of Business. University of Chicago. http://faculty.chicagobooth.edu/john.cochrane/research/papers/time_series_book.pdf

10. M. Franco, D. Blanco, W. Blequett, M. Guglia, E. Alvarado, Cointegration Methodology and Error Correction Model used to Forecast The Electricity Demand of The Venezuelan Electric System - Period 2004-2024, Transmission & Distribution Conference and Exposition: Latin America, 2006. TDC ‘06. IEEE/PES, vol., no., Aug. 2006, pp.1-8.

11. N.; Amjady, Short-Term Bus Load Forecasting of Power Systems by a New Hybrid Method, Power Systems, IEEE Transactions on, vol.22, no.1, Feb. 2007, pp.333-341.

12. Young-Min Wi, Sung-Kwan Joo, Kyung-Bin Song, Holiday Load Forecasting Using Fuzzy Polynomial Regression With Weather Feature Selection and Adjustment, Power Systems, IEEE Transactions on , vol.27, no.2, May 2012, pp.596-603.

13. Y. Chakhchoukh, P. Panciatici, L. Mili, New robust method applied to short-term load forecasting, PowerTech, 2009 IEEE Bucharest , vol., no., June 28 2009-July 2 2009, pp.1-6.

14. J. Durbin, S. J. Koopman Time Series Analysis by State Space Methods. (Oxford: Oxford University Press, 2001).

15. P. Reiss, F. Wolak, Structural Econometric Modeling: Rationales and Examples from Industrial Organization, In J. Heckman and E. Leamer (Ed.) Handbook of Econometrics Volume 6, (New York: Elsevier Science, 2008, pp 4277-4415).

16. D. Fay, J.V. Ringwood, On the Influence of Weather Forecast Errors in Short-Term Load Forecasting Models, Power Systems, IEEE Transactions on, vol.25, no.3, Aug. 2010, pp.1751,1758.