Filosofía de la mecánica de fractura: primera parte, MFEL

González, Leonardo

Departamento de Metalurgia - UNEXPO, Puerto Ordaz

Resumen:

La mecánica de fractura es una ciencia relativamente nueva y se puede decir que se inicia con la segunda guerra mundial, a causa de la fractura de una gran cantidad de acorazados Liberty que puso en peligro el éxito del desembarco del día D, 16 de junio de 1944, en las playas de Normandía (Francia). La mecánica de fractura es la ciencia que estudia el comportamiento de un sólido en presencia de una grieta. La mecánica de fractura se clasifica en Mecánica de Fractura Elástica Lineal (MFEL) y en Mecánica de Fractura Elasto-Plástica (MFEP). Esta primera parte está dedicada a la MFEL y en ella se desarrolla un novedoso modo de ver una grieta así como un factor de corrección de la ecuación de Griffith, el cual permitirá dar un nuevo enfoque tanto a la fractura frágil, basado en el radio de curvatura de la punta de la grieta, como a la ecuación de fatiga de Paris. Esto abre nuevos campos de investigación en MFEL que podría ser fructífero.

Palabras Claves: Mecánica de fractura/Grietas/Ecuación de Griffith/Factor de corrección/Grieta elíptica/Mecánica de Fractura Lineal Elástica (MFLE)/ Ecuación de Paris

Philosophy of fracture mechanics: part one, LEFM

Abstract:

Relatively, fracture mechanics is a new science and it can be considered that begins during the world war second, after a great deal of battleship fractured, even at dock, which put into danger the successful of landing operations during D-day, June 16 1944, at Normandy beaches (France). Fracture mechanics is the science which studies the behavior of a solid when a crack is present. In general, fracture mechanics is classified as Lineal Elastic Fracture Mechanics (LEFM) and Elasto-Plastic Fracture Mechanics (EPFM) or non-lineal fracture mechanics. In this part a novel model of seeing a crack and a Griffith’s equation correction factor has been developed, which let us to give a new interpretation of brittle fracture and Paris equation based in curvature radius at the crack tip. This point of view opens new fields of researching in fracture mechanics.

Keywords: Fracture mechanics/Crack/Griffith’s equation/Correction factor/Elliptical crack/ Lineal Elastic Fracture Mechanics (LEFM)/ Paris’ equation.

I.INTRODUCCION

Un sistema filosófico es un conjunto de ideas, basadas en la especulación y/o la experiencia, las cuales, estructuradas apropiadamente, ayudan a la comprensión del asunto objeto a estudio. A lo largo de la historia se han establecido, por filósofos y científicos, muchos sistemas filosóficos. En física, y particularmente en ciencia de materiales, hay dos grandes sistemas filosóficos, a saber: a) el sistema fenomenológico y el b) el sistema mecanicista. El primero responde a las preguntas: ¿qué está pasando?, ¿se puede elaborar una teoría elemental que permita explicar lo que está pasando? Los mejores ejemplos los tenemos en La Teoría de La Evolución de las Especies de Charles Darwin y todo el trabajo experimental de Michael Faraday. El segundo responde a las preguntas: ¿por qué está pasando lo que está pasando?, ¿se puede elaborar una teoría que permita predecir eventos no observados? El sistema mecanicista reduce el asunto objeto a estudio a la acción de fuerzas y energía y sus consecuencias. Los mejores ejemplos los tenemos en La teoría Electromagnética de James Clerk Maxwell, La Teoría de Gravitación Universal de Isaac Newton y La Teoría de la Relatividad de Albert Einstein.

La mecánica de fractura, como su nombre lo indica, es enfocada desde el punto de vista mecanicista y el cálculo de esfuerzos, alrededor de la punta de la grieta, es, por excelencia, el tema central. Sin embargo, considerando que la grieta no es otra cosa que la ruptura del enlace atómico, un sistema filosófico atomístico, basado en la teoría de enlaces atómicos, ha resultado altamente fructífero.

La mecánica de fractura se divide en dos grandes ramas: a) mecánica de fractura elástica lineal MFEL) y b) mecánica de fractura elasto-plástica (MFEP) o mecánica de fractura no lineal (MFNL). La primera utiliza, como parámetro fundamental de análisis, el “factor de intensidad de esfuerzo K” y el segundo “el valor de la integral J”,” valor de integral P”, “valor de integral M” y otros relacionados con la apertura de la grieta, tales como COD (crack opening displacement) y CTOD (crack tip opening displacement). El presente trabajo está dedicado a la MFEL y la segunda parte está dedicada a la MFEP. En esta parte se analizan las condiciones de deformación plana y esfuerzo plano, como premisas fundamentales para entender la MFEL y posteriormente la MFEP. Para ello se revisa el significado físico de la ley de Hooke y, usando notación tensorial sencilla, se revisan las ecuaciones elásticas de deformación y esfuerzo y se hace una corrección, la cual ha permanecido por décadas. Una novedosa interpretación del entorno de la grieta ha permitido incorporar un factor de corrección de la ecuación de Alan Arnold Griffith, desarrollada en 1921, el cual permite ver la evolución de la grieta como un fenómeno asociado al radio de curvatura de la punta y no solamente a su tamaño. Se hace un breve recuento histórico de la mecánica de fractura y del factor intensidad de esfuerzo y se da un nuevo enfoque a la ecuación de fatiga de Paul París y su equipo, basado en los nuevos conceptos introducidos, que abre un nuevo campo de investigación en el campo de la fatiga de materiales y su interpretación.

II. DESARROLLO

1. Evolucion

1.1. De Galileo Galilei a Thomas Young

En 1583, El fisico y matematico italiano Galileo Galilei escribio sobre la necesidad de medir la resistencia de los materiales empleados en la construccion de edificios y puentes. Sin embargo esto no pudo hacerse de manera sistematica por falta de recursos, de metodologia y de instrumental apropiado, lo que producia dispersiones muy grandes en los resultados. Para la fecha se usaba el torno de pedal en los talleres, el cual habia nacido en 1250 DC y perfeccionado por Leonardo Da Vinci a finales del siglo XV. 

En 1660, Robert Hooke, brillante físico inglés, estableció una correlación lineal entre carga (P) y desplazamiento ΔL (ΔL=L-L₀) en varillas metálicas, lo que dio lugar a la invención y construcción del resorte. En máquinas herramientas se había avanzado muy poco y se ensayaban 

grandes elementos estructurales, introduciendo así una variable geométrica en los ensayos, lo cual producía una variación en la pendiente, k, de la recta P=k.ΔL .Esta correlació lineal se conoce como ley de Hooke y los materiales que gozan de ella se llaman materiales hookenianos.

En 1807, Thomas Young, físico inglés, modificó los ensayos de Hooke trabajando con valores unitarios. Para esa fecha las máquinas herramientas habían alcanzado cierto desarrollo. En 1777, el inglés Jesé Ramsden construyó un torno de roscar de gran precisión, el cual se empleaba para la construcción de instrumentos científicos y probetas de ensayo cilíndricas.. Young tomaba en consideración la sección transversal de la probeta A₀ y una cierta longitud inicial L₀. De esta manera consideraba el esfuerzo σ = P/A₀ y la deformación  ε =ΔL/L₀ (adimensional). La relación de Hooke se convirtió en σ = E.ε, donde E toma el nombre de módulo de elasticidad o módulo de Young, por su gran aporte, el cual pasó a ser una propiedad del material. En un gráico σ vs ε el mismo material presentaba siempre la misma pendiente, esto es, el mismo módulo de Young. Los ingenieros civiles de la época no entendían como era posible esto, pero les facilitaba sus diseños

1.2. Origen atomístico del módulo de Young

Los átomos de un material se mantienen unidos mediante lo que se denomina enlaces atómicos. Estos enlaces se clasifican en: iónicos, covalentes, metálicos y de Van der Waals. En 1910, los físicos alemanes Max Born y Edwing Madelung desarrollaron la teoría del enlace iónico, basada fundamentalmente en interacciones de carácter electrostático siguiendo la ley de Coulomb. Básicamente se trata de atracciones entre iones positivos y negativos y repulsiones entre electrones periféricos por solapamiento de sus orbitales [1]. Una teoría para enlaces covalentes y metálicos es más complicada, pero puede seguirse pensando en acciones atractivas y repulsivas por resonancia [2]. Esto permite escribir la fuerza del enlace atómico como la resultante entre una fuerza atractiva, positiva, y una fuerza repulsiva, negativa, entre un par de átomos, de la siguiente manera:

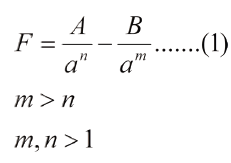
Donde A, B, m y n son constante y "a" es la distancia entre los núcleos atómicos.

Si ɸ es la energía potencial de interacción, entonces para una variación "da" se produce una variación de energía potencial ・dɸ・, de modo que dɸ = F.da, y así:

 

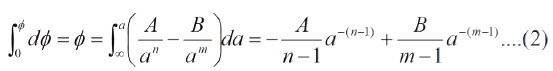
En la posicion de equilibrio para el cual a= a₀ se tiene F=0 y ɸ=ɸmin=ɸ₀, de modo que:

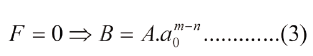
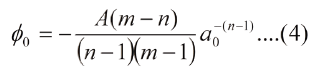
Observese que ɸ₀ es negativo, conforme con la convencion termodinamica de que el enlace atomico es exotermico, es decir, al unirse los atomos se produce desprendimiento de energia en forma de calor y, opuestamente, generar una grieta, ruptura de enlaces, requiere la incorporacion de energia externa, esto es, es un proceso endotermico. Observese tambien que al disminuir la distancia interatomica aumenta la energia de enlace y con ello las propiedades fisicas asociadas al enlace, tales como el punto de fusion y el modulo de Young, el cual pasa a ser una medida de la rigidez del material.

Es interesante conocer los valores de F para a<a₀, para ello consideremos las ecuaciones (1) y (3),

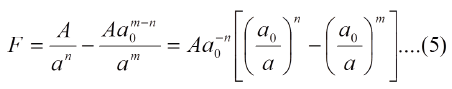
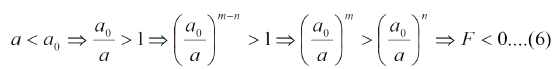
La relación (6) nos permite decir que para distancias interatómicas menores que las del equilibrio la fuerza resultante actuante es repulsiva.

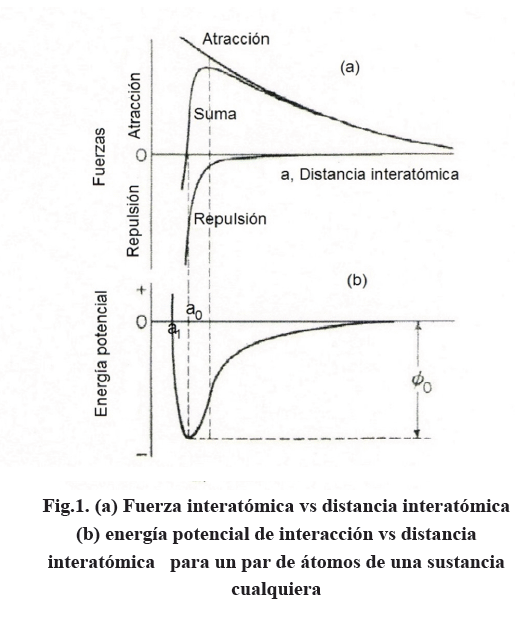
En la Fig.1 se tiene un esquema de las fuerzas interatómicas y la energía potencial de interacción en función de la distancia interatómica para un par de átomos de una sustancia cualquiera.

En la Fig.1 se puede observar que para distancias interatomicas muy grandes, las fuerzas y la energia potencial de interaccion se reducen a cero. Adicionalmente, existe un valor "a₀", dado por ec. (3) para el cual la energia de interaccion es minima y representa la distancia de equilibrio; tambien existe un valor a₁<a₀, para el cual ɸ=0, lo que permite escribir:

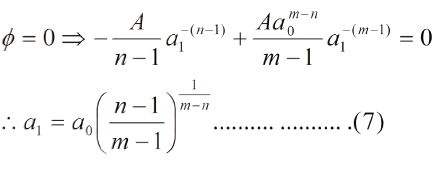
Para este valor la fuerza resultante es:

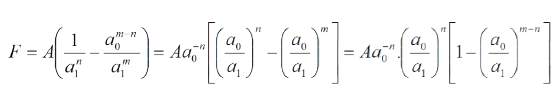
De la ec. (7) tenemos:

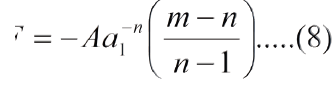
Que, como corresponde, es de repulsion.

Se puede observar de la  que, para un desplazamiento infinitesimal alrededor de ga0h la curva es aproximadamente lineal, por lo que se puede escribir, como una primera aproximacion, F.k.ƒ¢a, donde k es la pendiente de la recta y ƒ¢a=a-a0 es el desplazamiento, siguiendo asi un comportamiento hookeniano. La ofrece otro enfoque, como se muestra a continuacion:

Se puede observar de la Fig. (1a) que, para un desplazamiento infinitesimal alrededor de “a0” la curva es aproximadamente lineal, por lo que se puede escribir, como una primera aproximación, F≈k.Δa, donde k es la pendiente de la recta y Δa=a-a0 es el desplazamiento, siguiendo así un comportamiento hookeniano. La  Fig. (1b) ofrece otro enfoque, como se muestra a continuación:

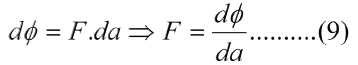
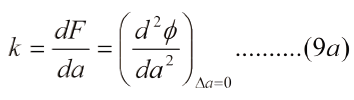
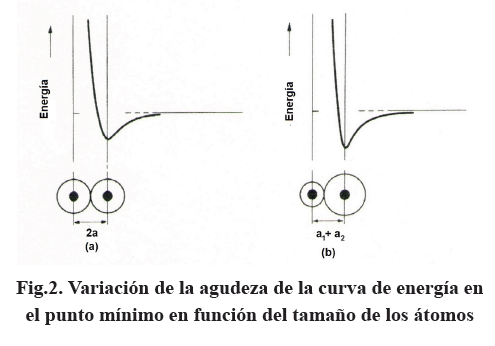
Como la segunda derivada está asociada a la curvatura, la ec. (9) señala que la constante de proporcionalidad “k” refleja la agudeza del mínimo de la curva de energía, Fig. (1b), el cual está próximo al punto de inflexión.

Al disminuir el tamaño de los átomos aumenta la energía de enlace, aumenta la rigidez, esto es, la pendiente de la recta, o sea k y E, y la agudeza de la curvatura en el valor mínimo es mayor, como se muestra en la Fig.2. Naturalmente, la profundidad da el valor de la energía potencial.

Para establecer una relación entre k y E se puede pensar en un cubo de lado “a0” con átomos en los vértices, de modo que el área de una cara es A0 y la fuerza F está actuando normalmente. Así tenemos:

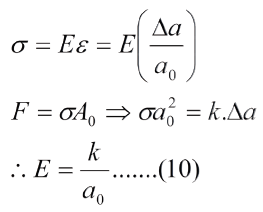
1.3. El origen natural de las grietas

Las deformaciones pueden ser elásticas o inelásticas, según que al quitar la carga ésta se recupere o no. En la deformación inelástica, la deformación que permanece se llama deformación plástica. Cuando la fractura se produce en el campo elástico se llama fractura frágil, de modo que el material se fractura sin deformación, pues toda la deformación elástica se recupera después de la fractura. Cuando la fractura se produce en el campo plástico se llama fractura dúctil y el material, después de la fractura, recupera la deformación elástica correspondiente, pero permanece la deformación plástica, la cual es fácil de reconocer observando la superficie de fractura en un microscopio electrónico de barrido (MEB).

La fractura frágil es producida por esfuerzos normales de tracción sobre planos cristalográficos denominados planos de clivaje. La fractura dúctil es producida por esfuerzos de corte sobre planos cristalográficos denominados planos de deslizamiento.

Como siempre ocurre con problemas que se pueden mostrar como complicados, para llegar a una solución aceptable, lo mejor es hacer un balance de energía. La grieta se puede formar, en un metal por ejemplo, durante la transformación líquido-sólido o durante el proceso de conformado del metal. En un caso los enlaces atómicos no se forman, en el otro se rompen. En ambos casos, la energía involucrada en el proceso queda almacenada en el entorno de la grieta, que en el caso de una fractura frágil es energía elástica. Como premisa fundamental se establece que el material es hookeniano.

Consideremos un ensayo de tracción en el que es válido la constancia de volumen, de modo que V=A₀.L₀ = A.L = Cte., donde A₀, es el área transversal inicial; L0 la longitud calibrada inicial; A y L las mismas magnitudes un instante cualquiera durante el ensayo. Al producirse un desplazamiento dL bajo la acción de la fuerza F, el material absorbe una energía dW, de modo que:

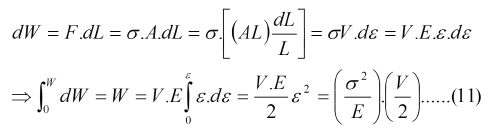
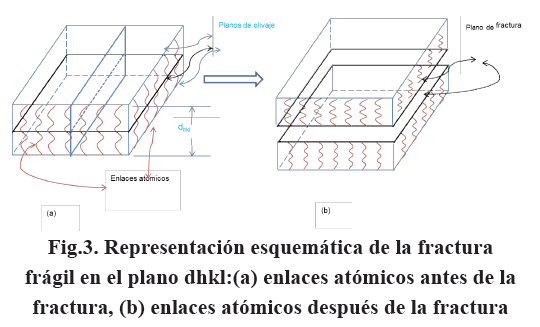
El volumen “V” a considerar es el volumen de enlaces atómicos entre dos planos de clivaje de área “A” y espaciados una distancia “dhkl”, así tenemos un volumen enlaces atómicos V= A._dhkl. En la ec. (11), el primer factor es la energía por unidad de volumen y el segundo factor es, atomísticamente, la mitad del volumen de los enlaces atómicos rotos. En la Fig.3 se tiene una representación esquemática de la fractura en un plano de clivaje.

En la Fig.3(a) se puede ver que medio volumen del sólido de energía elástica está asociado a media área del plano de clivaje. El plano de clivaje pasa a ser una sección principal del sólido de energía elástica. Si “V*” es el volumen de energía elástica y “A*” el área de la sección principal correspondiente al plano de clivaje, tenemos, en general:

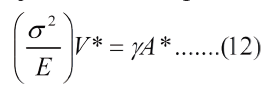
Si "s_ft" es el esfuerzo teorico para romper los enlaces atomicos, tenemos:

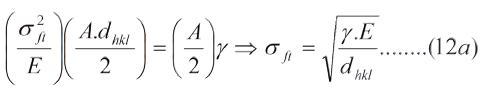
Cuando la ec. (12) se aplica a monocristales, como pronto veremos, los valores son del orden de 1010 Pa (10.000 MPa), los cuales superan en decenas de miles los valores experimentales obtenidos. Esto lleva a pensar que las grietas se forman durante los procesos de fabricación de las piezas, bien sea como grietas de contracción durante la solidificación del material o grietas de conformado durante la laminación, forja, extrusión, estampado, embutición y mecanizado.

Las grietas son la razón de ser de la mecánica de fractura y la mecánica de fractura elástica lineal es aplicable solamente a materiales hookenianos, algo que los libros sobre la materia no dicen explícitamente.

Antes de la decada de los 60 se hablaba de resiliencia y tenacidad, como la cantidad de energia absorbida por el material, en el campo elastico o plastico respectivamente, en un ensayo de traccion. De modo que la energia considerada hasta el momento es resiliencia.

La tenacidad es de esos conceptos que pareciera decir mucho y a la vez no decir nada. Para dar una interpretacion matematica es necesario introducir los conceptos de deformacion verdadera y esfuerzo verdadero como una deformacion instantanea e* y un esfuerzo instantaneo s*, referidos como el desplazamiento con respecto al valor momentaneo de longitud y al area instantanea respectivamente. Asi de* = dL/L y s* = P/A. Cuando esto se hace la curva es monotonicamente ascendente porque el area instantanea va disminuyendo progresivamente. Esto permite aproximar el area bajo la curva de inelasticidad a un trapezoide, de modo que si UT es la tenacidad, medida en traccion hasta la fractura, tenemos:

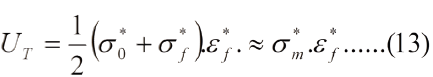
En la e. (13), s0* es el esfuerzo de fluencia verdadero; sf* es el esfuerzo de fractura verdadero; sm* es el esfuerzo maximo verdadero y ef* es la deformacion plastica verdadera en el momento de la fractura, esto es, la deformacion plastica total, llamada tambien ductilidad. No se olvide que la deformacion elastica, en el momento de la fractura, se recupera. Así pues, la tenacidad, medida en un ensayo de tracción, involucra tanto el esfuerzo máximo verdadero como la ductilidad.

La presencia de la grieta ha introducido conceptos nuevos, todos ellos equivalentes, como son: esfuerzo remanente; esfuerzo de fractura en presencia de una grieta; resistencia residual; tenacidad a la fractura.

1.4. La ley de Hooke en tres dimensiones. Esfuerzo plano. Deformación plana

Cuando una varilla metalica se carga en traccion en una direccion se alarga elasticamente en dicha direccion y se contrae en las otras dos, y reciprocamente. La razon de la contraccion al alargamiento se llama razon de Poisson, "µ", en honor al fisico y matematico frances del siglo XIX Simeon Denis Poisson. Los monocristales son, por naturaleza, anisotropicos de modo que sus propiedades dependen de la direccion en que se midan. Entre estas propiedades tenemos la velocidad del sonido, el modulo de Young E y la relacion de Poisson "µ". Sin embargo, un policristal, debido a su multidireccionalidad, es un material estadisticamente isotropo.

Consideremos una lámina y sobre ella un sistema cartesiano de referencia: 1≡X, 2≡Y, 3≡Z (espesor). Consideremos un material isótropo y hookeniano. Si la carga se aplica en la dirección “1”, entonces μ=-ε₂/ ε₁=-ε₃/ε₁; si en la dirección “2”, μ=-ε₁/ε₂=-ε₃/ε₂; si en la dirección “3”, μ=-ε₁/ε₃=- ε₂/ε₃. Como consecuencia de ello al aplicar la carga en la dirección "1" se produce una deformación directa ε₁=σ₁/E, y en la dirección “2”, ε₂=-με₁=μσ₁/E y en la dirección "3", ε₃ = με₁=μσ₁/E. Al aplicar la carga en la dirección “2”, el efecto en la dirección “1” es ε₁=-με₂=-μσ₂/E; así mismo al aplicarse la carga en la dirección "3", el efecto en la dirección “1” es ε₁ =-με₃=-μσ₃/E. Aplicando el principio de superposición podemos escribir ε₁ = σ₁/E -μσ₂/E-μσ₃/E = 1/E. [σ₁-μ(σ₂+σ₃). De manera genérica y usando notación tensorial:

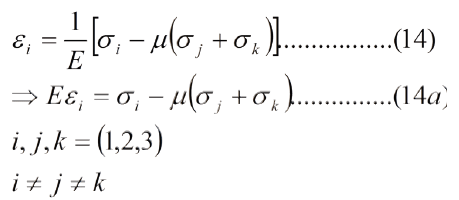
En un análisis experimental de tensiones lo que se mide son las deformaciones, y a través de éstas inferir sobre el estado de esfuerzos, por ello es conveniente expresar los esfuerzos en función de las deformaciones. Usemos el cálculo tensorial por comodidad y hagamos una sumatoria en la ec. (14):

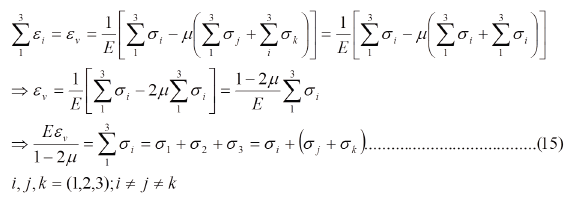
Multiplicando la ec. (15) por "µ" y sumandola a la ec. (14a) miembro a miembro, tenemos:

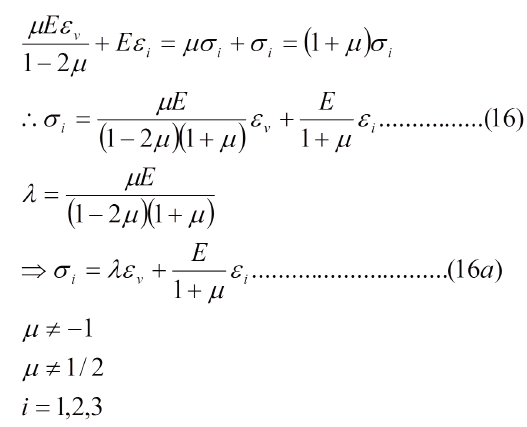
En la ec. (16a), "ε_v = Σε_i" es la deformación volumérica y "c " es la constante de Lamé en honor a Gabriel Lamé, matemático e ingeniero francés del siglo XIX. Para materiales isotrópicos, -1<μ<½ Aquélos materiales con valores negativos de "μ" reciben el nombre de materiales auxéticos y los materiales anisotrópicos con dos o tres ejes binarios de simetría reciben el nombre de materiales ortotrópicos, como la madera. El corcho usado para cerrar botellas de vino y champaña tienen un μ = 0,00, muy apropiado para el trabajo a realizar. El panal de las abejas, conformado por celdas hexagonales regulares, tiene un valor μ=+1,00, lo que ha llevado a algunos diseñdores a crear estructuras con efecto opuesto para producir estructuras auxéticas.

Las ecs. (14) y (16a) sirven para analizar dos casos muy particulares: los denominados deformacion plana y esfuerzo plano.

El espesor es una variable geometrica sumamente importante en mecanica de fractura. Consideremos un estado bidimensional (plano) de deformaciones, de modo que las deformaciones en la direccion del espesor, incluyendo las de corte, sean cero. En el presente caso, e₃ =0. Las ecuaciones tensoriales, para deformacion plana, se pueden escribir asi:

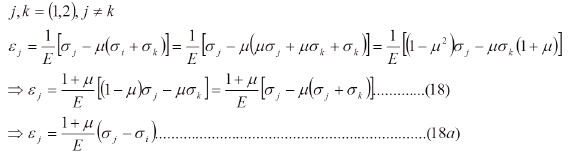
Observese que aun cuando la deformacion en la direccion del espesor es cero, el esfuerzo no lo es, viene dado por la ec. (17), lo cual genera un estado tridimensional de tensiones dado por la ec. (16a). Las deformaciones en las direcciones "1" y "2" vienen dadas por la ec. (18) o (18a).

Consideremos un estado bidimensional (plano) de esfuerzos, de modo que los esfuerzo, incluyendo los de corte, en la direccion del espesor sean cero. En el presente caso s₃ =0. Las ecuaciones tensoriales, para esfuerzo plano, a partir de la ec. (15a) se pueden escribir asi:

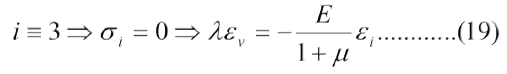
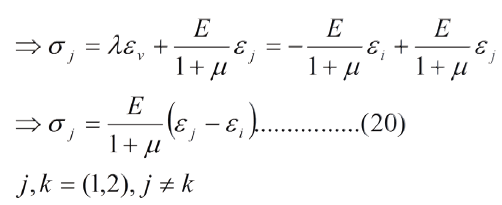
El esfuerzo en las direcciones "1" y "2" viene dado por la ec. (20). En la ec. (20) se puede convertir la diferencia de deformaciones en una suma, multiplicando el numerador y el denominador por (1-µ) y recordando que, para materiales isotropos, µ = -e_i/e_j,

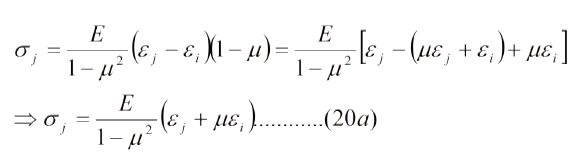
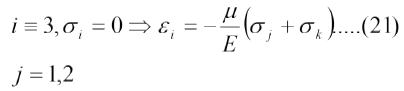
También se puede introducir la ec. (21) en la ec. (20):

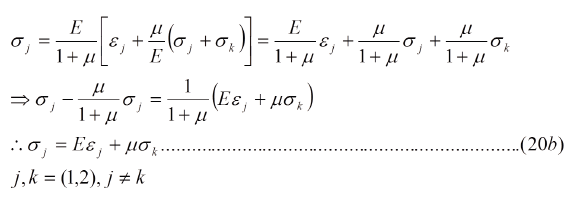
Conviene tener una expresión genérica para las deformaciones normales en la condición de esfuerzo plano. Para ello procedemos de la siguiente manera:

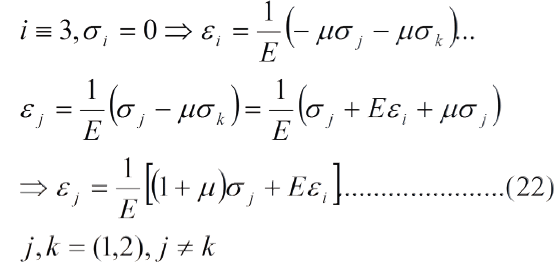
Obsérvese que aun cuando el esfuerzo en la dirección del espesor es cero, la deformación no lo es, viene dada por la ec. (21), lo cual genera un estado tridimensional de deformaciones dado por las ecs. (21) y (22).

Las láminas que tienen gran espesor y son sometidas a un estado bidimensional de esfuerzos (deformaciones) (L-T), casi no se deforman en la dirección del espesor, por lo que están en condiciones de deformación plana. Sin embargo existe un estado tridimensional de esfuerzos, dado por la ec. (16a).

Las láminas que tienen poco espesor y son sometidas a un estado bidimensional de esfuerzos (L-T), se deforman considerablemente en la dirección del espesor, el material no ofrece resistencia, por lo que están en un estado de esfuerzo plano. Las láminas de gran espesor no presentan efecto Poisson en el espesor, por lo que están sometidas a deformación plana. Hay un espesor límite por debajo del cual el material se encuentra en estado de esfuerzo plano y otro que por encima está en estado de deformación plana; intermedio es una mezcla y son los llamados espesores críticos.

Conviene apuntar que la ec. (20a) corrige algunos libros [3,4] que le asignan al subíndice “i”, en un cálculo convencional, los valores 1 y 2 (x e y), cuando en realidad tiene el valor fijo de 3 (espesor). Este error ha permanecido por décadas.

Toda la mecánica de fractura elástica lineal debería estar fundamentada en un estado de deformación plana, para la cual hay muy poca deformación plástica en la punta de la grieta. Toda la mecánica de fractura elasto-plástica debería estar fundamentada en un estado de esfuerzo plano, para el cual hay una gran deformación plástica en la punta de la grieta. Con frecuencia esto se olvida y se pretende obtener parámetros de evaluación críticos, válidos para cualquier espesor, cuando solamente son válidos para el espesor ensayado.

1.5. La grieta como centro de atención universal. Nuevos enfoques sobre fractura frágil

La fuerza es un vector que tiene un punto de aplicación, una dirección y un sentido. Como tal es un vector deslizante. Cuando actúa sobre una superficie, el punto de aplicación es el centroide del área. Cuando es una acción a distancia que actúa sobre un cuerpo, el punto de aplicación es el centro de gravedad del sólido. El álgebra de los vectores deslizantes es más compleja que la de los vectores libres, de modo que convertir uno en otro requiere, en mecánica de materiales, dar ciertos pasos audaces. Uno de ellos es definir el esfuerzo en un punto y otro es hablar de fuerza distribuida. Cuando esto se hace el esfuerzo se imagina como líneas de flujo que atraviesan la superficie, tal cual líneas de inducción magnética. Tales líneas de flujo pueden permanecer paralelas, en cuyo caso el esfuerzo es uniforme, o pueden aumentar su densidad superficial, concentrándose, en ciertos puntos particulares. En estos puntos el esfuerzo se eleva y el punto se llama concentrador de esfuerzo. En mecánica, los ángulos agudos y discontinuidades, como agujeros; en metalurgia, las inclusiones no metálicas son concentradores de esfuerzo.

En 1898, el fisico ingles G. Kirsch derivo las expresiones para determinar los esfuerzos alrededor de un hueco circular. A partir de estas expresiones se encuentra que en el diametro, perpendicular al esfuerzo remoto, el esfuerzo es tres veces el esfuerzo remoto s¥; es decir, el factor concentrador de esfuerzo K s es 3.

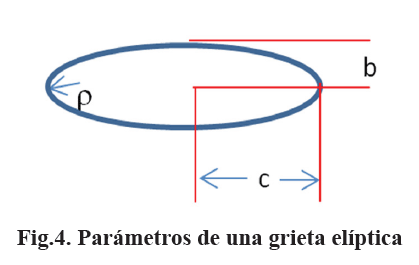
En 1907, Gury Vasilyevich Kolosov, matematico ruso, y en 1914, Charles Edward Inglis, metalurgista ingles, de manera independiente desarrollaron todo un analisis sobre el estado de esfuerzos alrededor de una grieta eliptica. Estos analisis senalaban que en la punta de la grieta el esfuerzo es infinito, lo que, obviamente, esta lejos de la realidad. Sin embargo ambos lograron encontrar una expresion para el factor concentrador de esfuerzo, Ks, en la punta de la grieta eliptica. Este valor esta dado por:

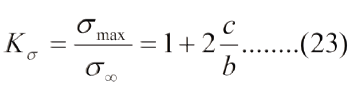
Donde s_max es el esfuerzo en la punta de la grieta y s_¥ es el esfuerzo remoto, perpendicular al eje mayor de la elipse. En la Fig.4 se tiene el significado de los simbolos empleados en la ec. (23). Una grieta de dos puntas, como las que se encuentran en el centro de la lamina, tiene una longitud "2c"; una grieta de una punta, como las que se encuentra en los bordes de la lamina, tiene una longitud "c";"b" es el semiancho de la grieta eliptica.

¿No es, acaso, una contradicción que en la punta de la grieta un análisis del campo de esfuerzos revele un valor infinito del esfuerzo y a la vez el análisis de concentrador de esfuerzo revele un valor máximo finito?

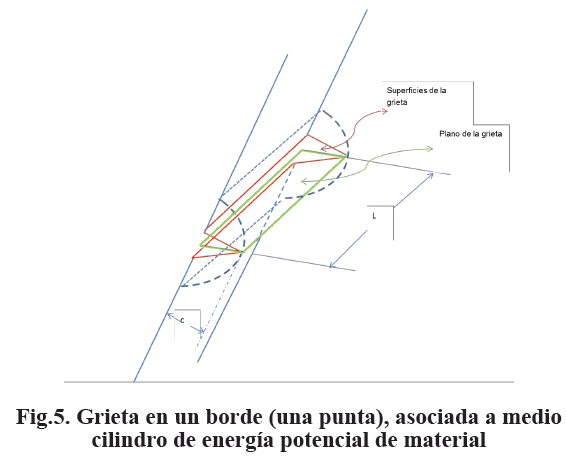
La grieta ya existe, los enlaces atómicos no llegaron a formarse y el material alrededor de la grieta quedó con una energía potencial equivalente a su ruptura. Se sigue con el pensamiento de que toda la energía involucrada en el proceso de fractura es energía elástica, es decir fractura frágil. El criterio que se establece para utilizar la ec. (12) es que el volumen elástico de material afectado por la grieta es aquel cilindro cuyo radio es “c” y cuya longitud es “L”. El plano de la grieta reemplaza al plano de clivaje; dos puntas representan una superficie y una punta representa media superficie del plano de grieta, la cual está asociada a medio volumen de cilindro, ambos asociados a medio volumen de enlaces atómicos no formados, como se muestra en la Fig.5 para una grieta en un borde. Esta nueva concepción separa el plano de la grieta de las superficies de fractura, asociando las energías correspondientes con el plano de la grieta. El plano de la grieta pasa a ser una sección principal del cilindro de energía elástica.

Debemos insistir, siguiendo la filosofia atomistica aqui presentada, que el esfuerzo asociado a la energia elastica, s_el, producto de la creacion de la grieta, no necesariamente es el esfuerzo de fractura, como veremos mas adelante. Podria ser si el tamano de la grieta creada, durante la formacion del solido, es el tamano critico "C_c ".

Así, de la ec. (12) tenemos:

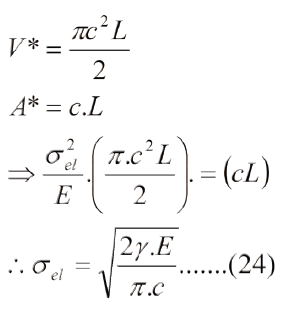
En 1924, Alan Arnold Griffith [5], ingeniero aeronáutico inglés, considerado el abuelo de la mecánica de fractura, continuó los trabajos de Inglis trabajando en láminas de vidrio sometidas a tracción, pero tomando en cuenta el efecto del tamaño de la grieta en el esfuerzo de fractura. Hizo muchos experimentos con grietas de diferentes tamaños, formas y ubicación. Para 1910, Max Born y Erwing Madelung, físicos alemanes, habían desarrollado la teoría para enlaces iónicos, de modo que Griffith era conocedor de ideas sobre enlaces atómicos y esto se observa al leer su trabajo [5]. El gran mérito de Griffith está en haber introducido el concepto de balance de energía, el cual se ha generalizado en todas las áreas de la ingeniería. Sin embargo, Griffith utiliza un cálculo basado en funciones hiperbólicas para llegar al esfuerzo de fractura.

Para llegar a la ecuación de Griffith se tiene que el volumen de energía elástica, que ahora se llama U_V, sigue siendo “V*”. La grieta tiene como superficie 2cL, como se muestra en la Fig.5, de modo que se tiene energía superficial U_S=2cLg. Si la grieta crece, entonces a una variación (disminución) de la energía de volumen dUv/dc le corresponde una variación (aumento) de energía de superficie dUS/ dc, de modo que:

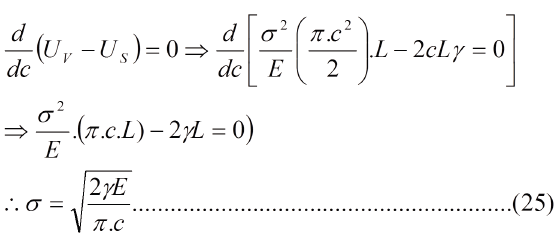
La ec. (25) es la famosa ecuación de Griffith para la condición de esfuerzo plano, la cual es similar a la ec. (24) pero de concepción completamente distinta. La dU_V/dc recibe el nombre de rapidez de liberación de energía de deformación elástica o fuerza motriz de la grieta, nombres asignados por el físico americano George Rankin Irwin en 1956.

La ec. (25) es una ecuación de crecimiento de grieta elástica y alcanzado el tamaño crítico se produce la fractura, esto es:

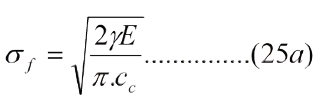
La ec. (24) representa el esfuerzo de traccion, asociado a la energia elastica almacenada por ausencia del material de la grieta. Esta afectado por el factor concentrador de esfuerzo K_s. Cuando se aplica un esfuerzo remoto s¥ este se ve afectado por Ks. Para que la grieta crezca, la suma de ambos debe ser igual al esfuerzo de fractura teorico. Asi tenemos:

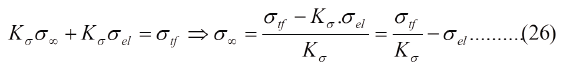
El factor concentrador de esfuerzo tambien se puede escribir en funcion del tamano de la grieta y del radio de curvatura "r" de la punta de la grieta eliptica, asi:

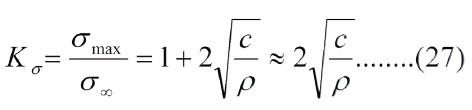
La ec. (27) señala que cuanto mayor es el tamaño de la grieta y más aguda es ésta mayor es el factor concentrador de esfuerzo. La ec. (26) indica que cuanto mayor es el factor concentrador de esfuerzo menor es el esfuerzo necesario para que la grieta crezca.

Reemplazando las ecs. (12), (24) y (27) en (26) tenemos:

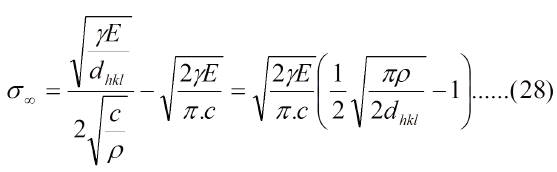
Puede verse, de la ec. (28) que a medida que la grieta crece el esfuerzo remoto disminuye, esto es la tenacidad o esfuerzo residual disminuye. Cuando la grieta alcance un tamano critico "C_c", el esfuerzo remoto "s¥" alcanza el valor de fractura "s_f", asi:

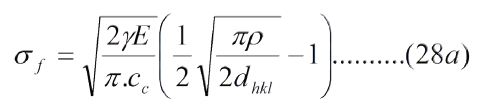
La ec. (28a) introduce un factor de correccion "W" en la ecuacion de Griffith, completamente novedoso, a saber:

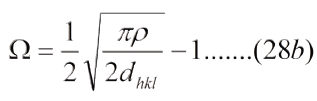
Este factor de corrección establece un intervalo de valores “ρ”: un “ρ_máx” para el cual “Ω” =1 y un “ρ_min” para el cual “Ω” =0, en materiales de fractura frágil. De modo que:

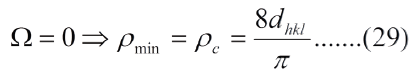
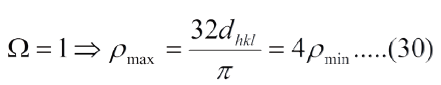
A medida que la grieta se hace mas aguda (^.."ρ" disminuye), el esfuerzo de fractura disminuye; a medida que la distancia entre los planos de clivaje aumenta (indices de Miller menores) el esfuerzo de fractura disminuye.

El factor de correccion en la ec. (28) nos indica algo sumamente importante, conocido por la experiencia, pero que se plantea, matematicamente, por primera vez: el esfuerzo necesario para la propagacion de la grieta puede llegar a ser cero, independientemente de su tamano, si esta tiene un radio de curvatura critico dado por la ec. (29).

1.6. Mecánica de fractura elástica lineal. El factor intensidad de esfuerzo. Un nuevo enfoque

Ha sido largo el camino para tener la vision de la mecanica de fractura que tenemos hoy. En esta tarea han participado mentes brillantes. En 1862, el matematico y astronomo ingles George Biddel Airy presento un metodo para determinar el estado de esfuerzos y deformaciones en una viga y demostro que siempre es posible encontrar una funcion ɸ(x₁,x₂) a partir de la cual se puede calcular los esfuerzos s_ij en una lamina bajo condicion de esfuerzo plano. A este tipo de funcion se le conoce como funcion de esfuerzos de Airy. Aunque Airy trabajo en el campo real, los grandes avances se han hecho en el campo complejo. Trabajando en este campo, el fisico y matematic

o ruso Nikolai Ivanovich Mushhelishvili, en 1930, desarrollo unas ecuaciones para conocer el campo de esfuerzos alrededor de la punta de una grieta, empleando condiciones muy generales de borde. Condiciones particulares de borde fueron desarrolladas por los cientifico Gury Vasilievich Kolosov, matematico ruso, en 1907; Charles Edward Inglis, metalurgista ingles, en 1914: Harold Malcolm Westergaard, fisico americano de origen danes, en 1939; George Rankin Irwin, cientifico americano, en 1958, considerado el padre de la mecanica de fractura, y Warner Tjardus Koiter, brillante conferencista y fisico holandes, en 1959, entre otros.

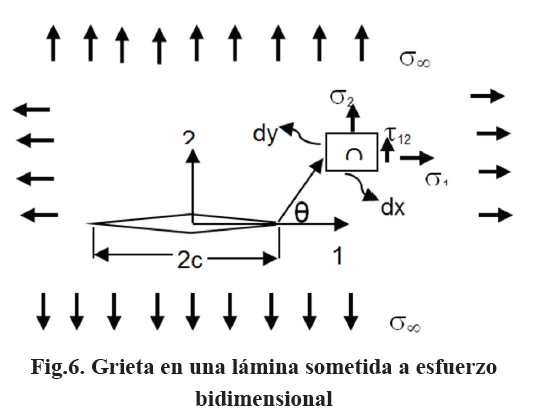
En la Fig.6 se tiene una representacion grafica de una grieta en una lamina de dimensiones infinitas sometida a un estado bidimensional de esfuerzos.

Para un punto Q(r,q.), ubicado en un plano perpendicular a la grieta, las ecuaciones que describen el campo de esfuerzos alrededor de la grieta, que hoy día se manejan, son las siguientes [6]:

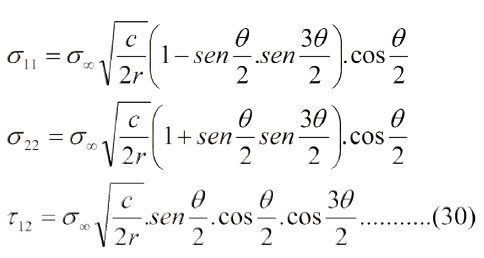
Las ecs. (30) se pueden resumir de la siguiente manera:

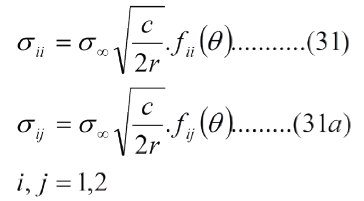
Para los puntos que están justo frente a la punta de la grieta, que son los que interesan en ingeniería, q.= 0, se tiene que f_ii(0) = 1 y f_ij(0) = 0. De modo que la ec. (31) se simplifica:

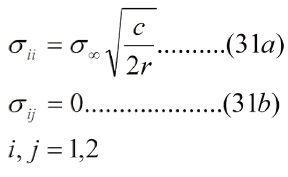
Puede verse que, frente a la punta de la grieta, los esfuerzos normales en las direcciones “1” y “2” son iguales, sin embargo en la mecánica de fractura convencional se le presta mayor atención al esfuerzo en la dirección “2” por considerar que es el que abre la grieta. La ec. (31a) sigue presentando el problema de dar un esfuerzo infinito en la punta de la grieta, lo que es inadmisible porque no existe un material que resista un esfuerzo considerado infinito y, por hipótesis, la grieta existe y se propaga con cierta velocidad. Para tratar de establecer una relación inversa entre el tamaño de la grieta y el esfuerzo remanente, George Rankin Irwin creó, en 1957, el concepto de “factor de intensidad de esfuerzo” “K”, definido en las ecs. (32) y (32a):

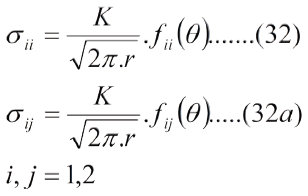
Desde luego, si se conoce gKh se conoce el campo de esfuerzos alrededor de la grieta mediante las ecs. (32) y (32a), pero no el campo de deformaciones para lo cual se necesita establecer la relacion e = f (s). Si se determina que esta es lineal, entonces se puede asociar las ecs. (32) con las ecs. (14). Justo frente a la punta de la grieta, q=0, f_ii =1 y f_ij =0, con lo cual se tiene:

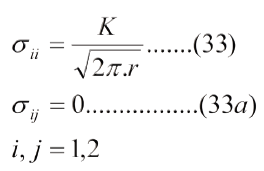
Comparando las ecs. (31a) y (33) e incorporemos un factor “ß” que da la experiencia, cuyo valor es 1,00 para grietas centrales y 1,12 para grietas en el borde se tiene:

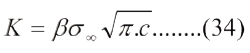
La ec. (34 guarda cierta relación con la ec. de Griffith y es la ecuación fundamental de la mecánica de fractura elástica lineal.

En nuestro aporte a la mecánica de fractura reescribamos la ec. (28):

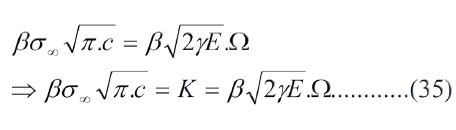
La definicion de K mediante la ec. (35) la liga con la macromecanica mediante los parametros "g" y "E" y con la micromecanica mediante los parametros "r" y d_hkl, es decir, no solo es un parametro de deformacion elastica sino que es para materiales hookenianos y fractura fragil.

La ec. (35) es mas amplia y concluyente que la ec. (34). La parte izquierda asocial un valor critico de "K" con un valor critico de tamano de grieta, conforme la mecanica de fractura convencional; la parte derecha de la ec. (35) asocia un valor critico de "K", que denominamos "K_rc", con un radio de curvatura de la grieta critico dado por la ec. (29), para el cual K_rc=0 y la grieta se propaga, catastroficamente, sin esfuerzo alguno. En otras palabras, grietas subcriticas con radio de curvatura criticos producen fracturas catastroficas. Sin embargo se trata de dos conceptos completamente opuestos. Mientras "K" pretende ser una propiedad del material, como lo es el esfuerzo de fluencia, para el que se establece un limite, obtenido experimentalmente en condiciones de deformacion plana, denominado valor critico "Kc", el valor K_rc=0. Es necesario superar el valor "Kc" para que se produzca una falla catastrofica. Por esta razon se hace necesario separar ambos conceptos.

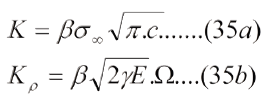
Adicionalmente, tanto  "g" como "E" son funciones de la temperatura, disminuyendo con el incremento de ésta y, en consecuencia, "K" disminuye con el incremento de temperatura, lo que es un hecho experimental, lo que también debe ocurrir con "K_r"

Las ecs. (30) son genericas en su derivacion y son aplicables a cualquier cuerpo cristalino o amorfo que contenga una grieta, sea este metal, roca, ladrillo, hielo, plastico, etc. A posteriori es que se relacionan con las ecs. (14) para seleccionar una condicion particular.

La mecanica de fractura convencional limita el valor del esfuerzo remoto, s_¥, a 80% s₀, donde s₀ es el esfuerzo de fluencia del material, para garantizar que se esta lejos de un comportamiento plastico.

George Biddel Airy llegó a ser muy famoso en su época, como astrónomo y como físico, por sus aciertos, y con frecuencia era consultado sobre diversos tópicos. En 1870, Airy fue consultado sobre cuál sería la mayor presión que debería de esperarse durante una tormenta en el fiordo de Tay, una porción del mar del norte en la costa oriental de Escocia, a fin de incorporar esta información al diseño y construcción de un puente ferroviario, remachado, sobre dicho fiordo, en la localidad de Dundee, Escocia. Su respuesta fue que ésta no debería ser mayor a 10 lb/ft² (5 kPa). El ingeniero diseñador y constructor, Thomas Bouch, no incorporó este valor en su diseño por considerarlo muy bajo. Se inició la construcción en 1871 y se puso en servicio el primero de junio de 1878. El 28 de diciembre de ese mismo año, durante una fuerte tormenta, y siendo cruzado por el ferrocarril de la North British Railway el puente colapsó. Bouch acusó a Airy de darle falsa información, pero la investigación reveló otra cosa. La presión que pudo incorporar la tormenta se estimó en 2,7 kPa; el material del puente era hierro colado y forjado, muy usado en la época, incluyendo la torre Eiffel. Sin embargo los defectos de fabricación eran notables y los remaches no cumplían con lo especificado [6].

Las vibraciones, al ser transmitidas directamente a las oscilaciones de los átomos, producen grietas subcríticas, en las áreas de concentración de esfuerzos, que pueden alcanzar el radio crítico, con lo cual, atendiendo a lo expuesto, producen fallas catastróficas. Si el tren no hubiera estado pasando en ese momento, con seguridad, el puente no se cae, pero lo hubiera hecho en otro momento, aun sin tormenta. Desde entonces varios puentes en USA y Canadá han colapsado, aun durante su construcción. Muchos accidentes catastróficos ocurridos en aviación, atribuidas a fatiga (presurización-despresurización), pueden ser consecuencia de grietas subcríticas, producidas por fatiga por vibración, con radios de curvatura críticos. Lo mismo puede decirse sobre la gran cantidad de barcos Liberty partidos en dos y severamente dañados, aun estando en los muelles, durante la segunda guerra mundial.

Normalmente d_hkl<< r, por lo que la ec. (35) puede escribirse:

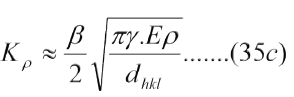
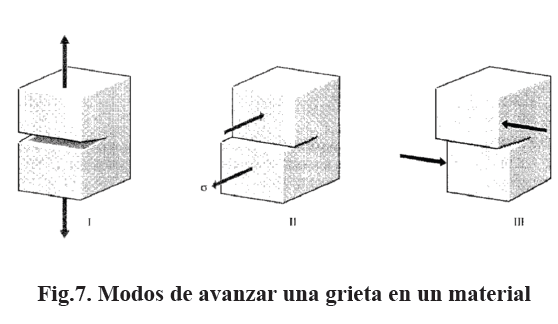
Pronto se reconoció que la grieta puede propagarse de tres modos: modo I, abriendo; modo II, deslizando; modo III torciendo o desgarrando, como se muestra en la Fig. 7. En el modo I el esfuerzo es de tensión, normal al plano de la grieta; en los modos II y III el esfuerzo es de corte en el plano de la grieta; en el modo II es perpendicular a la grieta y en el modo III es paralelo.

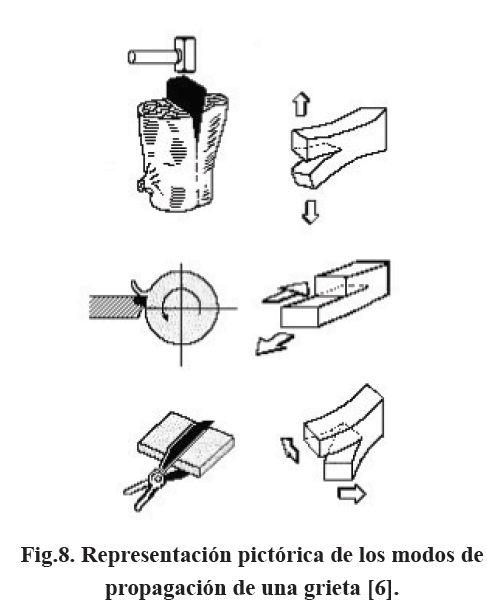
En la Fig.8 se tiene una presentación pictórica de estos modos de propagación de grietas [6].

Atendiendo a estos modos de propagación, al factor K se le designa por K_I, K_II y K_III respectivamente. Las ecs. (30) a 34 son para modo I. Las ecuaciones que se maneja para los modos II y III son las siguientes [6]:

Modo II:

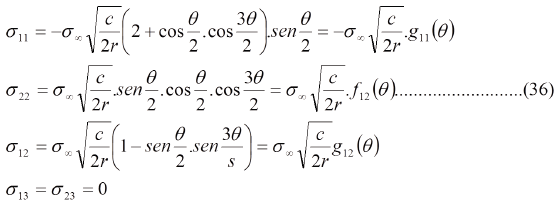
Definiendo K_II de la siguiente manera:

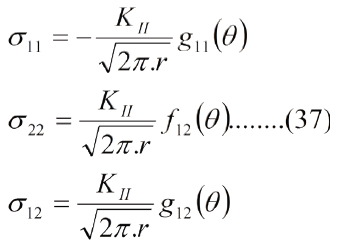
Para q= 0, frente a la punta de la grieta, tenemos, g₁₁ (q) =0, f₁₂(q) =0, g₁₂ (q)=1, por tanto:

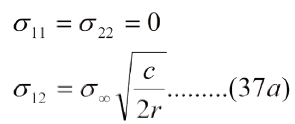
Comparando ecs. (37) y (37a) y haciendo s_¥= t_¥ (esfuerzo de corte remoto) e incorporando el factor "ß" tenemos:

Modo III:

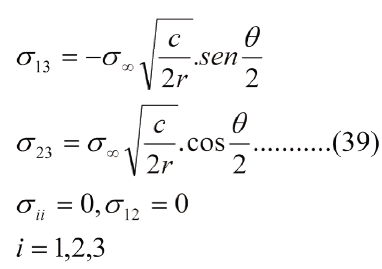
Definiendo K_III de la siguiente manera:

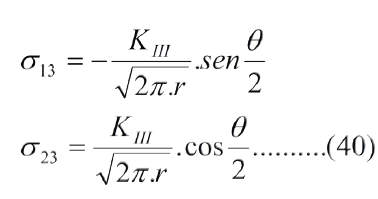
Frente a la punta de la grieta, q=0, sen(q/2)=0, cos(q/2) =1, por tanto:

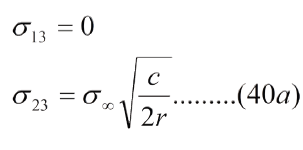
Comparando las ecs. (40) y (40a) y haciendo σ_∞= τ_∞ (esfuerzo de corte remoto) e incorporando el factor “β” tenemos:

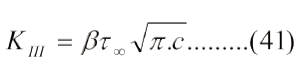
Con el enfoque dado aquí tendríamos las siguientes relaciones:

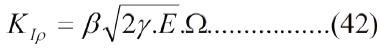
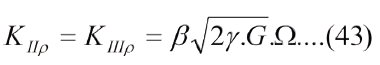
Donde "E" es, como de costumbre, el módulo de elasticidad en tracción (Young) y "G" el módulo de elasticidad en corte. Entre ambos hay una relación dada por la teoría de elasticidad, de modo que se puede emplear una sola constante elástica:

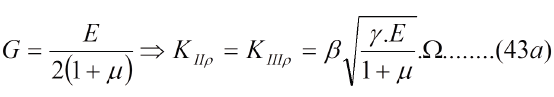
Los valores de "Kρ" así definidos no solo se refieren a materiales hookenianos sino que se aplica exclusivamente a la punta de la grieta y a fractura frágil, pues "Ω", como se recordará, se refiere exclusivamente a este tipo de material.

El trabajo de Alan Griffith permaneció a la sombra durante 26 años, hasta que en 1950 la ASM (American Society of Metals) publicó el libro pionero en fractura, "Fracturing of Metals", en el que aparecían dos trabajos relevantes: uno del extraordinario metalurgista físico americano Clarence Melvin Zener titulado "Micromechanics aspects of fracture initiation" y otro del ya citado George Rankin Irwin, "Dynamics fracturing of precracked materials". En el primero se hacía referencia al trabajo de Griffith. En 1959 se inician las "ICF" (International Conference of fracture) con la primera, ICF1, en Swampscott, condado de Essex (Massachussetts, USA). En 1962 se realizó ICF2 en Seattle (Estado de Washington). En estas conferencias participaron hombres de gran relevancia académica, tales como: Clarence Melvin Zener, Alan Howard Cottrell, Norman Petch, Egon Orowan, Morris Cohen, John Joseph Gilman, Charles Sanborn Barret, Frank McClintock y Takeo Yokobory que han dejado profunda huella en el campo de la mecánica de fractura [8]. En las décadas de los 60 y 70 el factor intensidad de esfuerzos K_IC, como parámetro evaluador de la fractura frágil, estaba ya bien establecido y actualmente existen desarrollos polinómicos que permiten calcularlo para diferentes geometrías. A ICF2 han seguido muchas en diferentes partes del mundo como Japón, Canadá, India, Rusia, Grecia, China, etc.

La mecánica de fractura elástica lineal nació para dar respuesta a la gran cantidad de fallas producidas en acero estructural de alta resistencia sometido a esfuerzos muy pequeños. Entre estas fallas tenemos las de fatiga, corrosión bajo tensión y las de corrosión-fatiga. En ambos casos el factor intensidad de esfuerzo juega un papel fundamental.

Como era natural, desde un comienzo, siempre se pensó que el fenómeno de la fatiga debería tener alguna relación funcional con el factor intensidad de esfuerzo, como por ejemplo:

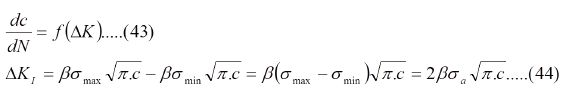
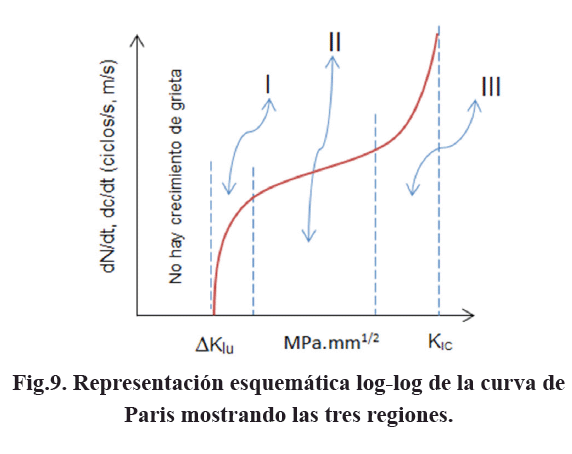
Donde “N” es el número de ciclos y “σ_a" es la amplitud del esfuerzo. En 1963, Paul Paris, de la universidad de Lehigh. USA, lideró proyectos de tesis doctorales en los que se realizaban ensayos de fatiga, en diversas condiciones, con diferentes tamaños iniciales de grieta y se trazaban las curvas c=f(N). En cada punto de estas curvas se tiene el tamaño de la grieta, con lo que se calcula “ΔK” según (43a) y mediante la tangente endicho punto se calcula dc/dN. Todos estos valores se tabulan y se traza una gráfica log-log, con lo que se obtiene una curva cuya forma genérica se muestra en la Fig.9, llamada impropiamente curva de Paris, en la que se distingue un “ΔK_I” umbral (“ΔK_Iu"), por debajo del cual no hay crecimiento de grieta; una región "I" de crecimiento relativamente lento de grieta; una región "II" de crecimiento estable o constante de grieta y una región "III" de crecimiento rápido o inestable hasta alcanzar el valor crítico "K_IC".

La región "II" tiene la forma genérica:

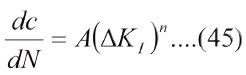
Donde "A" y "n" son constantes, dc/dN es la razón de propagación de la grieta con el número de ciclos, o si N=ν.t, donde “ν” es la frecuencia de aplicación de las cargas y “t” el tiempo, entonces dN=ν.dt y, por tanto:

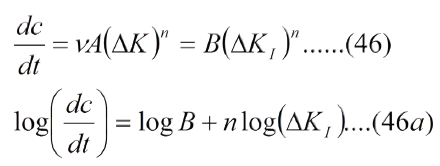
Donde "n" es la pendiente de la recta y "B" la ordenada en el origen en el intervalo "ΔK_I" de linealidad (región II).

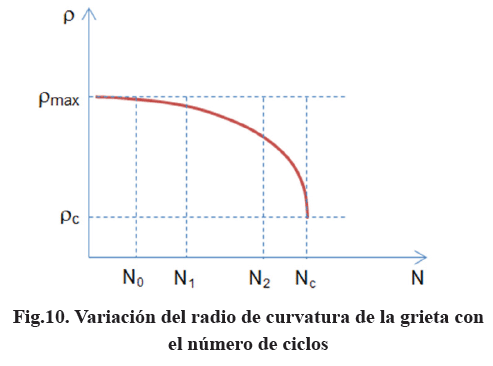
Para el enfoque dado en el presente trabajo se trazarí ρ=f(N), la cual debe tener la forma mostrada en la Fig. (10).

Por debajo de N₀ no hay crecimiento de grieta; entre N₀ y N₁ hay un crecimiento lento; entre N₁ y N₂ hay un crecimiento estable y constante y entre N₂ y Nc hay un crecimiento rápido hasta alcanzar la condición de inestabilidad.

Para determinar si la curva de Paris tiene la misma forma para dρ/dN derivemos la ec. (28) respecto de “N”. Se postula que “ρ” decrece con “N”, como se muestra en la Fig.(10):

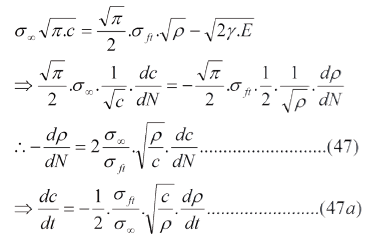
Por tanto -dρ/dN sigue un comportamiento similar a dc/dN. La ec (46) permite obtener una relación muy útil para dos instantes ti y tj de la existencia de cualquier grieta, siendo t_j > t_i, la cual es:

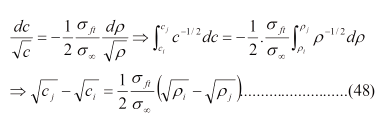
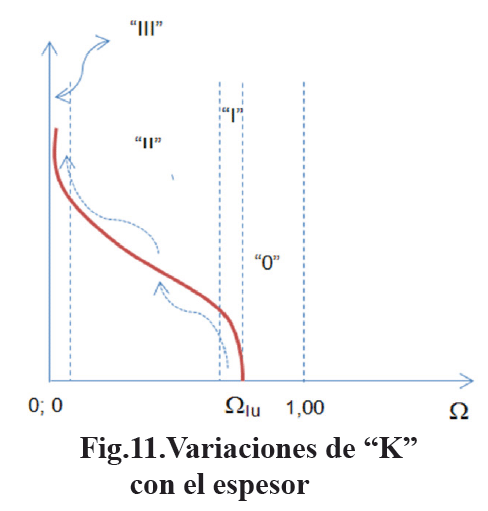
Si en un instante cualquiera se conoce la longitud de la grieta y su radio de curvatura, con conocer el radio de curvatura en otro instante se puede conocer su longitud para ese instante mediante la ec.(48). Obsérvese en la Fig.10 que en el punto "N_c", correspondiente a un "t_c", para el cual se alcanza el valor “ρ_c”, se tiene dρ/dt→∞ y por tanto dc/dt→∞. La curva dc/dt =f(K_Iρ) debe ser como se muestra en la Fig.11, tomando dc/dt vs Ω a partir de la ec. (42).

En la Fig.11, "Ω_Iu" es un factor de corrección umbral, al cual le corresponde un radio de curvatura umbral "ρ_Iu". Para Ω_Iu ≤Ω ≤1,00, los cambios en el radio de curvatura son mínimos y no se detectan cambios en el tamaño de la grieta, es la zona "0". En la zona "I" los radios de curvatura empiezan a disminuir y la grieta empieza a crecer lentamente; en la zona "II" hay un crecimiento sostenido y regular de la grieta; en la zona "III" hay un crecimiento rápido, hasta hacerse inestable, lo que conduce a la fractura.

En la zona "II", lineal, de crecimiento estable, se tiene:

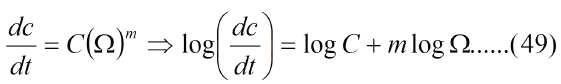
Consideremos dos instantes "t_i" y "t_j" del ensayo de fatiga, con t_i<t_j, en los cuales han transcurridos "N_i" y "N_j” ciclos a una frecuencia “ν”. En esos precisos instantes la grieta tiene los radios de curvatura ρ_i y ρ_j y sigue el curso mostrado en la Fig.10. A Partir de la ec. (42a) tenemos:

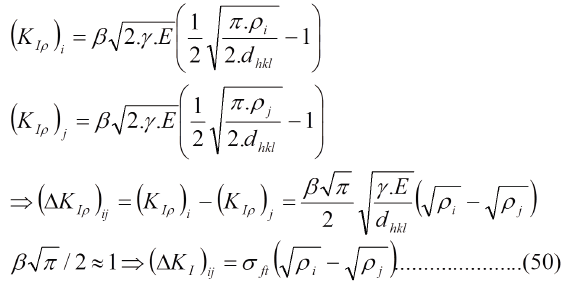
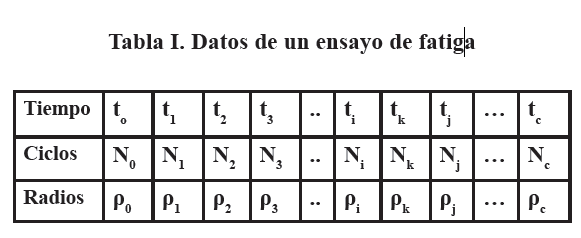
Para saber si se está en la región I, II o III consideremos un experimento de fatiga en el que se mide progresivamente el radio de curvatura y se tabulan como se muestra en la tabla I.

Para saber si una terna de puntos "ρ_i", "ρ_k", "ρ_j" forman parte de la región I, consideremos los intervalos (ρ_i, ρ_k), (ρ_k, ρ_j), de modo que debe verificarse:

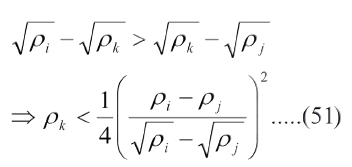
De la misma manera para que pertenezcan a la región II:

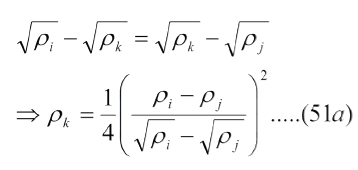
Para que pertenezcan a la región III:

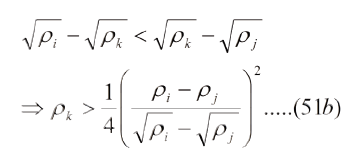
Por ejemplo, consideremos un acero estructural AISI 1020 cuyos plano de clivaje es el (100) de la ferrita, la cual tiene un parámetro de red de 0,30nm.

El intervalo de radios de curvatura es:

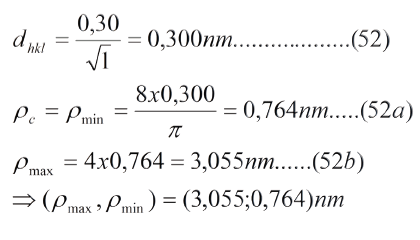
Supongamos que la grieta se inicia con un radio de curvatura umbral de 2,00nm. En base a lo expuesto, las siguientes secuencias de puntos pertenecen, de entre los muchos, a las regiones 0, I, II y III:

Región 0: 3,05; 3,00; 2,50; 2,30; 2,15nm

Región I: 2,00; 1,85; 1,80; 1,75; 1,70nm

Región II: 1,65; 1,55; 1,50; 1,35; 1,20nm

Región III: 1,10; 0,97; 0,80; 0,76 nm (radio crítico)

Como ya se ha apuntado, el espesor juega un papel importante en determinar el estado de esfuerzos y deformaciones de un sólido. En esta misma medida también tiene influencia en el factor intensidad de esfuerzo, como se muestra, esquemáticamente, en la Fig.11. Por debajo del espesor B₀ el material se encuentra bajo condición de esfuerzo plano y la tenacidad disminuye conforme disminuye el espesor; por encima de B₁ el material se encuentra bajo condición de deformación plana y la tenacidad permanece constante y corresponde al valor KIC; entre B₀ y B₁ se tiene una condición mixta. Por debajo de B₀ la fractura es por cizallamiento (dúctil); por encima de B₁ es por clivaje (frágil) y entre B₀ y B₁ es por quasiclivaje. A partir de B₀, a medida que aumenta el espesor aumentan las facetas de clivaje en la fractura y el material pierde tenacidad. Sin embargo, bajo condición de esfuerzo plano, a medida que aumenta el espesor aumenta la tenacidad, lo cual será explicado en la segunda parte del presente trabajo.

III. TECNICA EXPERIMENTAL. EJEMPLOS

El módulo de elasticidad se determina en un ensayo de tracción para lo cual se necesita unas probetas bien calibradas y bien preparadas, sin defectos superficiales, y rectificadas. Se necesita, así mismo, un extensómetro de gran precisión. La velocidad del ensayo debe ser baja.

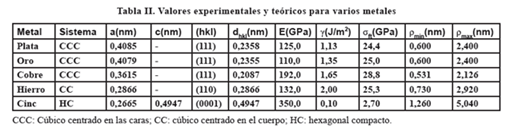
El ensayo para determinar los valores de tensión superficial en líquidos orgánicos es relativamente sencillo, pero en metales es más complejo. Un método que se usa es mediante el fenómeno de creep. Para ello se preparan muestras cilíndricas del material a ensayar de diferentes diámetros y longitud. Luego se seleccionan varias temperaturas de ensayo y se colocan las muestras en varios hornos de atmósfera controlada a temperaturas altas, cercanas al punto de fusión, bajo la acción de una carga "P" y se dejan durante varios días, midiendo el desplazamiento ΔL y calculando el esfuerzo instantáneo σ*. Por el efecto de creep las muestras tenderán a alargarse y por efecto de la tensión superficial las muestras tenderán a contraerse. Cuando ni se dilaten ni se contraigan se calcula σ σ*.ΔL =g. Luego se grafica g=f(T) y se extrapola a temperatura ambiente. Al desplazamiento “ΔL” es necesario sustraer la dilatación térmica. En la tabla II se tienen una serie de valores experimentales y los teóricos que de ellos se derivan, según el enfoque dado en este trabajo. Los valores de "d_hkl" se determinan mediante técnicas de difracción de rayos X.

Todos los datos disponibles actualmente de la MFEL están basados en el tamaño de grieta. Datos basados en el radio de curvatura, la esencia de los enfoques propuestos, no existen. Es un mundo nuevo por descubrir y experimentar. Aunque existen técnicas para replicar superficies de fractura, para su observación en microscopía electrónica de barrido (MEB), técnicas específicas para copiar una grieta y medir el radio de curvatura de la punta, con precisión, deben ser desarrolladas, pues pertenecen al campo de la nanotecnología. Una vez dominada la técnica los ensayos de mecánica de fractura resultarían más sencillos. Los trabajos de campo podrían ser más predictivos.

Los ensayos de fatiga demandarían establecer ρ=f(t), con ella dρ/dt y luego establecer dρdt=g(Ω). Esto abre nuevas líneas de investigación.

Ejemplos: 1) En ciertas ocasiones una pequeña piedra puede impactar el vidrio delantero de los automóviles. Muchas veces no ocasiona daños. Pero otras veces, lentamente, a partir del punto de impacto, surge una grieta que se propaga paulatinamente hasta cubrir todo el cristal. De no ser porque se trata de vidrios de seguridad la propagación sería instantánea. En base a lo expuesto, un núcleo de radio crítico se formó en el punto de impacto. 2) En cierta ocasión se colocó en dos pequeños jarrones de vidrio una flor en cada uno, también de vidrio, cuyo tallo terminaba en un corte elíptico. La base de los pequeños jarrones era suficientemente gruesa, para ofrecer estabilidad, en una proporción diámetro: altura=2:1. A los dos meses se formó una grieta en la base, en el punto de apoyo de la flor, y los jarrones colapsaron formando una superficie de fractura elíptica. En base a lo expuesto, el corte elíptico del extremo del tallo de la flor tenía una punta que formó, lentamente, un núcleo de radio crítico. 3) En metalurgia es frecuente tener grietas durante los cambios de fases en estado sólido, como las grietas de temple, pero hay uno en particular que se presenta en el estaño que da lugar a lo que se llama la peste del estaño. El estaño tiene dos variedades alotrópicas: por encima de 13,2°C se presenta el estaño blanco, tetragonal, conductor y dúctil; por debajo de 13,2°C se presenta el estaño gris, estructura tipo diamante, semiconductor y frágil. El paso del estaño blanco al gris se produce con una fuerte variación de densidad: de 7,30g/cm3 se pasa a 5,75g/cm3, lo cual produce una deformación volumétrica de 27% o sea 9% lineal, lo que sobrepasa el campo elástico. La máxima deformación elástica en el punto de resistencia a la tracción es de 4% y el resto, 5%, es deformación plástica. A esta deformación elástica le corresponde un esfuerzo de 1690MPa, suficientemente grande para producir fractura por clivaje, lo cual requiere de unos 400MPa. Sin embargo, la transformación pulveriza el estaño gris. En base a lo expuesto en el presente trabajo, la transformación produce infinidad de núcleos con radios de curvatura crítico que conduce a infinidad de microfracturas pulverizando el material.

IV. CONCLUSIONES

1. Usando una notación tensorial sencilla se encontró un error que por décadas ha permanecido en las ecuaciones de deformación elástica para esfuerzo plano. La ec. (20a) se escribe, en esta notación, así:

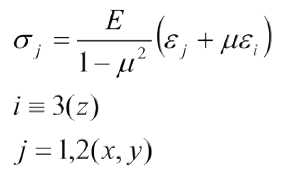
En la notación convencional (x, y, z) sería:

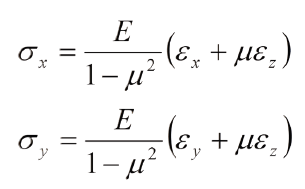
Y no como se suele escribir:

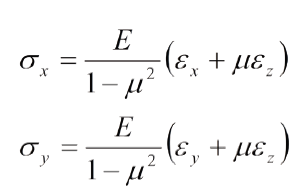
2. En una fractura por clivaje se establece una correspondencia entre el volumen del sólido de energía elástica, representado por un paralelepípedo cuyas bases son dos planos de clivaje contiguos, y el área de un plano intermedio que representa la sección de los enlaces atómicos,, equivalente a uno de clivaje, de modo que ,en el balance de energía, si "V*" es el volumen de energía, "A*" el área del plano de clivaje asociado, sección principal del sólido, y "g" la energia superficial, se tiene:

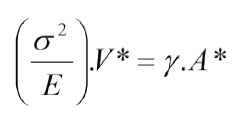
Esta ecuación es genérica y es otro de los aportes de este trabajo. Para una fractura por clivaje V*= d_hkl.A y A*=A, donde d_hkl es la distancia entre los planos de clivaje y "A" el área del plano de clivaje, igual al área de una base del paralelepípedo. si "σ_ft" es el esfuerzo de fractura teórico, se tiene:

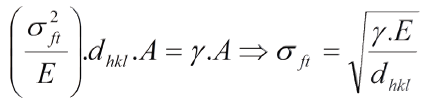
Este novedoso enfoque no necesita suponer que la curve de fuerza cohesiva de la Fig.1(a) sigue un comportamiento senoidal, como es lo usual, y hacer un proceso matemático más complicado.

3. Los valores de esfuerzo de fractura teóricos,σft, calculados en la tabla II, se consiguen solamente en filamentos libres de defectos (whiskers) y en uniones moleculares como las telarañas y los hilos de seda.

Las grietas son defectos intrínsecos que existen en el material, formadas durante el proceso de fabricación y conformación. La grieta es el resultado de la ruptura o la no existencia de enlaces atómicos y la formación de un enlace es un proceso exotérmico y termodinámicamente reversible. Cuando la grieta se forma, la energía asociada al enlace queda almacenada en el material bajo dos formas: energía de volumen y energía superficial, entre las cuales se establece una correspondencia. La energía de volumen es la energía almacenada en un cilindro cuyo diámetro es el tamaño de la grieta (dos puntas); la energía superficial es la energía asociada a la superficie del plano de la grieta, siendo éste una sección principal del cilindro de energía elástica. Para una grieta en un borde, "V*" es el volumen de un semicilindro de radio "c" y longitud L y "A*" es el área del plano de la grieta, de lados "c" y "L", de modo que:

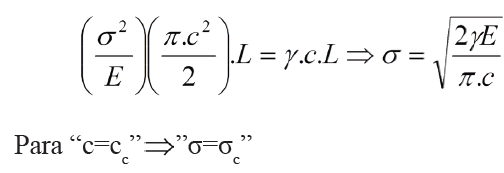
Este novedoso enfoque no necesita hacer un proceso de derivación matemática, como es lo usual, y una serie de conceptos introducidos en la década de los 50, para entender estos procesos, no hacen falta.

4. A partir del enfoque dado en 2, el esfuerzo elástico introducido también es afectado por el factor concentrador de esfuerzos en la punta de la grieta, al igual que el esfuerzo remoto, lo cual, manejado apropiadamente, conduce a un factor de corrección de la ecuación de Alan Arnold Griffith. Esta ecuación es:

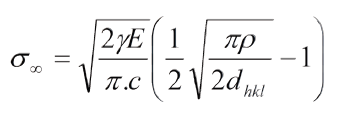
Donde σ_∞ es el esfuerzo remoto para que una grieta de tamaño "2c" (dos puntas) o "c" (una punta) y una punta de radio de curvatura “ρ” se propague. El factor de corrección, adimensional, viene dado por:

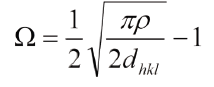
Este factor de corrección "Ω" varía entre 0 y 1, en materiales frágiles, lo que permite definir un intervalo de radios de curvaturas de la siguiente manera:

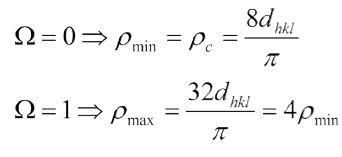
Donde "d_hkl" es distancia entre los planos de clivaje. De este modo, grietas de tamaño subcrítico producen catástrofes con esfuerzos muy pequeños.

5. Mediante el enfoque dado en el presente trabajo, se puede definir un factor intensidad de esfuerzo de la siguiente manera:

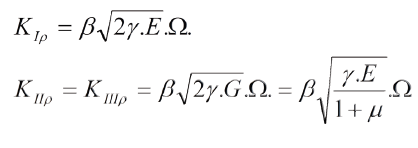
En contraste, la mecánica de fractura convencional define el factor intensidad de esfuerzo como:

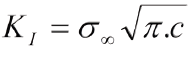
El valor crítico de K_I se determina experimentalmente y es un valor finito. Si una combinación de esfuerzo remoto y tamaño de grieta lo supera entonces se produce una falla catastrófica. Por el contrario, el valor crítico de K_Iρ está dado por las características cristalográficas del material. Cuando se alcanza este valor se tiene que K_Iρ =0 y la grieta se propaga catastróficamente sin esfuerzo.

6. Se postula que la grieta debe disminuir su radio de curvatura a medida que crece. En los intervalos (ρ_i,ρ_k), (ρ_k,ρ_j) se tiene ρ_i>ρ_k>ρ_j.

7. Con el modelo propuesto en el presente trabajo, la ecuación de fatiga, propuesta por Paris y su equipo, para la zona lineal, se puede escribir como:

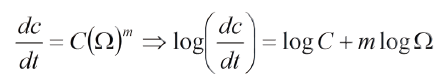
Los diferentes puntos en las tres regiones de la curva se determinan seleccionando intervalos de puntos (ρ_i,ρ_k), (ρ_k,ρ_j) del ensayo de fatiga, de modo que:

Región I:

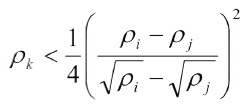
Región II:0

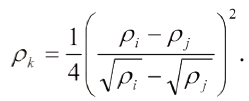
Región III:

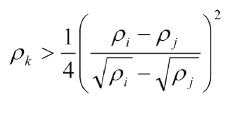
8. En un trabajo de campo se podría conocer la longitud de la grieta en cualquier momento, aun haciendo ésta recorridos complicados difíciles de medir. En un momento determinado "t_i" se mide “ρ_i" y "c_i"; con medir en otro instante “t_j” el radio de curvatura “ρ_j", la longitud "c_j" se determina por:

   

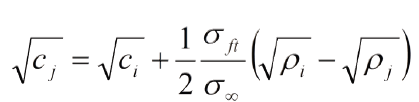
V. REFERENCIAS

1. Reed-Hill, Robert E., Physical Metallurgy Principles, D. Van Nostrand Company, Inc, USA, 1964, pp.40-57.

2. González, Leonardo, "El diámetro atómico Goldsmith y la ecuación de Pauling", Universidad, Ciencia y Tecnología V.14, N°. 54, Marzo 2010, Puerto Ordaz, Venezuela, pp. 5-18        [ Links ]

3. Dieter, George E., Mechanical Metallurgy, McGraw-Hill Book Company, International Student Edition, Japan,1961, p.39

4. Tuppeny, W.H, Kobayashi, A.S, Análisis Experimental de Tensiones, Ediciones Urmo, Bilbao, España, 1970, p. 25        [ Links ]

5. Griffith, Alan A., "The phenomena of rupture and flow in solids", Philosophy Transaction, vol. 221 A, Royal Society, London, January 1921, pp. 163-198        [ Links ]

6. Broek, David, Elementary Engineering Fracture Mechanics, Martinus Nijhoff Publishers, the Netherlands, 1986, pp. 79-81        [ Links ]

7. Balankin, Alexander, "Mecánica de Fractura: Pasado, Presente y Futuro", 5to. Congreso Nacional de Ingeniería Electromecánica y de Sistemas, Ciudad de México, noviembre 2000.         [ Links ]

8. Taplin, D.M.R, Saxena, Ashok, " ICF, The World Academy of Structural Integrity, Restrospective and Prospective", International Conference on Fracture and Strenght", Sendai, Japan, October 2010, published by Strenght, Fracture and Complexity, an International Journal, vol. 7, N°2, 2011.         [ Links ]