¿Qué constituye a los lenguajes natural y matemático?*

Wladimir Serrano Gómez

UPEL-Instituto Pedagógico de Miranda José Manuel Siso Martínez

RESUMEN

En este trabajo se discute la distinción entre lenguaje, lengua y habla matemáticos, apoyándose fundamentalmente en las ideas desarrolladas por Ferdinand de Saussure para el lenguaje natural en su Curso de lingüística general (publicado en 1916). Además, se discute una clasificación de los principios y reglas que rigen el lenguaje natural (Goodenough, 1971) con la intención de presentar una clasificación de los principios y reglas que rigen el lenguaje matemático; los cuales son agrupados en los sistemas (a) fonológico, (b) simbólico y gráfico, (c) sintáctico, (d) semántico y (e) expresivo y evocativo.

Palabras clave: lenguaje matemático - principios y reglas.

ABSTRACT

What’s made natural and mathematics languages? In this work it’s discuss the distinction between language, speech and mathematics’ language bases fundamentally in the Ferdinand de Saussure´s ideas about the natural language in his course called Course of general linguistic (published in 1916). Besides, It’s discuss a classification of the principles and rules that run the natural language. (Goodenough 1971) with the intention of presenting a principles and rules classification. Which are contained this systems: a) phonologic, b) symbolic and graphic, c) semantic and e) expressive and evocative.

Key words: mathematics’ language, principles, rules.

Recibido en noviembre 2004. Aceptado en abril 2005.

1. Introducción

La naturaleza del lenguaje matemático es entendida de formas muy diversas entre los profesores y estudiantes. Esta concepción guarda relación con el proceso de enseñanza/aprendizaje de la matemática así como con la comunicación que se lleva a cabo en el contexto del aula. La riqueza del lenguaje matemático no es, frecuentemente, utilizada con fines didácticos en las clases (en las discusiones, lo escrito en la pizarra, evaluaciones, etc.) y en los materiales escritos (libros de texto, guías de clase, compendios de problemas, etc.). En este sentido, el estudio de la naturaleza del lenguaje matemático y de los principios y reglas que lo rigen pueden aportar elementos importantes para la práctica escolar en sí, así como para el diseño de materiales escritos. El parangón entre el lenguaje matemático y el natural (o materno) permite, por una parte, ampliar la mirada y entender la naturaleza del primero, y por otra, aportar ideas sobre los principios que lo rigen. En esta tarea son fundamentales los trabajos de Saussure (1945) y de Goodeough (1971).

2. ¿Qué constituye al lenguaje natural?

El término lenguaje es bastante ambiguo. Se usa tanto para denotar la función comunicativa entre individuos, como para denotar un particular sistema de signos o símbolos o para describir el uso que se le da a este sistema en un contexto determinado. Saussure en su Curso de lingüística general (1945)¹ concibe al lenguaje (le langage) como constituido por dos entidades complementarias: lengua (la langue) y habla (la parole). Esta distinción ha dado lugar a un intenso debate en la lingüística desde la publicación del trabajo citado, considerado el punto de partida para el estudio científico del lenguaje e impuso una dicotomía en la lingüística de entonces (lingüística de la lengua y lingüística del habla)². Saussure llama habla al uso de la lengua por una persona en una situación específica, la entiende como un acto individual (Saussure, ob. cit., p. 30). En cambio, la lengua trasciende lo individual, consiste en una propiedad de la sociedad y adquiere cuerpo de “institución social” (p. 33); es decir la lengua es la totalidad de los sistemas lingüísticos que los miembros de una comunidad poseen (en su memoria). “Si pudiéramos abarcar la suma total de las imágenes verbales almacenadas en todos los individuos, llegaríamos al lazo social que constituye la lengua” (ob. cit., p. 30). En otras palabras: la lengua es un sistema de signos y el habla es la codificación de mensajes específicos, descifrados luego por quienes participan en el proceso de comunicación. En este sentido se dice que la lengua existe en un estado potencial, es un sistema de signos listo para ser utilizado en el habla, mientras que el habla existe a través de impresiones sonoras, dotadas de significado común al grupo social. Se puede pensar entonces en la lengua como un modelo lingüístico que determina el habla, y en el habla como un acto que incide también en el modelo lingüístico. Esta determinación recíproca hace variar la lengua muy lentamente, tanto que puede ser imperceptible para los hablantes (por ejemplo en la lengua materna) o llevarse a cabo durante siglos; se suceden variaciones en el vocabulario, cambios fonéticos, gramaticales, de significado, entre otros.En el habla se suceden las mismas variaciones mediadas por la interacción comunicativa, por el uso; aunque no todas ellas hacen variar la lengua (el habla en cuanto uso es susceptible de no aplicar las reglas de los sistemas lingüísticos que constituyen la “institución social”). El cuadro adjunto resume algunas de las propiedades de estas entidades tal como las concibe Saussure. Estos planos, lengua y habla, son inseparables en la práctica, en el acto comunicativo, y constituyen los dos aspectos del fenómeno lenguaje.

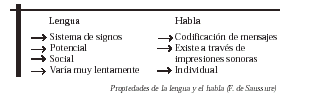
Esta distinción no es compartida por todos los lingüistas posteriores a Saussure. Algunos, como Hockett (1958), considerando el contraste y oposición que expone Saussure entre el aspecto social y el individual, entre un cuerpo de signos comunes a un grupo social y el habla como uso de ese cuerpo de signos, proponen estudiar la lengua individual: o el total de hábitos de habla de una persona específica en un tiempo dado. Así, la lengua individual de Hockett representa el sistema de signos y los usos que de él hace una persona en particular en cierto intervalo de tiempo y en un contexto dado. No obstante, lengua individual es un ente que interesa a la lingüística para estudios focales y a otras disciplinas, como la psicología, tal como lo señala Ullmann (1967). Incluso, lingüistas como Rulon Wells (En Benveniste, 1977, p. 176) critican separar esta ciencia como se hace en el curso: “si el habla es la fuente, el situs del cambio lingüístico, ¿en qué difiere la lingüística del habla de la lingüística diacrónica (de la lengua)?”. El lenguaje, y por ende el habla y la lengua (como la concibe Saussure³) constituyen un importante objeto de estudio y de reflexión por parte de profesores y alumnos; y en general de la educación matemática por cuanto ésta trata no sólo con el lenguaje matemático, sino con el natural (o materno), el corporal, gestual, entre otros. Al habla se puede acceder observando su registro y considerando, entre otros factores, el contexto; pero ¿cómo se accede a la lengua? ¿cómo definir con precisión el sistema de signos, sus reglas, su aceptación por un grupo social? Si se considera, por ejemplo, el contexto del aula de matemáticas, el problema no es menos complejo, se suscita en él una gran complejidad del sistema de signos del lenguaje matemático, variaciones en el vocabulario, diferencias de significado en símbolos, conceptos e ideas matemáticas y también en el uso dado al lenguaje matemático. Cada alumno, y el profesor, puede poseer sistemas distintos de lenguaje, en su lengua y habla matemática (como también en el lenguaje natural o materno). Sin embargo, “la lengua [...] sólo puede ser alcanzada mediante el habla; es, por consiguiente, analizando las expresiones específicas como cabe esperar identificar las unidades de que se compone la lengua” (Ullmann, 1967, p. 27). Esta tesis abre vías de indagación de fenómenos y problemas inherentes al lenguaje matemático empleado en el aula de matemáticas.

3. El lenguaje matemático escrito y la noción de lenguaje de F. de Saussure

Si consideramos al lenguaje matemático, su lengua la constituye el sistema de signos (símbolos matemáticos, gráficos, gestos, expresiones corporales, entre otros) compartidos por una comunidad (de matemáticos o una institución, como la escuela, un aula, etc.) y las reglas de uso de ese sistema; el habla matemática reúne los usos de ese sistema por un individuo en un contexto en particular. Pero, ¿qué aspectos del lenguaje “contempla” la comunicación matemática escrita?; precisamente, ¿“Contempla” el habla la manifestación escrita del lenguaje matemático? Si se entiende el habla (materializada) en dos modalidades, oral y escrita (incluyendo los gráficos), la noción de Saussure se “adapta” al lenguaje matemático escrito (o recíprocamente). Sin embargo, en esta “adaptación” las características del habla son afectadas en sus dos modalidades: oral y escrita. Si se ve a la lengua y al habla como partes inseparables del lenguaje, como las dos caras de una moneda, se espera que existan variaciones en las relaciones y naturaleza de sus características. Por ejemplo, el habla matemática no existe (o se manifiesta) exclusivamente a través de impresiones sonoras, como en el lenguaje natural, sino que aparte de ellas lo hace con impresiones de carácter gráfico y simbólico, e incluso informático (aunque muchas de estas impresiones también pueden ser verbalizadas), en correspondencia con el medio utilizado para enviar mensajes. En este sentido, el sistema de signos para el lenguaje matemático abarca signos del lenguaje natural, gráficos, visuales⁴, gestuales, etc., lo que confiere a este lenguaje una dificultad intrínseca.

El autor de estas líneas comparte la idea de que el carácter individual del habla se debe al uso del lenguaje por una persona en un contexto y no a la distinción de a quién se dirige el mensaje. Ahora, en qué sentido afecta el sistema lengua-habla matemática al carácter individual del habla matemática. La respuesta debe ser amplia y se encuentra en las características de la lengua matemática, en especial en su carácter social, en la noción general de sistemas de signos y reglas compartidos por una comunidad hablante.

4. Los principios y reglas que rigen el lenguaje natural (materno)

Goodenough (1971, pp. 159-163) clasifica las normas que rigen el comportamiento comunicativo o lingüístico en cinco sistemas: fonológico, morfológico, sintáctico, semántico y simbólico. Algunas de sus características se presentan en el cuadro siguiente.

 

Estos sistemas pueden verse como principios y reglas que rigen el lenguaje. No son “excluyentes” en el sentido de que las normas y principios que definen a un sistema poseen estrechas relaciones con las normas y principios de los demás sistemas. La idea de describir los principios y las reglas que rigen el lenguaje natural concuerda estrechamente con la definición que se dio del lenguaje en la página 28. Esto es, el lenguaje se vale de principios y reglas. Por otro lado, el lenguaje, entendido como una multitud de juegos de lenguaje en los que el uso es el medio para construir significados (página 49), permite ver que los principios, las reglas y el mismo sistema de signos son afectados por el uso y recíprocamente (bien sea modificándolos o aceptando otros). La lengua y el habla, entonces, se construyen atendiendo a los sistemas de signos, principios y reglas de una manera normativa, pero obedecen también al uso en un contexto. La clasificación de Goodenough puede facilitar el estudio del lenguaje (lengua y habla) “utilizado” en el aula. En particular, los sistemas SINTÁCTICO, SEMÁNTICO y SIMBÓLICO son de especial interés en la actividad escolar. Los principios que comprenden (en el contexto del aula) inciden en buena parte de la actividad matemática y no matemática desarrollada en el aula.

5. Los principios y reglas que rigen el lenguaje matemático

Goodenough se refiere al lenguaje natural o materno, pero considerando al lenguaje matemático ¿describen estos principios y reglas a todos sus objetos? La naturaleza de los objetos matemáticos, del habla matemática y su registro escrito implica adoptar, siguiendo la clasificación de Goodenough, nociones distintas de forma, principio sintáctico, normas de construcción de significado y la misma idea de símbolo. De esta forma cada sistema adquiere una dimensión distinta o bien por convenciones de una comunidad de hablantes de matemática (estudiantes, estudiantes y profesor, etc.) o por la naturaleza de los objetos matemáticos de que trata. Esta sección se propone distinguir algunas de estas diferencias y presentar una “adaptación” de los sistemas de Goodenough al lenguaje matemático que se aproxime a los principios y reglas que lo rigen y a la naturaleza de sus objetos. ¿Qué es fonema en el lenguaje matemático? El lenguaje matemático, en su manifestación verbal, emplea los fonemas que son propios al lenguaje natural: /e/, /cu/, /a/, /ci/, /on/, etc. ¿Cuáles son los principios y las normas para distinguir sonidos, entonación, acentos, así como para su organización? Éstas son básicamente las mismas que comprende el sistema fonológico del lenguaje natural.

 

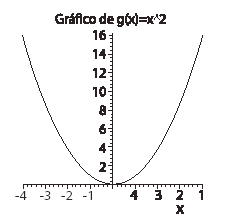
Sobre las reglas para el uso de símbolos y para la construcción de diagramas y gráficos: Estas reglas tienen que ver con el uso de una simbología adecuada y con la construcción de diagramas y gráficos⁶ (Ver los siguientes ejemplos).

Para la construcción de gráficos en el plano existen algunas reglas de uso común; por ejemplo, disponer el eje x de forma “horizontal”, representar “unidades” en cada eje, entre otras.

Sobre los principios sintácticos: éstos obedecen ya no sólo a las palabras en el lenguaje materno sino a los de los símbolos en el lenguaje matemático. Tienen que ver con el “orden correcto” y con la “validez” en las expresiones construidas.

Por ejemplo:

“(1+3).5” no puede ser escrito como sigue “(1+3).5”, “(1+3).5”, etc.

Naturalmente, los principios sintácticos guardan una estrecha relación con el significado, con el sistema semántico. Sobre los principios semánticos: éstos tienen que ver con las normas y convenciones relacionadas con el significado dado por el uso a palabras, símbolos, expresiones, gráficos o diagramas; se refieren a la relación entre los signos y los objetos a que hacen referencia. Aquí los fenómenos propios del lenguaje natural que suscitan malentendidos, como sinonimia, polisemia, homonimia, entre otros, tienen sus similares en el lenguaje matemático a través de las distintas representaciones de un mismo objeto o relación matemática o de una misma representación para denotar distintos objetos. Por ejemplo, la expresión:

“La función g (x) = x² no es inyectiva”.

Carece de sentido por el carácter ambiguo de su interpretación o la imprecisión en la definición de la función descrita. Se puede argüir por ejemplo que sig:   entonces sí es inyectiva. Pronto se advierte que existen infinitos casos en que g sí es inyectiva. El sentido se logra al definir “bien” la función g:

“La función g: R R tal que g (x) = x², no es inyectiva”.

Los malentendidos al utilizar el lenguaje matemático en el aula o incluso en producciones escritas como los libros de texto influyen en la enseñanza de las matemáticas, lo cual constituye un problema muy complejo. No sólo se construye significado a los objetos y relaciones matemáticas sino que el mismo trabajo en el aula (la actividad matemática) adquiere significados; por esta razón algunos investigadores conciben al aula como campo de interacciones simbólicas (ver por ejemplo los trabajos: Bauersfeld, 1988 y 1994). Sobre el sistema “simbólico” de Goodenough: Por otra parte, Goodenough (1971) también distingue un sistema (para el lenguaje natural) que denomina “simbólico”, el cual comprende principios que determinan usos expresivos y evocativos de las formas lingüísticas (sentimientos, emociones, etc.). En una primera mirada puede resultar difícil hacer un parangón con el lenguaje matemático. Sin embargo, si se piensa en expresiones como “esta prueba no es muy elegante”, “se puede demostrar por una vía más corta”, “tengo duda de si resolví bien el problema”, “no estoy seguro de la validez de esos argumentos”, etc. vemos que son bastante comunes en la actividad matemática de los estudiantes y profesores. Estos sentimientos y emociones con respecto al lenguaje o a la actividad matemática los abarcaremos en el sistema “expresivo y evocativo” del lenguaje matemático; no la llamaremos “simbólica”, tal como hizo Goodenough, para no generar confusiones con los símbolos y expresiones simbólicas del lenguaje matemático. El cuadro adjunto resume las características principales de cada sistema.

6. La lengua y el habla matemática

Las secciones anteriores permitieron describir el lenguaje matemático como un sistema regido por principios y reglas sobre los sonidos, símbolos, expresiones, diagramas, gráficos, significado, e incluso, sobre sentimientos y emociones con respecto al lenguaje y a la actividad matemática. En este marco, ¿cómo se manifiesta el habla matemática? ¿En qué consiste? ¿Qué la diferencia del habla materna?. La lengua matemática sirve para la codificación de mensajes matemáticos. Esta codificación se apoya en los principios y normas que rigen el lenguaje matemático. Como vimos, la lengua y el habla matemática se pueden manifestar a través de canales orales o escritos, de la representación escrita, de expresiones simbólicas, representaciones gráficas o combinaciones de éstos⁷. Así, la lengua matemática soporta al habla, tal como la langue a la parole en Saussure (en el lenguaje materno). Estas ideas permiten definir el lenguaje matemático como:constituido por la lengua y el habla matemática y se rige por los sistemas de principios y reglas (a) fonológico, (b) simbólico y gráfico, (c) sintáctico, (d) semántico y (e) expresivo y evocativo. definición que concuerda con la que se dio para el lenguaje en la página 28: el lenguaje consiste en “un sistema de signos y, de principios y reglas que lo rigen”. Estos principios y reglas, así como el sistema de signos, como se vio, son afectados por el uso, y recíprocamente (siguiendo al segundo Wittgenstein⁸). Consiste en una relación dialéctica.

7. Conclusión

En educación matemática la distinción de los principios y reglas que rigen el lenguaje matemático [organizadas en los sistemas (a) fonológico, (b) simbólico y gráfico, (c) sintáctico, (d) semántico y (e) expresivo y evocativo], la distinción entre lengua y habla matemática y, el uso del mismo lenguaje en un contexto, pueden contribuir a configurar aproximaciones teóricas sobre el uso de este lenguaje en el aula u otros contextos (libros de texto, comunidad escolar, etc.). En general, estas distinciones advierten lo complejo del sistema que conforma el lenguaje matemático en uso. Por otra parte, los profesores de matemáticas advirtiendo ello pudieran orientarse a desarrollar el sistema lengua-habla matemática (el lenguaje matemático) en los alumnos, atendiendo a los principios y reglas que lo rigen.

8. Referencias

1.- Bauersfeld, H. (1988). Interaction, construction, and knowledge: Alternative perspectives for mathematics education. En T. Coony y D. Grows (Eds.), Effective Mathematics Teaching (pp. 27-46). Reston, VA: National Council of Teachers of Mathematics / Erlbaum.         [ Links ]
2.- Bauersfeld, H. (1994). Theoretical perspectives on interaction in the mathematics
classroom. En R. Biehler; R. Scholz; R. Strässer y B. Winkelmann (Eds.). Didactics of Mathematics as a Scientific Discipline (pp. 133-146). Dordrecht, NL: Kluwer Academic Publishers.

3.- Bertín, J. (1988). La gráfica y el tratamiento gráfico de la información. Madrid: Taurus.         [ Links ]
4.- Eco, U. (1972). La estructura ausente. Barcelona: Lumen.         [ Links ]
5.- Goodenough, W. (1971). Cultura, lenguaje y sociedad. En: J. Kahn (Comp.) (1975),
El concepto de cultura: textos fundamentales (pp. 157-244). Barcelona: Anagrama.
6.- Hockett, C. (1958). A course in modern linguistics. New York: Macmillan.         [ Links ]
7.- Pimm, D. (1999). El lenguaje matemático en el aula. Madrid: Morata.         [ Links ]
8.- Saussure, F. (1945). Curso de lingüística general (20ª ed.). Buenos Aires: Losada. [Publicado originalmente en francés con el título Cours de linguistique générale,1916. Traducción de A. Alonso]         [ Links ]
9.- Ullmann, S. (1967). Semántica. Introducción a la ciencia del significado (2ª ed.). Madrid:
Aguilar. [Publicada originalmente en inglés con el título Semantics, an introduction to the science of meaning por Basil Blackwell and Mott Limited, Oxford, 1962]
10.- Wells, R. (1977). El sistema lingüístico de Ferdinand de Saussure. En: E. Benveniste,
et al., Ferdinand de Saussure. Fuentes manuscritas y estudios críticos. México:
Siglo Veintiuno Editores.
11.- Wittgenstein, L. (1963). Philosophical investigations. Oxford: Basil Blackwell.         [ Links ]
12.-Wittgenstein, L. (1998). Los cuadernos azul y marrón (3ª ed.). Madrid: Tecnos. [Traducción
de la segunda edición inglesa The Blue and brown books por Francisco Gracia, Basil Blackwell & Mott]

Notas

1 El original en francés fue publicado en 1916.

2 Antes de la publicación del curso la lingüística se ocupaba solamente del habla, no de la lengua tal como la concibe en su trabajo.

3 La caracterización que hace Saussure del lenguaje (como constituido por las entidades complementarias: lengua y habla) será la base para una distinción de ese tipo con respecto al lenguaje matemático. Idea que se desarrolla en las secciones que siguen.

4 Eco (1972, p. 217) no duda “de que se produzcan fenómenos de comunicación a nivel visual”. Sin embargo, advierte que no todos los fenómenos comunicativos pueden explicarse a través de categorías lingüísticas (ib.). Para Eco la semiótica sobrepasa el alcance de la lingüística.

5 Un comentario sobre la estructura Fonemas-Morfemas (vinculada a los sistemas FONOLÓGICO Y MORFOLÓGICO): Umberto Eco (1972) en su trabajo La estructura ausente habla del “mito de la doble articulación” (pp. 253-258). Para Eco, en la lengua materna (que llama verbal) existen elementos de primera y de segunda articulación. Los de primera articulación son los morfemas (él los denomina monemas), y los de segunda, los fonemas. Eco critica que basándose en el hecho de que en la lengua verbal existe la doble articulación, se niegue la dignidad de lengua a los sistemas de comunicación que no la poseen (más adelante se refiere a códigos cinematográficos, arquitectónico, retórico, entre otros). Este es el mito a que se refiere. La doble articulación, entonces, no es un dogma (p. 255).

6 Bertín (1988) en su trabajo La gráfica y el tratamiento gráfico de la información incluye como gráficos a los diagramas, a las redes y a los mapas. Y entiende la representación gráfica como un “sistema de signos”. Además, describe ocho variables para estudiar gráficos en el plano: x, y, tamaño, valor, grano, color, orientación y forma.

7 Por ejemplo: notas en gráficos, diagramación de textos matemáticos, etc.