Introducción
La resolución de problemas ha sido parte fundamental en la enseñanza de las matemáticas, permitiendo con ella satisfacer los requerimientos a la hora de enfrentar un suceso cotidiano. El pensamiento variacional se ha visto como una acción anexa al estudio de las matemáticas, haciendo su aparición en las etapas finales de cada proceso y dejando la resolución de problemas como la conclusión de la etapa preoperacional, sin embargo este pensamiento permite satisfacer las necesidades del individuo al momento de comprender las diferentes situaciones cotidianas que se presentan en situaciones problemas y no en operaciones concretas; evento que se refleja en resultados de evaluaciones externas como las pruebas de estado Evaluar para Avanzar en los estudiantes del grado sexto de la institución educativa José Odel Lizarazo Villamaga del municipio de Saravena - Arauca.
Para garantizar la viabilidad de esta, se define en la propuesta el diseño de guías de aprendizaje, el seguimiento a través de diarios de campos y la observación in situ, para identificar las debilidades en los procesos de enseñanza y aprendizaje en el aula, entre ellas, debilidades en la lectura de la situación y la comprensión de la misma. Siendo esta una de las limitaciones más evidentes en la investigación, junto a la trascripción y escritura de términos y conceptos matemáticos que alejan la identificación de la incógnita a resolver.
La implementación del método Pólya desde la etapa preoperacional del pensamiento matemático reconoce la lectura en sus diferentes niveles como fundamento en la apropiación de habilidades a la hora de resolver problemas, y la trascripción de dicha interpretación en interrogantes a resolver; todo ello alrededor del trabajo cooperativo y colaborativo desarrollando una interacción entre los sujetos y a través de ello la verificación de las opciones de respuesta. Llevando a los estudiantes a profundizar en la indagación, la exploración de hipótesis y el planteamiento de soluciones a las incógnitas identificadas.
En este sentido, el presente trabajo, analiza la incidencia del enfoque de resolución de problemas de George Pólya en el desarrollo del pensamiento variacional partiendo de una evaluación descriptiva del bajo desempeño en el desarrollo del pensamiento numérico - variacional como un indicador clave. El presente estudio tuvo como objetivo analizar la incidencia del enfoque de resolución de problemas matemáticos de George Pólya en el desarrollo del pensamiento variacional, visto como una de las problemáticas más recurrentes en la enseñanza de las matemáticas.
Metodología
Dando respuesta al planteamiento general de la investigación, el presente estudio se focalizó en la identificación de las dificultades de mayor relevancia en la resolución de problemas y el desarrollo del pensamiento variacional, aplicando el método de George Pólya. Este método permitió establecer su incidencia en la forma como se aborda el desarrollo de este pensamiento en la edad escolar, permitiendo describir el fenómeno in situ, que como lo nombra Bejarano (2016)), busca comprender y profundizar la problemática en su ambiente y con sus protagonistas.
La presente investigación se abordó desde un enfoque cualitativo, que permitió recolectar información a partir de diversos procesos que involucran la apreciación del fenómeno y la visión dada a este por la población focalizada para dicha acción. Como lo menciona Bejarano (2016), con la cualificación de la información se logró ahondar en las dificultades generales y particulares de los sujetos frente al desarrollo del pensamiento variacional y la resolución de problemas matemáticos.
Este proceso inductivo basado en la observación directa del fenómeno determina y describe nuevas perspectivas como fundamento teórico y recurre a la investigación acción, que según Hernández-Sampieri et al. (2014), “puede ser usado como recurso para reflexionar en torno a la ejecución de estrategias diseñadas e implementadas” (p. 8), en los estudiantes valorando la incidencia del método de George Pólya en la práctica de aula.
Estas características hicieron que la investigación no solamente abordara la descripción de un fenómeno, sino que además de ello, desde el paradigma naturalista, interpretara lo que observaba y se logró abarcar intereses o necesidades particulares y grupales frente al fenómeno u objeto de investigación, como lo fue la resolución de problemas matemáticos; de acuerdo al propósito investigativo, se direccionó la investigación en cuatro etapas fundamentales: un diagnóstico, un diseño, una implementación y se finaliza con la evaluación.
Para ello, se tomó como punto de partida los resultados de las pruebas de Evaluar para Avanzar 2022 del grado sexto de la institución, teniendo en cuenta que este grado comprende el ciclo 3 de formación escolar, donde se evidencia el paso de la básica primaria a básica secundaria.
Las categorías de análisis para la presente investigación fueron (ver Tabla 1): la competencia matemática, teniendo como centro la resolución de problemas desde el método de resolución de problemas de George Pólya y el desarrollo del pensamiento matemático, específicamente en el estudio del pensamiento variacional desde las razones de cambio y los patrones, de acuerdo con los estándares básicos de aprendizaje en matemáticas del Ministerio de Educación Nacional (2006).
Tabla 1 Categorías de Análisis.
| CATEGORÍA BASE | CATEGORÍA DE ANÁLISIS | SUBCATEGORÍAS DE ANÁLISIS |
|---|---|---|
| Competencia Matemática |
|
|
| Pensamiento Matemático | Pensamiento Variacional |
|
Nota. Categorías de análisis según los Estándares básicos de aprendizaje MEN-Colombia para la aplicación del método Pólya, elaboración propia 2023.
Para este estudio se implementaron, cuatro etapas que permitieron discriminar el fenómeno y a su vez, se convirtieron en una herramienta para generar mejoras en los aprendizajes, teniendo en cuenta las características específicas del grupo de estudiantes focalizados, como muestra la Figura 1, previa a una revisión de resultados de pruebas Saber.
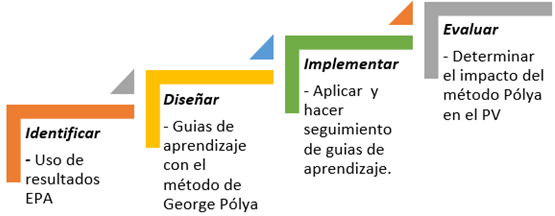
Nota. Fases de estudio para la implementación del método Pólya en el desarrollo del pensamiento variacional y la resolución de problemas, elaboración propia (2023).
Figura 1 Fases de la Investigación.
Fase 1. Identificación. Esta fase, permitió identificar las principales oportunidades de mejoramiento que se identifican en el proceso durante el desarrollo del pensamiento variacional visto desde el desarrollo de la competencia en la resolución de problemas. Para ello, se tomó como insumo los resultados obtenidos por los estudiantes focalizados durante la implementación de la prueba Evaluar para Avanzar en el primer semestre del 2022, por el Instituto Colombiano para la evaluación de la Calidad en la Educación ICFES. Esta prueba brindó al docente un panorama en el desarrollo de las competencias básicas en matemáticas en el ciclo 3 de la formación.
Fase 2. Diseño del Plan. Se trazó un plan ajustado a las características de los informantes claves, teniendo como marco el método de resolución de problemas de George Pólya, desde el diseño de una prueba diagnóstica la cual permitió determinar cuáles aspectos son relevantes para los informantes a la hora de resolver una situación problema y qué mecanismos implementan para la misma; otro instrumento dentro del plan, fue el diseño guías de aprendizaje basadas en los cuatro pasos de resolución de problemas propuestos por Pólya: conocer el problema, concebir un plan, ejecutar el plan y verificar; Como lo propone Santos-Valencia et al.(2018) en la aplicación de su caso específico que describe la resolución del problema mediante un trabajo ordenado y reflexivo para lograr el objetivo definido y que permite una comprensión más asertiva del enunciado del problema. Para finalizar se buscó establecer desde una prueba final, cómo el informante clave se apropió del método de acuerdo con el desarrollo del pensamiento variacional (ver Tabla 2).
Tabla 2 Diseño de la Propuesta.
Nota. Diseño de la propuesta d implementación del método Pólya en el desarrollo del pensamiento variacional y la resolución de problemas en los estudiantes de grado sexto de la I.E. José Odel Lizarazo-Villamaga , elaboración propia (2023).
Fase 3. Implementación del Plan. En tercer lugar, y siendo este no menos importante, se implementó el plan, que consistió en el trabajo de aula, para ello y basado en el método de acción-participación de Hernández-Sampieri et al. (2014), el docente acompañante, hizo seguimiento a cada una de las etapas anteriores, los estudiantes revisaron y desarrollaron guías de aprendizaje en la cual se vivenció los momentos claves desde el método de Pólya, conocer el problema, concebir un plan, ejecutar el plan y verificar el plan, desarrollando habilidades sociales, comprensión lectora y dinamizando la práctica educativa que para efectos de este estudio, fue la enseñanza de la matemática.
Para ello, se desarrolló trabajo en grupos de aprendizaje colaborativo, momento en el que cada estudiante aportó al cumplimiento de la meta de acuerdo a sus capacidades y habilidades y grupos de trabajo cooperativo, buscando que los estudiantes lograran explorar habilidades que les permitió desenvolverse, de tal manera que el ejercicio de la práctica de aula en matemática, fue un espacio enriquecedor tanto en lo social, como en lo competente al área en estudio y las habilidades comunicativas, ya que desde sus cualidades aportaron a la solución de la propuesta asignada para el espacio educativo. Además, de formar grupos de aprendizaje, se buscó que el estudiante fuera participativo y lograra después de un trabajo grupal construir sus propios criterios y de forma inversa, donde socializó sus propios planteamientos ante el grupo y pudo concretar en el trabajo grupos aprendizajes significativos, dado que la construcción del conocimiento es propia.
Fase 4. Evaluar. Por último, se planteó la etapa donde se evidencian los resultados de la propuesta diseñada, la cual luego de ejecutada emitió una radiografía de su implementación. Es por ello, que la evaluación del plan permitió monitorear la estrategia de forma inmediata teniendo como primer instrumento la observación de clase, en la cual el docente de forma directa y constante identificó los avances o las mejoras en la ejecución de la propuesta, haciendo un registro en el diario de campo; instrumento que permitió evidenciar los progresos de los informantes identificados previamente en el grupo focalizado, antes, durante y después de la propuesta. La evaluación, permitió tener un seguimiento más cercano del proceso, brindó herramientas para diseñar planes de mejora o fortalecer la propuesta de acuerdo con los resultados obtenidos, además de identificar la incidencia del método de Pólya como estrategia para el desarrollo del pensamiento variacional desde la resolución de problemas.
Resultados
De acuerdo a la implementación de la propuesta, el análisis de la información y la evaluación durante su estudio, este permite alcanzar resultados claros en la ejecución de cada fase y de acuerdo a las características tenidas en cuenta en cuanto a las necesidades de los informantes claves, que se tomaron de la población objeto de estudio; dicha población se encuentra la sede principal, donde acompañan 18 docentes de los cuales 2 orientan el área de matemáticas y un grupo de sexto grado con 40 estudiantes y de estos, se toma como muestra 8 estudiantes de grado sexto, como se relacionan a continuación (ver Tabla 3).
Tabla 3 Caracterización de Informantes.
| Grupo | Informante | Edad | Código |
|---|---|---|---|
| 601 | 01 | 15 años | INF01 |
| 601 | 02 | 12 años | INF02 |
| 601 | 03 | 14 años | INF03 |
| 601 | 04 | 12 años | INF04 |
| 601 | 05 | 11 años | INF05 |
| 601 | 06 | 15 años | INF06 |
| 601 | 07 | 14 años | INF07 |
| 601 | 08 | 11 años | INF08 |
Nota. Caracterización de estudiantes focalizados de grado sexto, sede principal, Institución educativa José Odel Lizarazo, Villamaga según resultados de pruebas Evaluar para Avanzar, elaboración propia 2023.
Con esta incidencia del método de George Pólya, se puede describir los resultados obtenidos durante la implementación de la prueba diagnóstica, propuesta para el desarrollo de dos ítems con situaciones aditivas, descritas a continuación así (ver Tabla 4):
Tabla 4 Resultados Informantes Prueba Diagnóstica.
| INFORMANTE | PRUEBA DIAGNÓSTICA | |
|---|---|---|
| La mamá de Sofía le pide que le haga el favor de comprar una bolsa de jabón en polvo en el supermercado y le entrega 50.000 pesos. Sofía llega al supermercado, observa los precios de algunos productos, un litro de aceite cuesta 8.000 pesos, un kilo de harina de trigo cuesta 3.000 pesos, una caja de cereal 15.000 pesos, una bolsa de jabón en polvo en 12.000 pesos y un cartón de huevos 15.000 pesos. ¿Cuánto le devuelven si solo compra el jabón en polvo? | Andrés desea festejar el cumpleaños para su mamá, cuenta con un ahorro de 50.000 pesos. Desea obsequiarle una loción que cuesta 30.000 pesos y un postre por 12.000 pesos ¿Cuánto le queda a Andrés para comprar las flores? | |
| INF01 | Reconoce los datos importantes en el planteamiento, propone una buena estrategia de solución (restar) pero, no reconoce el valor posicional de una unidad de mil. | Reconoce la estrategia de solución (resta), pero en ella no es claro la identificación del minuendo y el sustraendo, puesto que propone una sustracción de tres cifras en simultánea. |
| INF02 | Identifica los datos importantes para la solución del planteamiento, y ejecuta la operación acorde al planteamiento. Omite, la información distractora en su solución. | El informante plantea como solución una adición con los datos en los que el sujeto del planteamiento requiere disminuir a la cantidad inicial, sin embargo, el INF02, plantea la adición de estos como la solución, se puede observar que no es clara la estrategia, pues no logra comprender el problema. |
| INF03 | Identifica los datos importantes en el planteamiento, sin embargo, se observa que presenta dificultades en el manejo de la sustracción, puesto que, aunque la reconoce como solución, no demuestra habilidades en el desarrollo del algoritmo, por tanto, la solución propuesta no es acorde al planteamiento. | Identifica los datos importantes, pero no comprende el planteamiento, ya que, aunque propone una buena estrategia de solución (resta) se observa que no tiene dominio en la implementación de la sustracción. |
| INF04 | Este informante, nos muestra buenas habilidades en la solución de problemas, puesto que logra identificar los datos importantes y es clara la estrategia de solución (resta), dando una solución que es acorde al planteamiento. | la solución de problemas es clara la estrategia de solución, dando una solución que es acorde a las necesidades del planteamiento. |
| INF05 | Inicialmente, se observa que identifica los datos importantes y la estrategia de solución (resta) la ópera de forma correcta, sin embargo, en la presentación de la respuesta, los resultados en cuanto a cantidades numéricas no presentan buena escritura, puesto que omite 0s (ceros), es decir, escribe 50.00 por escribir 50.000 y escribe 38.00 por escribir 38.000. | Presenta dos propuestas de solución, sin embargo, una la encierra entre paréntesis y es tachada con tinta de lapicero, sin embargo, la propuesta de solución es acorde a lo solicitado, pero no es tenida en cuenta. Mientras que, en la segunda propuesta, el informante plantea una solución acorde a lo propuesto, sin embargo, en el momento de realizar la última operación, se identifica que no es claro el dominio del algoritmo de la sustracción. Además, podemos observar que, en la respuesta propuesta, el informante presenta nuevamente problemas en la escritura de cantidades numéricas. |
| INF06 | Se observa que identifica los datos importantes en el planteamiento, su propuesta de solución es acorde a la necesidad del planteamiento y su propuesta de solución cumple con el requerimiento del mismo. | Desarrolla la propuesta de solución en dos momentos con los datos importantes y acordes a la operación (resta), en el primer momento, obtiene el resultado esperado, sin embargo, para la implementación de la segunda operación (resta) se observa que presenta dificultades en el desarrollo del algoritmo matemático al presentar el valor, sin embargo, este no le impide presentar una conclusión en la cual ofrece un resultado, bien es escrito, acorde a la necesidad del planteamiento. |
| INF07 | En esta prueba, el informante tiene en cuenta los datos importantes, plantea como solución una resta, que es acorde al planteamiento, sin embargo, en el momento de desarrollar esta operación se evidencia que no se tiene dominio, pues las cantidades aumentan, en lugar de disminuir. Sin embargo, la conclusión propuesta presenta datos que son acordes a la necesidad del planteamiento. | Para el segundo ítem, se observa la misma situación del ítem 1, tiene en cuenta los datos importantes, identifica la estrategia, sin embargo, no tiene habilidades en la solución de estructuras aditivas. Teniendo en cuenta este patrón, se puede deducir, que el informante no posee habilidades claras en la solución de problemas matemáticos. |
| INF08 | Este informante, presenta dos propuestas que no son claras, en la primera, suma todos los datos sin tener en cuenta la funcionalidad en el planteamiento, luego en una segunda propuesta, toma los datos claves del planteamiento de forma abreviada, es decir, por escribir 50.000 escribe 50 y por escribir 12.000 escribe 12, y realiza una sustracción de forma correcta, sin embargo, en la conclusión nos presenta una solución acorde a la necesidad del planteamiento con los valores escritos de forma correcta. | Para el segundo ítem, no es claro la intensión de solución, aunque logra identificar y proponer una estrategia, no la concluye de forma óptima y por tanto su respuesta no es acorde al planteamiento. En este ítem, se puede observar que no se tuvo en cuenta los datos importantes, no reconoce el interrogante y no tiene claro el problema. |
Nota. Resultados Informantes Prueba Diagnóstica, mediante la aplicación de dos situaciones aditivas para la identificación de necesidades en la resolución de problemas, elaboración propia (2023).
De aquí, se evidenció en los estudiantes la dificultad en la comprensión de situaciones problemas, puesto que, en la práctica, el ejercicio de lectura fue agobiante para algunos informantes, tomando tiempos más extensos y repetitivos en la comprensión del planteamiento. Otro rasgo que se logró identificar fue la dificultad para la trascripción de información, en cuanto a la caligrafía y redacción, al expresar sus conclusiones ante el planteamiento. Se observó, por ejemplo, que pueden escribir un cero por un 6, o el 4 por un 1.
Otro rasgo significativo en la implementación de la prueba fue el manejo del espacio y problemas en la identificación del valor posicional un número. De esto, se dedujo, que pueden ser efectos postcovid-19, si se tiene en cuenta que, desde el grado cuarto de primaria, no tuvieron acompañamiento presencial hasta el grado sexto.
Por otra parte, en cuanto a los resultados de la propuesta, se evidenció que el dinamizar e incluir la resolución de problemas en la práctica de aula de matemáticas, fue fundamental en el desarrollo del pensamiento matemático y pensamiento lógico, además que permitió desarrollar habilidades de lecto-escritura, desde la lectura y comprensión de situaciones hasta la redacción en las conclusiones. Esto hizo que el estudiante profundizara en la lectura, enriqueciera su vocabulario con más información a la hora de redactar el texto que planteó una situación matemática y pudo desarrollar paulatinamente una conciencia lectora acorde a su etapa de formación.
Además de esto, esta propuesta permitió reconocer los siguientes aspectos en torno al método de solución de problemas de George Pólya: La competencia matemática en los estudiantes de la educación básica, jugó un papel importante puesto que esta permitió desarrollar habilidades en la solución de situaciones problemas haciendo parte fundamental en el aprendizaje y representando la estrategia de medición en las pruebas estandarizadas nacionales, llámense Saber 3° a 11°, Evaluar para Avanzar 2° a 11° del Instituto Colombiano para la Evaluación de la educación ICFES, entre otras. Ser competente en matemática, requiriendo del desarrollo de habilidades y destrezas en el uso del conocimiento matemático para dar solución a problemas que se presentan en la vida cotidiana, desde los ámbitos comunitarios, laborales y escolares. De esta manera, desarrollar habilidades en la resolución de problemas, juega un papel fundamental en el desarrollo de la competencia matemática. Dicho esta, se presentaron los resultados obtenidos a partir de la implementación del método de George Pólya en la solución de problemas.
En cuanto a la resolución de problemas, este es un propósito fundamental en la enseñanza de las matemáticas; está claro que, para dar solución a situaciones específicas e inspiradas en contextos cercanos, requirió que el estudiante indagara en sus conocimientos previos, vivencias similares o la exploración de nuevas hipótesis para dar respuesta a lo planteado en la situación. En este proceso, el estudiante se enfrentó a un sinfín de recursos propios del área, de tal modo que, de acuerdo con el progreso en sus habilidades matemáticas y a su desarrollo cognitivo, considerando las estrategias y mecanismos que permitieron dar solución al problema.
Como expresa García-Avella et al. (2017), otra forma de concebir la resolución de problemas es considerarla “como un proceso mediante el cual, una persona que se enfrenta a un problema trata de identificarlo, de delimitarlo, de explorar posibilidades de resolverlo, de elegir las estrategias adecuadas para lograrlo a partir de sus desarrollos individuales, de llevarlas a la práctica mediante la aplicación de métodos y técnicas apropiados.” (p.48). Estas técnicas, reflejaron la disposición del estudiante por encontrar la respuesta ante el planteamiento, así como a estructuras apropiadas durante su formación escolar, que con el paso del tiempo se omiten.
Desde su libro, (Polya, 1989) da pie a reflexionar en torno a las heurísticas, ¿Cuál es la incógnita?, ¿Cuáles son los datos? ¿Cuál es la condición? ¿Es la condición suficiente para determinar la incógnita? ¿Es suficiente? ¿Es redundante? ¿Contradictoria? Pues bien, tener clara la información que suministra el enunciado y entender cuál es la incógnita para solucionar, son garantía de satisfacer el planteamiento. Además, en el reconocimiento de los datos, la identificación de la incógnita podemos crear nuevos interrogantes que permitan darle una mirada más sencilla al planteamiento.
En cuanto a esto, se observa que el INF05 dio muestra del reconocimiento de la información suministrada en el planteamiento resaltando los datos que consideró importantes para la solución del planteamiento, e identificó con claridad el valor desconocido para la situación propuesta. De este informante clave, se observó que, para reconocer los datos, lo hace a través de la pregunta, la cual le permite profundizar en la información a tener en cuenta en la comprensión de problema, sin embargo, no se observa con reconoció la información numérica que representa cada interrogante.
Por otra parte, el INF04, destacó en el enunciado la información importante en el planteamiento. Si bien es cierto que usó la pregunta como estrategia para identificar la información, e intentó dar respuesta a esos interrogantes, se observó que los procedimientos precisos en cuanto al enunciado son coherentes frente al uso de algoritmos aritméticos básicos como la adición y la sustracción, reconociendo así, todos los elementos suministrados en el planteamiento tanto cualitativo como cuantitativo. En este primer paso, es importante identificar que cada problema tuvo una o más de una pregunta, por tanto, se precisó tener claridad de lo que pide el problema antes de proponer estrategias de solución, reconocer la información tanto cualitativa como cuantitativa y las condiciones dadas para la solución a la incógnita planteada conectando esta con una anteriormente vivenciada.
Por otra parte, en la segunda fase, se concibió un plan, permitiendo determinar los pasos a seguir luego de reconocer la información y datos necesarios para su solución, y hacer las preguntas como: ¿necesitas todos los datos para resolver la situación? ¿Conozco un problema similar? ¿Conozco el o los procedimientos matemáticos que se requiere para dar solución? Así mismo, el planteamiento pudo asemejarse con otro, y ser afín con resultados.
Por su parte, (Pólya, 1989) plantea: Si no puede resolver el problema propuesto, trate de resolver primero algún problema similar. ¿Podría imaginarse un problema análogo un tanto más accesible? ¿Un tanto más particular? ¿Un problema análogo? ¿Puede resolver una parte del problema? Considere sólo una parte de la condición; descarte la otra parte; ¿en qué medida la incógnita queda ahora determinada? ¿En qué forma puede variar? ¿Puede usted deducir algún elemento útil de los datos? ¿Puede pensar en algunos otros datos apropiados para determinar la incógnita? ¿Puede cambiar la incógnita? ¿Puede cambiar la incógnita o los datos, o ambos si es necesario, de tal forma que la nueva incógnita y los nuevos datos estén más cercanos entre sí? (p. 19).
En este sentido, el INF06 mostró en este segundo momento, cómo desde un nuevo planteamiento propuesto, pudo reescribir un problema con la misma información, reconocer los datos importantes en el enunciado genérico, usar de forma coherente las herramientas matemáticas que se requieren para su solución. Aquí, se observó cómo el informante con ahincó reescribe una situación problema con los mismos datos, además, destacó información, que para el caso en mención fue la cantidad de páginas que tenía un libro; de esta manera, logró distribuir la cantidad total de páginas de acuerdo con la condición propuesta en el nuevo enunciado.
Discusiones
La resolución de problemas matemáticos de George Pólya muestra una cercanía del estudiante con la situación problema, permitiendo dar solución al planteamiento propuesto mediante el uso de estrategias de resolución. Esta incidencia refleja que el ser recursivos y creativos en el uso del conocimiento matemático para elaborar una estrategia que permita encontrar el camino a la solución es importante y que se puede evidenciar usando recursos de ensayo error, diagramas, problemas similares, haciendo una lista de la información que tenemos, entre otras.
Cabe destacar que desde una revisión documental dentro del ámbito educativo en la incidencia del método de resolución de problemas de George Pólya y el desarrollo del pensamiento variacional en los estudiantes de la educación básica se conocen estudios como el de Díaz-Lozada & Díaz-Fuentes, (2018) que muestran la importancia de la resolución de problemas en el desarrollo del pensamiento matemático, en su trabajo: los Métodos de Resolución de Problemas y el Desarrollo del Pensamiento Matemático, donde refieren: “El desarrollo de la capacidad para la resolución de problemas matemáticos se potencia en la medida en que se combina con el estímulo de la capacidad para pensar en la resolución de problema. Es necesario que el estudiante desarrolle un modo de pensar que articule las dimensiones del pensamiento matemático, para ello, la instrucción heurística se puede convertir en una excelente estrategia de enseñanza” (p.11).
Esto hace que en los últimos años se haya alcanzado cierto beneplácito en el papel de la enseñanza de la Matemática en el desarrollo de la competencia en resolución de problemas, por encima de la transferencia de conocimientos matemáticos, haciendo que la enseñanza, haga un llamado a viva voz para reinventar y dinamizar la práctica de aula. Aunque numerosos autores han aportado métodos para resolver problemas, aún son escasas las propuestas concretas que ayuden a los docentes a utilizar los métodos de resolución de problemas y los recursos de la heurística para llevar a la práctica el tratamiento de la resolución de problemas con el fin de estimular el desarrollo del pensamiento matemático. Este artículo analiza la incidencia del método de resolución de problemas de George en el aprendizaje del pensamiento variacional.
En cuanto a la ejecución del plan, como parte del método de Pólya, se busca poner en marcha lo anteriormente mencionado. Estas estrategias sugieren que el estudiante ponga en práctica el plan elaborado y compruebe cada uno de los momentos diseñados para él, controlando cada paso y comprobando que sean correctos o no. Es por esto, que Pólya (1989) recalca que “reconsiderar la solución, reexaminar el resultado y el camino que los condujo a ella podría consolidar sus conocimientos y desarrollar aptitudes para resolver problemas” (p. 35). Asimismo, al dar importancia a la visión retrospectiva en cada uno de los detalles que componen la situación propuesta y la revisión de estrategia diseñada para tal solución incita a investigar en sus relaciones.
El autor Polya (1965) señala que: “la heurística moderna trata de comprender el método que conduce a la solución de problemas, en particular las operaciones mentales típicamente útiles en este proceso” (p. 102) estos métodos permiten al estudiante a incrementar el conocimiento, a generar procesos investigativos entorno al fenómeno planteado, a esquematizar las estrategias, dicho de otro modo, a definir procesos cognitivos y reflexivos útiles en la solución de problemas. Mientras que, al examinar la Solución, puede verificar el resultado y el razonamiento implementado para dar solución a la situación. Como se comenta en Barreriro et al. (2019), donde el proceso de resolución no se evidencia en un primer momento por el sujeto, teniendo en cuenta que muchas situcaciones se presentan en contextos extramatemáticos o intramatemáticos, tal como se presentan en las preubas externas a las que se enfrenta el estudiante de la zona rural, por ello, Pólya indica que este proceso es indispensable dado que posibilita la creación habilidades posteriores para resolver problemas con características similares.
Como lo cita Meneses-Espinal & Peñaloza (2017), es muy importante, si se tiene en cuenta que el estudiante tiene la posibilidad de revisar su trabajo y asegurarse de no haber cometido algún error; se puede orientar con preguntas como: ¿Es tu solución correcta? ¿Tu respuesta satisface lo establecido en el problema? ¿Puedes ver como extender tu solución a un caso general? Si al resolver los problemas los estudiantes emplean en forma consiente y cuidadosa cada uno de los anteriores pasos, aprenderán a diseñar y poner en práctica estrategias que les permitan alcanzar el éxito.
Se puede concluir, que desarrollar paulatinamente un proceso para resolver problemas, le permite al estudiante reconocer claramente la situación propuesta, identificar los datos que nos suministra el contexto de las situaciones problemas, además de inferir otros que se generan desde el uso de las heurísticas, y que no debe existir un patrón de solución único; sin embargo, algunos planteamientos pueden ser referentes de solución, debido a la similitud en sus características. Al igual que en la solución de problemas es indispensable como último paso la verificación, puesto que esta nos permite hacer una regresión de los procesos, y concluir de forma coherente ante la necesidad del planteamiento propuesto.
En cuanto el desarrollo del pensamiento Matemático y específicamente el pensamiento variacional, visto como la dupla del pensamiento numérico en la evaluación de pruebas de estado, y que, dentro del currículo matemático, juega un papel fundamental, teniendo en cuenta su transversalidad en el conocimiento matemático, porque brinda herramientas que se ajustan al estudio de conocimientos numéricos como el manejo de estructuras repetitivas.
Es claro que la transversalidad del pensamiento variacional que involucra, de acuerdo a Acosta et al. (2016), los elementos como la estrategia, los argumentos y la situcacióncon con el uso de sistemas numéricos representados en estructuras de variación y cambio se observa el cómo desde el planteamiento de una situación problema estas relaciones se hacen comunes en situaciones cotidianas, dado que existe una variable, quien es la encargada de generar el cambio o transforma los eventos involucrados en los problemas. De esta forma, el estudiante se aproxima a la noción de la función, como la de dependencia funcional entre magnitudes variables, ya que las funciones permiten analizar y modelar distintos fenómenos y procesos no sólo en problemas y situaciones del mundo de la vida cotidiana, sino también de las ciencias naturales y sociales y de las matemáticas mismas. (Ministerio de Educación Nacional de Colombia, 2006)
Como lo dice Mesa (2009) La razón de cambio involucra la variación de magnitudes que es necesario medir y comparar. Es por ello, que la gran parte de las actividades diseñadas en el aula para los estudiantes, buscan desarrollar de forma natural ecuaciones, ya que estos están asociados con el uso de un enunciado verbal traduciéndolo en una estructura matemática que busca satisfacer la solución al planteamiento. Es así, como el desarrollar situaciones problemas que estén en el marco de situaciones de cambio, contribuyen a que el estudiante desarrollo habilidades cognitivas y sea más fácil asociar situaciones similares en otros contextos.
De cara a futuros estudios en cuanto a la resolución de problemas desde el desarrollo del pensamiento variacional, se plantea la implementación en la enseñanza de la matemática, la resolución de problemas como un mecanismo para desarrollar habilidades en los estudiantes de tal modo que no se convierta en una competencia específica en el área que se plasma en un plan de área, sino que, por el contrario, sea la punta en la lanza de la práctica pedagógica. Además de ello se hace necesario desarrollar habilidades lectoras en los estudiantes en todas las áreas del conocimiento y hacer que la matemática se convierta no solo en el manejo de estructuras numéricas y simbólicas, sino que también sean parte de la comprensión, interpretación y solución de los fenómenos naturales, sociales y escolares. Para ello es necesario que se enfoque la evaluación de la matemática hacia la solución de problemas matemáticos y disminuir la solución de algoritmos.
Conclusiones
El desarrollo del pensamiento variacional en la educación básica, remarca su importancia en el abordaje inadecuado de este en el aula, ya que se desconocen las potencialidades que pueden brindar, no solamente en el referente del valor de una incógnita, que a su vez es importante en la resolución de problemas, sino también, porque es trasversal a los demás conocimientos y permite reconocer minuciosamente cada estructura numérica, las características de las formas y de los cuerpos, así como visibilizar el comportamiento de fenómenos sociales para la toma de decisiones, entre otras. Siendo este, esencial en el estudio de la matemática en un mundo que constantemente nos ofrece contextos y situaciones que varían, donde se requiere del conocimiento y de la habilidad para dar respuestas oportunas.
Este estudio, diseña una propuesta basada en el método de George Pólya, ya que es uno de los precursores en resolución de problemas y ofrece cuatro momentos para la resolución, que, para los niveles de la etapa de operaciones formales, en que se encuentran los informantes, son capaces de usar la lógica, y pueden desarrollar capacidades de formular hipótesis, sacar conclusiones y resolver problemas. Desde Pólya, comprender el plan, concebir un plan, ejecutar un plan y verificar, desarrollado desde las heurísticas, representa en los estudiantes una forma de aprender desde el descubrimiento, de lo que pueden encontrar, lo que pueden diseñar o lo que pueden ejecutar desde su conocimiento. Es aquí, como a la par, se propone desarrollar habilidades usando patrones, estableciendo la relación entre la información suministrada o creando estructuras que para el caso se convierten en estructuras algebraicas.
El estudio inicia con una prueba diagnóstica, que arroja como resultados estudiantes que desconocen los pasos mínimos para la solución de problemas, que presentan dificultades en el desarrollo de estructuras aditivas y se les dificulta establecer el orden en el valor posicional de las cantidades numéricas. Además, se observa que la falta de hábitos lectores hace que el estudiante omita información importante para la solución de un problema. Es pertinente hacer acompañamiento durante la implementación de la propuesta, ya que así se monitorea la evolución o involución de los informantes focalizados; el fomentar acciones que permitan a los estudiantes participar de forma activa y motivada por el descubrimiento o por asertividad en su intervención, desarrollando habilidades heurísticas para que se involucre en el aprendizaje.
En este sentido, el método de resolución de problemas de George Pólya, favorece el desarrollo de habilidades en solución de problemas, comprensión lectora, formulación de hipótesis, además de ser dinamizador en el aprendizaje de conocimiento matemático que no se rige por estructuras estáticas, sino que permite explorar otras formas de concebir o ver las matemáticas que en nuestros días ofrecen contextos variantes, es por ello que establecer nuevas relaciones, identificar la variable que ocasiona el cambio o definir el patrón que modela el sistema, permite generar un referente dinámico para futuras situaciones problema.















