Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Boletín Técnico
versión impresa ISSN 0376-723X
IMME v.44 n.2 Caracas jul. 2006
Evaluación rápida de la deriva máxima de piso en edificios sin muros de corte
Roberto Aguiar1, Anuar González2
1 Centro de Investigaciones Científicas. Escuela Politécnica del Ejército. Quito-Ecuador, email: raguiar@espe.edu.ec
2 Escuela de Ingeniería Civil. Universidad Técnica de Manabí. Portoviejo-Ecuador
Resumen
Se presenta una metodología para evaluar en forma rápida la deriva máxima de pisos en edificios de hormigón armado conformados por vigas y columnas, sin muros de corte, en la que cada uno de los parámetros que intervienen en el cálculo, han sido obtenidos a partir de sismos registrados en Colombia, Ecuador, Perú, Chile y Argentina. Además se ha considerado la forma como se construye en el Ecuador, la calidad del acero y el hormigón que usualmente se utiliza en las construcciones para la selección de las estructuras.
Posteriormente se obtiene la deriva máxima de piso de 72 edificios simétricos, de 1 a 6 pisos, ante la acción de 25 registros sísmicos, mediante análisis no lineal dinámico y se comparan los 1800 resultados obtenidos con los valores que se encuentran al aplicar la metodología rápida de evaluación.
Palabras claves: Deriva máxima de piso, deriva global, inelástico.
Quick evaluation of the maximum drift in buildings without shear walls
ABSTRACT
A methodology is presented to evaluate in quick form the maximum drift in buildings of reinforced concrete conformed by beams and columns, without shear walls, in which each one of the parameters that intervene in the calculation, has been obtained starting from earthquakes registered in Colombia, Ecuador, Peru, Chile and Argentina. It has also been considered the form like it is built in Ecuador, the quality of the steel and the concrete that it is usually used in the constructions for the selection of structures.
Later on the maximum drift of 72 buildings is obtained, from 1 to 6 floors, before the action of 25 seismic registrations, by means of dynamic non lineal analysis and the 1800 results obtained are compared with the values that are found when applying the quick methodology of evaluation.
Key words: Maximum derived of floor, global derive, inelastic.
Recibido: 09/01/06 Revisado: 04/05/06 Aceptado: 16/05/06
1. Introducción
En la última década del siglo pasado se dio gran importancia al desarrollo de métodos simplificados que reportan el punto de desempeño de una estructura ante una determinada acción sísmica, punto que está determinado por un desplazamiento lateral máximo o una deriva de piso máxima. Para el efecto se desarrollaron varios algoritmos para el Método del Espectro de Capacidad que fueron recomendados por el ATC-40 (1996).
Varias son las contribuciones realizadas para determinar el punto de desempeño empleando el Método del Espectro de Capacidad, entre las que se puede citar a las formuladas por Bertero (1995), Reinhorn (1997), Chopra y Goel (2002), entre otras. Lo cierto es que en todas estas metodologías se debe suministrar, a un programa de ordenador, la geometría de la estructura, el armado de los elementos y la calidad de los materiales. Información que demanda un tiempo considerable, pero es un poco menor a la que se suministra cuando se utilizan programas de análisis no lineal, paso a paso, pero la interpretación de resultados es más fácil que este último.
Con el propósito de encontrar el punto de desempeño en una forma rápida, se han propuesto ecuaciones empíricas, orientadas fundamentalmente a la evaluación de la vulnerabilidad sísmica de un conjunto de estructuras, las mismas que demandarían demasiado tiempo si se pretenden analizar con el Método del Espectro de Capacidad o peor aún con los algoritmos de análisis no lineal dinámico, paso a paso.
Una de las ecuaciones empíricas es la propuesta por Miranda (1997, 1999) y sirve para encontrar la deriva máxima de piso ![]() , empleando la siguiente ecuación.
, empleando la siguiente ecuación.
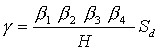 (1)
(1)
donde b1 es el valor de paso del sistema de un grado de libertad al sistema de múltiples grados de libertad; b2 es un factor de amplificación que permite determinar la distorsión máxima de entrepiso a partir de la deriva global de la estructura. La deriva global gg se define como la relación entre el desplazamiento lateral máximo en el tope del edificio dividido por la altura total del edificio; b3 es un factor que permite calcular los desplazamientos laterales máximos con comportamiento inelástico a partir de los máximos desplazamientos laterales con comportamiento elástico; b4 es un factor que sirve para determinar el cociente entre la distorsión máxima de entrepiso y la distorsión global pero calculado en una estructura con comportamiento inelástico con respecto a la misma relación pero calculada con comportamiento elástico; H es la altura total del edificio y Sd es el desplazamiento espectral elástico asociado al período efectivo Te de la estructura.
Una vez que se determina la deriva máxima de piso, ante una acción sísmica dada se puede inferir el desempeño de la misma, utilizando los valores recomendados por Ghobarah (2004) o por el comité VISION 2000 (1995). También se puede encontrar el desempeño utilizando las curvas de fragilidad propuestas por Aguiar y Bobadilla (2005) para cuatro niveles de daño denominadas: leve, moderado, extensivo y completo.
2. MODIFICACIÓN A LA ECUACIÓN PROPUESTA
Los modelos constitutivos de los materiales que han sido utilizados por la mayor parte de investigadores (Miranda 2000, Whittaker et al 1998, Nassar y Krawinkler 1991, Shimazaki y Sozen 1984, entre otros) para determinar alguno de los parámetros indicados en la ecuación (1) no han contemplado el deterioro de rigidez en la descarga, la pérdida de resistencia y el efecto de cierre de grietas (pinching). En efecto la mayor parte de ellos consideraron un modelo elasto perfectamente plástico o un modelo bilineal que contempla rigidez post fluencia.
Por este motivo es que se incorporó el parámetro b5 , que toma en cuenta la pérdida de rigidez, de resistencia y efecto pinching, quedando la ecuación (1) de la siguiente manera:
![]() (2)
(2)
La ecuación (2) es la que se utilizará para encontrar la deriva máxima de piso, bajo el título de metodología rápida y cuyos valores serán comparados con los que reporta el programa IDARC2D al realizar un análisis no lineal dinámico, paso a paso, pero antes de ello se describen a continuación los estudios realizados, en este artículo, para la determinación de cada uno de los parámetros.
3. PARÁMETRO b1
El factor b1 no es más que el factor de participación modal evaluado en el último piso, de tal manera que puede calcularse con la siguiente ecuación:
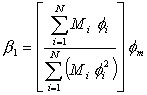 (3)
(3)
donde Mi es la masa del nivel i; fi es la ordenada de la forma modal fundamental en el nivel i; N es el número de pisos; fm es la amplitud del modo fundamental en la azotea. Pero el objetivo de la metodología rápida es evaluar cada parámetro con fórmulas simplificadas o valores propuestos por expertos es así que FEMA 356 propone los valores de b1 indicados en la tabla 1.
Tabla 1. Valores de b1 recomendados por FEMA 356
| Número de pisos | 1 | 2 | 3 | 5 | Más de 10 |
| b1 | 1.0 | 1.2 | 1.3 | 1.4 | 1.5 |
Existen fórmulas simplificadas para el cálculo de b1 como la propuesta por Algan (1982) la misma que se indica en la ecuación ( 4 ) pero fue deducida a partir de una viga de flexión de sección constante de tal manera que su aplicación tendrá mejor aproximación en edificios con muros de corte.
![]() (4)
(4)
Por otra parte, Miranda y Reyes (2002) resuelven un sistema acoplado de una viga de flexión con una viga de corte, de sección variable, en función del parámetro adimensional a0 que se indica a continuación:
 (5)
(5)
siendo GA0 la rigidez al corte y EL0 la rigidez a flexión. Para edificios con muros de corte el valor de a0 es menor a 2; para edificios con un sistema dual formado por muros de corte y vigas y columnas el valor de a0 se encuentra entre 1.5 y 6. Finalmente para edificios en base a vigas y columnas el valor de a0 está entre 5 y 20.
En la figura 1 se presentan las curvas que se obtienen a partir de los resultados de Miranda y Reyes (2002), para sección constante y para a0=2 que vendría a ser el límite superior de edificios con muros de corte; para a0=5 que es el límite inferior para el caso de edificios con vigas y columnas; para a0=10 que es un caso intermedio de edificios con vigas y columnas. En estos tres casos se ha considerado que la carga actuante es triangular. La carga lateral si influye en el valor de b1, en efecto, si la carga es uniforme distribuida se encuentran menores valores de b1. Se indica también las curvas que se obtiene con la propuesta de Algan y con la recomendada por FEMA 356.
En la figura 1, se observa que la propuesta de FEMA 356 presenta valores más altos que los obtenidos con la ecuación de Algan. Así mismo para edificios menores a 7 pisos, los valores de FEMA 356 se aproximan mejor, a los que se encuentra con Miranda y Reyes para a0=2 que son para estructuras con muros de corte. De tal manera que para edificios en base a un sistema de vigas y columnas, los valores recomendados por FEMA 356 son bastante altos. Al trabajar con los valores obtenidos para a0=5 se tendría un buen margen de seguridad para edificios en base a vigas y columnas de tal forma que se recomienda utilizar los valores indicados en la tabla 2 para esta tipología estructural.
Figura 1. Comparación de valores de b1
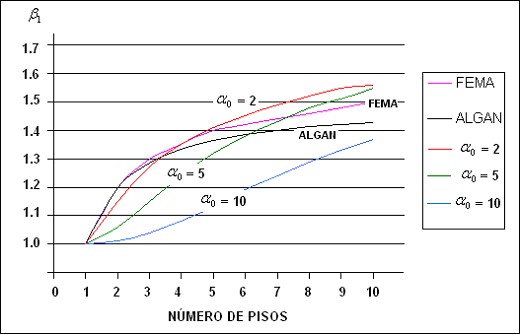
Tabla 2. Valores recomendados de b1para edificios en base a vigas y columnas
| Piso | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| b1 | 1.00 | 1.06 | 1.15 | 1.24 | 1.32 | 1.38 | 1.43 | 1.48 | 1.51 | 1.55 |
4. PARÁMETRO b2
Se analizaron 120 estructuras de hormigón armado de 1 a 10 pisos con la configuración en planta indicada en la figura 2. Las estructuras responden a una forma, como se construye en el Ecuador, cuya tendencia es no tener vigas descolgadas por este motivo el ancho de las vigas es mayor que el peralte, no son vigas banda ya que si aparece una pequeña dimensión fuera de la losa. En la tabla 3 se indican las dimensiones de las secciones transversales de columnas y vigas y la carga permanente; para todos los casos la carga transitoria fue de 200 kg/m2., y para el análisis sísmico se consideró la carga permanente más el 25% de la carga transitoria.
Figura 2. Planta tipo de edificios analizados
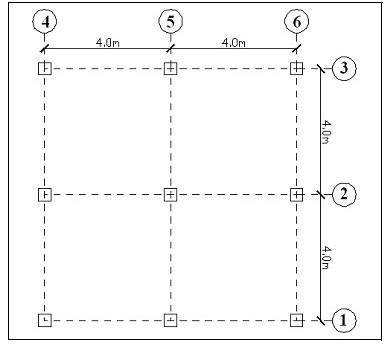
Tabla 3. Secciones y cargas de las estructuras
| NÚMERO DE PISOS | COLUMNAS | VIGAS | CARGA PERMANENTE (Kg./m2.) | ||
| Base (cm.) | Altura (cm.) | Base (cm.) | Altura (cm.) | ||
| 1 | 20 | 20 | 20 | 20 | 400 |
| 2 | 25 | 25 | 25 | 20 | 400 |
| 3 | 30 | 30 | 30 | 30 | 500 |
| 4 | 35 | 35 | 40 | 30 | 500 |
| 5 | 40 | 40 | 50 | 30 | 600 |
| 6 | 45 | 45 | 60 | 30 | 600 |
| 7 | 50 | 50 | 60 | 40 | 700 |
| 8 | 55 | 55 | 70 | 40 | 700 |
| 9 | 60 | 60 | 80 | 40 | 800 |
| 10 | 65 | 65 | 100 | 40 | 900 |
Tanto las secciones de vigas y columnas se mantienen constantes en todos los pisos así por ejemplo, para los edificios de 5 pisos las columnas son de 40cm./40cm., para todos los pisos, lo propio sucede con las vigas. La altura de los entrepisos es igual y vale 3.0 m., Bobadilla (2006).
La armadura longitudinal de las columnas varió de 1% a 2% y la armadura longitudinal de las vigas varió de 0.5% a 1.5%, los casos considerados de armado se indican en la tabla 4. Una vez seleccionado el porcentaje de armadura longitudinal de vigas y columnas se mantienen constantes estos valores en todos los vanos y pisos. El refuerzo transversal, tanto de vigas como de columnas es de 8 mm., de diámetro espaciado cada 10 cm., en los extremos del elemento y cada 20 cm., en el centro de la luz.
Tabla 4. Armadura longitudinal y transversal considerada en el estudio
| Caso | Cuantía de columna r en % | Cuantía de armadura inferior de viga r en % | Cuantía de la armadura superior de viga r en % |
| 1 | 1.0 | 0.50 | 0.75 |
| 2 | 1.0 | 0.75 | 1.00 |
| 3 | 1.0 | 1.00 | 1.25 |
| 4 | 1.0 | 1.25 | 1.50 |
| 5 | 1.5 | 0.50 | 0.75 |
| 6 | 1.5 | 0.75 | 1.00 |
| 7 | 1.5 | 1.00 | 1.25 |
| 8 | 1.5 | 1.25 | 1.50 |
| 9 | 2.0 | 0.50 | 0.75 |
| 10 | 2.0 | 0.75 | 1.00 |
| 11 | 2.0 | 1.00 | 1.25 |
| 12 | 2.0 | 1.25 | 1.50 |
Se encontró la respuesta no lineal, considerando nudos rígidos, ante la acción de 32 acelerogramas registrados en Colombia, Ecuador, Perú, Argentina y Chile, dando un total de 3840 datos con los cuales se obtuvo la relación entre la deriva máxima de piso con respecto a la deriva global, obteniéndose de esta manera el valor de b2. En la tabla 9 se indican los parámetros más importantes de 25 de los registros utilizados.
En la figura 3 se presentan los valores obtenidos de b2 para el caso 1 en que la armadura longitudinal de columnas es el 1% y la armadura de vigas es 0.5% en la parte inferior y 0.75% en la parte superior; se aprecia que los valores de b2 son superiores a la unidad y menores a 3.6. De igual forma se observa que hay más dispersión de b2 en edificios de mayor número de pisos. Los valores medios que se obtuvieron de los 3840 datos se indican en la figura 4, donde también se presenta la curva que mejor se ajusta a los puntos la misma que está definida por la siguiente ecuación:
![]() (6)
(6)
Figura 3. Valores de b2 obtenidos para el caso 1 de armadura longitudinal
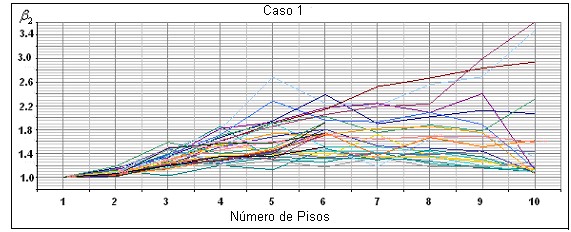
donde N es el número de pisos de la estructura. El valor de b2 tiene que ser mayor o igual a la unidad. En base a esta ecuación se halla el valor de b2 en la evaluación de la deriva máxima de piso, aplicando la metodología rápida.
Figura 4. Valores medios obtenidos y ajuste de curva para determinar b2
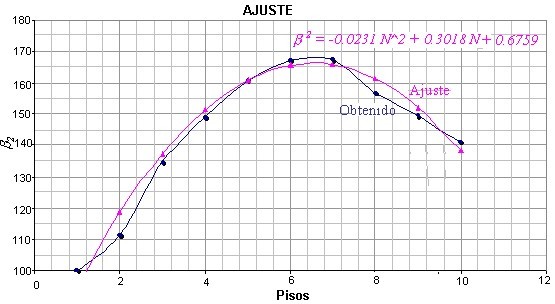
Se hace notar que el parámetro b2 se obtuvo del análisis de edificios de 1 a 10 pisos pero la comparación de la deriva máxima de piso utilizando la metodología rápida y el análisis no lineal se realizó con edificios de 1 a 6 pisos.
5. PARÁMETRO b3
El parámetro b3 relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico, en sistemas de un grado de libertad, con este recordatorio se debe manifestar que se han propuesto ecuaciones para el cálculo de b3 por parte de Miranda (2000), Nassar y Krawinkler (1991), entre otros, las mismas que fueron obtenidas en base a sismos registrados en los Estados Unidos de Norte América, razón por la cual era necesario encontrar una ecuación similar pero trabajando en base a registros sísmicos de Sur América, Guerrero (2005).
Aguiar y Guerrero (2005) en base al análisis de 63 acelerogramas registrados en Colombia, Perú, Chile y Argentina, recomiendan las siguientes ecuaciones para calcular b3, que son las que mejor se ajustan a los resultados obtenidos y que se indican en las figuras 5 y 6.
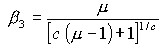 (7)
(7)
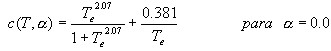 (8)
(8)
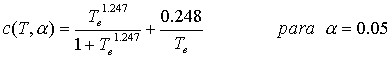 (9)
(9)
Siendo a la relación entre la rigidez post fluencia con respecto a la rigidez elástica de la curva de capacidad sísmica resistente que relaciona el cortante basal con el desplazamiento lateral máximo. Siempre se deberá considerar b3 mayor que 1.
Figura 5. Valores medios de b3 para a =0.05
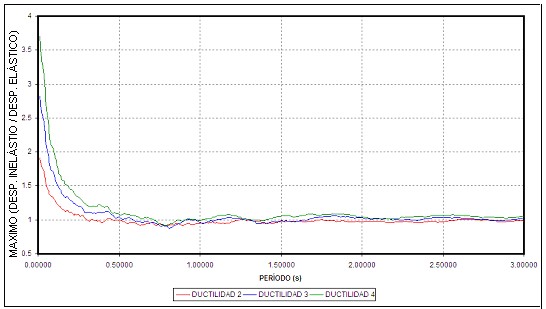
Figura 6. Valores medios de b3 para a =0.05
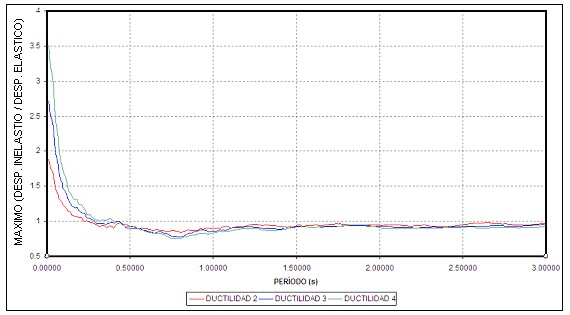
Para obtener b3 se obtuvieron los espectros de desplazamiento, elásticos e inelásticos para ductilidades de 2, 3 y 4 empleando el programa DEGTRA. Cada espectro se calculó con 300 puntos, se obtuvo espectros para a =0 y para a =0.05
El ajuste de las curvas se realizó empleando el método de Levenberg-Marquardt, utilizando para el efecto el programa Math Grapher. Este método también se empleó para la determinación de b2. A manera de ilustrar la bondad de las ecuaciones encontradas para el parámetro b3 en la figura 7 se presenta la curva de valores medios encontrada en el estudio y la curva ajustada para el caso de ductilidad igual a cuatro y el factor a =0, existiendo una buena correlación.
Figura 7. Valores medios de b3 y ajuste para ductilidad 4 y a =0
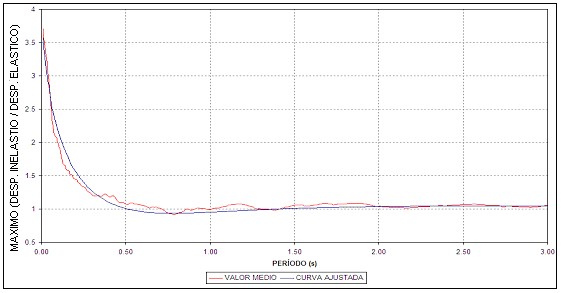
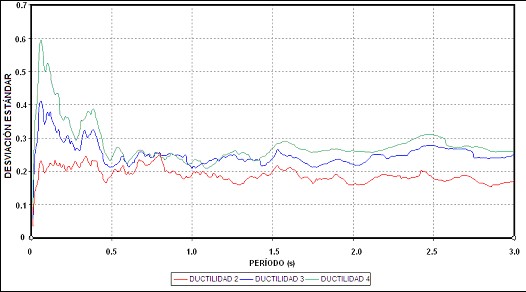
En la figura 8 se presenta la desviación estándar de los valores de b3 para a =0.05 se aprecia que para períodos cortos la desviación tiene un valor que está alrededor de 0.6 para una ductilidad de 4 y disminuye para las restantes ductilidades. Por esta razón se recomienda, al valor de b3 calculado con las ecuaciones (7) a (9), sumarle 0.5 para las construcciones de 1 piso y 0.3 para las de 2 pisos.
Figura 8. Valores de la desviación estándar de b3 para a =0
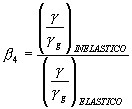
6. PARÁMETRO b4
Para el cálculo de b4 se analizaron 72 estructuras de 1 a 6 pisos, cuya configuración en planta, dimensiones y armado de sus elementos es la indicada en el apartado 4, ante la acción de 27 registros sísmicos de Colombia (9), Ecuador (1), Perú (7), Chile (8) y Argentina (2), de tal manera que se obtuvieron 1944 valores de b4 empleando la siguiente ecuación:
 (10)
(10)
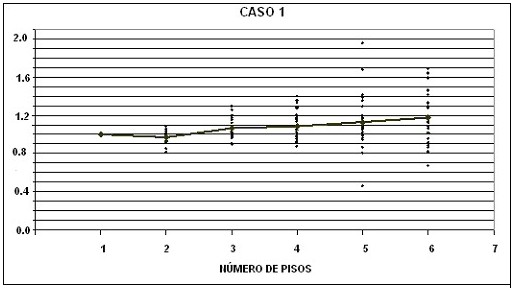
El parámetro b4 no es más que la relación del parámetro b2 calculado en el rango inelástico, con relación al parámetro b2 calculado en el rango elástico. En la figura 9 se presentan los valores obtenidos para el caso 1 de armado de las estructuras. Con línea continua se presenta la curva de valores medios para las estructuras 1 a 6 pisos.
Figura 9. Valores de b4 para las estructuras con armadura correspondiente al CASO 1
En la figura 10 se muestran las curvas de valores medios para cada una de los doce casos de armado y la curva media de todos ellos, la misma que se vuelve a enseñar en la figura 11 en la que se aprecia que la tendencia de los puntos medios es de tipo lineal, razón por la cual se ajustaron los puntos con una recta que es función del número de pisos N.
![]() (11)
(11)
Figura 10. Curvas de valores medios de b4 para cada caso de análisis
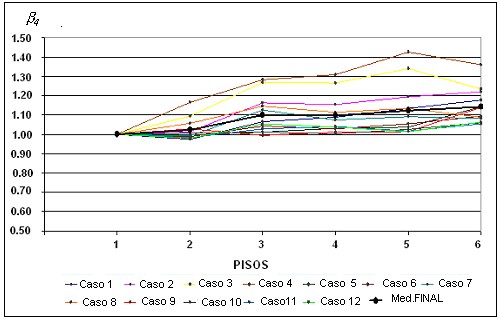
Figura 11. Ajuste de puntos obtenidos en el estudio con una recta

7. PARÁMETRO b5
Los estudios realizados para determinar los parámetros b2, b3 y b4no contemplan deterioro de rigidez en la descarga, deterioro de resistencia en un ciclo de histéresis y efecto de cierre de grietas. Estos tres factores son incluidos en el modelo numérico de cálculo de la deriva máxima de piso mediante el parámetro b5.
Lee et al (1999) analizaron la influencia de cada uno de los factores que intervienen en el modelo constitutivo, indicados en el párrafo anterior, con relación al modelo elasto perfectamente plástico, para ello utilizaron la nomenclatura indicada en la figura 12, en la que a1 es un factor que considera el incremento de rigidez en la post fluencia con respecto al modelo elasto perfectamente plástico, este factor si ha sido considerado en la determinación de los otros parámetros y se lo había denominado a por lo que no se lo incluye en la determinación de b5. El factor a2 indicado en la figura 12 considera la degradación de resistencia; el factor a3 considera el deterioro de rigidez en la descarga y el factor a4 el efecto de cierre de grietas
Figura 12. Modelos histeréticos: (a) Bilineal; (b) Degradación de Resistencia; (c) Degradación de rigidez en la descarga y (d) efecto de cierre de grietas
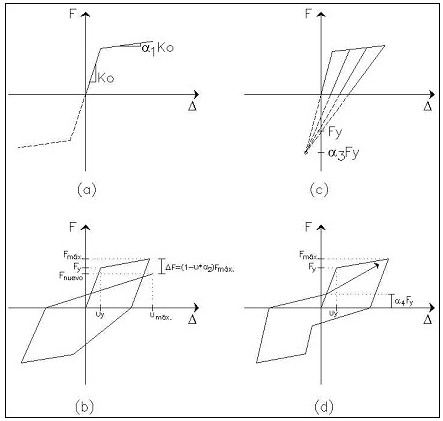
Lee et al (1999) en su estudio lo que hallaron fue en que porcentaje se incrementa o disminuye el factor de reducción de las fuerzas sísmicas Rm debido al modelo de histéresis pero al sacar la inversa se encuentra el factor de corrección con el que se obtienen los desplazamientos inelásticos.
Por efecto del deterioro de resistencia el valor de Rm disminuye con relación a los resultados que se obtienen del modelo elasto perfectamente plástico. Los valores para diferentes valores de a 2 se indican en la tabla 5. En la última columna de esta tabla se indica el valor promedio. Se aprecia que conforme se incrementa la ductilidad el valor disminuye.
Tabla 5. Efecto de la degradación de resistencia en Rm
| Ductilidad | a 2 =3% | a 2 =6% | a 2 =9% | a 2 =12% | Promedio |
| 2 | 9 | 96 | 94 | 91 | 94.75 |
| 3 | 97 | 94 | 92 | 89 | 93.00 |
| 4 | 96 | 93 | 90 | 87 | 91.50 |
| 5 | 95 | 91 | 88 | 85 | 89.75 |
| 6 | 95 | 91 | 87 | 84 | 89.25 |
En la tabla 6 se indica la variación de Rm en función de la demanda de ductilidad y del parámetro a 3. Se observa que este parámetro no cambia con la ductilidad y como era de esperarse mientras más pequeño es a 3 el factor Rm disminuye mas.
Tabla 6. Efecto de la degradación de rigidez en Rm
| Ductilidad | a 3 | a 3 | a 3 | a 3 | Promedio |
| 2 | 99 | 97 | 94 | 91 | 95.25 |
| 3 | 99 | 97 | 94 | 91 | 95.25 |
| 4 | 99 | 97 | 94 | 91 | 95.25 |
| 5 | 99 | 97 | 94 | 91 | 95.25 |
| 6 | 99 | 97 | 94 | 91 | 95.25 |
En la tabla 7 se aprecia la variación de Rm en función del parámetro a4 que cuantifica el efecto de cierre de grietas que se produce cuando un elemento ingresa al rango no lineal y empieza a deformarse en sentido contrario.
Tabla 7. Efecto del cierre de grietas en Rm
| Ductilidad | a 4 | a 4 | a 4 | a 4 | Promedi |
| 2 | 99 | 98 | 97 | 94 | 97.00 |
| 3 | 99 | 98 | 96 | 94 | 96.75 |
| 4 | 98 | 97 | 96 | 94 | 96.25 |
| 5 | 98 | 97 | 96 | 93 | 96.00 |
| 6 | 98 | 97 | 95 | 93 | 95.75 |
Al obtener la inversa del producto de los valores promedios indicados en la última columna de las tablas 5 a 7 se encuentra el parámetro a 5 y se indica en la tabla 8 para diferentes valores de ductilidad.
Tabla 8. Valores de b5 en función de la demanda de ductilidad
| Ductilidad | 1 | 2 | 3 | 4 | 5 | 6 |
| b5 | 1.00 | 1.14 | 1.17 | 1.19 | 1.22 | 1.23 |
8. PERÍODO EFECTIVO
El período efectivo Te con el cual se ingresa al espectro elástico para calcular el desplazamiento Sd, de acuerdo a FEMA 356 se evalúa con la siguiente ecuación:
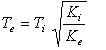 (12)
(12)
donde Ki es la rigidez inicial de la estructura que se la obtiene de la curva de capacidad sísmica resistente, que relaciona el cortante basal con el desplazamiento lateral máximo; Ke es una rigidez secante a la curva de capacidad que pasa por el punto cuya ordenada es igual a 0.6 del cortante de fluencia Vy; Ti es el período de vibración inicial de la estructura en el rango elástico. Emplear esta ecuación implica conocer la curva de capacidad sísmica resistente y para ello se debe suministrar la geometría de la estructura y la armadura longitudinal y transversal de cada uno de sus elementos, lo que demanda un tiempo apreciable que no estaría de acuerdo con la filosofía de la metodología rápida de evaluación de la deriva máxima de piso, por lo que se recomienda calcular tres valores de Te y hallar tres valores espectrales de Sd y por ende tres derivas de piso máximo con la ecuación (2) y de estas encontrar el valor medio.
Se propone el cálculo de Te con las siguientes ecuaciones, la primera es la obtenida de registros sísmicos con aceleraciones mayores al 15% de la aceleración de la gravedad en edificios de hormigón armado sin muros de corte, de tal manera que las estructuras sobrepasaron el punto de agrietamiento, la ecuación propuesta por Goel y Chopra (1997) es:
![]() (13)
(13)
Donde H es la altura total del edificio expresada en metros. La segunda ecuación que se propone para el cálculo de Te es la propuesta por el UBC-97 que se indica a continuación:
![]() (14)
(14)
De igual manera la altura total se expresa en metros. La tercera ecuación es la obtenida en México en edificios de hormigón armado sin muros de corte y está en función del número de pisos N.
![]() (15)
(15)
9. ESTRUCTURAS Y SISMOS DE ANÁLISIS
La geometría y armado de las 72 estructuras de 1 a 6 pisos que se analizaron se indicó en el apartado 4 de este artículo.
El hormigón utilizado tiene una resistencia máxima a la comprensión de 21 MPa y el acero un límite de fluencia de 420 MPa. Los acelerogramas con los cuales se obtuvo la deriva máxima de piso utilizando el programa IDARC2D, mediante análisis no lineal dinámico, se presentan en la tabla 9. Se destaca que es análisis no lineal dinámico ya que en el programa IDARC2D se puede realizar también un análisis no lineal estático para encontrar la curva de capacidad sísmica empleando la técnica del pushover.
Tabla 9. Parámetros más importantes de los sismos considerados en el estudio
| CÓDIGO | ESTACIÓN | PAÍS | FECHA | MAGNITUD | ACELERACIÓN MÁXIMA [gals] |
| 05a | CESAR VIZCARRA VARGAS | PERU | 23/06/2001 | 6.9 | -295.2 |
| 05b | CESAR VIZCARRA VARGAS | PERÚ | 23/06/2001 | 6.9 | 234.0 |
| 03b | PARQUE DE LA RESERVA | PERU | 17/10/1966 | 6.4 | -180.6 |
| 08b | ESTACIÓN SURCO | PERU | 03/10/1974 | 6.2 | -207.1 |
| 07a | PARQUE DE LA RESERVA | PERU | 03/10/1974 | 6.2 | -192.5 |
| 08a | ESTACION SURCO | PERU | 03/10/1974 | 6.2 | 192.3 |
| 09b | ESTACION ZARATE | PERU | 05/01/1974 | 6.6 | -156.2 |
| 31a | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | 518.4 |
| 31b | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | -680.1 |
| 32a | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | 554.9 |
| 32b | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | -477.8 |
| 33a | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -207.8 |
| 33b | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -141.5 |
| 35 | PEREIRA(MAZDA) RISARALDA(CMAZPA) | COLOMBIA | 19/02/1997 | 6.10 | 127.5 |
| 30a | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | 164.07 |
| 30B | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | -128.96 |
| 18a | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | 292.0 |
| 19 | COLBUN | CHILE | 09/03/1985 | 7.8 | 477.0 |
| 18b | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | -163.0 |
| 17b | VIÑA DEL MAR (UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | 356.0 |
| 17a | VIÑA DEL MAR (UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | -233.0 |
| 16b | LLOLLEO(UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | -698.0 |
| 15a | LLOLLEO | CHILE | 08/04/1985 | 7.2 | -167.0 |
| 14a | SAN FELIPE | CHILE | 09/03/1985 | 7.8 | -303.0 |
| 40 | ESMERALDAS | ECUADOR | 06/1989 | 6.1 | 210.19 |
10. ANÁLISIS NO LINEAL Y RESULTADOS
Se analizaron 1800 valores que corresponden a las 72 estructuras sometidas a los 25 registros indicados en la tabla 9. El análisis se realizó de dos maneras, la primera utilizando el programa IDARC2D y la segunda empleando la ecuación (2). Para el primer caso se encontró la respuesta no lineal, paso a paso, de un pórtico central del edificio, interesaba ver únicamente la distorsión máxima de piso y la demanda de ductilidad la misma que en la mayoría de los casos fue superior a 4. Posteriormente se evaluó la deriva máxima de piso por medio de la ecuación (2) empleando los parámetros b1 a b5 que han sido indicados en este artículo. Se destaca que en la metodología rápida se obtuvieron primero los espectros de desplazamiento elástico de cada uno de los sismos y los desplazamientos espectrales, Sd se hallaron para los tres períodos indicados en las ecuaciones (13) a (15) luego se obtuvo la deriva de piso máxima aplicando la ecuación (2) y finalmente se halló un promedio de estos valores.
Se denomina gID a la deriva máxima de piso obtenida con el programa IDARC2D y g a la deriva máxima de piso encontrada con la ecuación (2). Para poder visualizar los resultados en una sola figura se define la relación gID / g. Si esta relación tiende a 1 significa que la aproximación de la deriva máxima de piso que se encuentra en forma rápida con la ecuación (2) reporta muy buenos resultados. En la figura 13 se presenta esta relación para los 1800 puntos.
Figura 13. Relación gID / g encontrada en el estudio
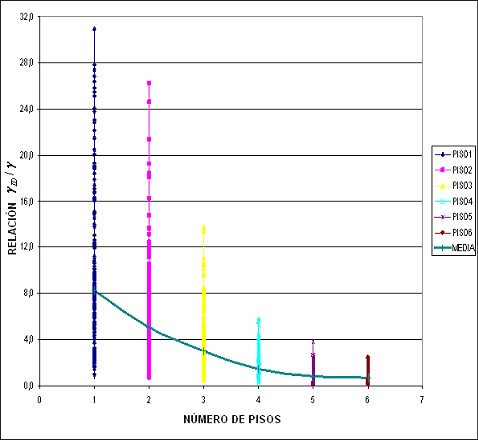
La línea continua de la figura 13, que une a todos los pisos, corresponde al valor medio encontrado con los valores de cada piso, se aprecia que una gran cantidad de puntos se encuentra bajo la línea de valores medios, el promedio sube por que existen valores que presentan una muy alta relación gID / g.
El valor medio para los edificios de 4, 5 y 6 pisos es prácticamente la unidad lo que significa que la evaluación de la deriva máxima de piso, con los parámetros propuestos en este estudio, para la metodología rápida es muy buena; para los edificios de 3 pisos el valor medio está alrededor de 3. que se considera aceptable. En cambio para las estructuras de 1 y 2 pisos la diferencia entre la deriva máxima que reporta el programa IDARC2D con la deriva máxima que se obtiene con la metodología rápida es considerable. Esto se debe a que las estructuras de 1 y 2 pisos tienen un período bastante bajo y los valores espectrales Sd asociados son bajos para los casos en que la relación gID / g es alta.
En la tabla 10 se indican los valores medios encontrados para las estructuras analizadas y que corresponde a la línea continua que une los diferentes pisos en la figura 12.
Tabla 10. Valores medios de gID / g
| Número de pisos | Valor medio |
| 1 | 8.22 |
| 2 | 5.03 |
| 3 | 2.96 |
| 4 | 1.41 |
| 5 | 0.81 |
| 6 | 0.67 |
11. CONCLUSIONES
En base a sismos registrados en Colombia, Ecuador, Perú, Chile y Argentina y tomando en cuenta la forma como se construye los edificios de hormigón armado en el Ecuador se han determinado varios parámetros que intervienen en la evaluación de la deriva máxima de piso mediante una sola ecuación, que se ha denominado metodología rápida. Posteriormente se analizaron 1800 resultados de las derivas máximas de piso que se obtuvieron al utilizar un programa de análisis no lineal dinámico, como es el IDARC2D y se compararon los resultados con los que se encuentran con la ecuación que contempla cinco parámetros y de los valores medios se desprenden las siguientes conclusiones:
-
Para los edificios de 4, 5 y 6 pisos los valores obtenidos con la metodología rápida, reporta resultados muy satisfactorios a los que se obtienen del análisis no lineal dinámico. El valor medio de los casos analizados establece que la deriva máxima de piso encontrada con la metodología rápida es prácticamente la misma que la reportada por el programa IDARC2D.
-
Para los edificios de 3 pisos se considera satisfactorio los resultados obtenidos con la metodología rápida ya que el valor medio está alrededor de tres.
-
Para las estructuras de 1 y 2 pisos la metodología rápida reporta valores bastante bajos en comparación con los que se hallan en el análisis no lineal dinámico.
12. AGRADECIMIENTOS
A los directivos de la Escuela Politécnica del Ejército por haber financiado el Proyecto de Investigación: Evaluación rápida de la deriva máxima de piso en edificios de hormigón armado.
13. REFERENCIAS
1. Aguiar R., y Bobadilla C., (2005), Curvas de fragilidad para estructuras de H/A de Ecuador menores a siete pisos, Revista CIENCIA. Escuela Politécnica del Ejército, 8 (2), 81-88, Quito, Ecuador. [ Links ]
2. Aguiar R., y Guerrero P., (2005), Relación entre desplazamiento máximo: inelástico a elástico en la evaluación del drift, Presentado a la Revista de la Sociedad Mexicana de Ingeniería Sísmica, 12 p, México. [ Links ]
3. Algan B., (1982), Drift and damage considerations in earthquake resistan design of reinforced concrete buildings, Ph.D thesis, University of Illinois, Urbana. Illinois. [ Links ]
4. American Society of Civil Engineers, (2000), Pre-standard and commentary for the seismic rehabilitation of buildings, FEMA 356, Federal Emergency Management Agency Washington, D.C. [ Links ]
5. ATC-40, (1996) Seismic evaluation and retrofit of concrete buildings, Applied Technology Council, Redwood City, California. [ Links ]
6. Bobadilla C., (2006) Curvas de Fragilidad y evaluación rápida de la vulnerabilidad sísmica de estructuras, Tesis de Grado. Escuela Politécnica del Ejército, Quito. [ Links ]
7. Bertero V., (1995), Tri-service manual methods in VISION 2000, Part 2, Appendix J, Structural Engineers Association of California, Sacramento. [ Links ]
8. Chopra A., Goel K., (2002), A modal pushover analysis procedure for estimating seismic demands for buildings, Earthquake Engineering and Structural Dynamics, Vol 31, 561-582. [ Links ]
9. FEMA (1997), NEHRP provisions for the seismic rehabilitation of buildings, Federal Emergency Management Agency. Rep. FEMA 273 (Guidelines) and 274 (Comentary), Washington, D.C. [ Links ]
10. Ghobarah A. (2004), On drift limits associated with different damage levels, International workshop on performance based seismic design. Department of Civil Engineering, Mc. Master University, June 28- July 1, 2004. [ Links ]
11. Goel R., and Chopra A., (1997), Period formulas for moment-resisting frame buildings, Journal of Structural Engineering, 123 (11), 1454-1461. [ Links ]
12. Guerrero P., (2005), Determinación rápida de la deriva de piso. Análisis de la relación entre el desplazamiento inelástico máximo esperado con el desplazamiento calculado para la respuesta elástica lineal en sistemas de 1 gdl, Tesis de Grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, Quito. [ Links ]
13. Lee L., Hang S., and Oh Y., (1999), Determination of ductility factor considering different hysteretic models, Earthquake Engineering and Structural Dynamics, 28, 957-977. [ Links ]
14. Math Grapher (2006), Internet: www.mathgrapher.com/Download/Trial [ Links ]
15. Miranda E., (1997), Estimation of maximum interstory drift demands in displacement-based design Seismic design methodologies for the next generation of codes, Krawinkler H., and Fajfar P., editor, Balkema. [ Links ]
16. Miranda E., (1999), Approximate seismic lateral deformation demands in multistory buildings, Journal of Structural Engineering, 125 (4), 417-425. [ Links ]
17. Miranda E., (2000), Inelastic displacement ratios for structures on firm sites, Journal of Structural Engineering, 126 (10), 1150-1159. [ Links ]
18. Miranda E., Reyes C., (2002), Aproximate lateral drift demands in multistory buildings with nonuniform stiffness, Journal of Structural Engineering, 128 (7), 840-849. [ Links ]
19. Nassar A., and Krawinkler H., (1991), Seismic demands for SDOF and MDOF systems, John Blume Earthquake Engineering. Ctr. Dept. of Civil Engineering, Rep. 95, Stanford University, Stanford, California. [ Links ]
20. Ordaz M., Montoya C., (2001), DEGTRA A4, Instituto de Ingeniería. Universidad Nacional Autónoma de México, México. [ Links ]
21. Reinhorn A., (1997), Inelastic analysis techniques in seismic evaluations, in P. Fajfar and K. Krawinkler (eds), Seismic design methodologies for the next generation of codes, 277-287, Balkema Rotterdam. [ Links ]
22. SEAOC (1995), Vision 2000 Report on performance based seismic engineering of buildings, Structural Engineers Association of California, Volume I, Sacramento. [ Links ]
23. Shimazaki K., and Sozen M., (1984), Seismic drift of reinforced concrete structures Res. Rep., Hazama-Gumi Ltd., Tokyo, Japan (in Japanese); and draft report (in English). [ Links ]
24. UBC (1997), Uniform Building Code, International Conference of Building Officials, ICBO, 3 Vol, Whittier, CA, USA. [ Links ]
25. Valles R., Reinhorn A., Kunnath S., Li C., and Madan A., (1996), IDARC2D Version 4.0: A computer program for the inelastic damage analysis of buildings, National Center for Earthquake Engineering Research. Headquartered at the State University of New York at Buffalo, Technical Report NCEER-96-0010, 189 p. New York. [ Links ]
26. Whittaker A., Constantinou M., and Tsopelas P., (1998), Displacement estimates for Performance-Based Seismic Design, Journal of Structural Engineering, 124 (8), 905-912. [ Links ]













