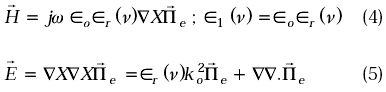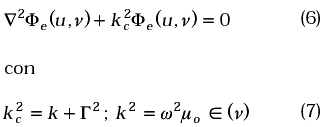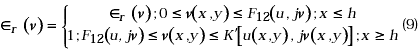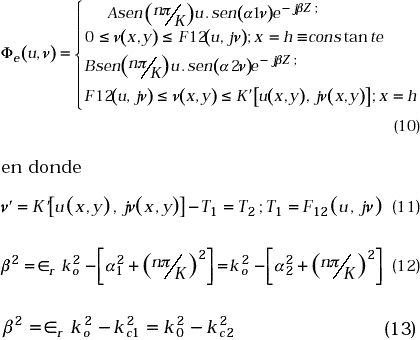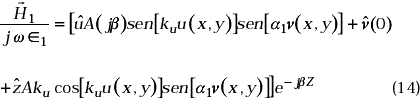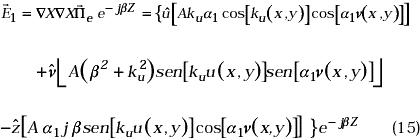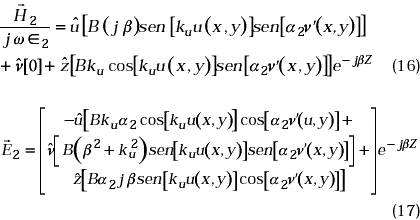A dispersion model of an open microstrip-line using the LSM propagation mode

Augusto Galo Durango

Departamento de Física, Facultad experimental de Ciencias, Universidad del Zulia. Maracaibo 4003, Venezuela

Abstract

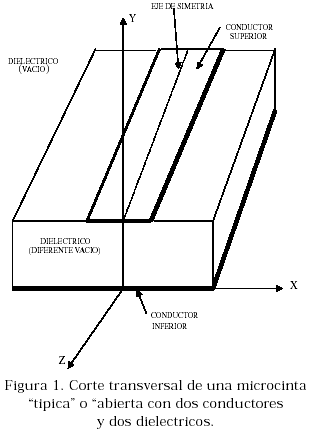
The study of one of the propagation modes, in the range of the microwave frequencies, of a transmission line conformed by two conductor planes, which is well known in the pertinent literature as an open or a “microstrip-line” is shown in this work. Open in the sense of that one of the conductors is exposed to the vacuum. That is, this device is basically conformed, if we have in account the thin film technology, of two conductive parallel planes and two dielectrics ones and this has been developed of the classical transmission line for low frequencies. The upper conductor plane has finite transversal dimensions with respect to the lower one. In the field of the Complex Variable Theory it is possible to study the LSM propagation mode in a P transformed plane, which was obtained from the physical plane (Z semiplane) of the microstrip-line through two consecutive Schwarz-Christoffel transformations. It is also possible to find the phase constant Г, the Electric and Magnetic fields and finally the equations for the LSM mode. Once this information is obtained, graphics will be made for the effective dielectric constant of the means as a function of the angular frequency and the W/h profile relation of the device. Finally, comparisons will be made with the results offered by others authors.

Key words: Dispersion Microstrip Mode LSM.

Modelo de dispersión de una microcinta abierta utilizando el modo de propagación LSM

Resumen

Se presenta en este trabajo el estudio de uno de los modos de propagación, en el rango de frecuencias de microondas, de una línea de transmisión de dos conductores planos conocida en la literatura pertinente como microcinta abierta o “microstrip-line”. Abierta en el sentido en que uno de los dos conductores está expuesto al vacío. Así, este dispositivo está conformado, teniendo en cuenta la tecnología de películas delgadas o “thin films”, de dos planos conductores paralelos y de dos dieléctricos y el cual ha evolucionado de la línea de transmisión clásica para frecuencias bajas. El conductor superior es de dimensiones mucho menores con respecto al conductor inferior. En el campo de la Teoría de Variable Compleja es posible estudiar el modo de propagación LSM en un plano transformado P, el cual se obtuvo del plano físico (semiplano Z) de la microcinta mediante dos transformaciones sucesivas Schwarz-Christoffel. También es posible encontrar en el mismo la constante de fase Г, los campos Eléctrico y Magnético, y, finalmente, las ecuaciones para el modo LSM. Una vez que se obtenga dicha información se realizarán gráficos para la constante dieléctrica efectiva Î_eff (w), de la Impedancia Zc, de la constante dieléctrica de los medios y de la relación de perfil w/h del dispositivo. Finalmente, se efectuarán comparaciones con los resultados presentados por otros autores.

Palabras clave: Dispersión Microcinta Modo LSM.

Recibido el 03 de Marzo de 2004

En forma revisada el 11 de Octubre de 2004

Introducción

En el plano físico Z de una microcinta típica o “abierta”, Figura 1, es imposible obtener en forma analítica los parámetros eléctricos, tales como Zc y Cc (impedancia y capacitancia características). Las soluciones no analíticas se deben principalmente por la no homogeneidad o discontinuidad en las condiciones de frontera del conductor tope y la interfaz dieléctrica. Debido a lo anterior no es posible conocer la solución para los campos Eléctrico y Magnético, los modos de propagación, la constante de fase, la energía de transmisión y la pérdida de potencia en conductores y dieléctricos en el mismo plano físico, a no ser por métodos aproximados y/o computacionales de relajación matricial , los cuales ofrecen, obviamente, a su vez soluciones de muy poca información analítica para procedimientos posteriores en sistemas más complejos o son de difícil solución y de alto consumo de tiempo en computadora. Así, por ejemplo, cuando es necesario estudiar arreglos de microcintas para el caso de la Antena Planar con Microcintas en Fase (Phased Array Antennas) o en un circuito MMIC (Monolithic Microwave Integrated Circuit) se presentan dificultades en encontrar los modos de propagación y, por ende, los campos EM (Electromagnéticos). En otras palabras, el desconocimiento no analítico de los campos EM provoca incertidumbre en el conocimiento de los campos reactivos (campos muy cercanos) que existen en tales sistemas y éstos, a su vez, impiden el acople óptimo entre la señal de entrada y la de salida o la transmisión/recepción de la señal EM en la antena. Hasta el presente, no se han podido desarrollar los sistemas con microcintas, a pesar de las expectativas existentes, para su utilización en la tecnología moderna de enlaces satelitales y terrestres a las longitudes de ondas milimétricas y submilimétricas. Otra de las principales dificultades al estudiar la microcinta es el comportamiento dispersivo de la constante de fase debido a la presencia de una interfaz dieléctrica la cual, a su vez, causa que existan modos híbridos que se propagan en dicho dispositivo, adicionales a los existentes debido a las pérdidas en los conductores. Teniendo en cuenta todo lo anterior, es necesario realizar un modelo matemático que solucione tales dificultades, en especial, que enfoque la solución del problema desde un punto de vista de resultados y ecuaciones analíticas. Parte de estas soluciones serán presentadas en el presente trabajo.

Realizando un breve recuento, entre los modelos computacionales de las tres últimas décadas muchos de ellos analizan el comportamiento dispersivo de la microcinta abierta y el análisis de los modos híbridos que en ella se propagan utilizando el Método de Momentos. Así, Denlinger [8] plantea el problema de condiciones de frontera asociado con la microcinta abierta en términos de una representación de modos empleando el método de Galerkin en el dominio espectral, el cual es una extensión del mencionado método de momentos. Este autor asume dos componentes de corrientes bases para el cálculo de las amplitudes de las distribuciones de corrientes en el dispositivo, pero las soluciones así obtenidas son altamente dependientes de las funciones bases que fueron asumidas. Itoh and Mitra [9] realizan una mejora en el modelo propuesto por Denlinger evitando las dificultades de éste y resuelven hasta el grado de exactitud deseado obteniendo con ello mejores resultados.

En forma alterna a lo antes expuesto, en el pasado hemos empleado las transformaciones conformes, en la teoría de Variable Compleja, como modelo matemático base para hallar la solución al campo EM para diferentes tipos de microcintas con uno y dos dieléctricos. Para el caso de un solo dieléctrico, ha sido posible encontrar los parámetros Zc y Cc del dispositivo, así como también el campo EM y el modo de propagación, todo ello en el plano de transformación P, Figura 2. Para el caso de dos dieléctricos, hemos realizado un ajuste de las ecuaciones presentadas en [12, 13] para obtener soluciones analíticas muy “aproximadas”, exactas para caso estático, y hemos tomado ventaja de las precisiones obtenidas en estos trabajos.

Con lo anterior enfocamos aquí, por primera vez, la búsqueda de uno de los dos modos de propagación: el modo LSM (Longitudinal Section Magnetic) o modo que no posee componente normal del campo Magnético en la dirección normal a la interfaz dieléctrica o, igualmente, el modo TM (Transverso Magnético) en dicha dirección. Este modo debería propagarse en forma híbrida con el modo LSE (Longitudinal Section Electric) o modo TE (Transverso Eléctrico) en la misma dirección.

Ventajas de este modelo

a) Se tiene en cuenta desde el comienzo el “efecto pestaña” o solución temprana del “efecto del campo EM en los bordes” del conductor superior.

b) Se obtiene una solución del tipo analítica, aunque las funciones involucradas son de difícil manejo.

c) Se efectúa el cálculo de los modos, campos y de las energías en términos de “funciones propias” o funciones potenciales en coordenadas Cartesianas en el plano de transformación P.

d) Las ecuaciones son más simples para el estudio futuro de acoples con otras microcintas de alimentación mediante otras guías o coaxiales.

Una vez que se planteen las ecuaciones generatrices o potenciales, en el plano de transformación P, es posible encontrar:

1. Los modos híbridos de propagación.

2. Los campos EM.

3. La constante de fase, Г = α + jβ, y su dependencia con la frecuencia de transmisión, w = 2πƒ, y con la constante dieléctrica relativa Î_r.

4) La dependencia de la misma constante dieléctrica relativa con la frecuencia o constante dieléctrica (relativa) efectiva Î_ff .

Metodología y Procedimiento

Modelo Matemático

Proponemos el modo LSM (Longitudinal Section Magnetic) como uno de los modos que pueden transmitirse en una microcinta con dos dieléctrico. En el modelo del modo LSM utilizamos la notación equivalente de onda o modo Ē_ν (u,ν), en el plano transformado P de la Figura 2, o modo con componente normal del campo Eléctrico a la interfaz dieléctrica o modo derivado del Potencial Hertziano Eléctrico. Empleando dicha figura podemos escribir para esta función

son la constante de fase compleja y las variables o coordenadas complejas en el plano de transformación P. La parte real de Г corresponde a la atenuación en dieléctricos y conductores, esto es,

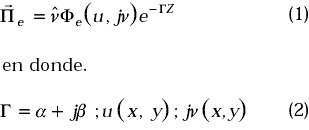
  α = α_d + α_c                                       (3)

La parte imaginaria corresponde a la parte oscilante de la energía. En un principio asumimos un sistema sin pérdidas, esto es, σ→ ¥. Los campos magnético y eléctrico pueden escribirse en términos del potencial Hertziano como:

y la ecuación de onda para la función potencial escalar es de la forma:

Para el caso de ondas no atenuadas, viajando en la dirección positiva de las z, la “profundidad de borde” en la superficie de los conductores tiende a cero para conductividad tendiendo a infinito y si no existen fuerzas de amortiguamiento

α→ 0; Î(ν) =  Î_R (ν) - j Î_I (ν) = Î_R (ν)    (8)

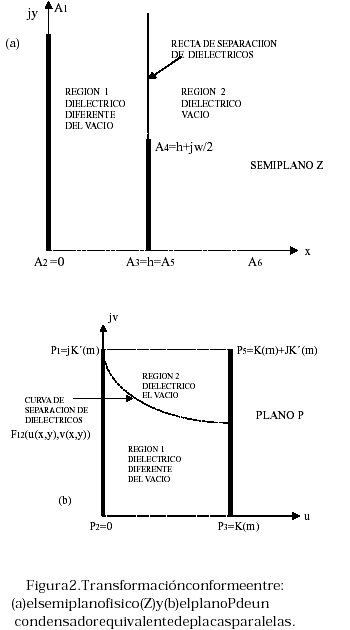
Definimos los números de ondas característicos para las regiones 1 y 2 de la Figura 2, respectivamente, como k_c1 y k_c2. Teniendo en cuenta lo anterior, el tipo de soluciones para la función potencial escalar en ambas regiones son del tipo de funciones armónicas, esto es, sen(k_uu(x,y))sen(k_uu(x,y)) y sen(α_1,2ν(x,y)). En donde, k_u indica el número de onda en la variable u y α_1,2(ν(x,y)) indica el número de onda en la variable n, para las dos regiones 1 y 2. Las soluciones a la ecuación (6) deberán, por supuesto, cumplir la ecuación para el caso estático o ecuación de Laplace. Cuando asumimos que

En la ecuación (9) observamos que la constante dieléctrica relativa estática toma los valores: Î_r(ν(x,y)) y 1 por debajo y por encima de la curva F₁₂(u,jν) respectivamente, dada en términos de funciones elípticas sn(u, jv), cn(u, jv) y dn(u, jv) [12]. Dicha curva separa los dos dieléctricos en el plano transformado P, Figura 2, pero la misma corresponde a una recta o frontera constante en el plano físico Z de la microcinta, x = h en la Figura 1. Igualmente K[u(x,y),jv(u,y)] y K´[u(x,y),jv(u,y)] son las integrales elípticas de la primera clase complementaria, las cuales corresponden a la frontera del polígono cerrado en el plano P, en cambio x = 0, x = ¥; y = 0, y = ¥ corresponden a las fronteras del polígono abierto en el plano Z. Lo anterior significa que si bien podemos escribir funciones potenciales en el plano P dentro de un entorno cerrado, propio para “auto funciones” y “auto valores”, la interfaz entre dieléctricos debe ser tomada del plano Z en donde corresponde a una recata, x = h, a través de las ecuaciones de transformación correspondientes [12]. Entonces, para las funciones generatrices o funciones potenciales escalares podemos escribir

Teniendo en cuenta las ecuaciones (4) y (10) en la región 1, del plano P,

Así mismo, el campo Eléctrico, se puede encontrar de la ecuación (5) como:

Igualmente, para la región (2), encontramos para el campo Magnético y Eléctrico,

Finalmente, las condiciones de continuidad de las componentes tangenciales del campo EM en la interfaz de los dos dieléctricos, en el plano de transformación P, recta x = h ≡ constante, permiten conocer la ecuación característica para el modo LSM.

Î₁ (ν)α₂ tan[α₁F₁₂(u,jν)] = -Î₀ α₁ tan[α₂ν′]            (18)

Procedimiento Numérico

Este consiste, principalmente en encontrar las constantes de fase o números de ondas en la variable v, esto es, α₁ y α₂. Así mismo, es de gran interés, para efectos de comparación con otros autores [2, 8, 9], encontrar la constante dieléctrica relativa (efectiva) como una función de la frecuencia.

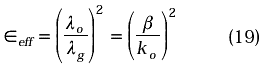
en donde λ_g es la longitud de onda de la guía.

La relaciones (12) y (18) forman un conjunto de ecuaciones trascendentales para las incógnitas α₁ y α₂, las cuales resolvemos por un programa realizado por el autor en QBASIC y el cual tiene en cuenta las transformaciones Schwarz-Christoffel tanto del entorno del dispositivo como de la curva que separa los dos dieléctricos o recta en el plano Z. Dado que tanto las integrales como las funciones elípticas están dadas en series de convergencia rápida, el anterior programa es así mismo de convergencia rápida.

Una vez que se han encontrado las constantes α₁ y α₂, es fácil conocer la constante de fase β(w) de (13), y el campo EM según las ecuaciones (14), (15), (16) y (17).

Resultados, Discusión de Resultados y Conclusiones

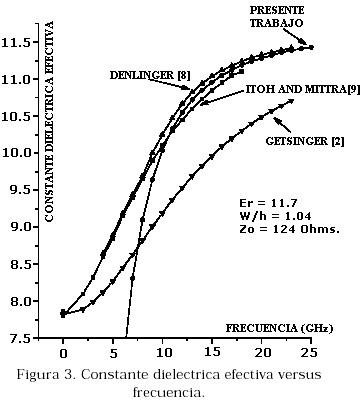
La Figura-3 muestran los resultados de Getsinger [2], Denlinger [8], Itho and Mitra [9] y del presente trabajo. Aquí también se emplea todo el cálculo numérico desarrollado en Fortran [12] y el cual hemos trasladado al Qbasic, en donde se realiza el estudio del dispositivo para el caso estático. Para frecuencia= 0 GHz, existe una excelente coincidencia en el valor de la constante dieléctrica efectiva estática, Î_eff = 7.8, entre lo expuesto por Getsinger [2] y Itoh and Mitra [9] y nuestros resultados, y una diferencia aproximada de 13% entre estos tres trabajos y lo expuesto por Denlinger [8]. Para otros valores de frecuencias, nuestros resultados están de acuerdo con los obtenidos por Itho and Mittra. Así, existe una coincidencia para una frecuencia de 10 GHz de la constante dieléctrica efectiva Î_eff (w) = 10.2. Para valores de frecuencia que están por encima de este valor nuestros resultados están aproximadamente 1% por encima de los presentados por estos dos autores y 1% por de bajo de los presentados por Denlinger. Para frecuencias mayores que 25 GHz los resultados coinciden, en menos del 1%, para Denlinger, Itho and Mitra y este trabajo. Para frecuencia mucho mayores a 25 GHz el comportamiento de estas tres curvas es asintótico con el valor estático Î_lr = 11.7 del dieléctrico entre los dos conductores y el dispositivo deja de tener el comportamiento “dispersivo”. Lo anterior significa, el hecho importante, que tanto el campo EM como la energía se propagan enteramente entre los dos conductores ya que solo “ven” un solo dieléctrico de constante dieléctrica relativa Î_lr = 11.7, esto es, en este rango de frecuencias la “microlínea” deja de tener su connotación de “línea de transmisión” para convertirse en una “guía de onda”, específicamente un “resonador”. Para frecuencias que están en el rango 6.5<=f(GHz)<=10 nuestros valores se encuentran por debajo de los presentados por Itho and Mitra y se presenta una divergencia sustancial para frecuencias cercanas a los 6.5 GHz. Lo anterior puede explicarse si tenemos en cuenta que en este modelo hemos asumido conductividad infinita, esto es cero pérdidas en los conductores o, lo que es lo mismo, la constante de fase Г = α + jβ es un complejo puro, α = 0. Esto es, este modelo muestra el dispositivo, para estas frecuencias, como una guía ideal, con una frecuencia de corte de aproximadamente 3.75 GHz (la cual no se observa en la Figura 3 debido al corrimiento del eje vertical). Cuando tenemos en cuenta las pérdidas en los conductores [13], los resultados son altamente convergentes con lo expuesto por [8] y [9].

La coincidencia entre los modelos [8], [9] y el nuestro se asienta principalmente en el hecho de que en los tres se enfoca el problema desde el punto de vista “dispersivo”. Todas las anteriores comparaciones se han efectuado para una muestra con Î_r = 11.7 y una relación de perfil W/h=1.04 (la cual corresponde a una impedancia característica del vacío de la microcinta de Zo=124 Ohmios).

En resumen, este modelo muestra claramente dos cosas importantes: simplicidad relativa y analiticidad con respecto a otros modelos existentes. La primera característica del modelo, simplicidad, conlleva a un cálculo de parámetros y ecuaciones del campo EM en una forma “relativamente simple” (coordenadas Cartesianas en el Plano de Transformación con un “auto valor” k_u en el plano transformado P y con los otros “autovalores no discretos” α_1,2[u(x,y),v(x,y)] referidos al plano físico de la microcinta en donde la curva de separación entre los dieléctricos es una recta). La segunda característica del modelo es el utilizar el potencial inherente de análisis y síntesis de las ecuaciones que son analíticas. Sin embargo, es necesario reconocer que las condiciones de ser un modelo “simple” y “analítico” están comprometidas por el empleo necesario de las funciones e integrales elípticas que están involucradas en el modelo, las cuales, por lo general, no son de fácil manejo.

Agradecimientos

Agradezco al CONDES (Consejo de Desarrollo Científico y Humanístico) por el apoyo en equipamiento al presente trabajo sin lo cual no hubiera sido posible el desarrollo y culminación del mismo.

Referencias Bibliográficas

1. Schneider, M.V. “Microstrip Lines for Microwave Integrated Circuits”. Bell System Technical Journal, Vol. 48 (1969), 1421-1444.        [ Links ]

2. Getsinger, W.J. “Microstrip Dispersion Model”. IEEE Trans. Vol. MTT- 21 (1973), 34-39.        [ Links ]

3. “Microwave Integrated Circuits”, Special Issue, IEEE Trans. on Electronic Devices, Vol. ED-15, July 1968.        [ Links ]

4. “Microwave Integrated Circuits”, Special Issue, IEEE Trans. Vol. MTT-19, July 1971.        [ Links ]

5. Mittra, R., Itoh T. “A new Technique for the Analysis of the Dispersion Characteristic of Microstrip Lines”. IEEE Trans. Vol. MTT-19 (1971), 4756.        [ Links ]

6. Yamashita, E., Mittra, R. “Variational Method for the Analysis of Microstrip Lines”. IEEE Trans. Vol. MTT-16 (1968), 251-256.        [ Links ]

7. Edwards, T.C., Owens, R.R. “2-18 GHz. Dispersions Measurements on 10-100 Ohms Microstrip Lines on Sapphire”. IEEE Trans. Vol. MTT-24 (1976), 506-513        [ Links ]

8. Denlinger, E.J. A Frequency Dependent Solution for Microstrip Transmission Lines” IEEE Trans. Vol. MTT-19 (1971), 30-39.        [ Links ]

9. Itoh, T., Mittra, R. Spectral-domain Approach for Calculating Dispersion.        [ Links ]

10. Characteristic of Microstrip Lines”. IEEE Trans. Vol. MTT-21 (1973), 496-498.        [ Links ]

11. Railton, C.J., Rozzi, T. “Complex Modes in Boxed Microstrip”. IEEE Trans. Vol. MMT-36 (1988), 865-874.        [ Links ]

12. Callarotti, R., Galo A. “On the Solution of a Microstrip Line with two Dielectrics” IEEE Trans. Vol. MTT-32, 4 (1984).        [ Links ]

13. Galo A. “Vectorial Wave Functions and Dyadic Green´s Functions for a Microstrip Line with two Dielectrics”. Revista Ciencia, Vol.1 (1993), 93-104.        [ Links ]