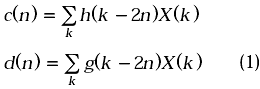A Wavelet based method to characterize electrical insulators under partial discharges 

José L. Paredes¹, Ender Luzardo² y Hildemaro Briceño 

¹Postgrado de Automatización e Instrumentación. ²Escuela de Ingeniería Eléctrica, Universidad de Los Andes. Mérida – Venezuela 5101. Tel: (0274) 240-2903, Fax: (0274) 240-3113. *E-mail: paredesj@ula.ve 

Abstract 

This paper introduces a wavelet packet based method to characterize electrical insulators under partial discharges. The proposed method applies the wavelet packet decomposition (WPD) on the insulator’s voltage signal, experimentally obtained when the electrical isolator is energized with high voltage. The wavelet coefficients outputted by the WPD are reorganized as a two-dimensional array, and well defined patterns are found that allow us to characterize electrical insulators under different working condition. In particular, the electrical insulators are exposed to different conditions of humidity and contamination similar to those found on air transmission lines. 

Key words: Wavelet Transform, electrical insulators, wavelet packets, partial discharges.

Caracterización de aisladores eléctricos sometidos a descargas parciales usando la transformada Wavelet 

Resumen 

En este artículo se expone un método de análisis de descargas parciales presentes en aisladores eléctricos de cerámica energizados con alta tensión. El método propuesto se basa en el uso de la transformada wavelet y la descomposición wavelet packet sobre señales de voltaje presente en aisladores. A través de una representación bidimensional de los coeficientes wavelets, ciertos patrones encontrados permiten caracterizar las condiciones de trabajo (humedad y contaminación) en las que pueden hallarse dichos aisladores cuando están conectados a líneas aéreas de transmisión. 

Palabras clave: Transformada Wavelet, aisladores eléctricos, wavelet packet, descargas parciales.

Recibido el 8 de Marzo 2004

En forma revisada el 6 de Junio 2005

1. Introducción 

Recientemente ha habido un gran interés en la aplicación de técnicas de representación de señales en el dominio tiempo-frecuencia para analizar transitorios presentes en señales de potencia. En particular, la transformada wavelet como herramienta matemática ha sido utilizada para analizar transitorios y perturbaciones en sistemas de potencia [1, 2], estudiar calidad de energía [3, 4] y más recientemente, para analizar el comportamiento de transformadores de potencia ante situaciones diversas [5, 6]. Todas estas aplicaciones explotan la capacidad que tiene la transformada wavelet de localizar en tiempo fenómenos transitorios (señales no estacionarias) y sus correspondientes componentes de frecuencia, así como la capacidad de realizar una representación multi-resolución de las diferentes señales en estudio. 

Una de las aplicaciones de gran interés en el área de potencia es el análisis de las perturbaciones producidas por descargas parciales, las cuales se manifiestan como transitorios en las señales de corriente y voltaje en un aislador eléctrico. Como es bien conocido, al producirse descargas eléctricas en un aislador, éstas pudieran producir el rompimiento del dieléctrico y como consecuencia producir arco o chispa generando una falla de aislamiento o afectando la vida útil del aislador.

En este artículo se hace un análisis en el dominio tiempo-frecuencia de la señal de voltaje en un aislador, adquirida en un montaje experimental en el que se energiza un aislador eléctrico de cerámica con tensiones entre 15 y 25 kV. En particular, se utiliza el análisis multi-resolución usando wavelet packet para determinar patrones en el dominio wavelet que permitan caracterizar las condiciones de trabajo del aislador eléctrico. Entendiéndose por condiciones de trabajo, situaciones reales de humedad y contaminación a la cual están sometidos estos aisladores cuando se encuentran en líneas áreas de transmisión. 

La organización de artículo es como sigue. En la Sección 2 se introduce brevemente los conceptos más relevantes de la transformada wavelet. Seguidamente, en la Sección 3 se describe el montaje experimental con el cual se obtuvieron los datos. La Sección 4 presenta el procesamiento de las señales obtenidas. En la sección 5 se presentan y analizan los resultados. Finalmente las conclusiones son expuestas en la Sección 6. 

2. Transformada Wavelet 

La transformada wavelet, al igual que cualquier otra transformada, representa la señal de interés en un nuevo dominio (dominio wavelet) a través de un conjunto bidimensional de coeficientes, denominados coeficientes wavelets. Estos coeficientes representan el grado de similitud entre la señal en estudio y un conjunto de señales ortogonales (bases de la transformada) de duración finita. Así, para cada instante t la señal continua en el tiempo x(t) se correlaciona con la función ψ_i,j(t) = 2^-j/2 ψ(2^-jt-i ),  i, j = 1,2,3… obteniéndose un conjunto de coeficientes C_i,j los cuales representan una medida de la similitud entre la señal original x(t) y la función ψ_i,j(t). Los parámetros i y j representan la localización en tiempo y en escala (frecuencia) respectivamente de la función ψ(t). La función ψ(t) se le conoce como wavelet fundamental o wavelet madre, y sobre ésta se definen el conjunto de funciones que forman la base ortogonal. Puede notarse que la base ortogonal esta constituida por versiones desplazadas y expandidas en tiempo de la wavelet madre [7]. 

Aunque el arreglo bidimensional de coeficientes, C_i,j, representa la señal x(t) tanto en tiempo como en frecuencia en el dominio wavelet, su representación es redundante y computacionalmente compleja. Además, es bien sabido que un conjunto de muestras tomadas de la señal banda base x(t) son suficientes para describir completamente la señal en tiempo continuó. Surge entonces la necesidad de extender los conceptos de la transformada wavelet continua a señales en tiempo discreto. Esto fue desarrollado por Mallat en [8], donde se describe un algoritmo computacionalmente eficiente para determinar la transformada wavelet discreta. 

A fin de sentar los fundamentos necesarios para esta aplicación en particular, a continuación se describe brevemente la transformada wavelet discreta. Para una descripción más detallada de la transformada wavelet tanto continua como discreta el lector es invitado a revisar [7]. 

2.1. Transformada Wavelet Discreta 

Sea una señal en tiempo discreto X(n) de tamaño 2^N muestras. Al aplicar la transformada wavelet discreta sobre la señal en estudio, ésta se hace pasar por un banco de filtros digitales, obteniéndose a la salida dos componentes. Una primera componente, conocida como coeficientes de aproximación, contiene las componentes de baja frecuencia de la señal de entrada y no es más que una aproximación de la señal en estudio. La segunda componente, conocida como coeficientes de detalles, contiene las componentes de alta frecuencia de la señal en estudio, es decir, los detalles (transitorios) que caracterizan a la señal de entrada. 

La descomposición de la señal X(n) en las componentes de baja y alta frecuencias se consigue al pasar X(n) por un filtro paso bajo y paso alto respectivamente, esto es

donde h(i) y g(i) son los coeficientes del filtro paso bajo y paso alto relacionados con las funciones escalar y wavelet respectivamente [7, pagina 11]. Puede notarse que en la ecuación (1) existe una operación de submuestreo implícito. Es decir, solo una de cada dos muestras se mantienen a la salida del filtro. Esta operación de submuestreo no produce perdida de información relevante de la señal, dado que las señales a la salida del filtro contiene la mitad de la frecuencia de la señal de entrada, por consiguiente su frecuencia de muestreo puede reducirse a la mitad. Así, se evita redundancia en la representación consiguiéndose a la salida de la descomposición wavelet los coeficientes de aproximación, c(n), y de detalles, d(n), de tamaño igual a la mitad del tamaño de la secuencia de entrada, es decir 2^N-1.

La ecuación (1) define un primer nivel de descomposición de la transformada wavelet, niveles sucesivos de descomposición se obtienen al aplicar progresivamente las operaciones de filtrado sobre la señal que resulta a la salida del filtro paso bajo.

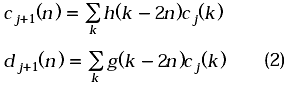
donde c_j y d_j representa los coeficientes de aproximación y de detalles en la j-ésima escala. En la medida que se avanza en la descomposición se consiguen representaciones de la señal de entrada a distintas resoluciones. Así, para j = 0 se tiene la resolución original de los datos de entrada, es decir C₀(n) = X(n) . A medida que j aumenta la resolución disminuye progresivamente. A esta descomposición sucesiva se le conoce como análisis multi-resolución [8]. 

Al igual que cualquier otra transformada, la transformada wavelet es reversible, es decir, a partir de los coeficientes de aproximación, c(n), y de detalles, d(n), es posible reconstruir la señal de entrada original mediante operaciones de filtrado paso bajo y paso alto. Esto es cierto si la wavelet satisface la propiedad de reconstrucción perfecta, condición que impone ciertas restricciones a los coeficientes de los filtros paso alto y paso bajo [7].  

En forma más general, la señal en la j-ésima resolución puede reconstruirse a partir de los coeficientes de detalles y de aproximación de la resolución j-esima + 1 de la siguiente manera

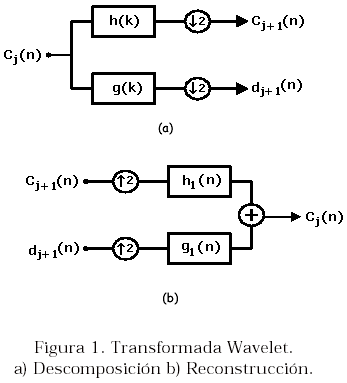
donde h₁(i) y g₁(i) son los coeficientes de los filtros de reconstrucción paso bajo y paso alto respectivamente. La Figura 1 ilustra la transformada wavelet y la correspondiente transformada wavelet inversa. Puede notarse que en la transformada wavelet inversa, previo al proceso de filtrado se hace necesario insertar ceros en los coeficientes de detalles y de aproximación (dicha operación es denotada con el símbolo ­ 2). Esto permite que el número de coeficientes a la entrada de cada filtro se duplique, obteniéndose a la salida una señal el doble del tamaño de la señal de entrada.

2.2. Limpieza de Señales (Denoising) 

Una de las aplicaciones de mayor interés de la transformada wavelet es la supresión de las componentes ruidosas que contaminan a la señal en estudio. El principio de esta metodología de limpieza de señales se fundamenta en el hecho de que las componentes de alta frecuencia de la señal (detalles y ruido) se encuentran concentrados en los coeficientes de detalles de la descomposición wavelet. Por tal motivo, si estos coeficientes se ponderan, por ejemplo se hacen cero si son menores que un cierto valor umbral de lo contrario mantienen su valor. En el proceso de reconstrucción, la señal reconstruida es una versión limpia de la señal contaminada. La escogencia del valor umbral apropiado para cada aplicación sigue siendo motivo de interés para investigadores, pues un valor umbral muy elevado elimina los detalles de interés para la señal en estudio, mientras que un umbral muy bajo deja pasar componentes ruidosas. En esta aplicación en particular se recurrió a métodos empíricos a fin de definir el valor umbral más apropiado.

2.3. Descomposición usando Wavelet Packet 

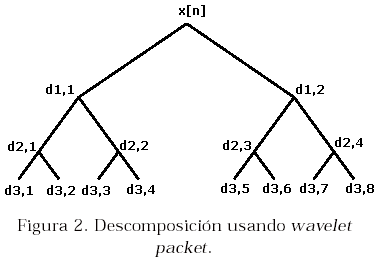
En la descomposición de una señal discreta usando wavelet Packet se procede a realizar un análisis multi-resolución tanto en los coeficientes de aproximación como en los coeficientes de detalles. Es decir, para cada nivel de descomposición, las componentes de alta frecuencia (coeficientes de detalles) también se hacen pasar sucesivamente por filtros paso bajo y paso alto obteniéndose un árbol de descomposición como el mostrado en la Figura 2. Así, en el j-ésimo nivel de descomposición usando wavelet packet se tendrán 2^j secuencias de salida conteniendo cada una 2^N-j coeficientes, siendo 2^N el numero de muestras de la señal original. La Figura 2 ilustra tres niveles de descomposición usando wavelet packet, donde los nodos del árbol representan los coeficientes wavelet, d_j,i, siendo j el nivel de descomposición e i la posición en el árbol a ese nivel. d_j,i puede verse como un vector fila de 2^N-j componentes.

A fin de facilitar el análisis y la interpretación de los resultados obtenidos con la descomposición de Wavelet Packet, se necesita una representación mas apropiada de los coeficientes. Sea A una matriz con 2^L filas y 2^N-L columnas donde L es el nivel máximo de descomposición. A cada fila de la matriz A se le asigna una de las secuencias de los coeficientes wavelet d_j,i. Es decir A(i,:)= d_j,i, para i = 1,2,3…2^L, donde se ha usado una notación similar a la utilizada en Matlab. Con esta representación cada columna contendrá las componentes de frecuencias de la señal en un instante determinado. Este arreglo bidimensional puede ser fácilmente representado como una imagen de N_g + 1 niveles de grises, esto es:

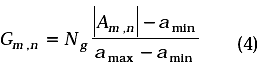
donde  N_g es igual a 255 para una imagen de 8 bits, a_min y a_max son los valores mínimos y máximos respectivamente de ½A_m,n½. Puede notarse que realizar el proceso de denoising descrito en la sección anterior es equivalente a realizar una segmentación de la imagen G_m,n donde las regiones quedan determinadas por el valor umbral. 

3. Montaje experimental para la obtención de los datos

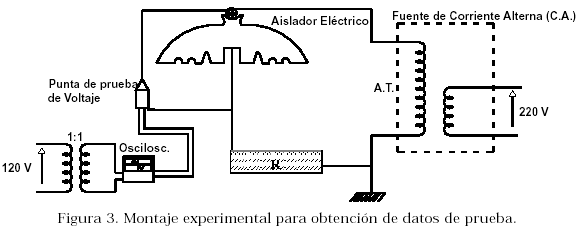
A fin de obtener las señales de prueba, cuando en un aislador se producen descargas eléctricas, se propone un esquema de conexión basado en la energización con alta tensión de una unidad de aislador eléctrico de cerámica, tal y como se muestra en la Figura 3.

En el montaje experimental, la resistencia R se usa para limitar la corriente y proteger el equipo de adquisición. Sobre el aislador se toman directamente muestras de voltaje a través de una punta de prueba atenuadora de un osciloscopio digital con una frecuencia de muestreo de 50 kHz. En [9] se menciona con detalle la metodología seguida para conseguir las señales de prueba. 

La implementación de este esquema de conexión se hizo con la intención de caracterizar los aisladores eléctricos sometidos a condiciones reales de operación, desde el punto de vista de una representación en el dominio tiempo-frecuencia de las señales producidas al ocurrir las descargas eléctricas. Es decir, analizar el efecto sobre la representación tiempo-frecuencia que tienen las distintas condiciones de operación real de estos aisladores eléctricos. Para ello se hizo necesario simular algunos estados o variaciones climáticas producto del sol, la lluvia, la humedad y la contaminación atmosférica, entre otros, a fin de poder estimar parámetros que puedan dar información apropiada sobre el estado de contaminación en que se encuentra determinado aislador en un momento dado. Para las simulaciones de las condiciones climáticas se establecieron cuatro estados, a saber:

1) Un estado “Limpio y Seco”: Este estado se logró lavando el aislador con agua destilada y luego un secado natural con puesta al sol. 

2) Un estado “Limpio y Húmedo”: El humedecimiento se hacia sobre el aislador en su estado “Limpio y Seco”, con agua destilada, en forma de rocío, sobre toda su superficie y de manera uniforme, simulando así el estado del aislador sometido a condiciones climatológicas cambiantes. 

3) Un estado “Contaminado y Seco”: Este estado se logró rociando el aislador “Limpio y Seco” sobre toda su superficie de manera uniforme con un contaminante y luego dejándolo secar al aire libre. El contaminante es una mezcla compuesta por Bentonita, Detergente Dodecil Sulfato de Sodio, sal y agua, siguiendo el estándar de contaminación propuesto en [10]; simulando así las condiciones normales de trabajo de un aislador colocado a la intemperie. 

4) Un estado “Contaminado y Húmedo”: El humedecimiento se hace sobre el aislador en su estado Contaminado y Seco en forma similar que el estado 2. 

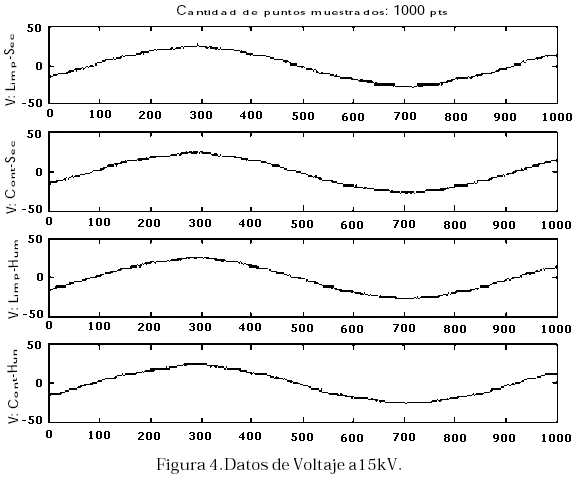
El procedimiento de montaje de los equipos que se llevó a cabo para la obtención de los datos experimentales se presenta con detalle en [9]. Se obtuvieron datos para tensiones de alimentación entre 15 y 25 kV. La Figura 4 muestra los datos de voltaje para las 4 condiciones climatológicas sometidas a prueba, para una tensión de alimentación de 15 kV.

En la Figura 4 se observa que las señales para distintas condiciones de trabajo del aislador son muy parecidas, por lo que no es posible determinar por simple inspección visual parámetros que caractericen las condiciones de contaminación ó de humedad del aislador, con lo cual resultaría muy difícil clasificar determinados datos sin tener previo conocimiento de su origen o procedencia.  

4. Análisis de las señales obtenidas usando la transformada Wavelet 

En la Figura 5 se presenta un diagrama de bloques que ilustra la forma en que fueron procesadas las señales de potencia obtenidas experimentalmente. Dicho procesamiento se inicia con una descomposición de Wavelet Packet, usando la wavelet Daubechies Db4 y cinco niveles de descomposición. Para determinar los niveles de descomposición, no se implemento alguna estrategia especifica sino se siguió sugerencia de otros investigadores quienes establecen que para la descomposición de señales de potencia es suficiente con realizar hasta cinco niveles de descomposición [2, 5].

Se continuó con un proceso de limpieza de la señal (denoising) para lo cual se determinó empíricamente el valor umbral igual al 66% del valor máximo de los coeficientes wavelet en cada nivel de la descomposición. Este criterio se mantuvo consistente para todos los datos analizados. Finalmente, los coeficientes wavelet se representan bidimensionalmente, obteniéndose una imagen de 32 x 32 píxeles.

5. Resultados 

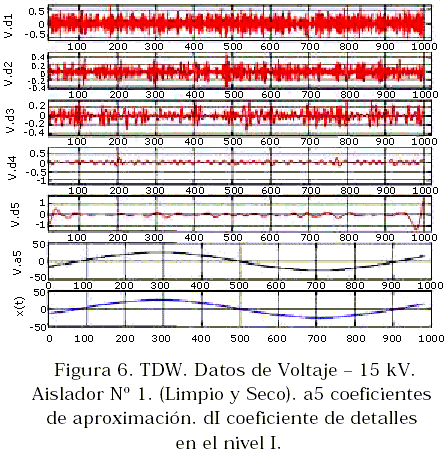
En la Figura 6 se muestra la transformada discreta wavelet aplicada a los datos experimentales de voltaje obtenidos sobre un aislador limpio y seco energizado a 15 kV. La señal original es pasada a través de los filtros paso-bajo y paso-alto, obteniéndose los coeficientes a1 y d1, respectivamente. La salida del filtro paso-bajo es de nuevo filtrada usando ambos filtros, obteniéndose así los coeficientes a2 y d2. Este proceso se repite hasta conseguir los coeficientes de aproximación a5 y de detalles d1, d2, d3, d4 y d5 como se muestran en la figura. Para propósitos de ilustrar la transformada, la operación de submuestreo ha sido omitida. Puede visualizar en la Figura 6 las componentes de frecuencias con su respectiva magnitud para cada nivel de descomposición y en el momento en que estas componentes aparecen a lo largo de la señal original.

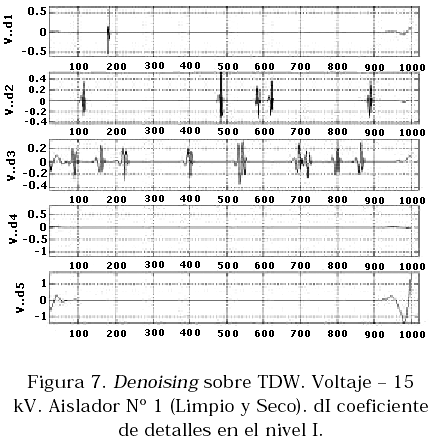
En la Figura 7 se muestra la técnica del Denoising aplicada a las señales de la Figura 6, pero sólo sobre los coeficientes de detalles, es decir, de ‘V..d1’ a ‘V..d5’, pues es en estos coeficientes donde se encuentran las componentes ruidosas de la señal así como también las señales transitorias producidas debido a las descargas eléctricas.

Mediante la técnica de denoising se ha podido eliminar parte de los datos que contenían los respectivos niveles de descomposición y que se consideran señales ruidosas, permitiendo observar sólo las componentes de alta frecuencia de mayor valor, que pudieran estar asociadas con transitorios generados al ocurrir las descargas parciales. Puede notarse que dichas descargas pueden ser capaces de romper la rigidez dieléctrica del aire, pudiendo alcanzar el voltaje disruptivo y por ende producir arco, el cual se manifiesta sobre las señales medidas como cambios abruptos (señales transitorias).

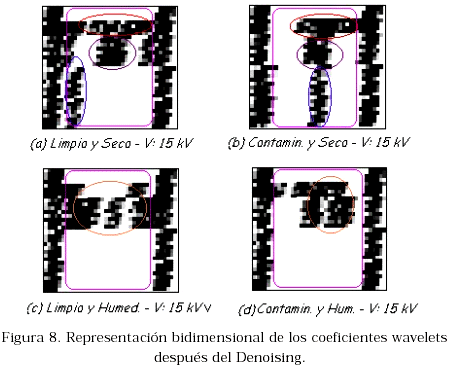
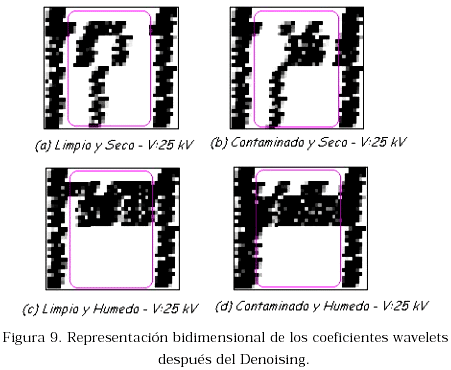
El tipo de representación propuesto para determinar patrones en el dominio tiempo-frecuencia que permitan caracterizar aisladores eléctricos en constante uso y expuestos a cualquier hora del día en las líneas aéreas de transmisión ante ciertas condiciones climáticas, se muestra en la figuras 8 y 9 para 15 kV y 25 kV respectivamente. El eje horizontal corresponde al eje del tiempo y el vertical a las componentes de frecuencia. Así, de la parte inferior a la superior de la grafica, la salida del proceso de filtrado con wavelet packet es mostrado, siendo las componentes bajas de frecuencia representada en la parte inferior mientras que las componentes de altas frecuencias son mostradas en la parte superior tal como se describió en la sección 2.3.

Cabe mencionar que la información de interés sobre la cual hay que enfocarse se encuentra dentro del recuadro; lo que se encuentre fuera de este recuadro no es considerado como información segura debido al efecto producido por la transformada wavelet en cada nivel de descomposición en los extremos de la señal. 

Puede notarse que en la representación bidimensional de los coeficientes wavelet se visualiza cierto comportamiento particular para cada una de las condiciones de operación del aislador, comportamiento que se repitió para todas las pruebas realizadas a los distintos aisladores. Note además, que algoritmos de reconocimiento de patrones basados en redes neuronales, clasificadores bayesianos, máquinas de soporte de vectorial [11], entre otros, pueden ser implementados en este dominio a fin de caracterizar automáticamente el estado del aislador evitando así recurrir a inspecciones visuales. Claramente se observa en la Figura 8, en el dominio wavelet, a diferencia del dominio temporal, las distintas condiciones de operabilidad de los aisladores eléctricos pueden ser fácilmente caracterizados con patrones específicos en el dominio tiempo-frecuencia. 

Adicionalmente puede notarse que en los estados húmedo, como era de esperar, se crean más componentes de alta frecuencia que en los estados secos, ya que se generan mayor cantidad de descargas eléctricas parciales; esto se visualiza en el arreglo bidimensional con coeficientes wavelet tomando valores elevados (componentes oscuras en la parte superior).

Para los estados contaminados se produce concentración de campo eléctrico, por consiguiente, disminución de la resistencia de aislamiento; esto se observa en el arreglo bidimensional como concentración de componentes hacia la parte central. Finalmente, para los estados limpio, las descargas parciales no aparecen tan rápido, es decir se tienen más componentes de baja frecuencia.

En síntesis se tiene que a medida que se contaminan los aisladores aparecen descargas parciales, a medida que se humedecen aparecen mayores descargas parciales y a medida que se humedece y se contaminan aparecen mayores concentraciones de componentes de frecuencia a mayor magnitud o descargas parciales más elevadas. Estas descargas parciales se manifiestan a su vez con coeficientes wavelet de elevado valor a altas frecuencias. 

6. Conclusiones 

En este artículo se ha analizado mediante una representación temporal-frecuencial las señales producidas debido a la ocurrencia de descargas eléctricas en un aislador sometido a diferentes condiciones de trabajo, condiciones similares a las encontradas en situaciones normales de operación. Es posible la caracterización a través de patrones en el dominio tiempo-frecuencia que permiten identificar las condiciones de trabajo del aislador, es decir, si el aislador está limpio-seco, contaminado-seco, limpio-húmedo o contaminado-húmedo. Se comprobó que efectivamente la transformada wavelet y la descomposición usando wavelet packet son herramientas con gran potencial para el análisis de señales de potencia. 

Agradecimiento 

Parte de este trabajo ha sido realizado gracias al apoyo del Laboratorio de Instrumentación y Desarrollo en Automatización e Instrumentación (LABIDAI) de la Escuela de Ingeniería Eléctrica. Universidad de Los Andes. 

Referencias Bibliográficas 

1. P. Pillay, A. Bhattacharjee Applications of Wavelet to Model Short-Term Power System Disturbances. IEEE Transactions on Power Systems. Vol. 11, No. 4, pp. 2031-2037, 1996.         [ Links ]

2. W.A. Wilkinson, M.D. Cox, Discrete Wavelet Analysis of Power System Transients. IEEE Transactions on Power Systems. Vol. 11, No. 4, pp. 2038-2044, 1996.         [ Links ]

3. G.T. Heydt, A.W. Galli. Transient Power Quality Problems Analyzed Using Wavelet, IEEE Transactions on Power Delivery. Vol. 12, No. 2, pp. 908-915, 1997.         [ Links ]

4. S. Santoso, E.J. Powers, M.W. Grady. Power Quality Disturbance Data Compression using Wavelet Transform Methods. IEEE Transactions on Power Delivery. Vol. 12, No. 2, pp. 1250-1256, 1997.         [ Links ]

5. O. A. Youssef. A Wavelet-Based Technique for Discrimination Between Faults and Magnetizing Inrush Currents in Transformers. IEEE Transactions on Power Delivery. Vol. 18, No. 1, pp.170-176, 2003.         [ Links ]

6. P. Kang, D. Birtwhistle. Condition Assessment of Power Transformer Onload Tap Changers Using Wavelet Analysis and Self-Organizing Map: Field Evaluation. IEEE Transactions on Power Deliver. Vol 18, No. 1, pp. 78-84, 2003.         [ Links ]

7. C.S. Burrus, R.A. Gopinath, H. Guo. Introduction to Wavelets and Wavelet Transforms. Printice Hall, New Jersey 1998.         [ Links ]

8. S.G. Mallat. A theory for multiresolution signal decomposition: The wavelet representation, IEEE Transactions on Pattern Anal. Machine Intell. Vol 11, No. 7, pp. 674-693, 1989.         [ Links ]

9. Ender Luzardo. Caracterización de Aisladores Eléctricos de Cerámica ante Descargas Parciales Usando la Transformada Wavelet. Proyecto de Grado. Escuela de Ingeniería Eléctrica. ULA. Mayo 2003.          [ Links ]

10. Norma ANSI/IEEE C62. 11 – 1987. pp. 27. IEEE Standard for metal-oxide surge arresters for AC power circuits.          [ Links ]

11. Tom M. Mitchell. Machine Learning. WCB/McGraw-Hill. P. 414.        [ Links ]