Robust control by extended static output feedback

Control robusto por realimentación estática de la salida extendida

Addison Ríos-Bolívar¹, Francisco Hidrobo², Julián Suárez³

¹Departamento de Control, Facultad de Ingeniería. ilich@ula.ve

²SUMA, Facultad de Ciencias. hidrobo@ula.ve

³LIC-Ciencias, Facultad de Ciencias. gebauer@ula.ve

Universidad de Los Andes. Mérida 5101, Venezuela. Tel. +58 274 240.28.47 - 29.14. Fax 274.240.28.11

Abstract

This paper presents a novel approach for the controller synthesis in linear time invariant systems (LTI) with uncertainty polytopical type, by means of the extended static feedback of the measured output. The method consists of designing feedback gains for the injection of the output and its derivative, which corresponds to the control signal. Conditions for the existence of such controllers are established. The uncertainty parameters are supposed to belong to a polytope. The stabilization problem is formulated in the context of linear matrix inequalities (LMI). Multiobjective performance indices in H2/H& are also considered, which are described as LMIs. The extended H2/H& conditions are obtained by means of the well known projection lemma. Performance of the proposed synthesis technique is illustrated by numerical example.

Key words: Static output feedback, robust control, polytopical uncertainty, linear matrix inequalities (LMI), H2/H& norms.

Resumen

Considerando los sistemas lineales invariantes en el tiempo (LTI) continuos con incertidumbres politópicas, esta contribución presenta un método para la síntesis de controladores por realimentación estática extendida de la salida medida. El método consiste en el diseño de ganancias de realimentación para la inyección de la salida y su derivada que corresponde a la señal de control. Se establecen condiciones para la existencia de este tipo de control. Los parámetros inciertos se suponen que pertenecen a un politopo. El problema de estabilización es formulado en el contexto de Desigualdades Matriciales Lineales (LMI). Índices de desempeño multiobjetivos en H2/H&, son también considerados, los cuales se describen como LMIs. Las condiciones de desempeño H2/H& extendidas se obtienen por medio del lema de proyección. El funcionamiento de la técnica propuesta es ilustrada por medio de un ejemplo numérico.

Palabras clave: Realimentación estática de la salida, control robusto, incertidumbre politópica, desigualdades matriciales lineales, normas H2/H&.

1. Introducción

El fin último de todo diseño de sistemas de control es su implantación práctica. Cuando se trata la síntesis de sistemas de control para los fines prácticos siempre se busca la mayor flexibilidad y simplificidad de implementación. De allí que el control por realimentación de la salida ha sido un tópico de mucho interés de investigación. Como se sabe, los controladores que ofrecen esas características se construyen a partir de la realimentación de estados, los cuales tienen el inconveniente de que no siempre es posible disponer de todos los estados. Por su parte, la realimentación estática de la salida presenta todas las bondades para una implementación sin muchas exigencias. El mayor inconveniente para la síntesis de control por realimentación estática de la salida (SOF) son sus condiciones de existencia de tales controladores [1]. El problema de SOF se refiere a lo siguiente: dado un sistema LTI encontrar una ganancia de realimentación estática de la salida tal que, en lazo cerrado, el sistema controlado exhiba las características deseadas de comportamiento; o en su defecto, determinar la no existencia de tal ganancia [2]. Aunque se conocen varias condiciones teóricas para la existencia de controladores por SOF, existe el inconveniente de lograr implantar algoritmos prácticos para la solución sin mayores requerimientos.

Así, el problema de control vía SOF se plantea de la siguiente manera: considérese el sistema LTI definido por

Problema 1

Dado el sistema (1), con (A;B) estabilizable, encontrar K para el control (2) de tal manera que la matriz A B_KC tenga todos sus autovalores en el semi-plano estable.

La selección de la ganancia K debe permitir satisfacer los requerimientos de funcionamiento según los objetivos de diseño del sistema de control. El primer detalle a definir es la existencia de tal ganancia de realimentación estática. Para ello han sido presentado varios resultados: [1-4]. Las condiciones establecidas no indican, de manera directa, los algoritmos de solución. Así, se han presentado varios métodos para la solución algorítmica del problema de SOF: [5-8]. Todas estas soluciones siguen manteniendo el problema de requerimientos exigentes desde el punto de vista computacional, limitando la aplicación práctica de las técnicas de SOF en procesos industriales.

En consecuencia, en este trabajo se presenta un método de diseño de controladores por SOF extendida para sistemas LTI con incertidumbres politópicas. La técnica consiste en el diseño de ganancias de realimentación para la inyección de la salida medida y su derivada, lo cual permite ampliar el espacio de sistemas controlables por SOF, y la ley de control se obtiene por solución numérica vía LMI con condiciones de normas

extendidas, las cuales son desarrolladas de acuerdo a las siguientes notaciones y resultados: R es el conjunto de números reales. Para una matriz A, A^T denota su transpuesta, tr(A) define la traza de la matriz A. L₂ es el espacio de Hilbert de señales vectoriales definidas en con producto escalar y tal que .

En las particiones de matrices simétricas * denota cada uno de sus bloques simétricos. i define la matriz identidad de dimensión apropiada.

Considérese el sistema LTI

medidas. Las matrices A, B, C, D son bien conocidas y de dimensiones apropiadas.

Para estudiar el desempeño de ese sistema, en la teoría moderna de control es tradicional aplicar criterios basados en normas. Adicionalmente, existen algunas modificaciones a los resultados clásicos considerados en la teoría de control robusto, tal es el caso de versiones mejoradas al Lema Real Acotado [9, 10], o en el caso de desempeño en

Lema 1.1 (Desempeño relajado) Considérese el sistema (3) con D= 0. Para P= P^T>0, las siguientes declaraciones son equivalentes i. A es estable y

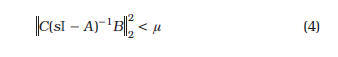
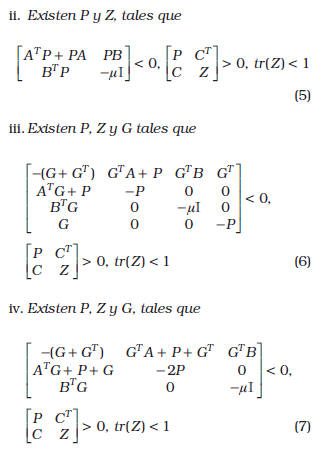
Prueba. Las equivalencias entre las declaraciones han sido mostradas en [11, 12]. Cuando existen relaciones entre la matriz dinámica del sistema y la matriz de Lyapunov se obtienen resultados más conservativos, tal como es el caso de sistemas con incertidumbres politópicas [13]. Esta situación se solventa, en cierto grado, desacoplando ambas matrices. Además, la declaración iv) en el Lema 1.1 provee una representación mejorada de la condición de desempeño en dada en [11]. De la misma forma que para el caso dado anteriormente, existen algunos resultados para mejorar el desempeño en tal como se muestra a continuación.

Lema 1.2 (Desempeño Relajado) Considérese el sistema (3). Con P = P^T>0 y la matriz G, las siguientes declaraciones son equivalentes:

 i. A es estable y

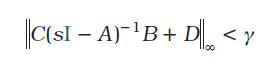
ii. Existe P, tal que

Prueba. Las condiciones i) y ii) representan el bien conocido Lema Real Acotado. La equivalencia entre ii) y iii) puede ser vista en [12].

Estos resultados serán útiles para el diseño de controladores robustos por realimentación estática de la salida extendida, tal como se mostrará a continuación.

2. Control por realimentación estática de la salida extendida

Considérese el sistema (1). Se define el control como:

donde K₀ y K₁ son las ganancias de realimentación a determinar para la salida y su derivada. En este caso, la derivada de la salida se utiliza en el contexto de la acción derivativa en controladores tipo PID. Así, el control estará dado por

donde I es la matriz identidad. Tal como se puede observar, la existencia del control depende de la invertibilidad de la matriz

que es una condición menos “fuerte” que las establecidas en el Problema 1 de SOF. Así, para el Control por realimentación estática de la salida extendida se establece el siguiente problema:

Problema 2

Dado el sistema (1), con (A;B) estabilizable. Encontrar para el control (11) de tal manera que la matriz tenga todos sus autovalores en el semi-plano estable.  

Lema 2.1. Sea Existe un control por realimentación estática de la salida extendida de la forma

sí y sólo si M tiene inversa generalizada (pseudoinversa Moore-Penrose), dada por En efecto, si 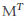es la matriz transpuesta de M, quien es de rango completo por columnas, entonces la matriz pseudoinversa Moore-Penrose

la cual, si existe, permite calcular la ley de control. Esta condición debilita y generaliza las establecidas en [14], dándole, además, solución al problema de SOF, en muchos más casos [15]. Por otro lado, el problema de estabilización mediante realimentación de la salida extendida se puede analizar en el ámbito de las LMIs. En efecto, si se considera el problema de estabilización por realimentación de la salida extendida en el contexto de LMIs, entonces, dado el sistema (1), encontrar 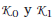de tal manera que el sistema en lazo cerrado sea estable en el sentido de Lyapunov, es decir si las siguientes BMI (desigualdades matriciales bilineales) se satisfacen:

donde Ac es la matriz dinámica de lazo cerrado. Este problema de estabilización ha sido tratado en [15], donde se presenta las fortalezas de las soluciones numéricas vía LMI.

3. Control en

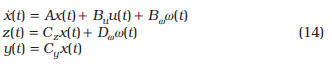
Considérese el sistema LTI definido por  donde es una perturbación desconocida, z(t) la salida controlada y y(t) la salida medida.

Problema 3

Dado el sistema (14), con (A;B_u) estabilizable. Encontrar para el control (11) de tal manera que la matriz dinámica Ac del lazo cerrado sea estable y que la norma-2 ó norma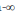 de la función de transferencia de la perturbación a salida controlada sea mínima en algún sentido, es decir

Aplicando el control dado por (11), entonces el sistema en lazo cerrado será

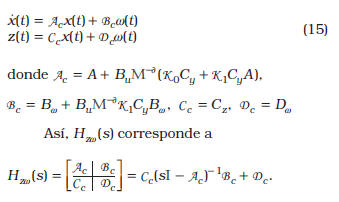
En este caso, la idea es obtener un controlador que nos permite alcanzar un índice de desempeño bajo la norma .

Acá se resuelve el problema de atenuación de los efectos de la perturbación a la salida controlada, sin considerar robustez por efecto de incertidumbres.

La síntesis de los controladores y las condiciones requeridas para ellos se pueden analizar en [15, 16].

En este caso, las condiciones son similares a las presentadas en la solución del Problema 2 vía LMI. Por otro lado, se amplía el espectro de los sistemas a ser estabilizados por realimentación de la salida. Además, allí existen condiciones para lograr un rechazo pleno de la perturbación. En efecto, si se selecciona de tal manera que 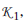. entonces se rechaza la perturbación. Por lo tanto, una vez seleccionado , se debe diseñar de tal manera que la matriz dinámica de lazo cerrado sea estable [15].

De igual manera, es posible tratar el problema de regulación o seguimiento de la salida, nuevamente con una adecuada selección de 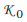, y una ganancia sobre la señal de referencia para asegurar un error nulo entre la salida y la señal a seguir.

4. Control robusto

Hasta ahora se ha considerado el diseño de controladores con objetivos de minimizar el efecto de las perturbaciones a las salidas controladas, tal como ha sido mostrado en [16]. A partir de este momento, estamos interesados en diseñar controladores robustos, en procesos donde existe incertidumbre en la matriz dinámica de la planta. Sea el sistema incierto

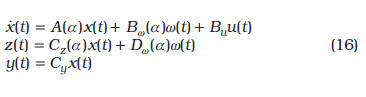
donde son los estados, . son perturbaciones desconocidas, son las entradas de control, son las salidas controladas, son las salidas medidas. Adicionalmente, las matrices desconocidas del sistema conforman un politopo incierto, es decir, pertenecen a

una cáscara convexa, con lo cual 

 

 

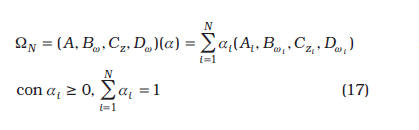
Puesto que está restringida a un conjunto unitario, ya que

entonces las matrices son funciones afines del vector de parámetros inciertos/ ' RN descrito por la combinación convexa de las matrices vértices Como se puede observar, las matrices B_u y C_y se consideran conocidas. Eso tiene correspondencia con el hecho de que ellas representan, desde el punto de vista práctico, los elementos fundamentales y precisos para la implantación de los sistemas de control, que son los actuadores y los sensores, respectivamente. Ahora, aplicando el control por realimentación de la salida estática extendida, y asumiendo que 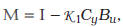, entonces

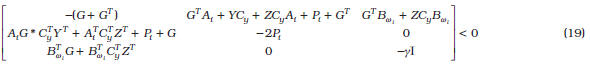
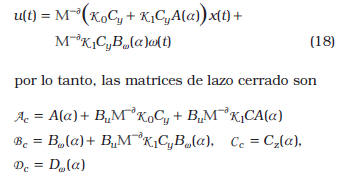
4.1. Control robusto

Del Lema 1.1 se obtienen los siguientes resultados

Teorema 4.1.

Sea el sistema (16) sobre el politopo (17) con D.(/) 0. Existe una ley de control por realimentación estática de la salida extendida de la forma (18), que garantiza un desempeño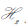 para el sistema en lazo cerrado, cumpliendo las condiciones formales, si se satisfacen las ecuaciones (19) (ver abajo) y (20)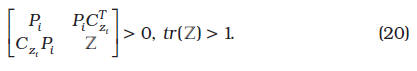

para lo cual las ganancias de la realimentación estática de la salida extendida se obtienen de

 

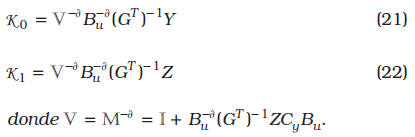
Prueba. A partir de cambios de variables se llega a la prueba. Asúmase que existe una solución factible para el problema de realimentación estática de la salida extendida, según el control (18). Entonces, a partir del Lema 1.1 y las matrices dinámicas del lazo cerrado, se tiene la ecuación (23) (abajo), si entonces por aplicación del Lema 1.1 se llega al resultado mostrado.

4.2. Control robusto

Del Lema 1.2 se deriva el siguiente resultado:

Teorema 4.2. Sea el sistema (16) sobre el politopo (17). Existe una ley de control por realimentación estática de la salida extendida de la forma (18), que garantiza un desempeño sub-óptimo para el sistema en lazo cerrado, satisfaciendo las condiciones formales, si se satisface la ecuación (24) (ver abajo),

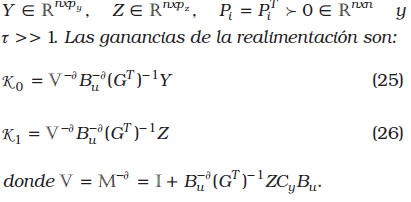
Prueba. Se sigue el mismo procedimiento del caso previo. Los resultados aquí obtenidos para el caso en   se pueden combinar a fin de obtener controladores con multiobjetivos. En las técnicas multiobjetivos clásicas, las expresiones de la forma A^TP + PA involucran productos entre las matrices de Lyapunov y las matrices de diseño, lo que se traduce en conservatismo. A fin de garantizar la convexidad del problema, es necesario hacer una consideración fundamental, reforzando todas las especificaciones a partir de una única función de Lyapunov. En el caso presentado, debido a las versiones extendidas de las caracterizaciones de las normas como LMIs, no se generan productos que involucren matrices de Lyapunov, y las matrices de diseño no dependerán de ellas, evitándose la necesidad de usar la misma matriz de Lyapunov para todas las especificaciones, lo que permite reducir el conservatismo.

5. Evaluación numérica

De manera ilustrativa, sea el sistema definido por, [8]:

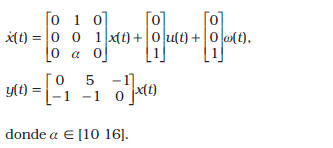
Aplicando los resultados del Teorema 4.2 se obtiene:

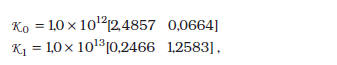
para un valor de 0,4244 de la minimización de la norma- para la función de transferencia

Así, la ley de control es

Evaluando, para la matriz dinámica de lazo cerrado es

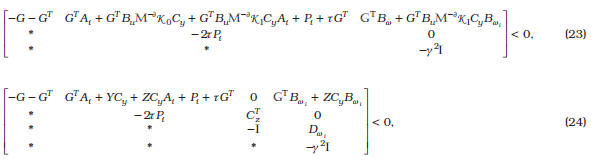
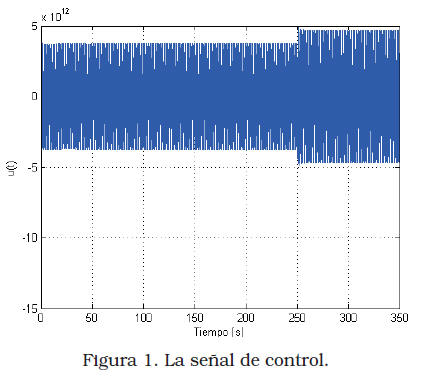
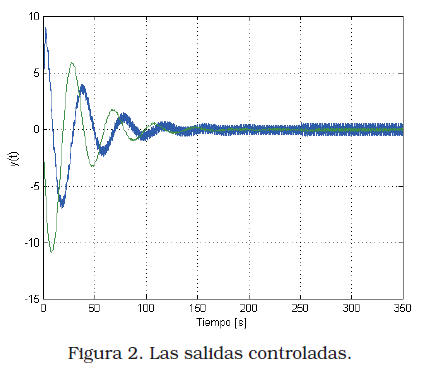
cuyos autovalores son –1,0486; –0,0305 ± 0,1573j. De esta manera, se evidencia la estabilización del sistema en lazo cerrado con una atenuación de la perturbación. Los resultados de la simulación se muestran en la Figura 1 y Figura 2, que corresponden al control y a la salida. Como se puede notar, las salidas son estabilizadas alrededor del cero, afectadas solamente por la presencia de la perturbación. Además, para evaluar la estabilización bajo cambios en el parámetro en t=250s, se produce una variación del mismo dentro de su rango estipulado, y como se puede notar, se mantiene la estabilidad del sistema por efectos de la acción del control.

6. Conclusiones

A partir de la salida y su derivada, se ha planteado y resuelto el problema de control robusto de sistemas lineales invariantes en el tiempo y con incertidumbres politópicas, por realimentación estática utilizando la inyección de ambas señales como entrada de control. La solución permite ampliar el espacio de los sistemas que pueden ser estabilizados por las técnicas tradicionales de realimentación estática de la salida, incorporando características de robustez. La utilización de la derivada de la salida se considera en el mismo contexto de la acción derivada en controladores PID. Además, con una adecuada selección de las ganancias de realimentación, tanto para la salida medida como para su derivada, es posible el rechazo de perturbaciones. Se han presentado las condiciones para la solución del problema, las cuales permiten alcanzar resultados en el marco del control en utilizando las caracterizaciones extendidas de estas normas, como desigualdades matriciales lineales. Las condiciones derivadas son análogas a los problemas de realimentación estática de la salida ya conocidos, pero se amplía el espectro de los sistemas lineales inciertos que pueden ser controlados por este tipo de realimentación.

Agradecimientos

Este trabajo ha sido financiado por el FONACIT bajo el proyecto No. 2005000170, y el CDCHT de la Universidad de Los Andes, a través del proyecto No. I-1206-09-02-B, por lo que gratamente se reconocen estos soportes.

Referencias bibliográficas

1. Syrmos, C., Abdallah, C., Dorato, P. and Grigoriadis, K., Static Output Feedback: A Survey, Automatica, Vol. 33, No. 2, pp. 125- 137, 1997.

2. Gadewadikar, J., Lewis, F. L. and Abu- Khalaf, M., Necessary and Sufficient Conditions for H8 Static Output-Feedback Control, Journal of Guidance, Control, and Dynamics, Vol. 29, No. 4, pp. 915-924, 2006.

3. Eremenko, A. and Gabrielov, A., Pole Placement by Static Output Feedback for Generic Linear Systems, SIAM J. Control Optim., Vol. 41, No. 1, pp. 303{312, 2002.

4. Chen, P.-C., Chang, K.-Y., Jeng, Y.-F. and Chang, W.-J., The Study on the Convex and LMI Conditions for Static Output Feedback Stabilization, Journal of Marine Science and Technology, Vol. 12, No. 3, pp. 171-174, 2004.

5. Ghaoui, L. E., Oustry, F. and AitRami, M., A Cone Complementarity Linearization Algorithm for Static Output-Feedback and Related Problems, IEEE Transactions on Automatic Control, Vol. 42, No. 8, pp. 1171-1176, 1997.

6. Yang, K., Orsi, R. and Moore, J. B., A Projective Algorithm for Static Output Feedback Stabilization, Proc. of IFAC Word Congress, Vol. 1, pp. CD-Rom, England, 2004.

7. Bernstein, D. S., The Optimal Projection Equations for Static and Dynamic Output Feedback: The Singular Case, IEEE Transactions on Automatic Control, Vol. 32, No. 12, pp. 1139-1143, 1987.

8. Henrion, D., Löfberg, J., Ko vara, M. and Stingl, M., Solving polynomial static output feedback problems with PENBMI, Proc. of the 44th IEEE Conference on Decision and Control, edited by IEEE, Vol. 1, pp. 7581-7586, Sevilla, Spain, 2005.

9. Shaked, U., Improved LMI Representations for the Analysis and the Design of Continuous- Time Systems with Polytopic Type Uncertainty, IEEE Trans. on Autom. Control, Vol. 46, No. 4, pp. 652-656, 2001.

10. He, Y., Wu, M. and She, J., Improved Bounded-Real-Lemma Representation and H8 Control of Systems With Polytopic Uncertainties, IEEE Trans. on Autom. Control, Vol. 52, No. 7, pp. 380-383, 2005.

11. Apkarian, P., Tuan, H. and Bernussou, J., Continuous-Time Analysis, Eigenstructure Assignment, and H2 Synthesis With Enhanced Linear Matrix Inequalities (LMI) Characterizations, IEEE Trans. on Autom. Control, Vol. 46, No. 12, pp. 1941-1946, 2001.

12. Wei, C., On Applications of the Projection Lemma to Analysis and Design of Continuous- Time Systems, Master’s thesis, National Sun Yat-Set University, 2003.         [ Links ]

13. Oliveira, M., Bernussou, J. and Geromel, J., A New Discrete-time Robust Stability Condition, Systems & Control Letters, Vol. 37, pp. 261-265, 1999.

14. Jinzhi,W. and Jifeng, Z., An LMI Approach to Static Output Feedback Stabilization for Linear Systems, Control Theory and Applications, Vol. 18, No. 6, pp. 843-846, 2001.

15. Ríos-Bolívar, A., Rivas-Echeverria, F. and Mousalli-Kayat, G., H8 control by extended static output feedback, ROCOM’09: Proc. of the 9th WSEAS international conference on Robotics, control and manufacturing technology, pp. 50-55,World Scientific and Engineering Academy and Society (WSEAS), Stevens Point, Wisconsin, USA, 2009.

16. Ríos-Bolívar, A., Rivas-Echeverria, F. and Mousalli-Kayat, G., Extended Static Output Feedback: An H2-H8 Control Setting, WSEAS Transactions on Systems and Control, Vol. 4, No. 7, pp. 286-295, 2009.

Recibido el 10 de Enero de 2010 En forma revisada el 18 de Julio de 2011