Adaptive ensemble of metamodels for the solution of modelling and global optimization problems

Ensamble adaptativo de metamodelos para la solución de problemas de modelado y optimización global

Daniel E. Finol, Néstor V. Queipo

Instituto de Cálculo Aplicado, Facultad de Ingeniería, Universidad del Zulia, Apartado 526. Maracaibo 4011-A, Venezuela. Telex LUZ-R-VE-64287. Tlf. (0261)7598701 Fax(0261)7512214. dfinol, nqueipo@ica.luz.ve

Abstract

The metamodeling approach is increasingly popular and has been shown to be useful in the analysis and optimization of computationally expensive simulation-based models in, for example, the aerospace, automotive and oil industries. Nevertheless, the problem of finding a metamodel that approximates a function (the original numeric model) from a sample of points (data), is inverse and nonlinear so that there are frequently multiple models that offer a reasonable fit to the data. This work proposes a method of modeling and global optimization with restrictions using an adaptive ensemble of metamodels (i.e., Radial Basis Functions, Kriging and Polynomial Regression), and its effectiveness is assessed comparing its performance (on 6 recognized test functions and an industrial application) with the individual use of the members of the ensemble. The performance of the proposed ensemble was robust: i) the average R2 per sample size is one of the two highest with one of the two smallest variances (modeling) and ii) in most case studies the metamodel exhibited one of the two best results (modeling and optimization).

Keywords: optimization, ensemble of metamodels, radial basis functions, kriging, polynomial regression.

Resumen

El enfoque de metamodelos es cada vez más popular y ha mostrado ser útil en el análisis y optimización de modelos computacionalmente costosos basados en simulaciones en, por ejemplo, las industrias petrolera, aeroespacial y automotriz. Sin embargo, el problema de encontrar un metamodelo que aproxime una función (el modelo numérico original) a partir de una muestra de puntos (datos), es inverso y no lineal de manera que con frecuencia existen múltiples metamodelos que ofrecen un razonable ajuste de los datos. Este trabajo ofrece una metodología para realizar modelado y optimización global con restricciones, usando un ensamble adaptativo de metamodelos (i.e., Funciones de Base Radial, Kriging y Regresión Polinómica), y su efectividad es evaluada comparando su desempeño (sobre 6 reconocidas funciones de prueba y una aplicación industrial) con el del uso aislado de los miembros del ensamble. El desempeño del enfoque de ensamble propuesto fue robusto: i) el promedio de R2 calculado por tamaño de muestra es uno de los dos mayores con una de las dos menores varianzas (modelado) y ii) es el único de los metamodelos que, en general, presenta uno de los dos mejores resultados en cada uno de los casos de estudio (modelado y optimización).

Palabras clave: optimización, ensamble de metamodelos, funciones de base radial, kriging, regresión polinómica.

Introducción

El enfoque de metamodelos es cada vez más popular y ha mostrado ser útil en el análisis y optimización de modelos computacionalmente costosos basados en simulaciones en, por ejemplo, las industrias petrolera [1, 2, 3, 4], aeroespacial [5] y automotriz [6]. Un metamodelo hace referencia a la idea de construir un modelo alternativo rápido (sustituto) a partir de datos de simulaciones numéricas. Sin embargo, el problema de encontrar un metamodelo que aproxime una función (el modelo numérico original) a partir de una muestra de puntos (datos), es inverso y no lineal de manera que con frecuencia existen múltiples metamodelos que ofrecen un razonable ajuste de los datos. El diseñador entonces enfrenta el problema de seleccionar un metamodelo pues, dependiendo del problema, un esquema particular de modelado (e.g. Regresión Polinómica, Splines, Funciones de Base Radial, o Kriging) puede ser mejor que los otros y, en general, no se sabe a priori cuál debe ser seleccionado [7, 8]. Dos estrategias han sido utilizadas en la selección de metamodelos: (1) seleccionar un metamodelo particular de un conjunto de candidatos [9, 10, 11] o (2) construir un ensamble de los metamodelos disponibles (promedio ponderado) con pesos calculados en base a medidas de desempeño globales [7] o locales [2, 12].

El enfoque de ensamble de metamodelos es una valiosa alternativa para resolver el problema de la selección del metamodelo, y hay evidencia de que puede proveer mejor capacidad promedio de predicción que usar un metamodelo aislado (e.g., [13]); en particular, es atractiva la variante que pondera (pesos) los metamodelos usando medidas de desempeño locales (varianza del error) considerando que el mejor desempeño en regiones del espacio de entrada puede ser exhibido por distintos metamodelos. Zerpa et al. [2] usaron una estimación analítica de la varianza del error como medida local de desempeño en la solución de un problema de optimización, mientras que Sánchez et al. [12] calcularon la varianza del error de forma empírica, en el contexto de problemas de modelado. Ambos se limitaron a casos de estudio de dimensiones cuatro [2] y seis [12] y no tomaron en consideración de manera explícita el grado de no-linealidad de los mismos.

Por otra parte, en el área de optimización no se ha establecido suficientemente si los resultados del enfoque basado en ensamble de metamodelos son mejores a los obtenidos usando metamodelos de manera aislada [2]. Nótese que Zerpa et al. [2] usaron un ensamble adaptativo de metamodelos pero la evaluación estuvo limitada a un solo caso de estudio de baja dimensionalidad. Una evaluación más completa permitiría establecer el potencial del enfoque de ensamble adaptativo de metamodelos para la solución de problemas complejos de modelado y optimización en ingeniería.

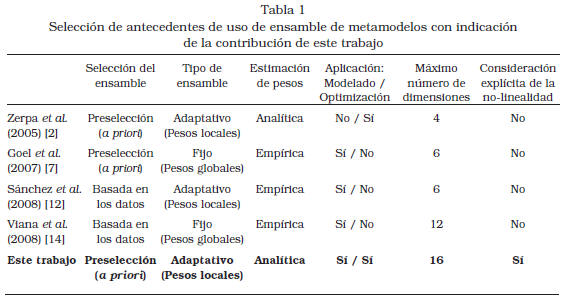
Este trabajo ofrece una metodología para realizar modelado y optimización global con restricciones usando un ensamble adaptativo de metamodelos, considerando reconocidas funciones de prueba de hasta dimensión 16 y de manera explícita su nivel de no-linealidad (Tabla 1).

Además, en contraste con Zerpa et al. [2] se evaluó empíricamente la confiabilidad de las estimaciones analíticas de la varianza del error de los metamodelos considerados, cuyos valores pueden estar significativamente sesgados y afectar la calidad del ensamble.

Ensamble adaptativo de metamodelos

El ensamble adaptativo de interés en este trabajo puede formularse mediante la expresión:

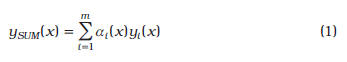
donde representa el peso del i-ésimo metamodelo en el punto x, es la predicción del i-ésimo metamodelo en el punto x, y m es el número de metamodelos. Específicamente los metamodelos considerados en este trabajo son:

Funciones de Base Radial (RBF), Regresión Polinómica (PRE) y Kriging (KRI) y los pesos se calculan de la siguiente manera:

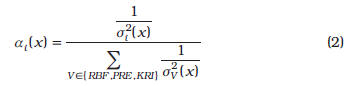
donde es la estimación de la varianza del error del metamodelo “i” en el punto x. Nótese que el peso de la predicción de cada metamodelo en el ensamble difiere según el punto de pronóstico considerado (adaptativo) y es inversamente proporcional a la varianza (estimada) de su error. A continuación se describen aspectos fundamentales de cada uno de los metamodelos utilizados, consideraciones sobre la estimación de la varianza del error de los metamodelos y detalles de la implementación de enfoque de ensamble de metamodelos propuesto.

Metamodelos

Cada uno de los metamodelos usados es un caso especial de la siguiente expresión: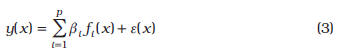

La Tabla 2 muestra las características de cada uno de los metamodelos usados. En la expresión para de Kriging, R es la matriz de correlaciones entre los puntos de la muestra, Y el vector de los valores de la función en la muestra, u es un vector de unos, es la estimación de máxima verosimilitud de la media y r(x) es el vector de correlaciones entre x y cada punto de la muestra. La correlación es modelada con una de distintas funciones parametrizadas (i.e., modelo Gaussiano, exponencial, exponencial generalizado, spline o esférico).

Estimación de la varianza del error de los metamodelos

La Tabla 3 especifica la función que proporciona la varianza estimada del error de cada metamodelo en cada punto del espacio.

En la expresión del estimador de la varianza de Kriging, es el estimador de máxima verosimilitud de la varianza del error (global). En la expresión para PRE y RBF, f (x) es el vector donde cada uno de sus elementos es una función de regresión evaluada en x; F es la matriz de diseño cuyos elementos son las funciones de regresión evaluadas en los puntos de la muestra; y es el estimador estándar de la varianza del error (usualmente conocido como Mean Square Error o, también, “Estimador Insesgado de la Varianza”). Para metamodelos lineales el estimador viene dado por SSE / (n – p); donde SSE es la suma del cuadrado de los errores, n el tamaño de la muestra y p el número de parámetros libres del metamodelo.

Para evaluar la confiabilidad de los estimadores de la varianza del error, se comparó el promedio de las estimaciones de las varianzas con el promedio del cuadrado de los errores sobre un conjunto de prueba suficientemente amplio. Diferencias significativas en los promedios citados implican estimadores poco confiables, lo que puede resultar en asignaciones inadecuadas de los pesos en el ensamble de metamodelos; esto ocurrió particularmente con el estimador de la varianza del error de los metamodelos RBF. Específicamente, se observó que la estimación de RBF de la varianza puntual del error presentaba, en general, valores significativamente por debajo del error cuadrático correspondiente (sesgo). Este sesgo era mayor que los observados para los otros métodos, lo que resultaría en una asignación inadecuada de los pesos. Para resolver este problema se experimentó con otros estimadores de la varianza global hasta encontrar uno apropiado, el cual se describe a continuación:

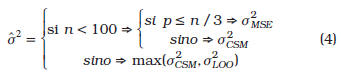
donde n es el tamaño de la muestra, p la dimensionalidad, es el estimador de validacióncruzada tipo Dejar-Uno-Afuera (Leave-One-Out) para metamodelos lineales y representa el estimador usado en los criterios de selección del modelo conocidos como Criterio de Información Bayesiana y Validación Cruzada Generalizada [17].

 

Implementación

El enfoque propuesto de ensamble adaptativo de metamodelos fue codificado en el ambiente de programación MATLAB [18]. Específicamente, los metamodelos utilizados correspondientes a Regresión Polinómica fueron los provistos por MATLAB; mientras que en el caso de Kriging y Funciones de Base Radial se usaron las herramientas DACE [16] y RBF2-Toolbox [17], respectivamente.

Casos de estudio

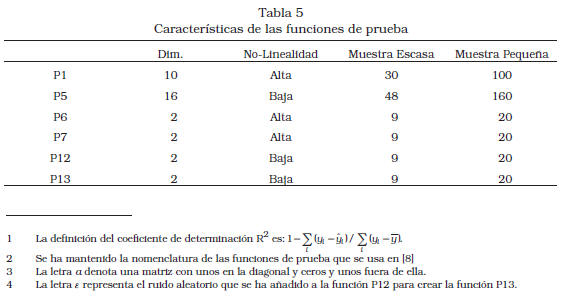
Se seleccionaron seis reconocidas funciones de prueba (Tabla 4) y una aplicación industrial que difieren en cuanto a su dimensionalidad y grado de no-linealidad. En la Tabla 5 se especifica la dimensión, grado de no-linealidad (alta y baja) y los tamaños de muestra usados (escasa y pequeña), para cada problema; las funciones de prueba fueron etiquetadas como de alta o baja no-linealidad, según que el R2 (coeficiente de determinación)1 de una regresión polinómica de primer o segundo grado fuera menor (alta) o mayor (baja) a 0,99 [8].

Aplicación industrial: Optimización de proceso de inyección de ASP (álcali-surfactante- polímero) [2, 12, 19].

La recuperación mejorada de petróleo utilizando ASP es uno de los métodos más promisorios para enfrentar uno de los retos más importantes de la industria petrolera: luego de métodos convencionales de recuperación por inyección de agua, el petróleo atrapado en el yacimiento puede ser hasta el 70% del petróleo originalmente en el yacimiento (POES). Este problema considera un proyecto a escala de campo (13 pozos, 9 productores y 4 inyectores; POES estimado en 395.427 barriles) con las siguientes variables de diseño: la concentración de cada uno de los compuestos químicos: álcali, surfactante y polímero; y el tiempo de inyección [2]; los rangos de estas variables son descritos en la Tabla 6.

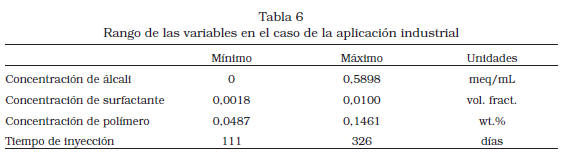
La función objetivo es la producción acumulada de petróleo para un horizonte de 487 días medida como porcentaje del POES y es evaluada utilizando el simulador UTCHEM de la Universidad de Texas [20]. Detalles adicionales de este caso de estudio se encuentran en [2].

Metodología de evaluación y medidas de desempeño

La evaluación fue realizada mediante los siguientes pasos:

1. Diseño del experimento y muestreo. Obtener el conjunto de puntos iniciales (muestra) para cada problema y tamaño de muestra, mediante el método conocido como hipercubo latino [21] y evaluarlos en el modelo original. Para cada función de prueba se escogieron dos muestras: Escasa y Pequeña, tal como se describe en la Tabla 5.

2. Construcción de metamodelos. Se construye cada metamodelo estimando sus parámetros a partir de la muestra. El ensamble de metamodelos, como se describió en la sección Ensamble adaptativo de metamodelos, es evaluado a partir de los metamodelos individuales y sus estimaciones de la varianza del error.

3. Optimización basada en metamodelos. El algoritmo de optimización utilizado es de naturaleza global denominado DIRECT (DIviding RECTangles) [22]. Nótese que el número de evaluaciones de la función objetivo no es un aspecto computacionalmente crítico en virtud de que la optimización está basada en el uso de metamodelos. Los métodos basados en gradiente (como el de Newton, etc.), aunque más eficientes, sólo encuentran óptimos locales.

4. Cálculo de medidas de desempeño. Para evaluar el enfoque propuesto en términos de modelado se utilizó el coeficiente de determinación R2 sobre conjuntos de prueba suficientemente amplios (entre 1600 y 2000 puntos) y en términos de optimización se calculó la diferencia entre el valor del óptimo encontrado utilizando el metamodelo y su verdadero valor. Nótese que mayores valores de R2 y menores diferencias con el óptimo indican mejor desempeño.

Análisis y discusión de resultados

Los resultados obtenidos se discuten en términos del desempeño en materia de modelado y optimización del ensamble de metamodelos sobre los casos de estudio.

Modelado

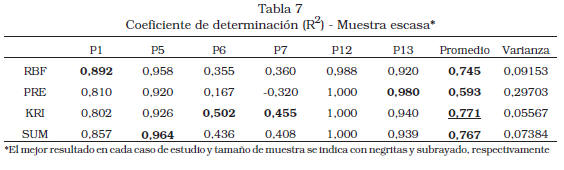
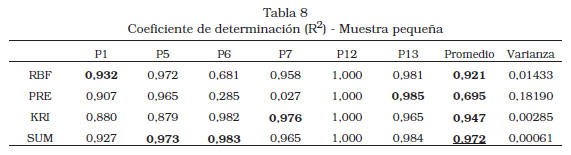
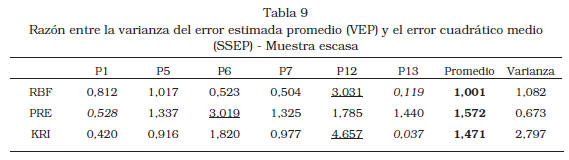
El ensamble (SUM) obtiene uno de los dos mejores resultados en todos los casos de estudio (Tabla 7 y la Tabla 8) excepto el correspondiente a P13-‘muestra escasa’; este último caso coincide con el de mayor desequilibrio (diferencia de VEP/SSEP5 entre metamodelos) entre las estimaciones de la varianza del error de los metamometamodelos (RBF, PRE, KRI y SUM) es el mejor en alguno de los problemas (RBF: P1; PRE: P13; KRI: P6-‘muestra escasa’ y P7; SUM: P5 y P6-‘muestra pequeña’), y el mayor R2 promedio lo obtienen, en el caso de muestra escasa, Kriging y, en el caso de la muestra pequeña, el ensamble. El ensamble de metamodelos ofreció un valor de R2 30,2% mayor que el promedio de los metamodelos individuales en la muestra escasa, y 17,6% mayor en la muestra pequeña. Además, la varianza de R2 para SUM fue la segunda menor en el caso de la muestra escasa (0,07384) y la menor con la muestra pequeña (0,00061).

Optimización

Distintos metamodelos ofrecen los mejores resultados dependiendo del problema considerado; sin embargo, el ensamble de metamodelos (SUM) presenta uno de los dos mejores resultados de optimización en la mayoría los casos (10 de 12). La Tabla 10 y la Tabla 11 muestran el óptimo de cada función, y su diferencia con el óptimo obtenido utilizando el algoritmo DIRECT y cada uno de los metamodelos (RBF, KRI, PRE y SUM).

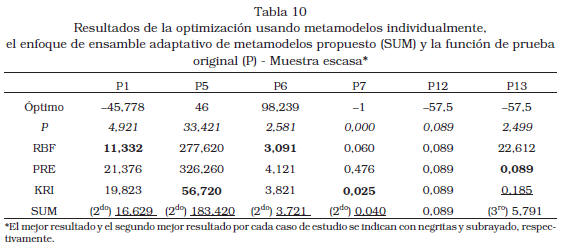
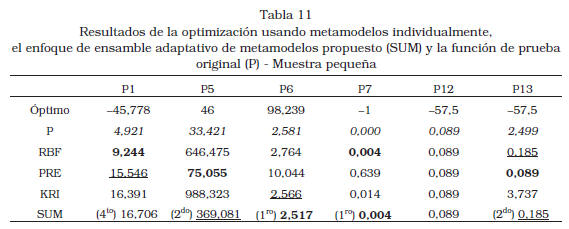
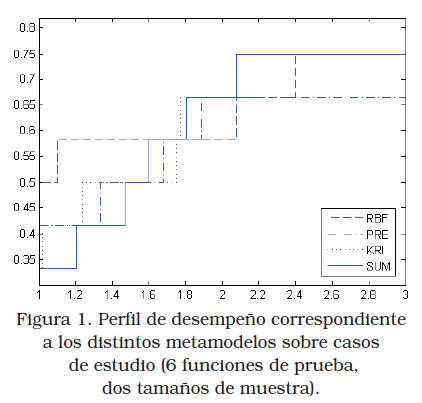
Además, se incluye el óptimo obtenido utilizando la función original (denotado P en la tabla). A manera de resumen la Figura 1 ilustra el desempeño relativo de los distintos metamodelos utilizando la metodología conocida como perfil de desempeño (performance profile) reportada en [23] y [24]. El citado perfil reporta para cada metamodelo la fracción (ordenada) del total de casos de estudio (12; 6 funciones de prueba con 2 tamaños de muestra) donde el error (diferencia entre el verdadero óptimo y el obtenido) estuvo dentro de una tolerancia dada (abscisa); esta tolerancia representa un múltiplo del mínimo error obtenido en cada caso. Dependiendo de la tolerancia distintos metamodelos exhiben un mejor desempeño; sin embargo, el ensamble presenta un perfil de desempeño robusto, vale decir, a partir de una tolerancia de 1,8 ningún otro metamodelo lo supera en número de casos de estudio exitosos.

Aplicación industrial

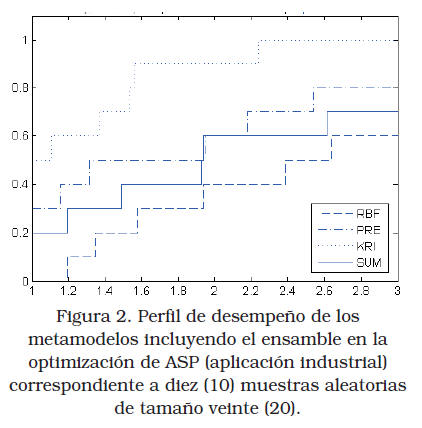
Para el caso ASP se realizaron optimizaciones basadas en metamodelos (KRI, PRE, RBF y SUM) para diez (10) muestras aleatorias de tamaño veinte (20), y se calcularon los errores con respecto al óptimo verdadero, i.e., porcentaje del POES = 39,81%, con cada punto porcentual representando 3.954 barriles de petróleo; el perfil de desempeño de los metamodelos se muestra en la Figura 2. El desempeño del ensamble exhibe las siguientes características: i) estuvo entre los dos mejores en tres de las diez muestras y en ningún caso ofreció el peor resultado y ii) ofreció el valor óptimo más cercano al verdadero (38,7%) con el peor resultado asociado con el metamodelo RBF (23,66%). Puede observarse que el uso de ensamble para obtener un desempeño robusto en la optimización basada en metamodelos puede fortalecerse, con mínimo costo computacional, incorporando la evaluación de los óptimos de los metamodelos individuales.

Conclusiones

La conclusión general de este trabajo es que el uso de un ensamble de metamodelos puede ser un mecanismo efectivo y robusto para el modelado y optimización de procesos complejos y representa una alternativa valiosa al uso de metamodelos de manera aislada. Específicamente, el desempeño del enfoque de ensamble propuesto (SUM) fue robusto: i) el promedio de R2 calculado por tamaño de muestra es uno de los dos mayores exhibiendo una de las dos menores varianzas (modelado), ii) es el único de los metamodelos que, en general, en cada caso de estudio, presenta uno de los dos mejores resultados y no ofrece el peor de los resultados (modelado y optimización) y iii) excepto en casos extremos, no se vio significativamente afectado por desequilibrios de las estimaciones de la varianza del error de los metamodelos.

Algunos aspectos a considerar en futuros trabajos en esta área son: a) establecer un mecanismo para el cálculo de los pesos que tome en cuenta la correlación entre los metamodelos (la expresión utilizada es óptima sólo si los metamodelos no están correlacionados), b) desarrollar estimaciones de la varianza del error de los metamodelos más ajustadas a la realidad, y c) evaluar más ampliamente el enfoque propuesto utilizando, otros metamodelos (e.g., máquinas de vectores de soporte) en el ensamble y otras aplicaciones industriales.

Referencias bibliográficas

 1. Queipo N., Goicochea J., y Pintos S.: “Surrogate modeling-based optimization of SAGD processes”, Journal of Petroleum Science and Engineering, Vol. 35, No. 1-2, Julio (2002) 83-93.  

2. Zerpa L., Queipo N., Pintos S., Salager J.: “An optimization methodology of alkalinesurfactant- polymer flooding processes using field scale numerical simulation and multiple surrogates”, Journal of Petroleum Science and Engineering 47 (2005) 197-208.         [ Links ]  

3. Queipo N., Verde A., Canelón J., y Pintos S.: “Efficient Global Optimization of Hydraulic Fracturing Designs”, Journal of Petroleum Science and Engineering Vol. 35 No. 3-4 (2002) 151-166.  

4. Queipo N., Pintos S., Rincón N., Contreras N. y Colmenares J.: “Surrogate modeling-based optimization for the integration of static and dynamic data into a reservoir description”, Journal of Petroleum Science and Engineering, Vol. 35 No. 3-4 (2002) 167-181.  

5. Queipo N., Haftka R., Shyy W., Goel T., Vaidyanathan R., Tucker P.: “Surrogatebased analysis and optimization”, Progress in Aerospace Sciences, Vol. 41, No. 1. (January 2005), 1-28.  

6. Craig KJ., Stander N., Dooge DA., Varadappa S.: “MDO of automotive vehicles for crashworthiness using response surface methods”, 9th AIAA/ISSMO symposium on multidisciplinary analysis and optimization, Atlanta, GA, AIAA Paper 2002-5607.  

7. Goel T., Haftka R., Shyy W., Queipo.; “Ensemble of Surrogates”. Structural and Multidisciplinary Optimization. Vol. 33, No. 3 (2007) 199-216.  

8. Jin R., Chen W., Simpson T.: “Comparative Studies of Metamodeling Techniques Under Multiple Modeling Criteria”, Journal of Structural Optimization, Vol. 23, No. 1 (2000) 1-13.  

9. Buckland ST., Burnham KP., Augustin NH.: “Model selection: an integral part of inference”, Biometrics 53 (1997): 275-290.  

10. Hoeting J., Madigan D., Raftery A., Volinsky C.T.: “Bayesian model averaging: a tutorial”, Statistical Science 14 (4) (1999):382-417.         [ Links ]  

11. Kass R.E., Raftery A.E.: “Bayes factors”, Journal of the American Statistical Association 90 (1995):773-795 Chapman & Hall, FL, (1993) pp. 126-142.  

12. Sánchez E., Pintos S., Queipo N.: “Toward an optimal ensemble of kernel based approximations with engineering applications”, Structural and Multidisciplinary Optimization 36(3), (2008) pp. 247-267.  

13. Madigan D., Raftery A.: “Model selection and accounting for model uncertainty in graphic models using Occam’s window”, Journal of the American Statistical Association 89 (1994):1535-1546.         [ Links ]  

14. Viana F., Haftka R., Steffen V., Butkewitsch S., Leal M.: “Ensemble of Surrogates: a Framework based on Minimization of the Mean Integrated Square Error”, Structures Structural Dynamics and Materials. (2008) AIAA 2008-1885.         [ Links ]  

15. Sacks, J., Welch, W., Mitchell, T., Wynn, H., “Design and Analysis of Computer Experiments”, Statistical Science, Vol. 4, No. 4 (1989) 409-435.  

16. Lophaven, S., Nielsen H., Sondergaard, J., “DACE A Matlab Kriging Toolbox Version 2.0”, Technical Report IMM-TR-2002-12, Technical University of Denmark (2002).  

17. Orr, J., "Introduction to Radial Basis Function Networks". Technical Report, Center for Cognitive Science, University of Edinburgh. (1996). http://anc.ed.ac.uk/rbf/rbf.html           [ Links ]

18. MATLAB® The language of technical computing, Versión 7.5, The MathWorks Inc., 2007.  

19. Nava E., Pintos S., y Queipo N. “A geostatistical perspective for the surrogate- based integration of variable fidelity models”. Journal of Petroleum Science and Engineering, (2010) 71: 56-66.  

20. UTCHEM-9.0 (2000) Utchem-9.0 a three-dimensional chemical flood simulator http:// www.cpge.utexas.edu/utchem/ (Jul)  

21. McKay M.D., Beckman R.J., Conover W.J.: “A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code”, Technometrics (American Statistical Association) 21 (2) (1979): 239-245.         [ Links ]  

22. Jones D., Perttunen C., Stuckman B.: “Lipschitzian optimization without the lipschitz constant”, Journal of Optimization Theory and Application, 79 (1993), pp. 157-181.

23. Dolan E., More J.J. “Benchmarking optimization software with performance profile. Mathematical Programing”, Mathematical Programing 91: 201213 (2002).  

24. Higham D.J., Higham N.J. MATLAB Guide. SIAM, Philadelphia, 2005. Second Edition.  

Recibido el 8 de Enero de 2010 En forma revisada el 17 de Octubre de 2011