Some results on a fractional q-integral operator involving generalized basic hypergeometric function

Leda Galué

Centro de Investigación de Matemática Aplicada (CIMA), Facultad de Ingeniería, Universidad del Zulia. Maracaibo, Venezuela. lgalue@hotmail.com

Abstract

In this paper the operator L(.) of the basic multiple hypergeometric function given by Yadav et al. is used in order to obtain the fractional q-integral operator L(.) of the generalized basic hypergeometric function _rΦ_s(.), also the q-Mellin transformfor the operator L(.) is presented. Various interesting special cases, involving q-special functions, have been derived as application of the main result.

Keywords: fractional q-integral operators, generalized basic hypergeometric function, q-Mellin transform, q-special functions.

AMS Subject Classification: 33D60, 33D90, 26A33.

Algunos resultados sobre un operador q-integral fraccional que incluye la función hipergeométrica básica generalizada

Resumen

En este trabajo el operador L(.) de la función hipergeométrica múltiple básica dado por Yadav et al. es usado con el fin de obtener el operador q-integral fraccional L(.) de la función hipergeométrica básica generalizada _rΦ_s(.), además se presenta la transformada q-Mellin del operador L(.). Varios casos especiales interesantes, que incluyen funciones q-especiales, han sido derivados como aplicación del resultado principal.

Palabras clave: operadores q-integrales fraccionales, función hipergeométrica básica generalizada, transformada q-Mellin, funciones q-especiales.

Recibido el 23 de Febrero de 2012

En forma revisada el 10 de Septiembre de 2012

1. Introduction

Nowadays, the fractional calculus theory is applied in almost all the areas of science and engineering. Operators of fractional calculus and their q-analogues have many applications, for example, they can used to solve dual integral and series equations which arise in crack problems in elasticity [1]. They find applications also in control systems, signal processing, bio-medical engineering, radars, sonars, etc. [2-4].

The concept of differ-integral of complex order n, which is a generalization of the ordinary n–th derivative and n times integral to any complex number, can be introduced in several ways. The most widely used definition of an integral of fractional order is via an integral transform, called the Riemann-Liouville operator of fractional integration: [5, p. 146]

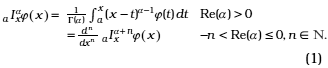
Many authors [5-19] have defined and studied operators of fractional integration through an integral transform. Some of these operators are:

1.1. Erdélyi-Kober Operator:

[10, p. 4, No. (20)]

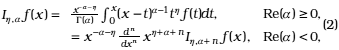
where n is the minor integer major that a.

1.2. Saxena operator: [17, p. 288, No. (1)]

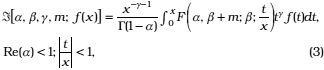
where F(a,b;c;x) denotes the Gauss hypergeometric function, and the parameters involved are complex numbers.

1.3. The operator L(.)

We consider the operator L(.) introduced by Delgado and Galué [8] in the following form:

As particular cases of this operator we have:

where   g ÎC, l,m₁ are non-negative integers, b₁ ≠0,-1,-2,..., with Á[-l,b₁, g, m₁; f(x)] as defined in (3).

with g ÎC, l is non-negative integer, b₁ ≠ 0,-1,-2,..., and I_g,l+1 f(x) as in (2).

In this paper the operator L(.) of the basic multiple hypergeometric function given by Yadav et al. is used in order to obtain the fractional q-integral operator L(.) of the generalized basic hypergeometric function _rf_s(.), also the q-Mellin transform for the operator L(.) is presented. Various interesting special cases, involving q-special functions, have been derived as application of the main result.

2. Basic hypergeometric series

In this section we present some definitions necessary for the development of the next sections.

2.1. The q-shifted factorial

The q-shifted factorial is defined as: [20]

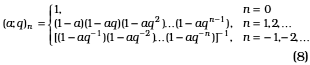
Also,

which converges for |q|<1 and diverges for a ≠ 0 and |q|≥1, and

2.2. Identities

We recall here the following q-identities [20, p. 233, No. (I.13); p. 235, No. (I.35)]:

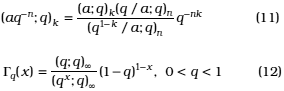
2.3. Generalized basic hypergeometric series

A generalization of the basic hypergeometric series ₂f₁ is given by: [20]

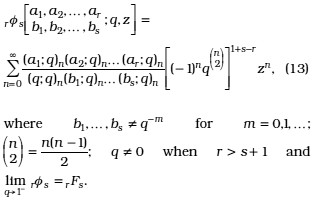
Some special cases of the _rf_s(.) are:

i) The two q-exponential functions, [20, p. 9, Nos. (1.3.15), (1.3.16)]

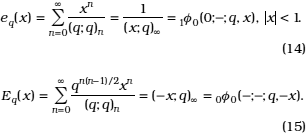
ii) q-analogues of Bessel functions, [20, p. 25]

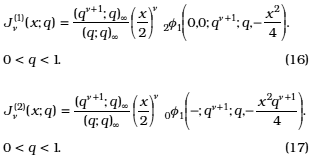
iii) The q-Laguerre polynomials defined by [20, p. 194]

iv) The little q-Jacobi polynomials: [21]

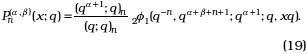
v) The Wall polynomials: [20, p. 196]

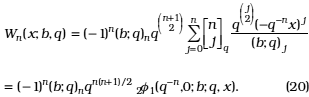
vi) The generalized Stieltjes-Wigert polynomials: [20, p. 196]

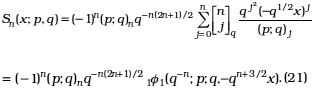
2.4. q-analogue of the Karlsson-Minton summation formula

Gasper (1981) derived a q-analogue of the Karlsson-Minton summation formula, which is given by: [20, p. 16, No. (1.9.10)]

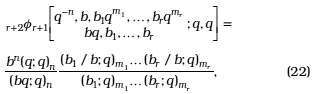
where m₁, m₂,...,m_r are non-negative integers, n ≥ m₁ +...+ m_r.

2.5. The basic multiple hypergeometric function

It was introduced by H.M. Srivastava [22] and is given by

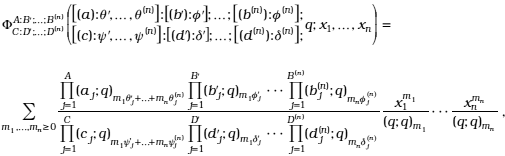
where the arguments x₁,..., x_n, the complex parameters

and the associated coefficients

are so constrained that the multiple serie (23) converges.

As particular case of (23) for n = 1, A = C = 0, f'_j = 1, j = 1,...,B', d'_j = 1, j = 1,...,D' we obtain

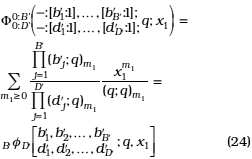
which is a general basic hypergeometric series [23].

2.6. The q-derivative operator

It is denoted by D_q and defined for fixed q by [20, p. 22]

2.7. q-Beta function

It is defined by [20, p. 18, No. (1.10.13), p. 19, No. (1.11.7)]

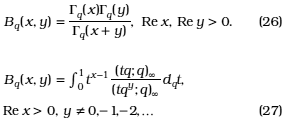
From these results we have

now applying (12), when x = u + n, Re(u) > 0, n Î Z,

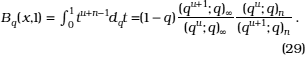
3. Fractional q-integral operator L(.) of the generalized basic hypergeometric series

R.K. Yadav, S.L. Kalla and G. Kaur [24] applied the operator L(.) to the basic multiple hypergeometric function and established the following result:

where g ÎC, l, m₁,...,m_r are non-negative integers, b₁,...,b_r ≠0,-1,-2,..., and l_i(i = 1,...,n) are arbitrary quantities.

From (30) and using (24) we get

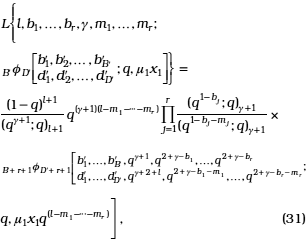
where g ÎC, l, m₁,...,m_r are non-negative integers, b₁,...,b_r ≠0,-1,-2,...

In the rest of the paper for convenience we will use the following notation:

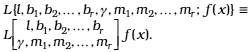
Lemma: Let be a fractional q-integral operator and _rf_s(.) the generalized basic hypergeometric series, as defined in (4) and (13) respectively, then

with l, m₁,...,m_r non-negative integers, l ≥ m₁+...+m_r; gÎC, Re(g + l + 1) > 0; b_j, g + l + 2 - b_j - m_j ≠ 0,-1,-2,..., j = 1,2,...,r; c₁, c₂,...,c_n ≠ q^-n for n = 0,1,2,...

Proof: From (5) we get

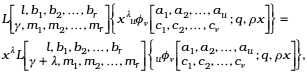
now, taking in (31) μ₁ = r, x₁ = x with _rf_s(.) as defined in (13), we have

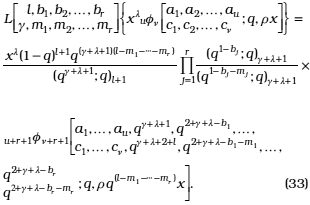
Now, using the results (11) and (10) joint with (12) we obtain respectively

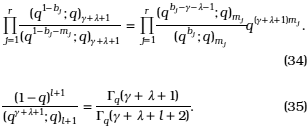
Then the substitution of (34) and (35) in (33) leads us to (32).

Particular cases: By replacing a₁,a₂,...,a_u,c₁,c₂,...,c_n in (32) by , respectively, and letting q ®1^- we obtain according to (6) and (7)

l, m₁ non-negative integres, l ≥ m₁; g Î C, Re(g + l + 1) > 0; b₁, g + l + 2 - b₁ - m₁ ≠ 0,-1,-2,...; c₁, c₂,...,c_n ≠ q^-n for n = 0,1,2,...

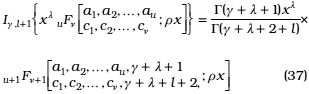
l non-negative integer; g Î C, Re(g + l + 1) > 0; b₁, g + l + 2 - b₁ ≠ 0,-1,-2,...; c₁, c₂,...,c_n ≠ q^-n for n = 0,1,2,...

Interestingly, by making a suitable change to the parameters a₁,a₂,...,a_u,c₁,c₂,...,c_n and the argument x in conjunction with definitions given in (14)-(21), we obtain the following results given in Table 1.

Where

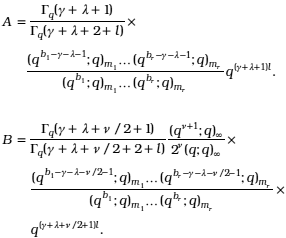
4. q-Mellin Transform of L(.)

In this section we establish the q-Mellin transform of the fractional q-integral operador

The q-Mellin Transform of f(x) is defined by [25]

Theorem 1. Let  be a fractional q-integral operator, as defined in (4), then

where M_q{f(x);s} denote the q-Mellin transform of f(x); l, m₁,...,m_r non-negative integers, l ≥ m₁+...+m_r; gÎC, Re(g - r - s + 1) > 0; b₁,...,b_r ≠0,-1,-2,...

Proof: From (5) and (46) we obtain,

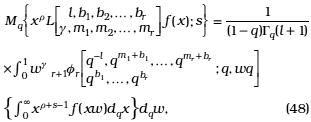
where we have interchanged the order of integration.

Making a change of variable in the inner integral and using (25) we have,

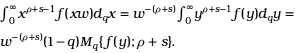
The substitution of this expression in (48) yields

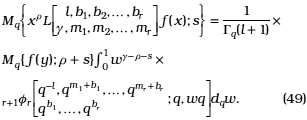
Now, applying (13),

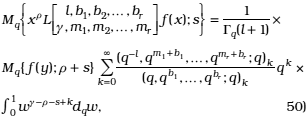
and from (29)

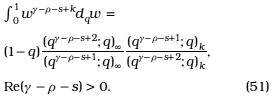
Then, (50) and (51) lead us to

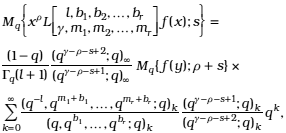
which using (13) can be written as

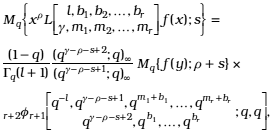
and by virtue of (22)

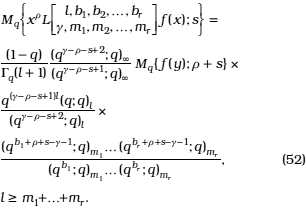
On the other hand, from (10) and (12)

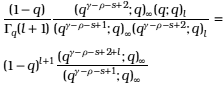
and using newly (12)

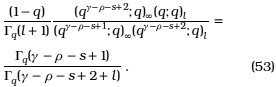
Finally, from the results (52) and (53) we get (47).

As particular case from this theorem we get

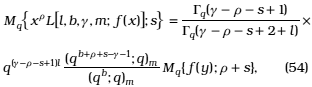
where l,m non-negative integers, l ≥ m; g Î C, Re(g - r - s + 1) > 0; b ≠ 0,-1,-2,...

Acknowledgement

The author would like to thanks to CONDES-Universidad del Zulia for financial support.

References

1. Sneddon I.N.: The use in mathematical physics of Erdélyi-Kober operators and some of their generalizations, Fractional calculus and its applications, Lecture Notes in Math., Vol. 457 (1975), 37-39.        [ Links ]

2. Tseng C.C.: Design of fractional order digital FIR differentiators. IEEE Signal Process. Letters, Vol. 8, No. 3 (2001), 77-79.        [ Links ]

3. Chen Y.Q. and Vinagre B.M.: A new IIR-type digital fractional order differentiator. Signal Processing, Vol. 83 (2003), 2359-2365.        [ Links ]

4. Vinagre B.M., Chen Y.Q. and Petras I.: Two direct Tustin discretization methods for fractional- order differentiator and integrator. J. Franklin Institute, Vol. 340, No. 5 (2003), 349-362.        [ Links ]

5. Ross B. (Ed): Fractional Calculus and Its Applications. Lecture Notes in Math., Springer- Verlag, Vol. 457, New York, 1975.        [ Links ]

6. Agarwal R.P.: Certain fractional q-integral and q-derivatives. Math. Proc. Camb. Phil. Soc., Vol. 66 (1969), 365-370.        [ Links ]

7. Al-Salam W.A.: Some fractional q-integrals and q-derivatives, Proc. Edin. Math. Soc., Vol. 15 (1966), 135-140.        [ Links ]

8. Delgado M. and Galué L.: Fractional q-integral operator involving basic hypergeometric function. Algebras Groups Geom., Vol. 25 (2008), 53-74.        [ Links ]

9. Galué L.: Generalized Erdélyi-Kober fractional q-integral operator. Kuwait Journal of Science & Engineering, Vol. 36, No. 2A (2009), 21-34.        [ Links ]

10. Kalia R.N. (Ed): Recent Advances in Fractional Calculus. Global Publishing Company, U.S.A., 1993.        [ Links ]

11. Kalla S.L., Galué L. and Srivastava H.M.: Further results on an H-function generalized fractional calculus. J. Fract. Calc., Vol. 4 (1993), 89-102.        [ Links ]

12. Kalla S.L. and Kiryakova V.: An H-function generalized fractional calculus based upon compositions of Erdélyi-Kober operators in Lp. Math. Japon., Vol. 35 (1990), 1151-1171.        [ Links ]

13. Kiryakova V.: Generalized Fractional Calculus and Applications. Longman (Pitman, Res. Notes in Math. Series # 301), London, U. K., 1994.        [ Links ]

14. McBride A.C. and Roach G.F. (Eds): Fractional Calculus. Res. Notes in Math., Vol. 138, Pitman, U. K., 1985.        [ Links ]

15. Saigo M.: A remark on integral operators involving the Gauss hypergeometric functions. Kyushu University Mathematics Reports of the College of General Education, Vol. XI, No. 2 (1978), 135-143.        [ Links ]

16. Samko S.G., Kilbas A.A. and Marichev O.I.: Fractional Integrals and Derivatives. Gordon and Breach Science Publishers, New York, 1993.        [ Links ]

17. Saxena R.K.: On fractional integration operators. Math. Zeitschr., Vol. 96, No. 4 (1967), 288-291.        [ Links ]

18. Saxena R.K. and Modi G.C.: Fractional q-integral operators associated with a basic analogue of Srivastava-Daoust’s function. Indian Journal of Pure Applied Mathematics, Vol. 16, No. 5 (1985), 491-497.        [ Links ]

19. Saxena R.K. and Gupta R.K.: Certain multidimensional fractional q-integral operators involving Srivastava’s generalized q-hypergeometric function of several variables. Pure and Applied Mathematica Sciences, Vol. XXXI, No. 1-2 (1990), 127-136.        [ Links ]

20. Gasper G. and Rahman M.: Basic Hypergeometric Series. Encyclopedia of Mathematics and its Applications, Vol. 35, Cambridge University Press, U. K., 1990.        [ Links ]

21. Srivastava H.M. and Agarwal A.K.: Generating functions for a class of q-polynomials. Annali di Matematica Pura ed Applicata, Vol. IV, No. 154 (1989), 99-109.        [ Links ]

22. Srivastava H.M. and Karlsson Per W.: Multiple Gaussian Hypergeometric Series. Jhon Wiley & Sons, New York, 1985.        [ Links ]

23. Slater, L.J.: Generalized Hypergeometric Functions. Cambridge University Press, Cambridge, 1966.        [ Links ]

24. Yadav R.K., Kalla S.L. and Kaur G.: On fractional q-integral operator involving the basic multiple hypergeometric functions. Algebras Groups and Geometries, Vol. 27, No.1 (2010), 97-116.        [ Links ]

25. Fitouhi A., Bettaibi N. and Brahim K.: The Mellin transform in quantum calculus. Constructive Approximation, Vol. 23, No. 3 (2006), 305-323.        [ Links ]