Determination of kinetic constants for the design of biological treatment dairy effluent in batch system

Carmen Cárdenas, Katina Landeta, Tomás Perruolo, Nancy Angulo, Suher Yabroudi, Alberto Trujillo, Paola Flores

Centro de Investigación del Agua, Facultad de Ingeniería, Universidad del Zulia. Apartado 98. Ciudad Universitaria, Maracaibo, Zulia, Venezuela. Telfs: (058-061) 597182-597181. (Fax) 597195 chcarden@gmail.com, kacalata@hotmail.com

Abstract

The behavior of a sequential batch reactor (SBR) at laboratory scale for treating wastewater from a dairy. Kinetic constants were determined which govern the process of degradation and biological growth, such as: maximum rate of substrate utilization (k), half rate constant (K_S), sludge yield coefficient (Y) and coefficient of extinction of microorganisms (k_d) using two kinetic models: Orozco and Michaelis-Menten. For the reactor operation was set hydraulic retention time (HRT) of 24 hours and a sludge age (q_c) of 20 days. According to the kinetic parameters estimated performance of the treatment system can be described by the model of Orozco, by which we obtain the following kinetic coefficients for the anaerobic stage, aerobic 1 and 2 respectively: 8,130; 1,350 and 0,765 d^–1 for “k”, 0,167; 0,449 and 0,767 mg VSS/mg COD for “Y” and 0,0114; 0,0017 and 0,0023 d^–1 for “k_d”.

Keywords: SBR system, dairy wastewater, kinetic coefficients.

Determinación de las constantes cinéticas para el diseño de tratamientos biológicos de un efluente lácteo en régimen discontinuo

Resumen

Se analizó el comportamiento de un reactor discontinuo secuencial (RBS) a escala de laboratorio durante el tratamiento de aguas residuales provenientes de una industria láctea. Se determinaron las constantes cinéticas que gobiernan el proceso de degradación y crecimiento biológico, tales como: tasa máxima de utilización de sustrato (k), constante de velocidad media (K_S), coeficiente de producción de lodos (Y) y coeficiente de desaparición de los microorganismos (k_d), utilizando para ello dos modelos cinéticos: Orozco y Michaelis-Menten. Para la puesta en marcha del reactor se estableció un tiempo de retención hidráulica (HRT) de 24 horas y una edad del lodo (q_c) de 20 días. De acuerdo a los parámetros cinéticos estimados la ejecución del sistema de tratamiento puede ser descrita por el modelo de Orozco, por medio del cual se obtuvieron los siguientes coeficientes cinéticos para las etapas anaerobia, aerobia 1 y aerobia 2 respectivamente: 8,130; 1,350 y 0,765 d^–1 para “k”, 0,167; 0,449 y 0,767 mg SSV/mg DQO para “Y” y 0,0114; 0,0017 y 0,0023 d^–1 para “k_d”.

Palabras clave: sistema RBS, efluente lácteo, parámetros cinéticos.

Recibido el 27 de Septiembre de 2012 En forma revisada el 7 de Octubre de 2013

Introducción

Se ha demostrado la gran variedad de aplicaciones de los reactores de cargas secuenciales (RBS) en procesos biológicos, gracias a sus ventajas de fácil operación, bajo costo y que no necesitan un tanque de sedimentación. Su utilización en el tratamiento de aguas residuales provenientes de las industrias lácteas, es una buena alternativa, debido a las altas concentraciones de aceites y grasas, materia orgánica y nutrientes, generalmente presentes en estos efluentes [1].

Debido al amplio uso que han tenido estos reactores en los procesos biológicos, el diseño de los mismos contempla entre otros factores, el estudio de la cinética, mediante el desarrollo de modelos matemáticos que caractericen el comportamiento de crecimiento microbiano y el proceso de degradación de la materia orgánica [2]. En la literatura existen varios modelos que describen la cinética de remoción de sustrato en el tratamiento biológico de las aguas residuales; a las condiciones de operación en las que se desarrolló esta investigación (alta concentración de sustrato y biomasa), se utilizaron las formulaciones de Michaelis-Menten y Jaramillo Orozco, las cuales representan suficientemente bien este proceso. En el caso de Orozco sus ecuaciones se cumplen para condiciones de sustrato limitado pero con altas densidades de biomasa [3] y la ecuación de Michaelis-Menten se emplea tanto para altos contenidos de sustrato como para bajos [4].

Ambos modelos han sido utilizados en estudios previos. En el trabajo de investigación realizado por Ramón y Gualdron [5] determinaron la estequiometría y cinética de reacción en reactores biológicos discontinuos y continuos en aguas residuales urbanas, en condiciones aerobias y anaerobias, utilizando para esto el modelo matemático de Orozco. Carta-Escobar y col. [2] estudiaron los parámetros cinéticos que describen el proceso de biodegradación de la materia orgánica en efluentes lácteos, para esto utilizaron dos dispositivos experimentales diferentes en régimen continuo y obtuvieron que los modelos cinéticos que describen el proceso son el de Michaelis-Menten y Chen-Hashimoto. Así mismo, Semprún y col. [6] emplearon las ecuaciones de Michaelis-Menten para determinar las constantes cinéticas que intervienen en el diseño del tratamiento biológico de lodos activados aplicado a un efluente lácteo, utilizando reactores por carga y de flujo continuo.

A continuación, se presentan los modelos cinéticos planteados por dos autores para reactores de flujo discontinuo, para la determinación de las constantes cinéticas.

1. Modelo cinético de Michaelis-Menten

Está dirigido a explicar la cinética de una reacción enzimática [3]. Se basa en estudios con cultivo puro. Sin embargo, se emplea para determinar la cinética de la degradación de sustratos mediante una población heterogénea de microorganismos, como los procesos de lodos activados [4].

La ecuación de Michaelis-Menten para la expresión de la velocidad de consumo específico de sustrato para un caso general, es la siguiente:

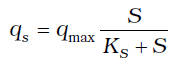      (1)

donde: q_s= Velocidad de consumo específico de sustrato (mg DQO/mg SSV.d)

q_max: Velocidad máxima de consumo específico de sustrato (mg DQO/mg SSV.d)

K_s: Constante de saturación (mg DQO/L) S: Concentración de sustrato (mg DQO/L).

De la ecuación (1) se desprenden dos interpretaciones físicas a saber:

– A altas concentraciones de sustrato (S>>K_S), despreciando K_S del denominador de la ecuación (1) al compararlo con S, y simplificando.

q = q_max         (2)

– A bajas concentraciones de sustrato (S << K_S), se elimina S del denominador en la ecuación (1) al compararlo con K_S, quedando la siguiente expresión:

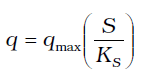(3)

La velocidad de consumo específico de sustrato puede ser expresada en términos de la ecuación de Monod por:

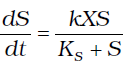    (4)

donde: k= Tasa máxima de utilización del sustrato por unidad de peso de microorganismos en (tiempo^–1) y X = Concentración de biomasa (mg SSV/L).

Linealizando la ecuación (4) queda:

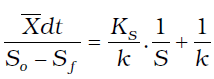      (5)

donde: = Concentración promedio de biomasa (mg SSV/L).

Graficando   se debe obtener una línea recta, en la cual el intercepto y pendiente de la línea son 1/k y K_S/k, 

respectivamente.

El balance de masa empleado para la tasa de producción de biomasa de una reacción de primer orden puede ser expresado como:

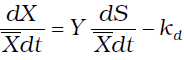      (6)

donde: K_d: Coeficiente de mortandad endógeno (día^–1); Y: Coeficiente estequiométrico de producción de biomasa (mg SSV/mg DQO).

Con los datos obtenidos experimentalmente se grafica de acuerdo a la ecuación (6). Donde la pendiente e 

intercepto 

del mejor ajuste lineal corresponde a Y y k_d respectivamente [4].

2. Modelo de Jaramillo Orozco

Supone que el parámetro de verdadero interés es la relación S/X, es decir, la disponibilidad de alimento por unidad de biomasa. Además supone que la tasa total de remoción de sustrato es poco significativa, y más bien debe emplearse la tasa neta de remoción de sustrato, dS/Xdt, que representa la tasa de remoción de sustrato por unidad de biomasa [3].

La remoción de sustrato soluble, viene gobernada por la siguiente ecuación:

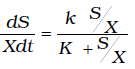      (7)

donde: K= Constante cinética de saturación (adimensional).

Linealizando la ecuación (7), utilizando el gráfico de Lineweaver-Burk:

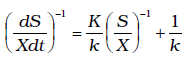  (8)

Se grafica , donde la pendiente determina el valor de K/k y el intercepto es igual a 1/k.

Los coeficientes Y y k_d, se obtienen de la ecuación de producción de biomasa.

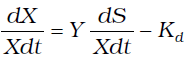    (9)

Al graficar , donde la pendiente determina el valor de Y y el intercepto el de K_d.

Parte experimental

Para la elaboración de esta investigación se empleó un RBS a escala piloto para tratar agua residual proveniente de una planta procesadora de productos lácteos, ubicada en la carretera Maracaibo-Villa del Rosario Km 79, estado Zulia, empleando ciclos de tratamiento con un tiempo de retención hidráulica (THR) de 24 horas y una edad de lodo (qc) de 20 días, donde cada ciclo estuvo constituido de las etapas: alimentación, mezcla anaerobia (5 horas), mezcla aerobia (6 horas), mezcla anóxica (3 horas), mezcla aerobia (6 horas), mezcla anóxica (3 horas), purga, sedimentación (1 hora) y vaciado. El reactor utilizado mostrado en la Figura 1, estaba conformado por un recipiente cilíndrico de polietileno de 85 cm de altura, 40 cm de diámetro y capacidad de 87 L; dos (02) válvulas de bola de 0,0127 m de plástico a diferentes alturas con la finalidad de permitir la descarga del agua tratada; una (01) bomba de recirculación del agua para el mezclado del lodo y el efluente de 186,425 W; un sistema de aireación, integrado por un compresor de aire de 82,737 KPa, conectado a un difusor punto burbuja de 28 cm de diámetro instalado por debajo del tanque.

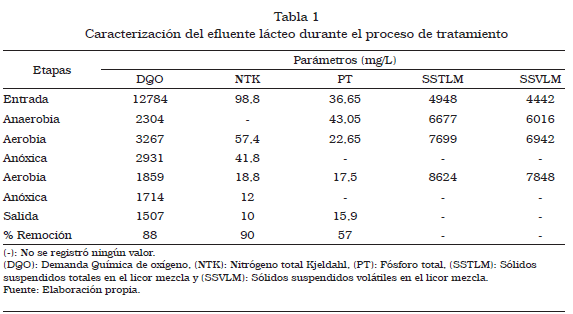
La toma de muestras para la determinación de las constantes cinéticas que describen el proceso se realizó a cada hora en la etapa anaerobia y en las dos (02) etapas aerobias. En la Tabla 1 se presentan las características del efluente lácteo utilizado en este estudio, durante el proceso de tratamiento. Todos los parámetros (Tabla 1) se analizaron de acuerdo a la metodología descrita en el Standard Methods for the examination of water and wastewater [7].

El lodo utilizado para dar partida al sistema fue obtenido de un reactor utilizado en el laboratorio de Ingeniería Ambiental del Centro de Investigación del Agua (CIA), para el tratamiento de un efluente lácteo. Se aclimató realizando procesos (ciclos) continuos de carga y descarga de una combinación de aguas residuales domésticas y el efluente lácteo en estudio. Al agua de alimentación se le fue incrementando proporcionalmente la cantidad del efluente lácteo, hasta cargar el reactor con un 100% del mismo. Dichos procesos involucraban etapas de aireación, mezclado, reposo y purga, a fin de estabilizar el lodo a las condiciones de trabajo. Al mismo tiempo se procedió a realizar mediciones de sólidos suspendidos totales (SST) y sólidos suspendidos volátiles (SSV) al licor mezcla, a fin de observar el crecimiento o decrecimiento de la biomasa a causa del nuevo efluente añadido. Alcanzadas las condiciones de equilibrio, es decir, una vez que la concentración de sólidos suspendidos en el reactor y la concentración materia orgánica del efluente (DBO y DQO), permanecieron relativamente constantes, se presumió que la masa microbiana se encontraba adaptada a ese desecho.

Determinación de las constantes cinéticas

Logradas las condiciones de estabilización del reactor se comenzó el tratamiento del líquido residual. Se registraron los valores de Demanda Bioquímica de Oxígeno (DBO), Demanda Química de Oxígeno (DQO) y Sólidos Suspendidos en el licor mezcla (SSLM) a través del tiempo y se ajustó la curva que mejor se adaptó [8]. Los valores de los coeficientes cinéticos fueron estimados por medio de análisis de regresión de los datos experimentales. En este estudio se determinó el coeficiente de velocidad media (K_S), la tasa máxima de degradación de sustrato (k), el coeficiente de producción de biomasa (Y) y la velocidad de decaimiento o muerte de microorganismos (k_d).

Discusión de resultados

Constantes de remoción de sustrato

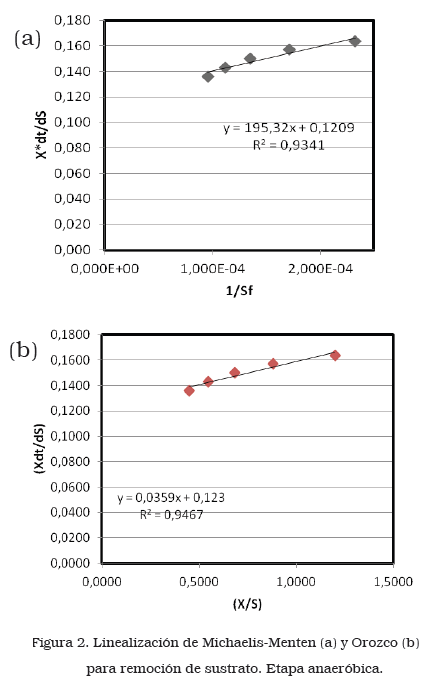
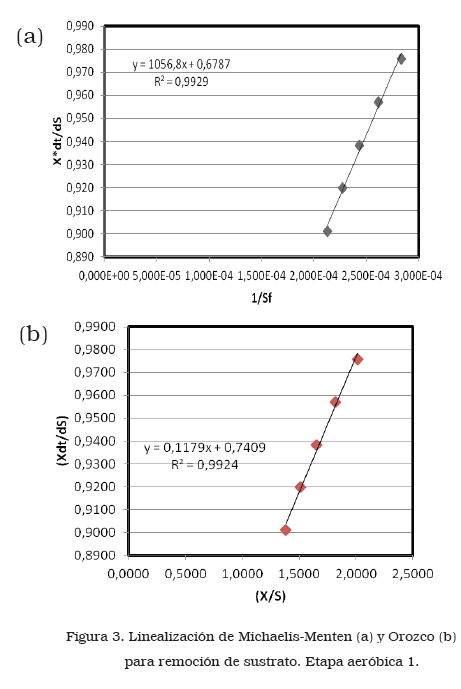
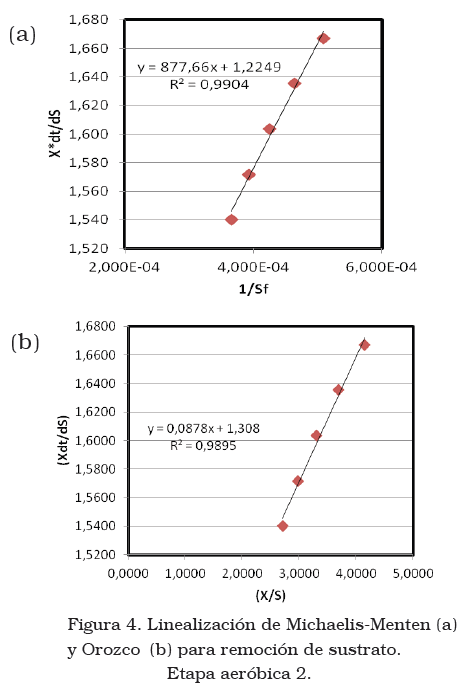
En las Figuras 2, 3 y 4 (a) se puede ver la representación gráfica de la ecuación (4) para el cálculo de las constantes cinéticas K_S y k obtenidas a partir del modelo cinético planteado por Michaelis- Menten. Así mismo, aplicando el modelo de Orozco, las constantes K y k se estimaron a través de la linealización de la ecuación (7) mostrada en las Figuras 2, 3 y 4 (b) para la etapa anaeróbica y las dos etapas aeróbicas respectivamente.

 

Constantes de producción de biomasa

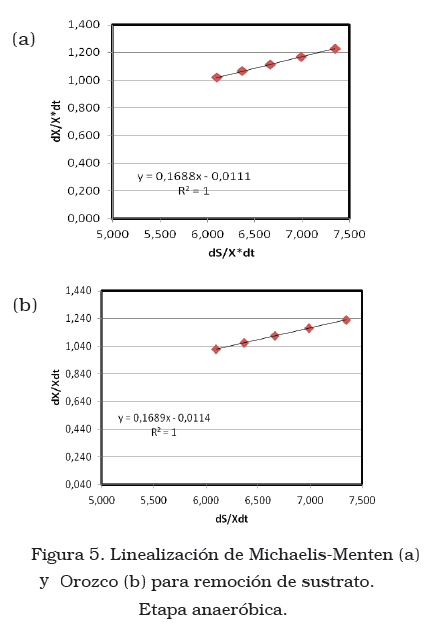
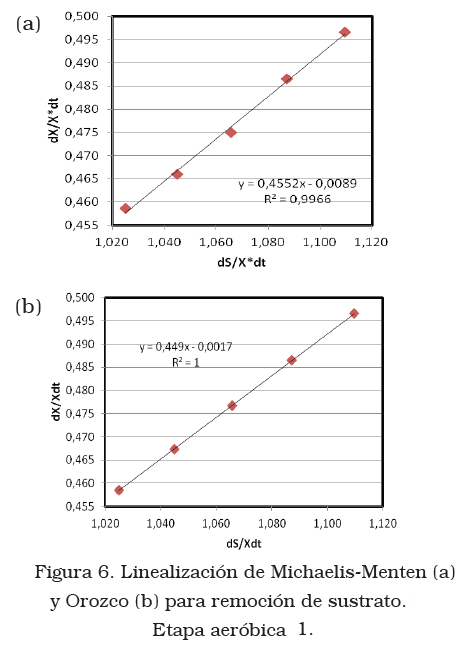
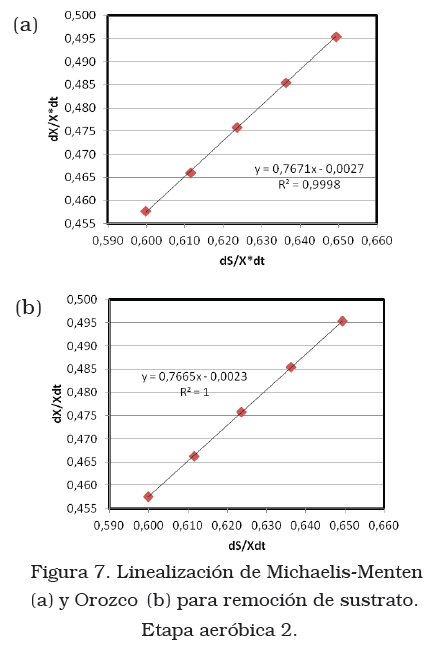
Las constantes Y y k_d representan el comportamiento de la biomasa activa contenida en el reactor, obtenidas mediante la representación gráfica de la ecuación de Michaelis-Menten (6) y de Orozco (9) como se muestra en las Figuras 5, 6 y 7.

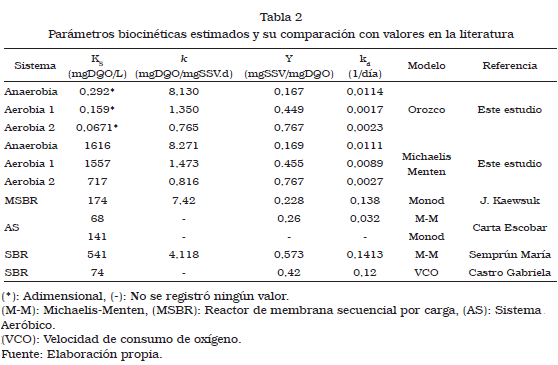
La Tabla 2 muestra una comparacion entre los coeficientes cineticos de otros estudios previos utilizando aguas residuales de una industria lactea y los obtenidos en esta investigacion.

En las etapas aerobias 1 y 2 la constante cinetica k en los dos modelos es menor en comparacion con la investigacion de Semprun y col. [6], esto puede ser atribuido a que en la etapa anaerobica previa a las etapas aerobias se removio mayor cantidad de materia organica, no obstante el proceso en general presento una buena remocion de DQO (88%). La constante K_S representa la afinidad de la biomasa por un determinado sustrato, donde el termino afinidad viene dado por µ_m/K_S, es decir altos valores de K_S corresponden con una baja afinidad del lodo por el sustrato [1].

Como se puede ver en la Tabla 2, los valores de K_S calculados en este estudio mediante el modelo de Michaelis-Menten son mayores que el alcanzado en las evaluaciones de Carta Escobar y col. [2] y Semprún y col. [6] utilizando el mismo modelo. Esto indica que la biomasa contenida en el reactor tiene poca afinidad para degradar este sustrato, siendo esta premisa contraria a los resultados obtenidos en cuanto a remoción de materia orgánica en este estudio; lo cual pone de manifiesto el hecho que puede estar ocurriendo en el reactor un proceso de acumulación de una parte de la materia orgánica en el lodo y el resto es degradada [9].

Para altas concentraciones de sustrato (Si ³ 12000 mg/L de DQO), como es el caso que se presenta en esta investigacion, la velocidad especifica de utilizacion de sustrato (q) es practicamente igual en cada una de las etapas del ciclo de tratamiento (Tabla 3) e independiente de la concentracion del mismo; por tanto para este intervalo de concentraciones el proceso de eliminacion de sustrato sigue una cinetica de orden cero [2].

De acuerdo a la bibliografía, las constantes cinéticas que describen el proceso de degradación mediante el modelo de Michaelis-Menten solo son válidas para un intervalo reducido de concentraciones de sustrato, ya que la velocidad de estos procesos decrece a elevadas concentraciones del mismo, existiendo un intervalo óptimo para cada sustrato [4]. Según Carta Escobar y col. [2], a estas condiciones se asume que la velocidad de consumo especifico es máxima (q_max), por lo tanto el hecho que las velocidades de consumo especifico sean iguales indica que el sistema estaba sobrecargado, siendo la velocidad máxima alcanzada.

En cuanto a los coeficientes cinéticos de producción de lodos, la constante Y está relacionada con la concentración de biomasa en el birreactor y representa la producción de lodo por kilogramo de sustrato total consumido. Al comparar los valores de Y obtenidos en este estudio por medio de ambas ecuaciones, estos son a excepción de la etapa anaerobia algo mayores que los encontrados en la literatura, lo que indica que este factor varía dependiendo del patrón metabólico usado en el proceso de conversión, donde los procesos aerobios son más eficientes que los anaerobios con respecto a la conversión de biomasa y por ello tiene un valor mayor de Y, por lo tanto, es lógico que en la etapa anaerobia sea bajo el valor de Y, ya que hay un menor crecimiento de los microorganismos con respecto a la biomasa presente en las etapas aerobias, debido a que en las fases aerobias los microorganismos acumulan los nutrientes (fósforo) necesarios para su crecimiento. Esto también indica que existe alto contenido de biomasa en el reactor [1, 6].

Comparando el coeficiente k_d con los valores reportados por otros autores, estos son menores (Tabla 2), lo cual de acuerdo al estudio de Kaewsuk y col. [1] una constante de saturación media o de afinidad (K_S) elevada se corresponde con una baja velocidad de decaimiento o muerte de las bacterias (k_d). Con relación a esto también se puede señalar según la bibliografía [10], cuando la operación de digestión es realizada con una alta relación sustrato/biomasa normalmente entre 0,05-1,5 mg DQO/mgSSVLM.d (45 mg DQO/ mgSSVLM.d en el caso de este estudio), los microorganismos disponen de una gran cantidad de material orgánico para consumir, por lo que no entran a la fase endógena o de extinción, y los lodos extraídos aún contienen gran cantidad de material orgánico biodegradable. Esto puede explicar los valores tan bajos del coeficiente de muerte endógena (k_d) en comparación con los estudios mencionados anteriormente.

Comparando las constantes cinéticas de ambos modelos en estudio se puede observar que la velocidad máxima de utilización de sustrato (k), el coeficiente de producción de lodos (Y) y la velocidad de decaimiento (k_d) son bastante confiables, ya que existe una gran similitud entre ellas en cada una de las etapas. En este caso en particular, la ecuación que mejor describe el proceso es la de Orozco, ya que actúa tanto en condiciones de abundancia como en condiciones de inanición [3]. El modelo descrito por Michaelis-Menten, presenta limitaciones a altas concentraciones de sustrato, como lo es la inhibición por sustrato, donde hay una disminución progresiva de la actividad a altas concentraciones. Esto puede indicar la existencia de dos sitios de unión entre sustrato y enzima; cuando hay poco sustrato, se ocupa el sitio de alta afinidad y sigue la cinética normal. A altas concentraciones, el segundo sitio de inhibición se ocupa inhibiendo la enzima [3]

Conclusiones

Los altos valores de k encontrados indican que la biomasa activa contenida en el reactor es apta o conveniente para degradar este tipo de sustrato. A pesar que hubo una notable disminución en el contenido de materia orgánica a través del proceso de tratamiento, los altos valores de KS en cada una de las etapas estudiadas indican que existe poca afinidad de los microorganismos para degradar el sustrato, por lo tanto esto puede significar que una cantidad de la materia orgánica se está acumulando en el lodo y el resto si es degradada. Altos valores del coeficiente de producción de lodos (Y) obtenidos indica alta biomasa en el reactor. En general, ambos modelos cinéticos tienen gran similitud entre los valores de las constantes, sin embargo el desempeño del sistema puede ser descrito por la ecuación de Orozco, debido a la limitación presente en el modelo descrito por Michaelis-Menten en cuanto a la alta concentración de sustrato. Se obtuvieron los siguientes coeficientes cinéticos para las etapas anaerobia, aerobia 1 y aerobia 2 respectivamente: 8,130; 1,350 y 0,765 d^–1 para “k”, 0,167; 0,449 y 0,767 mg SSV/mg DQO para “Y” y 0,0114; 0,0017 y 0,0023 d^–1 para “k_d”.

Agradecimiento

Los autores agradecen al Consejo de Desarrollo Científico y Humanístico de la Universidad del Zulia por el apoyo financiero a través del proyecto CC-0614-09 y al Centro de Investigación del Agua por el cofinanciamiento.

Referencias bibliográficas

1. Kaewsuk J., Thorasampan W, Thanuttamavong y Tae Seo Gyu:“Kinetic development and evaluation of membrane sequencing batch reactor (MSBR) with mixed cultures photosynthetic bacteria for dairy wastewater treatment”. Journal of Environmental Management. Vol. 91, (2010) 1161-1168.        [ Links ]

2. Carta Escobar F., Pereda J., Álvarez P., Romero F. y Durán M. M.: “Aerobic purification of dairy wastewater in continuous regime. Part II: Kinetic study of the organic matter removal in two reactor configurations”, Bioch. Engin. Journal.Vol. 22, (2005) 117-124.        [ Links ]

3. Orozco Jaramillo Álvaro: “Bioingeniería de Aguas Residuales”, Acodal, 2005.        [ Links ]

4. Ramalho R. S.: “Tratamiento de Aguas Residuales”, Illinois: Reverts S.A, 1991.        [ Links ]

5. Ramón J. A. y Gualdron L. D.: “Determinación de la estequiometria y cinética de reacción del proceso de degradación aerobia y anaerobia en el tratamiento biológico del agua residual en reactores continuos y discontinuos”, XXXI Congreso Interamericano AIDIS. Santiago, Chile, 2008.        [ Links ]

6. Semprún M., Romero Z. y Rojas A.: “Determinación de las constantes cinéticas para el diseño de tratamientos biológicos de un efluente lácteo”, Facultad de Ingeniería. Escuela de Ingeniería Civil. Universidad del Zulia. Maracaibo, Venezuela. 1983, 115 pág.        [ Links ]

7. APHA-AWWA-WEF. Standard Methods for the examination of water and wastewater. 20th Edition, 1999.        [ Links ]

8. García Silvia: “Coeficientes cinéticos en el tratamiento biológico”, Trabajo de Ascenso. Postgrado de Ingeniería Ambiental. LUZ. Maracaibo, Venezuela. 1991, 53 pág.        [ Links ]

9. Gutierrez M. S., Ferrari A., Benítez A., Hermida S. y Canetti R. M: “Carbon and nitrogen removal from dairy wastewater in a laboratory sequential batch reactor system”, 2nd Mercosur Congress on Chemical Engineering. 4th Mercosur Congress on Process Systems Engineering. ENPROMER. Costa Verde, Rio de Janeiro, Brasil, 2004, 10 pág.        [ Links ]

10. Componentes y sistemas para el tratamiento biológico de las aguas residuales. www.00cities.org/edrochac/residuales/lodosactivados5.pdf           [ Links ]